1 Introduction

Recently, the study of fractional calculus has attracted a great attention due to its potential applications in various fields [1–5]. As a branch of mathematical analysis, fractional calculus can be considered as the generalization of the conventional calculus. Most of the systems in interdisciplinary fields can be described via fractional calculus [6–14]. Moreover, fractional-order model can provide an explicit description and gives a further insight into physical process. That is, fractional-order systems can serve as a valuable tool in the modeling of many phenomena. Due to the fact that fractional calculus provides another good way to describe, predict, and control physical systems accurately, it has been applied to control system, physics, and system modeling. With the development of interdisciplinary applications, it has been investigated that various research fields can be elegantly described with the help of fractional derivatives, such as viscoelastic bodies, quantitative finance, dielectric polarization, electromagnetic waves, and polymer physics. On the other hand, there exist many significant differences between fractional-order system and the corresponding integer-order differential systems. As compared to the integer-order system, the fractional-order nonlinear system can display a richer dynamical behavior, such as showing various bifurcations under certain conditions which are different from the corresponding integer-order system.

Synchronization of chaos occurs in a process where in two (or many) chaotic systems (either equivalent or inequivalent) have a common behavior due to diffusive and multiplicative couplings [15, 16]. The idea underlying the phenomenon of synchronization of chaos is that two chaotic systems may evolve on different attractors, but when coupled, they initially start on different attractors and then somehow eventually follow a common trajectory. Such a synchronization between two systems is achieved when the trajectories of the systems are equal, which is the case when one of the two systems changes its trajectory to follow that of the other system or when both systems follow a new common trajectory. Nowadays, after the pioneering work of Pecora and Carroll [17], various types of chaos synchronization such as complete synchronization [18, 19], phase synchronization [20, 21], generalized synchronization [22, 23], lag synchronization [24, 25] projective synchronization [26, 27], Q–S synchronization [28], amplitude envelope synchronization [29], anticipated and lag synchronization [30, 31] have been described. There are many methods of synchronization, such as the active control, adaptive control, linear or nonlinear feedback control, and sliding mode control [32–49]. The fractional-order of the chaotic systems effects the transient performance of the chaotic synchronization, it has been investigated that the error in the synchronization of fractional-order systems decreases if the fractional order is increased. In other words, for the larger value of the fractional-order, synchronization starts earlier [50]. Using a nonlinear feedback control technique, [51] investigates that the chaotic and hyperchaotic systems with fractional orders are synchronized, while their integer orders do not, so the aim of the present article is to develop a technique which will serve the purpose of synchronization of fractional order as well as integer-order chaotic systems.

The main object of this paper is to study the synchronization of the fractional-order chaotic with different order and with unknown parameters using the modified adaptive sliding-mode controller. Synchronization controller and parameter identification technique are designed based on the Lyapunov stability method. Computer simulations based on the Adams–Bashforth–Moulton method support the theoretical findings. The organization of this paper is as follows. In Sect. 2, preliminaries of fractional-order calculus is presented. In Sect. 3, presents a methodology for the modified adaptive sliding-mode synchronization controller design. Two simulations examples are presented to verify the effectiveness of the proposed method in Sects. 4 and 5. Finally, a conclusion in Sect. 6 closes the work.

2 Properties of fractional derivative

Fractional calculus is a generalization of integration and differentiation to a non-integer-order integro-differential operator \({}_{a}D_{t}^{\alpha }\) defined by

$$ {}_{a}D_{t}^{\alpha }= \textstyle\begin{cases} \frac{{d^{\alpha }}}{{dt^{\alpha }}}, & R(\alpha ) > 0, \\ 1, &R(\alpha )= 0, \\ \int _{a}^{t} ( {d\tau } )^{ - \alpha },& R( \alpha ) < 0, \end{cases} $$
(1)

where α is the fractional order which can be a complex number, \(R(\alpha )\) denotes the real part of α and \(a < t\), a is the fixed lower terminal and t is the moving upper terminal. There exist several definitions for fractional derivatives and fractional integrals like the Riemann–Liouville, Caputo, Hadamard, Riesz, Griinwald–Letnikov [52–55]. The two most commonly used are Riemann–Liouville and Caputo definitions. Each definition uses Riemann–Liouville fractional integration and derivatives of whole order. The difference between the two definitions is in the order of evaluation. Caputo’s definition which is a modification of Riemann–Liouville definition has the advantage of dealing properly with initial value problems in which the initial conditions are given in terms of the field variables and their integer order which is the case in most physical processes. The commonly used definition is the Riemann–Liouville definition, defined by

$$ {}_{a}D_{t}^{\alpha }x ( t ) = \frac{{d^{n} }}{{dt^{n} }}J_{t}^{n - \alpha } x ( t ),\quad \alpha > 0, $$
(2)

where \(n = \lceil \alpha \rceil \), i.e., n is the first integer which is not less than α. \(J^{\varphi }\) is the fractional Riemann–Liouville integral operator which is described as follows:

$$ J_{t}^{\vartheta }\varphi ( t ) = \frac{1}{{\varGamma ( \vartheta )}} \int _{0}^{t} { \frac{{\varphi ( \upsilon )}}{{ ( {t - \upsilon } )^{1 -\vartheta } }}} \,d\upsilon, $$
(3)

with \(0< \vartheta \leq 1\), \(\varGamma (\cdot)\) is the gamma function. The Caputo differential operator of fractional order α is defined as

$$ {}^{c}D_{t}^{\alpha }x(t) = j_{t}^{n - \alpha } x^{n} (t),\quad \alpha > 0, $$
(4)

where \(n = \lceil \alpha \rceil \).

Lemma 1

For Riemann–Liouville derivatives if \(s> n\geq 0\), α and β are integers such that \(0\leq \alpha -1 \leq s <\alpha \), \(0 \leq \beta -1 \leq n<\beta \), then we obtain [1]

$$ {}_{a}D_{t}^{s} \bigl( { {}_{a}D_{t}^{ -n} x ( t )} \bigr) = {}_{a}D_{t}^{s - n} x ( t ). $$
(5)

Lemma 2

For Riemann–Liouville derivatives if \(s, n \geq 0\), α and β are integers such that \(0\leq \alpha -1 \leq s <\alpha \), \(0 \leq \beta -1 \leq n <\beta \), then we obtain [1]

$$ {}_{a}D_{t}^{s} \bigl( { {}_{a}D_{t}^{n} x ( t )} \bigr) = {}_{a}D_{t}^{s + n} x ( t ) - \sum _{j = 1}^{n} { \bigl[ {{}_{a}D_{t}^{n - j} x ( t )} \bigr]} _{t = a} \frac{{ ( {t - a} )^{ - s - j} }}{{\varGamma ( {1 - s - j} )}}. $$
(6)

3 Problem description

Given the fractional-order chaotic system, i.e., the drive system is

$$ D_{t}^{q} {x_{d}} =f(x_{d})+F(x_{d})\alpha , $$
(7)

where \(x_{d}\in R^{m}\) is the state vector of system (7), \(\alpha \in R^{k}\) is the unknown parameter vector of the system, \(f(x_{d}):R^{m} \rightarrow R^{m}\), \(F(x_{d}):R^{m} \rightarrow R^{m \times k}\). On the other hand, the controlled response system is given by

$$ D_{t}^{q} {x_{r}} =f(x_{r})+F(x_{r})\beta +u, $$
(8)

where \(x_{r}\in R^{n}\) is the state vector of the system, \(\beta \in R^{\ell }\) is the unknown parameter vector of the system, \(f(x_{r}):R^{n} \rightarrow R^{n}\), \(F(x_{r}):R^{n} \rightarrow R^{n \times \ell }\), \(U \in R^{n}\). When order \(m = n\), \(\ell = k\) and the functions \(f(x_{d}) = f(x_{r})\), \(F(x_{d}) = F(x_{r})\), the response system is identical to the drive system, and the synchronization problem has been well studied. When two systems satisfy the condition \(m \neq n\) (of course \(f(x_{d})\neq f(x_{r})\), and \(F(x_{d}) \neq F(x_{r})\)), that is, the order of the response system is lower or higher than that of the drive system, the synchronization is only attained in reduced order or increased order. The aim of this section is to address the synchronization of two coupled fractional-order chaotic systems via modified adaptive sliding mode control with different order, namely, reduced-order synchronization and increased-order synchronization.

3.1 Reduced-order synchronization of fractional-order chaotic systems

To achieving reduced-order synchronization of fractional-order chaotic systems via modified adaptive sliding mode control, we divide the drive system into two parts,

$$ D_{t}^{q} {x_{d_{\imath }}} =f_{\imath }(x_{d})+F_{\imath }(x_{d}) \alpha , $$
(9)

where \(x_{d_{\imath }}\in R^{n}\), \(f_{\imath }:R^{m}\rightarrow R^{n}\), and \(F_{\imath }:R^{m}\rightarrow R^{n\times k}\). Furthermore,

$$ D_{t}^{q} {x_{d_{\jmath }}} =f(x_{d_{\jmath }})+F(x_{d_{\jmath }})\alpha , $$
(10)

where \(x_{\jmath }\in R^{v}\), \(f_{\jmath }:R^{m} \rightarrow R^{v}\), \(F_{\jmath }:R^{m} \rightarrow R^{v\times k}\) and orders n, v satisfy \(n + v = m\). The dynamics of the reduced-order synchronization errors can be expressed as

$$ D_{t}^{p}{e}(t)=f(x_{r})+F(x_{r}) \beta -f_{\imath }(x_{d})-F_{\imath }(x_{d}) \alpha +u, $$
(11)

where \(e = x_{r} - x_{d_{\imath }}\). Our goal is to introduce a modified adaptive sliding-mode procedure to design the controller u to make the controlled uncertain response system synchronous with master system asymptotically, such that

$$ \lim_{t \to \infty } \Vert e \Vert = \lim_{t \to \infty } \Vert x_{r}- x_{d_{\imath }} \Vert = 0. $$
(12)

In accordance with the design procedure used for a modified adaptive sliding-mode control, if the nonlinear control function u is selected in (8) as follows:

$$\begin{aligned} u =&f_{\imath }(x_{d})+F_{\imath }(x_{d}) \alpha -f(x_{r})-F(x_{r})\beta +D_{t}^{p - 1} \biggl[F_{\imath }(x_{d}) (\hat{\alpha }-\alpha )-F(x_{r}) (\hat{\beta }- \beta ) \\ &{}- \bigl( {D_{t}^{p - 1} e( t )} \bigr) \frac{{( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1})} )}} - w(t)k \biggr], \end{aligned}$$
(13)

where α̂, β̂ are estimate values of the unknown parameters and \(k=[k_{1},k_{2},\ldots ,k_{n}]^{T}\) is a constant gain vector. Now, substituting u into the synchronization error system (11) yields a form that is comfortable for the oncoming stability analysis:

$$\begin{aligned} D_{t}^{p} e(t) =& D_{t}^{p - 1} \biggl[F_{\imath }(x_{d}) (\hat{\alpha }- \alpha )-F(x_{r}) (\hat{\beta }-\beta )- \bigl( {D_{t}^{p - 1} e( t )} \bigr) \frac{{( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1})} )}} \\ &{}- w(t)k \biggr]. \end{aligned}$$
(14)

Here \(w(t)\in R\) is a control input and can be determined as

$$ w(t) = \textstyle\begin{cases} {w^{+} (t)}, & {s(e) \ge 0}, \\ {w^{-} (t)}, & {s(e) < 0}, \end{cases}$$
(15)

where \(s=s(e)\) is a switching surface which introduces the desired sliding dynamics. The sliding surface function is designed as

$$ s(e)=ce, $$
(16)

where \(c=[c_{1}, c_{2},\ldots ,c_{n}]\) is a constant vector. There are necessary two conditions for the state trajectory on the sliding surface:

$$ s(e)=0\quad \mbox{and}\quad \dot{s}(e)=0. $$
(17)

The second condition is a necessary condition to constrain the state trajectory to stay on the switching surface \(s(e) = 0\). In accordance to the sliding-mode design strategy, we design the sliding mode as follows:

$$ w(t)= \biggl[\frac{s}{ \vert s \vert + \gamma } \biggr], $$
(18)

where \(\gamma >0\). The update laws parameters are defined as

$$ \begin{aligned} &\dot{\hat{\alpha }} = - \bigl[F_{\imath }(x_{d}) \bigr]^{T}\lambda , \\ &\dot{\hat{\beta }} = \bigl[F(x_{r}) \bigr]^{T} \lambda , \end{aligned} $$
(19)

where \(\lambda = s c^{T}\).

Theorem 1

Considering the error dynamic systems (14) with control laws (13) that obeys update laws parameters in (19). Then the error dynamic systems trajectories will converge to the sliding surface \(s(t) = 0\).

Proof

Consider the following Lyapunov candidate function:

$$ V = \frac{1}{2} \bigl[s^{2}+ \tilde{\alpha }^{T}\tilde{\alpha }+ \tilde{\beta }^{T} \tilde{\beta } \bigr], $$
(20)

where \(\tilde{\alpha }=\hat{\alpha }-\alpha \) and \(\tilde{\beta }=\hat{\beta }-\beta \). The time derivative of (20) is

$$ \dot{V} = \bigl[s\dot{e}^{T}c^{T}+{ \tilde{\alpha }}^{T} \dot{\tilde{\alpha }}+{\tilde{\beta }}^{T}\dot{\tilde{\beta }} \bigr]. $$
(21)

Using (6) in (21) yields V̇:

$$ \dot{V} = s \biggl[D_{t}^{p - 1} \bigl( D_{t}^{p} e \bigr) + \bigl( D_{t}^{p - 1} e( t ) \bigr) \frac{{ ( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1} )} )}} \biggr]^{T}c^{T}+{ \tilde{\alpha }}^{T}\dot{\tilde{\alpha }}+{ \tilde{\beta }}^{T}\dot{\tilde{\beta }}. $$
(22)

From (14) and (21), we obtain

$$\begin{aligned} \dot{V} =&s \biggl[ D_{t}^{p - 1} \biggl( D_{t}^{p - 1} \biggl[ F_{\imath }(x_{d}) \tilde{\alpha } - F(x_{r}) \tilde{\beta } - \bigl( D_{t}^{p - 1} e( t ) \bigr) \frac{{ ( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1} )} )}} \\ &{}-\frac{s}{ \vert s \vert + \gamma }k \biggr] \biggr) + \bigl( D_{t}^{p - 1} e( t ) \bigr) \frac{{ ( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1} )} )}} \biggr]^{T}c^{T} +{\tilde{\alpha }}^{T} \dot{\tilde{\alpha }}+{ \tilde{\beta }}^{T}\dot{\tilde{\beta }}, \end{aligned}$$
(23)

since \(\forall p \in [0, 1]\), \((1 - p) > 0\) and \((p- 1) < 0\). Now, using (5) and (19), (23) reduces to

$$\begin{aligned}& \begin{aligned}[b] \dot{V}={}&s \biggl[ \biggl( F_{\imath }(x_{d}) \tilde{\alpha } - F(x_{r}) \tilde{\beta }- \bigl( D_{t}^{q - 1} e( t ) \bigr) \frac{{ ( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1} )} )}} - \frac{s}{ \vert s \vert + \gamma }k \biggr) \\ &{}+ \bigl( D_{t}^{p - 1} e( t ) \bigr) \frac{{ ( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1} )} )}} \biggr]^{T}c^{T} +{\tilde{\alpha }}^{T} \dot{\tilde{\alpha }}+{\tilde{\beta }}^{T}\dot{ \tilde{\beta }}, \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned}& \dot{V}=s \biggl( F_{\imath }(x_{d}) \tilde{\alpha }- F(x_{r}) \tilde{\beta }- \frac{s}{ \vert s \vert + \gamma } k \biggr)^{T}c^{T} -\tilde{\alpha }^{T}F_{\imath }(x_{d})^{T} \lambda +\tilde{\beta }^{T}F(x_{r})^{T} \lambda . \end{aligned}$$
(25)

Then (25) yields

$$ \dot{V} = - ck \biggl[\frac{s^{2}}{ \vert s \vert +\gamma } \biggr] < 0. $$
(26)

Since \(s^{2}>0\) and \(|s|> 0\) both hold true, when \(e\neq 0\) and \(ck>0\), the inequality \(\dot{V}<0\) holds. According to the Lyapunov stability theory [56] V is positive-definite, and V̇ is negative-definite. Thus, the trajectories of the fractional error dynamical system (14) asymptotically converge to \(s(t) = 0\). Therefore, the state variables of the of the drive system (9) and the states variables of the response (8) system can be synchronized asymptotically and globally with the control law (13) and the adaptive parameter update laws (19). Here, the proof is completed. □

3.2 Increasing-order synchronization of fractional-order chaotic systems

To formulate the adaptive increasing-order problem, we consider response system as follows:

$$ D_{t}^{q} {x_{r}}_{\imath }=f_{\imath }({x_{r}}_{\imath })+F_{\imath }({x_{r}}_{\imath }) \beta +u_{\imath }({x_{d}},{x_{r}}_{\imath }), $$
(27)

the response system \({x_{r}}_{\imath }\in R^{n}\) is the state vector of system (27), \(\beta \in R^{\ell }\) is the vector of system parameters, \(f_{\imath }({x_{r}}_{\imath }):R^{n} \rightarrow R^{n}\), \(F_{\imath }({x_{r}}_{\imath }):R^{n} \rightarrow R^{n \times \ell }\), \(u_{\imath }(x_{d},{x_{r}}_{\imath })\in R^{n}\) is the control input, hence, the controlled response system is rewritten as follows:

$$ D_{t}^{q} {x_{r}} =f(x_{r})+F(x_{r})\beta +u(x_{d},x_{r}), $$
(28)

where

$$\begin{aligned}& x_{r}= \begin{pmatrix} {x_{r}}_{\imath }\\ {x_{r}}_{\jmath } \end{pmatrix}, \qquad f(x_{r})= \begin{pmatrix} f_{\imath }({x_{r}}_{\imath }) \\ 0 \end{pmatrix},\qquad F(x_{r})= \begin{pmatrix} F_{\imath }({x_{r}}_{\imath }) \\ 0 \end{pmatrix}, \\& u(x_{d},x_{r})= \begin{pmatrix} u_{\imath }(x_{d},{x_{r}}_{\imath }) \\ u_{\jmath }(x_{d},{x_{r}}_{\jmath }) \end{pmatrix},\quad {x_{r}}_{\jmath }, u_{\jmath }\in R^{m-n}. \end{aligned}$$

The dynamics of the add-order synchronization errors can be expressed as

$$ D_{t}^{p}{e}(t)=f(x_{r})+F(x_{r}) \beta -f(x_{d})-F(x_{d})\alpha +u, $$
(29)

where \(e = x_{r} - x_{d}\). Our aim is to design a suitable adaptive sliding-mode controller u to achieve the add-order synchronization between two different systems i.e.,

$$ \lim_{t \to \infty } \Vert e \Vert = \lim_{t \to \infty } \Vert x_{r}- x_{d} \Vert = 0. $$
(30)

In accordance with the design strategy for adaptive sliding-mode control, we choose the input signal vector as follows:

$$\begin{aligned} u =&f(x_{d})+F(x_{d}) \alpha -f(x_{r})-F(x_{r})\beta +D_{t}^{p - 1} \biggl[F(x_{d}) (\hat{\alpha }-\alpha )-F(x_{r}) (\hat{ \beta }-\beta ) \\ &{}- \bigl( {D_{t}^{p - 1} e( t )} \bigr) \frac{{( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1})} )}} -\frac{s}{ \vert s \vert + \gamma }k \biggr], \end{aligned}$$
(31)

where α̂, β̂ are estimate values of the unknown parameters and \(k=[k_{1},k_{2},\ldots ,k_{n}]^{T}\) is a constant gain vector. Substituting a particular expression for u and (31) into the error dynamics (29) yields a form that is convenient for the forthcoming stability analysis:

$$\begin{aligned} D_{t}^{p} e(t) =& D_{t}^{p - 1} \biggl[F(x_{d}) (\hat{\alpha }- \alpha )-F(x_{r}) ( \hat{\beta }-\beta )- \bigl( {D_{t}^{p - 1} e( t )} \bigr) \frac{{( t )^{ - ( {p - 1} ) - 1} }}{{\varGamma ( { - ( {p - 1})} )}} \\ &{}-\frac{s}{ \vert s \vert + \gamma }K \biggr]. \end{aligned}$$
(32)

The laws for updating parameters can be specified as follows:

$$ \begin{aligned} &\dot{\hat{\alpha }}=- \bigl[F(x_{d}) \bigr]^{T}\lambda , \\ &\dot{\hat{\beta }}= \bigl[F(x_{r}) \bigr]^{T} \lambda , \end{aligned} $$
(33)

where \(\lambda = s C^{T}\). The following theorem introduces the necessary conditions for verifying the stability of the error system in (29): Assume a positive Lyapunov function \(V=\frac{1}{2} (s^{2}+\tilde{\alpha }^{T}\tilde{\alpha }+ \tilde{\beta }^{T}\tilde{\beta } ]\), where \(\tilde{\alpha }=\hat{\alpha }-\alpha \) and \(\tilde{\beta }=\hat{\beta }-\beta \). With the choice of the updating laws (33) and reasonable control function u, the time derivative of V along the solution in (32) will be smaller than zero. In other words, the error vector will approach zero as time goes to infinity, and from Lyapunov stability theory [56], the states of the (28) system is asymptotically synchronized with the drive system (27). This completes the proof.

4 Reduced-order synchronization of fractional-order hyperchaotic Lorenz and fractional-order chaotic Lorenz systems via modified adaptive sliding mode control

To observe the reduced–order synchronization between the fractional-order hyperchaotic Lorenz [57] and fractional-order chaotic Lorenz [58] systems via modified adaptive sliding mode control, we assume that the \(x-y-z\) projection of the fractional-order hyperchaotic Lorenz systems is the drive system and it can be presented in the form of

$$ \begin{aligned} &D_{t}^{p_{1} } x_{1} = a_{1}( y_{1} - x_{1})+ w_{1}, \\ &D_{t}^{p_{2} } y_{1}= b_{1}x_{1} -x_{1} z_{1}-y_{1}, \\ &D_{t}^{p_{3} } z_{1} = x_{1} y_{1} - c_{1} z_{1}, \end{aligned} $$
(34)

and the response system can be presented in the form of

$$ \begin{aligned} &D_{t}^{p_{1} } x_{2} = a_{2}( y_{2} - x_{2})+u_{1}, \\ &D_{t}^{p_{2} } y_{2} = b_{2}x_{2} -x_{2} z_{2}-y_{2}+u_{2}, \\ &D_{t}^{p_{3} } z_{2} = x_{2} y_{2} - c_{2} z_{2}+u_{3}, \end{aligned} $$
(35)

where the variables \((u_{1},u_{2},u_{3})^{T}\) are controllers to be designed. Let \(e_{1}=x_{2}-x_{1}\), \(e_{2}=y_{2}-y_{1}\), \(e_{3}=z_{2}-z_{1}\). Then, we get the following error dynamic system between the drive (34) and response (35) systems:

$$ \begin{aligned} &D_{t}^{p_{1}}e_{1} = a_{2}( y_{2} - x_{2})-a_{1}( y_{1} - x_{1})- w_{1}+u_{1}, \\ &D_{t}^{p_{2}}e_{2} = b_{2}x_{2} -x_{2} z_{2}-y_{2}-b_{1}x_{1} +x_{1} z_{1}+y_{1}+u_{2}, \\ &D_{t}^{p_{3}}e_{3} = x_{2} y_{2} - c_{2} z_{2}-x_{1} y_{1} + c_{1} z_{1}+u_{3}. \end{aligned} $$
(36)

The goal of the modified adaptive sliding-mode control is to find an effective controller function \((u_{1},u_{2},u_{3})^{T}\) capable synchronizing the states of the response and drive systems with a parameter estimation update law. An appropriate sliding surface can be chosen as

$$ \begin{aligned} &s(e) = e_{1}+e_{3}, \\ &w(t) = \frac{s}{ \vert s \vert +0.01}. \end{aligned} $$
(37)

It is assumed that the constant vectors are \(c=(1,0,1)\), \(k = (2, 0, 40)^{T}\), and \(\gamma =0.01\). The adaptive sliding-mode controller of the error dynamic system (36) can be calculated as follows:

$$\begin{aligned}& \begin{aligned} u_{1}={}& {-}a_{2}( y_{2} - x_{2})+a_{1}( y_{1} - x_{1})+ w_{1} + D_{t}^{p_{1} - 1} \biggl[-\hat{a}_{2} (y_{2}-x_{2} )+ \hat{a}_{1} ( y_{1} - x_{1} ) \\ &{}- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} - \frac{2s}{ \vert s \vert +0.01} \biggr], \end{aligned} \\& \begin{aligned} u_{2} ={}&{-}b_{2}x_{2} +x_{2} z_{2}+y_{2}+b_{1}x_{1} -x_{1} z_{1}-y_{1}+ D_{t}^{p_{2} - 1} \biggl[-\hat{b}_{2}x_{2}+\hat{b}_{1}x_{1} \\ &{}- \bigl( {D_{t}^{p_{2} - 1} e_{2}( t )} \bigr){ \frac{{( t )^{ - ( {p_{2} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{2} - 1} )} )}} } \biggr], \end{aligned} \\& \begin{aligned} u_{3} ={}&{-}x_{2} y_{2} + c_{2} z_{2}+x_{1} y_{1} - c_{1} z_{1} + D_{t}^{p_{3} - 1} \biggl[ \hat{c}_{2}z_{2}-\hat{c}_{1} z_{1} \\ &{}- \bigl( {D_{t}^{p_{3} - 1} e_{3}( t )} \bigr){ \frac{{( t )^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3}- 1} )} )}} - \frac{40s}{ \vert s \vert +0.01} } \biggr]. \end{aligned} \end{aligned}$$
(38)

The adaptive laws for estimating the parameters \(\hat{a}_{1}\), \(\hat{b}_{1}\), \(\hat{c}_{1}\), \(\hat{a}_{2}\), \(\hat{b}_{2}\), and \(\hat{c}_{2}\) are chosen as follows:

$$ \begin{aligned} &\dot{\tilde{a}}_{1} = - (y_{1}-x_{1} )s, \\ &\dot{\tilde{b}}_{1} = x_{1}s, \\ &\dot{\tilde{c}}_{1} = z_{1}s, \\ &\dot{\tilde{a}}_{2} = (y_{2}-x_{2} )s , \\ &\dot{\tilde{b}}_{2} = x_{2}s, \\ &\dot{\tilde{c}}_{2} = -z_{2}s. \end{aligned} $$
(39)

Theorem 2

The state variables of the response system (35) and and the states variables of \((x-y-z)\)projection of the drive system (34) can be synchronized asymptotically and globally for all initial conditions using the control law (38) and the adaptive parameter update laws (39).

Proof

Substituting (38) into (36), this yields

$$ \begin{aligned} &D_{t}^{p_{1}}e_{1} = D_{t}^{p_{1} - 1} \biggl[-\tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} \\ &\hphantom{D_{t}^{p_{1}}e_{1} ={}}{}- \frac{2s}{ \vert s \vert +0.01} \biggr], \\ &D_{t}^{p_{2}}e_{2} = D_{t}^{p_{2} - 1} \biggl[-\tilde{b}_{2}x_{2}+ \tilde{b}_{1}x_{1} - \bigl( {D_{t}^{p_{2} - 1} e_{2}( t )} \bigr) { \frac{{( t )^{ - ( {p_{2} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{2} - 1} )} )}} } \biggr], \\ &D_{t}^{p_{3}}e_{3} = D_{t}^{p_{3} - 1} \biggl[ \tilde{c}_{2}z_{2}- \tilde{c}_{1} z_{1}- \bigl( {D_{t}^{p_{3} - 1} e_{3}( t )} \bigr) { \frac{{( t )^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3}- 1} )} )}} - \frac{40s}{ \vert s \vert +0.01} } \biggr], \end{aligned} $$
(40)

where \(\tilde{a}_{1}=\hat{a}_{1}-a_{1}\), \(\tilde{b}_{1}=\hat{b}_{1}-b_{1}\), \(\tilde{c}_{1}=\hat{c}_{1}-c_{1}\), \(\tilde{a}_{2}=\hat{a}_{2}-a_{2}\), \(\tilde{b}_{2}=\hat{b}_{2}-b_{2}\), and \(\tilde{c}_{2}=\hat{c}_{2}-c_{2}\). We select a Lyapunov function candidate in the form of

$$ {V} = \frac{1}{2} \bigl( {s^{2} + \tilde{a}^{2}_{1} + \tilde{b}^{2}_{1} + \tilde{c}^{2}_{1} + \tilde{a}^{2}_{2} + \tilde{b}^{2}_{2}+ \tilde{c}^{2}_{2}} \bigr). $$
(41)

Taking the derivative of (41) with respect to time using (6), one has

$$\begin{aligned} \dot{V} =& ( s \dot{s} + \tilde{a}_{1} \dot{\tilde{a}}_{1} + \tilde{b}_{1} \dot{ \tilde{b}}_{1}+ \tilde{c}_{1} \dot{\tilde{c}}_{1}+ \tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{b}_{2} \dot{\tilde{b}}_{2}+ \tilde{c}_{2} \dot{\tilde{c}}_{2} ) \\ =& \biggl( s{ \biggl[ {D_{t} ^{1 - p_{1} } } } \bigl( {D_{t} ^{p_{1} } e_{1}(t) }\bigr) + \bigl( {D_{t} ^{p_{1}-1 } e_{1}(t) }\bigr) { \frac{{(t)^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1} - 1})} )}}} \biggr] + s { \biggl[ {D_{t} ^{1 - p_{3} } } } \bigl( {D_{t} ^{p_{3} } e_{3}(t) } \bigr) \\ &{}+ \bigl( {D_{t} ^{p_{3}-1 } e_{3} (t)} \bigr) { \frac{{(t)^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3} - 1} )} )}}} \biggr] + \tilde{a}_{1} \dot{ \tilde{a}}_{1} +\tilde{c}_{1} \dot{\tilde{c}}_{1} +\tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{c}_{2} \dot{\tilde{c}}_{2} \biggr) \\ =&s { \biggl[ {D_{t} ^{1 - p_{1} } } } \biggl( D_{t}^{p_{1} - 1} \biggl[- \tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} \\ &{}- \frac{2s}{ \vert s \vert +0.01} \biggr] \biggr) + \bigl( {D_{t} ^{p_{1}-1 } e_{1}(t) } \bigr) { \frac{{(t)^{ - ( {p_{1} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{1} - 1} )} )}}} \biggr]+ s \biggl[D_{t}^{1 - p_{3} } \biggl(D_{t}^{1 - p_{3} } \biggl[\tilde{c}_{2}z_{2}-\tilde{c}_{1} z_{1} \\ &{}- \bigl(D_{t}^{ p_{3}-1 } e_{3} (t) \bigr) \frac{{(t)^{ - (p_{3} - 1) - 1} }}{{\varGamma ( - (p_{3} - 1))}}- \frac{40s}{ \vert s \vert +0.01} \biggr] \biggr)+ \bigl( {D_{t} ^{p_{3}-1 } e_{3}(t) } \bigr) { \frac{{(t)^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3} - 1} )})}}} \biggr] \\ &{} + \tilde{a}_{1} \dot{\tilde{a}}_{1} + \tilde{c}_{1} \dot{\tilde{c}}_{1} +\tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{c}_{2} \dot{ \tilde{c}}_{2}, \end{aligned}$$
(42)

since \(\forall p \in [0, 1]\), \((1 - p) > 0\) and \((p - 1) < 0\). Now, using (5) and introducing update laws (39), in (42) one obtains

$$\begin{aligned} \dot{V} =&s \biggl(-\tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \frac{2s}{ \vert s \vert +0.01} \biggr)+s \biggl(\tilde{c}_{2}z_{2}- \tilde{c}_{1} z_{1}- \frac{40s}{ \vert s \vert +0.01} \biggr) \\ &{}+\tilde{a}_{1} \bigl(- (y_{1}-x_{1} )s \bigr)+\tilde{c}_{1} (z_{1}s )+\tilde{a}_{2} \bigl( (y_{2}-x_{2} )s \bigr)+\tilde{c}_{2} (-z_{2}s ). \end{aligned}$$
(43)

Then (43) reduces to

$$ \dot{V} = -\frac{42 s^{2}}{ \vert s \vert +0.01}. $$
(44)

Since \(s^{2}>0\) and \(|s|> 0\) both hold true, when \(e\neq 0\) and \(ck>0\), the inequality \(\dot{V}<0\) holds. According to the Lyapunov stability theory [56], V is positive-definite, and V̇ is negative-definite. Thus, the trajectories of the fractional error dynamical system (36) asymptotically converge to \(s(t) = 0\). Therefore, the state variables of \((x-y-z)\) projection of the drive system (34) and the states variables of the response (35) system can be synchronized asymptotically and globally with the control law (38) and the adaptive parameter update laws (39). Here, the proof is completed. □

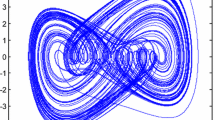
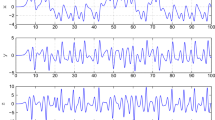
In the numerical simulations, the Adams–Bashforth–Moulton method is used to solve systems. The uncertain parameters are set to \(a_{1}=10\), \(b_{1}=28\), \(c_{1}=8/3\), \(a_{2}=10\), \(b_{2}=28\), \(c_{2} =8/3\). The initial values of the fractional-order drive and response systems (34)–(35) and the estimated parameters are, respectively, and arbitrarily set in simulations to \(x_{1}(0)=12\), y\(_{1}(0)=22\), \(z_{1}(0)=31\), \(w_{1}(0)=4\), \(x_{2}(0)=0\), \(y_{2}(0)=1\), and \(z_{2}(0)=2\) and \(\tilde{a}_{1}(0)=10\), \(\tilde{b}_{1}(0)=10\), \(\tilde{c}_{1}(0)=10\), \(\tilde{a}_{2}(0)=10\), \(\tilde{b}_{2}(0)=10\) and \(\tilde{c}_{2}(0)=10\). Figures 1–2 depict the modified adaptive sliding-mode synchronization of systems (34)–(35) via the adaptive control laws (38) and (39). Figure 1(a)–(c) displays the steady-state trajectories of the drive (34) and the response (35) systems. Figure 2 (a) displays the synchronization errors \(e_{1}\), \(e_{2}\), and \(e_{3}\) as functions of time t. Figure 2(b)–(c) displays the temporal response of the estimated parameter values \(\tilde{a}_{1}\), \(\tilde{b}_{1}\), \(\tilde{c}_{1}\), \(\tilde{a}_{2}\), \(\tilde{b}_{2}\), and \(\tilde{c}_{2}\) of the drive (34) and the response (35) systems.

Figure 1
figure 1

State trajectories of drive system (34) and response system (35): (a) signals \(x_{1}\) and \(x_{2}\); (b) signals \(y_{1}\) and \(y_{2}\); (c) signals \(z_{1}\) and \(z_{2}\). in \((x-y-z)\) projection

Full size image
Figure 2
figure 2

(a) error signals between the drive system (34) and the response system (35) systems, (b)–(c): Estimated values for unknown parameters in \((x-y-z)\) projection

Full size image

5 Increasing-order synchronization of fractional-order hyperchaotic Lü and fractional-order chaotic Lü systems via modified adaptive sliding mode control

This section investigates the increase–order synchronization behavior via modified adaptive sliding mode control. The drive system is assumed to be a fractional-order hyperchaotic Lü [59] while the fractional-order chaotic Lü [60] system is taken as the response. The definitions of both systems have unknown parameters:

$$ \begin{aligned} &D_{t}^{p_{1} } x_{1} = a_{1}( y_{1} - x_{1})+ w_{1}, \\ &D_{t}^{p_{2} } y_{1} = b_{1}y_{1} -x_{1} z_{1}, \\ &D_{t}^{p_{3} } z_{1} = x_{1} y_{1} - c_{1} z_{1}, \\ &D_{t}^{p_{4} } w_{1} = x_{1}z_{1} +r_{1} w_{1}, \end{aligned} $$
(45)

and

$$\begin{aligned} \begin{aligned} &D_{t}^{q_{1} } x_{2} = a_{2}(y_{2} - x_{2})+u_{1}, \\ &D_{t}^{q_{2} } y_{2} = -x_{2}z_{2}+b_{2}y_{2}+u_{2}, \\ &D_{t}^{q_{3} } z_{2} = x_{2}y_{2} - c_{2}z_{2}+u_{3}, \\ &D_{t}^{p_{4} } w_{2} = u_{4}, \end{aligned} \end{aligned}$$
(46)

where the variables \((u_{1},u_{2},u_{3}, u_{4})^{T}\) are controllers to be designed. Let \(e_{1}=x_{2}-x_{1}\), \(e_{2}=y_{2}-y_{1}\), \(e_{3}=z_{2}-z_{1}\) and \(e_{4}=w_{2}-w_{1}\). Then, we get the following error dynamic system between the drive (45) and response (46) systems:

$$ \begin{aligned} &D_{t}^{p_{1}}e_{1} = a_{2}( y_{2} - x_{2})-a_{1}( y_{1} - x_{1})- w_{1}+u_{1}, \\ &D_{t}^{p_{2}}e_{2} = -x_{2}z_{2}+b_{2}y_{2}-b_{1}y_{1} +x_{1} z_{1}+u_{2}, \\ &D_{t}^{p_{3}}e_{3} = x_{2} y_{2} - c_{2} z_{2}-x_{1} y_{1} + c_{1} z_{1}+u_{3}, \\ &D_{t}^{p_{4}}e_{4} = -x_{1}z_{1} -r_{1} w_{1}+u_{4}. \end{aligned} $$
(47)

The goal of the modified adaptive sliding-mode control method is to find proper control functions \(u_{i}\) (\(i = 1,2,3,4\)) capable of synchronizing the states of the response and drive systems with fully unknown parameters. Then, the switching surface is described as

$$ \begin{aligned} &s(e) = e_{1}+e_{3}, \\ &w(t) = \frac{s}{ \vert s \vert +0.01}. \end{aligned} $$
(48)

It is assumed that the constant vectors are \(c=(1,0,1,0)\), \(k = (7, 0,10,0)^{T}\), and \(\gamma =0.01\). The adaptive sliding-mode controller of the error dynamic system (47) can be calculated as follows:

$$ \begin{aligned} &\begin{aligned} u_{1}={}& {-}a_{2}( y_{2} - x_{2})+a_{1}( y_{1} - x_{1})+ w_{1} + D_{t}^{p_{1} - 1} \biggl[-\hat{a}_{2} (y_{2}-x_{2} )+ \hat{a}_{1} ( y_{1} - x_{1} ) \\ &{}- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} - \frac{7s}{ \vert s \vert +0.01} \biggr], \end{aligned} \\ &u_{2} =x_{2}z_{2}-b_{2}y_{2}+b_{1}y_{1} -x_{1} z_{1}+ D_{t}^{p_{2} - 1} \biggl[\hat{b}_{1}y_{1}-\hat{b}_{2}y_{2} - \bigl( {D_{t}^{p_{2} - 1} e_{2}( t )} \bigr) { \frac{{( t )^{ - ( {p_{2} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{2} - 1} )} )}} } \biggr], \\ &\begin{aligned} u_{3} ={}&{-}x_{2} y_{2} + c_{2} z_{2}+x_{1} y_{1} - c_{1} z_{1} + D_{t}^{p_{3} - 1} \biggl[ \hat{c}_{2}z_{2}-\hat{c}_{1} z_{1}- \bigl( {D_{t}^{p_{3} - 1} e_{3}( t )} \bigr) \frac{{( t )^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3}- 1} )} )}} \\ &{} - \frac{10s}{ \vert s \vert +0.01} \biggr], \end{aligned} \\ &u_{4} = x_{1}z_{1} +r_{1} w_{1}+ D_{t}^{p_{4} - 1} \biggl[ \hat{r}_{1}w1_{2}- \bigl( {D_{t}^{p_{4} - 1} e_{4}( t )} \bigr) { \frac{{( t )^{ - ( {p_{4} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{4}- 1} )} )}} } \biggr]. \end{aligned} $$
(49)

The adaptive laws for estimating the parameters \(\hat{a}_{1}\), \(\hat{b}_{1}\), \(\hat{c}_{1}\), \(\hat{a}_{2}\), \(\hat{b}_{2}\), and \(\hat{c}_{2}\) are chosen as follows:

$$\begin{aligned}& \dot{\tilde{a}}_{1} = - (y_{1}-x_{1} )s, \\& \dot{\tilde{b}}_{1} = -y_{1}s, \\& \dot{\tilde{c}}_{1} = z_{1}s, \\& \dot{\tilde{r}}_{1} = -w_{1}s, \\& \dot{\tilde{a}}_{2} = (y_{2}-x_{2} )s , \\& \dot{\tilde{b}}_{2} = y_{2}s, \\& \dot{\tilde{c}}_{2} = -z_{2}s. \end{aligned}$$
(50)

Theorem 3

The state variables of the of the drive system (45) and the states variables of the response (46) system can be synchronized asymptotically and globally for all initial conditions using the control law (49) and the adaptive parameter update laws (50).

Proof

Substituting (49) into (47), this yields

$$ \begin{aligned} &D_{t}^{p_{1}}e_{1} = D_{t}^{p_{1} - 1} \biggl[-\tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} \\ &\hphantom{D_{t}^{p_{1}}e_{1} ={}}{}- \frac{7s}{ \vert s \vert +0.01} \biggr], \\ &D_{t}^{p_{2}}e_{2} = D_{t}^{p_{2} - 1} \biggl[\tilde{b}_{1}y_{1}- \tilde{b}_{2}y_{2} - \bigl( {D_{t}^{p_{2} - 1} e_{2}( t )} \bigr) { \frac{{( t )^{ - ( {p_{2} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{2} - 1} )} )}} } \biggr], \\ &D_{t}^{p_{3}}e_{3} = D_{t}^{p_{3} - 1} \biggl[ \tilde{c}_{2}z_{2}- \tilde{c}_{1} z_{1}- \bigl( {D_{t}^{p_{3} - 1} e_{3}( t )} \bigr) \frac{{( t )^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3}- 1} )} )}} - \frac{10s}{ \vert s \vert +0.01} \biggr], \\ &D_{t}^{p_{4}}e_{4} = D_{t}^{p_{4} - 1} \biggl[ \tilde{r}_{1}w1_{2}- \bigl( {D_{t}^{p_{4} - 1} e_{4}( t )} \bigr) { \frac{{( t )^{ - ( {p_{4} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{4}- 1} )} )}} } \biggr], \end{aligned} $$
(51)

where \(\tilde{a}_{1}=\hat{a}_{1}-a_{1}\), \(\tilde{b}_{1}=\hat{b}_{1}-b_{1}\), \(\tilde{c}_{1}=\hat{c}_{1}-c_{1}\), \(\tilde{r}_{1}=\hat{r}_{1}-r_{1}\)\(\tilde{a}_{2}=\hat{a}_{2}-a_{2}\), \(\tilde{b}_{2}=\hat{b}_{2}-b_{2}\), and \(\tilde{c}_{2}=\hat{c}_{2}-c_{2}\). We select a Lyapunov function candidate in the form of

$$ {V} = \frac{1}{2} \bigl( {s^{2} + \tilde{a}^{2}_{1} + \tilde{b}^{2}_{1} + \tilde{c}^{2}_{1} + \tilde{r}^{2}_{1} + \tilde{a}^{2}_{2} + \tilde{b}^{2}_{2}+ \tilde{c}^{2}_{2}} \bigr). $$
(52)

Taking the derivative of (52) with respect to time using (6), one has

$$\begin{aligned} \dot{V} =& ( s \dot{s} + \tilde{a}_{1} \dot{\tilde{a}}_{1} + \tilde{b}_{1} \dot{ \tilde{b}}_{1}+ \tilde{c}_{1} \dot{\tilde{c}}_{1}+ \tilde{r}_{1} \dot{\tilde{r}}_{1}+\tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{b}_{2} \dot{ \tilde{b}}_{2}+ \tilde{c}_{2} \dot{\tilde{c}}_{2} ) \\ =& \biggl( s{ \biggl[ {D_{t} ^{1 - p_{1} } } } \bigl( {D_{t} ^{p_{1} } e_{1}(t) }\bigr) + \bigl( {D_{t} ^{p_{1}-1 } e_{1}(t) }\bigr) { \frac{{(t)^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1} - 1})} )}}} \biggr] + s { \biggl[ {D_{t} ^{1 - p_{3} } } } \bigl( {D_{t} ^{p_{3} } e_{3}(t) } \bigr) \\ &{}+ \bigl( {D_{t} ^{p_{3}-1 } e_{3} (t)} \bigr) { \frac{{(t)^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3} - 1} )} )}}} \biggr] + \tilde{a}_{1} \dot{ \tilde{a}}_{1} +\tilde{c}_{1} \dot{\tilde{c}}_{1} +\tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{c}_{2} \dot{\tilde{c}}_{2} \biggr) \\ =&s { \biggl[ {D_{t} ^{1 - p_{1} } } } \biggl( D_{t}^{p_{1} - 1} \biggl[- \tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \bigl( {D_{t}^{p_{1} - 1} e_{1}( t )} \bigr) \frac{{( t )^{ - ( {p_{1} - 1}) - 1} }}{{\varGamma ( { - ( {p_{1}- 1} )} )}} \\ &{}- \frac{7s}{ \vert s \vert +0.01} \biggr] \biggr) + \bigl( {D_{t} ^{p_{1}-1 } e_{1}(t) } \bigr) { \frac{{(t)^{ - ( {p_{1} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{1} - 1} )} )}}} \biggr]+ s \biggl[D_{t}^{1 - p_{3} } \biggl(D_{t}^{1 - p_{3} } \biggl[\tilde{c}_{2}z_{2}-\tilde{c}_{1} z_{1} \\ &{}- \bigl(D_{t}^{ p_{3}-1 } e_{3} (t) \bigr) \frac{{(t)^{ - (p_{3} - 1) - 1} }}{{\varGamma ( - (p_{3} - 1))}}- \frac{10s}{ \vert s \vert +0.01} \biggr] \biggr)+ \bigl( {D_{t} ^{p_{3}-1 } e_{3}(t) } \bigr) { \frac{{(t)^{ - ( {p_{3} - 1} ) - 1} }}{{\varGamma ( { - ( {p_{3} - 1} )})}}} \biggr] \\ &{} + \tilde{a}_{1} \dot{\tilde{a}}_{1} + \tilde{c}_{1} \dot{\tilde{c}}_{1} +\tilde{a}_{2} \dot{\tilde{a}}_{2} + \tilde{c}_{2} \dot{ \tilde{c}}_{2}, \end{aligned}$$
(53)

since \(\forall p \in [0, 1]\), \((1 - p) > 0\) and \((p - 1) < 0\). Now, using (5) and introducing update laws (50), (53) one obtains

$$\begin{aligned} \dot{V} =&s \biggl(-\tilde{a}_{2} (y_{2}-x_{2} )+\tilde{a}_{1} ( y_{1} - x_{1} )- \frac{7s}{ \vert s \vert +0.01} \biggr)+s \biggl(\tilde{c}_{2}z_{2}- \tilde{c}_{1} z_{1}- \frac{10s}{ \vert s \vert +0.01} \biggr) \\ &{}+\tilde{a}_{1} \bigl(- (y_{1}-x_{1} )s \bigr)+\tilde{c}_{1} (z_{1}s )+\tilde{a}_{2} \bigl( (y_{2}-x_{2} )s \bigr)+\tilde{c}_{2} (-z_{2}s ). \end{aligned}$$
(54)

Then, (54) reduces to

$$ \dot{V} = -\frac{17 s^{2}}{ \vert s \vert +0.01}. $$
(55)

Since \(s^{2}>0\) and \(|s|> 0\) both hold true, when \(e\neq 0\) and \(ck>0\), the inequality \(\dot{V}<0\) holds. According to the Lyapunov stability theory [56], V is positive-definite, and V̇ is negative-definite. Thus, the trajectories of the fractional error dynamical system (47) asymptotically converge to \(s(t) = 0\). Therefore, the state variables of the drive system (45) and the states variables of the response (46) system can be synchronized asymptotically and globally with the control law (49) and the adaptive parameter update laws (50). Here, the proof is completed. □

In the numerical simulations, the Adams–Bashforth–Moulton method to solve systems. The uncertain parameters are set to \(a_{1}=36\), \(b_{1}=20\), \(c_{1}=3\), \(a_{2}=36\), \(b_{2}=20\), \(c_{2} =3\). The initial values of the fractional-order drive and response systems (34)–(35) and the estimated parameters are respectively and arbitrarily set in simulations to \(x_{1}(0)=-1\), y\(_{1}(0)=0.2\), \(z_{1}(0)=-0.6\), \(w_{1}(0)=0.4\), \(x_{2}(0)=-2\), \(y_{2}(0)=4\), \(z_{2}(0)=-13\), and \(w_{1}(0)=0.1\) and \(\tilde{a}_{1}(0)=1\), \(\tilde{b}_{1}(0)=1\), \(\tilde{c}_{1}(0)=1\), \(\tilde{r}_{1}(0)=1\), \(\tilde{a}_{2}(0)=1\), \(\tilde{b}_{2}(0)=1\) and \(\tilde{c}_{2}(0)=1\). Figures 3–4 depict the modified adaptive sliding-mode add-order synchronization of the systems (45)–(46) via the adaptive control laws (49) and (50). Figure 3(a)–(d) displays the steady-state trajectories of the drive (45) and the response (46) systems. Figure 4(a) displays the synchronization errors \(e_{1}\), \(e_{2}\), \(e_{3}\), and \(e_{4}\) as functions of time t. Figure 4(b)–(c) displays the temporal response of the estimated parameter values \(\tilde{a}_{1}\), \(\tilde{b}_{1}\), \(\tilde{c}_{1}\), \(\tilde{r}_{1}\), \(\tilde{a}_{2}\), \(\tilde{b}_{2}\), and \(\tilde{c}_{2}\) of the drive (45) and the response (46) systems.

Figure 3
figure 3

State trajectories of drive system (45) and the response system (46): (a) signals \(x_{1}\) and \(x_{2}\); (b) signals \(y_{1}\) and \(y_{2}\); (c) signals \(z_{1}\) and \(z_{2}\); (d) signals \(w_{1}\) and \(w_{2}\)

Full size image
Figure 4
figure 4

(a): Error signals between drive (45) and response (46) systems, (b)–(c): Parameter estimates for the drive (45) and the response systems (46)

Full size image

6 Conclusion

In this paper, a new modification of the adaptive sliding-mode synchronization scheme has been proposed for fractional-order chaotic (hyperchaotic) systems with fully unknown parameters. A suitable controller and a parameters update law are designed to achieve the reduce- and add-order synchronization of two different order fractional-order chaotic (hyperchaotic) systems, based on the Lyapunov stability theorem. Simulations show that these kinds of reduce- and add-order order synchronization exists between many existing fractional-order chaotic (hyperchaotic) systems. Numerical simulations are also given to show the effectiveness of the proposed scheme.