1 Introduction

Many real-life biological models including prey–predator interactions often are governed by nonlinear differential equations. For these nonlinear differential systems analytical solutions are not always easy to investigate. One of the most challenging tasks is solving these nonlinear differential equations efficiently. There are several methods for converting continuous differential systems to their discrete counterparts. The most conventional way for this purpose is to implement standard difference methods such as Euler approximations and Runge–Kutta methods. However, numerical instabilities are observed with the implementation of standard finite difference schemes. In order to get rid of these numerical instabilities, one can implement nonstandard finite difference schemes introduced by Mickens [1].

Generally, a nonstandard finite difference scheme is based on the set of rules aimed at preserving the most dynamical properties of the associated continuous-time model, such as boundedness, positivity of solutions, stability of steady states, conservation laws, and bifurcations. In other words, the main advantage of these nonstandard finite difference schemes is to preserve the significant properties of their continuous analogs and consequently give reliable numerical results. On the other hand, the construction of these nonstandard finite difference schemes is not always a straightforward task and there are no general criteria for their construction, and these may be considered as major drawbacks for nonstandard finite difference schemes.

Predator–prey interactions belong to the most important ways that species interact in ecological communities. Predator–prey models can reasonably be seen as the building blocks for the ecosystems. Mathematical models governed by differential equations are more appropriate for the species in which populations are overlapped. In the case of non-overlapping generations, discrete-time models governed by difference equations are more suitable than differential equations. Discretization of differential equations is one way to produce discrete-time models governed by difference equations. Numerical methods are implemented to differential equations in order to produce discrete-time models for predator–prey systems. A discrete-time model is said to be dynamically consistent with its continuous counterpart if the two demonstrate a similar dynamical behavior, such as boundedness and persistence of solutions, stability behavior of steady states, chaos, and bifurcation [2]. Forward Euler approximations and piecewise constant arguments are more frequently used methods to obtain discrete-time counterparts of predator–prey models. But both of these methods are lacking the dynamical consistency with their continuous counterparts. Ushiki [3] proposed a discrete-time predator–prey model with implementation of forward Euler approximation, and it was investigated that the discrete-time system undergoes period-doubling bifurcation and the route to chaos was also discussed. Jing and Yang [4] implemented an Euler forward scheme to obtain a discrete version of the prey–predator system. Furthermore, in their paper they discussed period-doubling and Neimark–Sacker bifurcations. Similarly, Liu and Xiao [5] presented complex dynamics for a discrete Lotka–Volterra system after implementation of Euler method. For a similar type of investigations related to predator–prey systems the interested reader is referred to [6,7,8,9,10,11,12,13,14,15,16,17]. All these studies reveal that the discrete predator–prey models with implementation of Euler approximation are dynamically inconsistent with their continuous counterparts.

On the other hand, some other researchers implemented piecewise constant arguments to produce a discrete analog of the predator–prey system. Jiang and Rogers [18] implemented piecewise constant arguments to study the competitive case, and Krawcewicz and Rogers [19] investigated the cooperative case. Recently, Din [20,21,22] applied piecewise constant arguments to various classes of predator–prey system and investigated bifurcation and chaos control for discrete models. All these investigations reveal dynamical inconsistency between the discrete-time and continuous-time systems.

Keeping in view the dynamical consistency, Liu and Elaydi [2] studied competitive and cooperative systems of prey–predator type, and Al-Kahby et al. [23] investigated the dynamics of some biological systems with implementation of Mickens type nonstandard finite difference methods [1]. Moreover, Roeger and Allen [24], and Roeger [25,26,27] discussed the dynamics of May-Leonard competitive models in discrete cases. Moghadas et al. [28] proposed a nonstandard numerical scheme for a generalized Gause-type Lotka–Volterra system. For further applications of nonstandard finite difference schemes to various classes of Lotka–Volterra models we refer to [29,30,31,32,33,34,35] and the references therein.

Next, we consider the following Holling and Leslie type predator–prey model [36]:

$$ \begin{aligned} &x' ( t ) = x ( t ) \biggl( r \biggl( 1 - \frac{x ( t )}{k} \biggr) - \frac{\alpha x ( t ) y ( t )}{x^{2} ( t ) + \beta ^{2}} \biggr), \\ &y' ( t ) = sy ( t ) \biggl( 1 - \frac{hy ( t )}{x ( t )} \biggr), \end{aligned} $$
(1)

where x and y represent prey and predator population densities, respectively. Furthermore, the growth rate for prey species is considered to be logistic with intrinsic growth rate r and carrying capacity k, the consumption of prey is considered to be Holling type-III functional response, β denotes the half-saturation constant, s is the intrinsic growth rate for prey population, h represents the quantity of food which prey provides for the conversion of predator birth, and \(y / x\) denotes the Leslie–Gower term which measures the loss in the predator population due to rarity of its favorite food. Moreover, all parameters r, k, α, β, s, h are positive constants.

He and Lai [6] investigated stability, period-doubling bifurcation, Neimark–Sacker bifurcation and chaos control for a discrete counterpart of (1) with application of Euler forward approximation. Consequently, their investigation reveals the dynamical inconsistency between the discrete-time and continuous-time system because there is no chance of flip bifurcation in system (1). Keeping in view the dynamical consistency of model (1), the following discrete-time counterpart of (1) is proposed by implementing a Mickens type nonstandard finite difference scheme:

$$ \begin{aligned} &\frac{x_{n+ 1} - x_{n}}{\delta } = r x_{n} - \frac{x_{n} x_{n+ 1}}{k} - \frac{\alpha x_{n+ 1} x_{n} y_{n}}{x_{n} ^{2} + \beta ^{2}}, \\ &\frac{y_{n+ 1} - y_{n}}{\delta } = s y_{n} - \frac{sh y_{n} y_{n+ 1}}{x _{n}}, \end{aligned} $$
(2)

where \(\delta >0\) is step size for nonstandard finite difference method. Moreover, system (2) can be transformed into the following explicit form:

$$ \begin{aligned} &x_{n+ 1} = \frac{(1 + \delta r ) x_{n}}{1 + \frac{\delta r}{k} x _{n} + \frac{\alpha \delta x_{n} y_{n}}{x_{n}^{2} + \beta ^{2}}}, \\ &y_{n+ 1} = \frac{(1 +s \delta ) y_{n}}{1 + \frac{sh \delta y_{n}}{x _{n}}}. \end{aligned} $$
(3)

The remaining paper is organized as follows. In Sect. 2, dynamical behavior including positivity, boundededness and persistence of solutions, existence of equilibria and their stability for model (1) is carried out. In Sect. 3, we prove persistence of solutions, and a stability analysis of steady states for system (3) is also discussed. Neimark–Sacker bifurcation is investigated in Sect. 4 for model (3). Finally, numerical investigations are provided in Sect. 5.

2 Dynamics of system (1)

First, we discuss positivity, boundedness and permanence of solutions of system (1).

Lemma 2.1

All solutions of system (1) are positive and bounded with positive initial conditions. Moreover, assume that \(\alpha k^{2} < rh \beta ^{2}\), then system (1) is permanent.

Proof

Take into account system (1) with positive initial values, that is, \(x (0)= x_{0} >0\) and \(y (0)= y_{0} >0\). Then from system (1) with positive initial values it follows that

$$ x ( t )= x_{0} \exp \biggl( \int _{0}^{t} \biggl( r \biggl( 1 - \frac{x ( \xi )}{k} \biggr) - \frac{\alpha x ( \xi ) y ( \xi )}{x^{2} ( \xi ) + \beta ^{2}} \biggr) \,d\xi \biggr) >0 $$
(4)

and

$$ y ( t )= y_{0} \exp \biggl( \int _{0}^{t} s \biggl( 1 - \frac{hy ( \xi )}{x ( \xi )} \biggr) \,d\xi \biggr) >0. $$
(5)

Consider the following set:

$$ S:= \bigl\{ ( x, y ) \in \mathbb{R}^{2}: x >0, y >0 \bigr\} . $$

Then all solutions of system (1) starting in S remain in S for every \(t\geq 0\). Next, due to positivity of solutions and the first part (prey equation) of system (1) showing that \(x' ( t )= x ( t ) ( r ( 1 - \frac{x ( t )}{k} ) - \frac{\alpha x ( t ) y ( t )}{x ^{2} ( t ) + \beta ^{2}} ) \leq rx ( t ) ( 1 - \frac{x ( t )}{k} )\), one has \(x ( t ) \leq \{ x_{0}, k \}:= M_{1}\) for all \(t\geq 0\). Similarly it follows from the predator equation of system (1) that \(y' ( t )= sy ( t ) ( 1 - \frac{hy ( t )}{x ( t )} ) \leq sy ( t ) ( 1 - \frac{hy ( t )}{M_{1}} )\). Therefore, again one has \(y ( t ) \leq \{ y_{0}, \frac{M_{1}}{h} \}:= M_{2}\) for all \(t\geq 0\). In other words, for sufficiently large t we have \(\lim_{t\rightarrow \infty } \sup x ( t ) \leq k\) and \(\lim_{t\rightarrow \infty } \sup y ( t ) \leq \frac{k}{h}\). Then, again from system (1), it follows that \(x' ( t )= x ( t ) ( r ( 1 - \frac{x ( t )}{k} ) - \frac{\alpha x ( t ) y ( t )}{x^{2} ( t ) + \beta ^{2}} ) \geq x ( t ) ( r ( 1 - \frac{x ( t )}{k} ) - \frac{\alpha k^{2}}{h \beta ^{2}} )\). Furthermore, suppose that \(\alpha k^{2} < rh \beta ^{2}\), then it follows that \(\lim_{t\rightarrow \infty } \inf x ( t ) \geq k ( 1 - \frac{ \alpha k^{2}}{hr \beta ^{2}} ):= m_{1}\). Similarly, the second part of system (1) shows that \(y' ( t )= sy ( t ) ( 1 - \frac{hy ( t )}{x ( t )} ) \geq sy ( t ) ( 1 - \frac{hy ( t )}{m _{1}} )\), and therefore \(\lim_{t\rightarrow \infty } \inf y ( t ) \geq \frac{m_{1}}{h}\). Consequently, we obtain permanence for system (1). □

For the investigation of steady states of system (1), the zero growth isoclines are computed as follows:

$$ \begin{aligned} & x \biggl( r \biggl( 1 - \frac{x}{k} \biggr) - \frac{\alpha xy}{x ^{2} + \beta ^{2}} \biggr) =0, \\ & sy \biggl( 1 - \frac{hy}{x} \biggr) =0. \end{aligned} $$
(6)

Then obviously one has \((k, 0)\) as boundary equilibrium for system (1). In order to see the dynamical behavior of system (1) at \((k, 0)\), we first compute the Jacobian matrix of system (1) at \((k, 0)\) as follows:

$$ J ( k,0):= \begin{pmatrix} -r & - \frac{k^{2} \alpha }{k^{2} + \beta ^{2}} \\ 0 & s \end{pmatrix}. $$

Then one can easily see that \((k, 0)\) is a saddle point. Furthermore, the components of the interior steady state \((x^{*}, y^{*})\) are given by

$$ y^{*} = \frac{1}{h} x^{*}, $$

where \(x^{*}\) is a real root of the following cubic equation:

$$ x^{3} + \biggl( \frac{\alpha k-hkr}{hr} \biggr) x^{2} + \beta ^{2} x-k \beta ^{2} =0. $$

Denote \(\Delta =18 bcd- 4 b^{3} d+ b^{2} c^{2} - 4 c^{3} - 27 d^{2}\), where \(b = \frac{\alpha k-hkr}{hr}\), \(c = \beta ^{2}\) and \(d = -k \beta ^{2}\), then some simple calculation shows that \(\Delta = \frac{- 4 k ^{4} ( hr- \alpha )^{3} \beta ^{2} +h k^{2} r ( - 8 h^{2} r^{2} - 20 hr \alpha + \alpha ^{2} ) \beta ^{4} - 4 h^{3} r^{3} \beta ^{6}}{h^{3} r^{3}}\). Then \(\Delta <0\) if \(\alpha < hr\). Therefore, system (1) has a unique positive steady state if \(\alpha < hr\). Moreover, the variational matrix at interior equilibrium \((x^{*}, y ^{*})\) is computed as follows:

$$ J \bigl( x^{*}, y^{*} \bigr)= \begin{pmatrix} r- \frac{2 r x^{*}}{k} - \frac{2 x^{*} y^{*} \alpha \beta ^{2}}{ ( ( x^{*} )^{2} + \beta ^{2} )^{2}} & - \frac{( x^{*} )^{2} \alpha }{( x^{*} )^{2} + \beta ^{2}} \\ \frac{s}{h} & -s \end{pmatrix}. $$

According to the Routh–Hurwitz criterion \((x^{*}, y^{*})\) is a sink if and only if \(r-s- \frac{2 r x^{*}}{k} - \frac{2 x^{*} y^{*} \alpha \beta ^{2}}{ ( x^{* 2} + \beta ^{2} )^{2}} <0\). Furthermore, system (1) undergoes a Hopf bifurcation at \((x^{*}, y^{*})\) as s varies in a small neighborhood of \(s_{0}\) defined by

$$ s_{0} = r- \frac{2 r x^{*}}{k} - \frac{2 x^{*} y^{*} \alpha \beta ^{2}}{ ( x^{* 2} + \beta ^{2} )^{2}}. $$

Remark 2.1

There is no chance of flip bifurcation for system (1) about its positive equilibrium.

Proof

According to the necessary condition for the existence of the flip bifurcation, the determinant of the Jacobian matrix \(J ( x^{*}, y^{*} )\) must be zero, that is, \(\frac{2 r x^{*}}{k} + \frac{2 x^{*} y^{*} \alpha \beta ^{2}}{ ( x^{* 2} + \beta ^{2} ) ^{2}} + \frac{x^{* 2} \alpha }{h ( x^{* 2} + \beta ^{2} )} -r =0\). But zero growth isoclines for positive steady state satisfy \(r = \frac{r x^{*}}{k} + \frac{\alpha x^{*} y^{*}}{x^{* 2} + \beta ^{2}}\) and \(x^{*} = h y^{*}\). Putting in these values, we have \(\det J ( x^{*}, y^{*} )= \frac{r x^{*}}{k} + \frac{2 x^{*} y^{*} \alpha \beta ^{2}}{ ( x^{* 2} + \beta ^{2} )^{2}} >0\). □

3 Dynamics of system (3)

In this section, first of all we prove that system (3) is also permanent with similar parametric conditions to that for system (1).

Lemma 3.1

Assume that \(\alpha k^{2} < rh \beta ^{2}\), then system (3) is permanent.

Proof

Assume that \(x_{0} >0\) and \(y_{0} >0\), then every solution \(\{( x_{n}, y_{n} )\}\) of system (3) satisfies \(x_{n} >0\) and \(y_{n} >0\) for all \(n\geq 0\). Keeping in view the positivity of solutions of system (3), we have from this system \(x_{n+ 1} = \frac{(1 + \delta r ) x_{n}}{1 + \frac{\delta r}{k} x_{n} + \frac{\alpha \delta x_{n} y_{n}}{x_{n}^{2} + \beta ^{2}}} \leq \frac{(1 + \delta r ) x_{n}}{1 + \frac{\delta r}{k} x_{n}}\) and due to a comparison argument we have \(\lim_{n\rightarrow \infty } \sup x_{n} \leq k\) for all \(n\geq 0\). Similarly from the predator equation of system (3) we have \(y_{n+ 1} = \frac{(1 +s \delta ) y_{n}}{1 + \frac{s \delta y_{n}}{x _{n}}} \leq \frac{(1 +s \delta ) y_{n}}{1 + \frac{sh \delta y_{n}}{k}}\), and again by a simple comparison argument one has \(\lim_{n\rightarrow \infty } \sup y_{n} \leq \frac{k}{h}\) for all \(n\geq 0\). Now considering again the first equation of system (3) we obtain \(x_{n+ 1} = \frac{(1 + \delta r ) x_{n}}{1 + \frac{\delta r}{k} x_{n} + \frac{\alpha \delta x_{n} y_{n}}{x_{n}^{2} + \beta ^{2}}} \geq \frac{(1 + \delta r ) x_{n}}{1 + \frac{\delta r}{k} x_{n} + \frac{\alpha \delta k^{2}}{h \beta ^{2}}}\). Moreover, if we suppose that \(\alpha k^{2} < rh \beta ^{2}\), then again a comparison argument shows that \(\lim_{n\rightarrow \infty } \inf x _{n} \geq k ( 1 - \frac{\alpha k^{2}}{hr \beta ^{2}} ) = m _{1}\) for all \(n\geq 0\). On the other hand, the second equation of system (3) gives \(y_{n+ 1} = \frac{(1 +s \delta ) y_{n}}{1 + \frac{s \delta y_{n}}{x_{n}}} \geq \frac{(1 +s \delta ) y_{n}}{1 + \frac{sh \delta y_{n}}{m_{1}}}\) and it follows that \(\lim_{n\rightarrow \infty } \inf y_{n} \geq \frac{m_{1}}{h}\) for all \(n\geq 0\). Consequently, we obtain permanence for system (3). □

Next, we see the dynamics of model (3) at its steady states. First, the variational matrix of system (3) at boundary equilibrium \((k, 0)\) is computed as follows:

$$ V ( k,0)= \begin{pmatrix} 1 - \frac{r \delta }{1 +r \delta } & - \frac{k^{2} \alpha \delta }{ ( k^{2} + \beta ^{2} ) (1 +r \delta )} \\ 0 & 1 +s \delta \end{pmatrix}. $$

The eigenvalues of \(V ( k,0)\) are given by \(\lambda _{1} =1 - \frac{r \delta }{1 +r \delta }\) and \(\lambda _{2} =1 +s \delta \). Now, it is easy to observe that \(| \lambda _{2} | >1\) and \(| \lambda _{1} | <1\) for all \(r, \delta >0\). Therefore, \((k, 0)\) is a saddle point for system (3). Furthermore, the variational matrix \(V ( x^{*}, y^{*} )\) of system (3) at positive steady state is computed as follows:

$$ V \bigl( x^{*}, y^{*} \bigr)= \begin{pmatrix} \frac{1 + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2}}}{1 + \delta r} & - \frac{\alpha \delta x^{* 2}}{(1 +r \delta ) ( x^{* 2} + \beta ^{2} )} \\ \frac{s \delta }{h (1 +s \delta )} & \frac{1}{1 +s \delta } \end{pmatrix}. $$

Furthermore, the characteristic polynomial of \(V ( x^{*}, y^{*} )\) is computed as follows:

$$\begin{aligned} P ( \lambda ) =& \lambda ^{2} - \biggl( \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 +s \delta } \biggr) \lambda \\ &{} + \frac{s \alpha \delta ^{2} x^{* 2} ( x^{* 2} + \beta ^{2} ) +h ( ( x^{* 2} + \beta ^{2} )^{2} + 2 \alpha \delta x^{* 3} y^{*} )}{h ( x^{* 2} + \beta ^{2} ) ^{2} (1 +r \delta )(1 +s \delta )}. \end{aligned}$$
(7)

Moreover, due to some simple calculations, it follows from (7) that

$$ \begin{aligned} &P (1)= \frac{s \delta ^{2} ( \alpha x^{* 2} ( x^{* 2} + \beta ^{2} ) +h ( r ( x^{* 2} + \beta ^{2} ) ^{2} - 2 \alpha x^{* 3} y^{*} ) )}{h ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )(1 +s \delta )}, \\ &P ( - 1)= \frac{s \alpha \delta ^{2} x^{* 2} ( x^{* 2} + \beta ^{2} ) +h (2 +s \delta ) ( 2 ( x^{* 2} + \beta ^{2} )^{2} + \delta ( 2 \alpha x^{* 3} y^{*} +r ( x^{* 2} + \beta ^{2} )^{2} ) )}{h ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )(1 +s \delta )} \\ &\hphantom{P ( - 1)}>0 \end{aligned} $$
(8)

and

$$ P (0)= \frac{s \alpha \delta ^{2} x^{* 2} ( x^{* 2} + \beta ^{2} ) +h ( ( x^{* 2} + \beta ^{2} )^{2} + 2 \alpha \delta x^{* 3} y^{*} )}{h ( x^{* 2} + \beta ^{2} ) ^{2} (1 +r \delta )(1 +s \delta )}. $$

From (8) it follows that \(P (1)>0\) if and only if \(\alpha x^{* 2} ( x^{* 2} + \beta ^{2} ) +hr ( x^{* 2} + \beta ^{2} ) ^{2} - 2 \alpha h x^{* 3} y^{*} >0\). Keeping in view the relation \(x^{*} = h y^{*}\) and the existence condition \(hr > \alpha \) for a unique positive equilibrium point, we have

$$\begin{aligned} & \alpha x^{* 2} \bigl( x^{* 2} + \beta ^{2} \bigr) +hr \bigl( x ^{* 2} + \beta ^{2} \bigr)^{2} - 2 \alpha h x^{* 3} y^{*} \\ &\quad = \alpha x^{* 4} + \alpha \beta ^{2} x^{* 2} +hr x^{* 4} + 2 hr \beta ^{2} x^{* 2} +hr \beta ^{4} - 2 \alpha x^{* 4} \\ &\quad =( hr- \alpha ) x^{* 4} + \beta ^{2} ( \alpha + 2 hr ) x^{* 2} +hr \beta ^{4} >0. \end{aligned}$$

Lemma 3.2

Assume that \(\alpha < hr\), then the unique positive steady state \((x^{*}, y^{*})\) of system (3) is locally asymptotically stable if the following condition holds true:

$$ s \alpha \delta ^{2} x^{* 2} \bigl( x^{* 2} + \beta ^{2} \bigr) +h \bigl( \bigl( x^{* 2} + \beta ^{2} \bigr)^{2} + 2 \alpha \delta x ^{* 3} y^{*} \bigr) < h \bigl( x^{* 2} + \beta ^{2} \bigr)^{2} (1 +r \delta ) (1 +s \delta ). $$

Remark 3.1

Since \(P(-1)>0\), therefore there is no chance of period-doubling bifurcation for system (3) at its positive equilibrium.

4 Neimark–Sacker bifurcation

A Hopf (Neimark–Sacker) bifurcation is the production of a closed invariant curve from a steady state in dynamical systems with iterated maps, when the steady state (fixed point) changes stability via a pair of complex eigenvalues with unit modulus. Recently, many iterated maps have been studied for existence and direction of Neimark–Sacker bifurcation (cf. [37,38,39,40,41,42,43,44,45,46,47,48,49,50]).

In order to study the Neimark–Sacker bifurcation in system (3) at its positive steady state \((x^{*}, y^{*})\), we choose s as bifurcation parameter and system (3) is described by the following map:

$$ \begin{pmatrix} u \\ v \end{pmatrix} \rightarrow \begin{pmatrix} \frac{(1 + \delta r ) u}{1 + \frac{\delta r}{k} u+ \frac{\alpha \delta uv}{u^{2} + \beta ^{2}}} \\ \frac{(1 +s \delta ) v}{1 + \frac{sh \delta v}{u}} \end{pmatrix}. $$
(9)

We assume that

$$ s\equiv s_{1} = \frac{h ( 2 \alpha x^{* 3} y^{*} -r ( x ^{* 2} + \beta ^{2} )^{2} )}{ ( x^{* 2} + \beta ^{2} ) ( h ( x^{* 2} + \beta ^{2} ) (1 +r \delta ) - \alpha \delta x^{* 2} )} $$
(10)

and

$$ \biggl\vert \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x^{* 3} y ^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 + s_{1} \delta } \biggr\vert < 2. $$
(11)

Keeping in view (10) and (11), we define the following set:

$$ \mathbb{S}_{NB} = \bigl\{ ( r, k, \alpha , \beta , s _{1}, h ) \in \mathbb{R}_{+}^{6}: \mbox{(10) and (11) hold true} \bigr\} . $$

Suppose that \(( r, k, \alpha , \beta , s_{1}, h ) \in \mathbb{S}_{NB}\), then the map (9) can be written as follows:

$$ \begin{pmatrix} u \\ v \end{pmatrix} \rightarrow \begin{pmatrix} \frac{(1 + \delta r ) u}{1 + \frac{\delta r}{k} u+ \frac{\alpha \delta uv}{u^{2} + \beta ^{2}}} \\ \frac{ ( 1 + ( s_{1} + \tilde{s} ) \delta ) v}{1 + \frac{( s_{1} + \tilde{s} ) h \delta v}{u}} \end{pmatrix}, $$
(12)

where s̃ is small perturbation in s. Next, we take \(x = u- x^{*}\) and \(y = v- y^{*}\), where \((x^{*}, y^{*})\) is a unique positive fixed point of map (12), then one has the following map with fixed point at \((0, 0)\):

$$ \begin{pmatrix} x \\ y \end{pmatrix} \rightarrow \begin{pmatrix} \frac{(1 + \delta r )( x+ x^{*} )}{1 + \frac{\delta r}{k} ( x+ x^{*} ) + \frac{\alpha \delta ( x+ x^{*} )( y+ y^{*} )}{( x+ x^{*} )^{2} + \beta ^{2}}} \\ \frac{ ( 1 + ( s_{1} + \tilde{s} ) \delta ) ( y+ y^{*} )}{1 + \frac{( s_{1} + \tilde{s} ) h \delta ( y+ y^{*} )}{x+ x^{*}}} \end{pmatrix}. $$
(13)

An application of Taylor expansion about \((0, 0)\) shows that

$$ \begin{pmatrix} x \\ y \end{pmatrix} \rightarrow \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} f ( x, y ) \\ g ( x, y ) \end{pmatrix}, $$
(14)

where

$$\begin{aligned}& \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = \begin{pmatrix} \frac{1 + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2}}}{1 + \delta r} & - \frac{\alpha \delta x^{* 2}}{(1 +r \delta ) ( x^{* 2} + \beta ^{2} )} \\ \frac{( s_{1} + \tilde{s} ) \delta }{h (1 + ( s_{1} + \tilde{s} ) \delta )} & \frac{1}{1 + ( s_{1} + \tilde{s} ) \delta } \end{pmatrix}, \\& f ( x, y ) = a_{13} x^{2} + a_{14} xy+ a_{15} y^{2} + a_{16} x^{3} + a_{17} x^{2} y+ a_{18} x y^{2} + a_{19} y^{3} +O \bigl( \bigl( \vert x \vert + \vert y \vert \bigr)^{4} \bigr), \\& \begin{aligned} g ( x, y ) & = - \biggl( \frac{( s_{1} + \tilde{s} ) y^{*} \delta }{( x^{*} + ( s_{1} + \tilde{s} ) x^{*} \delta )^{2}} \biggr) x^{2} + \biggl( \frac{2( s_{1} + \tilde{s} ) \delta }{x^{*} (1 + ( s_{1} + \tilde{s} ) \delta )^{2}} \biggr) xy \\ &\quad {} - \biggl( \frac{h ( s_{1} + \tilde{s} ) \delta }{x^{*} (1 + ( s_{1} + \tilde{s} ) \delta )^{2}} \biggr) y^{2} + \biggl( \frac{( s_{1} + \tilde{s} ) y^{*} \delta }{( x^{*} + ( s_{1} + \tilde{s} ) x^{*} \delta )^{3}} \biggr) x^{3} \\ &\quad {} + \biggl( \frac{( s_{1} + \tilde{s} ) \delta ( - 2 + ( s_{1} + \tilde{s} ) \delta )}{x^{* 2} (1 + ( s_{1} + \tilde{s} ) \delta )^{3}} \biggr) x^{2} y+ \biggl( \frac{h ( s_{1} + \tilde{s} ) \delta (1 - 2( s_{1} + \tilde{s} ) \delta )}{x^{* 2} (1 + ( s_{1} + \tilde{s} ) \delta )^{3}} \biggr) x y^{2} \\ & \quad {}+ \biggl( \frac{h^{2} ( s_{1} + \tilde{s} )^{2} \delta ^{2}}{x^{* 2} (1 + ( s_{1} + \tilde{s} ) \delta )^{3}} \biggr) y^{3} +O \bigl( \bigl( \vert x \vert + \vert y \vert \bigr)^{4} \bigr), \end{aligned} \\& \begin{aligned} a_{13} & = \frac{k^{2} \delta (1 +r \delta ) ( -r x^{* 6} - 3 r x^{* 4} \beta ^{2} + 3 k x^{* 2} y^{*} \alpha \beta ^{2} - 3 r x^{* 2} \beta ^{4} -k y^{*} \alpha \beta ^{4} )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{3}} \\ &\quad {} + \frac{k^{2} \delta (1 +r \delta ) ( -r \beta ^{6} - 3 r x ^{* 5} y^{*} \alpha \delta +k x^{* 3} y^{* 2} \alpha ^{2} \delta +r x ^{* 3} y^{*} \alpha \beta ^{2} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{3}}, \end{aligned} \\& a_{14} = - \frac{2 k^{2} \alpha \delta (1 +r \delta ) ( -r x ^{* 4} ( x^{* 2} + \beta ^{2} ) \delta +k x^{*} ( x ^{* 2} \beta ^{2} + \beta ^{4} + x^{* 3} y^{*} \alpha \delta ) )}{ ( r x^{*} ( x^{* 2} + \beta ^{2} ) \delta +k ( x^{* 2} + \beta ^{2} + x^{*} y^{*} \alpha \delta ) )^{3}}, \\& a_{15} = \frac{x^{* 3} \alpha ^{2} \delta ^{2}}{ ( x^{* 2} + \beta ^{2} )^{2} ( 1 +r \delta )^{2}}, \\& \begin{aligned} a_{16} & = \frac{k^{2} \delta (1 +r \delta ) ( - 4 k^{2} x^{* 3} y^{*} \alpha \beta ^{2} + 4 k^{2} x^{*} y^{*} \alpha \beta ^{4} + r^{2} x^{* 8} \delta - k^{2} x^{* 4} y^{* 2} \alpha ^{2} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}} \\ &\quad {} + \frac{k^{2} \delta (1 +r \delta ) ( 4 r^{2} x^{* 6} \beta ^{2} \delta - 14 kr x^{* 4} y^{*} \alpha \beta ^{2} \delta + 6 r^{2} x ^{* 4} \beta ^{4} \delta + 4 kr x^{* 2} y^{*} \alpha \beta ^{4} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y ^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}} \\ &\quad {} + \frac{k^{2} \delta (1 +r \delta ) ( k^{2} y^{* 2} \alpha ^{2} \beta ^{4} \delta + 4 r^{2} x^{* 2} \beta ^{6} \delta + 2 kr y^{*} \alpha \beta ^{6} \delta + r^{2} \beta ^{8} \delta )}{ ( k x ^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}} \\ &\quad {} + \frac{k^{2} \delta (1 +r \delta ) ( 4 r^{2} x^{* 7} y^{*} \alpha \delta ^{2} - 4 kr x^{* 5} y^{* 2} \alpha ^{2} \delta ^{2} - 4 r ^{2} x^{* 5} y^{*} \alpha \beta ^{2} \delta ^{2} )}{ ( k x ^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}}, \end{aligned} \\& \begin{aligned} a_{17} & = \frac{k^{2} \delta (1 +r \delta ) ( 3 k x^{* 2} \alpha \beta ^{2} -k \alpha \beta ^{4} - 3 r x^{* 5} \alpha \delta + 2 k x^{* 3} y^{*} \alpha ^{2} \delta +r x^{* 3} \alpha \beta ^{2} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{3}} \\ &\quad {} + \frac{3 k^{3} x^{*} \alpha \delta ^{2} (1 +r \delta ) ( r x ^{* 6} + 3 r x^{* 4} \beta ^{2} - 3 k x^{* 2} y^{*} \alpha \beta ^{2} + 3 r x^{* 2} \beta ^{4} +k y^{*} \alpha \beta ^{4} )}{ ( k x ^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}} \\ &\quad {} + \frac{3 k^{3} x^{*} \alpha \delta ^{2} (1 +r \delta ) ( r \beta ^{6} + 3 r x^{* 5} y^{*} \alpha \delta -k x^{* 3} y^{* 2} \alpha ^{2} \delta -r x^{* 3} y^{*} \alpha \beta ^{2} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}}, \end{aligned} \\& a_{18} = \frac{k^{3} \alpha ^{2} \delta ^{2} (1 +r \delta ) ( -k x ^{* 6} + 2 k x^{* 4} \beta ^{2} + 3 k x^{* 2} \beta ^{4} - 4 r x^{* 7} \delta + 2 k x^{* 5} y^{*} \alpha \delta - 4 r x^{* 5} \beta ^{2} \delta )}{ ( k x^{* 2} +k \beta ^{2} +r x^{* 3} \delta +k x ^{*} y^{*} \alpha \delta +r x^{*} \beta ^{2} \delta )^{4}}, \end{aligned}$$

and

$$ a_{19} = - \frac{x^{* 4} \alpha ^{3} \delta ^{3}}{ ( x^{* 2} + \beta ^{2} )^{3} ( 1 +r \delta )^{3}}. $$

Moreover, the characteristic polynomial for ( a 11 a 12 a 21 a 22 ) is computed as follows:

$$\begin{aligned} P ( \rho ) =& \rho ^{2} - \biggl( \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 + ( s_{1} + \tilde{s} ) \delta } \biggr) \rho \\ &{} + \frac{( s_{1} + \tilde{s} ) \alpha \delta ^{2} x^{* 2} ( x ^{* 2} + \beta ^{2} ) +h ( ( x^{* 2} + \beta ^{2} ) ^{2} + 2 \alpha \delta x^{* 3} y^{*} )}{h ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )(1 + ( s_{1} + \tilde{s} ) \delta )}. \end{aligned}$$
(15)

Assume that \(\rho ( \tilde{s} )\) and \(\overline{\rho } ( \tilde{s} )\) are complex conjugate roots of (15), then we have

$$ \rho ( \tilde{s} )= \frac{p ( \tilde{s} ) +i \sqrt{4 q ( \tilde{s} ) - p^{2} ( \tilde{s} )}}{2}, $$

where

$$ p ( \tilde{s} ):= \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x ^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 + ( s_{1} + \tilde{s} ) \delta } $$

and

$$ q ( \tilde{s} ):= \frac{( s_{1} + \tilde{s} ) \alpha \delta ^{2} x^{* 2} ( x^{* 2} + \beta ^{2} ) +h ( ( x^{* 2} + \beta ^{2} )^{2} + 2 \alpha \delta x^{* 3} y^{*} )}{h ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )(1 + ( s_{1} + \tilde{s} ) \delta )}. $$

Furthermore, one has

$$ \bigl\vert \rho ( \tilde{s} ) \bigr\vert = \sqrt{\frac{( s_{1} + \tilde{s} ) \alpha \delta ^{2} x^{* 2} ( x^{* 2} + \beta ^{2} ) +h ( ( x^{* 2} + \beta ^{2} )^{2} + 2 \alpha \delta x ^{* 3} y^{*} )}{h ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )(1 + ( s_{1} + \tilde{s} ) \delta )}}. $$

Moreover, it follows that \(| \rho (0)| =1\), but \(\rho ^{i} (0) \neq 1\) for all \(i =1,2,3,4\) if and only if

$$ \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 + s_{1} \delta } \neq - 2, - 1,0,2. $$
(16)

Since \(( r, k, \alpha , \beta , s_{1}, h ) \in \mathbb{S} _{NB}\), we have \(0< \frac{1}{1 +r \delta } + \frac{2 \alpha \delta x ^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2} (1 +r \delta )} + \frac{1}{1 + s_{1} \delta } <2\). Thus condition (16) is automatically satisfied. Moreover, we assume that the following condition is satisfied:

$$ \biggl( \frac{d \vert \rho ( \tilde{s} ) \vert }{d \tilde{s}} \biggr)_{\tilde{s} =0} = - \frac{\delta ( x^{* 2} \alpha \delta -h ( x^{* 2} + \beta ^{2} ) (1 +r \delta ) )^{2}}{2 h (1 +r \delta ) ( h ( x^{* 2} + \beta ^{2} )^{2} - x^{* 2} \alpha ( x^{* 2} - 2 h x^{*} y^{*} + \beta ^{2} ) \delta )} \neq 0. $$
(17)

The following similarity transformation is considered in order to convert the linear part of (14) into its canonical form at \(\tilde{s} =0\):

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} a_{12} & 0 \\ \vartheta - a_{11} & - \varphi \end{pmatrix} \begin{pmatrix} w \\ z \end{pmatrix}, $$
(18)

where

$$ \vartheta := \frac{p (0)}{2},\qquad \varphi := \frac{\sqrt{4 q (0) - p ^{2} (0)}}{2}, $$

and

$$ a_{12} = - \frac{\alpha \delta x^{* 2}}{(1 +r \delta ) ( x^{* 2} + \beta ^{2} )},\qquad a_{11} = \frac{1 + \frac{2 \alpha \delta x^{* 3} y^{*}}{ ( x^{* 2} + \beta ^{2} )^{2}}}{1 + \delta r}. $$

Then from transformation (18) it follows that

$$ \begin{pmatrix} w \\ z \end{pmatrix} = \begin{pmatrix} \frac{1}{a_{12}} & 0 \\ \frac{\vartheta - a_{11}}{\varphi a_{12}} & - \frac{1}{\varphi } \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}. $$
(19)

Assuming \(\tilde{s} =0\), then from (18) and (19) we obtain the following normal form for the map (14):

$$ \begin{pmatrix} w \\ z \end{pmatrix} \rightarrow \begin{pmatrix} \vartheta & - \varphi \\ \varphi & \vartheta \end{pmatrix} \begin{pmatrix} w \\ z \end{pmatrix} + \begin{pmatrix} F ( w, z ) \\ G ( w, z ) \end{pmatrix}, $$
(20)

where

$$ F ( w, z ):= \frac{1}{a_{12}} f \bigl( a_{12} w,( \vartheta - a_{11} ) w- \varphi z \bigr) $$

and

$$ G ( w, z ):= \biggl( \frac{\vartheta - a_{11}}{\varphi a_{12}} \biggr) f \bigl( a_{12} w,( \vartheta - a_{11} ) w- \varphi z \bigr) - \frac{1}{\varphi } g \bigl( a_{12} w,( \vartheta - a_{11} ) w- \varphi z \bigr). $$

Taking into account the bifurcation theory of normal forms (cf. [51,52,53,54,55]) the first Lyapunov exponent at \(( w, z )=(0,0)\) is computed as follows:

$$ L = -\operatorname{Re} \biggl( \frac{(1 - 2 \rho (0)) \overline{\rho } (0 )^{2}}{1 - \rho (0)} \tau _{20} \tau _{11} \biggr) - \frac{1}{2} \vert \tau _{11} \vert ^{2} - \vert \tau _{02} \vert ^{2} +\operatorname{Re} \bigl( \overline{ \rho } (0) \tau _{21} \bigr), $$

where

$$\begin{aligned}& \tau _{20} = \frac{1}{8} \bigl[ F_{ww} - F_{zz} + 2 G_{wz} +i ( G_{ww} - G _{zz} - 2 F_{wz} )\bigr], \\& \tau _{11} = \frac{1}{4} \bigl[ F_{ww} + F_{zz} +i ( G_{ww} + G_{zz} ) \bigr], \\& \tau _{02} = \frac{1}{8} \bigl[ F_{ww} - F_{zz} - 2 G_{wz} +i ( G_{ww} - G _{zz} + 2 F_{wz} )\bigr], \end{aligned}$$

and

$$ \tau _{21} = \frac{1}{16} \bigl[ F_{www} + F_{wzz} + G_{wwz} + G_{zzz} +i ( G_{www} + G_{wzz} - F_{wwz} - F_{zzz} )\bigr]. $$

Due to the aforementioned computations, we have the following theorem.

Theorem 4.1

Suppose that (10), (11) and (17) hold true and \(L\neq 0\), then the positive steady state \((x^{*}, y^{*})\) of model (3) undergoes a Neimark–Sacker bifurcation when the bifurcation parameter s varies in a small neighborhood of \(s_{1}\) defined in (10). Furthermore, if \(L<0\), then an attracting invariant closed curve bifurcates from the equilibrium point for \(s> s_{1}\), and if \(L>0\), then a repelling invariant closed curve bifurcates from the equilibrium point for \(s< s_{1}\).

5 Numerical simulation and discussion

In order to dynamical consistency between (1) and (3), we take \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\) and \(h =0.5\) for both systems (1) and (3), then both systems (1) and (3) have unique positive steady state \(( x^{*}, y^{*} )=(0.519983,1.03997)\). Next, we take \(s =0.18\) for system (1), then the equilibrium point \(( x^{*}, y^{*} )=(0.519983,1.03997)\) is locally asymptotically stable and plots are depicted in Fig. 1. Furthermore, at \(s_{0} =0.1659505778939415\) system (1) undergoes Hopf bifurcation at its positive steady state \(( x^{*}, y^{*} )=(0.519983,1.03997)\) and plots are depicted in Fig. 2.

Figure 1
figure 1

Plots for system (1) with \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(s =0.18\) and \(( x_{0}, y_{0} )=(0.52,1.04)\)

Full size image
Figure 2
figure 2

Plots for system (1) with \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(s =0.1659505778939415\) and \(( x_{0}, y_{0} )=(0.52,1.04)\)

Full size image

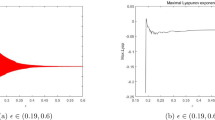
Furthermore, we take the step size \(\delta =0.1\) and \(s =0.18\) for system (3), then the equilibrium point \(( x^{*}, y^{*} )=(0.519983,1.03997)\) is locally asymptotically stable and plots are depicted in Fig. 3. In order to discuss the bifurcating behavior of the discrete-time model (3), we select \(\delta =0.1\) and \(s\in [0.05,0.25]\). Then model (3) undergoes a Neimark–Sacker bifurcation at \(s_{1} =0.15932296370369736\). Moreover, at \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(\delta =0.1\) and \(s =0.15932296370369736\) the variational matrix for model (3) is given as follows:

$$ V (0.519983,1.03997)= \begin{pmatrix} 1.01482 & - 0.0350006 \\ 0.0313649 & 0.984318 \end{pmatrix}. $$

With some simple computation one can obtain the eigenvalues for \(V (0.519983,1.03997)\), \(\lambda _{1} =0.999567 - 0.0294149 i\) and \(\lambda _{2} =0.999567 + 0.0294149 i\) such that \(| \lambda _{1,2} | =1\). Moreover, bifurcation diagrams for model (3) are given in Fig. 4. On the other hand, some phase portraits for model (3) are depicted in Fig. 5. Since we have chosen exactly similar parametric values for both continuous and discrete models except the step size \(\delta =0.1\) for the discrete model. In this case, the absolute difference between \(s_{0}\) and \(s_{1}\) is 0.00662761. The variation between \(| s _{0} - s_{1} | \) and δ is given in Table 1. From Table 1 it is obvious that for smaller step size δ the critical values of bifurcation parameter s for the emergence of a Hopf bifurcation and a Neimark–Sacker bifurcation are nearly identical, that is, \(| s_{0} - s_{1} | \rightarrow 0\) as \(\delta \rightarrow 0\). Furthermore, since system (1) is independent of δ, \(s_{0}\) is taken as \(s_{0} =0.1659505778939415\) in Table 1. Arguing as in [6], if we implement Euler forward approximation to system (1) with the aforementioned parametric values and step size \(\delta =0.1\), then this discrete-time model undergoes a Neimark–Sacker bifurcation at \(s_{1} =0.17688307136658987\) and thus we have \(| s_{0} - s_{1} | =0.0109325\).

Figure 3
figure 3

Plots for system (3) with \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(s =0.18\), \(\delta =0.1\) and \(( x_{0}, y_{0} )=(0.52,1.04)\)

Full size image
Figure 4
figure 4

Bifurcation diagrams for system (3) with \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(\delta =0.1\), \(s\in [0.05,0.25]\) and \(( x_{0}, y_{0} )=(0.52,1.04)\)

Full size image
Figure 5
figure 5

Phase portraits of system (3) for \(r =1.2\), \(k =1.5\), \(\alpha =0.45\), \(\beta =0.2\), \(h =0.5\), \(\delta =0.1 ( x_{0}, y_{0} )=(0.52,1.04)\) and with different values of s

Full size image
Table 1 Variation of \(s_{1}\) and \(| s_{1} - s_{0} | \) with different values of δ
Full size table

6 Concluding remarks

A dynamically consistent nonstandard finite difference scheme is proposed for a class of predator–prey models with implementation of Holling type-III functional response. Our investigations reveal that the discrete-time model has totally identical dynamical behavior to its continuous counterpart. Particularly, positivity, boundedness and persistence of solutions are preserved for the discrete model. The topological classification for both steady states are preserved. Furthermore, our proposed nonstandard finite difference scheme is also bifurcation preserving, that is, the continuous system undergoes a Hopf bifurcation and there is no chance of flip bifurcation, on the other hand, the discrete-time model undergoes a Neimark–Sacker bifurcation at its positive fixed point and there is no chance of a period-doubling bifurcation for this system. A discrete counterpart of the continuouspredator–prey model is discussed in [6] with implementation of an Euler forward approximation. According to these investigations the discrete-time model undergoes a period-doubling bifurcation at its positive fixed point and therefore the Euler method does not seem to be bifurcation preserving.