Abstract
In this paper, a prey-predator model with Allee effect and Holling type-I functional response is established, and its dynamical behaviors are studied in detail. The existence, boundedness and stability of the model are qualitatively discussed. Hopf bifurcation analysis is also taken into account. We further illustrate our theoretical analysis by means of numerical simulation. Using computer simulation, we found the position of each equilibrium point in the phase diagram that we drew. We found the threshold for undergoing a Hopf bifurcation in the bifurcation diagram. One of the interesting questions is which model with strong Allee effect is a bistable system.
Similar content being viewed by others
1 Introduction
Today, in order to comprehend the long-term behavior of a population, many researchers conduct extensive research on the dynamics of interacting prey-predator models. Various nonlinear ODE models are studied, and the interaction between predator and prey is analyzed [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The classic predator-prey model is the Lotka–Volterra model, which was independently proposed by Lotka in the United States in 1925 and Volterra in Italy in 1926. However, there are some specific classes among them, called the Gause type models [1, 2]. The research of predator-prey model and infectious disease model has always been a hot topic in biomathematics [1,2,3,4,5,6,7,8,9, 11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. In 1931, Allee discovered that the living state of the cluster is conducive to the growth of the population, but the density is too high and will inhibit the growth of the population and even become extinct due to resource competition. For each population, there must be an independent optimal density for growth and reproduction, the mechanism is called the Allee effect. There are also lots of people doing research on the predator-prey model with Allee effect in prey growth [3, 8, 9, 12, 14, 22, 24].
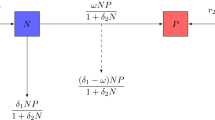
We consider the predator-prey model with Allee effect and Holling type-I functional response in predator growth [3] as follows:
where \(g(N) = r(1 - \frac{N}{K})(N - L)\) and \(p(N) = aN\), and the initial condition is \(N(0),P(0) > 0\). N is the prey population and P is the predator population, \(q(P)\) is the average loss rate of predators, c is the conversion efficiency from prey to predator, K is the carrying capacity, \(g(N)\) is the per capita prey growth rate, r is the intrinsic growth rate of prey, L is the Allee effect threshold, \(p(N)\) is the prey dependent functional response, and a is the prey capture rate by their predators. So we get
where a and m are all positive parameters. m is the intrinsic death rate of the predators.
2 Strong Allee effect
In order to reduce the number of parameters in the latter calculation, we can make model (2) dimensionless as follows:
where \(x = \frac{N}{K}\), \(y = P\), \(t = KrT\), \(\alpha = \frac{a}{Kr}\), \(\beta = \frac{L}{K}\), \(\gamma = \frac{ca}{r}\) and \(\delta = \frac{m}{Kr}\). It is easy to see \(0 \le x \le 1\). The threshold of the Allee type is β and satisfies the conditions \(0 < \beta < 1\) for a strong Allee effect [3].
3 Equilibria and existence
In order to find the equilibrium point of model (3), we consider the prey and predator nullcline of this model (3), to get
we easily see that model (3) exhibits four equilibrium points \(E_{s0} = (0,0)\), \(E_{s1} = (\beta ,0)\), \(E_{s2} = (1,0)\), \(E_{s^{*}} = (x_{*},y _{*})\). Here \(x_{*} = \frac{\delta }{\gamma } \), \(y_{*} = \frac{(1 - \frac{ \delta }{\gamma } )(\frac{\delta }{\gamma } - \beta )}{\alpha } \). For a positive equilibrium point, we have \(\beta < \frac{\delta }{\gamma } < 1\).
4 Boundedness of the model
Theorem 1
All the solutions of model which start in \(R_{ +}^{2}\) are uniformly bounded.
Proof
A function is defined by us that is \(\chi = x + \frac{\alpha }{ \gamma - \delta + \eta } y\). Therefore, the time derivative of the above equation along the solution of model (3) is
Now for each \(\eta > 0\) and \(0 \le x \le 1\), we have
Hence we can find \(\omega > 0\) such that
In summary, we have \(\frac{d\chi }{dt} \le - \eta \chi + \omega \), which implies that
Moreover, we have \(\lim \sup \chi (t) \le \frac{\omega }{\eta } < M\) as \(t \to \infty \), which is not related to the initial conditions. □
5 Local stability analysis
In this section, we will analyze the local stability of model (3).
Theorem 2
-
(1)
\(E_{s0}\) is locally asymptotically stable.
-
(2)
If \(\gamma < \frac{\delta }{\beta } \), then \(E_{s1}\) is the saddle point, otherwise it is the unstable node.
-
(3)
When \(\gamma < \delta \), \(E_{s2}\) is locally asymptotically stable and is a saddle point otherwise.
-
(4)
The positive equilibrium \(E_{s^{*}}\) is locally stable when \(\beta < \frac{2\delta - \gamma }{\gamma } \) and is unstable node otherwise.
Proof
It can be concluded by calculating the Jacobian matrix of model (3) at \(E_{s0}\)
Also we can find that \(E_{s0}\) is locally asymptotically stable.
By evaluating the Jacobian matrix of model (3) at \(E_{s1}\), we find
We find that the first eigenvalue \(\lambda _{1} = \beta - \beta ^{2}\) is positive, then \(E_{s1}\) is unstable as a saddle point if \((\beta - \beta ^{2})(\gamma \beta - \delta ) > 0\), that is, if \(\gamma > \frac{ \delta }{\beta } \), and is a stable saddle point otherwise.
We calculate the Jacobian matrix of model (3) at \(E_{s2}\); we have
We find that the first eigenvalue \(\lambda _{1} = \beta - 1\) is negative because of \(\beta < 1\), then \(E_{s2}\) is stable if \(\gamma < \delta \), and \(E_{s2}\) is a saddle point when \(\gamma > \delta \).
We calculate the Jacobian matrix of model (3) at \(E_{s^{*}}\) is given by
We can easily know that the characteristic polynomial is
Here \(T = (2 + 2\beta )x_{*} - 3x_{*}^{2} - \beta - \alpha y_{*}\) and \(D = (1 - \frac{\delta }{\gamma } )(\frac{\delta }{\gamma } - \beta ) \delta \).
Thus, we have the following conclusions.
-
(a)
If \(T < 0\) and \(\beta < \frac{2\delta - \gamma }{\gamma } \), then the positive equilibrium is locally asymptotically stable.
-
(b)
If \(T > 0\) and \(\beta > \frac{2\delta - \gamma }{\gamma } \), then the positive equilibrium is unstable.
□
6 Bifurcation analysis
6.1 Hopf bifurcation
From Theorem 2, model (3) undergoes a bifurcation if \(\beta = \frac{2 \delta - \gamma }{\gamma } \). The purpose of this section is to prove that model (3) will produce a Hopf bifurcation if \(\beta = \frac{2 \delta - \gamma }{\gamma } \).
First we choose β as the bifurcation parameter, and then analyze the conditions under which a Hopf bifurcation occurs at \(E_{s^{*}} = (x _{*},y_{*})\). Denote
when \(\beta = \beta _{0}\), we have \(T = (2 + 2\beta )x_{*} - 3x_{*} ^{2} - \beta - \alpha y_{*} = 0\). Thus, the Jacobian matrix \(J_{s^{*}}\) has a pair of imaginary eigenvalues \(\lambda = \pm i\sqrt{(1 - \frac{\delta }{\gamma } )(\frac{\delta }{\gamma } - \beta _{0}) \delta } \). Let \(\lambda = A(\beta ) \pm B(\beta )i\) be the roots of \(\lambda ^{2} - T\lambda + D = 0\), then
and
By the Poincare–Andronov Hopf bifurcation theorem, we know that model (3) undergoes a Hopf bifurcation at \(E_{s^{*}} = (x _{*},y_{*})\) when \(\beta = \beta _{0}\). However, the directionality of the Hopf bifurcation also require us to further analyze the normal form of the model.
Set \(x = X + x_{*}\) and \(y = Y + y_{*}\), to \((x_{*},y_{*})\) as origin of co-ordinates \((X,Y)\). We have the following model:
where
and
where \(P_{1}(X,Y)\), \(P_{2}(X,Y)\) are smooth functions of X and Y at least of order four.
Now, using the transformation \(u = X\), \(v = - \frac{1}{B}(a_{11}X + a_{12}Y)\), we obtain
where
so
set
where
So
If \(\sigma < 0\), the equilibrium \(E_{s^{*}}\) is destabilized through a Hopf bifurcation that is supercritical and a Hopf bifurcation that is subcritical otherwise [10].
7 Weak Allee effect
Next, we start to study a model with weak Allee effect and Holling type-I functional response in predator growth. For simplicity, we rewrite the dimensionless model in [3] in the following form:
8 Equilibria and existence
In order to find the equilibrium points of model (4), which follow from
we easily see that model (4) exhibits three equilibrium points, \(E_{w0} = (0,0)\), \(E_{w2} = (1,0)\), \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\). Here, \(\bar{x}_{*} = \frac{\delta }{\gamma } \), \(\bar{y}_{*} = \frac{(1 - \frac{ \delta }{\gamma } )(\frac{\delta }{\gamma } + \beta )}{\alpha } \). For a positive equilibrium point, we have \(\frac{\delta }{\gamma } < 1\).
9 Stability analysis
In this section, we will analyze the stability of model (4).
9.1 Local stability
Theorem 3
-
(1)
\(E_{w0}\) is a saddle point.
-
(2)
\(E_{w2}\) is stable for \(\gamma < \delta \), \(E_{w2}\) is a saddle point for \(\gamma > \delta \).
-
(3)
Positive equilibrium \(E_{w^{*}}\) is locally asymptotically stable when \(\beta > 1 - 2\bar{x}_{*}\), \(E_{w^{*}}\) is an unstable node when \(\beta < 1 - 2\bar{x}_{*}\).
Proof
It can be concluded by calculating the Jacobian matrix of model (4) at \(E_{w0}\) that
Hence \(E_{w0}\) is always a saddle point.
It can be concluded by calculating the Jacobian matrix of model (4) at \(E_{w2}\) that
We can find that the first eigenvalue \(\lambda _{1} = - \beta - 1\) is negative, hence \(E_{w2}\) is stable if \(\gamma < \delta \), and \(E_{w2}\) is a saddle point when \(\gamma > \delta \).
We calculate the Jacobian matrix of model (4) at \(E_{w^{*}}\) that is given by
The characteristic polynomial is
where \(\bar{T} = (2 - 2\beta )\bar{x}_{*} - 3\bar{x}_{*}^{2} + \beta - \alpha \bar{y}_{*}\) and \(\bar{D} = (1 - \frac{\delta }{\gamma } )(\frac{ \delta }{\gamma } + \beta )\delta \).
Thus, we have the following conclusions.
-
(a)
If \(\bar{T} < 0\) and \(\beta > 1 - 2\bar{x}_{*}\), we can find that \(E_{w^{*}}\) is locally asymptotically stable.
-
(b)
If \(\bar{T} > 0\) and \(\beta < 1 - 2\bar{x}_{*}\), we can find that \(E_{w^{*}}\) is unstable.
□
9.2 Global stability
Here we first prove that \(E_{w2} = (1,0)\) is globally stable when \(( \frac{\alpha + \gamma }{\alpha } )^{2} - \frac{4 \delta }{\alpha } < 0\).
Consider the Lyapunov function:
The derivative of V along the solution of model (4) is
If \(x^{2} - ( \frac{\alpha + \gamma }{\alpha } )x + \frac{ \delta }{\alpha } > 0\), then \(\dot{V} < 0\). So, \(\Delta = ( \frac{ \alpha + \gamma }{\alpha } )^{2} - \frac{4\delta }{\alpha } < 0\).
Next, we prove that \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) is globally stable for model (4). Here, we will prove the global stability of \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) based on the fact that \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) is locally asymptotically stable by using Th. 2 in [11]. In order to use this theorem better, we can rewrite model (4) as follows:
Here \(g(x) = (1 - x)(x + \beta )\) and \(p(x) = x\). Here \(g(x)\) and \(p(x)\) satisfy the following three conditions:
-
1.
\(g \in C([0,\infty ),\mathbb{R}) \cap C^{1}((0,\infty ),\mathbb{R})\), \(g(0) = (1 - 0)(0 + \beta ) > 0\), \(g(1) = 0\) and \((x - 1)g(x) < 0\) for \(x \in [0,1) \cup (1,\infty )\).
-
2.
\(p \in C([0,\infty ),\mathbb{R}) \cap C^{1}((0,\infty ),\mathbb{R})\), \(p(0) = 0\) and \(p'(x) = 1 > 0\) for all \(x \ge 0\).
-
3.
The positive equilibrium point \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) is calculated by \(\gamma p(\bar{x}_{*}) - \delta = 0\) and \(\bar{x}_{*}g( \bar{x}_{*}) - \alpha \bar{y}_{*}p(\bar{x}_{*}) = 0\), \(0 < \bar{x} _{*} < 1\), \(\bar{y}_{*} > 0\) and further \(\frac{d}{dx} ( \frac{xg(x)}{p(x)} ) = - (1 - x)(x + \beta ) < 0\), for all \(\bar{x}_{*} < x < 1\).
Here we explain the conditions. In fact, we can proceed from calculating from the local stability of \(E_{w^{*}}\). So we can find the prey nullcline \(y = \frac{(1 - x)(x + \beta )}{\alpha } \equiv r(x)\) is continuous curve, we say \(x = x_{1}\) is a local maximum point at the points \((0,\frac{ \beta }{\alpha } )\) and \((1,0)\) such that \(0 < x_{1} < 1\). Note that \(r(x) = \frac{xg(x)}{p(x)}\). We can find that the condition for satisfying local asymptotic stability of \(E_{*}\) is that \(x = \bar{x} _{*}\) on the right side of \(x = x_{1}\) and should intersect the prey nullcline, hence \(0 < \bar{x}_{*} < x < 1\) holds. Hypothesis \(x_{1}\) is the local maximum of \(y = r(x)\), we know that \(E_{w^{*}}\) is locally asymptotically stable, so that \(\frac{d}{dx}r(x) < 0\) for \(0 < x_{*} \le x \le 1\). Obviously, the above inequalities are still satisfied that \(r(x) = \frac{xg(x)}{p(x)}\).
Next, we apply Th. 2 in [11] to prove that \(E_{w^{*}}\) is globally stable under the assumption of local asymptotic stability.
Theorem 4
The following condition holds: \(\frac{d}{dx} ( \frac{f(x) - f(\bar{x}_{*})}{p(x) - p(\bar{x}_{*})} ) < 0\) for \(0 \le x \le 1\) and \(E_{w^{*}}\) is locally asymptotically stable. \(E_{w^{*}}\) is globally asymptotically stable where \(f(x) = \frac{d}{dx}(xg(x)) - \frac{p'(x)xg(x)}{p(x)}\).
Proof
For model (4), we can see that the definition of \(f(x)\) is
Hence we can calculate
We find \(- 2x{}^{2} + 4x\bar{x}_{*} - 2\bar{x}_{*}^{2} < 0\) for any \(x > 0\). □
10 Hopf bifurcation
Theorem 5
By selecting β as the bifurcation parameter, model (4) undergoes a Hopf bifurcation that occurs at \(E_{w^{*}} = ( \bar{x}_{*},\bar{y}_{*})\) if \(\beta = 1 - 2\bar{x}_{*}\).
Proof
If \(\bar{T} = (2 - 2\beta )\bar{x}_{*} - 3\bar{x}_{*} ^{2} + \beta - \alpha \bar{y}_{*} = 0\) and \(\det J_{w^{*}} > 0\), then use the implicit function theorem we have learned; when the stability of the equilibrium point \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) changes, Hopf bifurcation occurs, thereby generating a periodic orbit. Using these two conditions, the critical value of the Hopf bifurcation parameter is found to be \(\beta = 1 - 2\bar{x}_{*}\). Obviously given the condition by [4],
-
(i)
\(\bar{T} = (2 - 2\beta )\bar{x}_{*} - 3\bar{x}_{*}^{2} + \beta - \alpha \bar{y}_{*} = 0\),
-
(ii)
\(\det J_{*} > 0\), and
-
(iii)
\(\frac{d\bar{T}}{d\beta } \vert _{\beta = \beta _{0}} = - \frac{\delta }{\gamma } \ne 0\) at \(\beta = \beta _{0}\) model (4) undergoes a Hopf bifurcation around \(E_{w^{*}} = (\bar{x}_{*}, \bar{y}_{*})\).
□
11 Simulations tests
In this section, we numerically simulate the above theoretical derivation by MATLAB.
11.1 Strong Allee effect
The ODE model (3) has four parameters: α, β, γ, δ. We choose the parameters
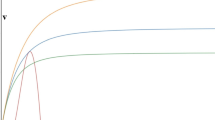
According to Fig. 1, we can find \(E_{s0} = (0,0)\) that it is asymptotically stable. If \(\gamma < \delta \) then \(\gamma = 0.36 < \delta = 0.4\), \(E_{s2} = (1,0)\) is asymptotically stable as shown in Fig. 2. If \(\beta < \frac{2\delta - \gamma }{\gamma } \) then \(0.2 < \frac{2*0.2 - 0.29}{0.29} \approx 0.379\), \(E_{s^{*}} = (x_{*},y_{*}) = (0.689,0.303)\) is asymptotically stable as shown in Fig. 3 we also find the saddle point \(E_{s1} = (0.2,0)\) like Fig. 1. Moreover, we find that there may be two stable equilibrium points; this is what we call a bistable system as shown in Fig. 4.
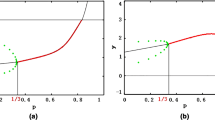
According to Fig. 5, we find that bifurcation occurs at approximately \(r = 0.3\), that is, a Hopf bifurcation. As we have demonstrated in the article, when \(\beta = 0.3\), model (3) undergoes a Hopf bifurcation.
11.2 Weak Allee effect
The ODE model (4) has four parameters: α, β, γ, δ. We choose the parameters
According to Fig. 6, we can find \(E_{w0} = (0,0)\) to be a saddle point. If \(\gamma < \delta \) then \(\gamma = 0.36 < \delta = 0.4\), \(E_{w2} = (1,0)\) is asymptotically stable as shown in Fig. 7. If \(\beta > 1 - 2x _{*}\) then \(0.2 > 1 - 2*0.556 = - 0.112\), \(E_{w^{*}} = (\bar{x}_{*}, \bar{y}_{*}) = (0.556,0.671)\) is asymptotically stable as shown in Fig. 8.
According to Fig. 9, we find that bifurcation occurs at approximately \(r = - 0.112\), that is, Hopf bifurcation. As we have demonstrated in the article, when \(\beta = - 0.112\), model (4) undergoes Hopf bifurcation.
12 Conclusions
In this paper, a prey-predator model with Allee effect in prey growth, a Holling type-I functional response in predator growth is given. The prey-predator model with strong Allee effect is analyzed, and the four equilibrium points and the conditions for each equilibrium point are obtained. We analyze the Hopf bifurcation occurring at \(E_{s^{*}} = (x _{*},y_{*})\) by choosing β as the bifurcation parameter, obtain the conditions for generating a Hopf bifurcation and further calculation of the Hopf bifurcation. If \(\sigma < 0\), the equilibrium \(E_{s^{*}}\) is destabilized through a Hopf bifurcation that is supercritical and the Hopf bifurcation is subcritical otherwise. The prey-predator model with weak Allee effect is also analyzed and we obtain stability conditions for three equilibrium points, the global stability of \(E_{w2} = (1,0)\) and \(E_{w^{*}} = (\bar{x}_{*},\bar{y}_{*})\) is proved. We also analyze the Hopf bifurcation occurring at \(E_{w^{*}} = (\bar{x}_{*}, \bar{y}_{*})\) by choosing β as the bifurcation parameter, the conditions for generating a Hopf bifurcation are obtained. Finally, using computer simulations we draw the position of each equilibrium point in the phase diagram, and we draw the bifurcation diagram under the strong and weak Allee effect. It is worth noting that there are some differences between the special case of bistability and the Allee effect as regards strength and weakness. If the positive equilibrium point of the model is stable, model (3) with strong Allee effect must be a bistable system. However, in the case of the weak Allee effect, the model is not necessarily a bistable system because the axial equilibrium point is unstable under certain conditions.
References
Caughley, G., Lawton, J.H.: Plant-herbivore systems. In: May, R.M. (ed.) Theoretical Ecology, pp. 132–166. Sinauer, Sunderland (1981)
Freedman, H.I.: Deterministic Mathematical Models in Population Ecology. Dekker, New York (1980)
Banerjee, M., Takeuchi, Y.: Maturation delay for the predators can enhance stable coexistence for a class of prey-predator models. J. Theor. Biol. 412, 154–171 (2017)
Gupta, R.P., Chandra, P.: Bifurcation analysis of modified Leslie–Gower predator-prey model with Michaelis–Menten type prey harvesting. J. Math. Anal. Appl. 398, 278–295 (2013)
Haque, M.: Ratio-dependent predator-prey models of interacting populations. Bull. Math. Biol. 71(2), 430–452 (2009)
Hu, D., Cao, H.: Stability and bifurcation analysis in a predator-prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal., Real World Appl. 33, 58–82 (2017)
Kar, T.K.: Modelling and analysis of a harvested prey-predator system incorporating a prey refuge. J. Comput. Appl. Math. 185(1), 19–33 (2006)
Allee, W.C.: Animal Aggregations: A Study in General Sociology. University of Chicago Press, Chicago (1931)
Manna, D., Maiti, A., Samanta, G.P.: A Michaelis–Menten type food chain model with strong Allee effect on the prey. Appl. Math. Comput. 311, 390–409 (2017)
Perko, L.: Diffrential Equations and Dynamical Systems, 3rd edn. Texts in Applied Mathematics, vol. 7. Springer, New York (2001)
Cheng, K.S., Hsu, S.B., Lin, S.S.: Some results on global stability of a predator-prey system. J. Math. Biol. 12, 115–126 (1981)
Cai, Y., Zhao, C., Wang, W., Wang, J.: Dynamics of a Leslie–Gower predator-prey model with additive Allee effect. Appl. Math. Model. 39, 2092–2106 (2015)
Ghosh, J., Sahoo, B., Poria, S.: Prey-predator dynamics with prey refuge providing additional food to predator. Chaos Solitons Fractals 96, 110–119 (2017)
Sen, M., Banerjee, M.: Rich global dynamics in a prey-predator model with Allee effect and density dependent death rate of predator. Int. J. Bifurc. Chaos 25(03), 1530007 (2015)
Li, Y.: Hopf bifurcations in general systems of Brusselator type. Nonlinear Anal., Real World Appl. 28, 32–47 (2016)
Yang, R., Zhang, C.: The effect of prey refuge and time delay on a diffusive predator-prey system with hyperbolic mortality. Complexity 21(S1), 446–459 (2016)
Ma, Z., Liu, J., Li, J.: Stability analysis for differential infectivity epidemic models. Nonlinear Anal., Real World Appl. 4(5), 841–856 (2003)
Li, X., Jiang, W., Shi, J.: Hopf bifurcation and Turing instability in the reaction-diffusion Holling–Tanner predator-prey model. IMA J. Appl. Math. 78(2), 287–306 (2013)
Wei, J.: Bifurcation analysis in a kind of fourth-order delay differential equation. Discrete Dyn. Nat. Soc. 2009(2), 332–337 (2014)
Sambath, M., Balachandran, K., Suvinthra, M.: Stability and Hopf bifurcation of a diffusive predator-prey model with hyperbolic mortality. Complexity 21(S1), 34–43 (2016)
Ma, Z., Wang, S., Wang, T., et al.: Stability analysis of prey-predator system with Holling type functional response and prey refuge. Adv. Differ. Equ. 2017(1), 243 (2017)
Wang, J., Shi, J., Wei, J.: Predator-prey system with strong Allee effect in prey. J. Math. Biol. 62(3), 291–331 (2011)
Rao, F., Castillo-Chavez, C., Kang, Y.: Dynamics of a diffusion reaction prey-predator model with delay in prey: effects of delay and spatial components. J. Math. Anal. Appl. 461(2), 1177–1214 (2018)
Feng, P., Kang, Y.: Dynamics of a modified Leslie–Gower model with double Allee effects. Nonlinear Dyn. 80(1–2), 1051–1062 (2015)
Cai, Y., Gui, Z., Zhang, X., et al.: Bifurcations and pattern formation in a predator-prey model. Int. J. Bifurc. Chaos 28(11), 1850140 (2018)
Zhang, H., Cai, Y., Fu, S., et al.: Impact of the fear effect in a prey-predator model incorporating a prey refuge. Appl. Math. Comput. 356, 328–337 (2019)
Yang, B., Cai, Y., Wang, K., et al.: Global threshold dynamics of a stochastic epidemic model incorporating media coverage. Adv. Differ. Equ. 2018(1), 462 (2018)
Cai, Y., Wang, K., Wang, W.: Global transmission dynamics of a Zika virus model. Appl. Math. Lett. 92, 190–195 (2019)
Huang, S., Tian, Q.: Marcinkiewicz estimates for solution to fractional elliptic Laplacian equation. Comput. Math. Appl. 78(5), 1732–1738 (2019)
Wang, J., Cai, Y., Fu, S., et al.: The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge. Chaos 29(8), 243 (2019)
Ye, Y., Liu, H., Wei, Y., et al.: Dynamic study of a predator-prey model with weak Allee effect and delay. Adv. Math. Phys. 2019, 7296461 (2019)
Funding
This work was supported by the National Natural Science Foundation of China (31560127), the Fundamental Research Funds for the Central Universities (31920180116, 31920180044, 31920170072), the Program for Yong Talent of State Ethnic Affairs Commission of China (No. [2014]121), Gansu Provincial First-class Discipline Program of Northwest Minzu University (No. 11080305) and Central Universities Fundamental Research Funds for the Graduate Students of Northwest Minzu University (Yxm2019109).
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ye, Y., Liu, H., Wei, Y. et al. Dynamic study of a predator-prey model with Allee effect and Holling type-I functional response. Adv Differ Equ 2019, 369 (2019). https://doi.org/10.1186/s13662-019-2311-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2311-1