1 Introduction

Researches on predation systems are always a popular issue in contemporary theoretical ecology and applied mathematics [1–12]. Results based on non-spatial systems have shown that the effect of prey refuge played an important role in determining the dynamical consequences of predator-prey systems [1, 3, 4, 7, 8, 10, 13–19]. Incorporating the effect of prey refuge into the considered predation system is initially done by modifying the originally functional response of predator to prey population, the functional response describes the per capita consumption rates of predators depending on prey density, and quantifies the energy transfer between trophic levels, like Holling I, II, III and IV functional response [20, 21]. The most widely reported conclusions are the community/interior/positive/coexistent equilibrium of the considered predation system being stabilized and the equilibrium density of prey and/or predator was enhanced by the addition of prey refuge [3, 8, 12, 19, 22, 23].

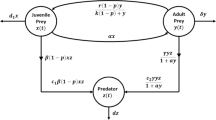
This paper is based on the following predator-prey system with prey self-limitation and the population growth of prey is logistic in the absence of predators:

$$ \textstyle\begin{cases} \dot{x}(t)=rx(1-\frac{x}{K})-f(x)y, \\ \dot{y}(t)=(cf(x)-d)y. \end{cases} $$
(1.1)

Here, \(x(t)\) and \(y(t)\) are the density of prey and predator populations at time t, respectively, and they are all positive numbers. The other parameters have the following biological meanings: r is the intrinsic per capita growth rate of prey population; K is the prey environmental carrying capacity; c is the efficiency with which predators convert consumed prey into new predators; d is the per capita death rate of predators. The function \(f(x)\) denotes a generalized functional response and represents the amount of prey killed per unit time by an individual predator. This paper applies a generalized representation of the functional response

$$f(x)=\frac{\lambda x^{n}}{1+\lambda hx^{n}}, $$

which is introduced by Real [21] and defined as Holling type functional response, where h is the handling time of predators, λ is the attack efficiency of predator to prey population, the exponent n describes the shape of the functional response, including the Holling II functional response for \(n=1\) and Holling III functional response for \(n=2\).

Incorporating a Holling type functional response into the system (1.1), the following predator-prey system could be obtained:

$$ \textstyle\begin{cases} \dot{x}(t)=rx(1-\frac{x}{K})-\frac{\lambda x^{n}y}{1+\lambda hx^{n}}, \\ \dot{y}(t)=(\frac{c\lambda x^{n}}{1+\lambda hx^{n}}-d)y. \end{cases} $$
(1.2)

In this paper, we extend the above model by incorporating the effect of prey refuge. Kot [24] gave a definition for the total number of prey caught V:

$$V= \lambda(T-hV)x, $$

where λ is the attack coefficient, h is the handling time required per prey, T is the total time and all parameters are positive. This definition proposes that the total number of prey caught by its predators is linearly proportional to prey’s density. However, most cases may be included in this representation. Hence, without loss of generality, this paper assumes that the total number of prey caught, \(V(x)\), is

$$ \textstyle\begin{cases} V(x)= \lambda T_{s}(x)x^{n}, \\ T_{s}(x)=T-hV(x), \end{cases} $$
(1.3)

where \(T_{s}(x)\) is the available search time and the other parameters are similar to Kot’s definition [24].

According to Maynard Simth [11] and Ma et al. [23], there exists a quantity βx of prey population which occupy refuges. By modifying the total number of prey caught V, it is given that

$$ \textstyle\begin{cases} V(x)= \lambda T_{s}(x)((1-\beta))x^{n}, \\ T_{s}(x)=T-hV(x). \end{cases} $$
(1.4)

Solving \(V(x)\) from the above equations, we have

$$V (x)=\frac{\lambda T(1-\beta)^{n}x^{n}y}{1+\lambda h(1-\beta)^{n}x^{n}}. $$

Thus, the modified functional response which incorporates the effect of prey refuge is given by

$$\frac{V (x)}{T}=\frac{\lambda(1-\beta)^{n}x^{n}y}{1+\lambda h(1-\beta)^{n}x^{n}}. $$

Based on the above analysis, the system (1.1) with the effect of prey refuge gets the following form:

$$ \textstyle\begin{cases} \dot{x}(t)=rx(1-\frac{x}{K})-\frac{\lambda(1-\beta)^{n}x^{n}y}{1+\lambda h(1-\beta)^{n}x^{n}}, \\ \dot{y}(t)=(\frac{c\lambda(1-\beta)^{n}x^{n}}{1+\lambda h(1-\beta)^{n}x^{n}}-d)y. \end{cases} $$
(1.5)

Before proceeding, we use the following change of variables:

$$\varphi:\bigl(R_{0}^{+}\bigr)^{2}\times R \rightarrow \bigl(R_{0}^{+}\bigr)^{2}\times R,\qquad \varphi(x,y,t)=\biggl(K \bar{x},Khr\bar{y},\frac{A+x^{n}}{r}\bar{t}\biggr) $$

and rewriting x̄, ȳ, t̄ as x, y, t, we obtain the equivalent form of the system (1.3)

$$ \textstyle\begin{cases} \dot{x}(t)=x(1-x)(A+x^{n})-x^{n}y, \\ \dot{y}(t)=B( x^{n}-C(A+x^{n}))y. \end{cases} $$
(1.6)

We have only three parameters, where \(A=\frac{1}{K^{n} \lambda h(1-\beta)^{n}}>0\), \(B=\frac{c}{hr}>0\), \(C=\frac{dh}{c}>0\).

2 Equilibria

The equilibrium points of the system (1.5) are \(E_{0}(0,0)\), \(E_{K}(K,0)\), \(\tilde{E}(\tilde{x},\tilde{y})\), where

$$\begin{aligned}& \tilde{x}=\frac{1}{1-\beta}\biggl[\frac{d}{\lambda(c-dh)}\biggr]^{1/n}, \\& \tilde{y}=\frac{cr}{d(1-\beta)}\biggl[\frac{d}{\lambda(c-dh)}\biggr]^{1/n} \biggl[1-\frac {1}{K(1-\beta)}\biggl(\frac{d}{\lambda(c-dh)}\biggr)^{1/n}\biggr]. \end{aligned}$$

The equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) is positive if and only if

$$\beta< 1-\frac{1}{K}\biggl(\frac{d}{\lambda(c-dh)}\biggr)^{1/n}. $$

If \(\beta>1-\frac{1}{K}(\frac{d}{\lambda(c-dh)})^{1/n}\), the equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) collapses with the point \(E_{K}(K,0)\).

Now, differentiating ỹ with respect to β, we observe that ỹ attains its maximum value at

$$\beta=1-\frac{2}{K}\biggl(\frac{d}{\lambda(c-dh)}\biggr)^{1/n}, $$

and then it decreases with further increases in β. Also we see that x̃ increases with β.

Again, in order to investigate the local stability and the existence of limit cycle, we should give the equilibrium points of the system (1.6). The equilibrium points of the system (1.6) can be obtained by solving the following equations:

$$ \textstyle\begin{cases} x(1-x)(A+x^{n})-x^{n}y=0, \\ B( x^{n}-C(A+x^{n}))y=0. \end{cases} $$
(2.1)

Clearly, it has three equilibrium points \(E_{0}(0,0)\), \(E_{1}(1,0)\), \(\bar{E}(\bar{x},\bar{y})\), where

$$\begin{aligned}& \bar{x}=\biggl(\frac{AC}{1-C}\biggr)^{1/n}, \\& \bar{y}= \frac{1}{C}\biggl(\frac{AC}{1-C}\biggr)^{1/n}\biggl[1-\biggl( \frac{AC}{1-C}\biggr)^{1/n}\biggr]. \end{aligned}$$

The equilibrium point \(\bar{E}(\bar{x},\bar{y})\) is positive if and only if \(A<\frac{1-C}{C}\).

If \(A=\frac{1-C}{C}\), the positive equilibrium point collapses with the equilibrium point \(E_{1}(1,0)\).

The equilibrium point \(\bar{E}(\bar{x},\bar{y})\) lies in the fourth quadrant when \(A>\frac{1-C}{C}\).

3 Positivity and boundedness of the solutions

In order to study the positivity and boundedness for the solutions of system (1.5), we denote the function on the right hand of system (1.5) as \(\mathbf{G}=(xg_{1},yg_{2})\) in which

$$\begin{aligned}& g_{1}(x,y)=r\biggl(1-\frac{x}{K}\biggr)-\frac{\lambda(1-\beta)^{n}x^{n-1} y}{1+\lambda h(1-\beta)^{n}x^{n}} , \\& g_{2}(x,y)=\frac{c \lambda(1-\beta)^{n}x^{n} }{1+\lambda h(1-\beta)^{n}x^{n}}-d . \end{aligned}$$

Clearly, \(G\in C^{1}(R^{2}_{+})\). Thus \(\mathbf{G}:R^{2}_{+} \rightarrow R^{2}\) is locally Lipschitz on \(R^{2}_{+}=\{(x,y)|x>0,y>0\}\). Hence the fundamental theorem of existence and uniqueness ensures existence and uniqueness of solution of the system (1.5) with the given initial conditions. The state space of the system is the non-negative cone in \(R^{2}_{+}\). In the theoretical ecology, positivity and boundedness of the system establishes the biological well behaved nature of the system.

Theorem 3.1

All the solutions of the system (1.5) with the given initial conditions are always positive and bounded.

Proof

Firstly, we wish to prove that \((x(t),y(t))\in R^{2}_{+}\) for all \(t \in[0,+\infty]\). We show this by the method of contradiction. Suppose this is not true. Hence, there must exist one \(\bar{t} \in[0,+\infty]\), such that \(x(\bar{t})\leq0\) and \(y(\bar{t})\leq 0\). From the system (1.5), we have

$$\begin{aligned}& x(t)=x(0)\exp\biggl( \int_{0}^{t} g_{1}(x,y)\,dt\biggr), \\& y(t)=x(0)\exp\biggl( \int_{0}^{t} g_{2}(x,y)\,dt\biggr). \end{aligned}$$

Since \((x(t),y(t))\) are well defined and continuous on \([0,\bar{t}]\), there must exist a \(M>0\) such that \(\forall t \in[0,\bar{t}]\)

$$\begin{aligned} \begin{aligned} &x(t)=x(0)\exp\biggl( \int_{0}^{t} g_{1}(x,y)\,dt\biggr)\geq x(0)\exp(-M\bar{t}), \\ &y(t)=x(0)\exp\biggl( \int_{0}^{t} g_{2}(x,y)\,dt\biggr) \geq y(0)\exp(-M\bar{t}). \end{aligned} \end{aligned}$$

It is clear that if we have the limit \(t \rightarrow\bar{t}\), we obtain

$$\begin{aligned}& x(\bar{t}) \geq x(0)\exp(-M\bar{t})>0, \\& y(\bar{t}) \geq y(0)\exp(-M\bar{t})>0, \end{aligned}$$

which is a contradiction. Hence, all the solutions of the system (1.5) are always positive.

Secondly, we will prove the boundedness.

Letting \(V(t)=x(t)+\frac{1}{c}y(t)\), then we obtain

$$\dot{V}(t)=rx\biggl(1-\frac{x}{K}\biggr)-\frac{\lambda(1-\beta)^{n}x^{n} y}{1+\lambda h(1-\beta)^{n}x^{n}}+ \frac{\lambda(1-\beta)^{n}x^{n} y}{1+\lambda h(1-\beta)^{n}x^{n}}-\frac{d}{c}y \leq-dV(t)+(d+r)K. $$

Integrating both sides of the above equation and applying the theorem of the differential inequality, we have

$$0< V(t)< \frac{(d+r)K}{d}\bigl(1-e^{-dt}\bigr)+V(0)e^{-dt}, \qquad V(0)=V\bigl(x(0),y(0)\bigr) $$

and \(\lim_{t \rightarrow+\infty} V(t)\leq\frac{(d+r)K}{d}\). □

4 Stability analysis

4.1 Local stability

The Jacobian matrix of the system (1.6) at the equilibrium point \(E_{1}(1,0)\) is given by

$$ J_{1}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -(A+1)&-1\\ 0&B(1-C-AC) \end{array}\displaystyle \right ). $$

The two eigenvalues of matrix \(J_{1}\) are \(-(A+1)\) and \(B(1-C-AC)\).

Hence, if \(A<\frac{1-C}{C}\), the equilibrium point \(E_{1}(1,0)\) is a saddle point. Otherwise, the equilibrium point \(E_{1}(1,0)\) is locally asymptotically stable.

For the positive equilibrium point \(\bar{E}(\bar{x},\bar{y})\), the Jacobian matrix is as follows:

$$ J_{2}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} A_{11}&A_{12}\\ A_{21}&0 \end{array}\displaystyle \right ). $$

Here

$$\begin{aligned}& A_{11}=\frac{(\bar{x})^{n}}{C}\bigl[\bigl(1-n(1-C)\bigr)-\bigl(2-n(1-C) \bigr)\bar{x}\bigr] , \\& A_{12}=-(\bar{x})^{n}< 0,\qquad A_{21}= \operatorname{Bn}(1-C) (\bar{x})^{n-1}\bar{y}>0 . \end{aligned}$$

Clearly \(\operatorname{Det}J_{2}=-A_{12}A_{21}>0\). Therefore, the sign of the eigenvalues of Jacobian matrix \(J_{2}\) depends only on \(\operatorname{Tr}J_{2}=A_{11}\).

Hence, the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) is locally asymptotically stable if and only if

$$ \bigl(1-n(1-C)\bigr)-\bigl(2-n(1-C)\bigr)\bar{x}< 0. $$
(4.1)

Case 1: If \(0< n<\frac{1}{1-C}\), then \(2-n(1-C)>0\) and \(1-n(1-C)>0\).

The inequality (4.1) can easily be solved as follows:

$$\bar{x}>\frac{1-n(1-C)}{2-n(1-C)}. $$

In other words

$$A>\frac{1-C}{C}\biggl[\frac{1-n(1-C)}{2-n(1-C)}\biggr]^{n}. $$

Hence, the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) is locally asymptotically stable.

The results of González-Olivares et al. [6] and Huang et al. [8] are special cases of ours for \(n=1\) and \(n=2\), respectively.

Case 2: If \(\frac{1}{1-C}\leq n \leq\frac{2}{1-C}\), then the inequality (4.1) holds.

Therefore, the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) is always asymptotically stable whenever the proportion of prey refuge is.

Case 3: If \(n>\frac{2}{1-C}\), then \(2-n(1-C)<0\) and \(1-n(1-C)<0\).

Hence, the inequality (4.1) is equivalent to the following condition:

$$\bar{x}< \frac{1-n(1-C)}{2-n(1-C)}. $$

It is easy to show that

$$A< \frac{1-C}{C}\biggl[\frac{1-n(1-C)}{2-n(1-C)}\biggr]^{n}. $$

Therefore, the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) is locally asymptotically stable under these assumptions.

4.2 Existence of limit cycle

Let us rewrite the system (1.6) in the following form:

$$ \textstyle\begin{cases} \dot{x}(t)=xg(x)-y p(x), \\ \dot{y}(t)=(q(x)-AC)y. \end{cases} $$
(4.2)

Here \(g(x)=(1-x)(A+x^{n})\), \(p(x)=x^{n}\), \(q(x)=(1-C)p(x)\).

We present a lemma [17] regarding uniqueness of limit cycle of the above system.

Lemma

[17]

Suppose the system (4.2) obeys

$$\frac{d}{dx}\biggl(\frac{xg'(x)+g(x)-xg(x)(p'(x)/p(x))}{q(x)-AC}\biggr)\leq0 $$

in \(0\leq x< \bar{x}\) and \(\bar{x}< x\leq1\). Then the system (4.2) has exactly one limit cycle which is globally asymptotically stable with respect to the set \(\{(x,y)|x>0,y>0\}\backslash \{E_{2}(\bar{x},\bar{y})\}\).

By employing the above lemma, we have

$$\begin{aligned}& \frac{d}{dx}\biggl(\frac{xg'(x)+g(x)-xg(x)(p'(x)/p(x))}{q(x)-AC}\biggr)\leq0 \\& \quad \Leftrightarrow\quad \frac{\varphi(x)}{((1-C)x^{n}-AC)^{2}}\leq0. \end{aligned}$$

Here

$$\begin{aligned} \varphi (x) =&-2(1-C)x^{2n}+A\bigl[2C(1+n)+(1-n) (n-2) (1-C) \bigr]x^{n} \\ &{}-An\bigl[1-n(1-C)\bigr]x^{n-1}-A^{2}C(n-2). \end{aligned}$$

This will be equivalent to prove that \(\varphi(x)\leq0\) for all \(x>0\).

Noticing that \(\varphi(0)=-A^{2}C(n-2)\leq0\) for \(n\geq2\) and

$$\begin{aligned} \varphi '(x) =&nx^{n-2}\bigl[-4(1-C)x^{n+1}+A \bigl(2C(1+n)+(1-n) (n-2) (1-C)\bigr)x \\ &{}-A(n-1) \bigl(1-n(1-C)\bigr)\bigr]. \end{aligned}$$

It is easy to show that \(x=0\) and \(x=\bar{x}\) are the solutions of the equation \(\varphi'(x)=0\).

Again \(\varphi''(\bar{x})=-nA\bar{x}^{n-2}[2C(1+n)+(n-1)(n-2)(1-C)]<0\).

Thus, \(x=\bar{x}\) is the maximum value point of the function \(\varphi(x)\).

Now, in order to prove \(\varphi(x)\leq0\), it is enough to show that \(\varphi(\bar{x})\leq0\).

$$\varphi(\bar{x})=-\frac{nA^{2}C}{\bar{x}}\bigl[\bigl(1-n(1-C)\bigr)-\bigl(2-n(1-C) \bigr)\bar{x}\bigr]< 0. $$

That is,

$$\bigl(1-n(1-C)\bigr)-\bigl(2-n(1-C)\bigr)\bar{x}>0. $$

Clearly, it is exactly the condition of the instability of the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\).

4.3 Global stability

In this section, we will prove the global stability of the positive equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) of the system (1.5).

We first choose a Lyapunov function defined as follows:

$$ W\bigl(x(t),y(t)\bigr)= \int_{\tilde{x}}^{x} \frac{u-\tilde{x}}{u}\, du+p \int_{\tilde{y}}^{y} \frac{w-\tilde{y}}{w}\, dw \quad (p>0). $$

By a simple computation, we obtain

$$\begin{aligned} \frac{dW}{dt} =&\frac{x-\tilde{x}}{x}\frac{dx}{dt}+p\frac{y-\tilde{y}}{y} \frac{dy}{dt} \\ =&(x-\tilde{x})\biggl[r\biggl(1-\frac{x}{K}\biggr)-\frac{\lambda(1-\beta)^{n}x^{n} y}{1+\lambda h(1-\beta)^{n}x^{n}} \biggr]+p(y-\tilde{y}) \biggl(\frac{c\lambda(1-\beta)^{n}x^{n} }{1+\lambda h(1-\beta)^{n}x^{n}}-d\biggr) \\ =&(x-\tilde{x})\biggl[r\biggl(1-\frac{\tilde{x}}{K}\biggr)+\frac{\lambda(1-\beta)^{n}\tilde{x}^{n-1} \tilde{y}}{1+\lambda h(1-\beta)^{n}\tilde{x}^{n}}-r \biggl(1-\frac{x}{K}\biggr)-\frac{\lambda(1-\beta)^{n}x^{n-1} y}{1+\lambda h(1-\beta)^{n}x^{n}}\biggr] \\ &{}+p(y-\tilde{y})\biggl[\frac{c\lambda(1-\beta)^{n}x^{n} }{1+\lambda h(1-\beta)^{n}x^{n}}-\frac{c\lambda(1-\beta)^{n}\tilde{x}^{n} }{1+\lambda h(1-\beta)^{n}\tilde{x}^{n}}\biggr] \\ =&-\frac{r}{K}(x-\tilde{x})^{2}-y(x-\tilde{x}) \biggl( \frac{\lambda (1-\beta)^{n}\tilde{x}^{n-1} }{1+c h(1-\beta)^{n}\tilde{x}^{n}}-\frac{\lambda(1-\beta)^{n}x^{n-1} }{1+\lambda h(1-\beta)^{n}x^{n}}\biggr) \\ &{}+(x-\tilde{x}) (y-\tilde{y})\frac{\lambda(1-\beta)^{n}\tilde{x}^{n-1} }{1+\lambda h(1-\beta)^{n}\tilde{x}^{n}}+pc\lambda(1-\beta) (y- \tilde{y}) \bigl(x^{n}-\tilde{x}^{n}\bigr) \\ =&-\frac{r}{K}(x-\tilde{x})^{2}- \lambda(1-\beta) (n-1) \tilde{x}^{n-2}y(x-\tilde{x})^{2} \\ &{}+\biggl[n c\lambda \tilde{x}^{n-1}(1-\beta)p-\frac{\lambda(1-\beta)\tilde{x}^{n-1} }{1+\lambda h(1-\beta)^{n}\tilde{x}^{n}}\biggr]. \end{aligned}$$

Selecting \(p=\frac{\lambda(1-\beta)^{n}\tilde{x}^{n-1}}{n c \lambda (1-\beta)^{n}\tilde{x}^{n-1}(1+\lambda h(1-\beta)^{n}\tilde{x}^{n})}>0\), then we have

$$\frac{dW}{dt}=-\frac{r}{K}(x-\tilde{x})^{2}- \lambda(1- \beta)^{n}(n-1)\tilde{x}^{n-2}y(x-\tilde{x})^{2}. $$

Thus, \(\frac{dW}{dt}<0\) if \(n \geq 1\). Hence, the positive equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) of the system (1.5) is globally asymptotically stable.

5 Main results

According to the above analysis, we can obtain the following results.

Theorem 5.1

Assuming that \(2\leq n<\frac{1}{1-C}\), then we have:

  1. (1)

    If \(0< A<\frac{1-C}{C}[\frac{1-n(1-C)}{2-n(1-C)}]^{n}\), the system (1.4) has a unique globally stable limit cycle surrounding the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) which is unstable.

  2. (2)

    If \(\frac{1-C}{C}[\frac{1-n(1-C)}{2-n(1-C)}]^{n}< A<\frac{1-C}{C}\), the system (1.4) has a globally asymptotically stable equilibrium point \(\bar{E}(\bar{x},\bar{y})\) at the first quadrant.

Theorem 5.2

Assuming that \(n>\frac{2}{1-C}\), then we have:

  1. (1)

    If \(0< A<\frac{1-C}{C}[\frac{1-n(1-C)}{2-n(1-C)}]^{n}\), the system (1.4) has a globally asymptotically stable equilibrium point \(\bar{E}(\bar{x},\bar{y})\) in the first quadrant.

  2. (2)

    If \(\frac{1-C}{C}[\frac{1-n(1-C)}{2-n(1-C)}]^{n}< A<\frac{1-C}{C}\), the system (1.4) has a unique globally stable limit cycle surrounding the interior equilibrium point \(\bar{E}(\bar{x},\bar{y})\) which is unstable.

In reference to the original parameters of the system (1.5), the above results can be expressed as follows.

Theorem 5.3

Assuming that \(2\leq n<\frac{c}{c-dh}\), then we have:

  1. (1)

    If \(0<\beta<1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac {2c-n(c-dh)}{c-n(c-dh)}]\), the prey and predator populations stably oscillate around the unique interior equilibrium point.

  2. (2)

    If \(1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac {2c-n(c-dh)}{c-n(c-dh)}]<\beta<1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}\), the two populations tend to reach a globally asymptotically stable equilibrium point at the first quadrant.

Theorem 5.4

Assuming that \(n>\frac{2c}{c-dh}\), then we have:

  1. (1)

    If \(0<\beta<1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac {2c-n(c-dh)}{c-n(c-dh)}]\), the two populations tend to reach a globally asymptotically stable equilibrium point in the first quadrant.

  2. (2)

    If \(1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac {2c-n(c-dh)}{c-n(c-dh)}]<\beta<1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}\), the prey and predator populations stably oscillate around the unique interior equilibrium point.

6 Bifurcation analysis

To obtain a complete classification of the qualitative behavior of the system (1.5), we analyze the bifurcation pattern and illustrate the results with one parameter, saying the effect of prey refuge β. The classification requires up to two codimension-one bifurcations: (i) Hopf-bifurcation point in which the coexistence equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) exchanges stability, (ii) the bifurcation point tracking a transcritical bifurcation between the coexistence equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) and the prey only equilibrium \(E_{K}(K,0)\), where these two equilibria coincide and exchange their stability to each other.

6.1 Hopf bifurcation

One-dimensional bifurcation analysis reveals the behavior of the system (1.5) when a particular system parameter is varied over a long range. Here we observe the behavior of the system (1.5) when the prey refuge intensity is varied.

By simple computation, the characteristic equation of the system (1.5) at the coexistence equilibrium point \(\tilde{E}(\tilde{x},\tilde{y})\) is

$$ \xi^{2}-\tilde{a}_{11} \xi+ \tilde{a}_{12}\tilde{a}_{21}=0, $$
(6.1)

in which

$$\begin{aligned}& \tilde{a}_{11}=r\biggl(1-\frac{2\tilde{x}}{K}\biggr)-\frac{n \lambda (1-\beta)^{n}\tilde{x}^{n-1}\tilde{y}}{(1+\lambda h(1-\beta)^{n}\tilde{x}^{n})^{2}} , \\& \tilde{a}_{12}=\frac{ \lambda(1-\beta)^{n}\tilde{x}^{n} }{ 1+\lambda h(1-\beta)^{n}\tilde{x}^{n} }>0 , \\& \tilde{a}_{21}=\frac{n c \lambda (1-\beta)^{n}\tilde{x}^{n-1}y}{(1+\lambda h(1-\beta)^{n}\tilde{x}^{n})^{2}}>0 . \end{aligned}$$

It can easily be observed from the characteristic equation (6.1) that the roots become purely imaginary when \(\tilde{a}_{11}=0\), i.e. \(\beta=\beta_{c}= 1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac{2c-n(c-dh)}{c-n(c-dh)}]\). In this case, \(\operatorname{Re}(\lambda)|_{\beta=\beta_{c}}=0\), \(\operatorname{Im}(\lambda)|_{\beta=\beta_{c}} \neq0\) and \(\frac{d}{d \beta}\operatorname{Re}(\lambda)|_{\beta=\beta_{c}}<0\) (we use the standard package of Mathematica to get these results) and hence the transversality condition for a Hopf bifurcation is satisfied. Therefore, there exists a Hopf bifurcation at \(\beta=\beta_{c}\). The negative sign of \(\frac{d}{d \beta}\operatorname{Re}(\lambda)|_{\beta=\beta_{c}}<0\) implies that the oscillations in the population densities dampen as the effect of prey refuge passes from lower value to higher value through \(\beta=\beta_{c}\).

Hence, we obtain the following results.

Theorem 6.1

The system (1.5) undergoes a Hopf bifurcation at \(\tilde{E}(\tilde{x},\tilde{y})\) when the effect of prey refuge β passes the threshold value \(\beta_{c}= 1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac{2c-n(c-dh)}{c-n(c-dh)}]\).

6.2 Transcritical bifurcation

In this section, we will consider the existence of a transcritical bifurcation for the system (1.5). In order to do this, we select the effect of prey refuge β as the bifurcation parameter. According to the analysis in Section 3, if \(1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}[\frac{2c-n(c-dh)}{c-n(c-dh)}] <\beta<1-\frac{1}{K}(\frac{d}{\lambda(c-dh)})^{1/n}\), the coexistence equilibrium Ẽ is stable but the axial equilibrium \(E_{K}\) is unstable. The two equilibria coincide a \(\beta=\beta_{0}=1-\frac{1}{K}(\frac{d}{\lambda(c-dh)})^{1/n}\) and exchange their stability when \(1-\frac{1}{K}(\frac{d}{\lambda(c-dh)})^{1/n}<\beta<1\).

Now, we will prove that the system (1.5) undergoes a transcritical bifurcation by using Sotomayer’s theorem [2]. For \(\beta=\beta_{0}\), the system (1.5) has only one axial equilibrium point \(E_{K}\). The Jacobian matrix evaluated at \(E_{K}\) is

$$ \mathbf{J}= Df(\tilde{x},\tilde{y};\beta_{0})= \begin{pmatrix} -r&-\frac{d}{c}\\ 0&0 \end{pmatrix}. $$

J has an eigenvalue \(\lambda=0\). Let V and W be the eigenvectors corresponding to the eigenvalue \(\lambda=0 \) for J and \(J^{T} \), respectively, then one can calculate

$$ \mathbf{V} = \begin{pmatrix} -\frac{d}{rc}\\1 \end{pmatrix} ,\qquad \mathbf{W} = \begin{pmatrix} 0\\1 \end{pmatrix} . $$

Using the expressions for V and W, we get

$$\begin{aligned}& W^{T}f_{\beta}(\tilde{x},\tilde{y};\beta_{0})=0, \\& W^{T}\bigl[Df_{\beta}(\tilde{x},\tilde{y}; \beta_{0})V\bigr]=-\frac{nd(c-dh)K}{c} \biggl(\frac{(c-dh)\lambda}{d} \biggr)^{\frac{1}{n}}\neq0, \\& W^{T}\bigl[D^{2}f(\tilde{x},\tilde{y}; \beta_{0}) (V,V)\bigr]=\frac {nd^{2}}{Krc^{2}}\neq0. \end{aligned}$$

Hence, according to Sotomayor’s theorem, the system (1.5) undergoes a transcritical bifurcation when the effect of prey refuge β passes through the threshold value \(\beta_{0}\).

Hence, we obtain the following results.

Theorem 6.2

The system (1.5) undergoes a transcritical bifurcation when the effect of prey refuge β passes the threshold value \(\beta_{0}=1-\frac{1}{K}(\frac{d}{\lambda(c-dh)})^{1/n}\).

7 Discussion

In this paper, we have considered a predator-prey system with a general functional response incorporating a prey refuge. Our analysis reveals that

  1. (i)

    The equilibrium point \(E_{K}(K,0)\) is locally asymptotically stable if the proportion of refuge using by prey is larger than \(1-\frac{1}{K}[\frac{d}{\lambda(c-dh)}]^{1/n}\). Therefore, when the refuge using by prey is high, the system predicts that the prey population reaches its carrying capacity and the predators go extinct, a dynamics also observed by Collings [5] for some certain parameters.

  2. (ii)

    The shape of the functional response plays an important role in determining the dynamic behavior of the system. If \(0< n<\frac{c}{c-dh}\), the effect of prey refuge has a stabilizing effect, which is consistent with results of González-Olivares and Ramos-Jiliberto [6] who has found a clear stabilizing effect on their considered system. Here, stabilization or the increase of stability refers to cases where a community equilibrium point changes from repeller to an attractor due to changes in the value of a control parameter [6]. However, if the exponent n is larger than \(\frac{2c}{c-dh}\), the stability of the interior equilibrium point changes from the globally asymptotically stable state to the unstable state surrounding a globally stable limit cycle as the refuge using by prey increases. The prey refuge can decrease the stability of the interior equilibrium point. We call this a destabilizing effect.