1 Introduction

The location of dense urban areas where the street is surrounded by rows of buildings is described as an urban street canyon. The deep geometry of street canyons can greatly affect the local air quality and climate. In the summer season, temperature in the street canyon is more affected by two primary sources, i.e., the hot wind flow and the heat released by burning fuel during traffic. To keep the air quality and thermal climate at an acceptable level in the street canyon, understanding the air flow pattern and the heat transfer in the street canyon is important. A number of research works have been conducted to investigate the heat transfer in the street canyons under hot weather in some urban cities [1,2,3] through the experimental and mathematical studies. The wind tunnel experiments of thermal effects on flow within and above urban street canyons were performed [4,5,6], and the convective heat transfer in street canyons was investigated numerically [7, 8]. The numerical simulations of heat transfer based on \(k-\varepsilon \) turbulence model were studied [9, 10], and thermal effects on fluid-dynamic in an urban street canyon were analyzed [11,12,13].

There are several factors affecting the heat transfer in street canyons. The experiments of wind speed effects in various aspect ratios and full-scale study were performed [14, 15]. The mean flow and turbulence structure were investigated [16, 17] in various directions of flow field, i.e., the perpendicular and ambient flows [18, 19]. The numerical studies based on \(k-\varepsilon \) turbulence model were conducted to investigate many characteristics of turbulent flows [20]. The flow distributions of skimming, wake, isolated, and vortex flows [21, 22] and the effects of buoyant flow in street canyons were examined [23, 24]. The influence of obstacles inside street canyons was considered by Hamlyn et al. [25]. They developed a simple network approach to simulate the dispersion among large groups of obstacles. The diffusive flow processes in the obstacle arrays and the pollutant dispersion in an urban canopy were studied. Salim et al. [26] proposed a numerical simulation of dispersion in street canyons of aspect ratio of the width to the height (W/H) about 1 lined with avenue-like tree planting. The effects of loosely-packed and densely-packed trees were considered in the models of dispersion in street canyons. Hang et al.[27] studied the impact of viaduct configurations and ground heating on pollutant dispersion in 2D street canyons based on CFD simulations. The flow to leeward and windward rooms of naturally-ventilated buildings was considered in street canyon models. The influences of absence and present of viaducts and road barriers on flow dispersion and the ground heating were investigated.

The majority of the aforementioned studies have already accessed the influences of the air flow and the building designs on heat transfer in street canyons. However, a few types of obstacles influencing the heat transfer [28, 29] in the street canyons have been reported. In some urban cities, the street canyon containing a skytrain above the main street has a significant effect on the local climate. In this study, we investigate the air flow and heat transfer in the region underneath the skytrain during traffic in the street canyon in the summer season. A mathematical model of the air flow and heat transfer in the street canyon is developed. The street canyon with the skytrain station is assumed to be surrounded by symmetrical buildings on both sides of the street. The effect of wind flow with three different levels of wind speed on the temperature distribution is investigated.

1.1 Governing equations

The airflow and heat transfer are described by the Reynolds-averaged Navier–Stokes equations (1)–(4) [30] and the heat conservation equation (5) [31]:

$$\begin{aligned}& \frac{\partial {\rho }}{\partial t}+\nabla \cdot (\rho \textbf{u}) =0, \end{aligned}$$
(1)
$$\begin{aligned}& \rho \frac{\partial {\textbf{u}}}{\partial t}+\rho (\textbf{u}\cdot \nabla )\textbf{u} =\nabla \cdot \biggl[-p\textbf{I}+(\mu -\mu _{T}) \bigl( \nabla \textbf{u}+\bigl( \nabla \textbf{u}^{T}\bigr)\bigr) \\& \hphantom{\rho \frac{\partial {\textbf{u}}}{\partial t}+\rho (\textbf{u}\cdot \nabla )\textbf{u} =}{}-\frac{2}{3}(\mu +\mu _{T}) (\nabla \cdot \textbf{u})\textbf{I}- \frac{2}{3}\rho {k}\textbf{I}\biggr]+\textbf{F}, \end{aligned}$$
(2)
$$\begin{aligned}& \rho \frac{\partial {k}}{\partial t}+\rho (\textbf{u}\cdot \nabla )k= \nabla \cdot \biggl[ \biggl(\mu +\frac{\mu _{T}}{ \sigma _{k}}\biggr)\nabla k\biggr]+P_{k}- \rho \varepsilon , \end{aligned}$$
(3)
$$\begin{aligned}& \rho \frac{\partial {\varepsilon }}{\partial t}+\rho (\textbf{u} \cdot \nabla )\varepsilon =\nabla \cdot \biggl[\biggl(\mu +\frac{\mu _{T}}{ \sigma _{\varepsilon }}\biggr)\nabla \varepsilon \biggr]+C_{\varepsilon 1}\frac{ \varepsilon }{k}P_{k}-C_{\varepsilon 2}\rho \frac{\varepsilon ^{2}}{k}, \end{aligned}$$
(4)
$$\begin{aligned}& \rho C_{p}\biggl(\frac{\partial {T}}{\partial t}+\textbf{u}\cdot \nabla T\biggr)+ \nabla \cdot \textbf{q}=0, \end{aligned}$$
(5)

where \(C_{\varepsilon {1}}\) and \(C_{\varepsilon {2}}\) are constants and other variables and parameters are described in Tables 1–3 in which the kinematic turbulent viscosity \(\mu _{T}\), the heat flux q, and the turbulent kinetic energy production \(P_{k}\) are respectively defined by

$$\begin{aligned}& \mu _{T} = \frac{c_{\mu }k^{2}}{\varepsilon }, \\& p_{k}= \mu _{T}\bigl[\nabla \textbf{u}:\bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr)\bigr], \\& \textbf{q} =-k_{T}\nabla {T}. \end{aligned}$$

To obtain a well-defined problem of the fluid flow with heat transfer phenomena in the street canyon, a set of boundary conditions [32] is established as follows.

Table 1 Nomenclature
Full size table
Table 2 Dependent variables
Full size table
Table 3 Model constants
Full size table

The boundary conditions of the turbulent airflow near walls are obtained by using wall functions. At the inlet boundary, we set

$$\textbf{u}=-U_{0}\textbf{n}, \qquad k=\frac{3}{2}(U_{\mathrm{ref}}I_{T})^{2}, \quad \text{and}\quad \varepsilon =C_{\mu }^{3/4}\frac{k^{3/2}}{L_{T}}. $$

At the outlet (open) boundary, we employ

$$\begin{aligned}& \biggl[-p\textbf{I}+(\mu +\mu _{T}) \bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr)-\frac{2}{3}(\mu +\mu _{T}) (\nabla \cdot \textbf{u}) \textbf{I}-\frac{2}{3}\rho {k}\textbf{I} \biggr]=0, \\& \nabla {k}\cdot \textbf{n}=0,\qquad \nabla {\varepsilon }\cdot \textbf{n}=0\quad \text{if } \textbf{u}\cdot \textbf{n}\geq 0, \\& k=\frac{3}{2}(I_{T}U_{\mathrm{ref}})^{2},\qquad \varepsilon =\frac{C_{\mu }^{3/4}}{L _{T}}\biggl(\frac{3(I_{T}U_{\mathrm{ref}})^{2}}{2}\biggr)^{\frac{3}{2}}\quad \text{if } \textbf{u}\cdot \textbf{n}< 0. \end{aligned}$$

At the walls including the perimeters of buildings, the skytrain station, and the sidewalks, we apply

$$\begin{aligned}& \biggl[(\mu +\mu _{T}) \bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr)- \frac{2}{3}(\mu +\mu _{T}) ( \nabla \cdot \textbf{u})\textbf{I}- \frac{2}{3}\rho {k}\textbf{I} \biggr]=- \rho \textbf{u}_{\mathrm{tang}}, \\& \textbf{u}\cdot \textbf{n}=0,\qquad \nabla {k}\cdot \textbf{n}=0,\quad \text{and}\quad \varepsilon =\rho \frac{C_{\mu }k^{2}}{\kappa _{v}\delta _{w}\mu }, \end{aligned}$$

where \(U_{\mathrm{ref}}\) is reference velocity, \(I_{T}\) and \(L_{T}\) are respectively turbulent intensity and turbulence length scale, \(\textbf{u}_{\mathrm{tang}}\) represents tangent velocity which is defined by \(\textbf{u}_{\mathrm{tang}}=\textbf{u}-(\textbf{u}\cdot {\textbf{n}}) \textbf{u}\), and \(C_{\mu }\), \(\kappa _{v}\), and \(\delta _{w}\) are constants.

For the temperature field, we assume the air temperature at the inlet boundary to be constant, i.e., \(T=T_{0}\). For the conditions at the open boundary, we set

$$\begin{aligned}& T=T_{0}, \quad \text{if } \textbf{n}\cdot \textbf{u}< 0, \\& -\textbf{n}\cdot \textbf{q}=0, \quad \text{if } \textbf{n}\cdot \textbf{u}\geq 0. \end{aligned}$$

Thermal insulation is applied on the perimeters of the buildings, the skytrain station, and the sidewalks, i.e.,

$$\begin{aligned}& -\textbf{n}\cdot \textbf{q}=0. \end{aligned}$$

On the street surface, we apply

$$\begin{aligned}& -\textbf{n}\cdot \textbf{q}=q_{0},\quad \text{and} \quad q_{0}=h(T - T0), \end{aligned}$$

where \(q_{0}\) represents inward heat flux due to traffic, h is heat transfer coefficient, and T0 is hot temperature generated on the street surface.

1.2 Finite element formulation

Firstly, we construct the total residual function for each equation in the above system and set it to zero, i.e.,

$$\begin{aligned}& \biggl(\frac{\partial \rho }{\partial {t}}, w^{p}\biggr)+\bigl(\nabla \cdot (\rho \textbf{u}), w^{p}\bigr) =0, \end{aligned}$$
(6)
$$\begin{aligned}& \biggl(\rho \biggl(\frac{\partial \textbf{u}}{\partial t}\biggr)+\rho (\textbf{u}\cdot \nabla ) \textbf{u},\textbf{w}^{u}\biggr) =\bigl(\nabla {p}, \textbf{w}^{u}\bigr) + ( \mu +\mu _{T}) \bigl(\nabla \cdot \bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr), \textbf{w}^{u}\bigr) \\& \hphantom{\biggl(\rho \biggl(\frac{\partial \textbf{u}}{\partial t}\biggr)+\rho (\textbf{u}\cdot \nabla ) \textbf{u},\textbf{w}^{u}\biggr) =}{}-\frac{2}{3}(\mu +\mu _{T}) \bigl((\nabla \cdot \textbf{u}) \textbf{I}, \textbf{w}^{u}\bigr) \end{aligned}$$
(7)
$$\begin{aligned}& \hphantom{\biggl(\rho \biggl(\frac{\partial \textbf{u}}{\partial t}\biggr)+\rho (\textbf{u}\cdot \nabla ) \textbf{u},\textbf{w}^{u}\biggr) =}{}-\frac{2}{3}\rho \bigl(k,\textbf{w}^{u}\bigr)+\bigl( \textbf{F},\textbf{w}^{u}\bigr), \end{aligned}$$
(8)
$$\begin{aligned}& \biggl(\rho \biggl(\frac{\partial k}{\partial t}\biggr)+(\textbf{u}\cdot \nabla )k\biggr),w ^{k}) = \biggl(\nabla \cdot \biggl[\biggl(\mu +\frac{\mu _{t}}{\sigma _{k}} \biggr)\nabla {k}\biggr],w ^{k}\biggr)+\bigl(P_{k},w^{k} \bigr) \\& \hphantom{\biggl(\rho \biggl(\frac{\partial k}{\partial t}\biggr)+(\textbf{u}\cdot \nabla )k\biggr),w ^{k}) =}{}-\bigl(\rho \varepsilon ,w^{k}\bigr), \end{aligned}$$
(9)
$$\begin{aligned}& \biggl(\rho \biggl(\frac{\partial \varepsilon }{\partial t}\biggr)+(\textbf{u}\cdot \nabla ) \varepsilon \biggr),w^{\varepsilon }) = \biggl(\nabla \cdot \biggl[\biggl(\mu + \frac{ \mu _{t}}{\sigma _{\varepsilon }}\biggr)\nabla {\varepsilon }\biggr],w^{\varepsilon }\biggr)+ \biggl(C_{\varepsilon {1}}\frac{\varepsilon }{k}P_{k},w^{\varepsilon }\biggr) \\& \hphantom{\biggl(\rho \biggl(\frac{\partial \varepsilon }{\partial t}\biggr)+(\textbf{u}\cdot \nabla ) \varepsilon \biggr),w^{\varepsilon }) =}{}-\biggl(C_{\varepsilon {2}}\rho \frac{\varepsilon ^{2}}{k},w^{\varepsilon }\biggr), \end{aligned}$$
(10)
$$\begin{aligned}& \biggl(\rho {C_{p}}\frac{\partial T}{\partial t}+\rho {C_{p}}\textbf{u} \cdot \nabla {T},w^{T}\biggr) = \bigl(q_{0},w^{T} \bigr)+\bigl(\nabla \cdot \textbf{q},w ^{T}\bigr), \end{aligned}$$
(11)

where \((\cdot ,\cdot )\) denotes the inner product on the square integrable function space, \(\textbf{w}^{u}\) is the vector of test functions for velocity field, \(w^{p}\), \(w^{T}\), \(w^{k}\), and \(w^{\varepsilon }\) are test functions for pressure, temperature, turbulent kinetic energy, and its dissipation rate, respectively.

By applying all Neumann boundary conditions to the above equations (6)–(11) and using Green’s theorem to reduce the second order derivatives to order one, we obtain the following variational statement:

Find \(\textbf{u} \in [H^{1}(\varOmega )]^{3}\), p, T, k and \(\varepsilon \in H^{1}(\varOmega )\) such that, for all test functions \(\textbf{w}^{u}\in [H^{1}_{0}(\varOmega )]^{3}\), \(w^{p}\), \(w^{T}\), \(w^{k}\), and \(w^{\varepsilon }\in H^{1}_{0}(\varOmega )\), all Dirichlet boundary conditions are satisfied and

$$\begin{aligned}& \int _{\varOmega }w^{p}\frac{\partial \rho }{\partial {t}}\,d\varOmega + \int _{\varOmega } w^{p}\bigl(\nabla \cdot (\rho \textbf{u}) \bigr)\,d\varOmega =0, \end{aligned}$$
(12)
$$\begin{aligned}& \rho \int _{\varOmega }\textbf{w}^{u}\frac{\partial \textbf{u}}{\partial {t}}\,d\varOmega +\rho \int _{\varOmega }\textbf{w}^{u}(\textbf{u}\cdot \nabla ) \textbf{u}\,d\varOmega = \int _{\varOmega }\textbf{w}^{u}\nabla (p)\,d\varOmega + (\mu + \mu _{T}) \int _{\partial \varOmega }\textbf{w}^{u}\bigl(\nabla \textbf{u} \\& \hphantom{\rho \int _{\varOmega }\textbf{w}^{u}\frac{\partial \textbf{u}}{\partial {t}}\,d\varOmega +\rho \int _{\varOmega }\textbf{w}^{u}(\textbf{u}\cdot \nabla ) \textbf{u}\,d\varOmega =}{}+(\nabla \textbf{u})^{T}\bigr)\cdot \textbf{n}\,ds- \int _{\varOmega }\nabla \textbf{u}\nabla \textbf{w}^{u}\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }\textbf{w}^{u}\frac{\partial \textbf{u}}{\partial {t}}\,d\varOmega +\rho \int _{\varOmega }\textbf{w}^{u}(\textbf{u}\cdot \nabla ) \textbf{u}\,d\varOmega =}{}-\frac{2}{3}(\mu -\mu _{T}) \int _{\varOmega }\textbf{w}^{u}(\nabla \cdot \textbf{u}) \textbf{I}\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }\textbf{w}^{u}\frac{\partial \textbf{u}}{\partial {t}}\,d\varOmega +\rho \int _{\varOmega }\textbf{w}^{u}(\textbf{u}\cdot \nabla ) \textbf{u}\,d\varOmega =}{}-\frac{2}{3}\rho \int _{\varOmega }\textbf{w}^{u}k\textbf{I}+ \int _{ \varOmega }\textbf{w}^{u}\cdot \textbf{F}\,d\varOmega , \end{aligned}$$
(13)
$$\begin{aligned}& \rho \int _{\varOmega }w^{k}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }w^{k}(\textbf{u}\cdot \nabla )k\,d\varOmega = \int _{\partial \varOmega }w^{k}\biggl[\biggl(\mu +\frac{\mu _{T}}{\sigma _{K}} \biggr)\biggr]\nabla {k}\cdot \textbf{n}\,d\partial \varOmega \\& \hphantom{\rho \int _{\varOmega }w^{k}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }w^{k}(\textbf{u}\cdot \nabla )k\,d\varOmega =}{}- \int _{\varOmega }\nabla {w^{k}}\biggl[\biggl(\mu + \frac{\mu _{T}}{\sigma _{K}}\biggr) \nabla {k}\biggr]\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }w^{k}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }w^{k}(\textbf{u}\cdot \nabla )k\,d\varOmega =}{}+ \int _{\varOmega }w^{k}{P_{k}}\,d\varOmega -\rho \int _{\varOmega }w^{k}\varepsilon \,d\varOmega , \end{aligned}$$
(14)
$$\begin{aligned}& \rho \int _{\varOmega }w^{\varepsilon }\frac{\partial {\varepsilon }}{ \partial {t}}\,d\varOmega +\rho \int _{\varOmega }w^{\varepsilon }(\textbf{u} \cdot \nabla )\varepsilon \,d\varOmega = \int _{\partial \varOmega }w^{\varepsilon }\biggl[\biggl(\mu +\frac{\mu _{T}}{\sigma _{\varepsilon }} \biggr)\biggr]\nabla {\varepsilon } \cdot \textbf{n}\,d\partial \varOmega \\& \hphantom{\rho \int _{\varOmega }w^{\varepsilon }\frac{\partial {\varepsilon }}{ \partial {t}}\,d\varOmega +\rho \int _{\varOmega }w^{\varepsilon }(\textbf{u} \cdot \nabla )\varepsilon \,d\varOmega =}{}- \int _{\varOmega }\nabla {w^{\varepsilon }}\biggl[\biggl(\mu + \frac{\mu _{T}}{ \sigma _{\varepsilon }}\biggr)\nabla {\varepsilon }\biggr]\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }w^{\varepsilon }\frac{\partial {\varepsilon }}{ \partial {t}}\,d\varOmega +\rho \int _{\varOmega }w^{\varepsilon }(\textbf{u} \cdot \nabla )\varepsilon \,d\varOmega =}{}+C_{\varepsilon {1}} \int _{\varOmega }w^{\varepsilon }\frac{\varepsilon }{k}{p_{k}}\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }w^{\varepsilon }\frac{\partial {\varepsilon }}{ \partial {t}}\,d\varOmega +\rho \int _{\varOmega }w^{\varepsilon }(\textbf{u} \cdot \nabla )\varepsilon \,d\varOmega =}{}-C_{\varepsilon {2}}\rho \int _{\varOmega }w^{\varepsilon }\frac{ \varepsilon ^{2}}{k}\,d\varOmega , \end{aligned}$$
(15)
$$\begin{aligned}& \rho {C_{p}} \int _{\varOmega }w^{T}\frac{\partial {T}}{\partial {t}}\,d\varOmega +\rho {C_{p}} \int _{\varOmega }w^{T}(\textbf{u}\nabla {T})\,d\varOmega = \int _{\varOmega }w^{T}{q_{0}}\,d\varOmega - \int _{\varOmega }w^{T}(\nabla \cdot \textbf{q})\,d\varOmega , \end{aligned}$$
(16)

which is difficult to find the solution in the infinite space \(H^{1}(\varOmega )=\operatorname{span}\{\phi _{i}\}_{1}^{\infty }\). We apply Galerkin approximation. We post the problem into an N finite-dimensional subspace and choose an N-dimensional subspace \(H_{N} = \operatorname{span}\{\phi _{i}\}_{1}^{N} \subset H^{1}(\varOmega )\) for \(u_{1}\), \(u_{2}\), \(u_{3}\), k, ε, T and the associated test functions \(w^{u_{i}}\), \(w^{T}\), \(w^{k}\), and \(w^{\varepsilon }\). Let \(\{\phi _{i}\}_{i=1}^{N}\) be the basis functions of \(H_{N}\), then any unknown function v with a test function w can be approximated in the form of \(v\approx v_{N} = \sum _{i=1}^{N}\phi _{i}(x)v_{i}(t)\) and \(w=\sum _{i=1}^{N}\phi _{i}(x)w_{i}\):

$$\begin{aligned}& \textbf{u}(x,t)\approx \textbf{u}_{N} =\sum _{n=1}^{N}\phi _{n}(x) \textbf{u}_{n}(t), \end{aligned}$$
(17)
$$\begin{aligned}& \textbf{w}^{u}\approx \textbf{w}^{u}_{N} =\sum _{l=1}^{N}\phi _{l}(x) \textbf{w}_{l}^{u}(t), \end{aligned}$$
(18)
$$\begin{aligned}& T(x,t)\approx T_{N} =\sum_{n=1}^{N} \phi _{n}(x)T_{n}(t), \end{aligned}$$
(19)
$$\begin{aligned}& w^{T}\approx w^{T}_{N} =\sum _{l=1}^{N}\phi _{l}(x)w_{l}^{T}(t), \end{aligned}$$
(20)
$$\begin{aligned}& k(x,t)\approx k_{N} =\sum_{n=1}^{N} \phi _{n}(x)k_{n}(t), \end{aligned}$$
(21)
$$\begin{aligned}& w^{k}\approx w^{k}_{N} =\sum _{l=1}^{N}\phi _{l}(x)w_{l}^{k}(t), \end{aligned}$$
(22)
$$\begin{aligned}& \varepsilon (x,t)\approx \varepsilon _{N} =\sum _{n=1}^{N}\phi _{n}(x) \varepsilon _{n}(t), \end{aligned}$$
(23)
$$\begin{aligned}& w^{\varepsilon }\approx w^{\varepsilon }_{N} =\sum _{l=1}^{N}\phi _{l}(x)w _{l}^{\varepsilon }(t). \end{aligned}$$
(24)

Next, we choose an M-dimensional subspace \(H_{M}\subset H^{1}(\varOmega )\) for p and the test function \(w^{p}\). Let \(\{\psi \}_{i=1}^{M}\) be the basis functions of \(H_{M}\), then

$$\begin{aligned}& p(x,t)\approx p_{M} =\sum_{m=1}^{M} \psi _{m}(x)p_{m}(t), \end{aligned}$$
(25)
$$\begin{aligned}& w^{p}\approx w^{p}_{M} =\sum _{m=1}^{M}\psi _{m}(x)w_{m}^{p}(t). \end{aligned}$$
(26)

By substituting equations (18), (20), (22), (24), and (26) into equations (6), (8), (9), (10), and (11), and noting that \(\textbf{w}^{u}\), \(w^{T}\), \(w^{k}\), \(w^{\varepsilon }\), and \(w^{p}\) are arbitrary, we then obtain

$$\begin{aligned}& \int _{\varOmega }\psi _{m}(\nabla \cdot \textbf{u})\,d\varOmega =0, \end{aligned}$$
(27)
$$\begin{aligned}& \rho \int _{\varOmega }\phi _{l}\frac{\partial \textbf{u}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla ) \textbf{u}\,d\varOmega \\& \quad = \int _{\partial \varOmega }\phi _{l}\cdot \bigl(-p+(\mu + \mu _{T}) \bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr) \bigr)\cdot \textbf{n}\,d\partial \varOmega \\& \qquad {}- \int _{\varOmega }\nabla \phi _{l}\cdot \bigl((\mu +\mu _{T}) \bigl(\nabla \textbf{u}+(\nabla \textbf{u})^{T}\bigr) \bigr) \\& \qquad {}+ \int _{\varOmega }\nabla \phi _{l}\cdot {p}\,d\varOmega + \int _{\varOmega }\phi _{l}\cdot \textbf{F}\,d\varOmega , \end{aligned}$$
(28)
$$\begin{aligned}& \rho \int _{\varOmega }\phi _{l}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla )kd \varOmega = \int _{\partial \varOmega }\phi _{l}\cdot \biggl[\biggl(\mu + \frac{\mu _{T}}{\sigma _{k}}\biggr)\nabla {k}\biggr]\cdot \textbf{n}\,d\partial \varOmega \\& \hphantom{\rho \int _{\varOmega }\phi _{l}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla )kd \varOmega =}{}- \int _{\varOmega }\nabla \phi _{l}\cdot \biggl[\biggl(\mu + \frac{\mu _{T}}{\sigma _{k}}\biggr)\nabla {k}\biggr]\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }\phi _{l}\frac{\partial {k}}{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla )kd \varOmega =}{}+ \int _{\varOmega }\phi _{l}p_{k}\,d\varOmega -\rho \int _{\varOmega }\phi _{l} \cdot \varepsilon \,{d}\varOmega , \end{aligned}$$
(29)
$$\begin{aligned}& \rho \int _{\varOmega }\phi _{l}\frac{\partial \varepsilon }{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla ) \varepsilon \,{d}\varOmega = \int _{\partial \varOmega }\phi _{l}\cdot \biggl[\biggl( \mu + \frac{\mu _{T}}{\sigma _{\varepsilon }}\biggr)\nabla {\varepsilon }\biggr] \cdot \textbf{n}\,d\partial \varOmega \\& \hphantom{\rho \int _{\varOmega }\phi _{l}\frac{\partial \varepsilon }{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla ) \varepsilon {d}\varOmega =}{}- \int _{\varOmega }\nabla \phi _{l}\cdot \biggl[\biggl(\mu + \frac{\mu _{T}}{ \sigma _{\varepsilon }}\biggr)\nabla {\varepsilon }\biggr]\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }\phi _{l}\frac{\partial \varepsilon }{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla ) \varepsilon {d}\varOmega =}{}+C_{\varepsilon {1}} \int _{\varOmega }\phi _{l}\cdot \frac{\varepsilon }{k}p_{k}\,d\varOmega \\& \hphantom{\rho \int _{\varOmega }\phi _{l}\frac{\partial \varepsilon }{\partial {t}}\,d\varOmega + \rho \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla ) \varepsilon {d}\varOmega =}{}-C_{\varepsilon {2}}\rho \int _{\varOmega }\phi _{l}\cdot \frac{ \varepsilon ^{2}}{k}\varOmega , \end{aligned}$$
(30)
$$\begin{aligned}& \rho {C_{p}} \int _{\varOmega }\phi _{l}\frac{\partial {T}}{\partial {t}}\,d\varOmega + \rho {C_{p}} \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla {T})\,d\varOmega = \int _{\varOmega }\phi _{l}\cdot {q_{0}}\,d\varOmega \\& \hphantom{\rho {C_{p}} \int _{\varOmega }\phi _{l}\frac{\partial {T}}{\partial {t}}\,d\varOmega + \rho {C_{p}} \int _{\varOmega }\phi _{l}\cdot (\textbf{u}\cdot \nabla {T})\,d\varOmega =}{}- \int _{\varOmega }\phi _{l}\cdot (\nabla \cdot \textbf{q})\,d\varOmega \end{aligned}$$
(31)

for all \(l=1,2,3,\ldots ,N\) and \(m=1,2,3,\ldots ,M\).

Next, by substituting equations (17), (19), (21), (23), and (25) into equations (27), (28), (29), (30), and (31), we have

$$\begin{aligned}& \sum _{n=1}^{N} \int _{\varOmega }\psi _{m}\biggl(\frac{\partial \phi _{n}}{ \partial {x_{i}}}\biggr)\,d\varOmega {U_{i}} =0 \end{aligned}$$
(32)
$$\begin{aligned}& \rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega \dot{U_{i}}+\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\cdot {u_{j}} \frac{ \partial {\phi _{n}}}{\partial {x_{i}}}\,d\varOmega {U_{i}} = \int _{\partial \varOmega }\phi _{l}\biggl[-\sum _{m=1}^{M}\psi _{m} \\& \hphantom{\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega \dot{U_{i}}+\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\cdot {u_{j}} \frac{ \partial {\phi _{n}}}{\partial {x_{i}}}\,d\varOmega {U_{i}} =}{}+(\mu +\mu _{T})\sum _{n=1}^{N}\biggl( \frac{\partial \phi _{n}}{\partial {x_{i}}}\biggr)\biggr]\cdot {\textbf{n}}\,d\partial \varOmega \\& \hphantom{\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega \dot{U_{i}}+\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\cdot {u_{j}} \frac{ \partial {\phi _{n}}}{\partial {x_{i}}}\,d\varOmega {U_{i}} =}{}+\sum _{m=1}^{M} \int _{\varOmega }\frac{\partial \phi _{l}}{\partial {x_{i}}}\psi _{m}\,d\varOmega {P} \\& \hphantom{\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega \dot{U_{i}}+\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\cdot {u_{j}} \frac{ \partial {\phi _{n}}}{\partial {x_{i}}}\,d\varOmega {U_{i}} =}{}-\sum _{n=1}^{N} \int _{\varOmega }(\mu -\mu _{T})\frac{\partial \phi _{l}}{\partial {x_{i}}} \frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {U_{i}} \\& \hphantom{\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega \dot{U_{i}}+\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\cdot {u_{j}} \frac{ \partial {\phi _{n}}}{\partial {x_{i}}}\,d\varOmega {U_{i}} =}{}+ \int _{\varOmega }\phi _{l}\cdot {\textbf{F}}\,d\varOmega \end{aligned}$$
(33)
$$\begin{aligned}& \rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega { \dot{K_{i}}}+ \rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}{u_{j}} \frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {K_{i}} \\& \quad =\sum _{n=1}^{N} \int _{\varOmega }\biggl[\biggl(\mu +\frac{\mu _{T}}{\sigma _{k}}\biggr)\phi _{l}\frac{\partial \phi _{n}}{ \partial {x_{i}}}\biggr]\cdot \textbf{n}\,d\partial \varOmega \\& \qquad {}-\sum _{n=1}^{N} \int _{\varOmega }\biggl(\mu +\frac{\mu _{T}}{\sigma _{k}}\biggr) \frac{ \partial \phi _{l}}{\partial {x_{i}}}\frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {K_{i}} \\& \qquad {}+ \int _{\varOmega }\phi _{l}{p_{k}}\,d\varOmega \\& \qquad {}-\rho \sum _{n=1}^{N}\phi _{l}\phi _{n}\,d\varOmega {E_{i}} \end{aligned}$$
(34)
$$\begin{aligned}& \rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega { \dot{E_{i}}}+ \rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}{u_{j}} \frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {E_{i}} \\& \quad =\sum _{n=1}^{N} \int _{\varOmega }\biggl[\biggl(\mu +\frac{\mu _{T}}{\sigma _{\varepsilon }}\biggr)\phi _{l}\frac{\partial \phi _{n}}{\partial {x_{i}}}\biggr]\cdot \textbf{n}\,d\partial \varOmega \\& \qquad {}-\sum _{n=1}^{N} \int _{\varOmega }\biggl(\mu +\frac{\mu _{T}}{ \sigma _{\varepsilon }}\biggr) \frac{\partial \phi _{l}}{\partial {x_{i}}}\frac{ \partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {E_{i}} \\& \qquad {}+C_{\varepsilon {1}} \int _{\varOmega }\phi _{l}{p_{k}}\,d\varOmega \\& \qquad {}-C_{\varepsilon {2}}\rho \sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega {E_{i}} \end{aligned}$$
(35)
$$\begin{aligned}& \rho {C_{p}}\sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega { \dot{T_{i}}}+\rho {C_{p}}\sum _{n=1}^{N} \int _{\varOmega }\phi _{l}{u _{j}} \frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {T_{i}} = \int _{\varOmega }\phi _{l}{q_{0}}\,d\varOmega \\& \hphantom{\rho {C_{p}}\sum _{n=1}^{N} \int _{\varOmega }\phi _{l}\phi _{n}\,d\varOmega { \dot{T_{i}}}+\rho {C_{p}}\sum _{n=1}^{N} \int _{\varOmega }\phi _{l}{u _{j}} \frac{\partial \phi _{n}}{\partial {x_{i}}}\,d\varOmega {T_{i}} =}{}- \int _{\varOmega }\phi _{l}\cdot (\nabla \cdot \textbf{q})\,d\varOmega \end{aligned}$$
(36)

for all \(n=1,2,3,\ldots,N\), \(m=1,2,3,\ldots,M\), and the superposed dot represents differentiation with respect to time.

2 Numerical examples

The street canyon model is mimicked from the urban region in which the skytrain station is above the main street surrounded by symmetrical buildings during traffic. To investigate the air flow on heat transfer in the street canyon, three levels of wind speed are chosen to be 7 km/h, 18 km/h, and 25 km/h corresponding to the gentle, moderate, and strong wind speeds respectively. We assume that no air flows in and out of the building and the skytrain station. Above the rooftop of the building on one side of the street canyon, the 35°C wind flows into the street canyon. On the other side and on the top surface of the street canyon, wind is allowed to flow in and out of the street canyon. The finite element solutions of the air flow and the temperature distribution are simulated using COMSOL Multiphysics [33].

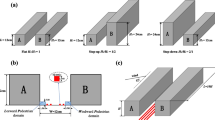
As the street canyon is surrounded by symmetrical buildings on both sides of the street, the 2D domain can be used to model the street canyon region. The computational domain is a vertical cross section of the air-flow area in a street canyon in which the street is surrounded by the 10-meter-tall buildings on both sides of the street. Figure 1(a) presents the dimension of the computational domain with its inlet boundary \(\partial \varOmega _{\mathrm{in}}\), and the outlet boundaries \(\partial \varOmega _{\mathrm{open}}\). The skytrain station with the width of 9 m and the height of 5 m is located at 12 m above the street. Two sidewalks with the width of 3 m are on both sides of the 9 m width street. The heat source due to traffic is applied on the surface of the street. Figure 1(b) shows a non-uniform domain mesh with a number of triangular-shaped elements with 48,125 degrees of freedom, 7899 nodes, and 15,100 elements. Due to the presence of two main regions including sidewalks and heat source on the street, the meshing on these regions is more delicate than the other portion of the street canyon in order to obtain accurate calculations at the vital parts in the heat transfer process.

Figure 1
figure 1

Geometric domain of the two dimensional of the street canyon: (a) defining the domain area, and (b) meshing the computational domain

Full size image

To investigate the effect of wind speed of the air flow on the temperature distribution, we run the simulation until we obtain the static pattern of the air flow for each case of the wind speed. The results shown in Fig. 2 and Fig. 3 indicate that the speed of the air flow has a significant effect on the temperature distribution in the cavity under the skytrain. The surface plot of the temperature distribution and its contour at the bottom left side next to the building are presented in Figs. 4 to 10. These results indicate that lower speed gives the higher heat accumulation in the cavity of the street canyon, especially at the region near the building above the sidewalk on the left side of the street. Figure 11 illustrates the patterns of the air flow obtained from three cases of wind speed. The results show the flow of air loop in the cavity of the street canyon. This flow may reduce the air quality in the street canyon and have a significant effect on the temperature accumulation in the summer season.

Figure 2
figure 2

The surface temperature (°C) at steady state when \(u=7\) km/h (gentle wind): (a) The entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 3
figure 3

The surface temperature (°C) at steady state of the zoom-in selected area: (a) \(u=7\) km/h (gentle wind), (b) \(u=18\) km/h (moderate wind) and (c) \(u=25\) km/h (strong wind)

Full size image
Figure 4
figure 4

The surface temperature (°C) at steady state when \(u=7\) km/h (gentle wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 5
figure 5

The surface temperature (°C) at steady state when \(u=18\) km/h (moderate wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 6
figure 6

The surface temperature (°C) at steady state when \(u=25\) km/h (strong wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 7
figure 7

The temperature contour (°C) at steady state when \(u=7\) km/h (gentle wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 8
figure 8

The temperature contour (°C) at steady state when \(u=18\) km/h (moderate wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 9
figure 9

The temperature contour (°C) at steady state when \(u=25\) km/h (strong wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 10
figure 10

The velocity vector (km/h) at steady state when \(u=7\) km/h (gentle wind): (a) Half of the entire computational domain, and (b) Zoom-in of the selected area

Full size image
Figure 11
figure 11

The velocity vector (km/h) at steady state state of the zoom-in selected area: (a) \(u=7\) km/h (gentle wind), (b) \(u=18\) km/h (moderate wind), and (c) \(u=25\) km/h (strong wind)

Full size image

3 Conclusions

An efficient mathematical model of the air flow and heat transfer in the skytrain-street canyon in which the street is surrounded by symmetrical buildings is developed. The air flow and heat transfer in the region underneath the skytrain during traffic in the summer season is analyzed numerically. The effect of wind speed of the air flow on the temperature distribution is investigated. The results show that our model can capture the air flow with heat transfer phenomena in the skytrain-street canyon effectively. The results of this research may help civil engineers in the optimization of the air control system in the urban street canyon with the skytrain.