1 Introduction

There are many forms of pollution, including air, water, thermal, noise, soil contamination, etc. [1, 2]. The air pollution is considered to be the world’s top environmental cause of mortality [3]. It has been reported that pollution has killed many million people in the world [4]. The critical air pollutants, including carbon dioxide, lead, nitrogen dioxide, ozone particles, and sulfur dioxide [5,6,7,8,9,10], come from factories, industries, and transportation. The transportation sector is responsible for a large portion of air pollution in large urban centers due to vehicle emissions. To protect public health, understanding how to keep the air quality acceptable in street canyons or other urban areas is important. Over the last few decades, many researchers have focused on the air quality control using both experimental and numerical models. As experimental studies cannot illustrate the pattern of pollutant dispersion accurately, numerical models have thus been used as a main tool over the last few decades to investigate the local sources of air pollution in street canyon environment under several aspects such as the presence of vegetation [11, 12] and dust [13], the surrounding airflow, and air pollutant dispersion [14,15,16,17,18,19,20,21,22,23,24]. Chan et al. proposed a two-dimensional model of air pollutant dispersion in an isolated street canyon [16]. Chang et al. applied the wind tunnel model to predict the pollutant dispersion in urban street canyons with different height arrangement [17]. Kim et al. studied the thermal effects on the flow and pollutant dispersion in urban street canyons [20]. In 2011, Liu proposed two numerical models to predict vehicle exhaust dispersion in urban areas with or without a wind field [25]. In his model, the effect of building and street canyon configuration and the turbulent energy produced by moving vehicles on the pollutant propagation were investigated. A few years later in 2014, numerical investigations on pollutant dispersion in street canyons with emission sources located near the ground level were performed by Madalozzo et al. using the pseudo-compressibility hypothesis of mass conservation, the Navier–Stokes equations, energy equation, and pollutant transport equation [26]. Their results show that temperature and street-canyon geometry affect both the wind flow patterns and pollutant concentration. Recently, Aristodemou et al. studied the effect of tall buildings on turbulent airflows and pollution dispersion at a seven-building site configuration using the mesh-adaptive large eddy simulation of incompressible turbulent flow [14]. Suebyat and Pochai investigated numerically air pollution in a heavy traffic area under the Skytrain platform in Bangkok, Thailand [27]. Pothiphan et al. studied the impact of wind speeds on heat transfer in a street canyon with a Skytrain station [28]. As the results obtained from existing models are mostly based on incompressible fluid flow with or without the pseudo-compressibility assumption in street canyons with rows of buildings, our understanding of traffic-related air pollution in the street canyon with Skytrain is very limited.

In this study, we investigate the effect of wind velocity on dispersion pattern of the traffic-related air pollution in the street canyon with Skytrain. For a single-pollutant approach to air pollution, namely, carbon dioxide, governing equations of the problem in adiabatic process are the Reynolds-averaged Navier–Stokes (RANS) equations of compressible turbulent flow and the convection–diffusion equations of the CO2 concentration. Finite element method is utilized for the solution of the problem. Nine wind conditions are chosen to demonstrate the impact of airflow on the pattern of CO2 dispersion in the study region.

2 Mathematical model

To describe the transport of CO2 in a street canyon with Skytrain, a transport model for an adiabatic system is developed. The compressible turbulent airflow and propagation of CO2 pollutant in the street canton with Skytrain Ω region are governed by the following initial boundary value problem (IBVP) which includes the Reynolds-averaged Navier–Stokes (RANS) equations and the convection–diffusion equations of the CO2 concentration [29], namely:

  • Mass conservation equation of compressible fluid:

    $$ \frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \vec{u})=0, $$
    (1)

  • Reynolds-averaged Navier–Stokes (RANS) equations:

    $$\begin{aligned}& \begin{aligned}[b] \rho \frac{\partial \vec{u}}{\partial t}+\rho (\vec{u}\cdot \nabla ) \vec{u} &=\nabla \cdot \biggl[-p\mathbf{I}+\mu _{e} \bigl(\nabla \vec{u}+( {\nabla \vec{u})}^{T} \bigr) \\ &\quad {}-\frac{2}{3}\mu _{e}(\nabla \cdot \vec{u})\mathbf{I}- \frac{2}{3} \rho k\mathbf{I} \biggr]+F, \end{aligned} \end{aligned}$$
    (2)
    $$\begin{aligned}& \rho \frac{\partial k}{\partial t}+\rho (\vec{u}\cdot \nabla )k = \nabla \cdot \biggl[ \biggl(\mu +\frac{\mu _{T}}{\sigma _{k}} \biggr) \biggr] \nabla k + P_{k} - \rho \epsilon , \\ \end{aligned}$$
    (3)
    $$\begin{aligned}& \rho \frac{\partial \varepsilon }{\partial t}+\rho (\vec{u}\cdot \nabla )\varepsilon = \nabla \cdot \biggl[ \biggl(\mu +\frac{\mu _{T}}{ \sigma _{\varepsilon }} \biggr) \biggr] \nabla \varepsilon + C_{\varepsilon _{1}}\frac{\varepsilon }{k}P_{k}-C_{\varepsilon _{2}} \rho \frac{ \varepsilon ^{2}}{k}, \end{aligned}$$
    (4)

  • Pollutant transport equation:

    $$ \frac{\partial c}{\partial t} - \nabla \cdot (\alpha \nabla c)+ \vec{u} \cdot \nabla c = S, $$
    (5)

    where ρ, u⃗, k, ε and c are unknown variables (see the details in Table 1), α denotes diffusion coefficient of CO2, and F and S respectively denote body force and pollution source, and \(\mu _{e}\) and \(P_{k}\) are the effective viscosity and turbulent kinetic energy production, which are respectively defined by

    $$\begin{aligned}& \mu _{e}=\mu +\mu _{t}\quad \mbox{with } \mu _{t}=\rho C_{\mu }k^{2}/\varepsilon ,\quad \mbox{and} \\& P_{k}=\mu _{t} \bigl(\nabla \vec{u}: \bigl(\nabla \vec{u}+(\nabla \vec{u})^{T}\bigr) \bigr). \end{aligned}$$

    Other constant model parameters are shown in Table 2.

    Table 1 Unknown variables
    Full size table
    Table 2 Model constants
    Full size table

In equation (2), F corresponding to body force due to concentration effect is defined by

$$ F = \rho \beta (c-c_{0}) \vec{g}, $$
(6)

where β is the coefficient of volumetric expansion due to concentration variation, g⃗ is the gravity acceleration vector, and \(c_{0}\) is a reference value for concentration. In adiabatic flow, pressure term p, a function of density ρ and the ratio of specific heat κ [30], is defined by

$$ p = \frac{1}{\kappa }\rho ^{\kappa }. $$
(7)

To completely define the initial boundary value problem (IVBP), the set of initial and boundary conditions [31] is established as follows:

  • The values of CO2 concentration at initial state \(t=0\text{ s}\) is assumed to be zero, i.e.,

    $$ c(\vec{x}, 0) = 0,\quad \forall \vec{x} \in \varOmega . $$

  • The pollutant emission sources are from traffic vehicles located near the ground level. On the inflow boundary of CO2 pollutant, we set

    $$ c(\vec{x}, t) = c_{0},\quad \forall \vec{x} \in \partial \varOmega _{S}. $$

  • On the inflow boundary of turbulent airflow \(\partial \varOmega _{ \mathrm{in}}\), we set

    $$ \vec{u}(\vec{x},t) = u_{0} \hat{u} ,\qquad k(\vec{x},t)= \frac{3}{2}(u_{\mathrm{ref}}I_{T})^{2},\qquad \varepsilon (\vec{x},t)={c_{\mu }}^{\frac{3}{4}}\frac{k^{\frac{3}{2}}}{L _{T}}, $$

    where û is the unit vector representing wind direction, \(I_{T}\) and \(L_{T}\) denote turbulent length scale and turbulent intensity, respectively, defined by

    $$ I_{T} = 0.16 \mathit{Re}^{\frac{1}{8}},\qquad L_{T} = c_{\mu }\frac{k^{ \frac{2}{3}}}{\varepsilon }. $$

  • On open (outlet) boundary \(\partial \varOmega _{\mathrm{out}}\), the conditions are set to be

    $$\begin{aligned} & \biggl[-\frac{\rho ^{\kappa }}{\kappa }\mathbf{I}+\mu _{e} \bigl(\nabla \vec{u}+({\nabla \vec{u})}^{T} \bigr)-\frac{2}{3}\mu _{e}(\nabla \cdot \vec{u})\mathbf{I}-\frac{2}{3}\rho k \mathbf{I} \biggr]\vec{n}=f_{0} \vec{n}, \end{aligned}$$
    (8)
    $$\begin{aligned} &\nabla k\cdot \vec{n}=0, \quad \mbox{and}\quad \nabla \varepsilon \cdot \vec{n}=0\quad \text{if } \vec{u}\cdot \vec{n}\geq 0, \end{aligned}$$
    (9)
    $$\begin{aligned} & k(\vec{x},t)=\frac{3}{2}(U_{\mathrm{ref}}I_{T})^{2}\quad \mbox{and}\quad \varepsilon (\vec{x},t)=C_{\mu }^{3/4} \frac{k^{3/2}}{L_{T}}\quad \text{if } \vec{u}\cdot \vec{n}< 0, \end{aligned}$$
    (10)
    $$\begin{aligned} &{-} \vec{n}\cdot \alpha \nabla c=0 \quad \text{if } \vec{n}\cdot \vec{u}\geq 0, \end{aligned}$$
    (11)
    $$\begin{aligned} &c(\vec{x},t) = c_{0}\quad \text{if } \vec{n}\cdot \vec{u}< 0. \end{aligned}$$
    (12)

  • In addition, we apply the near-wall condition on other boundaries \(\partial \varOmega _{w}\), including the walls of the Skytrain and surrounding buildings, and the surface of the road and the sidewalks, i.e.,

    $$\begin{aligned} &\vec{u}\cdot \vec{n}=0,\qquad \nabla k\cdot \vec{n}=0,\qquad \varepsilon =\rho \frac{C _{\mu }k^{2}}{\kappa _{v}\delta _{w}^{+}\mu }, \end{aligned}$$
    (13)
    $$\begin{aligned} &\biggl[\mu _{e} \bigl(\nabla \vec{u}+(\nabla \vec{u})^{T} \bigr)-\frac{2}{3}\mu _{e}(\nabla \cdot \vec{u})\mathbf{I}- \frac{2}{3}\rho k\mathbf{I} \biggr]\vec{n}=-\rho \frac{u_{\tau }}{\delta _{w}^{+}} \vec{u_{t}}, \end{aligned}$$
    (14)

    for \(\vec{u_{t}}=\vec{u}-(\vec{u}\cdot \vec{n})\vec{n}\) and \(u_{\tau }\) being the friction velocity.

3 Finite element formulation

The variational statement corresponding to the above IBVP is

Find \(\vec{u}\in [H^{1}(\varOmega )]^{3}\), \(\rho , k, \varepsilon , c \in H^{1}(\varOmega )\) that satisfy all boundary conditions, \(\forall \omega _{u}, \omega _{\rho }, \omega _{k}, \omega _{\varepsilon }, \omega _{c} \in H_{0}^{1}(\varOmega )\),

$$\begin{aligned} &\biggl(\frac{\partial \rho }{\partial t}, \omega _{\rho }\biggr)+\bigl(\nabla \cdot ( \rho \vec{u}),\omega _{\rho }\bigr)=0, \end{aligned}$$
(15)
$$\begin{aligned} &\biggl(\rho \frac{\partial {\vec{u}}}{\partial t},\omega _{u}\biggr)+\bigl(\rho ( \vec{u}\cdot \nabla )\vec{u},\omega _{u}\bigr)+(\mu _{e} \nabla \vec{u}, \nabla \omega _{u}) -\biggl\langle \mu _{e} \frac{\partial \vec{u}}{\partial \vec{n}}, \omega _{u}\biggr\rangle \\ &\quad = -\biggl(\nabla \frac{\rho ^{\kappa }}{\kappa }\vec{I}, \omega _{u} \biggr)+(\vec{F},\omega _{u}) , \end{aligned}$$
(16)
$$\begin{aligned} &\biggl(\rho \frac{\partial k}{\partial t},\omega _{k}\biggr)+\bigl(\rho ( \vec{u} \cdot \nabla )k,\omega _{k}\bigr)+\biggl(\biggl(\mu + \frac{\mu _{T}}{\sigma _{k}}\biggr)\nabla k ,\nabla \omega _{k}\biggr) \\ &\quad =(P_{k},\omega _{k})-(\rho \varepsilon ,\omega _{k}), \end{aligned}$$
(17)
$$\begin{aligned} &\biggl(\rho \frac{\partial \varepsilon }{\partial t},\omega _{\varepsilon }\biggr)+\bigl(\rho ( \vec{u}\cdot \nabla )\varepsilon ,\omega _{\varepsilon }\bigr)+\biggl(\biggl( \mu +\frac{\mu _{T}}{\sigma _{\varepsilon }}\biggr)\nabla \varepsilon ,\nabla \omega _{\varepsilon }\biggr) \\ &\quad =\biggl(C_{\varepsilon _{1}}\frac{\varepsilon _{1}}{k}P_{k} - C_{\varepsilon _{2}}\rho \frac{\varepsilon ^{2}}{k},\omega _{\varepsilon }\biggr), \end{aligned}$$
(18)
$$\begin{aligned} &\biggl(\rho \frac{\partial c}{\partial t},\omega _{c}\biggr)+(\alpha \nabla c, \nabla \omega _{c})+(\vec{u}\cdot \nabla c, \omega _{c}) = (s, \omega _{c}), \end{aligned}$$
(19)

where \((u,v)=\int _{\varOmega }uv\, d\varOmega \), \(H^{1}(\varOmega )\) is the Sobolev space \(W^{1,2}(\varOmega )\) with norm \(\|\cdot \|_{1,2,\varOmega }\), \(H_{0}^{1}(\varOmega )=\{v|v\in H^{1}(\varOmega )\mbox{ and } v=0\mbox{ on }\partial \varOmega \}\), and \(L^{2}(\varOmega )\) is the space of integrable functions.

The fourth term on the LHS of equation (15) is

$$\begin{aligned} \biggl\langle \mu _{e} \frac{\partial \vec{u}}{\partial \vec{n}}, \omega _{u}\biggr\rangle &= \int _{\partial \varOmega _{\mathrm{out}}} \omega _{u} \biggl( f_{0}+ \biggl(\frac{\rho ^{\kappa }}{\kappa }+\frac{2}{3}\mu _{e} \nabla \cdot \vec{u} + \frac{2}{3}\rho k\biggr) \mathbf{I} \biggr) \vec{n} \,ds \\ &\quad {} + \int _{\partial \varOmega _{w}} \omega _{u} \biggl( -\rho \frac{u_{\tau }}{ \delta _{w}^{+}} \vec{u}_{t}+ \biggl(\frac{2}{3}\mu _{e} \nabla \cdot \vec{u} + \frac{2}{3}\rho k\biggr) \mathbf{I} \biggr) \vec{n} \,ds. \end{aligned}$$
(20)

Applying the Galerkin approximation, we choose an N-dimensional subspace \(H_{N} \subset H^{1}(\varOmega )\) for u⃗, ρ, k, ε and \(H_{0} \subset H_{0}^{1}(\varOmega )\) for \(\omega _{u}\), \(\omega _{ \rho }\), \(\omega _{k}\), \(\omega _{\varepsilon }\), \(\omega _{c}\). Let \(\{\phi _{j} \}_{j=1}^{N}\) be a set of basis functions of \(H_{N}\) and \(H_{0}\). Then any unknown function f and test function h can be expressed in the following form:

$$ f \simeq f_{N} = \sum_{j=1}^{N} f_{j}(t) \phi _{j}(\vec{x}),\qquad h \simeq h_{N} = \sum_{i=1}^{N} h_{i} \phi _{i}(\vec{x}). $$

Here, we consider a two-dimensional problem. For a 2D linear triangular element, we have a system of nonlinear ordinary differential equations, for \(i = 1,2,3\),

$$\begin{aligned} & \sum_{j=1}^{3} \biggl( \int _{\varOmega }\phi _{i} \phi _{j}\, d \varOmega \biggr) \dot{\rho }_{j} + \biggl( \int _{\varOmega }( \nabla \cdot \vec{u})\phi _{i} \phi _{j} \,d\varOmega \biggr) \rho _{j}=0, \end{aligned}$$
(21)
$$\begin{aligned} &\sum_{j=1}^{3} \biggl( \int _{\varOmega }\phi _{i} \phi _{j}\, d \varOmega \biggr) \dot{\vec{u}}_{j} + \biggl( \int _{\varOmega }\phi _{i} (\vec{u} \cdot \nabla \phi _{j}) + \nu _{e} \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega \\ &\qquad {} -\frac{2}{3\rho } \int _{\partial \varOmega _{\mathrm{out}}} \mu _{e} \phi _{i} \frac{\partial \phi _{j}}{\partial n} \,ds -\frac{2}{3\rho } \int _{\partial \varOmega _{w}} \mu _{e} \phi _{i} \frac{\partial \phi _{j}}{ \partial n} \,ds \biggr) \vec{u}_{t} \\ &\quad = \frac{1}{\rho } \int _{\partial \varOmega _{\mathrm{out}}} \phi _{i} \biggl(f_{0}+ \frac{\rho ^{\kappa }}{\kappa } + \frac{2}{3}\rho ^{\kappa }\biggr) \mathbf{I} \,ds + \frac{1}{\rho } \int _{\partial \varOmega _{w}} \phi _{i} \biggl(- \rho \frac{u_{\tau }}{\delta _{w}^{+}} \vec{u}_{t} + \frac{2}{3} \rho k \biggr) \mathbf{I} \,ds \\ &\qquad {}- \frac{1}{\rho } \int _{\varOmega } \phi _{i} \biggl( \nabla \frac{\rho ^{\kappa }}{\kappa } \mathbf{I} + \vec{F}\biggr) \, d \varOmega , \end{aligned}$$
(22)
$$\begin{aligned} &\sum_{j=1}^{3} \biggl( \int _{\varOmega }\phi _{i} \phi _{j}\, d \varOmega \biggr) \dot{k}_{j}+ \biggl( \int _{\varOmega }\phi _{i} (\vec{u}\cdot \nabla )\phi _{j} \,d\varOmega + \int _{\varOmega }\biggl(\nu +\frac{\nu _{T}}{\sigma _{k}}\biggr) \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega \biggr) k_{j} \\ &\quad =\frac{1}{\rho } \int _{\varOmega }P_{k} \phi _{i} \,d\varOmega - \int _{ \varOmega } \varepsilon \phi _{i} \,d\varOmega , \end{aligned}$$
(23)
$$\begin{aligned} &\sum_{j=1}^{3} \biggl( \int _{\varOmega }\phi _{i} \phi _{j}\, d \varOmega \biggr) \dot{\varepsilon }_{j}+ \biggl( \int _{\varOmega }\phi _{i} (\vec{u}\cdot \nabla )\phi _{j} \,d\varOmega + \int _{\varOmega }\biggl(\nu +\frac{\nu _{T}}{ \sigma _{\varepsilon }}\biggr) \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega \biggr) \varepsilon _{j} \\ &\quad = \int _{\varOmega }\phi _{i} \biggl(C_{\varepsilon _{1}} \frac{\varepsilon }{ \rho k}P_{k} - C_{\varepsilon _{2}} \frac{\varepsilon ^{2}}{k} \biggr) \,d\varOmega , \end{aligned}$$
(24)
$$\begin{aligned} & \sum_{j=1}^{3} \biggl( \int _{\varOmega }\phi _{i} \phi _{j}\, d \varOmega \biggr) \dot{c}_{j}+ \biggl( \int _{\varOmega }\alpha \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega + \int _{\varOmega }\phi _{i} \vec{u}\cdot \nabla \phi _{j} \,d\varOmega \biggr) c_{j} = \int _{\varOmega }s \phi _{i} \, d \varOmega , \end{aligned}$$
(25)

or in matrix form as

$$ \mathbf{M}^{(e)} \dot{\mathbf{u}}+ \mathbf{A}^{(e)} \mathbf{u} = \mathbf{b}^{(e)} , $$
(26)

where \(\dot{\mathbf{u}}^{T}=(\dot{\rho }, \dot{\vec{u}}, \dot{k}, \dot{\varepsilon }, \dot{c})^{T}\), \(\mathbf{u}^{T}=(\rho , \vec{u}, k, \varepsilon , c)^{T}\), \(\mathbf{M}^{(e)}\) and \(\mathbf{A}^{(e)}\) are the element matrices, and \(\mathbf{b}^{(e)}\) denotes the load vector defined as follows:

$$\begin{aligned}& \mathbf{M}^{(e)} = \begin{bmatrix} M & 0 & \cdots & \cdots & \cdots & 0 \\ 0 & M & 0 & & & \vdots \\ \vdots & \ddots & \ddots & \ddots & & \vdots \\ \vdots & & \ddots & \ddots & \ddots & \vdots \\ \vdots & & & 0 & M & 0 \\ 0 & \cdots & \cdots & \cdots & 0 & M \end{bmatrix} _{21 \times 21} , \end{aligned}$$
(27)
$$\begin{aligned}& M = (m_{ij})_{3 \times 3} = \int _{\varOmega }\phi _{i} \phi _{j} \, d \varOmega , \end{aligned}$$
(28)
$$\begin{aligned}& \mathbf{A}^{(e)} = \begin{bmatrix} A_{\rho } & 0 & \cdots & \cdots & 0 \\ 0 & A_{\vec{u}} & 0 & & \vdots \\ \vdots & 0 & A_{k} & 0 & \vdots \\ \vdots & & 0 & A_{\varepsilon } & 0 \\ 0 & \cdots & \cdots & 0 & A_{c} \end{bmatrix} _{21 \times 21} , \end{aligned}$$
(29)
$$\begin{aligned}& A_{\rho } = ({}_{\rho }a_{ij})_{3 \times 3},\quad {}_{\rho }a_{ij} = \int _{\varOmega }( \nabla \cdot \vec{u})\phi _{i} \phi _{j} \, d \varOmega , \\& A_{\vec{u}} = ({}_{\vec{u}} a_{ij})_{3 \times 3}, \\& \quad {}_{\vec{u}} a_{ij} = \int _{\varOmega }\phi _{i} (\vec{u} \cdot \nabla \phi _{j}) + \nu _{e} \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega -\frac{2}{3\rho } \int _{\partial \varOmega _{\mathrm{out}}} \mu _{e} \phi _{i} \frac{\partial \phi _{j}}{ \partial n} \,ds-\frac{2}{3\rho } \int _{\partial \varOmega _{w}} \mu _{e} \phi _{i} \frac{ \partial \phi _{j}}{\partial n} \,ds, \\& A_{k} = ({}_{k} a_{ij})_{3 \times 3},\quad {}_{k} a_{ij} = \int _{\varOmega } \phi _{i} (\vec{u}\cdot \nabla )\phi _{j} \,d\varOmega + \int _{\varOmega }\biggl( \nu +\frac{\nu _{T}}{\sigma _{k}}\biggr) \nabla \phi _{i} \nabla \phi _{j} \, d \varOmega , \\& A_{\varepsilon } = ({}_{\varepsilon }a_{ij})_{3 \times 3},\quad {}_{\varepsilon }a_{ij} = \int _{\varOmega }\phi _{i} (\vec{u}\cdot \nabla )\phi _{j} \,d\varOmega + \int _{\varOmega }\biggl(\nu +\frac{\nu _{T}}{ \sigma _{\varepsilon }}\biggr) \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega , \\& A_{c} = ({}_{c} a_{ij})_{3 \times 3},\quad {}_{c} a_{ij} = \int _{\varOmega } \alpha \nabla \phi _{i} \nabla \phi _{j} \,d\varOmega + \int _{\varOmega }\phi _{i} \vec{u}\cdot \nabla \phi _{j} \,d\varOmega , \end{aligned}$$
(30)
$$\begin{aligned}& \mathbf{b}^{(e)} = \begin{bmatrix} b_{\rho } \\ b_{\vec{u}} \\ b_{k} \\ b_{\varepsilon } \\ b_{c} \end{bmatrix} _{21 \times 1} , \end{aligned}$$
(31)
$$\begin{aligned}& b_{\rho } = ({}_{\rho }b_{ij})_{3 \times 3},\quad {}_{\rho }b_{ij} = 0, \\& b_{\vec{u}} = ({}_{\vec{u}} b_{ij})_{3 \times 3}, \\& \quad {}_{\vec{u}} b_{ij} = \frac{1}{\rho } \int _{\partial \varOmega _{\mathrm{out}}} \phi _{i} \biggl(f _{0} + \frac{\rho ^{\kappa }}{\kappa } + \frac{2}{3}\rho ^{\kappa }\biggr) \mathbf{I} \,ds + \frac{1}{\rho } \int _{\partial \varOmega _{w}} \phi _{i} \biggl(- \rho \frac{u_{\tau }}{\delta _{w}^{+}} \vec{u}_{t} + \frac{2}{3} \rho k\biggr) \mathbf{I} \,ds \\& \hphantom{\quad {}_{\vec{u}} b_{ij} ={}}{}- \frac{1}{\rho } \int _{\varOmega } \phi _{i} \biggl(\nabla \frac{\rho ^{\kappa }}{\kappa } \mathbf{I} + \vec{F}\biggr) \, d \varOmega , \\& b_{k} = ({}_{k} b_{ij})_{3 \times 3},\quad {}_{k} b_{ij} = \frac{1}{ \rho } \int _{\varOmega }P_{k} \phi _{i} \,d\varOmega - \int _{\varOmega } \varepsilon \phi _{i} \,d\varOmega , \\& b_{\varepsilon } = ({}_{\varepsilon }b_{ij})_{3 \times 3},\quad {}_{\varepsilon }b_{ij} = \int _{\varOmega }\phi _{i} \biggl(C_{\varepsilon _{1}} \frac{\varepsilon }{\rho k}P_{k} - C_{\varepsilon _{2}} \frac{ \varepsilon ^{2}}{k} \biggr) \,d\varOmega , \\& b_{c} = ({}_{c} b_{ij})_{3 \times 3},\quad {}_{c} b_{ij} = \int _{\varOmega }s \phi _{i} \,d\varOmega . \end{aligned}$$
(32)

By assembling all element matrices and all element vectors, we obtain the global system

$$ \mathbf{M} \dot{\mathbf{u}}+ \mathbf{A} \mathbf{u} = \mathbf{F}, $$
(33)

which can be solved by a time integration scheme at any instant of time:

$$ \mathbf{M} \frac{\mathbf{u}_{n+1} - \mathbf{u}_{n}}{\triangle t} + \triangle (\mathbf{u}_{n}) \mathbf{u}_{n} = \mathbf{F}_{n}. $$
(34)

4 Numerical result

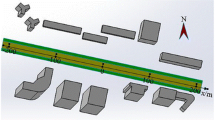
This section investigates numerically the effect of the airflow on air pollution dispersion within a street canyon having a Skytrain platform, 20- and 38-meter-tall buildings, and two 5-meter-width sidewalks. COMSOL Multiphysics Modelling software is applied to simulate the finite element approximation of solutions [29]. We assume that no airflow and pollutant emission occur in solid structures including buildings, a Skytrain platform and sidewalks, and emissions of carbon dioxide are only from traffic vehicles under the Skytrain. Figure 1 presents two-dimensional Skytrain–street-canyon analysis with five emission sources on the ground level. The Skytrain station with width of 21 m and height of 12 m is located 13 m above the traffic level. The computational domain with a nonuniform finite element mesh is shown in Fig. 2.

Figure 1
figure 1

Computational domain

Full size image
Figure 2
figure 2

Domain mesh

Full size image

The emission rate of 0.068 mol/m3, equivalent to the amount of pollutant from 20 vehicles, is chosen to analyze the impact of wind velocity on concentration distribution of air pollutants. Air is assumed to flow into the study region from the left-side rooftop. Figure 3 shows wind velocity with its streamlines and contour lines of carbon dioxide concentration obtained from the model with inflow wind speed of 10 km/h from southeast. The wind splits into two parts, upstream and downstream, when it approaches the Skytrain station. The downstream part flows into the Skytrain cavity in which three wind-circulation zones occur. A large circulation zone is below the Skytrain station and two small circulation zones are next to the buildings. This wind flow field has a significant impact on the dispersion and distribution of air pollutants in the Skytrain region. Air pollutants from traffic vehicles propagate into three wind-circulation zones and the area next to the building and Skytrain station. Figures 4 and 5 illustrate the effect of inflow features on the airflow pattern and distribution of air pollutant concentration, respectively. The inflow wind with speed of 5, 10, and 20 km/h gives different patterns of airflow and air pollutant concentration compared to those obtained from the models with other inflow conditions. The air pollutant concentration obtained from the model with wind blowing from northeast spreads throughout the Skytrain cavity and both sides of the Skytrain station while it distributes to the right-sided region for the inflow wind blowing from east and southeast. Figures 6 and 7 compare the profiles of wind velocity and air pollutant concentration at 1.5- and 2-meter heights above the ground obtained from the inflow wind models using 3 different speeds and 3 different wind blowing directions. The results indicate that a lower speed of the inflow wind blowing from both east and southeast gives a higher air pollutant concentration in the Skytrain cavity. It is also found that there is no significant difference of CO2 concentration in the Skytrain cavity for different speeds of the inflow wind blowing from the northeast.

Figure 3
figure 3

Velocity field and streamlines of wind and contour lines of CO2 concentration obtained from the model with the inlet wind magnitude of 5.40 knots (10 km/h) and the wind blowing from the southeast at 135 degrees

Full size image
Figure 4
figure 4

Velocity field and streamlines of wind obtained from the model with various features of inlet wind: wind speed of 5 km/h (first column), 10 km/h (second column), and 20 km/h (last column); and the wind blowing towards 3 different directions: (a) northeast; (b) east; (c) southeast

Full size image
Figure 5
figure 5

Contour lines of CO2 concentration obtained from the model with various features of inlet wind: wind speed of 5 km/h (first column), 10 km/h (second column), and 20 km/h (last column); and wind blowing towards 3 different directions: (a) northeast; (b) east; (c) southeast

Full size image
Figure 6
figure 6

Comparison of wind-velocity profiles and CO2-concentration profiles at 1.5-meter height above the ground obtained from model with various conditions of the inlet wind speed and its blowing direction

Full size image
Figure 7
figure 7

Comparison of wind-velocity profiles and CO2-concentration profiles at 2-meter height above the ground obtained from model with various conditions of the inlet wind speed and its blowing direction

Full size image

5 Conclusion

This paper demonstrates two-dimensional analysis of air pollution in the street canyon with a Skytrain platform using numerical modeling based on an initial boundary value problem (IBVP) governed by the Reynolds-averaged Navier–Stokes (RANS) equations of compressible turbulent airflow and the convection–diffusion equations of species concentration. The results indicate that the inflow wind on the rooftop of the building affects the airflow pattern in the Skytrain street canyon, leading to a change in concentration of air pollutants. The low wind speed is responsible for the concentrations of pollutants in the area under the Skytrain platform. Our modeling technique may help civil engineers to find technical solutions which will reduce air pollution emissions to more acceptable limits.