Abstract
This paper aims to investigate the effects of human behavior and contact heterogeneity on the spread of infectious diseases. For this purpose, a network-based SIRS epidemic model with a general feedback mechanism is proposed. In contrast to previous models, we consider the different fear degrees of individuals who have different potential number of contacts with others, when an epidemic prevails. The basic reproductive number that governs the global dynamics of the model is analytically derived. Accordingly, the permanence of the disease and stability conditions of the equilibria are studied in detail. It is shown that the general feedback mechanism cannot change the basic reproductive number, but theoretical and numerical results indicate that it plays an active role in reducing the disease damage. The obtained results generalize and improve some well-known ones.
Similar content being viewed by others
1 Introduction
Throughout human history, infectious diseases have been a serious threat to public health and social development. To better understand the dynamical mechanisms of the disease transmission, it is crucial to develop appropriate mathematical models. In the early days, the compartmental epidemic models (see Refs. [1, 2] and the references therein) are mostly based on the homogeneous mixing assumption. That is, all individuals mix uniformly and have the same contact rate. However, in modern society, individual behaviors and disease transmissions exhibit heterogeneity [3]. In this case, it is not sufficient to describe the features of disease transmission by using only traditional epidemic models. To further investigate the disease spreading characteristics, the idea of a complex network is introduced to the epidemic models.
In recent years, studies on the network-based models have attracted increasing attention [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The pioneering work regarding SIS and SIR epidemic models on complex heterogeneous networks were presented, respectively, by Pastor-Satorras et al. [17] and Moreno et al. [15]. Interestingly enough, these studies show that the spreading threshold will vanish in a heterogenous network with sufficiently large size. However, on some scale-free networks, Olinky and Stone [16] found the SIS epidemic model may have a non-infinitesimal threshold. Furthermore, in a finite size network [18], it was inferred that if the spreading rate is above a threshold value, the infection spreads and becomes endemic. Later, Wang and Dai [20] proved this conclusion rigorously by a monotone iterative technique. It is a pity that the results obtained in Refs. [18, 20] are based on the hypothesis that each infected node (individual) will contact every neighbor in one time step, that is, the infectivity of each infected node is equal to its degree. Since, in real life, individuals who have many acquaintances cannot contact all their acquaintances in one time step, Fu et al. [5] and Yang et al. [23] argued that this hypothesis is not always true. Zhang and Fu [27] further pointed out that the infectivity is nonlinear in the node degree. Moreover, for some infectious diseases, such as tuberculosis, it can last a lifetime. In order to reflect the effects of demographics and network structures, Zhu et al. [28], Li et al. [9] and Huang et al. [7] investigated the network-based SIS, SIRS and SIQRS epidemic models with birth and death rates and with nonlinear infectivity, respectively. They showed the disease dynamics of the models is completely determined by the epidemic thresholds. One can refer to Refs. [4, 6, 12, 29,30,31] for more work on nonlinear infectivity.
However, in the models mentioned above, the initiative response of people is not considered when an epidemic prevails. In reality, people will consciously decrease the number of contacts with others during the epidemic outbreaks. To describe this phenomenon, Liu and Yan et al. [14] introduced a feedback mechanism to investigate the spreading of an epidemic on exponential networks. Wang and Yan et al. [32] studied the modeling and controlling of epidemic spread on the small-world network with feedback mechanism. Zhang and Sun [25] proposed an SIS epidemic model with a new feedback mechanism on heterogeneous networks. They studied the stability of the equilibria and the effect of feedback mechanism. They later extended the model with a generalized feedback mechanism on weighted networks and obtained similar results [26]. By using Lyapunov’s direct method [9, 33] and constructing monotone iterative sequences [20, 29], Wei and Xu et al. [22] further obtained sufficient conditions for the global stability of the endemic equilibrium of the model proposed in Ref. [25]. Recently, Li and Liu et al. [11] presented an SIRS epidemic model with feedback mechanism on adaptive scale-free networks. They showed a threshold below which the disease-free equilibrium is globally asymptotically stable and above which the disease is permanent. Furthermore, Li et al. [11] and Zhang et al. [26] numerically found that the endemic equilibrium is globally asymptotically stable. However, to the best of our knowledge, the rigorous mathematical proof of this conclusion is not yet available.
Motivated by the above discussion, in this paper, we shall investigate the global dynamics of an SIRS epidemic model with a general feedback mechanism on complex heterogeneous networks. The rest of this paper is organized as follows: the model is formulated in the next section. In Sect. 3, we analyze the existence of equilibria and derive the basic reproductive number. In Sect. 4, we obtain the criteria for the global stability of the disease-free equilibrium and the permanence of the disease. In Sect. 5, the global stability of the endemic equilibrium is discussed in detail. In Sect. 6, numerical simulations are given to confirm the analytical findings. Finally, we conclude the paper in Sect. 7.
2 The model formulation
We consider the whole population and their contacts as a network. Each node of the network represents an individual. An edge connecting two nodes describes the potential contact, along which the infection may spread. For epidemic spreading of SIRS process, every node has three possible states: susceptible, infected and recovered. To account for the heterogeneity in the contacts among individuals, the population is divided into groups based on the number of potential contacts the individual has per unit of time (i.e., the node degree). That is, the kth group contains all degree k nodes for \(k=1,2,\ldots ,n\). Here n is the maximum node degree of the finite size network. Let \(S_{k}(t)\), \(I_{k}(t)\) and \(R_{k}(t)\) be the relative densities of susceptible, infected and recovered nodes in the kth group at time t, respectively. Let \(N_{k}(t):=S_{k}(t)+I_{k}(t)+R_{k}(t)\) for all \(t\geq 0\) and \(k=1,2,\ldots ,n\).
Using mean-field theory, the dynamics of the network-based SIRS model with a general feedback mechanism can be formulated by the following system:
where \(k=1,2,\ldots ,n\); \(b>0\) is the natural birth rate [8, 9, 28]; \(\lambda (k)>0\) is the degree-dependent infection rate [6, 28]; \(\omega >0\) is the rate of immunity-lost for recovered nodes; \(\mu >0\) is the death rate; \(\gamma >0\) is the recovery rate of the infected nodes; \(\varTheta (t)\) describes the probability that any given edge points to an infected node. According to Refs. [7, 27, 28],
where \(\varphi (k)\) is the infectivity of a node with degree k, that is, \(\varphi (k)\) denotes the average occupied edges from which a node with degree k can transmit the disease [16, 27]. \(\langle k\rangle =\sum_{k=1}^{n} kP(k)\) is the average degree of the network. Here \(P(k)\) denotes the probability that a randomly chosen node has degree k (i.e., the degree distribution). For convenience, the usual notation \(\langle \tilde{h}(k)\rangle =\sum_{k=1}^{n} \tilde{h}(k)P(k)\) is used.
The general feedback mechanism is assumed to be of the form \(U(\alpha (k),\varTheta (t))\), which satisfies the following general assumptions:
- (H1):
-
\(U(0,\varTheta (t))=U(\alpha (k),0)=1\);
- (H2):
-
\(U(\alpha (k),\varTheta (t))>0\) for \(\alpha (k)\geqslant 0\) and \(0\leqslant \varTheta \leqslant 1\);
- (H3):
-
\(\partial U/\partial \varTheta \leqslant 0\).
The assumptions (H1) and (H2) reflect the fact that, for \(\alpha (k)\) and \(\varTheta (t)\) small, the traditional term \(\lambda (k)S_{k}(t)\varTheta (t)\) dominates (i.e., the feedback mechanism is negligible), while for \(\alpha (k)\) and \(\varTheta (t)\) slightly large, the feedback mechanism \(U(\alpha (k), \varTheta (t))\) is at work. Here, \(\alpha (k)\) is a degree-dependent parameter measuring the fear degree of the kth group to infectious diseases. One can also note from (H3) that \(U(\alpha (k),\varTheta (t))\) is decreasing when \(\varTheta (t)\) is large and increasing when \(\varTheta (t)\) is small. Therefore, the function \(U(\alpha (k),\varTheta (t))\) can be used to interpret the initiative response of people when infectious diseases prevail. That is because people will decrease their contacts with others consciously, when the probability of contacting with infected people (i.e., \(\varTheta (t)\)) is becoming large. For example, \(U(\alpha (k),\varTheta (t))=e ^{-\alpha (k)\varTheta ^{q}(t)}\), \(U(\alpha (k),\varTheta (t))=1-\alpha (k) \varTheta ^{q}(t)\), where q is positive constant. The latter case where \(\alpha (k)=\alpha \) (a degree-independent constant) and \(q=1\) was considered by Li et al. [11] and Zhang et al. [25]. For notational convenience, let \(\phi _{k}(\varTheta (t))=U(\alpha (k),\varTheta (t))\) and \(\phi '_{k}( \varTheta )=\partial U/\partial \varTheta \).
In this paper, we assume that the birth rate equals the death rate, i.e., \(b=\mu \). It implies that deaths are balanced by births. Since adding (removing) nodes and edges resulting from the birth (death) only take a small proportion in the huge network, we further assume that the degree of each node is time invariant. These two assumptions are also presented in Refs. [8, 9, 11, 13, 28]. From a practical perspective, the initial conditions for system (2.1) satisfy
Consequently, for \(k=1,2,\ldots ,n\), we have \(S_{k}(t)+I_{k}(t)+R_{k}(t) \equiv 1\), \(t\geq 0\), and system (2.1) is equivalent to the following system:
To investigate the global dynamics of system (2.1), we only need to study the global dynamics of system (2.4).
3 Equilibria and the basic reproduction number
Obviously, system (2.4) has a disease-free equilibrium \(E^{0}=\{\overbrace{0,0,\ldots ,0}^{2n}\}\). Next, we follow the approach of van den Driessche and Watmough [34] or Diekmann et al. [35] to find the basic reproduction number, which is defined as the expected average number of secondary infections generated by an infected node during its infection time.
If we set
and \(\mathscr{V}(x)=(\mathscr{V}_{1}(x),\ldots ,\mathscr{V}_{n}(x), \mathscr{V}_{n+1}(x), \ldots ,\mathscr{V}_{2n}(x))^{T}\), system (2.4) can be written as
where
Here, \(\mathscr{F}_{i}(x)\) is the rate at which new infections occur in compartment i and \(\mathscr{V}_{j}(x)\) is the rate of transfer of individuals into or out of compartment j by all other means, \(j=1,2,\ldots ,2n\).
It is easy to show that the conditions (A1)–(A5) in Ref. [34] are satisfied by system (3.1). Note that the infected compartments are \(I_{k}\), \(k=1,2,\ldots ,n\). According to Lemma 1 in Ref. [34], we obtain \(F= [\frac{\partial \mathscr{F}_{i}}{\partial x_{j}}(E^{0}) ]_{1\leqslant i, j\leqslant n}\) and \(V= [\frac{\partial \mathscr{V}_{i}}{\partial x_{j}}(E^{0}) ]_{1\leqslant i, j\leqslant n} =(\mu +\gamma )\tilde{E_{n}}\), where
\(\tilde{E}_{n}\) is the \(n\times n\) identity matrix. Then, from Ref. [34], the basic reproduction number is \(\mathcal{R}_{0}=\rho (FV^{-1})=\frac{1}{\mu +\gamma }\rho (F)\), where \(\rho (\cdot )\) denotes the spectral radius of a matrix. Through a similarity transformation of the matrix F, the eigenvalues of the matrix F will not change. So, we have
To obtain the endemic equilibrium \(E^{*}=\{I_{1}^{*}, R_{1}^{*},I_{2} ^{*}, R_{2}^{*},\ldots ,I_{n}^{*}, R_{n}^{*}\}\) of system (2.4), we need to impose the requirement that the right side of system (2.4) be equal to zero. Then the equilibrium \(E^{*}\) should satisfy
where \(\varTheta ^{*}=\frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k)I _{k}^{*}\). It follows from (3.3) that
For simplicity, we also denote \(\varTheta ^{*}\) by Θ. Then from (3.4), we get the self-consistency equation:
Considering \(f(\varTheta ):=1-\frac{1}{\langle k\rangle }\sum_{k=1}^{n} \varphi (k)P(k)\frac{(\mu +\omega )\lambda (k) \phi _{k}(\varTheta )}{( \mu +\omega )(\mu +\gamma )+(\mu +\omega +\gamma )\lambda (k)\varTheta \phi _{k}(\varTheta )}\), then
Since \(\phi _{k}'(\varTheta )\leq 0\) and \(\phi _{k}(\varTheta )>0\) for \(0\leq \varTheta \leq 1\), we have \(f'(\varTheta )>0\). Note that \(f(1)>0\). Therefore, Eq. (3.5) has a unique nontrivial solution Θ (\(\varTheta \in (0,1)\)) if and only if \(f(0)<0\), that is, \(\mathcal{R}_{0}>1\). Substituting the nontrivial solution of (3.5) into (3.4), we can get \(I_{k}^{*}\). It follows from (3.3) and (3.4) that \(0< I_{k}^{*}, R_{k}^{*}<1 \) for \(k=1,2,\ldots ,n\). That is, the equilibrium \(E^{*}\) is well defined.
Summarizing the discussions above, the following theorem can be established.
Theorem 3.1
For system (2.4), there always exists a disease-free equilibrium \(E^{0}= \{\overbrace{0,0,\ldots ,0} ^{2n}\}\). If \(\mathcal{R}_{0}\leq 1\), there is no endemic equilibrium; Otherwise, system (2.4) has a unique endemic equilibrium \(E^{*}=\{I_{1}^{*}, R_{1}^{*},I_{2}^{*}, R_{2}^{*},\ldots ,I_{n}^{*}, R_{n}^{*}\}\), where
Remark 3.1
-
(a)
Theorem 3.1 shows that the existence of the endemic equilibrium \(E^{*}\) is completely determined by the basic reproduction number \(\mathcal{R}_{0}\). Although the general feedback mechanism cannot change the value of \(\mathcal{R}_{0}\), Eq. (3.4) shows the feedback mechanism can lower the final number of the infected nodes, i.e., it can reduce the endemic level.
-
(b)
If \(U(\alpha (k),\varTheta (t))=1\) (i.e., without feedback mechanism), then system (2.1) degenerates into system (2.1) in Ref. [9]. However, the value of \(\mathcal{R}_{0}\) is the same as that in Ref. [9]. This also means that the general feedback mechanism does not affect the basic reproduction number \(\mathcal{R}_{0}\).
-
(c)
If \(\varphi (k)=k\), \(\lambda (k)=\lambda k\) and \(U(\alpha (k), \varTheta (t))=1-\alpha \varTheta (t)\), then system (2.1) becomes system (1) in Ref. [11], and \(\mathcal{R}_{0}>1\) is simplified to \(\lambda >\frac{\langle k\rangle }{(\mu +\gamma )\langle k^{2}\rangle }=:\lambda _{c}\), which is consistent with Ref. [11].
4 Stability of the equilibrium \(E^{0}\) and permanence of the disease
In this section, the globally asymptotical stability of the disease-free equilibrium \(E^{0}\) and the permanence of the disease are investigated.
Before going into details, we first give the following lemma, which guarantees the solutions of system (2.4) are nonnegative. Let \(I_{k}(t)=x_{k}(t)\) and \(R_{k}(t)=x_{n+k}(t)\) for \(k=1,2,\ldots ,n\). Then we study system (2.4) for \(x:=(x_{1},x_{2},\ldots ,x_{2n}) \in \varOmega \), where
Lemma 4.1
The set Ω is positively invariant with respect to system (2.4), that is, \(x(0)\in \varOmega \) implies \(x(t)\in \varOmega \) for all \(t>0\).
The proof is shown in Appendix 1. Next, we will investigate the stability of the disease-free equilibrium \(E^{0}\).
Theorem 4.1
The disease-free equilibrium \(E^{0}\) of system (2.4) is locally asymptotically stable if \(\mathcal{R} _{0}<1\) and it is unstable if \(\mathcal{R}_{0}>1\).
Proof
Rewrite system (2.4) in a compact vector form:
with initial condition \(x(0)\in \varOmega \). Ax is the linear part, where A is the Jacobian matrix of system (2.4) at the trivial equilibrium \(E^{0}\) and satisfies
\(l_{i}=\frac{\lambda (i)}{\langle k\rangle }\), \(q_{j}=\varphi (j)P(j)\) (\(1\leq i,j\leq n\)), \(A_{12}=O_{n}\), \(A_{21}=\gamma \tilde{E}_{n}\), \(A_{22}=-(\mu +\omega )\tilde{E}_{n}\). Here, \(O_{n}\) and \(\tilde{E} _{n}\) stand for the \(n\times n\) zero and identity matrix, respectively. Note that \(\phi _{k}(\varTheta )=1+\phi _{k}'(\xi )\varTheta \), where \(0<\xi <\varTheta \). Then we have
Thus, the nonlinear part \(H(x)=-(h_{1},h_{2},\ldots , h_{n}, \overbrace{0,0, \ldots ,0}^{n} )^{T}\), \(h_{k}=\lambda (k)\varTheta [I_{k}+R_{k}-(1 -I _{k}-R_{k})\phi _{k}'(\xi )\varTheta ]\), for \(0<\xi <\varTheta \) and \(k=1,2,\ldots ,n \).
With the help of Lemma 3.1 in Ref. [10], the characteristic equation of the matrix A can easily be expressed in the following form:
This equation has a negative root \(-(\mu +\omega )\) with multiplicity n and a negative root \(-(\mu +\gamma )\) with multiplicity \(n-1\). Therefore, the stability of the disease-free equilibrium \(E^{0}\) completely depends on the sign of the root of \(\widetilde{\lambda }+ \mu +\gamma -\sum_{k=1}^{n}l_{k}q_{k} =\widetilde{\lambda }+ \mu +\gamma -\frac{\langle \lambda (k)\varphi (k)\rangle }{\langle k \rangle } =\widetilde{\lambda }-(\mu +\gamma )(\mathcal{R}_{0}-1)=0 \). Then \(\widetilde{\lambda }<0\) if \(\mathcal{R}_{0}<1\) and \(\widetilde{\lambda }>0\) if \(\mathcal{R}_{0}>1\). Thus, \(E^{0}\) is locally asymptotically stable if \(\mathcal{R}_{0}<1\) and it is unstable if \(\mathcal{R}_{0}>1\). The proof is completed. □
Remark 4.1
According to Theorem 4.1, we have (1) \(s(A)>0 \Leftrightarrow \mathcal{R}_{0}>1\), and (2) \(s(A)<0\Leftrightarrow \mathcal{R}_{0}<1\), where \(\widetilde{\lambda }_{1}, \widetilde{\lambda }_{2},\ldots ,\widetilde{\lambda }_{2n}\) are the eigenvalues of matrix A, \(s(A)=\max_{1\leq i\leq 2n}\operatorname{Re} \widetilde{\lambda }_{i}\).
Furthermore, we have the following result.
Theorem 4.2
If \(\mathcal{R}_{0}<1\), the disease-free equilibrium \(E^{0}\) of system (2.4) is globally asymptotically stable.
Proof
With the help of Theorem 4.1, it is sufficient to show that \(E^{0}\) is globally attractive for system (2.4). From the second equation of system (2.4) and Eq. (2.2), it follows that
This implies that
Since \(\varTheta (0)>0\), we have \(\varTheta (t)>0\), \(t>0\). Note that \(S_{k}(t)\leqslant 1\) and \(\phi _{k}(\varTheta )\leqslant \phi _{k}(0)=1\). Then we derive from (4.4) that
Now we consider the comparison system with \(G(0)=\varTheta (0)>0\):
Integrating from 0 to t, we get \(G(t)=G(0)\exp \{( \mu +\gamma )(\mathcal{R}_{0}-1)t \}\). Since \(\mathcal{R}_{0}<1\), \(\lim_{t\rightarrow +\infty }G(t)=0\). By comparison theorem, we have \(0<\varTheta (t)\leqslant G(t)\), \(t>0\). Hence, \(\varTheta (t)\rightarrow 0\), i.e., \(I_{k}(t)\rightarrow 0\), as \(t\rightarrow \infty \) for \(k=1,2,\ldots ,n\). Combining with the second equation of system (2.4), it obviously follows that \(\lim_{t\rightarrow +\infty }R_{k}(t)=0\). Consequently, the disease-free equilibrium \(E^{0}\) is globally attractive when \(\mathcal{R}_{0}<1\). The proof is completed. □
Finally, we apply the following two lemmas to study the uniform persistence of system (2.4).
Lemma 4.2
([36])
Let A be an irreducible \(n\times n\) matrix. If \(a_{ij}\geq 0\) whenever \(i\neq j\), then there exists an eigenvector u of A such that \(u>0\), and the corresponding eigenvalue is \(s(A)\).
Lemma 4.3
([30])
Consider a 2n-dimensional autonomous system
where à is a \(2n\times 2n\) matrix and \(\tilde{H}(y)\) is continuously differentiable in D.
Assume that
-
(i)
the compact convex set \(\varGamma \subset D\) is positively invariant with respect to system (4.6) and \(\mathbf{0} \in \varGamma \);
-
(ii)
there exists a positive integer \(m\leq 2n\) such that \(\lim_{y\rightarrow 0}\|\tilde{H}(y)\|/\sqrt{ \sum_{i=1}^{m} y_{i}^{2}}=0\);
-
(iii)
there exist a positive number r̃ and a real eigenvector u corresponding to a positive eigenvalue of \(\tilde{A} ^{T}\) such that \((y,u)\geq \widetilde{r}\sqrt{\sum_{i=1}^{m} y_{i}^{2}}\) for all \(y\in \varGamma \);
-
(iv)
\((\tilde{H}(y),u)\leq 0\) holds for all \(y\in \varGamma \).
Then for any \(y_{0}\in \varGamma -\{\mathbf{0}\}\) the solution \(\psi (t,y_{0})\) of system (4.6) satisfies \(\liminf_{t\rightarrow \infty }\|\psi (t, y_{0})\|\geq \sigma _{0}\), where \(\sigma _{0}>0\) is independent of the initial value \(y_{0}\). Moreover, there exists a constant solution of (4.6), \(y=y^{*}\) with \(y^{*}\in \varGamma -\{\mathbf{0}\}\).
Now, we verify that system (4.2) satisfies all the hypotheses of Lemma 4.3. It follows from Lemma 4.1 that condition (i) holds for (4.2) by selecting \(\varGamma =\varOmega \). It is clear that \(\lim_{x\rightarrow 0}\|H(x)\|/\sqrt{\sum_{i=1}^{n} x_{i} ^{2}}=0\), then condition (ii) follows.
For condition (iii), note that \(A_{11}^{T}=(a_{ji})_{n\times n}\) is irreducible and \(a_{ji}>0\) when \(j\neq i\), then from Lemma 4.2 and Eq. (4.3), there exists an eigenvector \(\widetilde{u}=(u_{1},u_{2},\ldots ,u_{n})^{T}\) of \(A_{11}^{T}\) such that \(u_{i}>0\) for all \(i=1,2,\ldots ,n\), and the corresponding eigenvalue is \(s(A_{11}^{T})=s(A)=(\mu +\gamma )(\mathcal{R}_{0}-1)\). If \(\mathcal{R}_{0}>1\), we have \(s(A_{11}^{T})=:\lambda _{0}>0\). Let \(u_{n+1}=\cdots =u_{2n}=0\) and \(u=(u_{1},u_{2},\ldots ,u_{2n})^{T}\), then \(A^{T}u=\lambda _{0}u\), that is, u is the eigenvector corresponding to a positive eigenvalue \(\lambda _{0}\) of \(A^{T}\). If we define \(\widetilde{r}=\min_{1\leq i\leq n}u_{i}>0\), then, for all \(x\in \varOmega \), we obtain \((x,u)\geq \widetilde{r}\sqrt{\sum_{i=1} ^{n} x_{i}^{2}}\), i.e., condition (iii) is satisfied.
Since \((H(x),u)=-\varTheta \sum_{k=1}^{n}\lambda (k)u_{k}[x_{k}+x_{n+k}+(1 -x_{k}-x_{n+k}) (-\phi _{k}'(\xi ))\varTheta ]\leq 0\) for all \(x\in \varGamma \), condition (iv) is also verified. Hence all the hypotheses of Lemma 4.3 are satisfied.
As shown above, the following result can be obtained.
Theorem 4.3
If \(\mathcal{R}_{0}>1\), system (2.4) is uniformly persistent, in the sense that there exists a constant \(0<\sigma _{0}\ll 1\) (independent of initial conditions) such that
for any solution of system (2.4) with (2.3).
Remark 4.2
Theorem 4.3 shows that the disease is permanent on the network if \(\mathcal{R}_{0}>1\). Moreover, it follows from Lemma 4.3 that, if \(\mathcal{R}_{0}>1\), there exists a constant solution of system (2.4), i.e., the endemic equilibrium of system (2.4). This is in agreement with Theorem 3.1.
5 Global stability of the endemic equilibrium
This section discusses the global stability of the endemic equilibrium \(E^{*}\) of system (2.4). Firstly, by constructing a Lyapunov function with the LaSalle invariant principle, we obtain the following theorem, which partly solves the stability problem in Ref. [11].
Theorem 5.1
If \(R_{0}>1\) and \(\alpha >\alpha _{0}:=\frac{ \lambda n}{4\mu }(1-\frac{1}{R_{0}})^{2}\), then the endemic equilibrium \(E^{*}\) of system (2.4) with \(\varphi (k)=k\), \(\lambda (k)= \lambda k\) and \(\phi _{k}(\varTheta )=1-\alpha \varTheta \) (i.e., system (1) in Ref. [11]) is globally asymptotically stable.
Proof
We choose \(\varphi (k)=k\), \(\lambda (k)=\lambda k\) and \(\phi _{k}(\varTheta )=1-\alpha \varTheta \) for system (2.4). It follows from (4.5) that \(\varTheta (t)>0\) for all \(t>0\). Then we define \(V : \varOmega \rightarrow \mathbb{R}\) by
where \(V=V(I_{1},I_{2},\ldots ,I_{n}, R_{1},R_{2},\ldots ,R_{n})\), \(A_{k}=\frac{kP(k)}{S_{k}^{*}\langle k\rangle }\), \(B_{k}=\frac{\omega kP(k)}{\gamma S_{k}^{*}\langle k\rangle }\), \(S_{k}^{*}=1-I_{k}^{*}-R _{k}^{*}\) and \(S_{k}(t)=1-I_{k}(t)-R_{k}(t)\), which satisfies
Here, \(\mu =\lambda k(1-\alpha \varTheta ^{*})S_{k}^{*}\varTheta ^{*}+\mu S _{k}^{*}-\omega R_{k}^{*}\). Moreover, recall that
Then the time derivative of V along the solution of system (2.4) for \(t>0\) is
It follows from (5.1) that
Using the identities \(\frac{\mathrm{d} R_{k}(t)}{\mathrm{d}t}=\gamma -\gamma S_{k}-(\mu +\omega +\gamma )R_{k}\) and \(\gamma =\gamma S_{k} ^{*}+(\mu +\omega +\gamma )R_{k}^{*}\), we have
Combining (5.2) with the identity \(\mu +\gamma =\frac{1}{ \langle k\rangle }\sum_{k=1}^{n} \lambda k^{2}P(k)(1-\alpha \varTheta ^{*})S_{k}^{*}\), we obtain
Note that \(\omega A_{k}=\gamma B_{k}\). Then, substituting (5.4)–(5.6) into (5.3), we get
where \(b_{k}=-\lambda \alpha k S_{k}^{*}\varTheta ^{*}\), \(c_{k}=\lambda \alpha k (S_{k}^{*})^{2}\), \(\tilde{X_{k}}=S_{k}-S_{k}^{*}\), \(\tilde{Y}=\varTheta -\varTheta ^{*}\) and \(\tilde{Z_{k}}=R_{k}-R_{k}^{*}\).
Note that \(\phi _{k}(\varTheta )=1-\alpha \varTheta >0\) and \(R_{0}=\frac{ \lambda \langle k^{2}\rangle }{(\mu +\gamma )\langle k\rangle }\). It follows from (3.3) that \((\mu +\gamma )I_{k}^{*}\leq \lambda k \varTheta ^{*}(1-\alpha \varTheta ^{*})\), Then \((\mu +\gamma )\frac{1}{\langle k\rangle }\sum_{k=1}^{n}kP(k)I_{k}^{*} \leq \lambda \varTheta ^{*}(1- \alpha \varTheta ^{*})\frac{1}{\langle k\rangle }\sum_{k=1}^{n}k^{2}P(k)\), i.e., \(\alpha \varTheta ^{*}\leq 1-\frac{1}{R_{0}}\). Since \(\alpha >\alpha _{0}:=\frac{\lambda n}{4\mu }(1-\frac{1}{R_{0}})^{2}\),
This implies that \(V'(t)\leq 0\). And \(V'(t)=0\) if and only if \(\tilde{X_{k}}=\tilde{Y}=\tilde{Z_{k}}=0\), i.e., \(S_{k}=S_{k}^{*}\), \(I_{k}=I_{k}^{*}\) and \(R_{k}=R_{k}^{*}\) for \(k=1,2,\ldots ,n\). Hence, the largest invariant subset in the set \(\{V'(t)=0\}\) is the singleton \(\{E^{*}\}\). According to the Lyapunov theorem (i.e., Theorem 3.1 in Ref. [33]) and the LaSalle invariant principle (i.e., Theorem 5.2.4 in Ref. [37]), the endemic equilibrium \(E^{*}\) is globally asymptotically stable. The proof is completed. □
Finally, we further study the global stability of \(E^{*}\) of system (2.4) by applying an iteration scheme [6, 7, 20, 29]. It follows from Theorem 4.3 that, if \(\mathcal{R}_{0}>1\), the infection will always exist in the population. Then a more general result is presented in the following theorem.
Theorem 5.2
Let \((I_{k}(t), R_{k}(t))\) be a solution of system (2.4) satisfying initial conditions (2.3). If \(\mathcal{R}_{0}>1\) and \(\gamma >\mu +\omega \), then \(\lim_{t\rightarrow +\infty }(I_{k}(t), R_{k}(t))=(I_{k}^{*}, R_{k} ^{*})\), where \((I_{k}^{*}, R_{k}^{*})\) is the unique positive equilibrium of system (2.4) satisfying (3.6) for \(k=1,2,\ldots ,n\).
The proof is shown in Appendix 2.
Remark 5.1
Theorems 5.1 and 5.2 show that the outstanding issue in Ref. [11] is partly solved. So the results we obtained improve and complement that of Ref. [11].
6 Numerical simulations
This section gives some numerical simulations to illustrate our analysis. All the simulations are based on a finite size scale-free network with the degree distribution \(P(k)=\eta k^{-\tau }\) (\(2< \tau \leq 3\)), where the constant η satisfies \(\sum_{k=1}^{n}\eta k^{-\tau }=1\), \(n=100\). Now we investigate the global behavior of system (2.4). Let \(I(t)=\sum_{k=1}^{n}I_{k}(t)P(k)\) and \(R(t)=\sum_{k=1}^{n}R_{k}(t)P(k)\) be the global average densities of the infected nodes and the removed nodes, respectively. In general, the nodes with higher degrees tend to be more susceptible to disease, so they tend to have a greater fear of disease than the nodes with lower degrees. Then we suppose that the ‘fear factor’ \(\alpha (k)=1-k^{-1/4}\), which is an increasing function of degree k. In Figs. 1, 2, 4 and 5, we choose \(\tau =2.6\), \(\lambda (k)=\lambda k\) and \(\varphi (k)=\frac{a k^{ \sigma }}{1+\nu k^{\sigma }}\), where \(a=0.3\), \(\sigma =0.75\) and \(\nu =0.02\).
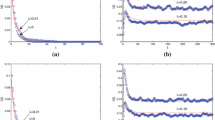
Figure 1 displays the time series \(I(t)\) with different forms of feedback mechanism. The initial values of Fig. 1(a) are given by \(I(0)=0.9\) and \(R(0)=0\). The parameters are chosen as \(\lambda =0.05\), \(\mu =0.01\), \(\omega =0.05\) and \(\gamma =0.05\), then \(\mathcal{R}_{0}=0.7059<1\). In Fig. 1(b), the initial values are \(I(0)=0.1\) and \(R(0)=0\), and the parameters are \(\lambda =0.06\), \(\mu =0.02\), \(\omega =0.04\) and \(\gamma =0.01\). Then \(\mathcal{R}_{0}=1.6942>1\). It can be seen from Fig. 1, regardless of the forms of feedback mechanism, whether the disease is disappearing or not is completely dependent on the basic reproductive number \(\mathcal{R}_{0}\). However, one can find that the feedback mechanism can decrease the final number of the infected nodes, i.e. it can weaken the epidemic spreading.
In the following, we only show \(U(\alpha (k),\varTheta (t))=1-\alpha (k) \varTheta ^{q}(t)\) (\(q=1/2\)) on behalf of other forms of the function \(U(\alpha (k),\varTheta (t))\). To further study the detailed outcome of Fig. 1, the time series of infected nodes with different degree should be examined. In Fig. 2, the initial value and parameters are the same as those of Fig. 1. One can see that when \(\mathcal{R}_{0}<1\) the infected nodes will ultimately disappear (i.e., the disease dies out) and when \(\mathcal{R}_{0}>1\) not only is the disease permanent but also the density of each infected node converges to a positive constant.
Now we explore the global behavior of the endemic equilibrium \(E^{*}\) of system (2.4). Here, \(\tau =2.9\), \(\lambda (k)= \lambda kA(k)\) [16] and \(\varphi (k)=\frac{a k^{\sigma }}{1+\nu k^{\sigma }}\), where \(a=20\), \(\sigma =0.65\) and \(\nu =14\), \(A(k)=\frac{k^{\epsilon }}{k(2+k^{\epsilon })}\), \(\epsilon =0.9\) and \(\lambda =0.32\). The initial value is \(I(0)=0.7\) and \(R(0)=0\). The other parameters are chosen as \(\mu =0.01\), \(\omega =0.085\), \(\gamma =0.096\). Then \(\gamma -(\mu +\omega )=0.001>0\) and \(\mathcal{R}_{0}=1.0676>1\). From Fig. 3, it is observed that when \(\mathcal{R}_{0}>1\) and \(\gamma >\mu +\omega \), the endemic equilibrium of system (2.4) is globally attractive, which is in agreement with Theorem 5.2.
Phase diagram of \(I(t)\) and \(R(t)\) with 20 different sets of random initial values for system (2.4)
Figure 4 shows the phase diagram of \(I(t)\) and \(R(t)\) with 20 different sets of randomly given initial values for system (2.4). It is clearly observed that all trajectories converge to the point \(O(0,0)\) and \(E^{*}(I^{*},R^{*})=E^{*}(0.0307, 0.0412)\) when \(\mathcal{R}_{0}<1\) and \(\mathcal{R}_{0}>1\), respectively. Here, \(I^{*}=\sum_{k=1}^{n}I_{k}^{*}P(k)\) and \(R^{*}=\sum_{k=1}^{n}R_{k} ^{*}P(k)\). The parameters are the same as those of Fig. 1. However, \(\gamma - \mu =0<\omega \), that is, the condition \(\gamma >\mu +\omega \) of Theorem 5.2 is not satisfied. Furthermore, we can repeat similar simulations to Fig. 3 in Ref. [22], when the value of α does not satisfy the assumption of Theorem 5.1. Therefore, we can infer that the endemic equilibrium \(E^{*}\) of system (2.4) is globally asymptotically stable only when \(\mathcal{R}_{0}>1\). We hope to tackle this question in the future.
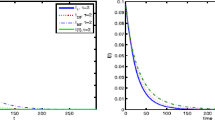
Evolutions of \(I(t)\) based on system (2.4) with varying α̂
Finally, we further investigate the influence of the personal initiative response (i.e., feedback mechanism) on the epidemic spreading. Let \(\hat{\alpha }=\sum_{k=1}^{n}\alpha (k)P(k)\) be changeable parameter, which is determined by the fear degree of the people to the infectious disease. In this case, we only study the effect of the parameter α̂ on the disease transmission. Figure 5 displays the evolutions of \(I(t)\) with different values of α̂. The initial value and parameters of Fig. 5 are the same as those of Fig. 1 except for the parameter \(\alpha (k)\). Although the parameter α̂ cannot affect the basic reproductive number \(\mathcal{R}_{0}\), Fig. 5 shows that when \(\mathcal{R}_{0}<1\), the larger the value of parameter α̂ is, the faster the disease will die out; and when \(\mathcal{R}_{0}>1\), the smaller the value of parameter α̂ is, the higher the endemic level will be. This result is consistent with those in Refs. [11, 22, 25].
7 Conclusions
In this paper, we have investigated the global dynamics of a network-based SIRS epidemic model with a general feedback mechanism. Some special cases of this model were studied in Refs. [9, 11]. The basic reproductive number \(\mathcal{R}_{0}\) is calculated by using the next generation matrix method. Interestingly, we find the basic reproductive number \(\mathcal{R}_{0}\) is the same as that in Ref. [9], that is, \(\mathcal{R}_{0}\) bears no relation to the general feedback mechanism.
Furthermore, we show that the basic reproductive number \(\mathcal{R} _{0}\) determines not only the existence of the endemic equilibrium \(E^{*}\) but also the global dynamics of the model. More specially, if \(\mathcal{R}_{0}<1\), the disease-free equilibrium \(E^{0}\) is globally asymptotically stable, namely, the disease will disappear eventually; if \(\mathcal{R}_{0}>1\), the disease is permanent and there exists a unique endemic equilibrium \(E^{*}\), which is globally attractive provided that \(\gamma >\mu +\omega \). With the help of Lyapunov’s direct method, we also obtain the global stability conditions for the epidemic equilibrium \(E^{*}\) of system (1) in Ref. [11], which partly solves the outstanding problem in Ref. [11].
Different from previous work [11, 25, 26], the degree-dependent parameter \(\alpha (k)\) is introduced to measure the fear degree of a susceptible individual who has k potential contacts with others, when epidemic diseases prevail. Both analytical and numerical results indicate that the feedback mechanism can reduce the average densities of infected nodes and accelerate the extinction of the disease. There is a biological meaning that people will consciously minimize their contacts with others during disease outbreaks. Hence, strengthening the individual self-protection awareness has an obvious effect on the suppression of diseases. We hope this work may be helpful in understanding the epidemic spreading in real society and designing appropriate strategies to control disease spread.
References
Hethcote, H.: The mathematics of infectious diseases. SIAM Rev. 42, 599–653 (2000)
Ma, Z.E., Zhou, Y.C., Wang, W.D., Jin, Z.: Mathematical Models and Dynamics of Infectious Diseases. China Science Press, Beijing (2004)
Pastor-Satorras, R., Castellano, C., Mieghem, P.V., Vespignani, A.: Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925 (2015)
Chu, X.W., Zhang, Z.Z., Guan, J.H., Zhou, S.G.: Epidemic spreading with nonlinear infectivity in weighted scale-free networks. Physica A 390, 471–481 (2011)
Fu, X.C., Small, M., Walker, D.M., Zhang, H.F.: Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Phys. Rev. E 77, 036113 (2008)
Huang, S.Y., Jiang, J.F.: Global stability of a network-based SIS epidemic model with a general nonlinear incidence rate. Math. Biosci. Eng. 13, 723–739 (2016)
Huang, S.Y., Chen, F.D., Chen, L.J.: Global dynamics of a network-based SIQRS epidemic model with demographics and vaccination. Commun. Nonlinear Sci. Numer. Simul. 43, 296–310 (2017)
Huang, S.Y., Jiang, J.F.: Epidemic dynamics on complex networks with general infection rate and immune strategies. Discrete Contin. Dyn. Syst., Ser. B 23, 2071–2090 (2018)
Li, C.H., Tsai, C.C., Yang, S.Y.: Analysis of epidemic spreading of an SIRS model in complex heterogeneous networks. Commun. Nonlinear Sci. Numer. Simul. 19, 1042–1054 (2014)
Li, C.H.: Dynamics of a network-based SIS epidemic model with nonmonotone incidence rate. Physica A 427, 234–243 (2015)
Li, T., Liu, X.D., Wu, J., Wan, C., Guan, Z.H., Wang, Y.M.: An epidemic spreading model on adaptive scale-free networks with feedback mechanism. Physica A 450, 649–656 (2016)
Liu, M.X., Chen, Y.M.: An SIRS model with differential susceptibility and infectivity on uncorrelated networks. Math. Biosci. Eng. 12, 415–429 (2015)
Li, K.Z., Zhu, G.H., Ma, Z.J., Chen, L.J.: Dynamic stability of an SIQS epidemic network and its optimal control. Commun. Nonlinear Sci. Numer. Simul. 66, 84–95 (2019)
Liu, Z.R., Yan, J.R., Zhang, J.G., Wang, L.: Epidemic dynamics with feedback mechanism in exponential networks. Chin. Phys. Lett. 23, 1343 (2006)
Moreno, Y., Pastor-Satorras, R., Vespignani, A.: Epidemic outbreaks in complex heterogeneous networks. Eur. Phys. J. B 26, 521–529 (2002)
Olinky, R., Stone, L.: Unexpected epidemic thresholds in heterogeneous networks: the role of disease transmission. Phys. Rev. E 70, 030902 (2004)
Pastor-Satorras, R., Vespignani, A.: Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001)
Pastor-Satorras, R., Vespignani, A.: Epidemic dynamics in finite size scale-free networks. Phys. Rev. E 65, 035108 (2002)
Sanz, J., Floría, L.M., Moreno, Y.: Spreading of persistent infections in heterogeneous populations. Phys. Rev. E 81, 056108 (2010)
Wang, L., Dai, G.Z.: Global stability of virus spreading in complex heterogeneous networks. SIAM J. Appl. Math. 68, 1495–1502 (2008)
Wang, Y., Cao, J.D.: Global dynamics of a network epidemic model for waterborne diseases spread. Appl. Math. Comput. 237, 474–488 (2014)
Wei, X.D., Xu, G.C., Zhou, W.S.: Global stability of an SIS epidemic model with feedback mechanism on networks. Adv. Differ. Equ. 2018, 60 (2018)
Yang, R., Wang, B.H., Ren, J., Bai, W.J., Shi, Z.W., Wang, W.X., Zhou, T.: Epidemic spreading on heterogeneous networks with identical infectivity. Phys. Lett. A 364, 189–193 (2007)
Zhang, J.H., Sun, J.T.: Exponential synchronization of complex networks with continuous dynamics and Boolean mechanism. Neurocomputing 307, 146–152 (2018)
Zhang, J.C., Sun, J.T.: Stability analysis of an SIS epidemic model with feedback mechanism on networks. Physica A 394, 24–32 (2014)
Zhang, J.C., Sun, J.T.: Analysis of epidemic spreading with feedback mechanism in weighted networks. Int. J. Biomath. 8, 1550007 (2015)
Zhang, H.F., Fu, X.C.: Spreading of epidemics on scale-free networks with nonlinear infectivity. Nonlinear Anal., Theory Methods Appl. 70, 3273–3278 (2009)
Zhu, G.H., Fu, X.C.: Global attractivity of a network-based epidemic SIS model with nonlinear infectivity. Nonlinear Anal., Theory Methods Appl. 36, 5808–5817 (2012)
Zhu, G.H., Fu, X.C., Chen, G.R.: Spreading dynamics and global stability of a generalized epidemic model on complex heterogeneous networks. Commun. Nonlinear Sci. Numer. Simul. 17, 2588–2594 (2012)
Zhu, G.H., Chen, G.R., Fu, X.C.: Effects of active links on epidemic transmission over social networks. Physica A 468, 614–621 (2017)
Shi, W., Jia, J.B., Yang, P., Fu, X.C.: Two novel immunization strategies for epidemic control in directed scale-free networks with nonlinear infectivity. Preprint (2018). arXiv:1806.01174
Wang, L., Yan, J.R., Zhang, J.G., Liu, Z.R.: Controlling disease spread on networks with feedback mechanism. Chin. Phys. 16, 2498 (2007)
Haddad, W.M., Chellaboina, V.S.: Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach. Princeton University Press, Princeton (2011)
Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)
Diekmann, O., Heesterbeek, J.A.P., Roberts, M.G.: The construction of next generation matrices for compartmental epidemic models. J. R. Soc. Interface 7, 873–885 (2010)
Lajmanovich, A., Yorke, J.A.: A deterministic model for gonorrhea in a nonhomogeneous population. Math. Biosci. 28, 221–236 (1976)
Hsu, S.B.: Ordinary Differential Equations with Applications. World Scientific, Singapore (2013)
Chen, F.D.: On a nonlinear nonautonomous predator–prey model with diffusion and distributed delay. J. Comput. Appl. Math. 180, 33–49 (2005)
Acknowledgements
The authors would like to thank Prof. Daozhou Gao for useful discussion of the mathematical modeling. The authors are deeply grateful to the editor and the reviewers for their valuable suggestions and comments, which greatly improved the quality of the paper.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 11601085, the Natural Science Foundation of Fujian Province under Grant 2017J01400 and 2018J01664, the Scientific Research Foundation of Fuzhou University under Grant GXRC-17026 and GXRC-18047.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Proof of Lemma 4.1
This appendix will show the set Ω is positively invariant for system (2.4). That is, we will show that if \(x(0)\in \varOmega \), then \(x(t)\in \varOmega \) for all \(t>0\). From (4.1), ∂Ω (the boundary of Ω) is composed of the following 3n sets:
and the respective outer normal vectors are
For an arbitrary compact set Ω̃, Nagumo had proved that the set Ω̃ is invariant for the system \(\mathrm{d}z/\mathrm{d}t=f(z)\), if the vector \(f(z)\) is tangent or pointing into Ω̃ for every point z on ∂Ω̃ [36]. Note that Ω is a compact set and, for \(1\leq i\leq n\),
Hence, through Nagumo’s result, we see that the set Ω is positively invariant.
Appendix 2: Proof of Theorem 5.2
This appendix will show the global attractivity of the endemic equilibrium \(E^{*}\) of system (2.4). In the following, k is fixed to be any integer in \(\{1,2,\ldots ,n\}\). From Theorem 4.3, there exist a small enough constant \(\xi _{0}\) (\(0<\xi _{0} \ll 1\)) and a large enough constant \(T_{0}>0\) such that \(I_{k}(t) \geq \xi _{0}\) for \(t>T_{0}\). Thus
Note that \(\phi _{k}(\varTheta )\leq \phi _{k}(0)=1\) for \(0\leq \varTheta \leq 1\). Then from the first equation of system (2.4), we have
By Lemma 2.1 in Ref. [38], we derive that \(\limsup_{t\rightarrow \infty }I_{k}(t)\leq \frac{\lambda (k)}{ \lambda (k)+\mu +\gamma }\). Then, for any given small constant \(0<\varepsilon _{1}^{(1)}<\frac{\mu +\gamma }{2[\lambda (k)+\mu + \gamma ]}\), by the comparison theorem, there exists a \(T_{1}^{(1)}>T_{0}\) such that \(I_{k}(t)\leq X_{k}^{(1)}-\varepsilon _{1}^{(1)}\) for \(t>T_{1}^{(1)}\), where
It then follows from the second equation of system (2.4) that
Similarly, for any given small constant \(0<\varepsilon _{1}^{(2)}< \min \{\frac{1}{2},\varepsilon _{1}^{(1)}, \frac{\mu +\omega }{2( \mu +\gamma +\omega )}\}\), there exists a \(T_{1}^{(2)}>T _{1}^{(1)}\) such that \(R_{k}(t)\leq Y_{k}^{(1)}-\varepsilon _{1}^{(2)}\) for \(t>T_{1}^{(2)}\), where
Since \(\varTheta (t)\leq \frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k)=\frac{\langle \varphi (k)\rangle }{\langle k\rangle }=:\beta \), \(\phi _{k}(\beta )\leq \phi _{k}(\varTheta )\). Substituting (B.2) into the first equation of system (2.4) gives
By Lemma 2.1 in Ref. [38], we derive that \(\liminf_{t\rightarrow \infty }I_{k}(t) \geq \frac{\lambda (k)(1 -Y_{k}^{(1)})\varepsilon _{0}\phi _{k}(\beta )}{\lambda (k)+\mu +\gamma }\). That is, for any given small constant \(0<\varepsilon _{1}^{(3)}< \min \{\frac{1}{3},\varepsilon _{1}^{(2)}, \frac{\lambda (k)(1 -Y_{k} ^{(1)})\varepsilon _{0}\phi _{k}(\beta )}{2[\lambda (k)+\mu +\gamma ]} \}\), there exists a \(T_{1}^{(3)}>T_{1}^{(2)}\) such that \(I_{k}(t)\geq x_{k}^{(1)}+\varepsilon _{1}^{(3)}\) for \(t>T_{1}^{(2)}\), where
From the second equation of system (2.4), we derive that \(\frac{\mathrm{d}R_{k}(t)}{\mathrm{d}t}\geq \gamma x_{k}^{(1)}-( \mu +\omega )R_{k}(t)\), \(t>T_{1}^{(3)}\). Similarly, for any given small constant \(0<\varepsilon _{1}^{(4)}<\min \{\frac{1}{4},\varepsilon _{1}^{(3)}, \frac{\gamma x_{k}^{(1)}}{2(\mu +\omega )}\}\), there exists a \(T_{1}^{(4)}>T_{1}^{(3)}\) such that \(R_{k}(t) \geq y_{k}^{(1)}+\varepsilon _{1}^{(4)}\) for \(t>T_{1}^{(4)}\), where
Note that \(\xi _{0}\) is a small enough constant, then \(0< x_{k}^{(1)} \ll 1\) and \(0< y_{k}^{(1)}\ll 1\). Then, from the discussion above, one obtains \(0< x_{k}^{(1)}< X_{k}^{(1)}<1 \) and \(0< y_{k}^{(1)}< Y_{k}^{(1)}<1 \) for \(t>T_{1}^{(4)}\). Accordingly, it follows from (2.2) that
where \(m_{1}=\frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k)x _{k}^{(1)}\) and \(M_{1}=\frac{1}{\langle k\rangle }\sum_{k=1}^{n} \varphi (k)P(k)X_{k}^{(1)}\). Again, from the first equation of system (2.4), we have
So, for any given constant \(0<\varepsilon _{2}^{(1)}<\min \{ \frac{1}{5},\varepsilon _{1}^{(4)}, \frac{\mu +\gamma +\lambda (k)y _{k}^{(1)}M_{1}\phi _{k}(m_{1})}{\lambda (k) M_{1}\phi _{k}(m_{1})+ \mu +\gamma }\}\), there exists a \(T_{2}^{(1)}>T_{1}^{(4)}\) such that
From the second equation of system (2.4) one then obtains \(\frac{\mathrm{d}R_{k}(t)}{\mathrm{d}t}\leq \gamma X_{k}^{(2)}-( \mu +\omega )R_{k}(t)\), \(t>T_{2}^{(1)}\). Hence, for any given constant \(0<\varepsilon _{2}^{(2)}<\min \{\frac{1}{6},\varepsilon _{2} ^{(1)}\}\), there exists a \(T_{2}^{(2)}>T_{2}^{(1)}\) such that
It follows from (B.1), (B.6) and (B.7) that \(X_{k}^{(2)}< X_{k}^{(1)}\) and \(Y_{k}^{(2)}< Y_{k}^{(1)}\).
Turning back to system (2.4), it can be seen that
So, for any given constant \(0<\varepsilon _{2}^{(3)}<\min \{ \frac{1}{7},\varepsilon _{2}^{(2)}, \frac{\lambda (k)(1 -Y_{k}^{(2)})m _{1}\phi _{k}(M_{1})}{\lambda (k) m_{1}\phi _{k}(M_{1})+\mu +\gamma }\}\), there exists a \(T_{2}^{(3)}>T_{2}^{(2)}\) such that \(I_{k}(t)\geq x_{k}^{(2)}\), where
Therefore, by (2.4), one has \(\frac{\mathrm{d}R_{k}(t)}{ \mathrm{d}t}\geq \gamma x_{k}^{(2)}-(\mu +\omega )R_{k}(t)\), \(t>T_{2}^{(3)}\). Then, for any given constant \(0<\varepsilon _{2}^{(4)}< \min \{\frac{1}{8},\varepsilon _{2}^{(3)}, \frac{\gamma x_{k}^{(2)}}{ \mu +\omega }\}\), there exists a \(T_{2}^{(4)}>T_{2}^{(3)}\) such that
Repeating the above procedure, we get four sequences: \(X_{k}^{(i)}\), \(Y _{k}^{(i)}\), \(x_{k}^{(i)}\), \(y_{k}^{(i)}\), \(i=1,2,\ldots \) . By induction, we know that the first two are monotone decreasing sequences and the last two are monotone increasing sequences. Then there exists a sufficiently large positive integer N such that, with \(n\geq N\),
Obviously, one has
Because the sequential limits of (B.10) exist, let \(\lim_{n\rightarrow \infty }H_{k}^{(n)}=H_{k}\), where \(H_{k}^{(n)}=(X _{k}^{(n)}, Y_{k}^{(n)}, x_{k}^{(n)}, y_{k}^{(n)}, M_{n}, m_{n})\) and \(H_{k}=(\bar{X}_{k}, \bar{Y}_{k}, \bar{x}_{k}, \bar{y}_{k}, M, m)\). Note that \(0<\varepsilon _{n}^{(i)}<\frac{1}{4n+i-4}\) (\(i=1,2,3,4\), \(n>1\)), then \(\varepsilon _{n}^{(i)}\rightarrow 0\) as \(n\rightarrow \infty \). Therefore, taking \(n\rightarrow \infty \), it follows from (B.10) that
where \(M=\frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k) \bar{X}_{k}\), \(m=\frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k) \bar{x}_{k}\), \(0< m\leq M<1\). Furthermore, we obtain from (B.12)
where \(D_{k}=[\lambda (k)M\phi _{k}(m)+\mu +\gamma ][\lambda (k)m\phi _{k}(M)+\mu +\gamma ]- \frac{[\lambda (k)]^{2} Mm\phi _{k}(M)\phi _{k}(m) \gamma ^{2}}{(\mu +\omega )^{2}}\). Here, we claim that \(D_{k}\neq 0\). Note that \(\bar{X}_{k}\) is the unique nonzero value determined by (B.12). If \(D_{k}=0\), then \(\lambda (k)m\phi _{k}(M)+(\mu +\gamma )=\frac{ \lambda (k)m\phi _{k}(M)\gamma }{\mu +\omega }\). By t symmetry, we have \(\lambda (k)M\phi _{k}(m)+(\mu +\gamma )=\frac{\lambda (k)M\phi _{k}(m) \gamma }{\mu +\omega }\). Obviously, it follows that \(\lambda (k)[m\phi _{k}(M)-M\phi _{k}(m)]=\frac{\lambda (k)[m\phi _{k}(M)-M\phi _{k}(m)] \gamma }{\mu +\omega }\), i.e. \(\mu +\omega =\gamma \). This is inconsistent with the assumed conditions of the theorem. Therefore, \(D_{k}\neq 0\).
Combining (B.13) with the expressions of M and m, one has
From (B.14), a direct computation leads to
Now we want to show that \(m=M\). Suppose it is not true, then there exists \(\tau _{0}\in (m,M)\) such that \(\phi _{k}(M)-\phi _{k}(m)=\phi _{k}'(\tau _{0})(M-m)\). Hence, it follows from (B.15) that
Since \(\phi _{k}'(\varTheta )\leq 0\) (\(0\leq \varTheta \leq 1\)) and \(\mu +\omega <\gamma \), each item on the left side of (B.16) is negative. This is apparently a contradiction. Consequently, \(m=M\). Then we have \(\frac{1}{\langle k\rangle }\sum_{k=1}^{n}\varphi (k)P(k)( \bar{X}_{k}-\bar{x}_{k})=0\), which implies that \(\bar{X}_{k}=\bar{x} _{k}\) for \(k=1,2,\ldots ,n\). From (B.11) and (B.12), we arrive at \(\lim_{t\rightarrow \infty }I_{k}(t)=\bar{X}_{k}=\bar{x}_{k}\) and \(\lim_{t\rightarrow \infty }R_{k}(t)=\bar{Y}_{k}=\bar{y}_{k}\). Note that Eq. (3.5) has a unique positive solution \(\varTheta ^{*}\) if \(\mathcal{R}_{0}>1\). Then, substituting \(M=m\) and \(\bar{X}_{k}= \bar{x}_{k}\) into (B.13), by virtue of (3.6) and (B.12), one can obtain \(\bar{X}_{k}=I_{k}^{*}\) and \(\bar{Y}_{k}=R_{k}^{*}\). As a result, the endemic equilibrium \(E^{*}\) of system (2.4) is globally attractive if \(\mathcal{R}_{0}>1\) and \(\gamma >\mu +\omega \).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, S., Chen, F. & Zhang, Y. Global analysis of epidemic spreading with a general feedback mechanism on complex networks. Adv Differ Equ 2019, 154 (2019). https://doi.org/10.1186/s13662-019-2095-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2095-3