An efficient numerical algorithm for solving the two-dimensional fractional cable equation

Abstract

In this paper, we consider an efficient numerical algorithm for solving the two-dimensional fractional cable equation. The stability and convergency of the numerical scheme are rigorously proved by the Fourier analysis. Then we find that the convergence order is $O(\tau^{2}+h_{x}^{4}+h_{y}^{4})$. Finally, numerical experiments are carried out to verify the accuracy and effectiveness of the new scheme.

1 Introduction

Fractional differential equations have been studied by many researchers in recent years. The fact shows that fractional differential equations can describe many phenomena and processes in various fields of science and engineering [1,2,3,4,5,6]. Since the fractional operators are nonlocal and have the character of history dependence and universal mutuality, it is not easy even impossible to obtain the analytical solutions of fractional differential equations, especially in high-dimensional domains. Therefore, there has been a growing interest in developing numerical methods for fractional differential equations [7,8,9,10,11,12,13,14,15,16,17].

The cable equation is one of the most fundamental equations for modelling neuronal dynamics. A recent study [18] has found that the diffusion of molecules through the cytoplasm of Purkinje cell dendrites is slowed at the macroscopic scale, primarily through temporary trapping by dendritic spines, and to a lesser extent through macromolecular crowding or binding [19, 20]. Henry et al. [21] derived a fractional cable equation to model electrotonic properties of spiny neuronal dendrites, which is similar to the traditional cable equation except that the order of derivative with respect to the space and/or time is fractional.

In this paper, we consider the following two-dimensional fractional cable equation:

$$\begin{aligned} \frac{\partial u(x,y,t)}{\partial t} =& {_{0}}D_{t}^{1-\gamma_{1}} \biggl[ \kappa_{1} \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+\kappa _{2} \frac{\partial^{2} u(x,y,t)}{\partial y^{2}} \biggr] \\ &{}-\kappa_{3} {_{0}}D_{t}^{1-\gamma_{2}}u(x,y,t) +f(x,y,t), \quad 0\leq x,y \leq L, 0< t\leq T, \end{aligned}$$

(1)

with the initial condition

$$\begin{aligned} u(x,y,0)=\psi (x,y),\quad 0\leq x,y \leq L, \end{aligned}$$

(2)

and the boundary conditions

$$\begin{aligned} u(0,y,t)=\phi_{1}(y,t), \qquad u(L,y,t)=\phi_{2}(y,t), \quad 0\leq y \leq L, 0\leq t\leq T, \end{aligned}$$

(3)

$$\begin{aligned} u(x,0,t)=\varphi_{1}(x,t), \qquad u(x,L,t)=\varphi_{2}(x,t), \quad 0\leq x \leq L, 0\leq t\leq T, \end{aligned}$$

(4)

where $0< \gamma_{1}, \gamma_{2} < 1$, $\kappa_{1}$, $\kappa_{2}$ and $\kappa_{3}$ are positive constants, and $f(x,y,t)$, $\psi (x,y)$, $\phi_{1}(y,t)$, $\phi_{2}(y,t)$, $\varphi_{1}(x,t)$ and $\varphi_{2}(x,t)$ are sufficiently smooth functions. The symbol ${_{0}}D_{t}^{1-\gamma }u(x,y,t)$ denotes the Riemann–Liouville fractional derivative of order $1-\gamma$ with respect to variable t, which is defined by

$$\begin{aligned} _{0}D^{1-\gamma }_{t} u(x,y,t)=\frac{1}{\varGamma (\gamma)} \frac{\partial }{\partial t} \int^{t}_{0}\frac{u(x,y,s)}{(t-s)^{1-\gamma }}\,ds,\quad 0< \gamma < 1. \end{aligned}$$

We mention some recent progress on the numerical treatment of the fractional cable equation. Liu et al. [22] presented two implicit numerical methods for the fractional cable equation and discussed the stability and convergence of these methods using the energy method. Lin et al. [23] constructed a finite difference/Legendre spectral scheme for the fractional cable equation. Hu et al. [24] proposed two implicit compact difference schemes for the fractional cable equation and analyzed the stability and convergence of the first scheme. Zheng et al. [25] used the discontinuous Galerkin finite element to approximate the fractional cable equation. Zhang et al. [26] presented discrete-time orthogonal spline collocation methods for the two-dimensional fractional cable equation. Irandoust-Pakchin et al. [27] employed the method of Chebyshev cardinal functions for solving the variable-order nonlinear fractional cable equation. Dehghan et al. [28] applied the element free Galerkin (EFG) method for solving fractional cable equation with the Dirichlet boundary condition. Zhu er al. [29] proposed two fully discrete schemes, based on Galerkin finite element schemes and the convolution quadrature method. Yu et al. [30] provided a fourth-order compact finite difference method for two-dimensional fractional cable equation. Liu et al. [31, 32] presented the finite element method for the nonlinear time-fractional cable equation. However, to the best of our knowledge, there is no numerical scheme with second-order accuracy in time for the two-dimensional fractional equation. Our scheme in this paper can reach to second-order accuracy in time. We integrate both sides of the fractional cable equation with respect to the time t, and then use the Riemann–Liouville fractional integral definition to discretize the fractional term.

The remainder of this paper is outlined as follows. In Sect. 2, we introduce the derivation of the new method for the solution of (1). The stability and convergence of the scheme are analyzed by the Fourier analysis in Sects. 3 and 4. In Sect. 5, some numerical experiments are presented to demonstrate our theoretical analyses.

2 Derivation of the numerical method

For three positive integer numbers $M_{1}$ $M_{2}$ and N, let $h_{x}={L}/{M_{1}}$, $h_{y}={L}/{M_{2}}$ and $\tau ={T}/{N}$ be the spatial and temporal step sizes, respectively. Denote $x_{i}=ih_{x}$, $y _{j}=jh_{y}$, $t_{k}=k\tau$ for $i=0,1,\ldots,M_{1}$, $j=0,1,\ldots,M _{2}$ and $k=0,1,\ldots,N$. The exact and approximate solutions at the point $(x_{i},y_{j},t_{k})$ are denoted by $u_{i,j}^{k}$ and $U_{i,j}^{k}$. We introduce the following notations:

$$\begin{aligned}& \delta_{x}^{2}u_{i,j}^{k}= \frac{u_{i-1,j}^{k}-2u_{i,j}^{k}+u_{i+1,j} ^{k}}{h_{x}^{2}} ,\qquad \mathcal{H}_{x}u_{i,j}^{k}= \biggl(1+\frac{h_{x}^{2}}{12}\delta_{x} ^{2} \biggr)u_{i,j}^{k}, \\& \delta_{y}^{2}u_{i,j}^{k}= \frac{ u_{i,j-1}^{k}-2u_{i,j}^{k}+u_{i,j+1} ^{k}}{h_{y}^{2}},\qquad \mathcal{H}_{y}u_{i,j}^{k}= \biggl(1+\frac{h_{y}^{2}}{12}\delta_{y} ^{2} \biggr)u_{i,j}^{k}. \end{aligned}$$

In this paper, we always suppose that $u(x,y,t)\in U(\varOmega)$, where

$$\begin{aligned} U(\varOmega) =& \biggl\{ u(x,y,t)\bigg|\frac{\partial^{6}u(x,y,t)}{\partial x^{6}}, {{\frac{\partial^{6}u(x,y,t)}{\partial y^{6}},}} \frac{\partial^{4}u(x,y,t)}{\partial x^{2}\partial t^{2}}, { {\frac{\partial^{4}u(x,y,t)}{\partial y^{2}\partial t^{2}},}} \frac{ \partial^{3}u(x,y,t)}{\partial t^{3}} \\ &{}\in \mathcal{C} (\varOmega) \biggr\} . \end{aligned}$$

Integrating both sides of (1) from $t_{k-1}$ to $t_{k}$, $k=1,2,\ldots,N$, we have

$$\begin{aligned}& u(x_{i},y_{j},t_{k})- u(x_{i},y_{j},t_{k-1}) \\& \quad =\frac{1}{\varGamma (\gamma_{1})} \biggl[ \kappa_{1} \int^{t_{k}}_{0}\frac{\partial^{2}u(x_{i},y_{j},s)}{ \partial x^{2}}(t_{k}-s)^{\gamma_{1}-1} \,ds +\kappa_{2} \int^{t_{k}}_{0}\frac{\partial^{2}u(x_{i},y_{j},s)}{\partial y^{2}}(t _{k}-s)^{\gamma_{1}-1}\,ds \biggr] \\& \qquad {} -\frac{1}{\varGamma (\gamma_{1})} \biggl[\kappa_{1} \int^{t_{k-1}}_{0}\frac{\partial^{2}u(x_{i},y_{j},s)}{ \partial x^{2}}(t_{k-1}-s)^{\gamma_{1}-1} \,ds \\& \qquad {} +\kappa_{2} \int^{t_{k-1}}_{0} \frac{\partial^{2}u(x_{i},y_{j},s)}{\partial y^{2}}(t_{k-1}-s)^{ \gamma_{1}-1} \,ds \biggr] \\& \qquad {}-\frac{1}{\varGamma (\gamma_{2})} \biggl[ \kappa_{3} \int^{t_{k}}_{0}u(x_{i},y_{j},s) (t_{k}-s)^{\gamma_{2}-1}\,ds - \kappa_{3} \int^{t_{k-1}}_{0}u(x_{i},y_{j},s) (t_{k-1}-s)^{\gamma_{2}-1}\,ds \biggr] \\& \qquad {}+ \int^{t_{k}}_{t_{k-1}} f(x_{i},y_{j},s) \,ds \\& \quad =I_{1}+I_{2}-I_{3}+I_{4}, \end{aligned}$$

(5)

where

$$\begin{aligned}& I_{1}=\frac{\kappa_{1}}{\varGamma (\gamma_{1})} \biggl[ \int^{t_{k}}_{0}\frac{\partial^{2}u(x_{i},y_{j},s)}{ \partial x^{2}}(t_{k}-s)^{\gamma_{1}-1} \,ds - \int^{t_{k-1}}_{0} \frac{\partial^{2}u(x_{i},y_{j},s)}{\partial x^{2}}(t_{k-1}-s)^{ \gamma_{1}-1} \,ds \biggr], \\& I_{2}=\frac{\kappa_{2}}{\varGamma (\gamma_{1})} \biggl[ \int^{t_{k}}_{0}\frac{\partial^{2}u(x_{i},y_{j},s)}{ \partial y^{2}} (t_{k}-s)^{\gamma_{1}-1} \,ds- \int^{t_{k-1}}_{0} \frac{\partial^{2}u(x_{i},y_{j},s)}{\partial y^{2}}(t_{k-1}-s)^{ \gamma_{1}-1} \,ds \biggr], \\& I_{3}=\frac{\kappa_{3}}{\varGamma (\gamma_{2})} \biggl[ \int^{t_{k}}_{0}u(x_{i},y_{j},s) (t_{k}-s)^{\gamma_{2}-1}\,ds - \int^{t_{k-1}}_{0}u(x_{i},y_{j},s) (t_{k-1}-s)^{\gamma_{2}-1}\,ds \biggr], \\& {{ I_{4}= \int^{t_{k}}_{t_{k-1}} f(x_{i},y_{j},s) \,ds.}} \end{aligned}$$

(6)

It follows from the Lagrange interpolation formula that

$$\begin{aligned} \frac{\partial^{2}u(x_{i},y_{j},s)}{\partial x^{2}} =&\frac{t_{k}-s}{ \tau }\frac{\partial^{2}u(x_{i},y_{j},t_{k-1})}{\partial x^{2}} + \frac{s-t _{k-1}}{\tau } \frac{\partial^{2}u(x_{i},y_{j},t_{k})}{\partial x^{2}} \\ &{}+O \bigl(\tau^{2} \bigr),\quad t_{k-1}\leq s \leq t_{k}. \end{aligned}$$

(7)

Using a Taylor expansion, we have

$$ \frac{\partial^{2}u(x_{i},y_{j},t_{k})}{\partial x^{2}}=\frac{\delta _{x}^{2}}{1+\frac{h_{x}^{2}}{12}\delta_{x}^{2}}u(x_{i},y_{j},t_{k})+O \bigl(h _{x}^{4} \bigr) $$

(8)

and

$$ \frac{\partial^{2}u(x_{i},y_{j},t_{k})}{\partial y^{2}}=\frac{\delta _{y}^{2}}{1+\frac{h_{y}^{2}}{12}\delta_{y}^{2}}u(x_{i},y_{j},t_{k})+O \bigl(h _{y}^{4} \bigr). $$

(9)

Based on (7) and (8), we can obtain the following approximation of $I_{1}$:

$$\begin{aligned} I_{1} =&\frac{\kappa_{1}}{\varGamma (\gamma_{1})} \Biggl[ \sum _{n=1}^{k} \int^{t_{n}}_{t_{n-1}} \biggl(\frac{t_{n}-s}{\tau } \frac{\delta_{x} ^{2}}{1+\frac{h_{x}^{2}}{12}\delta_{x}^{2}}u(x_{i},y_{j},t_{n-1}) + \frac{s-t _{n-1}}{\tau }\frac{\delta_{x}^{2}}{1+\frac{h_{x}^{2}}{12}\delta_{x} ^{2}}u(x_{i},y_{j},t_{n}) \biggr) \\ &{}\times (t_{k}-s)^{\gamma_{1}-1}\,ds \Biggr] \\ &{}- \frac{\kappa_{1}}{\varGamma (\gamma _{1})} \Biggl[\sum_{n=1}^{k-1} \int^{t_{n}}_{t_{n-1}} \biggl(\frac{t_{n}-s}{\tau } \frac{\delta_{x} ^{2}}{1+\frac{h_{x}^{2}}{12}\delta_{x}^{2}}u(x_{i},y_{j},t_{n-1}) + \frac{s-t _{n-1}}{\tau } \\ &{}\times \frac{\delta_{x}^{2}}{1+\frac{h_{x}^{2}}{12}\delta_{x}^{2}}u(x_{i},y _{j},t_{n}) \biggr) (t_{k-1}-s)^{\gamma_{1}-1}\,ds \Biggr]+R_{11} \\ =&\mu_{1}\sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b_{n}^{(\gamma _{1})} \bigr) \delta_{x}^{2}u(x_{i},y_{j},t_{k-n})+R_{11}, \end{aligned}$$

(10)

where

$$\begin{aligned}& \begin{aligned} &\mu_{1}=\frac{\kappa_{1}\tau^{\gamma_{1}}}{\varGamma (\gamma_{1}+2)}, \\ &a_{n}^{(\gamma_{1})}= \textstyle\begin{cases} 1,& n=0, \\ 2^{1+\gamma_{1}}-2,& n=1, \\ (n-1)^{1+\gamma_{1}}-2n^{1+\gamma_{1}}+(n+1)^{1+\gamma_{1}},& n=2,\ldots,k-1, \\ (1+\gamma_{1})k^{\gamma_{1}}+(k-1)^{1+\gamma_{1}}-k^{1+\gamma_{1}},& n=k, \end{cases}\displaystyle \\ &b_{n}^{(\gamma_{1})}= \textstyle\begin{cases} 0,& n=0, \\ 1,& n=1, \\ (n-2)^{1+\gamma_{1}}-2(n-1)^{1+\gamma_{1}}+n^{1+\gamma_{1}},& n=2,\ldots,k-1, \\ (1+\gamma_{1})(k-1)^{\gamma_{1}}+(k-2)^{1+\gamma_{1}}-(k-1)^{1+\gamma _{1}},& n=k, \end{cases}\displaystyle \end{aligned} \end{aligned}$$

(11)

and

$$ R_{11}=O \bigl(\tau^{2}+h_{x}^{4} \bigr) \Biggl[\sum_{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma_{1}-1}\,ds- \sum_{n=1} ^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma_{1}-1}\,ds \Biggr]. $$

(12)

Similarly, we obtain the following approximation for $I_{2}$ and $I_{3}$:

$$ I_{2}=\mu_{2}\sum _{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b_{n}^{( \gamma_{1})} \bigr)\delta_{y}^{2}u(x_{i},y_{j},t_{k-n})+R_{12}, $$

(13)

where

$$ \mu_{2}=\frac{\kappa_{2}\tau^{\gamma_{1}}}{\varGamma (\gamma_{1}+2)} $$

(14)

and

$$\begin{aligned}& \begin{aligned}&R_{12}=O \bigl(\tau^{2}+h_{y}^{4} \bigr) \Biggl[\sum_{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma_{1}-1}\,ds- \sum_{n=1} ^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma_{1}-1}\,ds \Biggr], \\ &I_{3}=\mu_{3}\sum _{n=0}^{k} \bigl(a_{n}^{(\gamma_{2})}-b_{n}^{( \gamma_{2})} \bigr)u(x_{i},y_{j},t_{k-n})+R_{13}, \end{aligned} \end{aligned}$$

(15)

where

$$ \mu_{3}=\frac{\kappa_{3}\tau^{\gamma_{2}}}{\varGamma (\gamma_{1}+2)} $$

(16)

and

$$ R_{13}=O \bigl(\tau^{2} \bigr) \Biggl[\sum _{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma_{2}-1}\,ds- \sum_{n=1} ^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma_{2}-1}\,ds \Biggr]. $$

For $I_{4}$, applying the trapezoidal rule leads to

$$ I_{4}=\frac{\tau }{2} \bigl[f(x_{i},y_{j},t_{k})+f(x_{i},y_{j},t_{k-1}) \bigr]+O \bigl(\tau^{3} \bigr). $$

(17)

Substituting (10), (13), (15) and (17) into (5) and multiplying both sides by $\mathcal{H}_{x}\mathcal{H} _{y}$, we have

$$\begin{aligned}& \mathcal{H}_{x}\mathcal{H}_{y} u(x_{i},y_{j},t_{k})- \mathcal{H}_{x} \mathcal{H}_{y} u(x_{i},y_{j},t_{k-1}) \\& \quad = \mu_{1} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma _{1})}-b_{n}^{(\gamma_{1})} \bigr) \mathcal{H}_{y}\delta_{x}^{2}u(x_{i},y _{j},t_{k-n}) \\& \qquad {} +\mu_{2} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b _{n}^{(\gamma_{1})} \bigr) \mathcal{H}_{x} \delta_{y}^{2}u(x_{i},y_{j},t _{k-n}) \\& \qquad {}-\mu_{3} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{2})}-b _{n}^{(\gamma_{2})} \bigr) \mathcal{H}_{x}\mathcal{H}_{y} u(x_{i},y_{j},t _{k-n}) \\& \qquad {} +\frac{\tau }{2}\mathcal{H}_{x}\mathcal{H}_{y} \bigl[f(x_{i},y _{j},t_{k})+f(x_{i},y_{j},t_{k-1}) \bigr]+R_{i,j}^{k} , \end{aligned}$$

(18)

where

$$\begin{aligned} R_{i,j}^{k} =&R_{11}+R_{12}+R_{13}+O \bigl(\tau^{3} \bigr) \\ =& O \bigl(\tau^{2}+h_{x}^{4}+h_{y}^{4} \bigr) \Biggl[\sum_{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma_{1}-1}\,ds- \sum_{n=1} ^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma_{1}-1}\,ds \Biggr] \\ &{}+O \bigl(\tau^{2} \bigr) \Biggl[\sum _{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma_{2}-1}\,ds- \sum_{n=1} ^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma_{2}-1}\,ds \Biggr]+O \bigl(\tau^{3} \bigr). \end{aligned}$$

Since

$$ \sum_{n=1}^{k} \int^{t_{n}}_{t_{n-1}}(t_{k}-s)^{\gamma -1}\,ds- \sum_{n=1}^{k-1} \int^{t_{n}}_{t_{n-1}}(t_{k-1}-s)^{\gamma -1}\,ds = \frac{1}{ \gamma } \bigl[(k\tau)^{\gamma }-(k\tau -\tau)^{\gamma } \bigr], $$

for $k\tau \leq T$,

$$ R_{i,j}^{k}= O \bigl(\tau^{2}+h_{x}^{4}+h_{y}^{4} \bigr). $$

(19)

Omitting the small term $R_{i,j}^{k}$ and replacing the function $u_{i,j}^{k}$ with its numerical approximation $U_{i,j}^{k}$ in (18), we can get the following difference scheme for (1):

$$\begin{aligned}& \mathcal{H}_{x}\mathcal{H}_{y} U_{i,j}^{k}- \mathcal{H}_{x}\mathcal{H}_{y} U_{i,j}^{k-1} \\& \quad = \mu_{1} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma _{1})}-b_{n}^{(\gamma_{1})} \bigr) \mathcal{H}_{y}\delta_{x}^{2}U_{i,j} ^{k-n} +\mu_{2} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b_{n} ^{(\gamma_{1})} \bigr) \mathcal{H}_{x}\delta_{y}^{2}U_{i,j}^{k-n} \\& \qquad {}-\mu_{3} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{2})}-b _{n}^{(\gamma_{2})} \bigr) \mathcal{H}_{x}\mathcal{H}_{y}U_{i,j}^{k-n} +\frac{ \tau }{2}\mathcal{H}_{x}\mathcal{H}_{y} \bigl(f_{i,j}^{k}+f_{i,j}^{k-1} \bigr). \end{aligned}$$

(20)

In addition, the initial and boundary value conditions can be written as

$$\begin{aligned}& \begin{aligned} & U_{i,j}^{0} =\psi (ih_{x},jh_{y}),\quad i=0,1,\ldots,M_{1}, j=0,1, \ldots,M_{2}, \\ &U_{0,j}^{k}=\phi_{1}(jh_{y},k\tau), \qquad U_{M_{1},j}^{k}=\phi_{2}(jh_{y},k \tau),\quad j=0,1,\ldots,M_{2}, k=1,2,\ldots,N, \\ &U_{i,0}^{k}=\varphi_{1}(ih_{x},k\tau), \qquad U_{i, M_{2}}^{k}=\varphi_{2}(ih _{x},k \tau),\quad i=0,1,\ldots,M_{1}, k=1,2,\ldots,N. \end{aligned} \end{aligned}$$

(21)

3 Stability analysis

In this section, we will analyze the stability of the scheme (20) by using the Fourier analysis. Let $\widetilde{U}_{ij}^{k}$ be the approximate solution of (20) and define

$$ \rho_{i,j}^{k} = U_{i,j}^{k}- \widetilde{U}_{i,j}^{k},\quad i=0,1,\ldots,M_{1}-1, j=0,1,\ldots,M_{2}-1, k=0,1,\ldots,N, $$

(22)

and

$$\begin{aligned} \rho^{k} =& \bigl[\rho_{11}^{k}, \rho_{12}^{k},\ldots, \rho_{1,M_{2}-1} ^{k}, \rho_{21}^{k},\rho_{22}^{k},\ldots, \rho_{2,M_{2}-1}^{k},\ldots, \rho_{M_{1}-1,1}^{k}, \\ &{}\rho_{M_{1}-1,2}^{k},\ldots, \rho_{M_{1}-1,M_{2}-1}^{k} \bigr]. \end{aligned}$$

(23)

With the above definition and regarding to (20), we can easily get the following roundoff error equation:

$$\begin{aligned}& \mathcal{H}_{x}\mathcal{H}_{y} \rho_{i,j}^{k}- \mathcal{H}_{x}\mathcal{H}_{y} \rho_{i,j}^{k-1} \\& \quad = \mu_{1} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma _{1})}-b_{n}^{(\gamma_{1})} \bigr) \mathcal{H}_{y}\delta_{x}^{2}\rho_{i,j} ^{k-n} +\mu_{2} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b_{n} ^{(\gamma_{1})} \bigr) \mathcal{H}_{x}\delta_{y}^{2}\rho_{i,j}^{k-n} \\& \qquad {} -\mu_{3} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{2})}-b _{n}^{(\gamma_{2})} \bigr) \mathcal{H}_{x}\mathcal{H}_{y}\rho_{i,j}^{k-n}. \end{aligned}$$

(24)

For $k=0,1,\ldots, N$, define the grid function

$$ \rho^{k}(x,y)= \textstyle\begin{cases} \rho_{i,j}^{k},& \textstyle\begin{array}{ll} x_{i}-\frac{h_{x}}{2}< x\leq x_{i}+\frac{h_{x}}{2},\quad i=1,2,\ldots,M_{1}-1, \\ y_{j}-\frac{h_{y}}{2}< y \leq y_{j}+\frac{h_{y}}{2}, \quad j=1,2,\ldots,M_{2}-1, \end{array}\displaystyle \\ 0,& \textstyle\begin{array}{ll} 0\leq x \leq \frac{h_{x}}{2} \quad \mbox{or} \quad L-\frac{h_{x}}{2}< x\leq L, \\ 0\leq y \leq \frac{h_{y}}{2} \quad \mbox{or} \quad L-\frac{h_{y}}{2}< y \leq L, \end{array}\displaystyle \end{cases} $$

where $\rho^{k}(x,y)$ can be expanded in a Fourier series

$$ \rho^{k}(x,y)=\sum^{\infty }_{l_{1}=-\infty } \sum^{ \infty }_{l_{2}=-\infty } \xi_{k}(l_{1},l_{2})e^{ q 2\pi (l_{1}x/L+l _{2}y/L)}, \quad k=1,2,\ldots,N, $$

(25)

in which

$$ q=\sqrt{-1},\qquad \xi_{k}(l_{1},l_{2})= \frac{1}{L^{2}} \int^{L}_{0} \int^{L}_{0}\rho^{k}(x,y)e ^{-q 2\pi (l_{1}x/L+l_{2}y/L)}\,dx\,dy. $$

We introduce the following norm [33]:

$$ {{ \bigl\Vert \rho^{k} \bigr\Vert _{2}= \biggl[ \int^{L}_{0} \bigl\vert \rho^{k}(x,y) \bigr\vert ^{2}\,dx\,dy \biggr]^{\frac{1}{2}}.}} $$

Using the Parseval equality, we have

$$ \bigl\Vert \rho^{k} \bigr\Vert _{2}= \Biggl({{\sum^{\infty }_{l_{1}=- \infty }}}\sum ^{\infty }_{l_{2}=-\infty } \bigl\vert \xi_{k}(l_{1},l_{2}) \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. $$

(26)

According to the above analysis, we suppose that the solution of Eq. (24) has the following form:

$$ \rho^{k}_{i,j}= \xi_{k}e^{q\sigma_{1}i h_{x}+q\sigma_{2} jh_{y}}, $$

(27)

where $\sigma_{1}=\frac{2\pi l_{1}}{L}$ and $\sigma_{2}=\frac{2\pi l_{2}}{L}$.

Substituting (27) into (24), we have

$$\begin{aligned}& (\omega_{1}+\mu_{1}\omega_{2}+ \mu_{2}\omega_{3}+\mu _{3}\omega_{1}) \xi_{k} \\& \quad = \bigl[\omega_{1}- \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{( \gamma_{1})} \bigr) \mu_{1}\omega_{2} - \bigl(a_{1}^{(\gamma_{1})}-b_{1} ^{(\gamma_{1})} \bigr)\mu_{2}\omega_{3} - \bigl(a_{1}^{(\gamma_{2})}-b _{1}^{(\gamma_{2})} \bigr) \mu_{3}\omega_{1} \bigr]\xi_{k-1} \\& \qquad {}-(\mu_{1}\omega_{2}+\mu_{2} \omega_{3})\sum_{n=2}^{k} \bigl(a_{n} ^{(\gamma_{1})}-b_{n}^{(\gamma_{1})} \bigr) \xi_{k-n}-\mu_{3}\omega_{1} \sum _{n=2}^{k} \bigl(a_{n}^{(\gamma_{2})}-b_{n}^{(\gamma_{2})} \bigr)\xi_{k-n}, \end{aligned}$$

(28)

where

$$\begin{aligned}& \begin{aligned} & \omega_{1}=\frac{1}{9} \biggl( \cos^{2}\frac{\sigma_{1}h _{x}}{2}+2 \biggr) \biggl(\cos^{2} \frac{\sigma_{2}h_{y}}{2}+2 \biggr), \\ &\omega_{2}=\frac{4}{3}\sin^{2}\frac{\sigma_{2}h_{y}}{2} \biggl(\cos ^{2}\frac{\sigma_{1}h_{x}}{2}+2 \biggr), \\ &\omega_{3}=\frac{4}{3}\sin^{2}\frac{\sigma_{1}h_{x}}{2} \biggl(\cos ^{2}\frac{\sigma_{2}h_{y}}{2}+2 \biggr). \end{aligned} \end{aligned}$$

(29)

Lemma 1

If $0< \gamma < 1$, the coefficients $a_{n}^{(\gamma)}$ and $b_{n}^{(\gamma)}$ ($n=0,1,\ldots,k$) satisfy

$$\begin{aligned}& \begin{aligned}&(1)\qquad a_{0}^{(\gamma)}-b_{0}^{(\gamma)}=1, \quad -1< a_{1}^{(\gamma)}-b_{1}^{(\gamma)}< 1, \qquad a_{n}^{(\gamma)}-b_{n}^{(\gamma)}< 0,\quad n=2, \ldots, k, \\ &(2)\qquad \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma)}-b_{n}^{(\gamma)} \bigr)=(1+ \gamma) \bigl[k^{\gamma }-(k-1)^{\gamma } \bigr]> 0, \\ &(3)\qquad \sum_{n=2}^{k} \bigl(a_{n}^{(\gamma)}-b_{n}^{(\gamma)} \bigr)> b _{1}^{(\gamma)}-a_{1}^{(\gamma)}-1. \end{aligned} \end{aligned}$$

(30)

Lemma 2

For $0< \gamma_{i} < 1$, if $a_{1}^{(\gamma_{i})}-b_{1}^{(\gamma_{i})}<0$, or if $0< a_{1}^{(\gamma _{i})}-b_{1}^{(\gamma_{i})}< \frac{1}{9(\mu_{1}+\mu_{2})+\frac{9}{4} \mu_{3}}$ ($i=1,2$), we have

$$ \omega_{1}- \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr) \mu _{1}\omega_{2} - \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr)\mu _{2}\omega_{3} - \bigl(a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} \bigr)\mu _{3}\omega_{1}>0. $$

(31)

Proof

From (11), (14), (16), and (29), we can get $\mu_{1}>0$, $\mu_{2}>0$, $\mu_{3}>0$, $\frac{4}{9}\leq \omega_{1} \leq 1$, $0\leq \omega_{2}\leq 4$ and $0\leq \omega_{3}\leq 4$.

• (i) When $a_{1}^{(\gamma_{i})}-b_{1}^{(\gamma_{i})}<0$, we can easily have

  $$ \omega_{1}- \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr) \mu _{1}\omega_{2} - \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr)\mu _{2}\omega_{3} - \bigl(a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} \bigr)\mu _{3}\omega_{1}>0. $$

• (ii) When $0< a_{1}^{(\gamma_{i})}-b_{1}^{(\gamma_{i})}< \frac{1}{9( \mu_{1}+\mu_{2})+\frac{9}{4}\mu_{3}}$

  $$\begin{aligned}& \omega_{1}- \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr) \mu _{1}\omega_{2} - \bigl(a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr)\mu _{2}\omega_{3} - \bigl(a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} \bigr)\mu _{3}\omega_{1} \\& \quad >\omega_{1}-\frac{1}{9(\mu_{1}+\mu_{2})+\frac{9}{4}\mu_{3}}( \mu_{1} \omega_{2}+\mu_{2}\omega_{3}+\mu_{3} \omega_{1}) \\& \quad > \frac{4}{9}-\frac{1}{9(\mu_{1}+\mu_{2})+ \frac{9}{4}\mu_{3}}(4\mu_{1}+4 \mu_{2}+\mu_{3}) \\& \quad =0. \end{aligned}$$

 □

Theorem 1

Suppose that $\xi_{k}$ ($k=1,2,\ldots,N$) are the solution of (28), under the conditions of Lemma 2, we have

$$ \vert \xi_{k} \vert \leq \vert \xi_{0} \vert ,\quad k=1,2,\ldots, N. $$

(32)

Proof

We prove (32) by means of mathematical induction.

For $k=1$ from (28), we can write

$$ \vert \xi_{1} \vert = \biggl\vert \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1} ^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b _{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b _{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \vert \xi_{0} \vert . $$

(33)

From Lemmas 1 and 2, the above equation leads to

$$\begin{aligned} \vert \xi_{1} \vert =&\frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma _{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{( \gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1} ^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+ \mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \\ \leq& \frac{\omega_{1}+ \vert a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \vert \mu_{1}\omega_{2} + \vert a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \vert \mu_{2}\omega_{3} + \vert a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma _{2})} \vert \mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2} \omega_{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \\ \leq& \frac{\omega_{1}+\mu_{1}\omega_{2} +\mu_{2}\omega_{3} + \mu_{3} \omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+\mu_{3} \omega_{1}} \vert \xi_{0} \vert = \vert \xi_{0} \vert . \end{aligned}$$

(34)

Now we suppose that

$$ \vert \xi_{n} \vert \leq \vert \xi_{0} \vert \quad (n=1,2,\ldots,k-1). $$

(35)

From (28) and (35), we have

$$\begin{aligned} \vert \xi_{k} \vert \leq& \biggl\vert \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1} ^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b _{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b _{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \vert \xi_{k-1} \vert \\ &{}+ \biggl\vert \frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1} \omega_{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \sum _{n=2} ^{k} \bigl\vert a_{n}^{(\gamma_{1})}-b_{n}^{(\gamma_{1})} \bigr\vert \vert \xi_{k-n} \vert \\ &{}+ \biggl\vert \frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2} \omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \sum _{n=2}^{k} \bigl\vert a_{n} ^{(\gamma_{2})}-b_{n}^{(\gamma_{2})} \bigr\vert \vert \xi_{k-n} \vert \\ \leq& \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \\ &{}+\frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \sum _{n=2} ^{k} \bigl\vert a_{n}^{(\gamma_{1})}-b_{n}^{(\gamma_{1})} \bigr\vert \\ &{}+\frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \sum _{n=2}^{k} \bigl\vert a_{n}^{( \gamma_{2})}-b_{n}^{(\gamma_{2})} \bigr\vert \\ \leq& \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \\ &{}+\frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \bigl(1+a_{1}^{( \gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr) \\ &{}+\frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \vert \xi_{0} \vert \bigl(1+a_{1}^{(\gamma_{2})}-b_{1} ^{(\gamma_{2})} \bigr) \\ =& \vert \xi_{0} \vert , \end{aligned}$$

which completes the proof. □

Theorem 2

Under the conditions of Lemma 2, the compact difference scheme (20) is stable.

Proof

From (26) and (32) we can write

$$\begin{aligned} \bigl\Vert \rho^{k} \bigr\Vert _{2}^{2}=\sum _{l_{1}=-\infty }^{\infty } \sum _{l_{2}=-\infty }^{\infty } \bigl\vert \xi_{k}(l_{1},l_{2}) \bigr\vert ^{2} \leq \sum_{l_{1}=-\infty }^{\infty } \sum_{l_{2}=-\infty } ^{\infty } \bigl\vert \xi_{0}(l_{1},l_{2}) \bigr\vert ^{2}= \bigl\Vert \rho^{0} \bigr\Vert _{2}^{2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \bigl\Vert \rho^{k} \bigr\Vert _{2}\leq \bigl\Vert \rho^{0} \bigr\Vert _{2},\quad k=1,2,\ldots, N, \end{aligned}$$

which means that the proposed scheme is stable. □

4 Convergence analysis

In this section, we discuss the convergence of the difference scheme (20). Similar to the stability analysis, we define the grid functions as follows:

$$\begin{aligned}& e^{k}(x,y)= \textstyle\begin{cases} e_{i,j}^{k},& \textstyle\begin{array}{ll} x_{i}-\frac{h_{x}}{2}< x\leq x_{i}+\frac{h_{x}}{2}, \quad i=1,2,\ldots,M_{1}-1, \\ y_{j}-\frac{h_{y}}{2}< y \leq y_{j}+\frac{h_{y}}{2},\quad j=1,2,\ldots,M_{2}-1, \end{array}\displaystyle \\ 0,& \textstyle\begin{array}{ll} 0\leq x \leq \frac{h_{x}}{2} \quad \mbox{or} \quad L-\frac{h_{x}}{2}< x\leq L, \\ 0\leq y \leq \frac{h_{y}}{2} \quad \mbox{or} \quad L-\frac{h_{y}}{2}< y \leq L, \end{array}\displaystyle \end{cases}\displaystyle \\& R^{k}(x,y)= \textstyle\begin{cases} R_{i,j}^{k},& \textstyle\begin{array}{ll} x_{i}-\frac{h_{x}}{2}< x\leq x_{i}+\frac{h_{x}}{2}, \quad i=1,2,\ldots,M_{1}-1, \\ y_{j}-\frac{h_{y}}{2}< y \leq y_{j}+\frac{h_{y}}{2}, \quad j=1,2,\ldots,M_{2}-1, \end{array}\displaystyle \\ 0,& \textstyle\begin{array}{ll} 0\leq x \leq \frac{h_{x}}{2} \quad \mbox{or} \quad L-\frac{h_{x}}{2}< x\leq L, \\ 0\leq y \leq \frac{h_{y}}{2} \quad \mbox{or} \quad L-\frac{h_{y}}{2}< y \leq L, \end{array}\displaystyle \end{cases}\displaystyle \end{aligned}$$

where $e^{k}(x,y)$ and $R^{k}(x,y)$ can be expanded in a Fourier series,

$$\begin{aligned}& e^{k}(x,y)=\sum^{\infty }_{l_{1}=-\infty } \sum ^{\infty }_{l_{2}=-\infty } \zeta_{k}(l_{1},l_{2})e^{q 2\pi (l_{1}x/L+l_{2}y/L)}, \quad k=1,2,\ldots,N, \end{aligned}$$

(36)

$$\begin{aligned}& R^{k}(x,y)=\sum^{\infty }_{l_{1}=-\infty } \sum ^{\infty }_{l_{2}=-\infty } \eta_{k}(l_{1},l_{2})e^{q 2\pi (l_{1}x/L+l_{2}y/L)}, \quad k=1,2,\ldots,N, \end{aligned}$$

(37)

in which

$$\begin{aligned}& \zeta_{k}(l_{1},l_{2})=\frac{1}{L^{2}} \int^{L}_{0} \int^{L}_{0}\zeta ^{k}(x,y)e^{-q 2\pi (l_{1}x/L+l_{2}y/L)} \,dx\,dy, \\& \eta_{k}(l_{1},l_{2})=\frac{1}{L^{2}} \int^{L}_{0} \int^{L}_{0}\eta ^{k}(x,y)e^{-q 2\pi (l_{1}x/L+l_{2}y/L)} \,dx\,dy. \end{aligned}$$

We introduce the following norm [33]:

$$\begin{aligned}& {{ \bigl\Vert e^{k} \bigr\Vert _{2}= \biggl[ \int^{L}_{0} \int^{L}_{0} \bigl\vert \zeta ^{k}(x,y) \bigr\vert ^{2}\,dx\,dy \biggr]^{\frac{1}{2}},}} \end{aligned}$$

(38)

$$\begin{aligned}& {{ \bigl\Vert R^{k} \bigr\Vert _{2}= \biggl[ \int^{L}_{0} \int^{L}_{0} \bigl\vert \eta^{k}(x,y) \bigr\vert ^{2}\,dx\,dy \biggr]^{\frac{1}{2}},}} \end{aligned}$$

(39)

where

$$\begin{aligned}& e^{k}= \bigl[e_{11}^{k},e_{12}^{k}, \ldots, e_{1,M_{2}-1}^{k},e_{21} ^{k},e_{22}^{k}, \ldots, e_{2,M_{2}-1}^{k},\ldots, e_{M_{1}-1,1}^{k},e _{M_{1}-1,2}^{k},\ldots, e_{M_{1}-1,M_{2}-1}^{k} \bigr], \\& R^{k}= \bigl[R_{11}^{k},R_{12}^{k}, \ldots, R_{1,M_{2}-1}^{k},R_{21} ^{k},R_{22}^{k}, \ldots, R_{2,M_{2}-1}^{k},\ldots, R_{M_{1}-1,1}^{k},R _{M_{1}-1,2}^{k},\ldots, R_{M_{1}-1,M_{2}-1}^{k} \bigr]. \end{aligned}$$

Applying the Parseval equality, we have

$$\begin{aligned}& \Vert e_{k} \Vert _{2}= \Biggl(\sum ^{\infty }_{l_{1}=-\infty }\sum^{\infty }_{l_{2}=-\infty }{{ \bigl\vert \zeta_{k}(l_{1},l_{2}) \bigr\vert ^{2}}} \Biggr)^{\frac{1}{2}}, \end{aligned}$$

(40)

$$\begin{aligned}& \Vert R_{k} \Vert _{2}= \Biggl(\sum ^{\infty }_{l_{1}=-\infty }\sum^{\infty }_{l_{2}=-\infty } \bigl\vert \eta_{k}(l_{1},l_{2}) \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}. \end{aligned}$$

(41)

From (19) there is a positive constant $C_{0}$ such that

$$ \bigl\vert R_{i,j}^{k} \bigr\vert \leq C_{0} \bigl(\tau^{2}+h_{x}^{4}+h_{y}^{4} \bigr). $$

(42)

Subtracting (20) from (18), we can obtain the following error equation:

$$\begin{aligned}& \mathcal{H}_{x}\mathcal{H}_{y} e_{i,j}^{k}- \mathcal{H}_{x}\mathcal{H}_{y} e_{i,j}^{k-1} \\& \quad = \mu_{1} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma _{1})}-b_{n}^{(\gamma_{1})} \bigr) \mathcal{H}_{y}\delta_{x}^{2}e_{i,j} ^{k-n} +\mu_{2} \sum_{n=0}^{k} \bigl(a_{n}^{(\gamma_{1})}-b_{n} ^{(\gamma_{1})} \bigr) \mathcal{H}_{x}\delta_{y}^{2}e_{i,j}^{k-n} \\& \qquad {} -\mu_{3} \sum_{l=0}^{k} \bigl(a_{n}^{(\gamma_{2})}-b _{n}^{(\gamma_{2})} \bigr) \mathcal{H}_{x}\mathcal{H}_{y}e_{i,j}^{k-n}+R _{i,j}^{k}, \\& \quad i=0,1,\ldots,M_{1}-1, j=0,1,\ldots,M_{2}-1, k=0,1, \ldots,N, \end{aligned}$$

(43)

and

$$\begin{aligned}& e_{i,j}^{0}=0,\quad 0\leq i \leq M_{1}, 0\leq j \leq M_{2}, \\& e_{0,j}^{k}=e_{M_{1},j}^{k}=0,\quad 0\leq j \leq M_{2}, 0\leq k \leq N, \\& e_{i,0}^{k}=e_{i,M_{2}}^{k}=0,\quad 0\leq i \leq M_{1}, 0\leq k \leq N, \end{aligned}$$

(44)

where $e_{ij}^{k} = u_{ij}^{k}-U_{ij}^{k}$.

According to the above analysis, we suppose that the solution of Eq. (43) has the following forms:

$$ e^{k}_{i,j}= \zeta_{k}e^{q\sigma_{1} ih_{x}+q\sigma_{2} jh_{y}}, \qquad R^{k}_{i,j}= \eta_{k}e^{q\sigma_{1}ih_{x}+q\sigma_{2} jh_{y}}. $$

(45)

Substituting the above relations into (43), we obtain

$$\begin{aligned} {{ \zeta_{k}}} =&\frac{\omega_{1}- (a _{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{ \omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} {{ \zeta_{k-1}}} \\ &{}+\frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}}\sum_{n=2}^{k} \bigl(a _{n}^{(\gamma_{1})}-b_{n}^{(\gamma_{1})} \bigr){{ \zeta_{k-n}}} \\ &{}+\frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \sum_{n=2}^{k} \bigl(a_{n}^{(\gamma_{2})}-b _{n}^{(\gamma_{2})} \bigr){{ \zeta_{k-n}}} \\ &{}+\frac{1}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+\mu_{3} \omega_{1}}\eta_{k}. \end{aligned}$$

(46)

Noting that $e^{0}=0$, we have

$$ {{\zeta_{0}}}={{\zeta_{0}(l_{1},l_{2})}}=0. $$

Due to the convergence of the series in the right hand side of (41), there is a positive constant $C_{1}$ such that

$$ \vert \eta_{k} \vert \equiv \bigl\vert \eta_{k}(l_{1},l_{2}) \bigr\vert \leq C_{1}\tau \bigl\vert \eta_{1}(l _{1},l_{2}) \bigr\vert \equiv C_{1}\tau \vert \eta_{1} \vert ,\quad k=1,2,\ldots, N. $$

(47)

Theorem 3

If $\zeta_{k}$ ($k=1,2,\ldots,N$) be the solutions of (46), under the conditions of Lemma 2, we have

$$\begin{aligned} \vert \zeta_{k} \vert \leq k \frac{9}{4} C_{1} \tau \vert \eta_{1} \vert ,\quad k=1,2, \ldots,N. \end{aligned}$$

Proof

For $k=1$ in (46), we have

$$ \vert \zeta_{1} \vert =\frac{1}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+ \mu_{3}\omega_{1}} \vert \eta_{1} \vert \leq \frac{9}{4} C_{1}\tau \vert \eta_{1} \vert . $$

Now we suppose that

$$ \vert \zeta_{n} \vert \leq n\frac{9}{4} C_{1}\tau \vert \eta_{1} \vert \quad (n=1,2,\ldots,k-1). $$

(48)

From (46) and (48), we have

$$\begin{aligned} {{ \vert \zeta_{k} \vert }} \leq& \biggl\vert \frac{\omega _{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega _{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega _{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega _{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+\mu_{3}\omega _{1}} \biggr\vert {{ \vert \zeta_{k-1} \vert }} \\ &{}+ \biggl\vert \frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1} \omega_{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \sum _{n=2} ^{k} \bigl\vert a_{n}^{(\gamma_{1})}-b_{n}^{(\gamma_{1})} \bigr\vert \vert { {\zeta_{k-n}|}} \\ &{}+ \biggl\vert \frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2} \omega_{3}+\mu_{3}\omega_{1}} \biggr\vert \sum _{n=2}^{k} \bigl\vert a_{n} ^{(\gamma_{2})}-b_{n}^{(\gamma_{2})}\bigr\vert {{ \vert \zeta_{k-n} \vert }} \\ &{}+\frac{1}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega_{3}+\mu_{3} \omega_{1}}\eta_{k} \\ \leq& \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \\ &{}\times (k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \\ &{}+\frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}}(k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \sum_{n=2}^{k} \bigl\vert a_{n}^{(\gamma_{1})}-b_{n}^{( \gamma_{1})} \bigr\vert \\ &{}+\frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}}(k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \sum_{n=2}^{k} \bigl\vert a_{n}^{(\gamma_{2})}-b_{n}^{(\gamma_{2})} \bigr\vert + \frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \\ \leq& \frac{\omega_{1}- (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} ) \mu_{1}\omega_{2} - (a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} )\mu_{2}\omega_{3} - (a_{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} )\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}} \\ &{}\times (k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \\ &{}+\frac{\mu_{1}\omega_{2}+\mu_{2}\omega_{3}}{\omega_{1}+\mu_{1}\omega _{2}+\mu_{2}\omega_{3}+\mu_{3}\omega_{1}}(k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \bigl(1+a_{1}^{(\gamma_{1})}-b_{1}^{(\gamma_{1})} \bigr) \\ &{}+\frac{\mu_{3}\omega_{1}}{\omega_{1}+\mu_{1}\omega_{2}+\mu_{2}\omega _{3}+\mu_{3}\omega_{1}}(k-1)\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \bigl(1+a _{1}^{(\gamma_{2})}-b_{1}^{(\gamma_{2})} \bigr)+\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert \\ =& \biggl[(k-1)\frac{9}{4}C_{1}\tau +\frac{9}{4}C_{1} \tau \biggr] \vert \eta _{1} \vert \\ =& k\frac{9}{4}C_{1}\tau \vert \eta_{1} \vert . \end{aligned}$$

 □

Theorem 4

Under the conditions of Lemma 2, the difference scheme (20) is convergent and the convergence order is $O(\tau^{2}+h _{x}^{4}+h_{y}^{4})$.

Proof

From the left hand of (39) and (42), we have

$$ \bigl\Vert R^{k} \bigr\Vert _{2}\leq \sqrt{M_{1}M_{2}h_{x}h_{y}}C_{0} \bigl(\tau^{2}+h _{x}^{4}+h_{x}^{4} \bigr)=LC_{0} \bigl(\tau^{2}+h_{x}^{4}+h_{x}^{4} \bigr). $$

(49)

Using Theorem 3 and the above inequality (49), for $k=1,2,\ldots,N$, we can obtain

$$\begin{aligned} \bigl\Vert e^{k} \bigr\Vert _{2}^{2} \leq& \sum_{l_{1}=-\infty }^{\infty } \sum _{l_{2}=-\infty }^{\infty }k^{2} \biggl(\frac{9}{4} \biggr)^{2}C _{1}^{2}\tau^{2} \bigl\vert \eta_{1}(l_{1},l_{2}) \bigr\vert ^{2} \\ =&k^{2} \biggl(\frac{9}{4} \biggr)^{2}C_{1}^{2} \tau^{2} \bigl\Vert R^{1} \bigr\Vert _{2}^{2} \\ \leq& k^{2} \biggl(\frac{9}{4} \biggr)^{2}C_{1}^{2} \tau^{2}L^{2}C_{0}^{2} \bigl( \tau^{2}+h_{x}^{4}+h_{x}^{4} \bigr)^{2}. \end{aligned}$$

$C_{0}$ and $C_{1}$ are defined as (42) and Theorem 3. Since $k\tau \leq T$, we have

$$\begin{aligned} \bigl\Vert e^{k} \bigr\Vert _{2}\leq C \bigl( \tau^{2}+h_{x}^{4}+h_{y}^{4} \bigr),\quad k=1,2,\ldots,N, \end{aligned}$$

in which $C=\frac{9}{4}TC_{0}C_{1}L$.

From the above discussion, the conditions of Lemma 2 are sufficient. However, numerical simulations for a wide range of $\gamma_{1}$ and $\gamma_{2}$ in the next section demonstrate that the stability and convergence of the scheme are generally established. □

5 Numerical experiments

In this section, some numerical results are given to testify the effectiveness and convergence orders of our new proposed scheme. To illustrate the accuracy of the method and for the comparison, we take the same spatial step $h_{x}=h_{y}=h$, and denote the $L_{2}$ and $L_{\infty }$ norm errors of the numerical solution as follows:

$$\begin{aligned}& e_{2}(h,\tau)=\max_{0\leq n\leq N} \bigl\Vert U^{n}-u^{n} \bigr\Vert , \\& e _{\infty }(h, \tau)=\max_{0\leq n\leq N} \bigl\Vert U^{n}-u^{n} \bigr\Vert _{ \infty }. \end{aligned}$$

Furthermore, the temporal convergence order and the spatial convergence order are defined by

$$\begin{aligned}& \textit{rate }1=\log_{2} \biggl( \frac{e_{2}(h,2\tau)}{e_{2}(h,\tau)} \biggr), \\& \textit{rate }2= \log_{2} \biggl( \frac{e_{\infty }(h,2\tau)}{e_{\infty }(h, \tau)} \biggr), \end{aligned}$$

when h is sufficiently small, and

$$\begin{aligned}& \textit{rate }3=\log_{2} \biggl( \frac{e_{2}(2h,\tau)}{e_{2}(h,\tau)} \biggr),\\& \textit{rate }4= \log_{2} \biggl( \frac{e_{\infty }(2h,\tau)}{e_{\infty }(h, \tau)} \biggr), \end{aligned}$$

when τ is sufficiently small, respectively.

Example 1

Consider the following two-dimensional fractional cable equation:

$$\begin{aligned} \frac{\partial u(x,y,t)}{\partial t} =& {_{0}}D_{t}^{1-\gamma_{1}} \biggl[ \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2} u(x,y,t)}{\partial y^{2}} \biggr] - {_{0}}D_{t}^{1-\gamma_{2}}u(x,y,t) +f(x,y,t), \\ &{}0< x,y< 1, 0< t\leq 1, \end{aligned}$$

(50)

with the initial condition

$$\begin{aligned} u(x,y,0)=0,\quad 0\leq x\leq 1, \end{aligned}$$

and the boundary conditions

$$\begin{aligned}& u(0,y,t)=0,\quad 0\leq t\leq 1, \\& u(1,y,t)=0,\quad 0\leq t\leq 1, \\& u(x,0,t)=0,\quad 0\leq t\leq 1, \\& u(x,1,t)=0,\quad 0\leq t\leq 1, \end{aligned}$$

where

$$f(x,y,t)= \biggl[2t+\frac{2}{\varGamma (2+\gamma_{1})}t^{1+\gamma_{1}}+\frac{4 \pi^{2}}{\varGamma (2+\gamma_{2})}t^{1+\gamma_{2}} \biggr]\sin (\pi x)\sin ( \pi y). $$

The exact solution of Eq. (50) is $u(x,t)=t^{2}\sin (\pi x)\sin ( \pi y)$.

We use the difference scheme (20) to solve the above equation. Firstly, the temporal errors and convergence orders are given in Table 1. We take the sufficiently small spatial step $h=\frac{1}{128}$ and various $\gamma_{1}$ and $\gamma_{2}$, respectively. It is observed that the scheme generates temporal convergence order, which is consistent with our theoretical analysis. Secondly, the spatial errors and convergence orders are tabulated in Table 2. We take the sufficiently small temporal step $\tau =\frac{1}{2000}$ and various $\gamma_{1}$ and $\gamma_{2}$, respectively. The results illustrate that our scheme has accuracy of $O(h^{4})$ in the spatial direction. That is in good agreement with our theoretical analysis.

Table 1 Numerical errors and convergence orders in time direction with $h=\frac{1}{128}$

Table 2 Numerical errors and convergence orders in spatial direction with $\tau =\frac{1}{2000}$

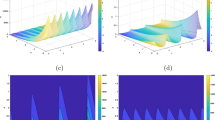
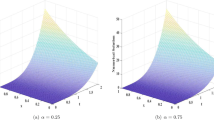
Figures 1 and 2 present the graphs of the numerical solution, the exact solution and the absolute error with $\gamma_{1}=0.3$, $\gamma_{2}=0.5$, $h_{x}=h_{y}=\frac{1}{64}$ and $\tau =\frac{1}{512}$. From these diagrams, it can be seen that our scheme gives a good approximation to the exact solution at mesh points.

Figure 1

Numerical and exact solutions with $\gamma_{1}= 0.3$, $\gamma _{2}=0.5$, $h_{x}=h_{y}=\frac{1}{64}$ and $\tau =\frac{1}{512}$ at $t=1$

Figure 2

Absolute error with $\gamma_{1}=0.3$, $\gamma_{2}=0.5$, $h_{x}= h _{y}=\frac{1}{64}$ and $\tau =\frac{1}{512}$ at $t=1$

The comparisons of our numerical solutions and the results of method developed in [26] for various $\gamma_{1}$ and $\gamma _{2}$ are shown in Table 3. It can be seen that the accuracy of our scheme is superior to the scheme proposed in [26] .

Table 3 Comparison of errors between the scheme (20) and the scheme given in [26]

6 Conclusion

In this paper, we proposed a new numerical method for the two-dimensional fractional cable equation. The stability and convergence of our scheme are obtained by the Fourier analysis. Numerical experiments are given to test the effectiveness of the new scheme and the results are in accordance with theoretical analyses. The application of the idea to more fractional differential equations will be considered in future work.