1 Introduction

It is well known that the neural networks are so important that they have been widely applied in various areas such as reconstructing moving images, signal processing, pattern recognition, optimization problems and so on (for reference, see [1–48]). During the recent years, more and more researchers have paid attention to a new model named state-dependent switching recurrent neural networks whose connection weights vary due to their states. Generally speaking, such switching neural networks have been entitled memristive neural networks or memristor-based neural networks. Therefore, let us recall the brief development of memristive neural networks in the following. In 1971, Dr. Chua (see [10]) firstly advised that a fourth basic circuit element should exist. Different from the other three elements—the resistor, the inductor, and the capacitor—the fourth one was named the memristor. According to Chua’s theory, the memristor must have important and distinctive ability. Precisely, with the rapid development of science, a prototype of the memristor had been built by some scientists from HP Labs until 2008 (see [11]). The memristor, which not only shares many properties of resistors but also shares the same unit of measurement, is a two-terminal element whose characteristic lies in its variable resistance called memristance. Memristance, depending on how much electric charge has been passed through the memristor in a special direction, is its distinctive ability. The ability contributes to its memorizing the passed quantity of electric charge. Therefore, since 2008, its potential applications have become more and more popular in many aspects such as generation computer, powerful brain-like neural computer, and so on. There is no doubt that it has initiated the worldwide concern with the emergence of the memristor (see [11–30]). For the neural networks, the first job is considering whether they are stable or not. Therefore, a lot of scholars have studied the memristive neural networks’ multitudinous stability such as asymptotical stability, global stability, and exponential stability (see [12, 13, 15, 17–20]). Moreover, as far as we know, the passivity theory plays an important role in the analysis of the stability of dynamical systems, nonlinear control, and other areas. Thus, some researchers have investigated passivity or dissipativity criteria on MRNNs (see [14, 16, 23–25, 27–30]).

On the other hand, neural networks with time-varying delays are unavoidable to subject to persistent disturbance. How to solve persistent disturbance for delayed neural networks is still an open problem. Therefore, He et al. [31] studied the problem of disturbance attenuating controller design for delayed cellular neural networks (DCNNs). In this paper, authors designed a feedback control law to guarantee disturbance attenuation for DCNNs by employing Lyapunov–Razumikhin theorem. However, firstly, this paper just discussed disturbance attenuation for delayed cellular neural networks, so the activation function was assumed only to be \(f(x(\cdot ))=0.5(|x(\cdot)+1|-|x(\cdot)-1|)\). As is well known to us, there are still Hopfield neural networks, except cellular neural networks. Both of them belong to recurrent neural networks. Thus, how to design disturbance attenuating controller for general neural networks is our first motivation. Secondly, it is noted that the results in this paper were derived for systems only with discrete delays. Another type of time delay is distributed delay. Systems with distributed delay can be applied in the modeling of feeding systems and combustion chambers in a liquid monopropellant rocket motor with pressure feeding. So, how to solve the persistent disturbance for delayed neural networks with both discrete and distributed time-varying delays remains some room to certain extent.

Motivated by the above mentioned discussion, the problem of disturbance attenuating controller design is extended for memristor-based neural networks. To the best of our knowledge, there has not been any paper to discuss the disturbance attenuating controller design for MRNNs, which motivates our study. Our objective is to give an effective feedback control law to ensure disturbance attenuation and obtain a description of the bounded attractor set for MRNNs with mixed time-varying delays. The main contribution of this paper lies in the following aspects: first of all, this paper is the first one to investigate the disturbance attenuating controller for MRNNs, which is sure to strengthen the systematic research theory for MRNNs and must further enrich the basis of application for MRNNs. Then, comparing to the existing paper [31] about the disturbance attenuating controller design, the studied systems not only contain the more general activation functions but also include both discrete time-varying delay and distribute time-varying delays;a feedback control law is designed in the simple form of linear matrix inequality (LMI) to ensure disturbance attenuation of memristor-based neural networks by employing multiple theories such as differential inclusions, set-valued maps, and Lyapunov–Razumikhin.

2 Problem statement and preliminaries

Throughout this paper, solutions of all the systems considered in the following are intended in Filippov’s sense (see [1, 36]). \([\cdot ,\cdot]\) represents the interval. The superscripts ‘−1’ and ‘T’ stand for the inverse and transpose of a matrix, respectively. \(P>0\) (\(P\geqslant0\), \(P<0\), \(P\leqslant0\)) means that the matrix P is symmetric positive definite (positive-semi definite, negative definite, and negative-semi definite). \(\Vert\cdot\Vert\) refers to the Euclidean vector norm. \(R^{n}\) denotes an n-dimensional Euclidean space. \(\mathcal{C}([-\rho,0],R^{n})\) represents a Banach space of all continuous functions. \(R^{{m}\times{n}}\) is the set of \(m\times n\) real matrices. ∗ denotes the symmetric block in a symmetric matrix. For matrices \(\mathcal{M}=(m_{ij})_{m\times{n}}\), \(\mathcal {N}=(n_{ij})_{m\times{n}}\), \(\mathcal{M}\gg\mathcal{N}\) (\(\mathcal{M}\ll \mathcal{N}\)) means that \(m_{ij}\gg{n}_{ij}\) (\(m_{ij}\ll{n}_{ij}\)) for \(i=1,2,\ldots,m\), \(j=1,2,\ldots,n\). And by the interval matrix \([\mathcal {M},\mathcal{N}]\), it follows that \(\mathcal{M}\ll\mathcal{N}\). For \(\forall\mathcal{L}=(l_{ij})_{m\times{n}}\in[\mathcal{M},\mathcal{N}]\), it means \(\mathcal{M}\ll\mathcal{L}\ll\mathcal{N}\), i.e., \(m_{ij}\lll _{ij}\ll{n}_{ij}\) for \(i=1,2,\ldots,m\), \(j=1,2,\ldots,n\). \(\operatorname{co}\{\Pi_{1},\Pi _{2}\}\) denotes the closure of the convex hull generated by real numbers \(\Pi_{1}\) and \(\Pi_{2}\). Let \(\bar{a}_{i}=\max\{\hat{a}_{i},\check{a}_{i}\} \), \(\underline{a}_{i}=\min\{\hat{a}_{i},\check{a}_{i}\}\), \(\bar {b}_{ij}=\max\{\hat{b}_{ij},\check{a}_{ij}\}\), \(\underline{b}_{ij}=\min \{\hat{b}_{ij},\check{b}_{ij}\}\), \(\bar{c}_{ij}=\max\{\hat {c}_{ij},\check{c}_{ij}\}\), \(\underline{c}_{ij}=\min\{\hat {c}_{ij},\check{c}_{ij}\}\), \(\bar{d}_{ij}=\max\{\hat{d}_{ij},\check {d}_{ij}\}\), \(\underline{d}_{ij}=\min\{\hat{d}_{ij},\check{d}_{ij}\}\). Matrix dimensions, if not explicitly stated, are assumed to be compatible with algebraic operations.

In this section, by Krichoff’s current law, a general class of memristor-based recurrent neural networks containing both persistent disturbances and mixed time-varying delays is introduced as follows:

$$\begin{aligned} \begin{gathered} \dot{x}_{i}(t) = -\breve{a}_{i}\bigl(x_{i}(t) \bigr)x_{i}(t)+\sum_{j=1}^{n} \breve {b}_{ij}\bigl(x_{i}(t)\bigr)f_{j} \bigl(x_{j}(t)\bigr)+\sum_{j=1}^{n} \breve {c}_{ij}\bigl(x_{i}(t)\bigr)f_{j} \bigl(x_{j}\bigl(t-\tau_{j}(t)\bigr)\bigr) \\ \hphantom{\dot{x}_{i}(t) =}{}+\sum_{j=1}^{n}\breve{d}_{ij} \bigl(x_{i}(t)\bigr) \int_{t-\rho _{j}(t)}^{t}f_{j}\bigl(x_{j}(s) \bigr)\,ds+\sum_{l=1}^{m}g_{il}h_{l}(t)+u_{i}(t), \quad t\geq 0,i=1,2,\ldots,n, \\ x_{i}(t)=\phi_{i}(t),\quad t\in[-\delta,0], \end{gathered} \end{aligned}$$
(1)

where \(x_{i}(t)\) represents the voltage of the capacitor \(C_{i}\), \(f_{i}(x_{i}(t))\in {R}^{n}\) is the nonlinear activation function, \(u_{i}(t)\) is the input, \(h_{l}(t)\) (\(l=1,2,\ldots,m\)) is the bounded disturbance. \(\tau_{i}(t)\) is the discrete time-varying delay, and \(\rho_{i}(t)\) is the distributed delay. They satisfy the following conditions: \(0\leq\tau_{i}(t)\leq\tau\), \(0\leq \rho_{i}(t)\leq\rho\) (τ and ρ are constants). \(\phi_{i}(t)\) is the initial condition and is bounded and continuously differential on \([-\delta,0]\) (\(\delta=\max\{\tau,\rho\}\)). \(g_{il}\) describes the weighting coefficients of the disturbance. \(\breve{a}_{i}\) describes the rate with which each neuron will reset its potential to the resting state in isolation when disconnected from the networks and external inputs. \(\breve{b}_{ij}\), \(\breve{c}_{ij}\), and \(\breve{d}_{ij}\) represent the element of the connection weight matrix, the discretely delayed connection weight matrices, and the distributed delays, respectively. They satisfy the following conditions:

$$\begin{aligned} &\breve{d}_{ij}\bigl(x_{i}(t)\bigr)= \textstyle\begin{cases} \hat{d}_{ij}, & \vert x_{i}(t) \vert \leq{T}_{i},\\ \check{d}_{ij},& \vert x_{i}(t) \vert >{T}_{i}, \end{cases}\displaystyle \qquad \breve{b}_{ij}\bigl(x_{i}(t)\bigr)= \textstyle\begin{cases} \hat{b}_{ij}, & \vert x_{i}(t) \vert \leq{T}_{i},\\ \check{b}_{ij},& \vert x_{i}(t) \vert >{T}_{i}, \end{cases}\displaystyle \\ &\breve{c}_{ij}\bigl(x_{i}(t)\bigr)= \textstyle\begin{cases} \hat{c}_{ij}, & \vert x_{i}(t) \vert \leq{T}_{i},\\ \check{c}_{ij},& \vert x_{i}(t) \vert >{T}_{i}, \end{cases}\displaystyle \qquad \breve{a}_{i}\bigl(x(t)\bigr)= \textstyle\begin{cases} \hat{a}_{i}, & \vert x_{i}(t) \vert \leq{T}_{i},\\ \check{a}_{i},& \vert x_{i}(t) \vert >{T}_{i}, \end{cases}\displaystyle \end{aligned}$$

in which switching jump \(T_{i}>0\), \(\hat{d}_{ij}\), \(\check{d}_{ij}\), \(\hat {b}_{ij}\), \(\check{b}_{ij}\), \(\hat{c}_{ij}\), \(\check{c}_{ij}\), \(\hat {a}_{i}\), \(\check{a}_{i}\), \(i,j=1,2,\ldots,n\), are all constant numbers.

Remark 2.1

The clear exposition about the relation between memristances and coefficients of switching system (1) has been given in the works [12, 18]. Thus, researchers can consult [12, 18] to get more information.

From the above description, the studied networks are state-dependent switching recurrent neural networks whose connection weights vary according to their states. To translate these state-dependent neural networks into the general ones, the next definitions are necessary.

Definition 2.1

Let \(E\subseteq{R}^{n}\), \(x\mapsto {F}(x)\) is called a set-valued map from \(E\hookrightarrow{R}^{n}\) if, for each point x of a set \(E\subseteq{R}^{n}\), there corresponds a nonempty set \(F(x)\subseteq{R}^{n}\).

Definition 2.2

A set-valued map F with nonempty values is said to be upper semi-continuous at \(x_{0}\in{E}\subseteq{R}^{n}\) if, for any open set N containing \(F(x_{0})\), there exists a neighborhood M of \(x_{0}\) such that \(F(M)\subseteq{N}\). \(F(x)\) is said to have a closed (convex, compact) image if, for each \(x\in{E}\), \(F(x)\) is closed (convex, compact).

Definition 2.3

For the differential system \(\frac {dx}{dt}=f(t,x)\), where \(f(t,x)\) is discontinuous in x, the set-valued map of \(f(t,x)\) is defined as follows:

$$\begin{aligned} F(t,x)=\bigcap_{\epsilon>0}\bigcap _{\mu(N)=0}\operatorname{co}\bigl[f\bigl(B(x,\epsilon)\setminus{N} \bigr)\bigr], \end{aligned}$$

where \(B(x,\epsilon)=\{y: \Vert y-x \Vert\leq\epsilon\}\) is the ball of center x and radius ϵ. Intersection is taken over all sets N of measure zero and over all \(\epsilon>0\); and \(\mu(N)\) is the Lebesgue measure of set N.

A Filippov solution of system (1) with initial condition \(x(0)=x_{0}\) is absolutely continuous on any subinterval \(t\in[t_{1},t_{2}]\) of \([0,T]\), which satisfies \(x(0)=x_{0}\), and the differential inclusion:

$$\begin{aligned} \frac{dx}{dt}\in{F}(t,x) \quad \mbox{for a.a. } t\in[0,T]. \end{aligned}$$

Firstly, by employing the theories of differential inclusions and set-valued maps, from (1), it follows that

$$\begin{aligned}& \begin{aligned} \dot{x}_{i}(t)&\in -\operatorname{co}\{\hat{a_{i}}, \check{a_{i}}\}x_{i}(t)+\sum_{j=1}^{n} \operatorname{co}\{ \hat{b}_{ij},\check{b}_{ij} \}f_{j}\bigl(x_{j}(t)\bigr)+\sum _{j=1}^{n}\operatorname{co}\{\hat {c}_{ij}, \check{c}_{ij}\}f_{j}\bigl(x_{j}\bigl(t- \tau_{j}(t)\bigr)\bigr) \\ &\quad {}+\sum_{j=1}^{n}\operatorname{co}\{ \hat{d}_{ij},\check{d}_{ij}\} \int_{t-\rho _{j}(t)}^{t}f_{j}\bigl(x_{j}(s) \bigr)\,ds+\sum_{l=1}^{m}g_{il}h_{l}(t)+u_{i}(t), \quad t\geq 0,i=1,2,\ldots,n, \end{aligned} \\& x_{i}(t)=\phi_{i}(t),\quad t\in[-\delta,0], \end{aligned}$$

or equivalently, for \(i,j=1,2,\ldots,n\), there exist \(a_{i}\in\operatorname{co}\{\hat {a}_{i},\check{a}_{i}\}\), \(b_{ij}\in\operatorname{co}\{\hat{b}_{ij},\check{b}_{ij}\} \), \(c_{ij}\in\operatorname{co}\{\hat{c}_{ij},\check{c}_{ij}\}\), and \(d_{ij}\in\operatorname{co}\{ \hat{d}_{ij},\check{d}_{ij}\}\) such that

$$ \begin{gathered} \dot{x}_{i}(t) = -a_{i} \bigl(x_{i}(t)\bigr)x_{i}(t)+\sum _{j=1}^{n}b_{ij}\bigl(x_{i}(t) \bigr)f_{j}\bigl(x_{j}(t)\bigr)+\sum _{j=1}^{n}c_{ij}\bigl(x_{i}(t) \bigr)f_{j}\bigl(x_{j}\bigl(t-\tau_{j}(t)\bigr) \bigr) \\ \hphantom{\dot{x}_{i}(t) =}{}+\sum_{j=1}^{n}d_{ij} \bigl(x_{i}(t)\bigr) \int_{t-\rho_{j}(t)}^{t}f_{j}\bigl(x_{j}(s) \bigr)\,ds+\sum_{l=1}^{m}g_{il}h_{l}(t)+u_{i}(t), \quad t\geq0,i=1,2,\ldots,n, \\ x_{i}(t)=\phi_{i}(t),\quad t\in[-\delta,0]. \end{gathered} $$
(2)

Clearly, \(\operatorname{co}\{\hat{a_{i}},\check{a_{i}}\}=[\bar{a},\underline{a}]\), \(\operatorname{co}\{ \hat{b}_{ij},\check{b}_{ij}\}=[\bar{b}_{ij},\underline{b}_{ij}]\), \(\operatorname{co}\{ \hat{c}_{ij},\check{c}_{ij}\}=[\bar{c}_{ij},\underline{c}_{ij}]\), \(\operatorname{co}\{ \hat{d}_{ij},\check{d}_{ij}\}=[\bar{d}_{ij},\underline{d}_{ij}]\) for \(i,j=1,2,\ldots,n\).

A solution \(x(t)=[x_{1}(t),x_{2}(t),\ldots,x_{n}(t)]^{T}\in{R}^{n}\)(in the sense of Filippov) of system (1) is absolutely continuous on any compact interval of \([0,+\infty]\), and for \(i=1,2,\ldots,n\),

$$ \begin{gathered} \dot{x}_{i}(t)\in -\operatorname{co}\{\hat{a_{i}}, \check{a_{i}}\}x_{i}(t)+\sum_{j=1}^{n} \operatorname{co}\{ \hat{b}_{ij},\check{b}_{ij} \}f_{j}\bigl(x_{j}(t)\bigr) \\ \hphantom{\dot{x}_{i}(t)\in} {}+\sum _{j=1}^{n}\operatorname{co}\{\hat {c}_{ij}, \check{c}_{ij}\}f_{j}\bigl(x_{j}\bigl(t- \tau_{j}(t)\bigr)\bigr)+\sum_{j=1}^{n}\operatorname{co}\{ \hat{d}_{ij},\check{d}_{ij}\} \int_{t-\rho _{j}(t)}^{t}f_{j}\bigl(x_{j}(s) \bigr)\,ds\\ \hphantom{\dot{x}_{i}(t)\in} {}+\sum_{l=1}^{m}g_{il}h_{l}(t)+u_{i}(t), \quad t\geq 0,i=1,2,\ldots,n, \\ x_{i}(t)=\phi_{i}(t),\quad t\in[-\delta,0]. \end{gathered} $$
(3)

For convenience, transform (1) into the compact form as follows:

$$\begin{aligned}& \begin{aligned} \dot{x}(t)&\in -\operatorname{co}\{\hat{A},\check{A}\}x(t)+\operatorname{co}\{ \hat{B},\check{B}\} f\bigl(x(t)\bigr)+\operatorname{co}\{\hat{C},\check{C}\}f \bigl(x\bigl(t-\tau(t)\bigr)\bigr) \\ &\quad {}+\operatorname{co}\{\hat{D},\check{D}\} \int_{t-\rho(t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)+u(t),\quad t\geq 0, \end{aligned} \\& x(t)=\phi(t),\quad t\in[-\delta,0], \end{aligned}$$

or equivalently, there exist \(A^{\ast}\in\operatorname{co}\{\hat{A},\check{A}\}\), \(B^{\ast}\in\operatorname{co}\{\hat{B},\check{B}\}\), \(C^{\ast}\in\operatorname{co}\{\hat{C},\check {C}\}\), and \(D^{\ast}\in\operatorname{co}\{\hat{D},\check{D}\}\) such that

$$ \begin{gathered} \dot{x}(t) = -Ax(t)+Bf\bigl(x(t)\bigr)+Cf\bigl(x \bigl(t-\tau(t)\bigr)\bigr) \\ \hphantom{\dot{x}(t) =}{}+D \int_{t-\rho (t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)+u(t),\quad t \geq0, \\ x(t)=\phi(t),\quad t\in[-\delta,0], \end{gathered} $$
(4)

where \(C^{\ast}=C(x)\), \(A^{\ast}=A(x)\), \(B^{\ast}=B(x)\), \(D^{\ast}=D(x)\), \(\hat{A}=(\hat{a}_{i})_{n\times{n}}\), \(\hat{B}=(\hat{b}_{ij})_{n\times {n}}\), \(\hat{C}=(\hat{c}_{ij})_{n\times{n}}\), \(\hat{D}=(\hat {d}_{ij})_{n\times{n}}\), \(\check{A}=(\check{a}_{i})_{n\times{n}}\), \(\check{B}=(\check {b}_{ij})_{n\times{n}}\), \(\check{C}=(\check{c}_{ij})_{n\times{n}}\), \(\check{D}=(\check{d}_{ij})_{n\times{n}}\), \(G=(g_{il})_{n\times{m}}\), \(x(t)=[x_{1}(t),x_{2}(t),\ldots,x_{n}(t)]^{T}\in{R}^{n}\), \(f(x(t))=[f_{1}(x_{1}(t)),f_{2}(x_{2}(t)), \ldots,f_{n}(x_{n}(t))]^{T}\in{R}^{n}\), \(f(x(t-\tau(t)))=[f_{1}(x_{1}(t-\tau_{1}(t))),f_{2}(x_{2}(t-\tau_{2}(t))), \ldots ,f_{n}(x_{n}(t-\tau_{n}(t)))]^{T}\in{R}^{n}\), \(y(t)=[y_{1}(t),y_{2}(t),\ldots ,y_{n}(t)]^{T}\in{R}^{n}\), \(u(t)=[u_{1}(t),u_{2}(t),\ldots,u_{n}(t)]^{T}\in{R}^{n}\). The bounded disturbance \(h(t)=[h_{1}(t),h_{2}(t),\ldots, h_{n}(t)]^{T}\in{R}^{n}\) is assumed to belong to the set \(\mathcal{H}=\{h|h^{T}h\leq1\}\).

Clearly, \(\operatorname{co}\{\hat{D},\check{D}\}=[\bar{D},\underline{D}]\), \(\operatorname{co}\{\hat {A},\check{A}\}=[\bar{A},\underline{A}]\), \(\operatorname{co}\{\hat{B},\check{B}\}=[\bar {B},\underline{B}]\), \(\operatorname{co}\{\hat{C},\check{C}\}=[\bar{C},\underline {C}]\), where \(\bar{A}=(\bar{a_{i}})_{n\times{n}}\), \(\underline{A}=(\underline {a}_{i})_{n\times{n}}\), \(\bar{B}=(\bar{b}_{ij})_{n\times{n}}\), \(\underline {B}=(\underline{b}_{ij})_{n\times{n}}\), \(\bar{C}=(\bar{c}_{ij})_{n\times {n}}\), \(\underline{C}=(\underline{c}_{ij})_{n\times{n}}\), \(\bar{D}=(\bar {d}_{ij})_{n\times{n}}\), \(\underline{D}=(\underline{d}_{ij})_{n\times{n}}\).

Let \(C=\frac{\underline{C}+\bar{C}}{2}\), \(A=\frac{\underline{A}+\bar {A}}{2}\), \(B=\frac{\underline{B}+\bar{B}}{2}\), \(D=\frac{\underline {D}+\bar{D}}{2}\), ∀ \(A^{\ast}\in\operatorname{co}\{\hat{A},\check{A}\}\), \(B^{\ast}\in\operatorname{co}\{ \hat{B},\check{B}\}\), \(C^{\ast}\in\operatorname{co}\{\hat{C},\check{C}\}\), \(D^{\ast}\in \operatorname{co}\{\hat{D},\check{D}\}\), \(A^{\ast}=A+\Delta{A}(t)\), \(B^{\ast}=B+\Delta {B}(t)\), \(C^{\ast}=C+\Delta{C}(t)\), \(D^{\ast}=D+\Delta{D}(t)\), (4) can be described as follows:

$$\begin{aligned} \begin{gathered} \dot{x}(t) = -\bigl(A+\Delta{A}(t)\bigr)x(t)+ \bigl(B+\Delta{B}(t)\bigr)f\bigl(x(t)\bigr)+\bigl(C+\Delta {C}(t)\bigr)f\bigl(x \bigl(t-\tau(t)\bigr)\bigr) \\ \hphantom{\dot{x}(t) =} {}+\bigl(D+\Delta{D}(t)\bigr) \int_{t-\rho(t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)-Fx(t),\quad t\geq 0, \\ x(t)=\phi(t),\quad t\in[-\delta,0]. \end{gathered} \end{aligned}$$
(5)

Moreover, if \(\hat{a}_{i}=\check{a}_{i}\), \(\hat{c}_{ij}=\check {c}_{ij}\), \(\hat{b}_{ij}=\check{b}_{ij}\), \(\hat{d}_{ij}=\check{d}_{ij}\) (\(i,j=1,2,\ldots,n\)), (5) can be expressed as follows:

$$\begin{aligned} \begin{gathered} \dot{x}(t) = -Ax(t)+Bf\bigl(x(t)\bigr)+Cf\bigl(x \bigl(t-\tau(t)\bigr)\bigr)\\ \hphantom{\dot{x}(t) =}{} +D \int_{t-\rho(t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)-Fx(t),\quad t\geq0, \\ x(t)=\phi(t),\quad t\in[-\delta,0]. \end{gathered} \end{aligned}$$
(6)

Suppose the state feedback to be \(u=-Fx\), then system (6) is changed into

$$\begin{aligned} \begin{gathered} \dot{x}(t) = -Ax(t)+Bf\bigl(x(t)\bigr)+Cf\bigl(x \bigl(t-\tau(t)\bigr)\bigr)\\ \hphantom{\dot{x}(t) =}{}+D \int_{t-\rho (t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)-Fx(t),\quad t\geq0, \\ x(t)=\phi(t),\quad t\in[-\delta,0]. \end{gathered} \end{aligned}$$
(7)

Moreover, throughout this paper, the neuron activation functions are assumed to satisfy the following assumption.

Assumption 2.1

The neuron activation function \(f(x(t))\) satisfies

$$ 0\leqslant\frac{f_{j}(a)-f_{j}(b)}{a-b}\leqslant{l_{j}}, \quad j=1,2,\ldots,n, $$
(8)

where \(l_{j}>0\) is a known real constant.

To get the main results in this paper, the definition of disturbance attenuation is introduced as follows.

Definition 2.4

Given system (6), the controller \(u=-Fx\) is called disturbance attenuating if systems (7) satisfy the following conditions:

  1. (1)

    When \(h(t)=0\), systems (7) are globally asymptotically stable;

  2. (2)

    When \(h(t)\neq0\), there exists a bounded attractor for systems (7).

Remark 2.2

The attractor of systems (7) is the invariant set Ω, which not only lies in the fact that all the trajectories beginning from it will retain in it for any \(h\in {\mathcal{H}}\), but also subjects to the condition that any trajectories beginning from outside the set will ultimately go into the set for any \(h\in\mathcal{H}\).

To establish the feedback controller for systems (7), the following lemmas will be used in this paper.

Lemma 2.1

(Lyapunov–Razumikhin theorem [35])

Consider the following functional differential equation:

$$ \dot{x}(t)=f(x_{t}),\quad t>0,\qquad x(t)= \phi(t),\quad t\in[-\tau,0]. $$
(9)

Assume that \(\phi\in{C}_{n,\tau}\) and the map \(f(\phi):{C}_{n,\tau }\mapsto{R}^{n}\) is continuous and Lipschitzian in ϕ and \(f(0)=0\). Suppose that \(u(s)\), \(\nu(s)\), \(w(s)\), and \(p(s)\in{R}^{+}\mapsto {R}^{+}\) are scalar, continuous, and nondecreasing functions, \(u(s)\), \(\nu(s)\), \(w(s)\) positive for \(s>0\), \(u(0)=\nu(0)=0\) and \(p(s)>s\) for \(s>0\). If there are a continuous function \(V:R^{n}\mapsto{R}\) and a positive number ρ such that, for all \(x_{t}\in{M}_{V(\rho)}:=\{\phi \in{C}_{n,\tau}:V(\phi(\theta))\leq\rho,\forall\theta\in[-\tau,0]\}\), the following conditions hold:

  1. (1)

    \(u( \Vert x \Vert )\leq{V}(x)\leq\nu( \Vert x \Vert )\);

  2. (2)

    \(\dot{V}(x(t))\leq-w( \Vert x \Vert )\), if \(V(x(t+ \theta ))< p (V (x(t) ) )\).

Then the solution \(x(t)\equiv0\) of (9) is asymptotically stable. Moveover, the set \({M}_{V(\rho)}\) is an invariant set inside the domain of attraction. Further, if \(u(s)\rightarrow\infty\) as \(s\rightarrow\infty\), then the solution \(x(t)\equiv0\) of (9) is globally stable.

Lemma 2.2

([27])

Let H, E, and \(G(t)\) be real matrices of appropriate dimensions with \(G(t)\) satisfying \(G(t)^{T}G(t)\leq{I}\). Then, for any scalar \(\varepsilon>0\),

$$ HG(t)E+\bigl(HG(t)E\bigr)^{T}\leq \varepsilon^{-1}HH^{T}+\varepsilon{E^{T}E}. $$
(10)

3 Main results

In this paper, the disturbance attenuation is investigated for memristive recurrent neural networks with mixed time-varying delays. According to Definition 2.4, the condition is constructed for the global asymptotic stability of systems (7) when \(h(t)=0\). Secondly, it is proved that there exists a bounded attractor for systems (7) when \(h(t)\neq0\). For convenience, denote \(L=\operatorname{diag}\{ l_{1},l_{2},\ldots,l_{n}\}\).

Theorem 3.1

Under Assumption 2.1, the memristive neural network (7) with \(h(t)=0\) under a disturbance attenuating controller \(u(t)=-Fx(t)\) is asymptotically stable if there exist matrices \(Q>0\), F, positive constants \(\varepsilon_{i}\) (\(i=0,1,2\)), and any given positive constant ϵ such that the following inequality holds:

$$ \begin{aligned}[b] \Omega&=-QA-AQ+\varepsilon_{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon _{0}LQL+\varepsilon_{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}LQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-QF-F^{T}Q+\epsilon^{-1}{Q}GG^{T}Q+ \epsilon{Q}\\ &< 0. \end{aligned} $$
(11)

Proof

Consider the following Lyapunov–Razumikhin function candidate:

$$\begin{aligned} V(t)=x(t)^{T}Qx(t). \end{aligned}$$
(12)

Taking the time-derivative of \(V(t)\) along the solution of (7) when \(h(t)=0\), the time-derivative of \(V(t)\) is

$$\begin{aligned} \dot{V}(t)=2x^{T}(t)Q\biggl[-Ax(t)+Bf\bigl(x(t)\bigr)+Cf\bigl(x \bigl(t-\tau(t)\bigr)\bigr)+D \int_{t-\rho (t)}^{t}f\bigl(x(s)\bigr)\,ds+u(t)\biggr]. \end{aligned}$$

If there exist positive constants \(\varepsilon_{i}\) (\(i=0,1,2\)), by employing Lemma 2.2, it is easy to obtain

$$\begin{aligned}& 2x^{T}(t)QBf\bigl(x(t)\bigr)\leq\varepsilon _{0}^{-1}x^{T}(t)QBQ^{-1}B^{T}Qx(t)+ \varepsilon_{0}f^{T}\bigl(x(t)\bigr)Qf\bigl(x(t)\bigr), \\& 2x^{T}(t)QCf\bigl(x\bigl(t-\tau(t)\bigr)\bigr)\leq\varepsilon _{1}^{-1}x^{T}(t)QCQ^{-1}C^{T}Qx(t)+ \varepsilon_{1}f^{T}(x\bigl(t-\tau(t)\bigr)Qf(x\bigl(t-\tau (t)\bigr), \\& \begin{aligned} 2x^{T}(t)QD \int_{t-\rho(t)}^{t}f\bigl(x(s)\bigr)\,ds&\leq \varepsilon_{2}^{-1}\rho (t)x^{T}(t)QDQ^{-1}D^{T}Qx(t)+ \varepsilon_{2}\rho(t)f^{T}\bigl(x(t)\bigr)Qf\bigl(x(t)\bigr) \\ &\leq\varepsilon_{2}^{-1}\rho{x}^{T}(t)QDQ^{-1}D^{T}Qx(t)+ \varepsilon_{2}\rho {f}^{T}\bigl(x(t)\bigr)Qf\bigl(x(t) \bigr). \end{aligned} \end{aligned}$$

Moreover, according to Assumption 2.1, it is not difficult to get

$$\begin{aligned}& 2x^{T}(t)QBf\bigl(x(t)\bigr) \leq\varepsilon _{0}^{-1}x^{T}(t)QBQ^{-1}B^{T}Qx(t)+ \varepsilon_{0}x^{T}(t)LQLx(t), \\& 2x^{T}(t)QCf\bigl(x\bigl(t-\tau(t)\bigr)\bigr) \leq\varepsilon _{1}^{-1}x^{T}(t)QCQ^{-1}C^{T}Qx(t)+ \varepsilon_{1}x^{T}\bigl(t-\tau(t)\bigr)LQLx\bigl(t-\tau (t) \bigr), \\& 2x^{T}(t)QD \int_{t-\rho(t)}^{t}f\bigl(x(s)\bigr)\,ds \leq \varepsilon_{2}^{-1}\rho {x}^{T}(t)QDQ^{-1}D^{T}Qx(t)+ \varepsilon_{2}\rho{x}^{T}(t)LQLx(t). \end{aligned}$$

Suppose \(p(s)=r\cdot{s}\) with \(r>1\) in Lemma 2.1, it is easy to get that \(p(s)>s\) for \(s>0\). Due to the condition \(V(x(\theta))\leq {p}(V(x(t)))\), \(\theta\in[t-\tau(t),t]\), that is, \(x^{T}(\theta)Qx(\theta )\leq{p}x^{T}(t)Qx(t)\). Thus, it is obvious that

$$\begin{aligned} x^{T}\bigl(t-\tau(t)\bigr)LQLx\bigl(t-\tau(t)\bigr)< rx^{T}(t)LQLx(t). \end{aligned}$$

In addition, choosing the controller to be \(u(t)=-Fx(t)\), it is easy to obtain

$$ \begin{aligned}[b] \dot{V}(t)&\leq{x}^{T}(t)\bigl[-QA-AQ+\varepsilon _{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon_{0}LQL +\varepsilon_{1}^{-1}QCQ^{-1}C^{T}Q \\ &\quad {}+\varepsilon_{1}rLQL +\varepsilon_{2}^{-1} \rho{Q}DQ^{-1}D^{T}Q+\varepsilon_{2} \rho{L}QL-QF-F^{T}Q\bigr]x(t). \end{aligned} $$
(13)

Because (11) holds, \(r>1\) is chosen to guarantee

$$ \begin{aligned}[b] &-QA-AQ+\varepsilon_{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon_{0}LQL+\varepsilon _{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}rLQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-QF-F^{T}Q+\epsilon^{-1}{Q}GG^{T}Q+ \epsilon{Q}< 0. \end{aligned} $$
(14)

Thus, combining (13) with (14), it is not difficult to obtain

$$\begin{aligned} \dot{V}(t)&\leq-{x}^{T}(t) \bigl(\epsilon^{-1}{Q}GG^{T}Q+ \epsilon{Q}\bigr)x(t)< 0. \end{aligned}$$
(15)

It is obvious that \(\dot{V}(t)\) is negative definite. According to Lyapunov stability theory, systems (7) when \(h(t)=0\) are asymptotically stable. This completes our first step. Next, when \(h(t)\neq0\), it is proved that there really exists a bounded attractor for systems (7). □

Theorem 3.2

Under Assumption 2.1, the memristive neural network (7) with \(h(t)\neq0\) has a disturbance attenuating controller \(u(t)=-Fx(t)\) with an attractor as \(\Phi=\{ x|x^{T}Qx\leq1\}\) if there exist matrices \(Q>0\), M, F, positive constants \(\varepsilon_{i}\) (\(i=0,1,2\)), and any given positive constant ϵ such that the following inequality holds:

$$\begin{aligned} \small\Delta= \left [ \begin{matrix} \Omega_{11} & QG&QB&QC&\sqrt{\rho}QD\\ \ast&-\epsilon{I}&0&0&0\\ \ast&\ast&-\varepsilon_{0}Q&0&0\\ \ast&\ast&\ast&-\varepsilon_{1}Q&0\\ \ast&\ast&\ast&\ast&-\varepsilon_{2}Q \end{matrix} \right ]< 0, \end{aligned}$$
(16)

where

$$\begin{aligned} \Omega_{11}=-QA-AQ+\varepsilon_{0}LQL+\varepsilon_{1}LQL+ \varepsilon_{2}\rho {L}QL+\epsilon{Q}-M-M^{T},\quad M=QF. \end{aligned}$$

Proof

Consider the same Lyapunov–Razumikhin function candidate:

$$\begin{aligned} V(t)=x^{T}(t)Qx(t). \end{aligned}$$
(17)

Taking the time-derivative of \(V(t)\) along the solution of (7) when \(h(t)\neq0\), the time-derivative of \(V(t)\) is

$$\begin{aligned} \begin{aligned} \dot{V}(t)&=2x^{T}(t)Q\biggl[-Ax(t)+Bf\bigl(x(t)\bigr)+Cf\bigl(x \bigl(t-\tau(t)\bigr)\bigr)\\ &\quad {}+D \int_{t-\rho (t)}^{t}f\bigl(x(s)\bigr)\,ds+Gh(t)+u(t)\biggr]. \end{aligned} \end{aligned}$$

After the same discussion as that in Theorem 3.1, let \(M=QF\), it is easy to obtain

$$ \begin{aligned}[b] \dot{V}(t)&\leq {x}^{T}(t)\bigl[-QA-AQ+\varepsilon _{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon_{0}LQL+\varepsilon _{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}rLQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-M-M^{T}\bigr]x(t)+2x^{T}(t)QGh(t). \end{aligned} $$
(18)

Applying Lemma 2.2 to the term \(2x^{T}(t)QGh(t)\), for the given positive ϵ, it is easy to get

$$\begin{aligned} 2x^{T}(t)QGh(t)\leq\epsilon^{-1}{x}^{T}(t){Q}GG^{T}Qx(t)+ \epsilon{h}^{T}(t)h(t). \end{aligned}$$

Because the bounded disturbances are assumed to belong to the set \(\mathcal{H}=\{h|h^{T}h\leq1\}\), it is easy to obtain

$$\begin{aligned} 2x^{T}(t)QGh(t)\leq\epsilon^{-1}{x}^{T}(t){Q}GG^{T}Qx(t)+ \epsilon. \end{aligned}$$

Thus, it follows that

$$\begin{aligned} \dot{V}(t)&\leq{x}^{T}(t)\bigl[-QA-AQ+\varepsilon _{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon_{0}LQL+\varepsilon _{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}rLQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-M-M^{T}+\epsilon^{-1}{Q}GG^{T}Q \bigr]x(t)+\epsilon. \end{aligned}$$
(19)

Applying the Schur complement to (16), it is equivalent to

$$ \begin{aligned}[b] \Delta&=-QA-AQ+\varepsilon_{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon _{0}LQL+\varepsilon_{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}LQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-M-M^{T}+\epsilon^{-1}{Q}GG^{T}Q+ \epsilon{Q}\\ &< 0. \end{aligned} $$
(20)

By choosing \(r>1\), it implies that

$$\begin{aligned} &-QA-AQ+\varepsilon_{0}^{-1}QBQ^{-1}B^{T}Q+ \varepsilon_{0}LQL+\varepsilon _{1}^{-1}QCQ^{-1}C^{T}Q+ \varepsilon_{1}rLQL \\ &\quad {}+\varepsilon_{2}^{-1}\rho{Q}DQ^{-1}D^{T}Q+ \varepsilon_{2}\rho {L}QL-M-M^{T}+\epsilon^{-1}{Q}GG^{T}Q< - \epsilon{Q}. \end{aligned}$$
(21)

Thus, it follows that

$$\begin{aligned} \dot{V}(t)&\leq-\epsilon{x}^{T}(t){Q}x(t)+\epsilon. \end{aligned}$$
(22)

Obviously, \(\dot{V}(t)\) is negative outside the set Φ, the trajectories beginning from outside the set Φ will ultimately access the set Φ for any \(h\in\mathcal{H}\). Therefore, Φ is the invariant set of systems (7). So far, condition (2) of disturbance attenuation has been constructed. Meanwhile, the disturbance attenuating controller \(u(t)=-Fx(t)\) with an attractor as \(\Phi=\{x|x^{T}Qx\leq1\}\) has been designed. This completes our proof. □

Remark 3.1

In comparison to the published paper [31], our paper’s contribution lies in three aspects: Firstly, the studied memristive neural networks are more popular at present; secondly, the activation function is not needed to be strict to be \(f(x(\cdot))=0.5(|x(\cdot)+1|-|x(\cdot)-1|)\), but rather it is relaxed to just satisfy Lipschitz conditions; thirdly, the discussed model not only contains discrete time-varying delay but also includes distributed time-varying delay. Therefore, our results are more general to be well applied.

Remark 3.2

Recently, many scholars have studied different kinds of control theories about MRNNS such as exponential synchronization control [12], finite-time synchronization control [13], exponential lag adaptive synchronization control [18], lag synchronization control [19], and so on. However, to the best of our knowledge, there has not been any paper to discuss the disturbance attenuating controller design for MRNNs. This paper is the first one to investigate the disturbance attenuating controller for MRNNs, which is sure to strengthen the systematic research theory for MRNNs and must further enrich the basis of application for MRNNs.

4 Numerical examples

In this section, one example is presented to demonstrate the effectiveness of our results.

Example 4.1

Consider a two-neuron memristive neural network containing both persistent disturbances and mixed time-varying delays:

$$\begin{aligned}& \begin{aligned} \dot{x}_{1}(t) &= -\breve{a}_{1}\bigl(x_{1}(t) \bigr)x_{1}(t)+\breve {b}_{11}\bigl(x_{1}(t) \bigr)f\bigl(x_{1}(t)\bigr)+\breve{b}_{12} \bigl(x_{1}(t)\bigr)f\bigl(x_{2}(t)\bigr)\\ &\quad {}+\breve {c}_{11}\bigl(x_{1}(t)\bigr)f\bigl(x_{1}\bigl(t- \tau(t)\bigr)\bigr)+\breve{c}_{12}\bigl(x_{1}(t)\bigr)f\bigl(x_{2} \bigl(t-\tau(t)\bigr)\bigr) \\ &\quad {}+\breve{d}_{11}\bigl(x_{1}(t) \bigr) \int _{t-\rho(t)}^{t}f\bigl(x_{1}(s)\bigr)\,ds+ \breve{d}_{12}\bigl(x_{1}(t)\bigr) \int_{t-\rho (t)}^{t}f\bigl(x_{2}(s)\bigr)\,ds \\ &\quad {}+g_{11}h_{1}(t)+g_{12}h_{1}(t)+u_{1}(t), \end{aligned} \\& \begin{aligned} \dot{x}_{2}(t) &= -\breve{a}_{2}\bigl(x_{2}(t) \bigr)x_{2}(t)+\breve {b}_{21}\bigl(x_{2}(t) \bigr)f\bigl(x_{1}(t)\bigr)+\breve{b}_{22} \bigl(x_{2}(t)\bigr)f\bigl(x_{2}(t)\bigr)\\ &\quad {}+\breve {c}_{21}\bigl(x_{2}(t)\bigr)f\bigl(x_{1}\bigl(t- \tau(t)\bigr)\bigr)+\breve{c}_{22}\bigl(x_{2}(t)\bigr)f\bigl(x_{2} \bigl(t-\tau(t)\bigr)\bigr) \\ &\quad {}+\breve{d}_{21}\bigl(x_{2}(t) \bigr) \int _{t-\rho(t)}^{t}f\bigl(x_{1}(s)\bigr)\,ds+ \breve{d}_{22}\bigl(x_{2}(t)\bigr) \int_{t-\rho (t)}^{t}f\bigl(x_{2}(s)\bigr)\,ds \\ &\quad {}+g_{21}h_{2}(t)+g_{22}h_{2}(t)+u_{2}(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned}& \breve{a}_{1}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} 1.01, & \vert x_{1}(t) \vert \leq1,\\ 0.97,& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{b}_{11}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} 1+\frac{2\pi}{5}, & \vert x_{1}(t) \vert \leq1,\\ 1+\frac{\pi}{5},& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \\& \breve{b}_{12}\bigl(x_{1}(t) \bigr)= \textstyle\begin{cases} 20.05, & \vert x_{1}(t) \vert \leq1,\\ 19.95,& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{c}_{11}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} -1.2\sqrt{2}\frac{\pi}{3}, & \vert x_{1}(t) \vert \leq1,\\ -1.4\sqrt{2}\frac{\pi}{3},& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \\& \breve{c}_{12}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} 0.12, & \vert x_{1}(t) \vert \leq1,\\ 0.09,& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{d}_{11}\bigl(x_{1}(t) \bigr)= \textstyle\begin{cases} -0.05, & \vert x_{1}(t) \vert \leq1,\\ 0.05,& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \\& \breve{d}_{21}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} -0.05, & \vert x_{1}(t) \vert \leq1,\\ 0.05,& \vert x_{1}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{a}_{2}\bigl(x_{2}(t)\bigr)= \textstyle\begin{cases} 1.01, & \vert x_{2}(t) \vert \leq1,\\ 0.97,& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \\& \breve{b}_{21} \bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} 0.12, & \vert x_{2}(t) \vert \leq1,\\ 0.95,& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{b}_{22}\bigl(x_{2}(t)\bigr)= \textstyle\begin{cases} 1+\frac{2\pi}{5}, & \vert x_{2}(t) \vert \leq1,\\ 1+\frac{\pi}{5},& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \\& \breve{c}_{21}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} 0.12, & \vert x_{2}(t) \vert \leq1,\\ 0.09,& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{c}_{22} \bigl(x_{2}(t)\bigr)= \textstyle\begin{cases} -1.2\sqrt{2}\frac{\pi}{3}, & \vert x_{2}(t) \vert \leq1,\\ -1.4\sqrt{2}\frac{\pi}{3},& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \\& \breve{d}_{21}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} -0.05, & \vert x_{2}(t) \vert \leq1,\\ 0.05,& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \qquad \breve{d}_{22}\bigl(x_{1}(t)\bigr)= \textstyle\begin{cases} -0.05, & \vert x_{2}(t) \vert \leq1,\\ 0.05,& \vert x_{2}(t) \vert >1, \end{cases}\displaystyle \\& g_{11}=g_{22}=1,\qquad g_{12}=g_{21}=0. \end{aligned}$$

Meanwhile, the discrete time-varying delay is assumed to be \(\tau (t)=1+0.4\operatorname{sin}(5t)\), and the distributed time-varying delay is supposed to be \(\rho(t)=0.81|\operatorname{cos}(t)|\). In addition, the activation functions are assumed to be \(f_{i}(x_{i})=0.5(|x_{i}+1|-|x_{i}-1|)\) (\(i=1,2\)). Moreover, the disturbance \(h(t)=[0.03\operatorname{cos}t;0.02\operatorname{sin}t]\). Particularly, if we choose that \(\varepsilon_{0}=\varepsilon_{1}=\varepsilon_{1}=\epsilon=1\), by solving LMI (16), we obtain

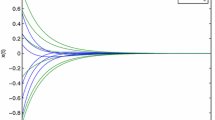
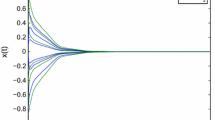
$$\begin{aligned}& Q=\left [ { \begin{matrix} {0.1278} & {-0.1204} \\ {-0.1204}& {1.4341} \end{matrix} } \right ],\qquad M=\left [ { \begin{matrix} {3.6433} & {-0.2134} \\ {-0.2134}& {6.6332} \end{matrix} } \right ],\\& F=\left [ { \begin{matrix} {30.8042} & {2.9171} \\ {2.4367}& {4.8701} \end{matrix} } \right ]. \end{aligned}$$

Figure 1 demonstrates the state trajectories of neural network (7) with \(u(t)=-Fx(t)\) when \(h(t)=0\). From Fig. 1, it shows that the neural networks are globally asymptotically stable under the feedback controller \(u(t)\). Figure 2 describes the disturbance attenuating controller \(u(t)=-Fx(t)\) with an attractor as \(\Phi=\{x|x^{T}Qx\leq1\}\) for neural network (7).

Figure 1
figure 1

State trajectories of neural network (1) with \(u(t)\) in case of \(h=0\)

Full size image
Figure 2
figure 2

The disturbance attenuating controller \(u(t)=-Fx(t)\) with an attractor as \(\Phi=\{x|x^{T}Qx\leq1\}\)

Full size image

Remark 4.1

Comparatively speaking, although the feedback controller law is established in the form of bilinear matrix inequality (BMI), it can be easily solved by alternatively fixing some parameters and optimizing the rest. However, the LMIs in [31] are at least four, which is obviously difficult to be solved.

5 Conclusions

In this paper, the famous differential inclusions, set-valued maps, and Lyapunov–Razumikhin are employed to design a feedback controller law for MRNNs. A feedback controller law is obtained with less computation burden. In the future, other approach, such as the delay-partitioning technique, can be employed to further reduce the conservativeness of the obtained result.