1 Introduction

The concept of fractional differentiation appeared for the first time in a famous correspondence between L’Hospital and Leibniz, in 1695. Many mathematicians have further developed this area and we can mention the studies of Euler, Laplace, Abel, Liouville and Riemann. However, the fractional calculus remained for centuries a purely theoretical topic, with little if any connections to practical problems of physics and engineering. In recent years, the fractional calculus has been recognized as an effective modeling methodology for researchers [1]. As is well known, fractional calculus is a generalization of classical calculus to non-integer order. Compared with an integer-order system, a fractional-order system is a better option for engineering physics.

Fractional systems have been paid much attention to, for example, the fractional optimal control problems [2], stability analysis of Caputo-like discrete fractional systems [3, 4], fractional description of financial systems [5], fractional chaotic systems [6]. Especially, stabilization problem of fractional-order systems is a very interesting and important research topic. In recent years, more and more researchers and scientists have begun to address this problem [7–23]. With the help of the Lyapunov direct method, Mittag-Leffler stability and generalized Mittag-Leffler stability was studied [10, 20]. The Lyapunov direct method deals with the stability problem of fractional-order systems have been extended [11, 24]. Reference [25] studied the global Mittag-Leffler stability for a coupled system of fractional-order differential equations on network with feedback controls. Robust stability and stabilization of fractional-order interval systems with \(0<\alpha<1\) order have been studied [15]. Necessary and sufficient conditions on the asymptotic stability of the positivity continuous time fractional-order systems with bounded time-varying delays are investigated by the monotonic and asymptotic property [14]. The stabilization problem of a class of fractional-order chaotic systems have been addressed [12]. Pseudo-state stabilization problem of fractional-order nonlinear systems has attracted the attention of some researchers [7–9, 13, 16]. Moreover, any equilibrium of a general fractional-order nonlinear system described by either Caputo’s or Riemann-Liouville’s definition can never be finite-time stable was proved [26]. Finite-time fractional-order adaptive intelligent backstepping sliding mode control have been proposed to deal with uncertain fractional-order chaotic systems [27]. The time-optimal control problem for a class of fractional-order systems was proposed [28]. In addition, robust controller design problem for a class of fractional-order nonlinear systems with time-varying delays was investigated [29] and state feedback \(H_{\infty}\) control of commensurate fractional-order systems was studied [30].

Backstepping design method has been widely applied in stabilizing a general class of integer-order nonlinear systems. Backstepping design offers a choice of design tools for accommodation of uncertain nonlinearities [31]. It is well known that the backstepping design has been reported for nonlinear systems in strict-feedback form or triangular form [31–36]. Systematic design of globally stable and adaptive controllers for a class of parametric strict-feedback form are investigated by the backstepping design procedure [34]. The overparametrization and partial overparametrization problems were soon eliminated by elegantly introducing the tuning functions [33, 35]. On the other hand, with the aids of this frequency distribute model and the indirect Lyapunov method, the adaptive backstepping control of fractional-order systems were established [37–39]. As far as we know, there are few results on the generalization of backstepping into fractional-order systems. It was pointed out that the well-known Leibniz rule is not satisfied for fractional-order systems. Then an interesting question arises: when the states of system are not Leibniz rule, how to deal with the stabilization problem through design of tuning functions and adaptive feedback control law? So far, the stabilization problem of fractional-order nonlinear systems remains an open problem.

In this paper, we investigate the Mittag-Leffler stabilization problem of a class of fractional-order nonlinear systems. Compared with the existing results, the main contributions of this paper are as follows: (1) The backstepping design is extended to fractional-order nonlinear systems with unknown control coefficients, and an adaptive control scheme with tuning functions is proposed. It is proved that the stabilization problem of fractional-order nonlinear systems can be solved by the designed control scheme. (2) The Mittag-Leffler stabilization problem is achieved using a systematic design procedure and without any growth restriction on nonlinearities. (3) The controller is designed to ensure that the pseudo-state of the fractional-order system convergence to the equilibrium. (4) Successfully overcoming the difficulty of the fractional-order system without the Leibniz rule, and the tuning function is constructed to avoid overparameterization.

The remainder of this paper is organized as follows: Section 2 the problem formulation, some necessary concepts and some necessary lemmas are given. In Section 3, as the main part of this note, an adaptive controller and tuning functions are designed by using the backstepping method for fractional-order nonlinear systems. In Section 4, two numerical simulations are provided to illustrate the effectiveness of the proposed results. Finally, Section 5 concludes this study.

2 Problem formulation and preliminary results

In this paper, we consider the stabilization problem of the following nonlinear fractional systems:

$$ \begin{aligned} &D^{q} x_{i}=b_{i}x_{i+1}+ \theta^{T}\varphi_{i}(x_{1},\ldots,x_{i}), \quad i=1, \ldots,n-1, \\ &D^{q} x_{n}=\varphi_{0}(x)+\theta^{T} \varphi_{n}(x_{1},\ldots,x_{n})+b_{n} \beta_{0}(x)u, \end{aligned} $$
(1)

where \(x=[x_{1},\ldots,x_{n}]^{T}\in R^{n}\), \(D^{q}\) is the Caputo fractional derivative of order \(0< q\leq1\), \(\theta\in R^{p}\) is an unknown constant parameter and \(b_{i},i=1,2,\ldots,n\), are unknown constants, called unknown control coefficients. \(u\in R\) is the control input, \(\varphi _{0}\), \(\beta_{0}\) and the components of \(\varphi_{i}\), \(1\leq i\leq n\) are smooth nonlinear functions in \(R^{n}\) and \(\beta_{0}(x)\neq0\) for all \(x\in R^{n}\).

Remark 1

It is worth pointing out that if let the unknown constants \(b_{i}=1\) (\(i=1,\ldots,n\)) and \(q=1\) in (1), the systems (1) reduces to the well-known parametric strict-feedback system. Moreover, if \(b_{i}=1\) (\(i=1,\ldots,n\)) and \(\varphi_{0}(x)\) is a constant, then system (1) will become the parametric strict-feedback form of fractional-order nonlinear system.

Definition 1

([40])

The fractional-order derivative \(D_{t}^{q}\) (\(q>0\)) of \(g(t)\) in Caputo sense is defined as

$$ {}^{C}_{t_{0}} D_{t}^{q}g(t)= \frac{1}{\Gamma(n-q)} \int_{t_{0}}^{t}(t-s)^{n-q-1}g^{(n)}(s) \,ds, $$
(2)

where \(n-1< q\leq n\in N\).

Remark 2

For simplicity, the symbol \(D^{q}\) is shorted for \({}^{C}_{t_{0}} D_{t}^{q}\), where t is the time.

  1. (1)

    If C is a constant, then \(D^{q} C=0\).

Similar to integer-order differentiation, fractional-order differentiation in Caputo’s sense is a linear operation:

  1. (2)

    \(D^{q}(\mu g(t)+\omega h(t))=\mu D^{q} g(t)+\omega D^{q} h(t)\),

where μ and ω are real numbers.

  1. (3)

    Leibniz rule:

    $$D^{q}\bigl( g(t)h(t)\bigr)=\sum_{r=0}^{\infty} \frac{\Gamma(q+1)}{\Gamma(r+1)\Gamma (q-r+1)}D^{q-r}g(t)D^{r}h(t). $$

Note that the sum is infinite and contains integrals of fractional order for \(r>[q]+1\).

Remark 3

The well-known Leibniz rule \(D^{q}(fg) = (D^{q} f)g + f(D^{q} g)\) is not satisfied for differentiation of non-integer orders.

Lemma 1

([13])

Let \(V: D \rightarrow R\) be a continuous positive definite function defined on a domain \(D\subset R^{n}\) that contains the origin. Let \(B_{d} \subset D\) for some \(d > 0\). Then there exist class-K functions \(\gamma_{1}\) and \(\gamma_{2}\) defined on \([0,d]\), such that

$$\begin{aligned} \gamma_{1} \bigl( \Vert x \Vert \bigr)\leq V(x)\leq \gamma_{2} \bigl( \Vert x \Vert \bigr), \end{aligned}$$
(3)

for all \(x\in B_{d}\). If \(D=R^{n}\), the functions \(\gamma_{1}\) and \(\gamma_{2}\) will be defined on \([0,\infty)\).

Lemma 2

([7, 11] (Mittag-Leffler stability))

Let \(x(t)=0\) be the equilibrium point of the fractional-order system \(D^{q} x=f(x,t),x\in\Omega\), where Ω is neighborhood region of the origin. Assume that there exists a fractional Lyapunov function \(V(t,x(t)):[0,\infty)\times R^{n}\rightarrow R\) and class-K functions \(\gamma_{i},i=1,2,3\) satisfying

$$\begin{aligned} \mathrm{(i)}&\quad \gamma_{1} \bigl( \Vert x \Vert \bigr)\leq V \bigl(t,x(t) \bigr)\leq\gamma_{2} \bigl( \Vert x \Vert \bigr); \\ \mathrm{(ii)}&\quad D^{q} V \bigl(t,x(t) \bigr)\leq-\gamma_{3} \bigl( \Vert x \Vert \bigr). \end{aligned}$$

Then the fractional-order system is asymptotically Mittag-Leffler stable. Moreover, if \(\Omega=R^{n}\), the fractional-order system is globally asymptotically Mittag-Leffler stable.

Lemma 3

([24])

Let \(x(t)\in R\) be a real continuously differentiable function. Then, for any time instant \(t\geq t_{0}\),

$$ \frac{1}{2}~_{t_{0}} D_{t}^{\alpha}x^{2}(t)\leq x(t) _{t_{0}} D_{t}^{\alpha}x(t),\quad \forall\alpha\in(0,1). $$
(4)

Remark 4

In the case when \(x(t)\in R^{n}\), Lemma 3 is still valid. That is, \(\alpha\in(0,1)\) and \(t \geq t_{0}\), \(\frac {1}{2}D^{\alpha}x^{T}(t)x(t)\leq x^{T}(t)D^{\alpha}x(t)\). In addition, let \(x(t)\in R\) be a real continuously differentiable function. Then, for any \(p = 2^{n} , n \in N\), \(D^{\alpha}x^{p}(t)\leq px^{p-1}(t)D^{\alpha}x(t)\), where \(0<\alpha<1 \) (see [7]).

3 Backstepping design

In this section, we will give the backstepping design procedure of fractional-order systems.

Theorem 1

The fractional-order nonlinear system (1) can be asymptotically Mittag-Leffler stable by the adaptive feedback control

$$\begin{aligned} &u = -\frac{1}{b_{n}\beta_{0}} \biggl(b_{n-1}z_{n-1}+c_{n}z_{n}+ \varphi_{0}+\hat{\theta}^{T}\varphi_{n}+ \frac{b_{n-2}}{b_{n-1}}D^{q}z_{n-2}+\frac{c_{n-1}}{b_{n-1}}D^{q}z_{n-1} \biggr). \end{aligned}$$
(5)
$$\begin{aligned} &\alpha_{i}(x_{1},\ldots,x_{i},\hat{\theta}) = -\frac{1}{b_{i}} \biggl(b_{i-1}z_{i-1}+c_{i}z_{i}+ \hat{\theta}^{T}\varphi_{i}+\frac{b_{i-2}}{b_{i-1}}D^{q}z_{i-2} +\frac{c_{i-1}}{b_{i-1}}D^{q}z_{i-1} \biggr), \\ &\quad 2\leq i\leq n-1, \end{aligned}$$
(6)

where \(\alpha_{1}(x_{1},\hat{\theta})=-\frac{c_{1}}{b_{1}}z_{1}-\frac{1}{b_{1}}\hat {\theta}^{T}\varphi_{1}(x_{1})\), and \(c_{1},c_{2},\ldots,c_{n}\) are positive constants. θ̂ is the estimate of the unknown parameter θ, \(\tilde{\theta}=\hat{\theta}-\theta\) and update laws

$$ D^{q}\hat{\theta}=\tau_{n}=\Gamma z_{1} \varphi_{1}+ \sum_{k=1}^{n-1}\Gamma z_{k+1} \biggl(\varphi_{k+1}-\frac{1}{\tilde{\theta}b_{k}}D^{q}( \hat{\theta}\varphi_{k}) \biggr), $$
(7)

where \(\Gamma=\operatorname{diag}[p_{1},\ldots,p_{m}]>0\) is the gain matrix of the adaptive law.

Proof

The design procedure is recursive. Its ith-order subsystem is stabilized with respect to a Lyapunov function \(V_{i}\) by the design of a stabilizing function \(\alpha_{i}\) and a tuning function \(\tau_{i}\). The update law for the parameter estimate θ̂ and the feedback control u are designed at the final step.

Step 1: Let \(z_{1} =x_{1}\) and \(z_{2}=x_{2}-\alpha_{1}\), we rewrite \(D^{q} x_{1}=b_{1}x_{2} + \theta^{T}\varphi_{1}(x_{1})\) as

$$ D^{q} z_{1}=b_{1}(z_{2} + \alpha_{1} )+\theta^{T}\varphi_{1}(x_{1}). $$
(8)

Choose a Lyapunov function candidate as \(V_{1}=\frac{1}{2}z_{1}^{2}+\frac {1}{2}\tilde{\theta}^{T}\Gamma^{-1}\tilde{\theta}\), where \(\tilde{\theta }=\hat{\theta}-\theta\) is the parameter estimate error. We have

$$ D^{q} V_{1}\leq z_{1} \bigl[b_{1}(z_{2}+\alpha_{1})+\hat{ \theta}^{T}\varphi_{1} \bigr]+\tilde{\theta}^{T} \Gamma^{-1} \bigl(D^{q} \hat{\theta}-\tau_{1} \bigr), $$
(9)

where

$$ \tau_{1}=\Gamma z_{1}\varphi_{1}(x_{1}). $$
(10)

To make \(D^{q} V_{1}\leq- c_{1}z_{1}^{2}\), we would choose

$$ \alpha_{1}(x_{1},\hat{\theta})=- \frac{1}{b_{1}} \bigl(c_{1}z_{1}+\hat{ \theta}^{T}\varphi_{1}(x_{1}) \bigr). $$
(11)

However, we retain \(\tau_{1}\) as the first tuning function and \(\alpha_{1}\) as the first stabilizing function. We have

$$ D^{q}V_{1}\leq-c_{1}z_{1}^{2}+b_{1}z_{1}z_{2}+ \tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{1} \bigr). $$
(12)

The second term \(b_{1}z_{1}z_{2}\) in \(D^{q}V_{1}\) will be canceled at the next step.

Substituting (11) into (8) yields

$$ D^{q}z_{1}=-c_{1}z_{1}+b_{1}z_{2}+( \theta-\hat{\theta})^{T}\varphi_{1}(x_{1}). $$
(13)

Step 2: Let \(z_{3} =x_{3} -\alpha_{2}\), we rewrite \(D^{q}x_{2} =b_{2}x_{3} + \theta ^{T}\varphi_{2}(x_{1},x_{2})\) as

$$ D^{q}z_{2}=b_{2}(z_{3}+ \alpha_{2})+\theta^{T}\varphi_{2}+\frac{1}{b_{1}} \bigl(c_{1}D^{q}z_{1}+D^{q}(\hat{ \theta}\varphi_{1}) \bigr). $$
(14)

Choose a Lyapunov function candidate as follows: \(V_{2} = V_{1} + \frac {1}{2}z_{2}^{2}\). We have

$$\begin{aligned} D^{q} V_{2} \leq& -c_{1}z_{1}^{2}+z_{2} \bigl[b_{1}z_{1}+b_{2}(z_{3}+ \alpha_{2})+\hat{\theta}^{T}\varphi_{2} \bigr]+ \frac{z_{2}}{b_{1}} \bigl[c_{1}D^{q}z_{1}+D^{q}( \hat{\theta}\varphi_{1}) \bigr] \\ & {}+ \tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q} \hat{\theta}-\tau_{2} \bigr), \end{aligned}$$
(15)

where

$$\begin{aligned} \tau_{2}=\Gamma \biggl(z_{1} \varphi_{1}+z_{2}\varphi_{2}-\frac{z_{2}}{\tilde{\theta}b_{1}}D^{q}( \hat{\theta}\varphi_{1}) \biggr)=\tau_{1}+\Gamma z_{2} \biggl(\varphi_{2}-\frac{1}{\tilde{\theta}b_{1}}D^{q}( \hat{\theta}\varphi_{1}) \biggr). \end{aligned}$$
(16)

Then, to make \(D^{q}V_{2} \leq-c_{1} z_{1}^{2} -c_{2} z_{2}^{2}\), we would choose

$$ \alpha_{2}(x_{1},x_{2},\hat{ \theta})=-\frac{1}{b_{2}} \biggl(b_{1}z_{1}+c_{2}z_{2}+ \hat{\theta}^{T}\varphi_{2}+\frac{c_{1}}{b_{1}}D^{q}z_{1} \biggr). $$
(17)

However, we retain \(\tau_{2}\) as the second tuning function and \(\alpha _{2}\) as the second stabilizing function. The resulting \(D^{q}V_{2}\) is

$$ D^{q}V_{2}\leq-c_{1}z_{1}^{2}-c_{2}z_{2}^{2}+b_{2}z_{2}z_{3}+ \tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{2} \bigr). $$
(18)

The third term in \(D^{q}V_{2}\) will be canceled at the next step.

Substituting (17) into (14) yields

$$ D^{q}z_{2}=-b_{1}z_{1}-c_{2}z_{2}+b_{2}z_{3}+( \theta-\hat{\theta})^{T}\varphi_{2}+\frac{1}{b_{1}}D^{q}( \hat{\theta}\varphi_{1}). $$
(19)

Step 3: Let \(z_{4} =x_{4}-\alpha_{3}\), we rewrite \(D^{q}x_{3} =b_{3}x_{4} + \theta ^{T}\varphi_{3}(x_{1},x_{2},x_{3})\) as

$$ D^{q}z_{3}=b_{3}(z_{4}+ \alpha_{3})+\theta^{T}\varphi_{3}+\frac{1}{b_{2}} \bigl(b_{1}D^{q}z_{1}+c_{2}D^{q}z_{2}+D^{q}( \hat{\theta}\varphi_{2}) \bigr). $$
(20)

Choose a Lyapunov function as \(V_{3} = V_{2} + \frac{1}{2}z_{3}^{2}\). We have

$$\begin{aligned} D^{q} V_{3} \leq& -c_{1}z_{1}^{2}-c_{2}z_{2}^{2}+z_{3} \bigl[b_{2}z_{2} +b_{3}(z_{4}+ \alpha_{3})+\hat{\theta}^{T}\varphi_{3} \bigr] \\ &{}+\frac{z_{3}}{b_{2}} \bigl(b_{1}D^{q}z_{1}+c_{2}D^{q}z_{2}+D^{q}( \hat{\theta}\varphi_{2}) \bigr)+\tilde{\theta}^{T} \Gamma^{-1} \bigl(D^{q}\hat{\theta}-\tau_{3} \bigr), \end{aligned}$$
(21)

where

$$\begin{aligned} \tau_{3} = \tau_{2}+\Gamma z_{3} \varphi_{3}-\Gamma\frac{z_{3}}{\tilde{\theta}b_{2}} D^{q}(\hat{\theta} \varphi_{2})=\tau_{2}+\Gamma z_{3} \biggl( \varphi_{3}-\frac{1}{\tilde{\theta}b_{2}}D^{q}(\hat{\theta} \varphi_{2}) \biggr). \end{aligned}$$
(22)

Then, to make \(D^{q}V_{3} \leq-c_{1}z_{1}^{2}- c_{2}z_{2}^{2}-c_{3}z_{3}^{2}\), we would choose

$$\begin{aligned} \alpha_{3}(x_{1},x_{2},x_{3}, \hat{\theta})=-\frac{1}{b_{3}} \biggl(b_{2}z_{2}+c_{3}z_{3}+ \hat{\theta}^{T}\varphi_{3}+\frac{b_{1}}{b_{2}}D^{q}z_{1}+ \frac{c_{2}}{b_{2}}D^{q}z_{2} \biggr). \end{aligned}$$
(23)

However, we retain \(\tau_{3}\) as the third tuning function and \(\alpha_{3}\) as the third stabilizing function. The resulting \(D^{q}V_{3}\) is

$$\begin{aligned} D^{q}V_{3} \leq& -c_{1}z_{1}^{2}-c_{2}z_{2}^{2}-c_{3}z_{3}^{2}+b_{3}z_{3}z_{4}+ \tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{3} \bigr). \end{aligned}$$
(24)

Substituting (23) into (20) yields

$$\begin{aligned} D^{q}z_{3} = & -b_{2}z_{2}-c_{3}z_{3}+b_{3}z_{4}+( \theta-\hat{\theta})^{T}\varphi_{3}+\frac{1}{b_{2}}D^{q}( \hat{\theta}\varphi_{2}). \end{aligned}$$
(25)

Step i (\(i\geq2\)): Let \(z_{i+1} =x_{i+1}-\alpha_{i}\), we rewrite \(D^{q}x_{i} =b_{i}x_{i+1}+\theta^{T}\varphi_{i}(x_{1},\ldots,x_{i})\) as

$$\begin{aligned} D^{q}z_{i} = b_{i}(z_{i+1}+ \alpha_{i})+\theta^{T}\varphi_{i}+ \frac{1}{b_{i-1}} \bigl(b_{i-2}D^{q}z_{i-2}+c_{i-1}D^{q}z_{i-1}+D^{q}( \hat{\theta}\varphi_{i-1}) \bigr). \end{aligned}$$
(26)

Choose a Lyapunov function of the form \(V_{i}= V_{i-1} + \frac {1}{2}z_{i}^{2}\). Then

$$\begin{aligned} D^{q}V_{i} \leq& -\sum _{k=1}^{i-1}c_{k}z_{k}^{2} +z_{i} \bigl[b_{i-1}z_{i-1}+b_{i}(z_{i+1}+ \alpha_{i})+\hat{\theta}\varphi_{i} \bigr] \\ &{}+\frac{z_{i}}{b_{i-1}} \bigl(b_{i-2}D^{q}z_{i-2}+c_{i-1}D^{q}z_{i-1} +D^{q}(\hat{\theta}\varphi_{i-1}) \bigr)+\tilde{ \theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{\theta}- \tau_{i} \bigr), \end{aligned}$$
(27)

where

$$\begin{aligned} \tau_{i}=\tau_{i-1}+\Gamma z_{i} \biggl(\varphi_{i}-\frac{1}{\tilde{\theta}b_{i-1}}D^{q}(\hat{\theta} \varphi_{i-1}) \biggr). \end{aligned}$$
(28)

Then, to make \(D^{q}V_{i}\leq-\sum_{k=1}^{i}c_{k}z_{k}^{2}\), we would choose

$$\begin{aligned} \alpha_{i}(x_{1},\ldots,x_{i}, \hat{\theta}) = &-\frac{1}{b_{i}} \biggl(b_{i-1}z_{i-1}+c_{i}z_{i}+ \hat{\theta}^{T}\varphi_{i}+\frac{b_{i-2}}{b_{i-1}}D^{q}z_{i-2}+ \frac{c_{i-1}}{b_{i-1}}D^{q}z_{i-1} \biggr). \end{aligned}$$
(29)

However, we retain \(\tau_{i}\) as the ith tuning function and \(\alpha_{i}\) as the ith stabilizing function. The resulting \(D^{q}V_{i}\) is

$$\begin{aligned} D^{q}V_{i} \leq& -\sum _{k=1}^{i}c_{k}z_{k}^{2}+b_{i}z_{i}z_{i+1}+ \tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{i} \bigr). \end{aligned}$$
(30)

Substituting (29) into (26) yields

$$\begin{aligned} D^{q}z_{i} = & -b_{i-1}z_{i-1}-c_{i}z_{i}+b_{i}z_{i+1}+( \theta-\hat{\theta})^{T}\varphi_{i}+\frac{1}{b_{i-1}}D^{q}( \hat{\theta}\varphi_{i-1}). \end{aligned}$$
(31)

Step n: With \(z_{n} =x_{n}- \alpha_{n-1}\), we rewrite \(D^{q}x_{n} =\varphi _{0}(x)+\theta^{T}\varphi_{n}(x)+b_{n}\beta_{0}(x)u\) as

$$\begin{aligned} D^{q}z_{n} = \varphi_{0}+ \theta^{T}\varphi_{n}+b_{n}\beta_{0}(x)u+ \frac{1}{b_{n-1}} \bigl(b_{n-2}D^{q}z_{n-2}+c_{n-1}D^{q}z_{n-1}+D^{q} \bigl(\hat{\theta}^{T}\varphi_{n-1} \bigr) \bigr), \end{aligned}$$
(32)

and we now design the Lyapunov function as \(V_{n}= V_{n-1} + \frac {1}{2}z_{n}^{2}\); we have

$$\begin{aligned} D^{q}V_{n} \leq& -\sum _{k=1}^{n-1}c_{k}z_{k}^{2}+z_{n} \bigl[b_{n-1}z_{n-1}+\varphi_{0}+ \theta^{T}\varphi_{n}+b_{n}\beta_{0}(x)u \bigr] \\ &{}+\frac{z_{n}}{b_{n-1}} \bigl(b_{n-2}D^{q}z_{n-2}+c_{n-1}D^{q}z_{n-1}+D^{q} \bigl(\hat{\theta}^{T}\varphi_{n-1} \bigr) \bigr) \\ &{} +\tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{n-1} \bigr). \end{aligned}$$
(33)

To eliminate \(\hat{\theta} - \theta\) from \(D^{q}V_{n}\) we choose the update law

$$\begin{aligned} D^{q}\hat{\theta} =\tau_{n}= \tau_{n-1}+\Gamma z_{n} \biggl(\varphi_{n}- \frac{1}{\tilde{\theta}b_{n-1}}D^{q}(\hat{\theta}\varphi_{n-1}) \biggr), \end{aligned}$$
(34)

we rewrite \(D^{q}V_{n}\) as

$$\begin{aligned} D^{q}V_{n} \leq& -\sum _{k=1}^{n-1}c_{k}z_{k}^{2} +\tilde{\theta}^{T}\Gamma^{-1} \bigl(D^{q}\hat{ \theta}-\tau_{n} \bigr). \end{aligned}$$
(35)

Finally, we choose

$$\begin{aligned} u = -\frac{1}{b_{n}\beta_{0}} \biggl(b_{n-1}z_{n-1}+c_{n}z_{n}+ \varphi_{0}+\hat{\theta}^{T}\varphi_{n}+ \frac{b_{n-2}}{b_{n-1}}D^{q}z_{n-2}+\frac{c_{n-1}}{b_{n-1}}D^{q}z_{n-1} \biggr). \end{aligned}$$
(36)

We have

$$ D^{q}V_{n}\leq-\sum _{k=1}^{n}c_{k}z_{k}^{2}. $$
(37)

Substituting (36) into (32) yields

$$\begin{aligned} D^{q}z_{n} = -b_{n-1}z_{n-1}-c_{n}z_{n}+( \theta-\hat{\theta})^{T}\varphi_{n}+\frac{1}{b_{n-1}}D^{q} \bigl(\hat{\theta}^{T}\varphi_{n-1} \bigr). \end{aligned}$$
(38)

According to Lemma 1, for the Lyapunov function \(V_{n}\), there exist class-K functions \(\gamma_{1}\) and \(\gamma_{2}\) such that \(\gamma _{1}( \Vert \eta \Vert )\leq V_{n}(\eta)\leq\gamma_{2}( \Vert \eta \Vert )\) where \(\eta=[z_{1},\ldots,z_{n},\tilde{\theta}]\).

Unless \(z_{i}=0\), we have \(D^{q}V_{n}\leq0\), thus there exists a class-K function \(\gamma_{3}\) such that \(D^{q}V_{n}\leq-\gamma_{3}( \Vert \eta \Vert )\).

According to Lemma 2, the z-system is asymptotically Mittag-Leffler stable. □

Remark 5

In this paper, we constructed the virtual controllers and tuning functions to deal with the fractional stabilization problem, the backstepping technique has been extended to fractional-order systems. It should be noted that the Mittag-Leffler stability implies asymptotic stability [11]. Therefore, the Lyapunov direct method can be applied to obtain the asymptotical stability of the closed-loop system.

4 Simulation results

In this section, two examples are given to verify the effectiveness of the proposed scheme.

Example 1

We consider the following fractional-order nonlinear system:

$$\begin{aligned} \begin{aligned} &D^{q}x _{1} = 3x_{2}+2x_{1}^{2}, \\ &D^{q}x _{2} = u-2x_{1}^{2}- 2x_{2}\sin(x_{1}), \end{aligned} \end{aligned}$$
(39)

where \(b_{1}=3\), \(\theta=2\), \(\varphi_{1}=2x_{1}^{2}\), \(\varphi _{3}=-x_{1}^{2}-x_{2}\sin(x_{1})\), \(\Gamma=1\) and we choose \(q=0.96\).

Step 1: Let \(z_{1} =x_{1}\) and \(z_{2}=x_{2}-\alpha_{1}\), we rewrite \(D^{q} x_{1}=3x_{2}+2x_{1}^{2} \) as

$$ D^{q} z_{1}=3z_{2} +3 \alpha_{1}+2x_{1}^{2}, $$
(40)

choose the Lyapunov function \(V_{1}=\frac{1}{2}z_{1}^{2}+\frac{1}{2}(\hat {\theta}-2)^{T}\Gamma^{-1}(\hat{\theta}-2)\). Then

$$ D^{q} V_{1}\leq z_{1} \bigl(3z_{2}+3\alpha_{1}+2x_{1}^{2} \bigr)+(\hat{\theta}-2)^{T} \bigl(D^{q} \hat{\theta}- \tau_{1} \bigr), $$
(41)

where \(\tau_{1}=x_{1}^{3}\). Meanwhile, we choose

$$ \alpha_{1}=-\frac{k_{1}}{3}z_{1}- \frac{\hat{\theta}}{3}x_{1}^{2}. $$
(42)

Then

$$ D^{q}V_{1}\leq-k_{1}z_{1}^{2}+3z_{1}z_{2}+( \hat{\theta}-2)^{T}D^{q}(\hat{\theta}-\tau_{1}). $$
(43)

The second term \(3z_{1}z_{2}\) in \(D^{q}V_{1}\) will be canceled at the next step.

Substituting (42) into (40) yields

$$ D^{q}z_{1}=-k_{1}z_{1}+3z_{2}+(2- \hat{\theta})x_{1}^{2}. $$
(44)

Step 2: Since \(z_{2} =x_{2} -\alpha_{1}\), we have

$$ D^{q}z_{2}=u-2x_{1}^{2}-2x_{2}\sin(x_{1})+ \frac{k_{1}}{3} \bigl(3x_{2}+2x_{1}^{2} \bigr)+ \frac{2\hat{\theta}}{3}x_{1} \bigl(3x_{2}+2x_{1}^{2} \bigr). $$
(45)

Choose the Lyapunov function \(V_{2} = V_{1} + \frac{1}{2}z_{2}^{2}\). Then

$$\begin{aligned} D^{q} V_{2} \leq& -k_{1}z_{1}^{2}+z_{2} \biggl[3z_{1}+u-2x_{1}^{2}-2x_{2}\sin(x_{1})+ \frac{k_{1}}{3} \bigl(3x_{2}+2x_{1}^{2} \bigr)+ \frac{2\hat{\theta}}{3}x_{1} \bigl(3x_{2}+2x_{1}^{2} \bigr) \biggr] \\ &{}+(\hat{\theta}-2)^{T} \bigl(D^{q}\hat{\theta}- \tau_{2} \bigr). \end{aligned}$$
(46)

Then, to make \(D^{q}V_{3} \leq-k_{1}z_{1}^{2}- k_{2}z_{2}^{2}\), we would choose

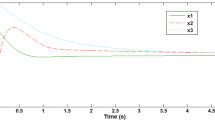
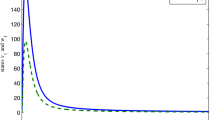
$$\begin{aligned} u = -k_{2}z_{2}-3z_{1}+2x_{1}^{2}+2x_{2}\sin(x_{1})- \frac{k_{1}}{3} \bigl(3x_{2}+2x_{1}^{2} \bigr)- \frac{2\hat{\theta}}{3}x_{1} \bigl(3x_{2}+2x_{1}^{2} \bigr). \end{aligned}$$
(47)

In this simulation, \(k_{1}=3\), \(k_{2}=2\). The results for the initial state condition \(x_{1}(0)=1, x_{2}(0)=-1\) are given in Figures 1-3.

Figure 1
figure 1

The state trajectories \(\pmb{x_{1}, x_{2}}\) .

Full size image
Figure 2
figure 2

Control input u .

Full size image
Figure 3
figure 3

Parameter estimate θ .

Full size image

Example 2

We consider the following fractional-order nonlinear system:

$$\begin{aligned} \begin{aligned} &D^{q}x _{1} = b_{1}x_{2}+ \theta x_{1}^{2}, \\ &D^{q} x_{2} = b_{2}x_{3}+\theta x_{1}x_{2}, \\ &D^{q}x _{3} = u, \end{aligned} \end{aligned}$$
(48)

where \(b_{1}=b_{2}=1\), \(\theta=2\), \(\varphi_{1}(x_{1})=x_{1}^{2}\), \(\varphi _{2}(x_{1},x_{2})=x_{1}x_{2}\) and \(\Gamma=1\), we choose \(q=0.96\).

Step 1: Let \(z_{1} =x_{1}\) and \(z_{2}=x_{2}-\alpha_{1}\), we rewrite \(D^{q} x_{1}=x_{2} + 2x_{1}^{2}\) as

$$ D^{q} z_{1}=z_{2} + \alpha_{1} +2x_{1}^{2}. $$
(49)

Choose the Lyapunov function \(V_{1}=\frac{1}{2}z_{1}^{2}+\frac{1}{2}(\hat {\theta}-2)^{T}(\hat{\theta}-2)\). Then

$$ D^{q} V_{1}\leq z_{1} \bigl(z_{2}+\alpha_{1}+\hat{\theta}^{T}x_{1}^{2} \bigr)+(\hat{\theta}-2)^{T} \bigl(D^{q} \hat{\theta}- x_{1}^{3} \bigr), $$
(50)

we choose

$$\begin{aligned} &\tau_{1}(x_{1})= x_{1}^{3}, \end{aligned}$$
(51)
$$\begin{aligned} &\alpha_{1}(x_{1},\hat{\theta})=-k_{1}x_{1}- \hat{\theta}^{T}x_{1}^{2}, \end{aligned}$$
(52)

we arrive at

$$ D^{q}V_{1}\leq-k_{1}z_{1}^{2}+z_{1}z_{2}+( \hat{\theta}-2)^{T} \bigl(D^{q}\hat{\theta}- \tau_{1} \bigr). $$
(53)

The second term \(z_{1}z_{2}\) in \(D^{q}V_{1}\) will be canceled at the next step. Notice that \(D^{q}z_{2} =D^{q}x_{2} - D^{q} \alpha_{1}\), that is,

$$ D^{q}z_{2}=x_{3}+2x_{1}x_{2}+k_{1} \bigl(x_{2}+2x_{1}^{2} \bigr)+D^{q} \bigl( \hat{\theta}^{T}x_{1}^{2} \bigr). $$
(54)

Let \(z_{3}=x_{3}-\alpha_{2}\), choose a Lyapunov function as \(V_{2} = V_{1} + \frac {1}{2}z_{2}^{2}\). Then

$$\begin{aligned} D^{q} V_{2} \leq-k_{1}z_{1}^{2}+z_{2} \bigl[z_{1}+z_{3}+2x_{1}x_{2}+ \alpha_{2}+k_{1} \bigl(x_{2}+2x_{1}^{2} \bigr) \bigr]+ (\hat{\theta}-2)^{T} \bigl(D^{q}\hat{\theta}- \tau_{2} \bigr), \end{aligned}$$
(55)

where \(D^{q}\hat{\theta}=\tau_{2}=\tau_{1}-\frac{z_{2}}{\hat{\theta}-2}D^{q}(\hat {\theta}^{T}x_{1}^{2})\). Then, to make \(D^{q}V_{2} \leq-k_{1} z_{1}^{2} -k_{2} z_{2}^{2}+z_{2}z_{3}+(\hat{\theta}-2)^{T}(D^{q}\hat{\theta}-\tau_{2})\), we would choose

$$ \alpha_{2}(x_{1},x_{2},\hat{ \theta})=-x_{1}-k_{2} \bigl(x_{2}+k_{1}x_{1}+ \hat{\theta}x_{1}^{2} \bigr)-2x_{1}x_{2}-k_{1} \bigl(x_{2}+2x_{1}^{2} \bigr). $$
(56)

Choose the Lyapunov candidate function \(V_{3}=V_{2}+\frac{1}{2}z_{3}^{2}\). Then

$$\begin{aligned} D^{q} V_{3} \leq& -k_{1}z_{1}^{2}-k_{2}z_{2}^{2}+z_{3} \bigl[z_{2}+u+x_{2}+2x_{1}^{2}+k_{2} \bigl(x_{3}+2x_{1}x_{2}+k_{1} \bigl(x_{2}+2x_{1}^{2} \bigr) \bigr) \\ &{}+4\hat{\theta}x_{1} \bigl(x_{2}+2x_{1}^{2} \bigr)+k_{1} \bigl(x_{3}+2x_{1}x_{2}+4x_{1} \bigl(x_{2}+2x_{1}^{2} \bigr) \bigr) \bigr] \\ &{}+ ( \hat{ \theta}-2)^{T} \bigl(D^{q}\hat{\theta}- \tau_{3} \bigr), \end{aligned}$$
(57)

where \(D^{q}\hat{\theta}=\tau_{3}=\tau_{2}-\frac{z_{3}}{\hat{\theta}-2}D^{q}(\hat {\theta}^{T}x_{1}x_{2})\), we choose

$$\begin{aligned} u =&-z_{2}-k_{3}z_{3}-x_{2}-2x_{1}^{2}-k_{2} \bigl(x_{3}+2x_{1}x_{2}+k_{1} \bigl(x_{2}+2x_{1}^{2} \bigr) \bigr) \\ &{}-4\hat{\theta}x_{1} \bigl(x_{2}+2x_{1}^{2} \bigr)-k_{1}k_{2} \bigl(x_{3}+2x_{1}x_{2}+4x_{1} \bigl(x_{2}+2x_{1}^{2} \bigr) \bigr), \end{aligned}$$
(58)

we obtain

$$ D^{q}V_{3}\leq-\sum_{i=1}^{3}k_{i}z_{i}^{2}. $$
(59)

In this simulation, \(k_{1}=k_{2}=k_{3}=1\). The results for the initial state condition \(x_{1}(0)=1\), \(x_{2}(0)=-2\), \(x_{3}(0)=-1\) are given in Figures 4-6.

Figure 4
figure 4

The state trajectories \(\pmb{x_{1}}\) , \(\pmb{x_{2}}\) , \(\pmb{x_{3}}\) .

Full size image
Figure 5
figure 5

Control input u .

Full size image
Figure 6
figure 6

Parameter estimate θ .

Full size image

5 Conclusions

The problem of Mittage-Leffler stabilization has been investigated for a class of fractional-order nonlinear systems with the unknown control coefficients. The backstepping design scheme is extended to fractional-order systems, and an adaptive control law is proposed with fractional-order update laws to achieve an asymptotical Mittag-Leffler stabilization for the close-loop system, and the tuning function is constructed to avoid overparameterization. Finally, the effectiveness of the proposed method has been verified by some simulation examples.