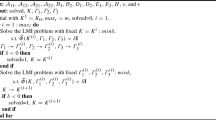Asymptotical stabilization of the nonlinear upper triangular fractional-order systems

Abstract

This paper introduces a simple method of the design of the output feedback stabilizing controller (OFSC) for the nonlinear upper triangular fractional-order systems (NUTFOS). The OFSC which makes the closed-loop system asymptotically stable is given based on the fractional indirect Lyapunov method and the static gain control method. Furthermore, an algorithm is established to design OFSC for the NUTFOS. Finally, an example is presented to verify the validity of the proposed method.

1 Introduction

Fractional-order systems (FOS) have received a great deal of attention from mathematicians, physicists, chemists, biologists, and so on [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. It has been the huge development of the theory and the applications in many fields, especially in control. The feedback control design problem is a hot topic for nonlinear fractional-order systems, such as linear matrix inequality (LMI) methods [15,16,17,18,19,20,21], adaptive backstepping control scheme [22,23,24], the static gain control method [25,26,27], etc.

Linear matrix inequality (LMI) methods have been used to discuss the feedback control design problem of fractional-order systems; see [17,18,19,20,21]. The existence conditions and design methods of the state feedback controller, static output feedback controller, and observer-based controller for asymptotically stabilizing such uncertain linear FOS were derived in [17]. The fuzzy output feedback stabilization for uncertain FOS was considered in [18]. The output feedback normalization and stabilization for singular FOS were investigated in [19]. Based on a fractional-order indirect Lyapunov method, a new singular system approach, and linear matrix equality (LMI) methods, the problem of output feedback sliding mode control for nonlinear FOS was studied in [20]. A robust fixed-order dynamic output feedback controller for uncertain linear time-invariant FOS was designed in [21].

Adaptive backstepping control scheme has been also used to considered the feedback control design problem of FOS; see [22,23,24]. Mittag–Leffler stability of nonlinear FOS was solved via fractional-order backstepping in [22]. A novel fractional order adaptive backstepping output feedback control scheme for nonlinear FOS was presented via a state estimation filter and the indirect Lyapunov method in [23]. A fractional order adaptive backstepping control scheme was presented for an incommensurate FOS in the presence of input saturation in [24].

FOS in the triangular form plays an important role in describing many complicated physical phenomena, especially in modeling the circuitry system [28,29,30]. Recently, the static gain control method has been introduced to study the feedback control design problem of FOS especially fractional-order triangular systems; see [25,26,27]. Both the state feedback stabilizing controller (SFSC) and the OFSC were designed for both lower triangular and upper triangular linear FOS in [25]. Using the static gain control method and the fractional indirect Lyapunov method, design problems of both the SFSC and the OFSC for the nonlinear lower triangular FOS were investigated in [26]. The SFSC for the NUTFOS was designed in [27].

Based on the above discussions, fewer works have been done to investigate the OFSC for the NUTFOS. In this paper, we study the design of the OFSC for the NUTFOS. The main contributions are as follows:

• Via the fractional indirect Lyapunov method and the static gain control method, the OFSC which makes the closed-loop system asymptotically stable is designed.

• A novel algorithm of designing OFSC for the NUTFOS is established.

• The OFSC for the NUTFOS is linear. The conditions for the existence of the OFSC are very easy to verify.

• The design scheme in this paper is simple because most of works in the design procedure of this paper can be completed by using MATLAB toolbox.

The rest of this paper is organized as follows. Section 2 presents some necessary preliminaries. Section 3 introduces the NUTFOS, investigates the design of the OFSC for the NUTFOS, and establishes an algorithm to design OFSC for the NUTFOS. Section 4 gives an illustrative example to verify our simple method, which is followed by the conclusion in Sect. 5.

2 Preliminaries

In this section, we first give some basic preliminaries. Throughout this paper, $D^{\alpha }_{t}$ denotes Caputo fractional derivative, which is referred in [2, 26, 31].

Definition 2.1

([2])

Let $h(t)$ be a continuous function. Then $\alpha >0$-order Caputo fractional derivative of $h(t)$ is given by

$$ D^{\alpha }_{t}h(t)=\frac{1}{\varGamma (n-\alpha )} \int _{0}^{t}\frac{h ^{(n)}(s)}{(t-s)^{\alpha -n+1}}\,ds. $$

Remark 2.1

The Leibniz rule of Caputo fractional derivative is given in [2]. However, it implies that the form of the Leibniz rule of classical derivative is not appropriate for Caputo fractional derivative.

Several fundamental conclusions of Caputo fractional derivative are given in the following.

Lemma 2.1

([26])

Let $s_{i} (t)\ (i=1, 2, \ldots, n)$ be continuous and derivable functions and $s(t)= (s_{1} (t), s_{2} (t), \ldots, s_{n} (t) ) ^{T}\in \mathbb{R}^{n}$. Then, for any $t\geq 0$,

$$ \frac{1}{2} {D^{\alpha }_{t}} \bigl(s^{T} (t)Ps(t) \bigr)\leq s^{T} (t)P { D^{\alpha }_{t}}s(t) $$

(1)

holds, where $\alpha \in (0,1]$ and $P\in \mathbb{R}^{n\times n}$ is a positive definite matrix.

Remark 2.2

([26])

Inequality (1) is equivalent to

$$ { D^{\alpha }_{t}} \bigl(s^{T} (t)Ps(t) \bigr)\leq \bigl({ D^{ \alpha }_{t}}s(t) \bigr)^{T} P s(t)+s^{T} (t)P{ D^{\alpha }_{t}}s(t). $$

(2)

Finally, we recall the fractional indirect Lyapunov theorem for FOS [31].

Lemma 2.2

([31])

Let $s=0$ be an equilibrium point of the nonautonomous FOS

$$ D^{\alpha }_{t}s(t)=f(t,s),\quad s_{0}\in \mathbb{R}^{n}, $$

(3)

where $0<\alpha <1$. Assume that there exist a Lyapunov function $V(t,v(t))$ and class-$\mathcal{K}$ functions $\beta _{1}, \beta _{2}$, and $\beta _{3}$ satisfying

$$\begin{aligned} &\beta _{1}\bigl( \Vert s \Vert \bigr)\leq V\bigl(t,s(t)\bigr)\leq \beta _{2}\bigl( \Vert s \Vert \bigr), \\ &D^{\alpha }_{t}V\bigl(t,s(t)\bigr)\leq -\beta _{3} \bigl( \Vert s \Vert \bigr). \end{aligned}$$

Then system (3) is asymptotically stable.

3 Main results

In this section, the OFSC for the NUTFOS is designed. Firstly, we introduce the NUTFOS. Then, we investigate the design of the OFSC for the systems by the fractional indirect Lyapunov method and the static gain control method and establish an algorithm to design the OFSC for the systems.

3.1 Problem description

In this subsection, the NUTFOS are presented.

Consider the following NUTFOS:

$$ \textstyle\begin{cases} D^{\alpha }_{t} v_{1}(t)=v_{2}(t)+g_{1}(t, v(t)), \\ D^{\alpha }_{t} v_{2}(t)=v_{3}(t)+g_{2}(t, v(t)), \\ \vdots \\ D^{\alpha }_{t} v_{n-2}(t)=v_{n-1}(t)+g_{n-2}(t, v(t)), \\ D^{\alpha }_{t} v_{n-1}(t)=v_{n}(t), \\ D^{\alpha }_{t} v_{n}(t)=u(t), \\ y=v_{1}(t), \end{cases} $$

(4)

where $\alpha \in (0,1]$, $v(t)=(v_{1}(t),v_{2}(t),\ldots,v_{n}(t))^{T} \in \mathbb{R}^{n}$ denotes the state, $u\in \mathbb{R}$ denotes the input, and $y\in \mathbb{R}$ denotes the output. In this paper, $v_{i}, w_{i}, \bar{e}_{i}$, and $\bar{w}_{i}$ denote $v_{i}(t), w _{i}(t), \bar{e}_{i}(t)$, and $\bar{w}_{i}(t)$, respectively. The functions $g_{i}: \mathbb{R}\times \mathbb{R}^{n}\to \mathbb{R}\ (i=1,2, \ldots,n-2)$ are continuous and satisfy the following.

Assumption 3.1

$$ \bigl\vert g_{i}(t,v) \bigr\vert \leq c \bigl( \vert v_{i+2} \vert + \vert v_{i+3} \vert +\cdots + \vert v_{n} \vert \bigr),\quad i=1,2, \ldots,n-2, $$

(5)

where $c\geq 0$.

3.2 OFSC design

In this subsection, the design of the OFSC for system (4) is given in terms of the fractional indirect Lyapunov method and the static gain control method, and an algorithm to the proposed method is examined.

Firstly, we present the design of the OFSC for system (4).

Theorem 3.1

Under Assumption 3.1, system (4) is asymptotically stabilized by a linear OFSC.

Proof

Examine the following linear observer:

$$ \textstyle\begin{cases} D^{\alpha }_{t} w_{1}=w_{2}+\frac{a_{1}l}{R}(v_{1}-w_{1}), \\ D^{\alpha }_{t} w_{2}=w_{3}+\frac{a_{2} l^{2}}{R^{2}}(v_{1}-w_{1}), \\ \vdots \\ D^{\alpha }_{t} w_{n-1}=w_{n}+\frac{a_{n-1}l^{n-1}}{R^{n-1}}(v_{1}-w _{1}), \\ D^{\alpha }_{t} w_{n}=u+\frac{a_{n}l^{n}}{R^{n}}(v_{1}-w_{1}), \end{cases} $$

(6)

where $R>1, l>0$, and $a_{j} > 0\ (j=1,2,\ldots,n)$ are coefficients of the Hurwitz polynomial

$$ \bar{p}(k)=k^{n}+a_{1} k^{n-1}+\cdots +a_{n-1}k+a_{n}. $$

Set

$$ h_{i}=\frac{v_{i}-w_{i}}{R^{n+1-i}}, \qquad\bar{w}_{i}=\frac{w_{i}}{R ^{n+1-i}},\quad i=1,2,\ldots,n. $$

By (4) and (6), we obtain

$$\begin{aligned} & D^{\alpha }_{t} h=\frac{1}{R}\bar{A}(l)h+G, \end{aligned}$$

(7)

$$\begin{aligned} & D^{\alpha }_{t} \bar{w}=\frac{1}{R}\bar{ \varOmega } \bar{w}+\frac{1}{R}Fu+ \frac{1}{R}\bar{C}(l)h, \end{aligned}$$

(8)

where

$$\begin{array}{rl}& h=\left(\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_n\end{array}\right),\overline{A}(l)=\left(\begin{array}{ccccc}-a_{1}l& 1& 0& \cdots & 0\\ -a_2{l}^2& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -a_{n-1}{l}^{n-1}& 0& 0& \cdots & 1\\ -a_n{l}^n& 0& 0& \cdots & 0\end{array}\right),\\ & G=\left(\begin{array}{c}\frac{g_1}{R^n}\\ \frac{g_2}{R^{n-1}}\\ ⋮\\ \frac{g_{n-2}}{R^3}\\ 0\\ 0\end{array}\right),\overline{w}=\left(\begin{array}{c}{\overline{w}}_1\\ {\overline{w}}_2\\ ⋮\\ {\overline{w}}_n\end{array}\right),\\ & \overline{\Omega }=\left(\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\\ 0& 0& 0& \cdots & 0\end{array}\right),F=\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right),\\ & \overline{C}(l)=\left(\begin{array}{ccccc}{a}_{1}l& 0& 0& \cdots & 0\\ a_2{l}^2& 0& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{n-1}{l}^{n-1}& 0& 0& \cdots & 0\\ a_n{l}^n& 0& 0& \cdots & 0\end{array}\right).\end{array}$$

We set $R>1$ such that the system consisting of (7), (8) and

$$ u=-(b_{1} \bar{w}_{1}+b_{2} \bar{w}_{2}+b_{3} \bar{w}_{3}+\cdots +b _{n} \bar{w}_{n}) $$

(9)

is asymptotically stable at $h=0$ and $\bar{w}=0$, where $b_{j}>0\ (j=1,2, \ldots,n)$ are the coefficients of the Hurwitz polynomial

$$ \bar{q}(k)=k^{n}+b_{n} k^{n-1}+\cdots +b_{2} k+b_{1}. $$

In forms of $\bar{w}_{i}$ and (9), we obtain

$$ u=-\frac{1}{R^{n}}\bigl(b_{1} w_{1}+b_{2} R w_{2}+b_{3} R^{2} w_{3}+\cdots +b_{n} R^{n-1} w_{n}\bigr). $$

(10)

By (8) and (9), we have

$$ D^{\alpha }_{t} \bar{w}=\frac{1}{R}\bar{B} \bar{w}+\frac{1}{R}\bar{C}(l)h, $$

(11)

where

$$\overline{B}=\left(\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\\ -b_1& -b_2& -b_3& \cdots & -b_n\end{array}\right).$$

Let Lyapunov function $\bar{V}_{1}=h^{T} \bar{P}(l)h$, where $\bar{P}(l)>0$ is a positive definite matrix and satisfies $\bar{P}(l) \bar{A}(l)+\bar{A}^{T} (l) \bar{P}(l)=-I$. Then we have

$$\begin{aligned} { D^{\alpha }_{t}}\bar{V}_{1}|_{(7)} &\leq \bigl({ D ^{\alpha }_{t}}h \bigr)^{T} \bar{P}(l) h+h^{T} \bar{P}(l) { D^{ \alpha }_{t}}h \\ &=\biggl(\frac{1}{R}\bar{A}(l)h+G\biggr)^{T} \bar{P}(l) h+h^{T} \bar{P}(l) \biggl( \frac{1}{R}\bar{A}(l)h+G\biggr) \\ &\leq -\frac{1}{R} \Vert h \Vert ^{2} +2 \bigl\Vert \bar{P}(l) \bigr\Vert \cdot \Vert h \Vert \cdot \Vert G \Vert . \end{aligned}$$

From (5) and the expressions of $h_{i}$ and $\bar{w}_{i}$, for any $i\ (i=1,2,\ldots,n)$, we have

$$\begin{aligned} \biggl\vert \frac{g_{i}}{R^{n-i+1}} \biggr\vert &\leq \frac{c}{R^{n-i+1}}\bigl( \vert v _{i+2} \vert + \vert v_{i+3} \vert +\cdots + \vert v_{n} \vert \bigr) \\ &\leq \frac{c}{R^{2}}\sum_{j=1}^{n} \frac{ \vert v_{j} \vert }{R^{n-j+1}} \\ &=\frac{c}{R^{2}}\sum_{j=1}^{n}\bigl( \vert h_{j} \vert + \vert \bar{w}_{j} \vert \bigr) \\ &\leq \frac{c\sqrt{n}}{R^{2}} \Vert h \Vert +\frac{c\sqrt{n}}{R^{2}} \Vert \bar{w} \Vert , \end{aligned}$$

where $R>1$ and $\sum_{j=1}^{n}|h_{j}|\leq \sqrt{n}\|h\|$.

Hence, we get

$$\begin{array}{rl}{D}_t^{\alpha }{\overline{V}}_1{|}_{(\text{7})}& \le -\frac{1}{R}{\parallel h\parallel }^2+2\parallel \overline{P}(l)\parallel \cdot \parallel h\parallel (\frac{c\sqrt{n}}{R^2}\parallel h\parallel +\frac{c\sqrt{n}}{R^2}\parallel \overline{w}\parallel )\parallel \left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\\ 0\\ 0\end{array}\right)\parallel \\ & \le -\frac{1}{R}{\parallel h\parallel }^2+\frac{2nc}{R^2}\parallel \overline{P}(l)\parallel \cdot {\parallel h\parallel }^2+\frac{nc}{R^2}\parallel \overline{P}(l)\parallel ({\parallel h\parallel }^2+{\parallel \overline{w}\parallel }^2)\\ & \le -\frac{1}{R}{\parallel h\parallel }^2+\frac{3nc}{R^2}\parallel \overline{P}(l)\parallel \cdot {\parallel h\parallel }^2+\frac{nc}{R^2}\parallel \overline{P}(l)\parallel \cdot {\parallel \overline{w}\parallel }^2.\end{array}$$

(12)

Set Lyapunov function $\bar{V}_{2}=\bar{w}^{T} \bar{Q}\bar{w}$, where $\bar{Q}>0$ is a positive definite matrix $\bar{Q}>0$ and satisfies $\bar{Q}\bar{B}+\bar{B}^{T} \bar{Q}=-I$. Then we have

$$\begin{aligned} { D^{\alpha }_{t}}\bar{V}_{2}|_{(11)} &\leq \bigl({ D ^{\alpha }_{t}}\bar{w} \bigr)^{T} \bar{Q} \bar{w}+\bar{w}^{T} \bar{Q} { D^{\alpha }_{t}}\bar{w} \\ &=\biggl(\frac{1}{R}\bar{B}\bar{w}+\frac{1}{R}\bar{C}(l)h \biggr)^{T} \bar{Q} \bar{w}+\bar{w}^{T} \bar{Q} \biggl( \frac{1}{R}\bar{B}\bar{w}+\frac{1}{R} \bar{C}(l)h\biggr) \\ &\leq -\frac{1}{R} \Vert \bar{w} \Vert ^{2} + \frac{2}{R} \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \cdot \Vert h \Vert \cdot \Vert \bar{w} \Vert \\ &\leq -\frac{1}{R} \Vert \bar{w} \Vert ^{2} + \frac{1}{R} \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \bigl( \Vert h \Vert ^{2}+ \Vert \bar{w} \Vert ^{2}\bigr). \end{aligned}$$

(13)

Choose Lyapunov function $\bar{V}=\bar{V}_{1}+\bar{V}_{2}$. By (12) and (13), we obtain

$$\begin{aligned} { D^{\alpha }_{t}}\bar{V}|_{(7)(11)} \leq{} &{-} \frac{1}{R}\bigl(1- \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \bigr) \Vert h \Vert ^{2} +\frac{3nc}{R^{2}} \bigl\Vert \bar{P}(l) \bigr\Vert \cdot \Vert h \Vert ^{2} \\ & {}-\frac{1}{R}\bigl(1- \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \bigr) \Vert \bar{w} \Vert ^{2}+\frac{nc}{R ^{2}} \bigl\Vert \bar{P}(l) \bigr\Vert \cdot \Vert \bar{w} \Vert ^{2} \\ ={}&{-}\frac{1}{R^{2}}\bigl[\bigl(1- \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \bigr)R-3nc \bigl\Vert \bar{P}(l) \bigr\Vert \bigr] \Vert h \Vert ^{2} \\ & {}-\frac{1}{R^{2}}\bigl[\bigl(1- \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \bigr)R-nc \bigl\Vert \bar{P}(l) \bigr\Vert \bigr] \Vert \bar{w} \Vert ^{2}. \end{aligned}$$

Set $l>0$ and $R>1$ satisfying

$$ \bigl\Vert \bar{Q}\bar{C}(l) \bigr\Vert \leq \delta,\qquad R>\frac{3n}{1-\delta } \bigl(c \bigl\Vert \bar{P}(l) \bigr\Vert +\eta \bigr), $$

where δ satisfies $0<\delta <1$ and $\eta >0$.

Thus, from Lemma 2.2, we get ${ D^{\alpha }_{t}}\bar{V} |_{\text{( 7)(11)}}<-\frac{\eta }{R^{2}}(\|h\|^{2}+\|\bar{w}\| ^{2})$, which implies that system (7) and (11) is asymptotically stable at $h=0$ and $\bar{w}=0$. Therefore, closed-loop system (4), (8), and (9) is asymptotically stable at $v=0$ and $\bar{w}=0$. Closed-loop system (4), (6), and (10) is also asymptotically stable at $v=0$ and $w=0$. Thus, it can be concluded that system (6) and (10) is the linear output dynamic compensator of system (4). This completes the proof. □

Based on the above analysis, we establish an algorithm to construct an OFSC for system (4).

Algorithm 3.1

The algorithm is divided into the following five steps:

• (1) Let $a_{j}>0, b_{j}>0\ (j=1,2,\ldots,n)$ be the coefficients of the Hurwitz polynomials

  $$\begin{aligned} &\bar{p}(k)=k^{n}+a_{1} k^{n-1}+\cdots +a_{n-1} k+a_{n},\\ & \bar{q}(k)=k ^{n}+b_{n} k^{n-1}+\cdots +b_{2} k+b_{1}. \end{aligned}$$

  Then we get $\bar{A}(l), \bar{C}(l)$, and B̄.

• (2) Solving the equation

  $$ \bar{B}^{T} \bar{Q}+\bar{Q} \bar{B}=-I $$

  leads to $\bar{Q}>0$.

• (3) Choose an appropriate constant l such that $\delta =\|\bar{Q}\bar{C}(l)\|<1$.

• (4) Solve the equation

  $$ \bar{P}(l)\bar{A}(l)+\bar{A}^{T} (l) \bar{P}(l)=-I. $$

  Then we obtain $\bar{P}(l)>0$.

• (5) Let

  $$ R>\frac{3n}{1-\delta }c \bigl\Vert \bar{P}(l) \bigr\Vert . $$

  Then a linear OFSC for system (4) is u, where u is defined as in (10), and $w_{1}, w_{2},\ldots, w_{n}$ are the states of system (6).

Remark 3.1

The different research problems of this paper and [27] are on the design problem of the OFSC output and the SFSC for the same system (4). The OFSC for the NUTFOS is studied in this paper, and the SFSC for the NUTFOS is considered in [27]. In fact, the design process of the OFSC is more complicated than that of the SFSC.

4 An example

In this section, we give an example to verify our simple method.

Example 4.1

Consider the following nonlinear FOS:

$$ \textstyle\begin{cases} D^{\alpha }_{t} v_{1}=v_{2}-\frac{\sin {v_{1}}}{c+ce^{-t}}v_{3}, \\ D^{\alpha }_{t} v_{2}=v_{3}, \\ D^{\alpha }_{t} v_{3}=u, \\ y=v_{1}, \end{cases} $$

(14)

where $\alpha \in (0,1]$.

By Algorithm 3.1, choose $a_{1}=99/100$, $a_{2}=261/1000$, $a_{3}=81/5000$, $b_{1}=100$, $b_{2}=120$, $b_{3}=21$. Then

$$\begin{array}{rl}& \overline{A}(l)=\left(\begin{array}{ccc}-99l/100& 1& 0\\ -261l^2/1000& 0& 1\\ -81l^3/5000& 0& 0\end{array}\right),\overline{C}(l)=\left(\begin{array}{ccc}99l/100& 0& 0\\ 261l^2/1000& 0& 0\\ 81l^3/5000& 0& 0\end{array}\right),\\ & \overline{B}=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -100& -120& -21\end{array}\right),\overline{Q}=\left(\begin{array}{ccc}4& -1/2& -1\\ -1/2& 1& -1/2\\ -1& -1/2& 1\end{array}\right).\end{array}$$

Set $l=0.9$ and $c=3000$. Then, we get $R=6.5$. Therefore, the linear output feedback stabilizer for system (14) is

$$ u=-\frac{100}{R^{3}}w_{1}-\frac{120}{R^{2}}w_{2}- \frac{21}{R}w_{3}, $$

(15)

where $w_{1}$, $w_{2}$, and $w_{3}$ are the states of the following system:

$$ \textstyle\begin{cases} D^{\alpha }_{t} w_{1}=w_{2}+\frac{99l}{100R}(v_{1}-w_{1}), \\ D^{\alpha }_{t} w_{2}=w_{3}+\frac{261l^{2}}{1000R^{2}} (v_{1}-w_{1}), \\ D^{\alpha }_{t} w_{3}=-\frac{100}{R^{3}}w_{1}-\frac{120}{R^{2}}w _{2}-\frac{21}{R}w_{3} +\frac{81l^{3}}{5000R^{3}}(v_{1}-w_{1}). \end{cases} $$

(16)

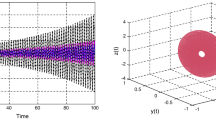
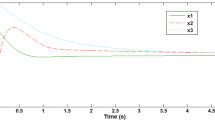
Figures 1, 2, and 3 show the state trajectories of the system consisting of (14), (15), and (16) with the order $\alpha =0.9$ for the initial condition $(v_{1}(0), v_{2}(0), v _{3}(0), w_{1}(0), w_{2}(0), w_{3}(0))=(-0.03, 0.2, 0.6, 0.1, 0.5, 0.04)$, which shows the asymptotic stability of the system.

Figure 1

Trajectories of $v_{1}$ and $w_{1}$

Figure 2

Trajectories of $v_{2}$ and $w_{2}$

Figure 3

Trajectories of $v_{3}$ and $w_{3}$

5 Conclusion

By using the fractional indirect Lyapunov method and the static gain control method, a simple method of design problem of the OFSC for the NUTFOS has been investigated in this paper. We have obtained the OFSC making the closed-loop system asymptotically stable and established an algorithm to design output stabilizing controller for the NUTFOS. Finally, an example has been given to verify the validity of the simple method.

In future works, one can study the controllability of the nonlinear upper triangular fractional-order systems.