1 Introduction

Recently, dynamical neural networks (DNNs) have been widely applied in all kinds of science and engineering fields, such as image and signal processing, pattern recognition, associative memory and combinational optimization, see [1–5]. In practical applications, DNNs are always designed to be globally asymptotically or exponentially stable. There have been many excellent results with respect to the stability of DNNs in the existing works, see [6–16].

During the implementation of DNNs, the effects of measurement errors, parameter fluctuations and external disturbances are inevitable. Hence, it is significant that the designed neural networks are globally robustly stable. In Refs. [17–34], the global robust stability conditions were presented for integer-order neural networks (INNs).

Recently, in Refs. [6–8], the stability of a class of FNNs with delays was discussed, and some sufficient conditions were presented by applying Lyapunov functional approach. In Ref. [9], Wang et al. investigated the global asymptotic stability of FNNs with impulse effects. In Ref. [11], Yang et al. discussed the finite-time stability for FNNs with delay. By employing the Mittag-Leffler stability theorem, Ref. [35] considered the global projective synchronization for FNNs and presented the Mittag-Leffler synchronization condition in terms of LMIs. In Ref. [12], Wu et al. discussed the global Mittag-Leffler stabilization for FNNs with bidirectional associative memory based on Lyapunov functional approach. Ref. [13] considered the boundedness, Mittag-Leffler stability and asymptotical ω-periodicity of fractional-order fuzzy neural networks, some Mittag-Leffler stability conditions were developed. In addition, Ref. [32] investigated the robust stability of fractional-order Hopfield DNNs with the norm-bounded uncertainties, and some conditions were presented. It should be noted that, in the above papers with respect to FNNs, the Lyapunov function for solving the stability of FNNs is the absolute value function \(V(t)=\sum^{n}_{i=1}\delta_{i}|x_{i}|\), see [8–13, 32], or the quadratic function \(V(t)=x^{T}Px\), see [14] and [35]. Obviously, the activation function of neural networks is not applied in the Lyapunov function, hence, the obtained stability results in the above papers have a certain degree of conservatism.

Motivated by the discussion above, in this paper, we investigate the global robust Mittag-Leffler stability for FNNs with the interval uncertainties. The innovations of this paper are mainly the following aspects: (1) a new inequality for the Caputo derivative of integer-order integral function with the variable upper limit is developed; (2) the proof of the existence of equilibrium point is presented by means of the properties of Brouwer degree; (3) the integral item \(\int ^{z_{i}(t)}_{0}f_{i}(s)\,ds \) is utilized in the construction of Lyapunov functional; (4) the criteria of the global robust Mittag-Leffler stability are established in terms of LMIs.

The rest of this paper is organized as follows. In Section 2, some definitions, lemmas and a system model are given. In Section 3, the proof of global robust Mittag-Leffler stability of equilibrium point for FNNs with interval uncertainties is presented. In Section 4, two numerical examples are provided to demonstrate the correctness of the proposed results. Some conclusions are drawn in Section 5.

Notation: R denotes the set of real numbers, \(R^{n}\) denotes the n-dimensional Euclidean space, \(R^{n\times m}\) is the set of all \(n\times m\) real matrices, N is the set of integers and C is the set of complex numbers. Given the vectors \(x= (x_{1},\ldots,x_{n} )^{T}, y= (y_{1},\ldots,y_{n} )^{T}\in R^{n}\). The norm of a vector \(x\in R^{n}\) by \(\|x\|=(\sum_{i=1}^{n}x_{i}^{2})^{\frac{1}{2}}\), \(A^{T}\) represents the transpose of matrix A, \(A^{-1}\) represents the inverse of matrix A, \(\|A\|\) represents the induced norm of matrix A. \(A>0\) (\(A<0\)) means that A is positive definite (negative definite). \(\lambda_{\max}(A)\) and \(\lambda_{\min}(A)\) represent the maximum and minimum eigenvalues of matrix A, respectively. E denotes an identity matrix.

2 Preliminaries and model description

2.1 Fractional-order integral and derivative

Definition 2.1

[36]

The Riemann-Liouville fractional integral of order α for a function \(f(t):[0,+\infty)\rightarrow R\) is defined as

$$ ^{R} _{0} I^{\alpha}_{t}f(t)= \frac{1}{\Gamma(\alpha)} \int_{0}^{t}\frac{f(\tau )}{(t-\tau)^{1-\alpha}}\,d\tau, $$

where \(\alpha>0 \), \(\Gamma(\cdot)\) is the gamma function.

Definition 2.2

[36]

Caputo’s fractional derivative of order α for a function \(f\in C^{n}([0,+\infty],R) \) is defined by

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}f(t)= \frac{1}{\Gamma(n-\alpha)} \int_{0}^{t}\frac {f^{n}(\tau)}{(t-\tau)^{\alpha-n+1}}\,d\tau, \end{aligned} $$

where \(t\geqslant0 \) and n is a positive integer such that \(n-1<\alpha<n \). Particularly, when \(0<\alpha<1\),

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}f(t)= \frac{1}{\Gamma(1-\alpha)} \int_{0}^{t}\frac{ f {'}(\tau)}{(t-\tau)^{\alpha}}\,d\tau. \end{aligned} $$

Lemma 2.1

[36]

  1. (i)

    \(\underline{_{0}^{c} D^{\alpha}_{t}( {}_{0}^{R} I^{\beta}_{t}x(t))= {}_{0}^{c}D^{\alpha-\beta}_{t}x(t)}\), where \(\alpha\geq\beta\geq0\). Especially, when \(\alpha=\beta\), \(\underline{_{0}^{c} D^{\alpha}_{t}( {}_{0}^{R} I^{\beta}_{t}x(t))= x(t)}\).

  2. (ii)

    Let \([0,T]\) be an interval on the real axis R, \(n=[\alpha]+1\) for \(\alpha\notin N\) or \(n=\alpha\) for \(\alpha\in N\). If \(x(t)\in C^{n}[0,T]\), then

    $$ \begin{aligned} _{0}^{R} I^{\alpha}_{t} \bigl( {}_{0}^{c} D^{\alpha}_{t}x(t) \bigr) =x(t)-\sum_{k=0}^{n-1}\frac{x^{(k)}(0)}{k!}t^{k}. \end{aligned} $$

    In particular, if \(0< \alpha<1\) and \(x(t)\in C^{1}[0,T]\), then \(_{0}^{R} I^{\alpha}_{t} {}_{0}^{c} D^{\alpha}_{t}x(t)=x(t)-x(0)\).

Definition 2.3

[16]

The Mittag-Leffler function with two parameters has the following form:

$$ \begin{aligned} E_{\alpha,\beta}(z)=\sum ^{\infty}_{k=0} \frac{z^{k}}{\Gamma(k\alpha+\beta)}, \end{aligned} $$

where \(\alpha>0\), \(\beta>0 \), and \(z\in C\). For \(\beta=1\),

$$ \begin{aligned} E_{\alpha,1}(z)=E_{\alpha}(z)=\sum ^{\infty}_{k=0}\frac{z^{k}}{\Gamma (k\alpha+1)}, \end{aligned} $$

especially, \(E_{1,1}(z)=e^{z}\).

Lemma 2.2

[16]

Let \(V(t)\) be a continuous function on \([0,+\infty)\) satisfying

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}V(t) \leq-\theta V(t), \end{aligned} $$

where \(0<\alpha< 1\), and θ is a constant. Then

$$ \begin{aligned} V(t)\leq V(0)E_{\alpha} \bigl(-\theta t^{\alpha} \bigr),\quad t\geq0. \end{aligned} $$

Lemma 2.3

[35]

Suppose that \(x(t)\in R^{n}\) is a continuous and differentiable function, \({P\in R^{n\times n}}\) is a positive definite matrix. Then, for \(\alpha\in(0,1)\), the following inequality holds:

$$ \begin{aligned} \frac{1}{2} {}_{0}^{c}D^{\alpha}_{t} \bigl[ x^{T}(t) P x(t) \bigr]\leq x^{T}(t)P_{0}^{c}D^{\alpha}_{t}x(t). \end{aligned} $$

2.2 A new inequality

In this section, we develop an inequality (see Lemma 2.5) with respect to the Caputo derivative of the integer-order integral function.

Lemma 2.4

Suppose that \(f:R\rightarrow R\) and \(g:R\rightarrow R\) are continuous functions, and \(f(0)=0\), \(tf(t)\geq0\), \(g(t)\geq0\), \(t\in R\). Then, for \(t\in R\),

$$ \operatorname{Sign} \biggl( \int^{t}_{0}f(s)\,ds \biggr)=\operatorname{Sign} \biggl( \int^{t}_{0}g(s)f(s)\,ds \biggr), $$

where \(\operatorname{Sign}(\cdot)\) is the sign function.

Proof

Case 1. Let \(t\geq0\), then \(f(s)\geq0\), \(s\in(0,t)\). Obviously, \(\int^{t}_{0}f(s)\,ds\geq0\). According to \(g(s)\geq0\), it is easy to obtain that \(\int^{t}_{0}g(s)f(s)\,ds\geq 0\). Thus, \(\operatorname{Sign}(\int^{t}_{0}f(s)\,ds)=\operatorname{Sign}(\int^{t}_{0}g(s) f(s)\,ds)\).

Case 2. Let \(t<0\), then \(f(s)<0\), \(s\in(t, 0)\), and \(\int^{t}_{0}f(s)\,ds= -\int^{0}_{t}f(s)\,ds \geq0\). Noting that \(\int^{t}_{0}g(s)f(s)\,ds=- \int^{0}_{t}g(s)f(s)\,ds \geq0\), we have \(\operatorname{Sign}(\int^{t}_{0}f(s)\,ds)=\operatorname{Sign}(\int^{t}_{0}g(s)f(s)\,ds)\).

From Cases 1 and 2, it follows that

$$ \operatorname{Sign} \biggl( \int^{t}_{0}f(s)\,ds \biggr)=\operatorname{Sign} \biggl( \int^{t}_{0}g(s)f(s)\,ds \biggr),\quad t\in R. $$

The proof is completed. □

Lemma 2.5

Suppose that \(z:R\rightarrow R\) is a continuous and differentiable function, and \(g:R\rightarrow R\) is a continuous and monotone nondecreasing function. Then, for \(\alpha\in(0,1)\), the following inequality holds:

$$ \begin{aligned} _{0}^{c} D^{\alpha}_{t} \biggl[ \int_{0}^{z(t)}g(s)\,ds \biggr]\leq g \bigl(z(t) \bigr)_{0}^{c} D^{\alpha}_{t} z(t),\quad t\geq0. \end{aligned} $$
(1)

Proof

Obviously, inequality (1) is equivalent to

$$ \begin{aligned} g \bigl(z(t) \bigr)_{0}^{c} D^{\alpha}_{t}z(t)-{}_{0}^{c} D^{\alpha}_{t} \biggl[ \int^{z(t)}_{0}g(s)\,ds \biggr]\geq0. \end{aligned} $$
(2)

By Definition 2.2, we have

$$ \begin{aligned} _{0}^{c} D^{\alpha}_{t}z(t)= \frac{1}{\Gamma(1-\alpha)} \int^{t}_{0}\frac {z'(s)}{(t-s)^{\alpha}}\,ds, \end{aligned} $$
(3)

and

$$ \begin{aligned}[b] _{0}^{c} D^{\alpha}_{t} \biggl[ \int^{z(t)}_{0}g(s)\,ds \biggr]&=\frac{1}{\Gamma (1-\alpha)} \int^{t}_{0}\frac{(\int^{z(s)}_{0}g(u)\,du)'}{(t-s)^{\alpha }}\,ds \\ &=\frac{1}{\Gamma(1-\alpha)} \int^{t}_{0}\frac {g(z(s))z'(s)}{(t-s)^{\alpha}}\,ds. \end{aligned} $$
(4)

Take (3) and (4) into (2), then it can be rewritten as

$$ \begin{aligned} \frac{g(z(t))}{\Gamma(1-\alpha)} \int^{t}_{0}\frac{z'(s)}{(t-s)^{\alpha }}\,ds- \frac{1}{\Gamma(1-\alpha)} \int^{t}_{0}\frac {g(z(s))z'(s)}{(t-s)^{\alpha}}\,ds\geq0. \end{aligned} $$
(5)

Further, we can get

$$ \begin{aligned} \frac{1}{\Gamma(1-\alpha)} \int^{t}_{0}\frac {g(z(t))-g(z(s))}{(t-s)^{\alpha}}z'(s) \,ds \geq0. \end{aligned} $$
(6)

Equation (6) can be changed as follows:

$$ \begin{aligned} \frac{1}{\Gamma(1-\alpha)} \int^{t}_{0}\frac {g(z(t))-g(z(s))}{(t-s)^{\alpha}(z(t)-z(s))} \bigl(z(t)-z(s) \bigr)\,d \bigl(z(t)-z(s) \bigr) \leq0. \end{aligned} $$
(7)

Set \(\tau=z(t)-z(s)\), \(w(s)=\frac{g(z(t))-g(z(s))}{(t-s)^{\alpha}(z(t)-z(s))}=\bar{w}(\tau) \). g is a monotone nondecreasing function, hence, \(\bar{w}(\tau)\geq0\).

As a result, (7) can be transformed into

$$ \begin{aligned} \frac{1}{\Gamma(1-\alpha)} \int^{z(t)-z(0)}_{0}\bar{w}(\tau)\tau \,d\tau\geq0. \end{aligned} $$
(8)

By Lemma 2.4 and (8), (2) is true if

$$ \begin{aligned} \int^{z(t)-z(0)}_{0}\tau \,d\tau\geq0. \end{aligned} $$
(9)

It is easy to calculate that

$$ \begin{aligned} \int^{z(t)-z(0)}_{0}\tau \,d\tau =\frac{1}{2} \bigl(z(t)-z(0) \bigr)^{2}\geq0. \end{aligned} $$
(10)

The proof is completed. □

2.3 System description

In this paper, we consider a FNNs model described by

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}x_{i}(t)=-C_{i}x_{i}(t)+ \sum^{n}_{j=1}a_{ij}g_{j}(x_{j(t)})+I_{i},\quad i=1,2, \ldots, n. \end{aligned} $$
(11)

Equation (11) can be written equivalently as follows:

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}x(t)=-Cx(t)+Ag \bigl(x(t) \bigr)+I, \end{aligned} $$
(12)

where \(\underline{x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}\in R^{n}}\) is the state vector associated with the neurons, \(C=\text{diag}(c_{1},c_{2},\ldots,c_{n}) \) is a positive diagonal matrix, \(A=(a_{ij})_{n\times n}\) is the interconnection weight matrix, \(g(x)=(g_{1}(x_{1}),g_{2}(x_{2}),\ldots, g_{n}(x_{n}))^{T}\in R^{n}\) and \(I=(I_{1},I_{2},\ldots,I_{n})^{T}\) denote the neuron activation function and constant input vector, respectively.

The parameters C, A are assumed to be interval as \(C\in C_{I}\), \(A\in A_{I}\), where \(C_{I}:=\{C=\text{diag}(c_{i})_{n\times n}:0<\underline{C}\leq{C}\leq\overline{C}, \textit{i.e.}, 0<\underline{c}_{i}\leq c_{i}\leq\overline{c}_{i},i=1,2,\ldots,n\}\), \(\underline{C}=\text{diag}(\underline{c}_{i})_{n\times n}\), \(\overline{C}=\text{diag}(\overline{c}_{i})_{n\times n}\). \(A \in A_{I}\), \(A_{I}:=\{A=(a_{ij})_{n\times n}:\underline{A}\leq{A}\leq\overline{A}, \textit{i.e.}, \underline{a}_{i}\leq a_{i}\leq\overline{a}_{i},i=1,2,\ldots,n\}\), \(\underline{A}=(\underline{a}_{ij})_{n\times n}\), \(\overline{A}=(\overline{a}_{ij})_{n\times n}\).

In this paper, we make the following hypothesis for the neuron activation function \(g_{i}\):

\((H_{1})\) :

\(g_{i}\) is a continuous and monotone nondecreasing function.

Lemma 2.6

[24]

Let \(x\in R^{n}\) and \(A\in A_{I}\), then, for any positive diagonal matrix Q, the following inequality holds:

$$ \begin{aligned} x^{T} \bigl(QA+A^{T}Q \bigr)x \leq x^{T} \bigl(QA^{\ast}+A^{\ast T}Q+\big\| QA_{\ast}+A^{T}_{\ast}\big\| _{2}E \bigr)x, \end{aligned} $$

where \(A^{\ast}=\frac{1}{2}(\overline{A}+\underline{A})\), \(A_{\ast}=\frac {1}{2}(\overline{A}-\underline{A})\).

Definition 2.4

Mittag-Leffler stability

An equilibrium point \(x^{\ast}\) of the neural network system (12) is said to be Mittag-Leffler stable if there exist constants \(M>0\), \(\lambda>0\), \(\alpha\in(0,1)\) and \(b>0\) such that, for any solutions \(x(t)\) of (12) with initial value \(x_{0}\), the following inequality holds:

$$ \begin{aligned} \big\| x(t)-x^{\ast}\big\| \leq \bigl\{ M \big\| x_{0}-x^{\ast}\big\| E_{\alpha} \bigl(- \lambda t^{\alpha} \bigr) \bigr\} ^{b},\quad t\geq 0. \end{aligned} $$

Definition 2.5

[32]

The neural network system (12) is said to be globally robust Mittag-Leffler stable if the unique equilibrium point is globally Mittag-Leffler stable for \(C\in C_{I}\) and \(A\in A_{I}\).

3 Main results

Theorem 3.1

Let assumption \((H_{1})\) hold. If there exists a positive diagonal matrix \(Q=\operatorname{diag}(q_{1}, \ldots,q_{n})>0\) such that

$$ \begin{aligned} \Phi=Q A^{\ast}+A^{\ast T}Q+ \big\| Q A_{\ast}+A_{\ast}^{T}Q\big\| E < 0, \end{aligned} $$
(13)

then system (12) has a unique equilibrium point which is globally robustly Mittag-Leffler stable.

Proof

The process of proof is divided into three steps.

Step 1: In this step, we prove the existence of equilibrium point of system (12).

For \(C\in C_{I}\) and \(A\in A_{I}\), set

$$ \begin{aligned} W(x)&=Cx-Ag(x)-I \\ &=Cx-A \bigl(g(x)-g(0) \bigr)-I-Ag(0) \\ &=Cx-Af(x)-\widetilde{W}, \end{aligned} $$

where \(f(x)=g(x)-g(0)\), \(\widetilde{W}=Ag(0)+I\). It is easy to check that \(x^{*}\in R^{n}\) is an equilibrium point of (12), if and only if, \(W(x^{*}) = 0\). Let \(\mathcal{H}(\lambda, x)=Cx-\lambda A f(x)-\lambda\widetilde{W}\), \(\lambda\in[0, 1]\). Obviously, \(\mathcal{H}(\lambda, x)\) is a continuous homotopy mapping on x.

By Lemma 2.6 and (13), we can obtain that

$$ \begin{aligned} &f^{T}(x)Q \mathcal{H}(\lambda,x) \\ &\quad= f^{T}(x)Q Cx-\lambda f^{T}(x)Q Af(x)-\lambda f^{T}(x)Q\widetilde{W} \\ &\quad=f^{T}(x)Q Cx-\frac{\lambda}{2}f^{T}(x) \bigl(Q A+A^{T}Q \bigr)f(x)-\lambda f^{T}(x)Q \widetilde{W} \\ &\quad\geq f^{T}(x)Q Cx-\frac{\lambda}{2}f^{T}(x) \bigl(Q A^{\ast}+A^{\ast T}Q+\big\| Q A_{\ast}+A_{\ast}^{T}Q \big\| E \bigr)f(x)-\lambda f^{T}(x)Q \widetilde{W} \\ &\quad\geq f^{T}(x)Q Cx-\lambda f^{T}(x)Q \widetilde{W} \\ &\quad=\sum^{n}_{i=1}f_{i}(x_{i})q_{i}c_{i} \biggl(x_{i}-\frac{\lambda \widetilde{W}_{i}}{c_{i}} \biggr) \\ &\quad\geq \sum^{n}_{i=1}\big| f_{i}(x_{i})\big| q_{i} \underline{c}_{i} \biggl(| x_{i}|-\bigg| \frac{\widetilde{W}_{i}}{ \overline{c}_{i}}\bigg| \biggr). \end{aligned} $$

Under assumption \((H_{1})\), we have

$$ \begin{aligned} \underline{\lim_{| x_{i}|\rightarrow +\infty}f_{i}(x_{i})q_{i}c_{i}x_{i}=+ \infty.} \end{aligned} $$

This implies that, for each \(i\in\{ 1,2,\ldots, n\}\),

$$ \lim_{| x_{i}|\rightarrow+\infty} \big| f_{i}(x_{i})\big| q_{i}\underline{c}_{i} \biggl(| x_{i}|-\bigg| \frac{ \widetilde{W}_{i}}{ \overline{c}_{i} }\bigg| \biggr)=+\infty. $$
(14)

Let

$$ \begin{aligned} L_{i}=\sum ^{n}_{j=1,j\neq i} \sup \biggl\{ \big| f_{j}(x_{j})\big| q_{j} \underline{c}_{j} \biggl(| x_{j}|+\bigg| \frac{\widetilde{W}_{j}}{\overline{c}_{j}}\bigg| \biggr): | x_{j}|\leq\bigg| \frac{\widetilde{W}_{j}}{\overline{c}_{j}}\bigg| \biggr\} . \end{aligned} $$
(15)

By (14), there exists \(l_{i}> |\frac{\widetilde{W}_{j}}{\overline{c}_{j}}|\) such that, for any \(| x_{i}|> l_{i}\),

$$ \begin{aligned} &\Psi_{i}=\big| f_{i}(x_{i}) \big| q_{i}\underline{c}_{i} \biggl(| x_{i}|- \bigg| \frac{ \widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr)-L_{i}>0. \end{aligned} $$

Set \(\Omega=\{x\in R^{n}:| x_{i}|< l_{i}+1,i=1,2,\ldots,n\}\). It is easy to find that Ω is an open bounded convex set independent of λ. For \(x\in \partial\Omega\), define

$$ \begin{gathered} \Theta_{+}= \biggl\{ i \in\{1,2,\ldots,n \}: | x_{i}|\geq\bigg| \frac{\widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr\} , \\ \Theta_{-}= \biggl\{ i \in\{1,2,\ldots,n\}: | x_{i} |< \bigg| \frac{ \widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr\} , \end{gathered} $$

and there exists \(i_{0}\in\{1,2,\ldots,n\}\) such that \(| x_{i_{0}}|= l_{i_{0}}+1\).

By the definition of \(L_{i}\) in (15), we have

$$ \begin{aligned} & \big| f_{i_{0}}(x_{i_{0}})\big| q_{i_{0}}\underline{c}_{i_{0}} \biggl(| x_{i_{0}}|-\bigg| \frac{ \widetilde{W}_{i_{0}}}{\overline{c}_{i_{0}}}\bigg| \biggr)+\sum_{i\in\Theta _{-}}\big| f_{i}(x_{i})\big| q_{i}\underline{c}_{i} \biggl(| x_{i}|-\bigg|\frac{\widetilde {W}_{i}}{\overline{c}_{i}}\bigg| \biggr) \\ &\quad\geq\big| f_{i_{0}}(x_{i_{0}})\big| q_{i_{0}} \underline{c}_{i_{0}} \biggl(| x_{i_{0}}|- \bigg| \frac{ \widetilde{W}_{i_{0}}}{\overline{c}_{i_{0}}}\bigg| \biggr)-L_{i_{0}} \\ &\quad=\Psi_{i_{0}}>0. \end{aligned} $$

On the other hand,

$$ \begin{aligned} \sum_{i\in\Theta_{+}\setminus\{i_{0}\}}\big| f_{i}(x_{i})\big| q_{i}\underline{c}_{i} \biggl(| x_{i}|-\bigg|\frac{ \widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr)>0. \end{aligned} $$

Thus, for \(x\in\partial\Omega\) and \(\lambda\in[0,1]\), it follows that

$$ \begin{aligned} &f^{T}(x)Q \mathcal{H}(\lambda,x) \\ &\quad\geq \sum^{n}_{i=1}\big| f_{i}(x_{i})\big| q_{i}\underline{c}_{i} \biggl(| x_{i}|-\bigg| \frac{\widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr) \\ &\quad=\sum_{i\in\Theta _{+}\setminus\{i_{0}\}}\big| f_{i}(x_{i}) \big| q_{i}\underline{c}_{i} \biggl(| x_{i}|- \bigg| \frac{\widetilde{W}_{i}}{\overline{c}_{i}}\bigg| \biggr)+\big| f_{i_{0}}(x_{i_{0}})\big| q_{i_{0}} \underline{c}_{i_{0}} \biggl(| x_{i_{0}}|- \bigg|\frac{\widetilde {W}_{i_{0}}}{\overline{c}_{i_{0}}}\bigg| \biggr) \\ &\quad\quad{}+\sum_{i\in\Theta_{-}}\big| f_{i}(x_{i}) \big| q_{i}\underline{c}_{i} \biggl(| x_{i}|- \bigg| \frac{\widetilde {W}_{i}}{\overline{c}_{i}}\bigg| \biggr) \\ &\quad>0. \end{aligned} $$

This shows that \(\mathcal{H}(\lambda,x)\neq0\) for any \(x\in \partial\Omega\), \(\lambda\in[0,1]\). By utilizing the property of Brouwer degree (Lemma 2.3(1) in [15]), it follows that \(\operatorname{deg}(\mathcal {H}(1,x),\Omega,0)=\operatorname{deg}(\mathcal{H}(0, x),\Omega,0)\), namely, \(\operatorname{deg}(W(x),\Omega,0)=\operatorname{deg}(Cx,\Omega,0)\). Noting that \(\operatorname{deg}(W(x),\Omega,0)=\operatorname{deg}(Cx,\Omega,0)=\operatorname{Sign}|C|\neq 0\), where \(|C|\) is the determinant of C, and applying Lemma 2.3(2) in [15], we can obtain that \(W(x)=0 \) has at least a solution in Ω. That is, system (12) has at least an equilibrium point in Ω.

Step 2: In this step, we verify the uniqueness of equilibrium point of system (12).

Let \(x^{\prime}\) and \(x^{\prime\prime}\in R^{n}\) be two different equilibrium points of system (12). Then

$$ \begin{aligned} C \bigl(x^{\prime}-x^{\prime\prime} \bigr)=A \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr). \end{aligned} $$

Multiplying by \(2(f(x^{\prime})-f(x^{\prime\prime}))^{T}Q\) yields

$$ \begin{aligned}[b] 0&< 2 \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr)^{T}Q C \bigl(x^{\prime}-x^{\prime \prime} \bigr) \\ &=2 \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr)^{T}Q A \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime \prime} \bigr) \bigr) \\ &= \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr)^{T} \bigl(Q A+A^{T}Q \bigr) \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr) \\ &\leq \bigl(f \bigl(x^{\prime} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr)^{T}\Phi \bigl(\underline{f \bigl(x^{\prime }} \bigr)-f \bigl(x^{\prime\prime} \bigr) \bigr) \\ &< 0. \end{aligned} $$
(16)

Obviously, this is contradiction. Hence, \(x^{\prime}=x^{\prime\prime}\), namely, system (12) has a unique equilibrium point in Ω.

Step 3: In this step, we prove that the equilibrium point of system (12) is globally robustly Mittag-Leffler stable.

Assume that \(x^{\ast} \in R ^{n}\) is the unique equilibrium point of system (12). Let \(z_{i}(t)=x_{i}(t)-x_{i}^{\ast}\), then system (12) can be changed as follows:

$$ \begin{aligned}[b] ^{c}_{0}D^{\alpha}_{t}z_{i}(t)&=-c_{i}z_{i}(t)+ \sum_{j=1}^{n} a_{ij} \bigl(g_{j} \bigl(z_{j}(t)+x_{j}^{\ast} \bigr)-g_{j} \bigl(x_{j}^{\ast} \bigr) \bigr) \\ &=\underline{-c_{i}z_{i}(t)+\sum _{j=1}^{n} a_{ij}f_{j} \bigl(z_{j}(t) \bigr)}, \end{aligned} $$
(17)

where \(f_{j}(z_{j}(t))=g_{j}(z_{j}(t)+x_{j}^{\ast})-g_{j}(x_{j}^{\ast})\).

By assumption \((H_{1})\), \(f_{i}\) is monotone nondecreasing and \(f_{i}(0)=0\). Hence, for any \(z_{i} \in R\), we have

$$ 0\leq \int^{z_{i}}_{0}f_{i}(s)\,ds\leq z_{i} f_{i}(z_{i}). $$
(18)

For \(C\in C_{I}\) and \(A\in A_{I}\), consider the following Lyapunov functional \(V: R^{n}\rightarrow R\) of Lur’e-Postnikov type [37]:

$$ \begin{aligned} V \bigl(z(t) \bigr)=z^{T}(t)C^{-1}z(t)+2 \beta\sum^{n}_{i=1} q_{i} \int ^{z_{i}(t)}_{0}f_{i}(s)\,ds, \end{aligned} $$

where

$$ \beta>\frac{1}{\lambda_{m}}\big\| \underline{C}^{-1} \overline{A} \big\| ^{2}>0, $$
(19)

\(\lambda_{m} =\lambda_{\min}(-\Phi)>0\). Note that under condition (19), being \(\|C^{-1}A\|^{2}=\lambda_{\max} ((C^{-1}A)^{T}(C^{-1}A))\), it follows that

$$ \lambda=\lambda_{\min} \bigl(\beta(-\Phi)- \bigl(C^{-1}A \bigr)^{T} \bigl(C^{-1}A \bigr) \bigr)>0. $$
(20)

Calculate the fractional-order derivative of \(V(z(t))\) with respect to time along the solution of system (17). By Lemmas 2.3, 2.5 and 2.6, it can be obtained that

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}V \bigl(z(t) \bigr)={}&^{c}_{0}D^{\alpha}_{t} \bigl[z^{T}(t)C^{-1}z(t) \bigr]+2\beta \sum ^{n}_{i=1} q_{i} {^{c}_{0}D^{\alpha}_{t}} \biggl[ \int ^{z_{i}(t)}_{0}f_{i}(s)\,ds \biggr] \\ \leq{}& 2z^{T}(t){C^{-1}} ^{c}_{0}D^{\alpha}_{t}z(t)+2 \beta\sum^{n}_{i=1} q_{i}f_{i}^{T} \bigl(z_{i}(t) \bigr)^{c}_{0}D^{\alpha}_{t}{z_{i}(t)} \\ ={}&{-}2z^{T}(t)z(t)+2z^{T}(t)C^{-1}Af \bigl(z(t) \bigr) \\ &-2\beta f^{T} \bigl(z(t) \bigr) (QC)z(t)+2\beta f^{T} \bigl(z(t) \bigr) (Q A)f \bigl(z(t) \bigr) \\ \leq{}&{-}2z^{T}(t)z(t)+2z^{T}(t)C^{-1}Af \bigl(z(t) \bigr) \\ &-2\beta f^{T} \bigl(z(t) \bigr) (QC)z(t)+\beta f^{T} \bigl(z(t) \bigr)\Phi f \bigl(z(t) \bigr), \end{aligned} $$

where \(2\beta f^{T}(z(t))(QC)z(t)\geq0\) on the basis of assumption \((H_{1})\). By adding and subtracting \(-f^{T} (z(t)) [(C^{-1}A)^{T} (C^{-1}A) ]f(z(t))\), and accounting for (20), we get

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}V \bigl(z(t) \bigr)\leq{}&{-}2z^{T}(t)z(t)+ 2z^{T}(t)C^{-1}Af \bigl(z(t) \bigr) \\ &-f^{T} \bigl(z(t) \bigr) \bigl[ \bigl(C^{-1}A \bigr)^{T} \bigl(C^{-1}A \bigr) \bigr]f(z(t) \\ &-f^{T} \bigl(z(t) \bigr) \bigl[\beta(-\Phi)- \bigl(C^{-1}A \bigr) \bigl(C^{-1}A \bigr)^{T} \bigr]f \bigl(z(t) \bigr) \\ &-2\beta f^{T} \bigl(z(t) \bigr) (Q C)z(t) \\ \leq{}&{-}z^{T}(t)z(t)-\big\| z(t)-C^{-1}Af\bigl(z(t)\bigr)\big\| ^{2} \\ &- \lambda f^{T} \bigl(z(t) \bigr)f \bigl(z(t) \bigr) -2\beta f^{T} \bigl(z(t) \bigr) (Q C)z(t) \\ \leq{}&{-}z^{T}(t)z(t)-2\beta f^{T} \bigl(z(t) \bigr) (Q C)z(t) \\ ={}&{-}\sum^{n}_{i=1}z^{2}_{i}(t)- 2\beta\sum^{n}_{i=1}c_{i} q_{i} z_{i}(t) f_{i} \bigl(z_{i}(t) \bigr). \end{aligned} $$

By (18), we have

$$ \begin{aligned} ^{c}_{0}D^{\alpha}_{t}V \bigl(z(t) \bigr) &\leq-\underline{c} \Biggl[z^{T}(t)C^{-1}z(t)+2 \beta\sum^{n}_{i=1} q_{i} \int ^{z_{i}(t)}_{0}f_{i}(s)\,ds \Biggr] \\ &\leq-\underline{c}V \bigl(z(t) \bigr), \end{aligned} $$

where \(\underline{c}=\min\{\underline{c}_{i}:1\leq i\leq n\}\). By applying Lemma 2.2, we obtain that

$$ \begin{aligned} V \bigl(z(t) \bigr)\leq V(0)E_{\alpha} \bigl(- \underline{c}t^{\alpha} \bigr), \quad t>0. \end{aligned} $$

Noting that

$$ \begin{aligned} V \bigl(z(t) \bigr)= &\sum ^{n}_{i=1} \frac{1}{c_{i}}z^{2}_{i}(t)+2 \beta\sum^{n}_{i=1} q_{i} \int^{z_{i}(t)}_{0}f_{i}(s)\,ds \geq\sum ^{n}_{i=1}\frac{1}{c_{i}}z^{2}_{i}(t) \geq \frac{1}{\overline{c}}\big\| z(t)\big\| ^{2}, \end{aligned} $$

where \(\overline{c}=\max\{\overline{c}_{i}:1\leq i\leq n\}\), we have

$$ \big\| z(t)\big\| ^{2}\leq\overline{c} V(0)E_{\alpha} \bigl(- \underline{c}t^{\alpha} \bigr),\quad t>0. $$

This implies that

$$ \begin{aligned} &\big\| x(t)-x^{\ast}\big\| ^{2} \\ &\quad\leq \overline{c} \Biggl( \big\| x(0)-x^{\ast}\big\| ^{2}+2\beta\sum ^{n}_{i=1} q_{i} \int^{x(0)-x^{\ast}}_{0}f_{i}(s)\,ds \Biggr) E_{\alpha} \bigl(-\underline{c}t^{\alpha} \bigr) \\ &\quad\leq\overline{c} \bigl(\big\| x(0)-x^{\ast}\big\| ^{2}+2\beta \overline{q} f^{T} \bigl(x(0)-x^{\ast} \bigr) \bigl(x(0)-x^{\ast} \bigr) \bigr)E_{\alpha} \bigl(- \underline{c}t^{\alpha} \bigr), \end{aligned} $$

where \(\overline{q}=\max\{\overline{q}_{i}:1\leq i\leq n\}\).

Hence

$$ \begin{aligned} \big\| x-x^{\ast}\big\| \leq M \big\| x(0)-x^{\ast} \big\| \bigl(E_{\alpha} \bigl(-\underline{c} t^{\alpha} \bigr) \bigr)^{\frac{1}{2}}, \end{aligned} $$

where \(M= (\overline{c}+2\beta \overline{q}\overline{c}\frac{f^{T} (x(0)-x^{\ast})(x(0)-x^{\ast})}{\|x(0)-x^{\ast}\|^{2}} )^{\frac{1}{2}}\). According to Definitions 2.4 and 2.5, the equilibrium point of system (12) is globally robustly Mittag-Leffler stable. The proof is completed. □

4 Numerical examples

Example 1

Consider a fractional-order neural network (12) with the following parameters:

$$\begin{gathered} \alpha=0.98 ,\quad\quad \underline{C}=\operatorname{diag}(1,1),\qquad\overline{C}=\operatorname{diag}(3,3),\\ \underline{A}= \begin{pmatrix}-18&0\cr-1&-19 \end{pmatrix} ,\qquad \overline{A}= \begin{pmatrix}-16&2\\ 1&-17 \end{pmatrix} ,\\ I=(20,10)^{T}.\end{gathered}$$

Choose the activation function with respect to \(\underline{g_{i}(x_{i})=0.5x_{i}+\tanh(x_{i})}\), \(i=1,\ldots, n\). Obviously, \(g_{i}\) is a monotone nondecreasing function.

By applying appropriate LMI solver to acquire a feasible numerical solution of (13), we can get that Q could be as follows:

$$Q=\left (\textstyle\begin{array}{c@{\quad}c} 1.0624 & 0\\ 0 & 0.8924 \end{array}\displaystyle \right )>0. $$

The condition of Theorem 3.1 holds. Thus, system (12) with the above parameters is globally robustly Mittag-Leffler stable.

To verify the above result, we divide a numerical simulation into three cases:

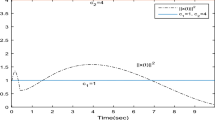
Case 1: \(C=\underline{C}\in C_{I} \), \(A=\underline{A}\in A_{I}\), \(x^{*}=(0.8024,0.3089)\), see Figure 1.

Figure 1
figure 1

The state trajectory x of neural network ( 17 ) in Case 1 of Example 1 .

Full size image

Case 2: \(C= \bigl({\scriptsize\begin{matrix}{}2&0\cr0&2 \end{matrix}} \bigr) \in C_{I}\), \(A= \bigl({\scriptsize\begin{matrix}{}-17&1\cr0&-18 \end{matrix}} \bigr) \in A_{I}\), \(x^{*}=(0.8419,0.3535)\), see Figure 2.

Figure 2
figure 2

The state trajectory x of neural network ( 17 ) in Case 2 of Example 1 .

Full size image

Case 3: \(C=\overline{C}\in C_{I}\), \(A=\overline{A}\in A_{I}\), \(x^{*}=(0.8899,0.4037)\), see Figure 3.

Figure 3
figure 3

The state trajectory x of neural network ( 17 ) in Case 3 of Example 1 .

Full size image

From Figures 1, 2, 3, we can see that the state trajectories converge to a unique equilibrium point. This is consistent with the conclusion of Theorem 3.1.

Example 2

Consider a fractional-order neural network (12) with the following parameters:

$$\begin{gathered} \alpha=0.7 , \quad\quad \underline{C}=\operatorname{diag}(1,2,3), \qquad \overline{C}=\operatorname{diag}(3,4,5),\\ \underline{A}= \begin{pmatrix}-30&-1&0\\1&-11&0\\0&0&-8 \end{pmatrix} ,\qquad \overline{A}= \begin{pmatrix}-28&1&0\\3&-9&0\\0&0&-6 \end{pmatrix} ,\\ I=(10,8,10)^{T},\qquad g_{i}(x_{i})=0.5x_{i}+\arctan(x_{i}). \end{gathered}$$

Obviously, \(g_{i}\) is a monotone nondecreasing function. Choose the positive definite diagonal matrix \(Q=\operatorname{diag}(5,8,11)\), then we have

$$ \begin{aligned} \Phi&= Q A^{\ast}+A^{\ast T}Q+\big\| Q A_{\ast}+A_{\ast}^{T}Q\big\| E \\ &= \begin{pmatrix}-263.6580&16.000&0\\16.000&-133.6580&0\\0&0&-127.6580 \end{pmatrix} \\ &< 0. \end{aligned} $$

The condition of Theorem 3.1 is satisfied. Thus, system (12) with the above parameters is globally robustly Mittag-Leffler stable.

To verify the above result, we divide a numerical simulation into three cases:

Case 1: \(C=\underline{C}\in C_{I} \), \(A=\underline{A}\in A_{I}\), \(x^{*}=(0.2336,0.5032,0.8613)\), see Figure 4.

Figure 4
figure 4

The state trajectory x of neural network ( 17 ) in Case 1 of Example 2 .

Full size image

Case 2:

$$ \begin{gathered} C=\operatorname{diag}(2,3,4),\qquad A= \begin{pmatrix}-29&0&0\\2&-10&0\\0&0&-7 \end{pmatrix} \in A_{I},\\ x^{*}=(0.2383,0.5589,0.9464), \end{gathered}$$

see Figure 5.

Figure 5
figure 5

The state trajectory x of neural network ( 17 ) in Case 2 of Example 2 .

Full size image

Case 3: \(C=\overline{C}\in C_{I}\), \(A=\overline{A}\in A_{I}\), \(x^{*}=(0.2495,0.6496,1.1050)\), see Figure 6.

Figure 6
figure 6

The state trajectory x of neural network ( 17 ) in Case 3 of Example 2 .

Full size image

From Figures 4, 5, 6, we can see that the state trajectories converge to a unique equilibrium point. This is consistent with the conclusion of Theorem 3.1.

5 Conclusion

In this paper, the global robust Mittag-Leffler stability issue has been investigated for a class of FNNs with parameter uncertainties. A new inequality with respect to the Caputo derivative of an integer-order integral function with the variable upper limit has been developed. The sufficient condition in terms of LMIs has been presented to ensure the existence, uniqueness and robust Mittag-Leffler stability of equilibrium point.

It would be interesting to extend the results proposed in this paper to FNNs with delays and parameter uncertainties. This issue will be the topic of our future research.