1 Introduction

Complex networks [1, 2] have attracted considerable attention as a fundamental tool in understanding the dynamical behaviors of real systems, such as internet, World Wide Web, food webs, electrical power grids, metabolic networks, scientific citation web and fractal networks [3]. The dynamics of complex networks has been an interesting issue with focus on the interplay between the local node dynamics and the overall topological structures. As a typical collective behavior, synchronization of complex networks has been widely investigated because of many applications in engineering [4]. Among many types of synchronization of complex networks, inner synchronization inside a network and outer synchronization between two coupled networks are striking. Generally the method of synchronization is to transform the networked systems into some low dimensional systems and obtain the criteria of synchronization by the master stability function or linear matrix inequality [5, 6]. When the inner synchronization may not happen inside a network with unappropriate topological connections and node dynamics, some controlling (e.g., the adaptive, feedback, pinning and impulsive control) methods are employed for realizing the synchronization (see [7–11] and many references cited therein).

To study the outer synchronization between two coupled networks, Li et al. applied the open-plus-closed-loop control to achieve outer synchronization [12]. This original work theoretically and numerically demonstrated the feasibility of this type of synchronization. In reality, when the trains arrive at the platform in subway systems, the inner and outer doors simultaneously open or close, showing that both inner synchronization and outer synchronization happen. Afterwards, the expanded works on the outer synchronization, such as introducing the adaptive control, effect of noise and fractional-order node dynamics, can be found in the literature [13–17].

It should be noted that all of the above-mentioned works on the synchronization focus on the known node dynamics and topological connections. This assumption cannot be used in many real networks with evolving or adaptive couplings, e.g., flocks of robots [18]. Recently the synchronization of dynamical networks with unknown information has received increasing attention. Zheng used the impulsive control to study the synchronization of uncertain complex-variable chaotic delayed systems [19]. Wu and Lu studied the outer synchronization and parameter identification between two networks with time-varying connections by designing the adaptive controllers [20]. By designing the nonlinear controllers, we achieved the generalized outer synchronization between two uncertain networks where the couplings of each network are unknown nonlinear functions [21].

During the studies on the synchronization of complex networks, most of the existing works studied the complete synchronization. Apart from this type of synchronization, lag synchronization is an interesting phenomenon, which is referred to as the coincidence of the states between two coupled systems, where one system is delayed by a finite time. Presently lag synchronization has been observed in lasers, neural models and electronic circuits [22] and applied in secure communication [23]. Recently the lag synchronization of coupled networks has become a new issue in the research of complex networks. Li et al. studied the successive lag synchronization on nonlinear dynamical networks by the linear feedback control [24]. Zhao et al. considered the lag synchronization between two different networks based on the state observer and designed the corresponding adaptive controllers [25]. Projective lag synchronization in drive-response dynamical networks was studied by proposing a hybrid feedback control method [26, 27]; however they did not consider the parameter identification. To reduce the number of control nodes, the lag synchronization by pinning control was studied in [28, 29].

Inspired by the above discussions, we study lag synchronization in drive-response dynamical networks by the method proposed in [26, 27] and identify the unknown parameter in the node dynamics. By designing the hybrid feedback controllers, we achieve the lag synchronization. With the proposed controllers and update laws for the system parameter, we obtain two theorems on the lag synchronization and identify the unknown system parameter when the lag synchronization happens. In addition, this control method is effective for the drive system with and without mismatched terms. Our findings may help a deeper understanding of the consensus or agreement of the connected agents.

The rest of this paper is organized as follows. In Sections 2 and 3, preliminaries and network models are given. Section 4 studies the lag synchronization by linear and adaptive feedback control. Numerical examples are shown to verify the efficiency of the proposed adaptive schemes in Section 5. Finally, conclusions are drawn in Section 6.

Notations: Throughout this paper, some necessary notations are first introduced. The norm of a vector x is \(\|x\|=\sqrt{x^{T}x}\). The norm of a matrix A is \(\|A\|=\sqrt{\lambda_{\max}(A^{T}A)}\), where \(\lambda_{\max}(A^{T}A)\) denotes the maximal eigenvalue of matrix \(A^{T}A\). ⊗ is the Kronecker product. \(I_{n}\) is an identity matrix of size n.

2 Preliminaries

Consider the following uncertain dynamical system:

$$ \dot{x}(t)=f\bigl(x(t),\theta\bigr)\triangleq f_{1}\bigl(x(t) \bigr)+f_{2}\bigl(x(t)\bigr)\theta, $$
(1)

where \(x\in R^{n}\) is the state vector, \(\theta\in R^{m}\) is an unknown system parameter vector. \(f_{1}: R^{n}\rightarrow R^{n}\) is a continuous vector function and \(f_{2}: R^{n}\rightarrow R^{n\times m}\) is a continuous matrix function.

Assumption 1

There exists a positive constant L satisfying

$$(y-x)^{T}\bigl(f(y,\theta)-f(x,\theta)\bigr)\leq L (y-x)^{T}(y-x), $$

where \(x, y\in R^{n}\) are time-varying vectors.

Lemma 1

(LaSalle invariance principle) [30]

Let \(\Omega\subset D\) be a compact set that is positively invariant with respect to \(\dot{x}=f(x)\). Let \(V: D\rightarrow R\) be a continuously differentiable function such that \(\dot{V}(x)\leq0\) in Ω. Let E be the set of all points in Ω where \(\dot{V}(x)=0\). Let M be the largest invariant set in E. Then every solution starting in Ω approaches M as \(t\rightarrow\infty\).

3 Model presentation

The uncertain drive-response coupled networks with the designed controllers is given by

$$\begin{aligned}& \dot{x}^{d}(t)=f_{1}\bigl(x^{d}(t) \bigr)+f_{2}\bigl(x^{d}(t)\bigr)\theta+\Delta(t), \end{aligned}$$
(2)
$$\begin{aligned}& \dot{y}_{i}^{r}(t)=f_{1}\bigl(y_{i}^{r}(t) \bigr)+f_{2}\bigl(y_{i}^{r}(t)\bigr)\tilde{ \theta}(t) +\sum_{j=1}^{N}a_{ij} \Gamma y_{j}^{r}(t)+u_{i}(t),\quad i=1,2, \ldots,N, \end{aligned}$$
(3)

where \(x^{d}=(x_{1}^{d},x_{2}^{d},\ldots,x_{n}^{d})^{T}\in R^{n}\) is the state vector of the drive system. \(f_{1}\), \(f_{2}\) have the same meanings in Eq. (1). \(\Delta(t)\) is the nonlinear mismatched term. \(y_{i}^{r}=(y_{i1}^{r},y_{i2}^{r},\ldots,y_{in}^{r})^{T}\in R^{n}\) denotes the state vector of the ith node. \(\theta=(\theta^{(1)},\theta^{(2)},\ldots ,\theta^{(m)})^{T}\in R^{m}\) is the unknown parameter vector. \(\tilde{\theta}(t)=(\tilde{\theta }^{(1)}(t),\tilde{\theta}^{(2)}(t),\ldots,\tilde{\theta}^{(m)}(t))^{T}\in R^{m}\) is the estimation of the unknown parameter θ. \(\Gamma\in R^{n\times n}\) is an inner coupling matrix measuring the interactions of variables. \(A=(a_{ij})_{N\times N}\) is the coupling configuration matrix denoting the topological structures of networks. The entries \(a_{ij}\) are defined as follows: \(a_{ij}> 0\) if there is a link between node i and node j (\(i\neq j\)); otherwise \(a_{ij}= 0\) (\(i\neq j\)), and the diagonal entries \(a_{ii}=-\sum_{j=1,j\neq i}^{N}a_{ij}\), \(i=1,2,\ldots,N\). \(u_{i}(t)\) (\(i=1,2,\ldots,N\)) are the controllers to be designed.

The lag synchronization error is defined as \(e_{i}(t)=y_{i}^{r}(t)-x^{d}(t-\tau )\), \(i=1,2,\ldots,N\), where \(\tau>0\) is a constant denoting time delay or lag. Then the lag synchronization between the reference node (2) and the dynamical networks (3) is achieved if

$$\lim_{t\rightarrow\infty} \big\| y_{i}^{r}(t)-x^{d}(t- \tau)\big\| = 0,\quad i=1,2,\ldots,N. $$

4 Lag synchronization analysis

4.1 Linear feedback control

In this subsection, we study the lag synchronization in drive-response networks (2) and (3) with the designed linear feedback controllers. The main results are summarized in the following theorem.

Theorem 1

Suppose that Assumption 1 holds. If the controllers are designed as follows:

$$ \left\{ \textstyle\begin{array}{l} u_{i}(t)=u_{i1}(t)+u_{i2}(t), \\ u_{i1}(t)=\Delta(t-\tau), \\ u_{i2}(t)=-d_{i}e_{i}(t)\quad (i=1,2,\ldots,N), \\ \dot{\tilde{\theta}}(t)=-\sum_{i=1}^{N}f_{2}^{T} (y_{i}^{r}(t)) e_{i}(t), \end{array}\displaystyle \right . $$
(4)

where \(d_{i}\ (i=1,2,\ldots,N)>0\) are feedback gains satisfying \(d_{\min}=\min_{i=1,\ldots,N}\{d_{i}\}\geq L+\lambda_{\max}((P+P^{T})/2)+1\) with \(P=A\otimes\Gamma\), then the lag synchronization in drive-response networks (2) and (3) is achieved and the unknown parameter θ can be identified.

Proof

From networks (2) and (3), we obtain the following error dynamical system:

$$ \dot{e}_{i}(t)=f\bigl(y_{i}^{r}(t),\theta \bigr)-f\bigl(x^{d}(t-\tau),\theta\bigr) +f_{2} \bigl(y_{i}^{r}(t)\bigr)\bar{\theta}(t) +\sum_{j=1}^{N} a_{ij}\Gamma e_{j}(t)-d_{i}e_{i}(t), $$
(5)

where \(\bar{\theta}(t)=\tilde{\theta}(t)-\theta\).

Consider the following Lyapunov function:

$$\begin{aligned} V(t) =&\frac{1}{2}\sum_{i=1}^{N}e_{i}^{T}(t)e_{i}(t)+ \frac{1}{2}\bar{\theta }^{T}(t) \bar{\theta}(t). \end{aligned}$$

The time derivative of \(V(t)\) along the trajectories of error system (5) gives

$$\begin{aligned} \dot{V}(t) =&\sum_{i=1}^{N} e_{i}^{T}(t) \bigl[f\bigl(y_{i}^{r}(t), \theta\bigr)-f\bigl(x^{d}(t-\tau ),\theta\bigr) +f_{2} \bigl(y_{i}^{r}(t)\bigr)\bar{\theta}(t)-d_{i}e_{i}(t) \bigr] \\ &{}+\sum_{i=1}^{N}\sum _{j=1}^{N} e_{i}^{T}(t)a_{ij}\Gamma e_{j}(t)- \sum_{i=1}^{N}\bar{\theta }^{T}f_{2}^{T}\bigl(y_{i}^{r}(t) \bigr)e_{i}(t) \\ \leq&\sum_{i=1}^{N}(L-d_{i})e_{i}^{T}(t)e_{i}(t)+ \sum_{i=1}^{N}\sum _{j=1}^{N}e_{i}^{T}(t)a_{ij} \Gamma e_{j}(t) \\ \leq&\bigl(L+\lambda_{\max}\bigl(\bigl(P+P^{T}\bigr)/2 \bigr)-d_{\min}\bigr)e^{T}(t)e(t), \end{aligned}$$

where \(e(t)=(e_{1}^{T}(t),e_{2}^{T}(t),\ldots,e_{N}^{T}(t))^{T}\). According to the conditions, we obtain \(\dot{V}(t)\leq-e^{T}(t)e(t)\). Then the set

$$E= \bigl\{ e_{i}(t)=0, \tilde{\theta}(t)=\theta, i=1,2,\ldots, N \bigr\} $$

is the largest invariant set of the set \(\widehat{E}=\{\dot{V}(t)=0\}\) for error system (5). Based on the LaSalle invariance principle, the orbits converge asymptotically to the set E, which means that the lag synchronization is achieved. It also gives that the system parameter vector θ can be identified by the updating laws (4) when the lag synchronization is achieved. □

Remark 1

In this theorem, we design a hybrid feedback control method to realize lag synchronization, including \(u_{i1}(t)\) being the nonlinear feedback control and \(u_{i2}(t)\) being the linear feedback control.

Remark 2

For this linear feedback control, the expected feedback gains \(d_{i}\) need satisfy \(d_{i}\geq L+\lambda_{\max}((P+P^{T})/2)+1\). As many studies on the linear feedback control show [24, 28], the theoretical values of \(d_{i}\) are much bigger than those needed in practice. To deal with the shortcoming of linear feedback control, we will use the adaptive technique to achieve the lag synchronization.

4.2 Adaptive feedback control

In this subsection, we apply the adaptive controllers to achieve the lag synchronization and identify the unknown parameter in the node dynamics. The corresponding adaptive controllers and update laws are then designed.

Theorem 2

Suppose that Assumption 1 holds. The lag synchronization in drive-response networks (2) and (3) is achieved and the unknown parameter θ is also identified with the following adaptive controllers and the corresponding updating laws:

$$ \left\{ \textstyle\begin{array}{l} u_{i}(t)=u_{i1}(t)+u_{i2}(t), \\ u_{i1}(t)=\Delta(t-\tau), \\ u_{i2}(t)=-d_{i}(t)e_{i}(t)\quad (i=1,2,\ldots,N), \\ \dot{d}_{i}(t)=h_{i}e_{i}^{T}(t) e_{i}(t), \\ \dot{\tilde{\theta}}(t)=-\sum_{i=1}^{N}f_{2}^{T} (y_{i}^{r}(t)) e_{i}(t), \end{array}\displaystyle \right . $$
(6)

where \(h_{i}\) are arbitrary positive constants.

Proof

Choose the Lyapunov function candidate as follows:

$$ V(t)=\frac{1}{2}\sum_{i=1}^{N} e_{i}^{T}(t)e_{i}(t)+\frac{1}{2}\sum _{i=1}^{N}\frac {1}{h_{i}} \bigl(d_{i}(t)-d_{i}^{*}\bigr)^{2}+\frac{1}{2} \bar{\theta}^{T}(t) \bar{\theta}(t), $$

where \(d_{i}^{*}\) (\(i=1,2,\ldots,N\)) are sufficiently large positive constants to be determined later. The derivative of \(V(t)\) yields

$$\begin{aligned} \dot{V}(t) =&\sum_{i=1}^{N}e_{i}^{T}(t) \dot{e}_{i}(t)+ \sum_{i=1}^{N} \frac {1}{h_{i}}\bigl(d_{i}(t)-d_{i}^{*}\bigr) \dot{d}_{i}(t)+\bar{\theta}^{T}(t) \dot{\bar{\theta }}(t) \\ =&\sum_{i=1}^{N} e_{i}^{T}(t) \bigl[ f\bigl(y_{i}^{r}(t),\theta\bigr)-f \bigl(x^{d}(t-\tau),\theta\bigr) +f_{2}\bigl(y_{i}^{r}(t) \bigr)\bar{\theta}(t)-d_{i}(t)e_{i}(t) \bigr] \\ &{}+\sum_{i=1}^{N}\sum _{j=1}^{N} e_{i}^{T}(t)a_{ij}\Gamma e_{j}(t)- \sum_{i=1}^{N}\bar{\theta }^{T}(t)f_{2}^{T}\bigl(y_{i}^{r}(t) \bigr)e_{i}(t) +\sum_{i=1}^{N} \bigl(d_{i}(t)-d_{i}^{*}\bigr)e_{i}^{T}(t) e_{i}(t) \\ \leq&\sum_{i=1}^{N}\bigl(L-d^{*} \bigr)e_{i}^{T}(t)e_{i}(t)+ \sum _{i=1}^{N}\sum_{j=1}^{N}e_{i}^{T}(t)a_{ij} \Gamma e_{j}(t) \\ \leq& \bigl[L+\lambda_{\max}\bigl(\bigl(P+P^{T}\bigr)/2 \bigr)-d^{*} \bigr]e^{T}(t)e(t), \end{aligned}$$

where \(d^{*}=\min_{i=1,\ldots,N}\{d_{i}^{*}\}\). Taking \(d^{*}\geq L+\lambda_{\max}((P+P^{T})/2)+1\), we obtain \(\dot{V}(t)\leq -e^{T}(t)e(t)\). Then the set

$$E= \bigl\{ e_{i}(t)=0, \tilde{\theta}(t)=\theta, d_{i}(t)=d_{i}^{*}, i=1,2,\ldots , N \bigr\} $$

is the largest invariant set of the set \(\widehat{E}=\{\dot{V}(t)=0\}\). According to the LaSalle invariance principle of differential equation, the orbits asymptotically converge to the set E. It shows that the system parameter vector θ can be identified by the updating laws (6) when the lag synchronization is achieved. □

Remark 3

It is noted that the mismatched term \(\Delta(t)\) has no effect on the derivative of Lyapunov function \(V(t)\), which shows that this method is robust for some control systems with parameters perturbation and noise disturbance.

5 Numerical analysis

In this section, we will provide numerical examples to show the effectiveness of the proposed control schemes obtained in the previous sections, which includes the linear and adaptive feedback controls. In the numerical simulations, the node dynamical equations are taken as the Lorenz chaotic system [31], which is given by

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}^{d} = \theta^{(1)}(x_{2}^{d} - x_{1}^{d}), \\ \dot{x}_{2}^{d} = \theta^{(2)}x_{1}^{d} -x_{2}^{d}- x_{1}^{d}x_{3}^{d},\\ \dot{x}_{3}^{d} = x_{1}^{d}x_{2}^{d} - \theta^{(3)}x_{3}^{d}. \end{array}\displaystyle \right . $$

Then the system can be rewritten in the following form:

$$ \left ( \textstyle\begin{array}{c} \dot{x}_{1}^{d} \\ \dot{x}_{2}^{d} \\ \dot{x}_{3}^{d} \end{array}\displaystyle \right )=\underbrace{\left ( \textstyle\begin{array}{c} 0 \\ -x_{1}^{d}x_{3}^{d}-x_{2}^{d} \\ x_{1}^{d}x_{2}^{d} \end{array}\displaystyle \right )} _{f_{1}(x^{d})}+\underbrace{\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} x_{2}^{d} - x_{1}^{d} & 0 & 0 \\ 0 & x_{1}^{d} & 0 \\ 0 & 0 & -x_{3}^{d} \end{array}\displaystyle \right )} _{f_{2}(x^{d})}\underbrace{\left ( \textstyle\begin{array}{c} \theta^{(1)} \\ \theta^{(2)} \\ \theta^{(3)} \end{array}\displaystyle \right )} _{\theta}. $$

We introduce the quantity \(E(t)=\max_{i=1,\ldots,N}\| y_{i}^{r}(t)-x^{d}(t-\tau)\|\) to measure the lag synchronization process and take the inner coupling matrix \(\Gamma=I_{3}\).

5.1 Lag synchronization by linear feedback control

In this subsection, we use the linear feedback control schemes (4) in Theorem 1 to realize the lag synchronization and to identify the unknown parameter in the node dynamics. We choose an undirected coupling network, and the coupling matrix is

$$ A=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -4 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 1 & -5 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & -5 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & -4 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & -5 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & -5 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 & -6 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & -5 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & -4 & 1 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & -5 \end{array}\displaystyle \right ]. $$

According to Theorem 1, the estimation of the unknown parameter \(\tilde {\theta}(t)\) reads as

$$\left ( \textstyle\begin{array}{c} \dot{\tilde{\theta}}^{(1)}(t) \\ \dot{\tilde{\theta}}^{(2)}(t) \\ \dot{\tilde{\theta}}^{(3)}(t) \end{array}\displaystyle \right )=\left ( \textstyle\begin{array}{c} -\sum_{i=1}^{N}(y_{i2}^{r}(t) - y_{i1}^{r}(t))e_{i1}(t) \\ -\sum_{i=1}^{N}y_{i1}^{r}(t)e_{i2}(t) \\ \sum_{i=1}^{N}y_{i3}^{r}(t)e_{i3}(t) \end{array}\displaystyle \right ). $$

Based on the results obtained in [32] on the Lorenz system, one can choose a positive constant \(L=68\) such that Assumption 1 holds. According to Theorem 1, the feedback gains \(d_{i}\geq L+\lambda_{\max}((P+P^{T})/2)+1\). We then take \(d_{i}=80\), \(i=1,2,\ldots,10\), for numerical simulations and employ the mismatched terms as \(\Delta (t)=(\sin(t),0,0.2\cos(t))^{T}\). The real values for the system parameter θ are set as \(\theta^{(1)}=10\), \(\theta^{(2)}=28\), \(\theta ^{(3)}=8/3\). The initial values are randomly chosen in \((-2,2)\). The numerical results are presented in Figures 1 and 2. Figure 1 displays the time evolution of the lag synchronization error \(E(t)\) with a delay \({\tau=0.01}\), indicating that the lag synchronization between the drive and response networks is achieved. Figure 2 shows the identification of the uncertain system parameter θ, which means that the unknown parameter is successfully estimated. In addition, we increase the network size \(N\leq 50\) and the lag \(0<\tau\leq1\) and see that these two quantities have a little effect on the lag synchronization.

Figure 1
figure 1

Time evolution of the lag synchronization error \(\pmb{E(t)}\) .

Full size image
Figure 2
figure 2

The estimated unknown parameter \(\pmb{\tilde{\theta }=(\tilde{\theta}^{(1)}, \tilde{\theta}^{(2)}, \tilde{\theta}^{(3)})^{T}}\) by linear feedback control with \(\pmb{\tau=0.01}\) .

Full size image

5.2 Lag synchronization by adaptive feedback control

In this subsection, we apply the adaptive technique to control the lag synchronization by using the controllers and corresponding laws (6) in Theorem 2. In this numerical example, we take a directed network as follows:

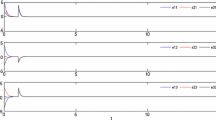
$$ A=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -3 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & -5 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & -5 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & -3 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & -4 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & -5 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 & 1 & 0 & -5 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & -4 & 1 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 1 & -5 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & -5 \end{array}\displaystyle \right ]. $$

The mismatched terms are chosen as \(\Delta(t)=(\sin(t),\cos(t),0)^{T}\), and the initial values are chosen randomly in \((-5,5)\). The corresponding numerical results are shown in Figures 3, 4, 5. The time evolution of lag synchronization error \(E(t)\) is depicted in Figure 3. From Figure 4, the proposed adaptive controllers and update laws can identify the unknown system parameter. Figure 5 shows the curves of the adaptive feedback gains \(d_{i}\) for \(i=1,2,\ldots,10\), which converge to some constants when the lag synchronization is achieved. These results show that the required lag synchronization has been realized with our designed control laws (6). Compared to the linear feedback control, the adaptive control method is better for realizing the lag synchronization and identifying the unknown parameter.

Figure 3
figure 3

Time evolution of the lag synchronization error \(\pmb{E(t)}\) .

Full size image
Figure 4
figure 4

The estimated unknown parameter \(\pmb{\tilde{\theta }=(\tilde{\theta}^{(1)}, \tilde{\theta}^{(2)}, \tilde{\theta}^{(3)})^{T}}\) by adaptive feedback control with \(\pmb{\tau=0.05}\) .

Full size image
Figure 5
figure 5

Time evolution of feedback gains \(\pmb{d_{i}(t)}\) with \(\pmb{h_{i}=10}\) , \(\pmb{i=1,2,\ldots,10}\) .

Full size image

6 Conclusions

In the current study, we have studied lag synchronization in drive-response dynamical networks with an uncertain parameter vector in the node dynamics by the hybrid feedback control method. By employing the linear and adaptive feedback controllers, we have designed two types of control schemes and updated laws for the system parameter and derived two criteria on the lag synchronization. Simultaneously, we have identified the unknown system parameter when the lag synchronization is achieved. In the numerical simulations, we have provided two examples to show the validity of the proposed control schemes. Our hybrid control method is effective for the driving system with parameter perturbation and noise disturbance and it also holds that the disturbance is in the response networks. In the future, how to derive the domain of the lag in the synchronization of drive-response networks is underway.