1 Introduction

A genetic regulatory network (GRN) is a dynamic system to depict the interactions between genes (mRNA) and proteins. Since GRNs play a key role in the area of cell and molecular biology, they have received increasing attention in the community of mathematical biology in recent years (see references [1–10]). An important topic related to mathematical analysis of GRNs is to investigate the stability of GRNs. Wu et al. [1] and Wang [3] conducted robust stability analysis of GRNs by using stochastic analysis approach. Wang et al. [6] investigated the mean-square exponential stability of stochastic GRNs with time-varying delays by constructing a Lyapunov-Krasovskii functional. Although this stability analysis leads to conclusions on whether solutions of GRNs converge to an equilibrium point when a GRN system becomes stable, this analysis does not give the convergence rate of the system. For many GRN systems, slow convergence rates are undesirable, and high convergence rates (e.g., exponential rates) are needed. Therefore, it is necessary to study the exponential stability for a GRN system.

The aim of this study is to investigate the mean-square exponential stability of the solution of a GRN model with diffusion process, impulses, degradation reactions, time-varying delays, and fBm of extrinsic noise. Stability analysis for such a comprehensive GRN model is rare in the literature. For example, Wu et al. [1], Wang [3], Wang et al. [4], and Wang et al. [5] studied the stability and convergence of GRNs with stochastic perturbation and time delays but without diffusion and reaction. Although Ma et al. [9, 10] investigated the asymptotic stability of GRNs with diffusion, reaction, and delays, the systems of their study [9, 10] are deterministic. In [7], finite-time robust stochastic stability was considered under stochastic perturbation, reaction, diffusion, and delays. In addition, like in [1, 3–5], the stochastic perturbation in [7] was described using a standard Brownian motion instead of a fractional Brownian motion.

Our study uses fBm to describe extrinsic noise introduced into the GRNs for mean-square exponential stability analysis, which is a novelty of this paper. We denote an fBm as \(B^{H}(t)\), where H is the Hurst parameter. The fBm has a long-memory in comparison with standard Brownian motion (\(H=\frac{1}{2}\)) [11]. In [12], it was shown that a fractional Brownian motion can be used to describe a subdiffusive dynamics process. Experimental data of chromatin mobilizations show that an fBm is more appropriate to model gene movements than a standard Brownian motion [13]. Therefore, introducing the long-term correlations described by an fBm in GRNs is an important contribution to the literature.

Another contribution of this study is to introduce impulses into stochastic GRNs to describe sudden changes in the amount of mRNA and proteins. According to [14–16], an impulse is referred to the phenomenon that a system state is changed abruptly at a given time. The changes may be caused by abrupt change of physical environments, such as intake of drug or nutriment and exertion of the external force. For example, it was pointed out in [17] that metaphase progression can be controlled by external mechanical impulses through different mechano-chemical cellular reactions. We have not found references of stability analysis of stochastic GRNs with impulses. Therefore, out study differs from the existing studies (e.g., Zhou et al. [7], Wang et al. [4], Ma et al. [9], Han et al. [10]) on the following two aspects: (a) a diffusion-reaction process driven by a fractional Brownian motion is considered, and (b) the impulses are involved.

The rest of this paper is organized as follows: In Section 2, we introduce the impulsive stochastic GRNs and define the exponential stability. Sufficient conditions of exponential stability in the mean-square sense for trivial solutions of GRNs are established in Section 3. Section 4 illustrates our analysis by a numerical example.

2 GRNs and preliminaries

In Section 2.1, we first define a deterministic GRN with time-varying delays and then introduce an impulse and stochastic perturbation into the deterministic model to define the model that is investigated in this study. The preliminaries needed for the exponential stability analysis are given in Section 2.2.

2.1 Deterministic and stochastic GRNs

A deterministic GRN is defined as follows [10]:

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial\tilde{m}_{i}(t,x)}{\partial t} = \sum_{k=1}^{l}\frac {\partial}{\partial x_{k}} (D_{ik}\frac{\partial\tilde {m}_{i}(t,x)}{\partial x_{k}} ) - a_{i}\tilde{m}_{i}(t,x) + \sum_{j=1}^{n} w_{ij}g_{j}(\tilde{p}_{j}(t-\sigma(t),x)) + q_{i}, \\ \frac{\partial\tilde{p}_{i}(t,x)}{\partial t} = \sum_{k=1}^{l}\frac {\partial}{\partial x_{k}} (D_{ik}^{*}\frac{\partial\tilde {p}_{i}(t,x)}{\partial x_{k}} ) - c_{i}\tilde{p}_{i}(t,x) + b_{i}\tilde {m}_{i}(t-\tau(t),x), \quad i=1,2,\ldots,n, \end{array}\displaystyle \right . $$
(1)

where \(\tilde{m}_{i}(t,x)\) and \(\tilde{p}_{i}(t,x)\) denote the concentrations of the ith mRNA and protein, respectively; \(x=(x_{1}, x_{2}, \ldots, x_{l})^{T}\in Q\subset R^{l}\); \(Q = \{x: |x|\leq L_{k}, k=1,2, \ldots, l\}\) is a compact set in \(R^{n}\) with smooth boundary ∂Q; \(L_{k}\) is a positive constant; \(D_{ik}>0\) and \(D_{ik}^{*}>0\) are diffusion coefficient matrices of mRNA and protein, respectively; \(b_{i}\) is a constant; \(a_{i}\) and \(c_{i}\) represent the degradation rates of the mRNA and protein, respectively; \(w_{ij}\) is defined as follows:

$$w_{ij} = \left \{ \textstyle\begin{array}{l@{\quad}l} \delta_{ij}, & j \text{ is an activator of gene } i, \\ -\delta_{ij}, & j \text{ is a repressor of gene } i , \\ 0, & \text{there is no link from gene } j \text{ to } i , \end{array}\displaystyle \right . $$

where \(\delta_{ij}\) is the dimensionless transcriptional rate of transcriptional factor j to gene i; \(g_{j}\) is the activation function of the \(g_{j}(s) = \frac{s^{h}}{1+s^{h}}\), where h is the Hill coefficient; \(q_{i} = \sum_{j\in I_{j}}\delta_{ij}\), where \(I_{j}\) denote the set of all repressors of gene j; and \(\sigma(t)\) and \(\tau(t)\) are the time-varying delays satisfying

$$ \begin{aligned} &0\leq\tau(t)\leq\bar{\tau}, \qquad \dot{\tau}(t)\leq \mu_{1} < 1, \\ &0\leq\sigma(t)\leq\bar{\sigma}, \qquad \dot{\sigma}(t)\leq \mu_{2} < 1, \end{aligned} $$
(2)

where τ̄, σ̄, \(\mu_{1}\), and \(\mu_{2}\) are nonnegative real numbers, and \(\bar{\mu} = \mu_{1}\vee\mu_{2}\) is assumed.

Considering the time delays, we can give the initial conditions associated with (1) as follows:

$$\begin{aligned}& \tilde{m}_{i}(t,x) = \varphi_{i}(t,x),\quad x\in Q, s \in[-d,0], i=1,2,\ldots,n, \\& \tilde{p}_{i}(t,x) = \varphi_{i}^{*}(t,x),\quad x\in Q, s \in[-d,0], i=1,2,\ldots,n, \end{aligned}$$

where \(d = \bar{\sigma}\vee\bar{\tau}\), and \(\varphi_{i}(t,x), \varphi _{i}^{*}(t,x) \in C^{1}([-d,0]\times Q,R)\). Moreover, the following Dirichlet boundary conditions are considered:

$$\begin{aligned}& \tilde{m}_{i}(t,x) = 0,\quad x\in\partial Q, t\in[-d,0], \\& \tilde{p}_{i}(t,x) = 0,\quad x\in\partial Q, t\in[-d,0]. \end{aligned}$$

Let \(m^{*}=(m_{1}^{*}, m_{2}^{*}, \ldots, m_{n}^{*})\) and \(p^{*}=(p_{1}^{*}, p_{2}^{*}, \ldots, p_{n}^{*})\) denote the unique solution of (1) and the equilibrium point \((m^{*}, p^{*})\) of system (1) to the origin. Using the transformations \(m_{i} = \tilde{m}_{i}-m_{i}^{*}\) and \(p_{i} = \tilde{p}_{i}-p_{i}^{*}\) (\(i=1,2,\ldots,n\)), we can transform (1) into the matrix form as follows:

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial m(t,x)}{\partial t} = \sum_{k=1}^{l}\frac{\partial }{\partial x_{k}} (D_{k}\frac{\partial m(t,x)}{\partial x_{k}} ) - Am(t,x) + Wf(p(t-\sigma(t),x)), \\ \frac{\partial p(t,x)}{\partial t} = \sum_{k=1}^{l}\frac{\partial }{\partial x_{k}} (D_{k}^{*}\frac{\partial p(t,x)}{\partial x_{k}} ) - Cp(t,x) + Bm(t-\tau(t),x), \end{array}\displaystyle \right . $$
(3)

where

$$\begin{aligned}& A = \operatorname{diag}(a_{1}, a_{2},\ldots,a_{n}), \qquad B = \operatorname{diag}(b_{1},b_{2}, \ldots,b_{n}),\qquad C = \operatorname{diag}(c_{1}, c_{2},\ldots,c_{n}), \\& D_{k} = \operatorname{diag}(D_{1k}, D_{2k}, \ldots, D_{nk}),\qquad m(t,x) = \bigl(m_{1}(t,x), m_{2}(t,x),\ldots,m_{n}(t,x)\bigr)^{T}, \\& D_{k}^{*} = \operatorname{diag}\bigl(D_{1k}^{*}, D_{2k}^{*}, \ldots, D_{nk}^{*}\bigr),\qquad p(t,x) = \bigl(p_{1}(t,x), p_{2}(t,x),\ldots,p_{n}(t,x) \bigr)^{T}, \\& f\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr) = \bigl(f_{1}\bigl(p\bigl(t- \sigma(t),x\bigr)\bigr), f\bigl(p_{2}\bigl(t-\sigma(t),x\bigr)\bigr), \ldots, f_{n}\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr)\bigr)^{T}, \\& f_{i}\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr) = g_{i} \bigl(p_{i}\bigl(t-\sigma(t),x\bigr)+p_{i}^{*}\bigr) -g_{i}\bigl(p_{i}^{*}\bigr),\quad i=1,2,\ldots,n. \end{aligned}$$

Now we introduce impulses and stochastic perturbation into account, and equations (3) become

$$ \left \{ \textstyle\begin{array}{l} dm(t,x)= \sum_{k=1}^{l}\frac{\partial}{\partial x_{k}} (D_{k}\frac {\partial m(t,x)}{\partial x_{k}} )\,dt - Am(t,x) \,dt+ Wf(p(t-\sigma (t),x))\,dt \\ \hphantom{dm(t,x)={}}{}+ S(t,m(t,x),p(t,x))\,dB^{H}(t),\quad t\neq t_{k}, t\geq0, \\ dp(t,x) = \sum_{k=1}^{l}\frac{\partial}{\partial x_{k}} (D_{k}^{*}\frac{\partial p(t,x)}{\partial x_{k}} )\,dt - Cp(t,x)\,dt + Bm(t-\tau(t),x)\,dt,\quad t\neq t_{k}, t\geq0, \\ \varDelta m(t_{k},x) = m(t_{k}^{+},x)-m(t_{k},x) = U_{k}m(t_{k},x),\quad k\in N, \\ \varDelta p(t_{k},x) = p(t_{k}^{+},x)-m(t_{k},x) = V_{k}p(t_{k},x),\quad k\in N, \end{array}\displaystyle \right . $$
(4)

where \(m(t_{k}^{+},x) = \lim_{t\rightarrow t_{k}^{+}}m(t,x)\), \(p(t_{k}^{+},x) = \lim_{t\rightarrow t_{k}^{+}}p(t,x)\), \(t_{k}\) represent the moments when impulses occur, \(t_{k}< t_{k+1}\), \(\lim_{t\rightarrow\infty} t_{k} =\infty\), and \(B^{H}(t)\) denotes an n-dimensional fBm with Hurst parameter \(H\in (0,\frac{1}{2}]\).

2.2 Preliminaries

In this section, we introduce some necessary definitions, assumptions, and lemmas needed for the subsequent discussion. Let \((\varOmega , \mathscr {F},P)\) be a complete probability space with filtration \(\{\mathscr {F}_{t}\}_{t\geq0}\) satisfying the usual conditions (i.e., it is increasing and right continuous, and \(\mathscr{F}_{0}\) contains all P-null sets). For convenience, let \(A^{T}\) denotes the transpose of a matrix A, \(\lambda_{\max}(A)\) and \(\lambda_{\min}(A)\) denote the largest and smallest eigenvalues of a square matrix A, respectively.

The vector norm \(\Vert \cdot \Vert \) is defined as

$$\begin{aligned}& \bigl\Vert y(t,x)\bigr\Vert = \biggl( \int_{Q}y^{T}(t,x)y(t,x)\,dx \biggr)^{1/2}, \quad \forall y(t,x)\in C^{1}\bigl([0,+\infty]\times Q,R^{n} \bigr), \\& \bigl\Vert z(t,x)\bigr\Vert _{d} = \biggl( \int_{Q}\sup_{-d\leq t\leq0}z^{T}(t,x)z(t,x) \,dx \biggr)^{1/2},\quad \forall z(t,x)\in C^{1}\bigl([-d,0] \times Q,R^{n}\bigr), \end{aligned}$$

and for a real square matrix \(A=(a_{ij})_{n\times n}\), its norm \(\Vert A\Vert _{p}\) (\(p=1,2,\infty\)) is defined as

$$ \Vert A\Vert _{1}=\max_{j}\sum _{i=1}^{n}|a_{ij}|,\qquad \Vert A\Vert _{2}=\sqrt{\lambda_{\max }\bigl(A^{T}A\bigr)}, \qquad \Vert A\Vert _{\infty}=\max_{i}\sum _{j=1}^{n}|a_{ij}|, $$

and we write \(\Vert A\Vert _{p} = \Vert A\Vert \) (\(p=1,2,\infty\)) without causing any confusion.

Definition 1

According to [18], the trivial solution of system (4) with initial values \(\varphi(t,x)\), \(\varphi^{*}(t,x)\in C^{1}([-d,0]\times Q,R^{n})\) is said to be exponentially stable in the mean-square sense if there exist constants \(\alpha, \alpha', M, M' > 0\) such that

$$ E\bigl\Vert m(t,x)\bigr\Vert ^{2}\leq M\Vert \varphi \Vert ^{2}e^{-\alpha t}, \qquad E\bigl\Vert p(t,x)\bigr\Vert ^{2}\leq M'\bigl\Vert \varphi^{*}\bigr\Vert ^{2}e^{-\alpha' t},\quad t\geq0, $$

where

$$ \Vert \varphi \Vert =\sup_{s\in[-\bar{\tau},0],x\in Q} \bigl\Vert m(s,x)\bigr\Vert ,\qquad \bigl\Vert \varphi ^{*}\bigr\Vert =\sup_{s\in[-\bar{\sigma},0],x\in Q} \bigl\Vert p(s,x)\bigr\Vert . $$

Furthermore, we assume that \(\Vert \psi \Vert = \Vert \varphi \Vert \vee \Vert \varphi^{*}\Vert \). As a result, the following lemma follows directly from Green’s second identity [19].

Lemma 1

Let \(R_{1}>0\) and \(R_{2} >0\) be a pair of diagonal matrices. Then

$$\begin{aligned}& \int_{Q}\frac{\partial m^{T}(t,x)}{\partial t}R_{1}\sum _{k=1}^{l}\frac {\partial}{\partial x_{k}} \biggl(D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad = \int_{Q} m^{T}(t,x) R_{1}\sum _{k=1}^{l}\frac{\partial }{\partial x_{k}} \biggl(D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx, \\& \int_{Q}\frac{\partial p^{T}(t,x)}{\partial t}R_{2}\sum _{k=1}^{l}\frac {\partial}{\partial x_{k}} \biggl(D_{k}^{*} \frac{\partial p(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad = \int_{Q} p^{T}(t,x) R_{2}\sum _{k=1}^{l}\frac{\partial }{\partial x_{k}} \biggl(D_{k}^{*} \frac{\partial p(t,x)}{\partial x_{k}} \biggr)\,dx. \end{aligned}$$

Lemma 2

Let \(x,y\in R^{n}\) be two n-dimensional column vectors, and \(A_{3}=(a_{ij})\in R^{n\times n}\) be a positive definite matrix. Then we have

$$ x^{T}A_{3}y \leq x^{T}A_{4}x + y^{T}A_{5}y, $$

where \(A_{4} = \frac{1}{2}\operatorname{diag} ( \sum_{i}|a_{i1}|, \sum_{i}|a_{i2}|, \ldots, \sum_{i}|a_{in}| )\) and \(A_{5} = \frac{1}{2}\operatorname{diag} ( \sum_{i}|a_{1i}|, \sum_{i}|a_{2i}|, \ldots, \sum_{i}|a_{ni}| )\) are positive definite diagonal matrices, and \(|a|\) is the absolute value of a real number a.

Proof

$$\begin{aligned} x^{T}A_{3}y =& (x_{1},\ldots,x_{n}) \left ( { \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} {{a_{11}}}& \cdots&{{a_{1n}}}\\ \vdots&{}& \vdots\\ {{a_{n1}}}& \cdots&{{a_{nn}}} \end{array}\displaystyle } \right )\left ( { \textstyle\begin{array}{@{}c@{}} {{y_{1}}}\\ \vdots\\ {{y_{n}}} \end{array}\displaystyle } \right ) \\ \leq& \frac{1}{2} \bigl[ \bigl(|a_{11}|x_{1}^{2}+|a_{21}|x_{1}^{2}+ \cdots+|a_{n1}|x_{1}^{2} \bigr) + \bigl(|a_{12}|x_{2}^{2}+|a_{22}|x_{2}^{2}+ \cdots+|a_{n2}|x_{2}^{2} \bigr) \\ &{}+\cdots+ \bigl(|a_{1n}|x_{n}^{2}+|a_{2n}|x_{n}^{2}+ \cdots+|a_{nn}|x_{n}^{2} \bigr) \\ &{}+ \bigl(|a_{11}|y_{1}^{2}+|a_{21}|y_{2}^{2}+ \cdots+|a_{n1}|y_{n}^{2} \bigr) + \bigl(|a_{12}|y_{1}^{2}+|a_{22}|y_{2}^{2}+ \cdots+|a_{n2}|y_{n}^{2} \bigr) \\ &{}+\cdots+ \bigl(|a_{1n}|y_{1}^{2}+|a_{2n}|y_{2}^{2}+ \cdots+|a_{nn}|y_{n}^{2} \bigr) \bigr] \\ =& x^{T} \operatorname{diag} \biggl(\frac{1}{2}\sum _{i} {|{a_{i1}}|},\ldots,\frac{1}{2}\sum _{i} {|{a_{in}}|} \biggr)x +y^{T}\operatorname{diag} \biggl(\frac{1}{2}\sum_{i} {|{a_{1i}}|},\ldots,\frac{1}{2}\sum_{i} {|{a_{ni}}|} \biggr)y \\ =& x^{T}A_{4}x + y^{T}A_{5}y. \end{aligned}$$

The proof is completed. □

To investigate the mean-square exponential stability of trivial solution for system (4), we introduce the following conditions:

(A1):

The function \(f(p(t,x))\) satisfies the Lipschitz condition: there exists a positive constant K such that

$$ \bigl\Vert f\bigl(p(t,x)\bigr)-f\bigl(p(s,x)\bigr)\bigr\Vert \leq K\bigl\Vert p(t,x)-p(s,x)\bigr\Vert , \quad \forall s,t\in[0,+\infty). $$
(A2):

The noise intensity \(S(t,m(t,x),p(t,x))\) in equation (4) satisfies the condition

$$\begin{aligned}& \operatorname{trace}\bigl[S^{T}\bigl(t,m(t,x),p(t,x)\bigr)S \bigl(t,m(t,x),p(t,x)\bigr)\bigr] \\& \quad \leq m^{T}(t,x)A_{1}m(t,x)+p^{T}(t,x)A_{2}p(t,x), \end{aligned}$$

where \(A_{1}\) and \(A_{2}\) are known matrices.

(A3):

There exist positive definite matrices \(P_{1}\), \(P_{2}\), \(Q_{1}\), \(Q_{2}\) such that the following linear matrix inequalities are satisfied:

$$ \begin{aligned} &{-}\frac{\pi^{2}}{2}P_{1}D_{L} - 2P_{1}A + 2Q_{3} + \frac{2}{1-\bar{\mu}}Q_{6} + Ht^{2H-1}Q_{1} >0, \\ &{-}\frac{\pi^{2}}{2}P_{2}D_{L}^{*} - 2P_{2}C + 2Q_{5} + \frac{2K}{1-\bar{\mu}}Q_{4} + Ht^{2H-1}Q_{2}>0, \end{aligned} $$
(5)

where \(Q_{3}\), \(Q_{4}\), \(Q_{5}\), \(Q_{6}\) of the same forms as \(A_{4}\), \(A_{5}\) in Lemma 2 are positive definite diagonal matrices, and

$$\begin{aligned}& D_{L} = \operatorname{diag} \Biggl( \sum _{k=1}^{l}\frac{D_{1k}}{L_{k}^{2}}, \sum _{k=1}^{l}\frac {D_{2k}}{L_{k}^{2}}, \ldots,\sum _{k=1}^{l}\frac{D_{nk}}{L_{k}^{2}} \Biggr), \\& D_{L}^{*} = \operatorname{diag} \Biggl( \sum _{k=1}^{l}\frac{D_{1k}^{*}}{L_{k}^{2}}, \sum _{k=1}^{l}\frac{D_{2k}^{*}}{L_{k}^{2}}, \ldots, \sum _{k=1}^{l}\frac {D_{nk}^{*}}{L_{k}^{2}} \Biggr). \end{aligned}$$
(A4):

\(\rho\equiv\sup_{k\in N}(t_{k}-t_{k-1})<\infty\),

$$ 0< \lambda\rho< -\ln \biggl[\lambda_{5}( \beta_{1}+\beta_{2})+\frac{d}{1-\bar{\mu }} ( \lambda_{6}K+\lambda_{7} ) \biggr], $$
(6)

where \(\beta_{1}\equiv\sup_{k\in N}\Vert I+U_{k}\Vert ^{2}\), \(\beta_{2}\equiv\sup_{k\in N}\Vert I+V_{k}\Vert ^{2}\), \(\lambda_{5}=\max\{\lambda_{\max}(P_{1}), \lambda_{\max }(P_{2})\}\), \(\lambda_{6}=\lambda_{\max}(Q_{4})\), \(\lambda_{7}=\lambda_{\max}(Q_{6})\).

(A4∗):

\(\rho\equiv\sup_{k\in N}(t_{k}-t_{k-1})<\infty\), \(0<\lambda\rho <-\ln [\lambda_{5}(\beta_{1}+\beta_{2})+ d ( \lambda_{6}K+\lambda _{7} ) ]\).

(A5):

There exists a positive constant η such that

$$ \frac{\ln(1/\lambda_{4})}{t_{k}-t_{k-1}}\leq\eta\leq\alpha,\quad k=1,2,\ldots, $$
(7)

where \(\lambda_{4}=\min\{\lambda_{\min}(P_{1}), \lambda_{\min}(P_{2}) \}\), and α will be defined in (21).

3 Exponential stability

In this section, we establish conditions of the exponential stability for system (4) by constructing a suitable Lyapunov function.

Theorem 1

If assumptions (A1)-(A5) hold, then the trivial solution of system (4) is globally exponentially stable in the mean-square sense.

Proof

Define a Lyapunov function as follows:

$$ V\bigl(t,m(t,x),p(t,x)\bigr) = V_{1}\bigl(m(t,x),p(t,x)\bigr) + V_{2}(t) + V_{3}(t), $$

where

$$\begin{aligned}& V_{1}\bigl(m(t,x),p(t,x)\bigr) = \int_{Q} \bigl(m^{T}(t,x)P_{1}m(t,x) + p^{T}(t,x)P_{2}p(t,x) \bigr) \,dx, \\& V_{2}(t) = \frac{2}{1-\bar{\mu}} \int_{Q} \int_{t-\sigma (t)}^{t}f^{T}\bigl(p(s,x) \bigr)Q_{4}f\bigl(p(s,x)\bigr)\,ds\,dx, \\& V_{3}(t) = \frac{2}{1-\bar{\mu}} \int_{Q} \int_{t-\tau(t)}^{t} m^{T}(s,x)Q_{6}m(s,x) \,ds\,dx. \end{aligned}$$

Using Itô’s formula, we have

$$\begin{aligned} dV_{1} =& 2 \int_{Q} m^{T}(t,x)P_{1} \Biggl[\sum _{k=1}^{l}\frac{\partial }{\partial x_{k}} \biggl(D_{k}\frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dt - Am(t,x) \,dt \\ &{} + Wf\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr)\,dt + S\bigl(t,m(t,x),p(t,x) \bigr)\,dB^{H}(t) \Biggr]\,dx \\ &{} + Ht^{2H-1} \int_{Q} \operatorname{trace} \bigl(S^{T} \bigl(t,m(t,x),p(t,x)\bigr)P_{1}S\bigl(t,m(t,x),p(t,x)\bigr) \bigr)\,dx \,dt \\ &{}+ 2 \int_{Q} p^{T}(t,x)P_{2} \Biggl[\sum _{k=1}^{l}\frac{\partial}{\partial x_{k}} \biggl(D_{k}^{*}\frac{\partial p(t,x)}{\partial x_{k}} \biggr) - Cp(t,x) + Bm\bigl(t- \tau(t),x\bigr) \Biggr]\,dx\,dt \\ =& 2\sum_{k=1}^{l} \int_{Q} m^{T}(t,x)P_{1}\frac{\partial}{\partial x_{k}} \biggl(D_{k}\frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx\,dt -2 \int _{Q}m^{T}(t,x)P_{1}Am(t,x)\,dx\,dt \\ &{} + 2 \int_{Q} m^{T}(t,x)P_{1}Wf\bigl(p\bigl(t- \sigma(t),x\bigr)\bigr)\,dx\,dt +2 \int_{Q} p^{T}(t,x)P_{2}Bm\bigl(t- \tau(t),x\bigr)\,dx\,dt \\ &{} + 2\sum_{k=1}^{l} \int_{Q} p^{T}(t,x)P_{2}\frac{\partial}{\partial x_{k}} \biggl(D_{k}^{*}\frac{\partial p(t,x)}{\partial x_{k}} \biggr)\,dx\,dt -2 \int _{Q} p^{T}(t,x)P_{2}Cp(t,x)\,dx\,dt \\ &{} + Ht^{2H-1} \int_{Q} \operatorname{trace} \bigl(S^{T} \bigl(t,m(t,x),p(t,x)\bigr)P_{1}S\bigl(t,m(t,x),p(t,x)\bigr) \bigr)\,dx \,dt \\ &{} + 2 \int_{Q} S\bigl(t,m(t,x),p(t,x)\bigr)\,dx\,dB^{H}(t). \end{aligned}$$
(8)

According to the Dirichlet boundary conditions, Green’s formula, and Lemma 1, we have

$$\begin{aligned}& 2\sum_{k=1}^{l} \int_{Q} m^{T}(t,x)P_{1}\frac{\partial}{\partial x_{k}} \biggl(D_{k}\frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad = 2\sum_{k=1}^{l} \int_{Q} \frac{\partial}{\partial x_{k}} \biggl( m^{T}(t,x)P_{1}D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \qquad {}-2\sum_{k=1}^{l} \int_{Q} \biggl( \frac{\partial m^{T}(t,x)}{\partial x_{k}}P_{1}D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad = 2\sum_{k=1}^{l} \int_{\partial Q} \biggl( m^{T}(t,x)P_{1}D_{k} \frac {\partial m(t,x)}{\partial x_{k}} \biggr)_{k=1}^{l}\cdot\mathbf{n}\,dx \\& \qquad {}-2\sum _{k=1}^{l} \int_{Q} \biggl( \frac{\partial m^{T}(t,x)}{\partial x_{k}}P_{1}D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad = -2\sum_{k=1}^{l} \int_{Q} \biggl( \frac{\partial m^{T}(t,x)}{\partial x_{k}}P_{1}D_{k} \frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \\& \quad \leq-\frac{\pi ^{2}}{2} \int_{Q} m^{T}(t,x)P_{1}D_{L}m(t,x) \,dx, \end{aligned}$$
(9)

where n denotes the outer normal vector of ∂Q, and

$$\begin{aligned}& \biggl( m^{T}(t,x)P_{1}D_{k}\frac{\partial m(t,x)}{\partial x_{k}} \biggr)_{k=1}^{l} \\& \quad = \biggl( m^{T}(t,x)P_{1}D_{1} \frac{\partial m(t,x)}{\partial x_{1}}, m^{T}(t,x)P_{1}D_{2} \frac{\partial m(t,x)}{\partial x_{2}}, \ldots, m^{T}(t,x)P_{1}D_{l} \frac{\partial m(t,x)}{\partial x_{l}} \biggr). \end{aligned}$$

Similarly, we get

$$ 2\sum_{k=1}^{l} \int_{Q} p^{T}(t,x)P_{2}\frac{\partial}{\partial x_{k}} \biggl(D_{k}^{*}\frac{\partial m(t,x)}{\partial x_{k}} \biggr)\,dx \leq-\frac{\pi^{2}}{2} \int_{Q} p^{T}(t,x)P_{2}D_{L}^{*}p(t,x) \,dx. $$
(10)

Substituting (9) and (10) into (8) and using Lemma 2, we obtain

$$\begin{aligned} dV_{1} \leq& -\frac{\pi^{2}}{2} \int_{Q} m^{T}(t,x)P_{1}D_{L}m(t,x) \,dx\,dt -2 \int _{Q}m^{T}(t,x)P_{1}Am(t,x)\,dx\,dt \\ &{} + 2 \int_{Q}m^{T}(t,x)Q_{3}m(t,x)\,dx\,dt + 2 \int_{Q} f^{T}\bigl(p\bigl(t-\sigma (t),x\bigr) \bigr)Q_{4}f\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr)\,dx\,dt \\ &{} - \frac{\pi^{2}}{2} \int_{Q} p^{T}(t,x)P_{2}D_{L}^{*}p(t,x) \,dx\,dt -2 \int_{Q} p^{T}(t,x)P_{2}Cp(t,x)\,dx\,dt \\ &{} + 2 \int_{Q} p^{T}(t,x)Q_{5}p(t,x)\,dx\,dt + \int_{Q} m^{T}\bigl(t-\tau(t),x\bigr)Q_{6}m \bigl(t-\tau (t),x\bigr)\,dx\,dt \\ &{} + Ht^{2H-1} \int_{Q} m^{T}(t,x)Q_{1}m(t,x)\,dx\,dt + Ht^{2H-1} \int_{Q} p^{T}(t,x)Q_{2}p(t,x)\,dx\,dt \\ &{} + 2 \int_{Q} S\bigl(t,m(t,x),p(t,x)\bigr)\,dx\,dB^{H}(t). \end{aligned}$$
(11)

Now, we calculate the differential of \(V_{2}(t)\) and \(V_{3}(t)\):

$$\begin{aligned} dV_{2} =& \frac{2}{1-\bar{\mu}} \int_{Q} f^{T}\bigl(p(t,x)\bigr)Q_{4}f \bigl(p(t,x)\bigr)\,dx\,dt \\ &{}-\frac{2(1-\dot{\sigma}(t))}{1-\bar{\mu}} \int_{Q} f^{T}\bigl(p\bigl(t-\sigma (t),x\bigr) \bigr)Q_{4}f\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr)\,dx\,dt \\ \leq& \frac{2K}{1-\bar{\mu}} \int_{Q} p^{T}(t,x)Q_{4}p(t,x)\,dx\,dt \\ &{}- 2 \int_{Q} f^{T}\bigl(p\bigl(t-\sigma(t),x\bigr) \bigr)Q_{4}f\bigl(p\bigl(t-\sigma(t),x\bigr)\bigr)\,dx\,dt, \end{aligned}$$
(12)

and

$$\begin{aligned} dV_{3} =& \frac{2}{1-\bar{\mu}} \int_{Q} m^{T}(t,x)Q_{6}m(t,x)\,dx\,dt \\ &{}- \frac{2(1-\dot{\tau}(t))}{1-\bar{\mu}} \int_{Q} m^{T}\bigl(t-\tau (t),x \bigr)Q_{6}m\bigl(t-\tau(t),x\bigr)\,dx\,dt \\ \leq& \frac{2}{1-\bar{\mu}} \int_{Q} m^{T}(t,x)Q_{6}m(t,x)\,dx\,dt \\ &{}- 2 \int_{Q} m^{T}\bigl(t-\tau(t),x\bigr)Q_{6}m \bigl(t-\tau(t),x\bigr)\,dx\,dt, \end{aligned}$$
(13)

where Lemma 2 is applied. Combining (11), (12), and (13) and taking the expectation of both sides, we derive that

$$\begin{aligned} \mathbb{E}\,dV =& \sum_{i=1}^{3} \mathbb{E}\,dV_{i} \\ \leq& -\frac{\pi^{2}}{2} \mathbb{E} \int_{Q} m^{T}(t,x)P_{1}D_{L}m(t,x) \,dx\,dt -2\mathbb{E} \int_{Q}m^{T}(t,x)P_{1}Am(t,x)\,dx\,dt \\ &{} + 2\mathbb{E} \int_{Q}m^{T}(t,x)Q_{3}m(t,x)\,dx\,dt + \frac{2K}{1-\bar{\mu }}\mathbb{E} \int_{Q} p^{T}(t,x)Q_{4}p(t,x)\,dx\,dt \\ &{} -\frac{\pi^{2}}{2} \mathbb{E} \int_{Q} p^{T}(t,x)P_{2}D_{L}^{*}p(t,x) \,dx\,dt -2\mathbb{E} \int_{Q} p^{T}(t,x)P_{2}Cp(t,x)\,dx\,dt \\ &{} +2\mathbb{E} \int_{Q} p^{T}(t,x)Q_{5}p(t,x)\,dx\,dt + \frac{2}{1-\bar{\mu }}\mathbb{E} \int_{Q} m^{T}(t,x)Q_{6}m(t,x)\,dx\,dt \\ &{} +Ht^{2H-1}\mathbb{E} \int_{Q} m^{T}(t,x)Q_{1}m(t,x)\,dx\,dt \\ &{}+ Ht^{2H-1}\mathbb {E} \int_{Q} p^{T}(t,x)Q_{2}p(t,x)\,dx\,dt \\ =& \mathbb{E} \int_{Q} m^{T}(t,x)\varPi _{1}m(t,x)\,dx\,dt + \mathbb{E} \int_{Q} p^{T}(t,x)\varPi _{2}p(t,x)\,dx\,dt, \end{aligned}$$
(14)

where \(\varPi _{1} = -\frac{\pi^{2}}{2}P_{1}D_{L} - 2P_{1}A + 2Q_{3} + \frac{2}{1-\bar {\mu}}Q_{6} + Ht^{2H-1}Q_{1}\), \(\varPi _{2} = -\frac{\pi^{2}}{2}P_{2}D_{L}^{*} - 2P_{2}C + 2Q_{5} + \frac{2K}{1-\bar{\mu}}Q_{4} + Ht^{2H-1}Q_{2}\). This implies that

$$\begin{aligned} \mathbb{E}\,dV \leq&\lambda_{1}\mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} + \lambda_{2}\mathbb {E}\bigl\Vert p(t,x)\bigr\Vert ^{2} \\ \leq&\lambda_{3} \bigl( \mathbb{E} \bigl\Vert m(t,x)\bigr\Vert ^{2} + \mathbb {E}\bigl\Vert p(t,x) \bigr\Vert ^{2} \bigr), \end{aligned}$$
(15)

where \(\lambda_{1} = \lambda_{\max}(\varPi _{1})\), \(\lambda_{2} = \lambda_{\max }(\varPi _{2})\), and \(\lambda_{3} = \max\{\lambda_{1}, \lambda_{2}\}\).

On the other hand, for \(V(t,m(t,x),p(t,x))\), we have the estimates

$$\begin{aligned} \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr) \geq& \mathbb{E}V_{1} \bigl(m(t,x),p(t,x)\bigr) \\ =& \mathbb{E} \int_{Q} \bigl(m^{T}(t,x)P_{1}m(t,x) + p^{T}(t,x)P_{2}p(t,x) \bigr)\,dx \\ \geq &\lambda_{4}\bigl(\mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} + \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2}\bigr) \end{aligned}$$

and

$$\begin{aligned} \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq& \lambda_{5}\bigl( \mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} + \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2}\bigr) \\ &{}+\frac{\lambda_{6}K}{1-\bar{\mu}} \int_{t_{k}-\sigma (t_{k})}^{t_{k}}\mathbb{E}\bigl\Vert p(s,x)\bigr\Vert ^{2}\,ds \\ &{}+ \frac{\lambda_{7}}{1-\bar{\mu}} \int_{t_{k}-\tau(t_{k})}^{t_{k}}\mathbb {E}\bigl\Vert m(s,x)\bigr\Vert ^{2}\,ds,\quad k=0,1,2,\ldots, \end{aligned}$$
(16)

where \(\lambda_{5}\), \(\lambda_{6}\), \(\lambda_{7}\), and \(\lambda_{4}\) were defined in assumption (A4) and (A5), respectively. Thus, we obtain

$$ \mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} + \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2} \leq\frac{1}{\lambda _{4}} \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr). $$
(17)

Substituting (17) into (15), we have

$$\begin{aligned} \mathbb{E}\,dV\bigl(t,m(t,x),p(t,x)\bigr) \leq&\frac{\lambda_{3}}{\lambda_{4}} \mathbb {E}V\bigl(t,m(t,x),p(t,x)\bigr)\,dt \\ \equiv&\lambda\mathbb{E}V \bigl(t,m(t,x),p(t,x)\bigr)\,dt, \end{aligned}$$
(18)

where \(\lambda=\frac{\lambda_{3}}{\lambda_{4}}\). Integrating the both sides of inequality (18) from \(t_{k-1}\) to t (\(t\in(t_{k-1},t_{k}]\), \(k=1,2,\ldots\)), we obtain

$$ \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq V\bigl(0,m(0,x),p(0,x) \bigr)\cdot e^{\lambda t},\quad t\in[0,t_{1}], $$
(19)

and

$$\begin{aligned}& \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr) \\& \quad \leq V\bigl(t_{k-1}^{+},m \bigl(t_{k-1}^{+},x\bigr),p\bigl(t_{k-1}^{+},x\bigr)\bigr)\cdot e^{\lambda (t-t_{k-1})},\quad t\in(t_{k-1},t_{k}], k=2,3,\ldots. \end{aligned}$$
(20)

We define the function r as follows:

$$ r(z) = (z+\lambda)\rho+ \ln \biggl[\lambda_{5}(\beta_{1}+ \beta_{2})+\frac {d}{1-\bar{\mu}} ( \lambda_{6}K + \lambda_{7} )e^{zd} \biggr],\quad z\in [0,+\infty). $$

Then, we have

$$ r'(z) = \rho+ \frac{d^{2}(\lambda_{6}K + \lambda_{7})e^{zd}}{\lambda _{5}(1-\bar{\mu})(\beta_{1}+\beta_{2})+d(\lambda_{6}K + \lambda_{7})e^{zd}}>0,\quad z\in[0,\infty), $$

and \(r(z)\rightarrow+\infty\) (\(z\rightarrow+\infty\)). Moreover, from (6) we have \(r(0)<0\). Thus, there exists a unique positive number α such that \(r(\alpha) = 0\), that is,

$$ (\alpha+\lambda)\rho= -\ln \biggl[\lambda_{5}( \beta_{1}+\beta_{2})+\frac {d}{1-\bar{\mu}} ( \lambda_{6}K + \lambda_{7} )e^{\alpha d} \biggr]. $$
(21)

For \(t\in[0,t_{1}]\), we have by (19) that

$$\begin{aligned} \begin{aligned} \mathbb{E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq{}& \lambda_{5}\bigl( \mathbb{E}\bigl\Vert m(0,x)\bigr\Vert ^{2} + \mathbb{E}\bigl\Vert p(0,x)\bigr\Vert ^{2}\bigr) \\ &{}+\frac{\lambda_{6}K}{1-\bar{\mu}} \int_{-\sigma (0)}^{0}\mathbb{E}\bigl\Vert p(s,x)\bigr\Vert ^{2}\,ds \\ &{} + \frac{\lambda_{7}}{1-\bar{\mu}} \int_{-\tau(0)}^{0}\mathbb {E}\bigl\Vert m(s,x)\bigr\Vert ^{2}\,ds \\ \leq{}& \biggl(2\lambda_{5} + \frac{d}{1-\bar{\mu}}(\lambda_{6}K + \lambda_{7}) \biggr)\Vert \psi \Vert ^{2}e^{\lambda t}. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} \leq& \frac{1}{\lambda_{4}}\mathbb {E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq\frac{1}{\lambda_{4}} \biggl(2\lambda_{5} + \frac {d}{1-\bar{\mu}}(\lambda_{6}K + \lambda_{7}) \biggr)\Vert \psi \Vert ^{2}e^{\lambda t} \\ =& \frac{1}{\lambda_{4}} \biggl(2\lambda_{5} + \frac{d}{1-\bar{\mu}}( \lambda _{6}K + \lambda_{7}) \biggr)e^{(\lambda+\alpha)\rho} \Vert \psi \Vert ^{2}e^{-\alpha\rho } \\ \leq& \frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha t}, \quad t\in[0,t_{1}], \end{aligned}$$
(22)

where \(M_{1} = (2\lambda_{5} + \frac{d}{1-\bar{\mu}}[\lambda_{6}K + \lambda_{7}] )e^{(\lambda+\alpha)\rho}>0\), and α is defined in (21). Similarly, we can conclude that

$$ \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2} \leq M_{1}\Vert \psi \Vert ^{2}e^{-\alpha t},\quad t \in[0,t_{1}]. $$
(23)

Equations (22) and (23) then yield

$$ \begin{aligned} &\sup_{t_{1}-\tau(t_{1})\leq s\leq t_{1},x\in Q}\mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2}\leq \frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha(t_{1}-\tau(t_{1}))} \leq\frac {M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha t_{1}}e^{\alpha\bar{\tau}}, \\ &\sup_{t_{1}-\sigma(t_{1})\leq s\leq t_{1},x\in Q}\mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2}\leq \frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha(t_{1}-\sigma(t_{1}))} \leq\frac {M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha t_{1}}e^{\alpha\bar{\sigma}}. \end{aligned} $$
(24)

From the last two equations of system (4) we conclude that

$$\begin{aligned}& \mathbb{E}\bigl\Vert m\bigl(t_{k}^{+},x\bigr)\bigr\Vert ^{2}=\mathbb{E}\bigl\Vert (I+U_{k})m(t_{k},x) \bigr\Vert ^{2} \\& \hphantom{\mathbb{E}\bigl\Vert m\bigl(t_{k}^{+},x\bigr)\bigr\Vert ^{2}}\leq \bigl\Vert (I+U_{k})\bigr\Vert ^{2}\cdot\mathbb{E}\bigl\Vert m(t_{k},x)\bigr\Vert ^{2}\leq\beta_{1}\mathbb {E}\bigl\Vert m(t_{k},x) \bigr\Vert ^{2}, \\& \mathbb{E}\bigl\Vert p\bigl(t_{k}^{+},x\bigr)\bigr\Vert ^{2}=\mathbb{E}\bigl\Vert (I+V_{k})p(t_{k},x) \bigr\Vert ^{2} \\& \hphantom{\mathbb{E}\bigl\Vert p\bigl(t_{k}^{+},x\bigr)\bigr\Vert ^{2}}\leq \bigl\Vert (I+V_{k})\bigr\Vert ^{2}\cdot\mathbb{E}\bigl\Vert p(t_{k},x)\bigr\Vert ^{2}\leq\beta_{2}\mathbb {E}\bigl\Vert p(t_{k},x) \bigr\Vert ^{2}, \\& \quad k=1,2,\ldots. \end{aligned}$$
(25)

Thus, according to (21)-(25), we have

$$\begin{aligned}& \mathbb{E}V\bigl(t_{1}^{+},m\bigl(t_{1}^{+},x \bigr),p\bigl(t_{1}^{+},x\bigr)\bigr) \\& \quad \leq \lambda_{5}\bigl(\mathbb{E}\bigl\Vert m \bigl(t_{1}^{+},x\bigr)\bigr\Vert ^{2}+\mathbb {E}\bigl\Vert p\bigl(t_{1}^{+},x\bigr)\bigr\Vert ^{2}\bigr) \\& \qquad {}+ \frac{\lambda_{6}K}{1-\bar{\mu}} \int_{t_{1}-\sigma(t_{1})}^{t_{1}} \mathbb {E}\bigl\Vert p(s,x)\bigr\Vert ^{2}\,ds +\frac{\lambda_{7}}{1-\bar{\mu}} \int_{t_{1}-\tau(t_{1})}^{t_{1}}\mathbb {E}\bigl\Vert m(s,x)\bigr\Vert ^{2}\,ds \\& \quad \leq \lambda_{5}\bigl(\beta_{1}\mathbb{E}\bigl\Vert m(t_{1},x)\bigr\Vert ^{2}+\beta_{2}\mathbb {E} \bigl\Vert p(t_{1},x)\bigr\Vert ^{2}\bigr) \\& \qquad {}+ \frac{\lambda_{6}K}{1-\bar{\mu}} \int_{t_{1}-\sigma(t_{1})}^{t_{1}} \mathbb {E}\bigl\Vert p(s,x)\bigr\Vert ^{2}\,ds +\frac{\lambda_{7}}{1-\bar{\mu}} \int_{t_{1}-\tau(t_{1})}^{t_{1}}\mathbb {E}\bigl\Vert m(s,x)\bigr\Vert ^{2}\,ds \\& \quad \leq \biggl[\lambda_{5}(\beta_{1} + \beta_{2}) + \frac{\lambda_{6} K\bar{\sigma }}{1-\bar{\mu}}e^{\alpha\bar{\sigma}} + \frac{\lambda_{7}\bar{\tau }}{1-\bar{\mu}}e^{\alpha\bar{\tau}} \biggr]\frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha t_{1}} \\& \quad \leq \biggl[\lambda_{5}(\beta_{1} + \beta_{2}) + \frac{d}{1-\bar{\mu}} (\lambda_{6}K+ \lambda_{7} )e^{\alpha d} \biggr]\frac{M_{1}}{\lambda _{4}}\Vert \psi \Vert ^{2}e^{-\alpha t_{1}} \\& \quad = e^{-(\lambda+\alpha)\rho}\frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-\alpha t_{1}}. \end{aligned}$$
(26)

Now, we will show that

$$ \mathbb{E}V\bigl(t_{k}^{+},m\bigl(t_{k}^{+},x \bigr),p\bigl(t_{k}^{+},x\bigr)\bigr) \leq e^{-(\lambda+\alpha)\rho } \frac{M_{1}}{\lambda_{4}^{k}}\Vert \psi \Vert ^{2}e^{-\alpha t_{k}},\quad k=1,2, \ldots. $$
(27)

It is obvious that (27) is true when \(k=1\) by (26). We assume that (27) holds for \(k=i\), that is,

$$ \mathbb{E}V\bigl(t_{i}^{+},m\bigl(t_{i}^{+},x\bigr),p \bigl(t_{i}^{+},x\bigr)\bigr) \leq e^{-(\lambda+\alpha)\rho }\frac{M_{1}}{\lambda_{4}^{i}} \Vert \psi \Vert ^{2}e^{-\alpha t_{i}}. $$

Then, for \(t\in(t_{i},t_{i+1}]\), we get

$$\begin{aligned} \mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} \leq& \frac{1}{\lambda_{4}}\mathbb {E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq\frac{1}{\lambda_{4}} \mathbb {E}V\bigl(t_{i}^{+},m\bigl(t_{i}^{+},x\bigr),p \bigl(t_{i}^{+},x\bigr)\bigr)e^{\lambda(t-t_{i})} \\ \leq& e^{-(\lambda+\alpha)\rho}\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i}}e^{\lambda\rho} = e^{-\alpha\rho} \frac{M_{1}}{\lambda _{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i}} \\ \leq& e^{-\alpha(t-t_{i})}\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i}} =\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t}. \end{aligned}$$
(28)

Similarly, we have

$$ \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2} \leq \frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t}. $$
(29)

In addition, from (28) and (29) it follows directly that

$$ \begin{aligned} &\sup_{t_{i+1}-\bar{\tau}\leq s\leq t_{i+1},x\in Q}\mathbb {E} \bigl\Vert m(t,x)\bigr\Vert ^{2}\leq\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha (t_{i+1}-\tau(t_{i+1}))} \leq\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i+1}}e^{\alpha\bar{\tau}}, \\ &\sup_{t_{i+1}-\bar{\sigma}\leq s\leq t_{i+1},x\in Q}\mathbb {E}\bigl\Vert p(t,x)\bigr\Vert ^{2}\leq\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha (t_{i+1}-\sigma(t_{i+1}))} \leq\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i+1}}e^{\alpha\bar{\sigma}}. \end{aligned} $$
(30)

By (21), (25), and (28)-(30) we obtain

$$\begin{aligned}& \mathbb{E}V\bigl(t_{i+1}^{+},m\bigl(t_{i+1}^{+},x\bigr),p \bigl(t_{i+1}^{+},x\bigr)\bigr) \\& \quad = \lambda_{5} \bigl[\mathbb{E}\bigl\Vert m \bigl(t_{i+1}^{+},x\bigr)\bigr\Vert ^{2}+\mathbb {E}\bigl\Vert p\bigl(t_{i+1}^{+},x\bigr)\bigr\Vert ^{2} \bigr]+ \frac{\lambda_{6}K}{1-\bar{\mu}} \int _{t_{i+1}-\sigma(t_{i+1})}^{t_{i+1}}\mathbb{E}\bigl\Vert p(s,t)\bigr\Vert ^{2}\,ds \\& \qquad {} +\frac{1}{1-\bar{\mu}} \int_{t_{i+1}-\tau(t_{i+1})}^{t_{i+1}}\mathbb {E}\bigl\Vert m(s,t)\bigr\Vert ^{2}\,ds \\& \quad \leq \lambda_{5} \bigl[\beta_{1}\mathbb{E}\bigl\Vert m(t_{i+1},x)\bigr\Vert ^{2}+\beta_{2} \mathbb {E}\bigl\Vert p(t_{i+1},x)\bigr\Vert ^{2} \bigr] \\& \qquad {}+ \frac{\lambda_{6}K}{1-\bar{\mu}} \int _{t_{i+1}-\sigma(t_{i+1})}^{t_{i+1}}\mathbb{E}\bigl\Vert p(s,t)\bigr\Vert ^{2}\,ds \\& \qquad {} +\frac{\lambda_{7}}{1-\bar{\mu}} \int_{t_{i+1}-\tau (t_{i+1})}^{t_{i+1}}\mathbb{E}\bigl\Vert m(s,t)\bigr\Vert ^{2}\,ds \\& \quad \leq \biggl[\lambda_{5}(\beta_{1} + \beta_{2}) + \frac{\lambda_{6}K\bar{\sigma }}{1-\bar{\mu}}e^{\alpha\bar{\sigma}} + \frac{\lambda_{7}\bar{\tau }}{1-\bar{\mu}}e^{\alpha\bar{\tau}} \biggr]\frac{M_{1}}{\lambda _{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i+1}} \\& \quad \leq \biggl[\lambda_{5}(\beta_{1} + \beta_{2}) + \frac{d}{1-\bar{\mu}} (\lambda_{6}K \lambda_{7} )e^{\alpha d} \biggr]\frac{M_{1}}{\lambda _{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i+1}} \\& \quad = e^{-(\lambda+\alpha)\rho}\frac{M_{1}}{\lambda_{4}^{i+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{i+1}}, \end{aligned}$$

which shows that (27) holds for \(k = i+1\). Therefore, (27) is true for every \(k=1,2,\ldots \) . Hence, for \(t\in(t_{k},t_{k+1}]\), we can conclude by (27) that

$$\begin{aligned} \mathbb{E}\bigl\Vert m(t,x)\bigr\Vert ^{2} \leq& \frac{1}{\lambda_{4}}\mathbb {E}V\bigl(t,m(t,x),p(t,x)\bigr) \leq\frac{1}{\lambda_{4}} \mathbb{E} V\bigl(t_{k}^{+},m\bigl(t_{k}^{+},x\bigr),p \bigl(t_{k}^{+},x\bigr)\bigr)e^{\lambda(t-t_{k})} \\ \leq& e^{-(\lambda+\alpha)\rho}\frac{M_{1}}{\lambda_{4}^{k+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{k}}e^{\lambda\rho} =e^{-\alpha\rho} \frac{M_{1}}{\lambda _{4}^{k+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{k}} \\ \leq& e^{-\alpha(t-t_{k})}\frac{M_{1}}{\lambda_{4}^{k+1}}\Vert \psi \Vert ^{2}e^{-\alpha t_{k}} =\frac{M_{1}}{\lambda_{4}^{k+1}}\Vert \psi \Vert ^{2}e^{-\alpha t} \\ \leq& \frac{M_{1}}{\lambda_{4}}e^{\eta t_{k}}\Vert \psi \Vert ^{2}e^{-\alpha t} \leq \frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-(\alpha-\eta) t},\quad k=1,2,\ldots. \end{aligned}$$
(31)

Similarly, we have

$$ \mathbb{E}\bigl\Vert p(t,x)\bigr\Vert ^{2} \leq \frac{M_{1}}{\lambda_{4}^{k+1}}\Vert \psi \Vert ^{2}e^{-\alpha t} \leq \frac{M_{1}}{\lambda_{4}}\Vert \psi \Vert ^{2}e^{-(\alpha-\eta) t}, \quad k=1,2, \ldots, $$
(32)

which, together with (22), (23), and (31), show that the trivial solution of system (4) is globally exponentially stable in the mean square sense. □

Remark 1

If the time delays are constant functions with respect to t, that is, \(\tau(t) =\tau\), \(\sigma(t) = \sigma\), then Theorem 1 reduces to the following result.

Corollary 1

If assumptions (A1)-(A3), (A4∗), and (A5) hold, then the trivial solution of system (4) with \(\tau(t) =\tau\), \(\sigma(t) = \sigma\) is globally exponentially stable in the mean-square sense.

Remark 2

Because the fBm becomes the standard Brownian motion when \(H = \frac{1}{2}\), the exponential stability conditions derived in Theorem 1 for the GRNs with fBm will become mean-square exponential stability conditions for the GRNs with standard Brownian motion, which, to the best our knowledge, has not been reported in the literature. Based on Theorem 1, the following result for the GRNs with standard Brownian motion can be obtained.

Corollary 2

If assumptions (A1), (A2), (A4), and (A5) hold and Eq. (5) in (A3) is replaced by the equations

$$\begin{aligned}& -\frac{\pi^{2}}{2}P_{1}D_{L} - 2P_{1}A + 2Q_{3} + \frac{2}{1-\bar{\mu}}Q_{6} + \frac{1}{2}Q_{1} >0, \\& -\frac{\pi^{2}}{2}P_{2}D_{L}^{*} - 2P_{2}C + 2Q_{5} + \frac{2K}{1-\bar{\mu}}Q_{4} + \frac{1}{2}Q_{2}>0, \end{aligned}$$

then the trivial solution of system (4) is globally exponentially stable in the mean-square sense.

4 Numerical simulations

In this section, we illustrate our results in a numerical example. Without loss of generality, we consider a two-dimensional system (\(n=2\), \(l=1\)) and choose the parameters of system (4) as follows:

$$\begin{aligned}& A = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.2 & 0\\ 0 & 0.3 \end{array}\displaystyle \right ],\qquad B = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.2 & 0\\ 0 & 0.2 \end{array}\displaystyle \right ], \\& C = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.5 & 0\\ 0 & 0.4 \end{array}\displaystyle \right ],\qquad D = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.1 & 0\\ 0 & 0.2 \end{array}\displaystyle \right ], \\& D_{k}^{*} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.2 & 0\\ 0 & 0.2 \end{array}\displaystyle \right ],\qquad U_{k} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.15 & 0\\ 0 & 0.15 \end{array}\displaystyle \right ], \\& V_{k} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.1 & 0\\ 0 & 0.1 \end{array}\displaystyle \right ],\qquad W = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.3 & 0\\ 0 & 0.2 \end{array}\displaystyle \right ], \\& \sigma(t) = \left [ \textstyle\begin{array}{@{}c@{}} 0.1+0.2|\sin t|\\ 0.1+0.1|\sin t| \end{array}\displaystyle \right ],\qquad \tau(t) = \left [ \textstyle\begin{array}{@{}c@{}} 0.1+0.1|\sin t|\\ 0.1+0.2|\sin t| \end{array}\displaystyle \right ], \\& f(x) = \frac{x^{2}}{1+x^{2}},\qquad t_{k}=0.2k, \qquad H=0.4, \qquad S(t,m,p) = -0.1(m+p). \end{aligned}$$

By using MATLAB to solve the inequalities given in conditions (A1)-(A5), we get the following feasible solution:

$$\begin{aligned}& P_{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.1005 & 0\\ 0 & 0.1201 \end{array}\displaystyle \right ],\qquad P_{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.1526 & 0\\ 0 & 0.1628 \end{array}\displaystyle \right ], \\& Q_{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 2.2341 & 0\\ 0 & 3.6024 \end{array}\displaystyle \right ],\qquad Q_{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 4.0292 & 0\\ 0 & 2.8485 \end{array}\displaystyle \right ], \\& \varPi _{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.3761 & 0\\ 0 & 0.4841 \end{array}\displaystyle \right ],\qquad \varPi _{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.5773 & 0\\ 0 & 0.2709 \end{array}\displaystyle \right ]. \end{aligned}$$

We know that the conditions of Theorem 1 are satisfied. By Theorem 1 we can conclude that the trivial solution of system (4) is exponential stability in the mean-square sense.

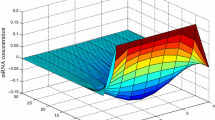
In order to show the exponential stability of the trivial solution of system (4), the system is solved numerically using the Euler method. The numerical results are presented in Figures 1-4. Figures 1(b), 2(b), 3(b), 4(b) plot the exponential stability of the trivial solution at \(x=0.2\). The four figures show that the concentrations of both mRNA and protein are exponentially stable, indicating effectiveness of the results derived in Theorem 1.

Figure 1
figure 1

Contour plot and sectional view of mRNA concentration \(\pmb{m_{1}(t,x)}\) .

Full size image
Figure 2
figure 2

Contour plot and sectional view of mRNA concentration \(\pmb{m_{2}(t,x)}\) .

Full size image
Figure 3
figure 3

Contour plot and sectional view of protein concentration \(\pmb{p_{1}(t,x)}\) .

Full size image
Figure 4
figure 4

Contour plot of and sectional view protein concentration \(\pmb{p_{2}(t,x)}\) .

Full size image

5 Conclusions

In this paper, we analyze the mean-square exponential stability for the comprehensive GRNs with (a) diffusion-reaction, (b) time-varying delay, (c) impulsive control, and (d) fBm for extrinsic noise. The stability analysis is a more challenging than the previous analysis reported in the literature that considered only one or two of the four model components. Our derived conditions of the mean-square exponential stability have a simple form and can be used for evaluating the exponential stability of GRNs in a numerically straightforward manner.