1 Introduction

In order to explain the complex dynamic behavior of genetic regulatory systems, the authors of [1] presented a model of ordinary differential system for the transcript factors (TFs). Furthermore, taking account of the delay between changes in the transcription rate of either gene and changes in the concentration of the corresponding protein, Smolen et al. [2] generalized the ordinary differential system to the following delayed differential system:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{d[TF\mbox{-}A]}{dt} = ( \frac{k_{1,f}[TF\mbox{-}A]^{2}}{[TF\mbox{-}A]^{2}+K_{1,d}(1+[TF\mbox{-}R]/K_{R,d})} )(t-\tau )-k_{1,d}[TF\mbox{-}A]+r,\\ \frac{d[TF\mbox{-}R]}{dt} = ( \frac{k_{2,f}[TF-A]^{2}}{[TF\mbox{-}A]^{2}+K_{2,d}(1+[TF\mbox{-}R]/K_{R,d})} )(t-\tau)-k_{2,d}[TF\mbox{-}R], \end{array}\displaystyle \right . $$
(1.1)

where [TF-A] denotes the level of the transcriptional activators, [TF-R] denotes the level of the protein that represses transcription by binding to TA-REs (the responsive elements of the TFs), \(k_{1,f}\) is the maximal transcription rate of TF-A, \(k_{2,f}\) is the maximal synthesis rate, \(k_{1,d}\) and \(k_{2,d}\) are degradation rates, \(K_{1,d}\) and \(K_{2,d}\) are the dissociation constants of TF-A dimer from TF-REs, r is a basal rate of synthesis of activator at negligible dimer concentration, and \(K_{R,d}\) is the dissociation constant of TF-R monomers from TF-REs. For simplicity, letting

$$\begin{aligned}[b] &x_{1}=[TF\mbox{-}A],\qquad x_{2}=[TF\mbox{-}R],\qquad K_{R,d}=q, \quad\mbox{and}\\ &k_{i}=k_{i,f},\qquad p_{i}=K_{i,f},\qquad l_{i}=k_{i,d} \quad \mbox{for } i=1,2, \end{aligned} $$

system (1.1) can be translated to

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dx_{1}}{dt} = \frac{k_{1}x_{1}^{2}(t-\tau)}{x_{1}^{2}(t-\tau )+p_{1}(1+x_{2}(t-\tau)/q)}-l_{1}x_{1}(t)+ r,\\ \frac{dx_{2}}{dt} = \frac{k_{2}x_{1}^{2}(t-\tau)}{x_{1}^{2}(t-\tau )+p_{2}(1+x_{2}(t-\tau)/q)}-l_{2}x_{2}(t). \end{array}\displaystyle \right . $$
(1.2)

Recently, the authors of [3] and [4] studied Hopf bifurcation and global attractivity of system (1.2), respectively. Moreover, in the past decade, a great deal of mathematical effort in other gene regulatory network models has been devoted to the study of stability and bifurcations (see references [5–12]). However, limited work has been done on the global exponential stability of positive periodic solutions for genetic regulatory system (1.2) with time-varying coefficients and delays. Thus, considering that parameters periodically vary due to changes of external environment, we modify the genetic regulatory system (1.2) as follows:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dx_{1}}{dt} = \frac{k_{1}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{1}(t)(1+x_{2}(t-\tau(t))/q(t))}-l_{1}(t)x_{1}(t)+ r(t),\\ \frac{dx_{2}}{dt} = \frac{k_{2}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{2}(t)(1+x_{2}(t-\tau(t))/q(t))}-l_{2}(t)x_{2}(t), \end{array}\displaystyle \right . $$
(1.3)

where q, r, τ, \(k_{1}\), \(k_{2}\), \(l_{1}\), \(l_{2}\), \(p_{1}\), \(p_{2}\) are all nonnegative continuous ω-periodic functions.

In the real-world phenomena, the periodic variation of the environment (e.g., temperature, moisture, pressure, seasonal effects of weather, reproduction, food supplies, mating habits, etc.) plays a pivotal role in determining the dynamics, so that some classic models, such as the Nicholson blowflies model [13, 14], hematopoiesis model [15, 16], etc., have been generalized to the nonautonomous nonlinear delay differential equation with time-varying coefficients and delays. Consequently, it is worth studying the model of gene regulatory system with time-varying coefficients and delays.

It is convenient to introduce some notation. Given a bounded continuous function f defined on R, we define \(f^{+}\) and \(f^{-}\) as

$$f^{-}=\inf_{t\in{R}}f(t), \qquad f^{+}=\sup_{t\in{R}}f(t). $$

Let \(R^{n}\) (\(R_{+}^{n}\)) be the set of all (nonnegative) real vectors; by \(x=(x_{1},\ldots,x_{n})^{T}\in R^{n}\) we denote a column vector, in which the symbol \(({}^{T})\) denotes the transpose of a vector. We denote by \(|x|\) the absolute-value vector \(|x|=(|x_{1}|,\ldots,|x_{n}|)^{T}\) and define \(\|x\|=\max_{1\leq i\leq n}|x_{i}|\). For \(\tau^{+}>0\), we denote by \(C= C([-\tau^{+},0], R^{2})\) the Banach space equipped with the supremum norm, that is, \(\|\varphi\|=\sup_{-\tau^{+}\leq t\leq0}\max_{1\leq i\leq2}|\varphi_{i}(t)|\) for all \(\varphi(t)=(\varphi _{1}(t),\varphi_{2}(t))^{T} \in C\). Let \(C_{+}=\{\varphi\in C| \varphi(t)\in R_{+}^{2} \mbox{ for } t\in [-\tau^{+},0]\}\). If \(x_{i}(t)\) is defined on \([t_{0}-\tau^{+},\nu)\) with \(t_{0}, \nu\in R\) and \(i =1,2 \), then we define \(x_{t}\in C \) as \(x_{t}=(x_{t}^{1}, x_{t}^{2} )^{T}\) where \(x^{i}_{t}(\theta)=x_{i}(t+\theta)\) for all \(\theta\in[-\tau^{+} ,0]\) and \(i =1,2\).

It is biologically reasonable to assume that only positive solutions of system (1.3) are meaningful and therefore admissible. The initial conditions associated with system (1.3) are of the form

$$ x_{t_{0}} =\varphi, \qquad \varphi=(\varphi_{1}, \varphi_{2} )^{T}\in C_{+}, \quad\mbox{and}\quad \varphi_{i}(0)>0,\quad i =1,2. $$
(1.4)

We denote by \(x_{t}(t_{0}, \varphi)=x(t; t_{0}, \varphi)\) a solution of the initial value problem (1.3) and (1.4). Also, let \([t_{0},\eta(\varphi))\) be the maximal right-interval of the existence of \(x_{t}(t_{0}, \varphi)\).

Definition 1.1

Let \(x^{*}(t)\) be a solution of (1.3). For any given initial value φ that satisfies (1.4), if there are positive constants λ, \(K_{\varphi}\), and \(T_{\varphi}>t_{0}\) such that every solution \(x(t; t_{0},\varphi)\) to system (1.3) satisfies

$$\bigl|x_{i} (t; t_{0},\varphi)-x^{*}_{i}(t)\bigr|\leq K_{\varphi}e^{-\lambda(t-t_{0})} \quad \mbox{for } t>T_{\varphi}, i =1,2, $$

then \(x^{*}(t)\) is said to be globally exponentially stable.

The objective of this paper is twofold. The first is getting the attracting set for system (1.3). The other is deriving conditions on the existence, uniqueness, and global exponential stability of positive periodic solutions. Finally, we give an example and its numerical simulations to illustrate our main results.

2 Preliminary results

In this section, we derive the following lemmas, which will be used to prove our main results in Section 3.

Lemma 2.1

Suppose that \(r^{-}>0\) and \(l_{i}^{-}>0\) (\(i=1,2\)) and define the positive constants

$$B_{1}=\frac{r^{-}}{l_{1}^{+}},\qquad C_{1}=\frac{k_{1}^{+}+r^{+}}{l_{1}^{-}},\qquad B_{2}=\frac {k_{2}^{-}B_{1}^{2}}{l_{2}^{+}(B_{1}^{2}++p_{2}^{+}(1+C_{2}/q^{-}))},\qquad C_{2}=\frac{k_{2}^{+}}{l_{2}^{-}}. $$

Then there exists a unique positive global solution \(x(t;t_{0},\varphi)\) to initial value problem (1.3) and (1.4) on the interval \([t_{0}-\tau ^{+},+\infty)\). Moreover, there exist \(t_{0}(\varphi)>t_{0}\) such that for any \(t>t_{0}(\varphi)\),

$$ B_{i}\leq x_{i}(t;t_{0},\varphi)\leq C_{i},\quad i=1,2. $$
(2.1)

Proof

Set \(x(t)= x(t; t_{0}, \varphi)=(x_{1}(t),x_{2}(t))^{T} \mbox{ for all } t\in [t_{0},\eta(\varphi)) \). From the variation-of-constants formula we have

$$ \left \{ \textstyle\begin{array}{@{}l} x_{1}(t) = \varphi_{1}(0)e^{-\int_{t_{0}}^{t}l_{1}(s)\,ds} +\int_{t_{0}}^{t} e^{-\int_{s}^{t}l_{1}(u)\,du}[\frac{k_{1}(s)x_{1}^{2}(s-\tau(s))}{x_{1}^{2}(s-\tau (s))+p_{1}(s)(1+x_{2}(s-\tau(s))/q(s))}+r(s)]\,ds,\\ x_{2}(t) = \varphi_{2}(0)e^{-\int_{t_{0}}^{t}l_{2}(s)\,ds} +\int_{t_{0}}^{t} e^{-\int_{s}^{t}l_{2}(u)\,du}\frac{k_{2}(s)x_{1}^{2}(s-\tau(s))}{x_{1}^{2}(s-\tau (s))+p_{2}(s)(1+x_{2}(s-\tau(s))/q(s))}\,ds \end{array}\displaystyle \right . $$
(2.2)

for \(t\in[t_{0},t_{0}+\tau^{+}]\).

Since the initial value φ satisfies (1.4), Eq. (2.2) leads to \(x_{i}(t)>0 \) (\(i=1,2\)) for \(t\in[t_{0}, t_{0}+\tau^{+}]\). Then, by the method of steps we obtain that \(x(t;t_{0},\varphi)\) is positive and exists on \([t_{0}-\tau^{+},+\infty)\).

In what follows, we prove that (2.1) holds for \(t>t_{0}(\varphi)\). In view of the first equation of (1.3), we get

$$\frac{dx_{1}}{dt}=\frac{k_{1}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{1}(t)(1+x_{2}(t-\tau(t))/q(t))}-l_{1}(t)x_{1}(t)+ r(t) \leq k_{1}^{+}+r^{+}-l_{1}^{-}x_{1}(t) $$

and

$$\frac{dx_{1}}{dt}=\frac{k_{1}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{1}(t)(1+x_{2}(t-\tau(t))/q(t))}-l_{1}(t)x_{1}(t)+ r(t) \geq r^{-}-l_{1}^{+}x_{1}(t), $$

which, by the comparison principle, imply that there exists \(t_{1}>t_{0}\) such that for any \(t>t_{1}\), \(B_{1}\leq x_{1}(t)\leq C_{1}\). From the second equation of (1.3) we have

$$\frac{dx_{2}}{dt} = \frac{k_{2}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{2}(1+x_{2}(t-\tau(t))/q(t))}-l_{2}(t)x_{2}(t)\leq k_{2}^{+}-l_{2}^{-}x_{2}(t), $$

which yields that there exists \(t_{2}>t_{1}\) such that for any \(t>t_{2}\), \(x_{2}(t)\leq C_{2}\). So for \(t>t_{2}+\tau^{+}\), \(x_{2}(t)\) satisfies

$$\frac{dx_{2}}{dt} = \frac{k_{2}(t)x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{2}(1+x_{2}(t-\tau(t))/q(t))}-l_{2}(t)x_{2}(t)\geq \frac {k_{2}^{-}B_{1}^{2}}{B_{1}^{2}+p_{2}^{+}(1+C_{2}/q^{-})}-l_{2}^{+}x_{2}(t). $$

Consequently, there exists \(t_{3}>t_{2}\) such that for any \(t>t_{3}\), \(x_{2}(t)\geq B_{2}\). The proof is now completed. □

Lemma 2.2

Suppose that \(q^{-}>0\), \(r^{-}>0\), \(l_{i}^{-}>0 \) (\(i=1,2\)), and

$$ -l_{i}^{-}+ k_{i}^{+}(D_{i}+E_{i})< 0,\quad i=1,2, $$
(2.3)

where \(D_{i}=\frac {2C_{1}^{3}+2C_{1}(B_{1}^{2}+p_{i}^{-}(1+B_{2}/q^{+}))}{(B_{1}^{2}+p_{i}^{-}(1+B_{2}/q^{+}))^{2}}\), \(E_{i}=\frac{C_{1}^{2}p_{i}^{+}/q^{-}}{(B_{1}^{2}+p_{i}^{-}(1+B_{2}/q^{+}))^{2}}\) (\(i=1,2\)). Moreover, let \(x(t)=x(t;t_{0},\varphi)\), \(\widetilde{x}(t)=\widetilde {x}(t;t_{0},\psi)\). Then, there exist positive constants λ, \(K_{\varphi,\psi}\), and \(t_{\varphi,\psi}>t_{0}\) such that

$$ \bigl|x_{i} (t)-\widetilde{x}_{i}(t)\bigr|\leq K_{\varphi,\psi} e^{-\lambda (t-t_{0})} \quad\textit{for all } t>t_{\varphi,\psi}, i =1,2. $$
(2.4)

Proof

For \(i=1,2\), define the continuous functions \(\Gamma _{i}(u)\) as

$$\Gamma_{i}(u)=u-l_{i}^{-}+k_{i}^{+} \bigl(D_{i}e^{u\tau^{+}}+E_{i}e^{u\tau^{+}}\bigr), \quad u\in[0,1]. $$

Then, in view of (2.3), we obtain

$$\Gamma_{i}(0)=-l_{i}^{-}+k_{i}^{+}(D_{i}+E_{i})< 0, \quad i=1,2, $$

which implies that there exist two constants \(\eta>0\) and \(\lambda\in (0,1]\) such that

$$ \Gamma_{i}(\lambda)=\lambda-l_{i}^{-}+k_{i}^{+} \bigl(D_{i}e^{\lambda\tau^{+}}+E_{i}e^{\lambda \tau^{+}}\bigr)< - \eta< 0,\quad i=1,2. $$
(2.5)

Set \(y(t)=x(t)-\widetilde{x}(t)=(y_{1}(t),y_{2}(t))^{T}\), where \(y_{i}(t)=x_{i}(t)-\widetilde{x}_{i}(t)\), \(t\in[t_{0}-\tau^{+},+\infty)\), \(i=1,2\). Then

$$\begin{aligned} \frac{dy_{i}}{dt} =&-l_{i}(t)y_{i}(t)+k_{i}(t) \biggl[\frac{x_{1}^{2}(t-\tau (t))}{x_{1}^{2}(t-\tau(t))+p_{i}(t)(1+x_{2}(t-\tau(t))/q(t))} \\ &{}-\frac{\widetilde{x}_{1}^{2}(t-\tau(t))}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau(t))/q(t))}\biggr], \quad t>t_{0}, i=1,2. \end{aligned}$$
(2.6)

It follows from Lemma 2.1 that there exists \(t_{\varphi,\psi}>t_{0}\) such that

$$ B_{i}\leq x_{i}(t), \widetilde{x}_{i}(t) \leq C_{i} \quad \mbox{for all } t\in \bigl[t_{\varphi,\psi}-\tau^{+},+\infty\bigr), i=1,2. $$
(2.7)

We consider the Lyapunov functional

$$ V_{i}(t)=\bigl|y_{i}(t)\bigr|e^{\lambda(t-t_{0})} , \quad i=1,2. $$
(2.8)

In view of (2.7), for all \(t>t_{\varphi,\psi}\) and \(i=1,2\), calculating the upper left derivative of \(V_{i}(t)\) along the solution \(y_{i}(t)\) of (2.6), we have

$$\begin{aligned} D^{-}\bigl(V_{i}(t)\bigr) \leq&\lambda\bigl|y_{i}(t)\bigr| e^{\lambda(t-t_{0})}+e^{\lambda (t-t_{0})}k_{i}(t)\biggl|\frac{x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{i}(t)(1+x_{2}(t-\tau(t))/q(t))} \\ &{}-\frac{\widetilde{x}_{1}^{2}(t-\tau(t))}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau (t))/q(t))}\biggr|-l_{i}(t)\bigl|y_{i}(t)\bigr|e^{\lambda(t-t_{0}) } \\ \leq&\bigl(\lambda-l_{i}(t)\bigr)\bigl|y_{i}(t)\bigr| e^{\lambda(t-t_{0})}+e^{\lambda (t-t_{0})}k_{i}(t) \\ &{}\times\biggl[\biggl|\frac{x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau(t))+p_{i}(t)(1+x_{2}(t-\tau (t))/q(t))} \\ &{}-\frac{x_{1}^{2}(t-\tau(t))}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau(t))/q(t))}\biggr| \\ &{}+\biggl|\frac{x_{1}^{2}(t-\tau(t))}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau(t))/q(t))} \\ &{}-\frac{\widetilde{x}_{1}^{2}(t-\tau(t))}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau(t))/q(t))}\biggr|\biggr] \\ \leq&e^{\lambda(t-t_{0})}k_{i}(t)\biggl[ \frac{x_{1}^{2}(t-\tau(t))}{x_{1}^{2}(t-\tau (t))+p_{i}(t)(1+x_{2}(t-\tau(t))/q(t))} \\ &{}\times\frac{(x_{1}(t-\tau(t)+\widetilde{x}_{1}(t-\tau(t)))|y_{1}(t-\tau (t))|+p_{i}(t)|y_{2}(t-\tau(t))|/q(t)}{\widetilde{x}_{1}^{2}(t-\tau (t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau(t))/q(t))} \\ &{}+\frac{(x_{1}(t-\tau(t))+\widetilde{x}_{1}(t-\tau(t)))|y_{1}(t-\tau (t))|}{\widetilde{x}_{1}^{2}(t-\tau(t))+p_{i}(t)(1+\widetilde{x}_{2}(t-\tau (t))/q(t))}\biggr]+\bigl(\lambda-l_{i}(t) \bigr)\bigl|y_{i}(t)\bigr| e^{\lambda(t-t_{0})} \\ \leq&e^{\lambda(t-t_{0})}k_{i}^{+}\biggl[ \frac{C_{1}^{2}(2C_{1}|y_{1}(t-\tau (t))|+p_{i}^{+}|y_{2}(t-\tau(t))|/q^{-})}{(B_{1}^{2}+p_{i}^{-}(1+B_{2}/q^{+}))^{2}} \\ &{}+\frac{2C_{1}|y_{1}(t-\tau(t))|}{B_{1}^{2}+p_{i}^{-}(1+B_{2}/q^{+})}\biggr]+\bigl(\lambda -l_{i}^{-} \bigr)\bigl|y_{i}(t)\bigr| e^{\lambda(t-t_{0})} \\ =&k_{i}^{+}\bigl(D_{i}V_{1}\bigl(t-\tau(t)\bigr) e^{\lambda\tau(t)}+E_{i}V_{2}\bigl(t-\tau(t)\bigr) e^{\lambda\tau(t)}\bigr)+\bigl(\lambda-l_{i}^{-}\bigr)V_{i}(t) \\ \leq&\bigl(\lambda-l_{i}^{-}\bigr)V_{i}(t)+k_{i}^{+} \bigl( D_{i}V_{1}\bigl(t-\tau(t)\bigr) e^{\lambda\tau ^{+}}+E_{i}V_{2} \bigl(t-\tau(t)\bigr) e^{\lambda\tau^{+}}\bigr). \end{aligned}$$
(2.9)

We now claim that

$$\begin{aligned} V_{i}(t) =&\bigl|y_{i}(t)\bigr|e^{\lambda(t-t_{0})} \\ < &e^{\lambda t_{\varphi,\psi}}\Bigl(\max_{1\leq i\leq2} \max_{t\in[t_{0}-\tau^{+},t_{\varphi,\psi}]}\bigl|x_{i}(t)- \widetilde{x}_{i}(t)\bigr|+1\Bigr) \\ :=&K_{\phi,\psi} \quad\mbox{for all } t>t_{\varphi,\psi}, i=1,2. \end{aligned}$$
(2.10)

Contrarily, there must exist \(t_{4}>t_{\varphi,\psi} \) and \({i}\in\{1,2\} \) such that

$$ V_{{i}}(t_{4})=K_{\varphi,\psi} \quad\mbox{and} \quad V_{{j}}(t)< K_{\varphi,\psi } \quad\mbox{for all } t\in\bigl[t_{0}- \tau^{+},t_{4}\bigr), {j}=1,2. $$
(2.11)

From (2.9) and (2.11) we get

$$\begin{aligned} 0 \leq&D^{-}\bigl(V_{{i}}(t_{4})\bigr) \\ \leq&\bigl(\lambda-l_{i}^{-}\bigr)V_{i}(t_{4})+k_{i}^{+} \bigl( D_{i}V_{1}\bigl(t_{4}-\tau(t_{4}) \bigr) e^{\lambda \tau^{+}}+E_{i}V_{2}\bigl(t_{4}- \tau(t_{4})\bigr) e^{\lambda\tau^{+}}\bigr) \\ < &\bigl\{ \lambda-l_{i}^{-}+k_{i}^{+}\bigl( D_{i} e^{\lambda\tau^{+}}+E_{i} e^{\lambda\tau ^{+}}\bigr)\bigr\} K_{\varphi,\psi}. \end{aligned}$$

Thus,

$$0\leq\lambda-l_{i}^{-}+k_{i}^{+}\bigl( D_{i} e^{\lambda\tau^{+}}+E_{i} e^{\lambda\tau^{+}}\bigr), $$

which contradicts (2.5). Hence, (2.10) holds. It follows that

$$ \bigl|y_{i}(t)\bigr|< K_{\varphi,\psi}e^{-\lambda(t-t_{0})} \quad\mbox{for all } t>t_{\varphi,\psi}, i=1,2. $$
(2.12)

The proof is completed. □

3 Main results

In this section, we establish sufficient conditions on the existence, uniqueness, and global exponential stability of positive ω-periodic solutions for system (1.3).

Theorem 3.1

Suppose that all conditions in Lemma  2.2 are satisfied. Then system (1.3) has exactly one positive ω-periodic solution \(\widetilde {x}(t)\). Moreover, \(\widetilde{x}(t)\) is globally exponentially stable.

Proof

Let \(x(t)= x(t; t_{0}, \varphi)=(x_{1}(t),x_{2}(t))^{T} \) be a solution of system (1.3) and (1.4). By Lemma 2.1 we obtain that there exists \(s_{\varphi}>t_{0}\) such that

$$B_{i}\leq x_{i}(t)\leq C_{i} \quad \mbox{for all } t\geq s_{\varphi}-\tau^{+}, i=1,2. $$

By the periodicity of coefficients and delay for system (1.3) we have that, for any natural number h,

$$\begin{aligned} &\bigl[x_{1}\bigl(t+(h+1)\omega\bigr) \bigr]' \\ &\quad= \frac{k_{1}(t+(h+1)\omega)x_{1}^{2}(t+(h+1)\omega-\tau (t))}{x_{1}^{2}(t+(h+1)\omega-\tau(t))+p_{1}(t+(h+1)\omega )(1+x_{2}(t+(h+1)\omega-\tau(t))/q(t+(h+1)\omega))} \\ &\qquad{}-l_{1}\bigl(t+(h+1)\omega\bigr)x_{1}\bigl(t+(h+1) \omega\bigr)+ r\bigl(t+(h+1)\omega\bigr) \\ &\quad= \frac{k_{1}(t)x_{1}^{2}(t+(h+1)\omega-\tau(t))}{x_{1}^{2}(t+(h+1)\omega-\tau (t))+p_{1}(t)(1+x_{2}(t+(h+1)\omega-\tau(t))/q(t))} \\ &\qquad{}-l_{1}(t)x_{1}\bigl(t+(h+1)\omega\bigr)+ r(t) \end{aligned}$$
(3.1)

and

$$\begin{aligned} &\bigl[x_{2}\bigl(t+(h+1)\omega\bigr) \bigr]' \\ &\quad= \frac{k_{2}(t+(h+1)\omega)x_{1}^{2}(t+(h+1)\omega-\tau (t))}{x_{1}^{2}(t+(h+1)\omega-\tau(t))+p_{2}(t+(h+1)\omega )(1+x_{2}(t+(h+1)\omega-\tau(t))/q(t+(h+1)\omega))} \\ &\qquad{}-l_{2}\bigl(t+(h+1)\omega\bigr)x_{2}\bigl(t+(h+1) \omega\bigr) \\ &\quad= \frac{k_{2}(t)x_{1}^{2}(t+(h+1)\omega-\tau(t))}{x_{1}^{2}(t+(h+1)\omega-\tau (t))+p_{2}(t)(1+x_{2}(t+(h+1)\omega-\tau(t))/q(t))} \\ &\qquad{}-l_{2}(t)x_{2}\bigl(t+(h+1)\omega\bigr), \end{aligned}$$
(3.2)

where \(t+(h+1)\omega\in[t_{0},+\infty)\), \(i=1,2\). Thus, for any natural number h, we obtain that \(x(t+(h+1)\omega)=(x_{1}(t+(h+1)\omega ),x_{2}(t+(h+1)\omega))^{T}\) is a solution of system (1.3) for all \(t\geq t_{0}-\tau^{+}-(h+1)\omega\), \(i=1,2\). Hence, \(x(t+\omega)\) (\(t\in[t_{0}-\tau^{+} ,+\infty)\), \(i=1,2\)) is also a solution of system (1.3) with initial values

$$\psi_{i}(s)=x_{i}(s+t_{0}+\omega),\quad s\in \bigl[-\tau^{+},0\bigr], i=1,2. $$

It follows from the proof of Lemma 2.2 that there exists a constant \(s_{\varphi}>t_{0}\) such that, for any nonnegative integer h and \(t+h\omega\geq s_{\varphi}\),

$$\begin{aligned} \bigl|x_{i}\bigl(t+(h+1)\omega;t_{0},\varphi\bigr) -x_{i}(t+h\omega;t_{0},\varphi )\bigr| =&\bigl|x_{i}(t+h \omega;t_{0},\psi) -x_{i}(t+h\omega;t_{0}, \varphi)\bigr| \\ \leq& K_{\varphi}e^{-\lambda(t+h\omega-t_{0})},\quad i=1,2, \end{aligned}$$

where \(K_{\varphi}=e^{\lambda s_{\varphi}}(\max_{1\leq i\leq2}\max_{s\in[t_{0}-\tau^{+}, s_{\varphi}]}|x_{i}(s;t_{0},\psi)-x_{i}(s;t_{0},\varphi)|+1)\).

Now, we show that \(x_{i}(t+q\omega;t_{0},\varphi) \) (\(i=1,2\)) is convergent on any compact interval as \(q\rightarrow+\infty\). Let \([a,b]\subset R\) be an arbitrary subset of R. Choose a nonnegative integer \(q_{0}\) such that \(t+q_{0}\omega\geq s_{\varphi}\) for \(t\in[a,b]\). Then, for \(t\in[a,b]\) and \(q>q_{0}\), we have

$$x_{i}(t+q\omega)=x_{i}(t+q_{0}\omega)+ \sum _{h=q_{0}}^{q-1}\bigl[x_{i}\bigl(t+(h+1) \omega\bigr)-x_{i}(t+h\omega)\bigr],\quad i=1,2. $$

Then \(x_{i}(t+q\omega)\) converges uniformly to a continuous function, say \(\widetilde{x}_{i}(t)\), on \([a,b]\). Because of arbitrariness of \([a,b]\), we see that \(x_{i}(t+q\omega)\rightarrow \widetilde{x}_{i}(t)\) as \(q\rightarrow+\infty\) for \(t\in R\), \(i=1,2\). Moreover,

$$ B_{i}\leq\widetilde{x}_{i}(t)\leq C_{i} \quad \mbox{for all } t\in R, i=1,2. $$
(3.3)

It remains to show that \(\widetilde{x}(t)=(\widetilde{x}_{1}(t),\widetilde {x}_{2}(t))^{T}\) is an ω-periodic solution of system (1.3). The periodicity is obvious since

$$\widetilde{x}_{i}(t+\omega)=\lim_{q\rightarrow+\infty}x_{i}(t+ \omega +q\omega)=\lim_{q+1\rightarrow+\infty}x_{i}\bigl(t+(q+1)\omega \bigr)=\widetilde{x}_{i}(t) ,\quad i=1,2, $$

for all \(t\in R\). Now, note that \(x(t+q\omega)\) is a solution to system (1.3), that is,

$$\begin{aligned} &x_{1}(t+q\omega) -x_{1}(t_{0}+q\omega) \\ &\quad= \int_{t_{0}}^{t}\biggl[ \frac{k_{1}(s)x_{1}^{2}(s+q\omega-\tau(s))}{x_{1}^{2}(s+q\omega -\tau(s))+p_{1}(s)(1+x_{2}(s+q\omega-\tau(s))/q(s))} -l_{1}(s)x_{1}(s+q\omega)+ r(s) \biggr]\,ds \end{aligned}$$

and

$$\begin{aligned}[b] &x_{2}(t+q\omega) -x_{2}(t_{0}+q\omega) \\ &\quad= \int_{t_{0}}^{t}\biggl[ \frac{k_{2}(s)x_{1}^{2}(s+q\omega-\tau(s))}{x_{1}^{2}(s+q\omega -\tau(s))+p_{2}(s)(1+x_{2}(s+q\omega-\tau(s))/q(s))} -l_{2}(s)x_{2}(s+q\omega)\biggr]\,ds \end{aligned} $$

for \(t\geq t_{0}\). Letting \(q\rightarrow+\infty\) gives us

$$\left \{ \textstyle\begin{array}{@{}l} \widetilde{x}_{1}(t) -\widetilde{x}_{1}(t_{0}) = \int_{t_{0}}^{t}[ \frac {k_{1}(s)\widetilde{x}_{1}^{2}(s-\tau(s))}{\widetilde{x}_{1}^{2}(s-\tau (s))+p_{1}(s)(1+\widetilde{x}_{2}(s-\tau(s))/q(s))}-l_{1}(s)\widetilde {x}_{1}(s)+ r(s)]\,ds,\\ \widetilde{x}_{2}(t) -\widetilde{x}_{2}(t_{0}) = \int_{t_{0}}^{t}[ \frac {k_{2}(s)\widetilde{x}_{1}^{2}(s-\tau(s))}{\widetilde{x}_{1}^{2}(s-\tau (s))+p_{2}(s)(1+\widetilde{x}_{2}(s-\tau(s))/q(s))}-l_{2}(s)\widetilde{x}_{2}(s)]\,ds \end{array}\displaystyle \right . $$

for \(t\geq t_{0}\), that is, \(\widetilde{x}(t)\) is a solution to system (1.3) on \([t_{0}-\tau^{+}, +\infty)\). Finally, from (2.1) and (3.3), again using a similar argument as in the proof (2.12), we can prove that \(\widetilde{x}(t)\) is globally exponentially stable. This completes the proof of the main theorem. □

4 An example

In this section, we give an example and numerical simulations to demonstrate the results obtained in previous sections.

Example 4.1

Considerthe following genetic regulatory system with time-varying coefficients and delays:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dx_{1}}{dt} = \frac{\frac{1}{10}(2+\sin t)x_{1}^{2}(t-2|\sin t|)}{x_{1}^{2}(t-2|\sin t|)+(1+\sin t)(1+x_{2}(t-2|\sin t|))}-(10+\cos t)x_{1}(t)+ 11,\\ \frac{dx_{2}}{dt} = \frac{\frac{1}{10}(2+\cos t)x_{1}^{2}(t-2|\sin t|)}{x_{1}^{2}(t-2|\sin t|)+(1+\cos t)(1+x_{2}(t-2|\sin t|))}-(10+\sin t)x_{2}(t). \end{array}\displaystyle \right . $$
(4.1)

Obviously, \(r^{-}=r^{+}=11\), \(q^{-}=q^{+}=1\), \(k_{i}^{-}=0.1\), \(k_{i}^{+}=0.3\), \(l_{i}^{-}=9\), \(l_{i}^{+}=11\), \(p_{i}^{-}=0\), \(p_{i}^{+}=2\) (\(i=1,2\)). From (2.1) and (2.3) we obtain \(B_{1}=1\), \(C_{1}=11.3/9\), \(B_{2}=1/264\), \(C_{2}=0.1/3\), \(D_{i}\approx 6.46968\), \(E_{i}\approx3.15284\) (\(i=1,2\)), and

$$ -l_{i}^{-}+ k_{i}^{+}(D_{i}+E_{i}) \approx-6.11325< 0, \quad i=1,2, $$
(4.2)

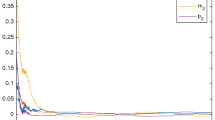
which imply that the genetic regulatory system (4.1) satisfies all conditions of Theorem 3.1. Therefore, system (4.1) has a unique positive 2π-periodic solution \(\widetilde{x}(t)\), which is globally exponentially stable with the exponential convergent rate \(\lambda \approx0.5\). The numerical simulations in Figure 1 strongly support the conclusion.

Figure 1
figure 1

Numerical solutions \(\pmb{x(t)=(x_{1}(t),x_{2}(t))^{T}}\) of system ( 4.1 ) for initial value \(\pmb{\varphi(s)\equiv(5,4)^{T}, (3,2)^{T}, (0.5,0.5)^{T}}\) , \(\pmb{s\in [-2,0]}\) .

Full size image

Remark 4.1

To the best of our knowledge, rare authors studied the problems of the global exponential stability of positive periodic solutions for genetic regulatory system with time-varying coefficients and delays. It is obvious that all results in [3, 4] and the references therein cannot be applicable to prove that all solutions of system (4.1) converge exponentially to a positive periodic solution since the system has time-varying coefficients and delays. This implies that the results of this paper are generalization and complement of previously known results.