Abstract
In this paper, by using a fixed point theorem and differential inequality techniques, we consider the existence and global exponential stability of an equilibrium point for a class of fuzzy bidirectional associative memory neural networks with time-varying delays in leakage terms on time scales. We also present a numerical example to show the feasibility of obtained results. The results of this paper are completely new and complementary to the previously known results.
MSC:34B37, 34N05.
Similar content being viewed by others
1 Introduction
The bidirectional associative memory (BAM) neural networks were first introduced by Kosto in 1988 [1]. These are special recurrent neural networks that can store bipolar vector pairs and are composed of neurons arranged in two layers. The neurons in one layer are fully interconnected to the neurons in the other layer, while there are no interconnections among neurons in the same layer.
In recent years, due to their wide range of applications, for example, pattern recognition, associative memory, and combinatorial optimization, BAM neural networks have received much attention. There are lots of results on the existence and stability of an equilibrium point, periodic solutions or almost periodic solutions of BAM neural networks [2–10].
Based on traditional cellular neural networks, Yang and Yang proposed a fuzzy cellular neural network, which integrates fuzzy logic into the structure of traditional cellular neural networks and maintains local connectedness among cells [11]. The fuzzy neural network has fuzzy logic between its template input and/or output besides the sum of product operation. Studies have revealed that the fuzzy neural network is very useful for image processing problems, which is a cornerstone in image processing and pattern recognition. Besides, in reality, time delays often occur due to finite switching speeds of the amplifiers and communication time and can destroy a stable network or cause sustained oscillations, bifurcation or chaos. Hence, it is important to consider both the fuzzy logic and delay effect on dynamical behaviors of neural networks. There have been many results on the fuzzy neural networks with time delays [12–17]. Moreover, time delay in the leakage term also has a great impact on the dynamics of neural networks. As pointed out by the author in [18], time delay in the stabilizing negative feedback term has a tendency to destabilize a system. Therefore, it is meaningful to consider fuzzy neural networks with time delays in the leakage terms [19–24].
In fact, both continuous and discrete systems are very important in implementation and applications. To avoid the trouble of studying the dynamical properties for continuous and discrete systems respectively, it is meaningful to study those on time scales, which was initiated by Stefan Hilger in his PhD thesis, in order to unify continuous and discrete analyses. Lots of scholars have studied neural networks on time scales and obtained many good results [25–34]. However, to the best of our knowledge, there is no paper published on the stability of fuzzy BAM neural networks with time delays in the leakage terms on time scales.
Motivated by the above, in this paper, we integrate fuzzy operations into BAM neural networks with time delays in the leakage terms and study the stability of considered neural networks on time scales. By using a fixed point theorem and differential inequality techniques, we consider the existence and global exponential stability of an equilibrium point for the following BAM neural network with time-varying delays in leakage terms on time scales:
where  is a time scale; n, m are the number of neurons in layers; and denote the activations of the i th neuron and the j th neuron at time t; and represent the rate at which the i th neuron and the j th neuron will reset their potential to the resting state in isolation when they are disconnected from the network and the external inputs; and denote the leakage delays; , are the input-output functions (the activation functions); and are transmission delays; , , and ; , are elements of feedback templates; , denote the elements of fuzzy feedback MIN templates and , are the elements of fuzzy feedback MAX templates; , are fuzzy feed-forward MIN templates and , are fuzzy feed-forward MAX templates; , denote the input of the i th neuron and the j th neuron; , denote biases of the i th neuron and the j th neuron, , , ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operations, respectively.
is a time scale; n, m are the number of neurons in layers; and denote the activations of the i th neuron and the j th neuron at time t; and represent the rate at which the i th neuron and the j th neuron will reset their potential to the resting state in isolation when they are disconnected from the network and the external inputs; and denote the leakage delays; , are the input-output functions (the activation functions); and are transmission delays; , , and ; , are elements of feedback templates; , denote the elements of fuzzy feedback MIN templates and , are the elements of fuzzy feedback MAX templates; , are fuzzy feed-forward MIN templates and , are fuzzy feed-forward MAX templates; , denote the input of the i th neuron and the j th neuron; , denote biases of the i th neuron and the j th neuron, , , ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operations, respectively.
The initial condition of (1.1) is of the form
where , denote positive real-valued continuous functions on and , respectively.
For the sake of convenience, we introduce some notations. For matrix D, denotes the transpose of D, denotes the spectral radius of D. A matrix or a vector means that all entries of D are greater than or equal to zero, can be defined similarly. For matrices or vectors D and E, (respectively ) means that (respectively ).
Throughout this paper, we assume that the following condition holds:
-
(H)
and there exist positive constants , such that
for all , , .
The organization of the rest of this paper is as follows. In Section 2, we introduce some preliminary results which are needed in the later sections. In Section 3, we establish some sufficient conditions for the existence and uniqueness of the equilibrium point of (1.1). In Section 4, we prove the equilibrium point of (1.1) is globally exponentially stable. In Section 5, we give an example to illustrate the feasibility and effectiveness of our results obtained in previous sections.
2 Preliminaries
In this section, we state some preliminary results.
Definition 2.1 [25]
Let  be a nonempty closed subset (time scale) of ℝ. The forward and backward jump operators and the graininess are defined, respectively, by
be a nonempty closed subset (time scale) of ℝ. The forward and backward jump operators and the graininess are defined, respectively, by
Lemma 2.1 [25]
Assume that are two regressive functions, then
-
(i)
and ;
-
(ii)
;
-
(iii)
;
-
(iv)
.
Lemma 2.2 [25]
Let f, g be Δ-differentiable functions on T, then
-
(i)
for any constants , ;
-
(ii)
.
Lemma 2.3 [35]
Assume that for , then .
Definition 2.2 [35]
A function is called regressive if
for all . The set of all regressive and rd-continuous functions will be denoted by ℛ. We define the set .
Lemma 2.4 [35]
Suppose that , then
-
(i)
for all ;
-
(ii)
if for all , , then for all .
Lemma 2.5 [35]
If and , then
and
Lemma 2.6 [35]
Let , and assume that is continuous at , where with . Also assume that is rd-continuous on . Suppose that for each , there exists a neighborhood U of such that
where denotes the derivative of f with respect to the first variable. Then
-
(i)
implies ;
-
(ii)
implies .
Definition 2.3 A point is said to be an equilibrium point of (1.1) if is a solution of (1.1).
Lemma 2.7 [17]
Let be defined on R, . Then, for any , , , we have the following estimations:
and
where , .
Definition 2.4 [36]
A real matrix is said to be an M-matrix if , , and all successive principal minors of A are positive.
Lemma 2.8 [36]
Let be a matrix with nonpositive off-diagonal elements, then the following statements are equivalent:
-
(i)
A is an M-matrix;
-
(ii)
there exists a vector such that ;
-
(iii)
there exists a vector such that ;
-
(iv)
there exists a positive definite diagonal matrix D such that .
Lemma 2.9 [36]
Let be an matrix with , then , where denotes the spectral radius of A and is the identity matrix of size l.
Definition 2.5 Let be an equilibrium point of (1.1). If there exists a positive constant λ with such that for , there exists such that for an arbitrary solution of (1.1) with initial value satisfies
where , , . Then the equilibrium point is said to be globally exponentially stable.
3 Existence and uniqueness of an equilibrium point
In this section, we study the existence and uniqueness of an equilibrium point of (1.1).
Theorem 3.1 Let (H) hold. Suppose further that , where , , and
, . Then (1.1) has one unique equilibrium point.
Proof Let be an equilibrium point of (1.1), then we have
where , . Define a mapping as follows:
where
for , . Obviously, we need to show that is a contraction mapping on . In fact, for any and , we have
and
It follows that
Let N be a positive integer. In view of (3.1), we have
Since , we obtain , which implies that there exist a positive integer M and a positive constant such that
Hence, we have
which implies that . Since , it is obvious that the mapping is a contraction mapping. By the fixed point theorem of a Banach space, Φ possesses a unique fixed point in , that is, there exists a unique equilibrium point of (1.1). The proof of Theorem 3.1 is completed. □
4 Global exponential stability of an equilibrium point
In this section, we study the global exponential stability of the equilibrium point of (1.1).
Theorem 4.1 Let (H) and hold. Suppose further that
(H5) , where
and
Then the equilibrium point of (1.1) is globally exponentially stable.
Proof By Theorem 3.1, (1.1) has a unique equilibrium point . Suppose that is an arbitrary solution of (1.1) with the initial condition . Let , where , , , . Then (1.1) can be rewritten as
where and
The initial condition of (4.1) is the following:
We rewrite (4.1) as follows:
and
Multiplying both sides of (4.2) by and integrating on , where , we get
Similarly, multiplying both sides of (4.3) by and integrating on , we get
For a positive constant with , we have for . Take . In view of (H5), it is obvious that . Hence, we have
We claim that
To prove this claim, we show that for any , the following inequality holds:
which means that for , we have
and for , we have
By way of contradiction, assume that (4.7) does not hold. Firstly, we consider the following two cases.
Case One: (4.8) is not true and (4.9) is true. Then there exist and such that
Hence, there must be a constant such that
Note that in view of (4.4), we have
which is a contradiction.
Case Two: (4.8) is true and (4.9) is not true. Then there exist and such that
Hence, there must be a constant such that
Note that in view of (4.5), we have
which is also a contradiction.
By the above two cases, for other cases of negative proposition of (4.7), we can obtain a contradiction. Therefore, (4.7) holds. Let , then (4.6) holds. Hence, we have that
which means that the equilibrium point of (1.1) is globally exponentially stable. The proof of Theorem 4.1 is completed. □
5 Example
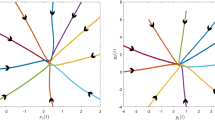
In this section, we present an example to illustrate the feasibility of our results.
Example 5.1 Let . Consider the following fuzzy BAM system with delays in leakage terms on a time scale  :
:
where time delays , , , , are defined as those in system (1.1) and the coefficients are as follows:
and are identity matrices. By calculating, we have . We can verify that for and , all the conditions of Theorem 3.1 and Theorem 4.1 are satisfied. Hence, for or , (5.1) always has one unique equilibrium point, which is globally exponentially stable.
References
Kosko B: Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18: 49-60. 10.1109/21.87054
Zhao HY: Global stability of bidirectional associative memory neural networks with distributed delays. Phys. Lett. A 2002, 297: 182-190. 10.1016/S0375-9601(02)00434-6
Li YK: Existence and stability of periodic solution for BAM neural networks with distributed delays. Appl. Math. Comput. 2004, 159: 847-862. 10.1016/j.amc.2003.11.007
Park JH, Park CH, Kwon OM, Lee SM: A new stability criterion for bidirectional associative memory neural networks of neutral-type. Appl. Math. Comput. 2008, 199: 716-722. 10.1016/j.amc.2007.10.032
Zhou Q: Global exponential stability of BAM neural networks with distributed delays and impulses. Nonlinear Anal., Real World Appl. 2009, 10: 144-153. 10.1016/j.nonrwa.2007.08.019
Li YK: Global exponential stability of BAM neural networks with delays and impulses. Chaos Solitons Fractals 2005, 24: 279-285.
Zheng B, Zhang Y, Zhang C: Global existence of periodic solutions on a simplified BAM neural network model with delays. Chaos Solitons Fractals 2008, 37: 1397-1408. 10.1016/j.chaos.2006.10.029
Xia Y, Cao JD, Lin M: New results on the existence and uniqueness of almost periodic solution for BAM neural networks with continuously distributed delays. Chaos Solitons Fractals 2007, 31: 928-936. 10.1016/j.chaos.2005.10.043
Zhang L, Si L: Existence and exponential stability of almost periodic solution for BAM neural networks with variable coefficients and delays. Appl. Math. Comput. 2007, 194: 215-223. 10.1016/j.amc.2007.04.044
Liu C, Li C, Liao X: Variable-time impulses in BAM neural networks with delays. Neurocomputing 2011, 74: 3286-3295. 10.1016/j.neucom.2011.05.005
Yang T, Yang L, Wu C, Chua L: Fuzzy cellular neural networks: theory. Proceedings of IEEE International Workshop on Cellular Neural Networks and Applications 1996, 181-186.
Yuan K, Cao JD, Deng J: Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays. Neurocomputing 2006, 69: 1619-1627. 10.1016/j.neucom.2005.05.011
Zhang Q, Xiang R: Global asymptotic stability of fuzzy cellular neural networks with time-varying delays. Phys. Lett. A 2008, 372: 3971-3977. 10.1016/j.physleta.2008.01.063
Song Q, Cao JD: Dynamical behaviors of discrete-time fuzzy cellular neural networks with variable delays and impulses. J. Franklin Inst. 2008, 345: 39-59. 10.1016/j.jfranklin.2007.06.001
Wang J, Lu J: Global exponential stability of fuzzy cellular neural networks with delays and reaction-diffusion terms. Chaos Solitons Fractals 2008, 38: 878-885. 10.1016/j.chaos.2007.01.032
Li YK, Yang L, Wu WQ: Periodic solutions for a class of fuzzy BAM neural networks with distributed delays and variable coefficients. Int. J. Bifurc. Chaos 2010, 20: 1551-1565. 10.1142/S0218127410026708
Liu Y, Tang W: Exponential stability of fuzzy cellular neural networks with constant and time-varying delays. Phys. Lett. A 2004, 323: 224-233. 10.1016/j.physleta.2004.01.064
Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Dynamics. Kluwer Academic, Dordrecht; 1992.
Li X, Cao JD: Delay-dependent stability of neural networks of neutral type with time delay in the leakage term. Nonlinearity 2010, 23: 1709-1726. 10.1088/0951-7715/23/7/010
Li X, Rakkiyappan R, Balasubramanian P: Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations. J. Franklin Inst. 2011, 348: 135-155. 10.1016/j.jfranklin.2010.10.009
Li X, Fu X, Balasubramaniam P, Rakkiyappan R: Existence, uniqueness and stability analysis of recurrent neural networks with time delay in the leakage term under impulsive perturbations. Nonlinear Anal., Real World Appl. 2010, 11: 4092-4108. 10.1016/j.nonrwa.2010.03.014
Balasubramaniam P, Vembarasan V, Rakkiyappan R: Leakage delays in T-S fuzzy cellular neural networks. Neural Process. Lett. 2011, 33: 111-136. 10.1007/s11063-010-9168-3
Balasubramaniam P, Kalpana M, Rakkiyappan R: Global asymptotic stability of BAM fuzzy cellular neural networks with time delays in the leakage term, discrete and unbounded distributed delays. Math. Comput. Model. 2011, 53: 839-853. 10.1016/j.mcm.2010.10.021
Liu BW: Global exponential stability for BAM neural networks with time-varying delays in the leakage terms. Nonlinear Anal., Real World Appl. 2013, 14: 559-566. 10.1016/j.nonrwa.2012.07.016
Hilger S: Analysis on measure chains - a unified approach to continuous and discrete calculus. Results Math. 1990, 18: 18-56. 10.1007/BF03323153
Zhang Z, Liu K: Existence and global exponential stability of a periodic solution to interval general bidirectional associative memory (BAM) neural networks with multiple delays on time scales. Neural Netw. 2011, 24: 427-439. 10.1016/j.neunet.2011.02.001
Li YK, Chen XR, Zhao L: Stability and existence of periodic solutions to delayed Cohen-Grossberg BAM neural networks with impulses on time scales. Neurocomputing 2009, 72: 1621-1630. 10.1016/j.neucom.2008.08.010
Li YK, Gao S: Global exponential stability for impulsive BAM neural networks with distributed delays on time scales. Neural Process. Lett. 2010, 31: 65-91. 10.1007/s11063-009-9127-z
Zhang JM, Fan M, Zhu HP: Existence and roughness of exponential dichotomies of linear dynamic equations on time scales. Comput. Math. Appl. 2010, 59: 2658-2675.
Lakshmikantham V, Vatsala AS: Hybrid systems on time scales. J. Comput. Appl. Math. 2002, 141: 227-235. 10.1016/S0377-0427(01)00448-4
Li YK, Zhao KH: Robust stability of delayed reaction-diffusion recurrent neural networks with Dirichlet boundary conditions on time scales. Neurocomputing 2011, 74: 1632-1637. 10.1016/j.neucom.2011.01.006
Li YK, Zhang TW: Global exponential stability of fuzzy interval delayed neural networks with impulses on time scales. Int. J. Neural Syst. 2009, 19: 449-456. 10.1142/S0129065709002142
Li YK, Zhao KH, Ye Y: Stability of reaction-diffusion recurrent neural networks with distributed delays and Neumann boundary conditions on time scales. Neural Process. Lett. 2012, 36: 217-234. 10.1007/s11063-012-9232-2
Li YK, Wang C: Uniformly almost periodic functions and almost periodic solutions to dynamic equations on time scales. Abstr. Appl. Anal. 2011., 2011: Article ID 341520
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston; 2001.
Berman A, Plemmons R: Nonnegative Matrices in the Mathematical Science. Academic Press, New York; 1979.
Acknowledgements
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 10971183.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors typed, read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Y., Yang, L. & Sun, L. Existence and exponential stability of an equilibrium point for fuzzy BAM neural networks with time-varying delays in leakage terms on time scales. Adv Differ Equ 2013, 218 (2013). https://doi.org/10.1186/1687-1847-2013-218
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-218