Abstract
Environmental fluctuations and toxin-producing phytoplankton are crucial factors affecting marine ecosystems. In this paper, we propose a stochastic phytoplankton-toxin phytoplankton–zooplankton model to study the effect of environmental fluctuations on extinction and persistence of the population. The results show that large environmental fluctuations may lead to the extinction of the population, and small environmental fluctuation can keep population weakly persistent in the mean. We also find that the noise-induced extinction of one phytoplankton population may lead to the density increase of the other phytoplankton population in two competitive phytoplankton populations. By constructing appropriate Lyapunov functions, we obtain the sufficient conditions for the existence of an ergodic stationary distribution of the model. Finally, numerical simulations are carried out to support our main results.
Similar content being viewed by others
1 Introduction
Plankton includes plants and animals that float along at the mercy of the sea’s tides and currents. There are two main types of plankton, phytoplankton and zooplankton. Phytoplankton include microscopic organisms such as diatoms and dinoflagellates as well as blue-green algae. Zooplankton depends on the phytoplankton and other particulate matter that is found in the water for food. Phytoplankton is the chief source of food for the zooplankton. The significance of plankton for the wealth of the ocean ecosystems and ultimately for the planet itself is nowadays widely recognized. Therefore, many scholars have studied models of plankton [1, 2]. Caraballo et al. [1] considered a model in which one predator (zooplankton) has two preys of different sizes (phytoplankton). The authors first proved the existence of a global pullback attractor and then estimated the fractal dimension of the attractor by using Leonov’s theorem and constructing a proper Lyapunov function. In addition, many science researcher have devoted their efforts to investigating plankton dynamics through laboratory experiments and field studies. The studies show that many types of phytoplankton can release toxic chemicals, which have an important effect on plankton; see [3,4,5,6,7,8] and the references therein. Mathematical modeling is an important tool to study plankton dynamics and to understand the various mechanisms involved in toxin-producing phytoplankton [9, 10]. For example, Chattopadhayay et al. [6] using field studies and mathematical models confirmed that toxin-producing plankton may act as a biological control for planktonic blooms. Turner and Tester [7] revealed that the interplay between toxic phytoplankton and the zooplankton grazing on them gives rise to various situations, since, in some cases, the toxic phytoplankton does not cause any harm, but in other cases it causes serious damage if grazed. Therefore, the study of the toxin-producing phytoplankton population is an interesting and important topic in marine ecology. Mukhopadhyay et al. [11] investigated a nutrient-plankton model in an aquatic environment in the context of phytoplankton bloom and they observed that the zooplankton populations try to avoid the areas where toxin-producing phytoplankton density is high. Jin and Ma [12] considered the two plankton species having competitive and allelopathic effects on each other. In particular, Banerjee and Venturino [13] proposed the following model:
Here \(\varPi _{1}\), \(\varPi _{2}\) and ζ, respectively, denote the phytoplankton, toxin-producing phytoplankton and zooplankton populations. \(\rho _{i}\) denotes the growth rate of species i (\(i=1,2\)), \(K_{i}\) is the environmental carry capacity of species i (\(i=1,2\)), ã represents the action of the second population upon the growth rate of the first population, b̃ stands for the action of the first population upon the growth rate of the second population, \(\alpha _{1}\) is the capture rate, \(\frac{\alpha _{2}\varPi _{2}}{\beta _{2}+ \varPi _{2}^{2}}\) is the Monod–Haldane function, which represents zooplankton populations consuming the toxic-phytoplankton populations, \(e_{1}\) denotes the nutrition conversion rate for the \(\varPi _{1}\) to the ζ, \(e_{2}\) represents the effect of consuming \(\varPi _{2}\) on ζ, μ is the death rate of the zooplankton population. All parameters are assumed to be nonnegative and constant in time. And we assume that the zooplankton is able to recognize the two phytoplankton populations and when the toxic phytoplankton is ingested too much, and it will kill too much zooplankton; then the latter will decrease its consumption. This is modeled via a Monod–Haldane type functional response \(\frac{\alpha _{2}\varPi _{2}}{\beta _{2}+\varPi _{2}^{2}}\) [14], which increases to a maximum and then decreases again for larger values of the toxin-producing phytoplankton population. For more information, see Ref. [13] and the references therein.
Model (1.1) can be simplified to a dimensionless form with a reduced number of parameters by means of the transformation \(P(t)=K_{1}\varPi _{1}(t)\), \(T(t)=\sqrt{\beta _{2}}\varPi _{2}(t)\), \(Z(t)=e_{2}\sqrt{ \beta _{2}}\zeta (t)\), \(t=\frac{\tau }{e_{2}\alpha _{2}\beta _{2}\sqrt{ \beta _{2}}}\), then we obtain the following system:
Here
are positive constants.
It is well known that environmental fluctuation plays an important role in the study of ecosystems. Therefore, many authors have introduced stochastic white noise into deterministic models to describe the effect of random noise [15,16,17,18,19,20,21,22,23,24,25,26,27]. For example, Han et al. [16] obtained two systems admitting a unique random attractor under some conditions. They also obtained conditions under which coexistence of species exists for the random system. Yuan et al. [19] considered a nutrient-phytoplankton model with toxin-producing phytoplankton under environmental fluctuations. The obtained results suggested that toxin-producing phytoplankton and environmental fluctuations play a key role in the termination of algal blooms. Colucci et al. [20] studied semi-Kolmogorov models for plankton. For the random semi-Kolmogorov system they also obtained sufficient conditions for the existence of a global random attractor. Therefore, it is meaningful to further incorporate the environmental fluctuation into the underlying model (1.2), which could provide us a deeper understanding for the realistic aquatic ecosystems. Inspired by the above-mentioned facts, we get the following stochastic model:
where \(B_{i}(t)\) are standard Brownian motions. \(\sigma _{i}^{2}\) denotes the intensity of the white noise. Recently, a few studies about the effect of environmental fluctuations on aquatic ecosystems have been carried out, it is worth noting that in this paper, we split the phytoplankton, identifying the toxic-producing subpopulation, in other words, the considered system includes three species: phytoplankton, toxic phytoplankton, and zooplankton; we investigate the effect of the environmental fluctuations on this system. To the best of our knowledge, the results about the stochastic phytoplankton-toxin phytoplankton–zooplankton model are few. We will devote our main attention to the analysis of model (1.3). First, we study the persistence or extinction of the populations. Then we prove the existence of a stationary distribution.
The rest of this paper is organized as follows. Some related preliminaries are given in the next section. In Sect. 3, we prove the existence of the global positive solution and establish the threshold between weakly persistence in the mean and extinction in Sect. 4. Sufficient conditions for the stationary distribution and its ergodic of model (1.3) are established by using a Lyapunov function in Sect. 5. Finally, in order to illustrate our results, some numerical simulations and discussions are presented in Sect. 6.
2 Preliminaries
From now on, unless otherwise specified, let \((\varOmega ,\mathscr{F},\{ \mathscr{F}_{t}\}_{t\geq 0},P)\) denote a complete probability space with a filtration \(\{\mathscr{F}_{t}\}_{t\geq 0}\) satisfying the usual conditions (i.e. it is right continuous and \(\mathscr{F}_{0}\) contains all P-null sets). Let us consider an n-dimensional stochastic differential equation:
with the initial \(x(0)=x_{0}\in R^{n}\), where \(W(t)\) denotes an m-dimensional standard Wiener process. A definite a \(C^{2}\)-function V, applying Itõ’s formula, yields
where
Definition 2.1
-
(i)
Population \(x(t)\) is said to be extinct if \(\lim_{t\rightarrow \infty }x(t)=0\) almost surely.
-
(ii)
Population \(x(t)\) is said to be weakly persistent in the mean if there exists a constant \(N>0\) such that \(\limsup_{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}{x(s)\,ds}\leq N\) almost surely.
-
(iii)
Population \(x(t)\) is said to be strongly persistent in the mean if there exists a constant \(N>0\) such that \(\limsup_{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}{x(s)\,ds}\geq N\) almost surely.
-
(iv)
Population \(x(t)\) is said to be persistent in the mean if there exists a constant \(N>0\) such that \(\lim_{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}{x(s)\,ds}= N\) almost surely.
Next, we will present some lemmas which will be used in the following sections.
Lemma 2.1
([30])
Let \(M=\{M_{t}\}_{t}\geq 0\) be a real-valued continuous local martingale, then
and
Lemma 2.2
([31])
Let \(X(t)\in R_{+}\) and \(g(t)\) be two stochastic process satisfying \(\lim_{t\rightarrow \infty } \frac{g(t)}{t}=0\) a.s.
-
(i)
If there exist three positive constants \(t_{0}\), β and \(\beta _{0}\) such that, for all \(t\geq t_{0}\),
$$ \ln X(t)\leq \beta t-\beta _{0} \int _{0}^{t}{X(s)\,ds}+g(t), $$then
$$ \limsup_{t\rightarrow +\infty }\frac{1}{t} \int _{0}^{t}{X(s)\,ds} \leq \frac{\beta }{\beta _{0}}, \quad \textit{a.s.} $$ -
(ii)
If there exist three positive constants \(t_{0}\), β and \(\beta _{0}\) such that, for all \(t\geq t_{0}\),
$$ \ln X(t)\geq \beta t-\beta _{0} \int _{0}^{t}{X(s)\,ds}+g(t), $$then
$$ \liminf_{t\rightarrow +\infty }\frac{1}{t} \int _{0}^{t}{X(s)\,ds} \geq \frac{\beta }{\beta _{0}}, \quad \textit{a.s.} $$
3 Existence and uniqueness of globally positive solution
In this section, we show that there is a unique local positive solution for the system (1.3) and then we prove that this solution is global by constructing a suitable Lyapunov function. To the best of our knowledge, in order to guarantee that a stochastic differential equation has a unique local positive solution, the coefficients of the equation should satisfy the linear growth condition and the local Lipschitz condition. Therefore, we establish the following theorem.
Theorem 3.1
For any positive initial value \((P(0),T(0),Z(0)) \in R_{+}^{3}\), there exists a unique global positive solution of model (1.3), and the solution remains in the region \(R_{+}^{3}\) with probability one.
Proof
Let \(u(t)=\ln P(t)\), \(v(t)=\ln T(t)\), \(w(t)=\ln Z(t)\), by use of the Itô formula, we get
with initial values \(u(0)=\ln P(0)\), \(v(0)=\ln T(0)\), \(w(0)=\ln Z(0)\). Obviously, model (3.1) meets the local Lipschitz condition. Hence there exists a unique local solution \((u(t),v(t),w(t))\) for \(t\in [0,\tau _{e})\), where \(\tau _{e}\) is the explosion time. The system (1.3) is equivalent to the system (3.1). So, for the system (1.3) there exists a local solution \((P(t),T(t),Z(t))\) on \(t\in [0,\tau _{e})\), for an arbitrary initial value \((P(0),T(0),Z(0))\in R_{+}^{3}\). Now, we need to prove \(\tau _{e}=\infty \) a.s. Let \(k_{0}>0\) be sufficiently large such that each component of the initial value \((P(0),T(0),Z(0))\) lies within the interval \([\frac{1}{k_{0}},k_{0}]\) when \(k\geq k_{0}\). Define the stopping time
Throughout this paper we set \(\inf \emptyset =\infty \) (as usual ∅ denotes the empty set). Clearly, \(\tau _{k}\) is increasing as \(k\rightarrow \infty \). Set \(\tau _{\infty }= \lim_{k \rightarrow \infty } \tau _{k}\), hence \(\tau _{\infty } \leq \tau _{e}\) a.s. If we can show that \(\tau _{\infty }= \infty \) a.s., then \(\tau _{e} =\infty \) a.s. The proof will go by contradiction. If this statement is false, then there exist a pair of constants \(T >0\) and \(\varepsilon \in (0,1)\) such that \(P\{\tau _{k} \leq T\} \geq \varepsilon \) for any \(k\geq k_{0}\).
Define a \(\mathcal{C}^{2}\)-function \(V:R^{3}_{+}\rightarrow R_{+}\) as follows:
where \(V_{1}(P,T,Z)=AP-\ln P-1-\ln A\), \(V_{2}(P,T,Z)=T-1-\ln T\), \(V_{3}(P,T,Z)=B(Z-1-\ln Z)\), A, B are positive constants to be determined later. Obviously, this function is nonnegative.
An application of the Itô formula to \(V_{1}\) yields
Analogously
and
Hence
Choose \(A=\frac{ce+2e}{cm}\), \(B=\frac{(c+2)e+m}{m^{2}} \), then
Then \(dV\leq M\,dt+\sigma _{1}A(P-1)\,dB_{1}(t)+\sigma _{2}(T-1)\,dB_{2}(t)+ \sigma _{3}B(Z-1)\,dB_{3}(t)\).
Integrating both sides from 0 to \(\tau _{k} \wedge T\), and taking the expectation, we get
By the definition of stopping time, substituting k and \(\frac{1}{k}\) into \(V(P(0),T(0),Z(0))\), which implies that
Next,
Letting \(k\rightarrow \infty \) gives
which contradicts the assumption; then we must have \(P(\tau _{\infty }= \infty )=1\). Therefore, the solution will not explode in a finite time with probability one. This completes the proof. □
4 Weakly persistent in the mean and extinction
In this section, we will study the long time behavior of stochastic model (1.3) and show that the population will be weakly persistent in the mean when the intensity of noises is small. Otherwise, if the intensity of noises is sufficiently large, the population will become extinct with probability one.
Theorem 4.1
Let \((P(t),T(t),Z(t))\) be a solution of model (1.3).
-
(i)
If \(r_{1}>\frac{\sigma _{1}^{2}}{2}\), \(r_{2}> \frac{\sigma _{2}^{2}}{2}\) and \(r_{1}(e-m)>e\frac{\sigma _{1}^{2}}{2}+r _{1}\frac{\sigma _{3}^{2}}{2}\), then the populations \(P(t)\), \(T(t)\) and \(Z(t)\) are weakly persistent in the mean.
-
(ii)
If \(r_{1}>\frac{\sigma _{1}^{2}}{2}\), \(r_{2}< \frac{\sigma _{2}^{2}}{2}\) and \(r_{1}(e-m)>e\frac{\sigma _{1}^{2}}{2}+r _{1}\frac{\sigma _{3}^{2}}{2}\), then the populations \(P(t)\) and \(Z(t)\) are weakly persistent in the mean, the population \(T(t)\) is extinct.
-
(iii)
If \(r_{1}<\frac{\sigma _{1}^{2}}{2}\), \(r_{2}> \frac{\sigma _{2}^{2}}{2}\), then the populations \(P(t)\) and \(Z(t)\) are extinct, the population \(T(t)\) is weakly persistent in the mean.
-
(iv)
If \(r_{1}<\frac{\sigma _{1}^{2}}{2}\), \(r_{2}< \frac{\sigma _{2}^{2}}{2}\), then the population \(P(t)\), \(T(t)\) and \(Z(t)\) are extinct.
Proof
By using Itô’s formula in (1.3), we have
and from (4.1), we furthermore obtain
integrating both sides of (4.4) from 0 to t gives the following inequality:
denoting \(\varTheta (t)=M_{1}(t)+\ln P(0)=\sigma _{1}B_{1}(t)+\ln P(0)\). We can get \(\lim_{t\rightarrow \infty }\frac{\varTheta (t)}{t}=0\). By Lemmas 2.1 and 2.2, we have
So, following the above conditions \(r_{1}>\frac{\sigma _{1}^{2}}{2}\), we see that the population \(P(t)\) is weakly persistent in the mean.
From (4.2), we have
integrating both sides of (4.7) from 0 to t gives the following inequality:
letting \(f(t)=M_{2}(t)+\ln T(0)=\sigma _{2}B_{2}(t)+\ln T(0)\). It is easy to get \(\lim_{t\rightarrow \infty }\frac{f(t)}{t}=0\). Similarly, we have
For \(r_{2}>\frac{\sigma ^{2}_{2}}{2}\), the population \(T(t)\) is weakly persistent in the mean.
According to a similar method in [32], we can get
and
From (4.1), we can get
Applying Lemma 2.1, combining with (4.10), yields
Similarly, from (4.3), we have
Together with (4.12) and (4.13), this yields
The condition \(r_{1}(e-m)>e\frac{\sigma _{1}^{2}}{2}+r_{1}\frac{\sigma _{3}^{2}}{2}\) implies that \(\frac{1}{c}(r_{1}- \frac{\sigma _{1}^{2}}{2})-\frac{r_{1}}{ce}(m+\frac{\sigma _{3}^{2}}{2})>0\), hence, the population \(Z(t)\) is weakly persistent in the mean, thus we complete the proof of (i).
In (ii), we have only to prove that \(r_{2}<\frac{\sigma _{2}^{2}}{2}\) implies \(\lim_{t\rightarrow +\infty }T(t)=0\) a.s.
If \(r_{2}<\frac{\sigma _{2}^{2}}{2}\), from (4.8), we can obtain
dividing both sides of (4.14) by t and taking the limit, by Lemma 2.1, we have \(\lim_{t\rightarrow +\infty }\frac{\ln T(t)}{t}<0\) a.s.; thus the population \(T(t)\) is extinct.
(iii) If \(r_{1}<\frac{\sigma _{1}^{2}}{2}\), \(r_{2}> \frac{\sigma _{2}^{2}}{2}\), from the above proof, we know that the population \(P(t)\) is extinct, the population \(T(t)\) is weakly persistent in the mean. From (4.3), it is easy to see that
We denote \(G(t)=\sigma _{3}B_{3}(t)+\ln Z(0)\). We get \(\lim_{t\rightarrow \infty }\frac{G(t)}{t}=0\). Dividing both sides of (4.15) by t and taking the limit, we have \(\lim_{t\rightarrow +\infty }\frac{\ln Z(t)}{t}<0\) a.s., that is, the population \(Z(t)\) is extinct.
The result of (iv) comes from the proofs (ii) and (iii), so we omit it. The proof is complete. □
Remark 4.1
From (i), (ii) of Theorem 4.1, we know all populations preserve some stability under small noise and large noise may lead to the extinction of the toxic-phytoplankton population. From (iii) of Theorem 4.1, we find that the noise-induced extinction of \(P(t)\) contributes the density increase of \(T(t)\), thus noise-induced extinction of nontoxic phytoplankton may lead to more serious outbreaks of the toxic phytoplankton and furthermore if there is excessive consumption of toxin phytoplankton by zooplankton this will lead to its extinction. The results also reflect that if the reproduction rate of the population is dominated by the environmental noise, the population will go in extinction. Otherwise, the population will be weakly persistent in the mean.
Remark 4.2
By \(r_{1}=\frac{\rho _{1}}{e_{2}\alpha _{2}\beta _{2}\sqrt{\beta _{2}}}\), \(r_{2}=\frac{\rho _{2} }{e_{2}\alpha _{2}\beta _{2}\sqrt{\beta _{2}}}\), \(e=\frac{e_{1}K_{1}\alpha _{1}}{e_{2}\alpha _{2}\beta _{2}\sqrt{\beta _{2}}}\), \(m=\frac{\mu }{e_{2}\alpha _{2}\beta _{2}\sqrt{\beta _{2}}}\), we can know that the \(r_{i}\) (\(i=1,2\)) are proportional to \(\rho _{i}\) (the growth rate of species i), respectively; m is proportional to μ (the death rate); e is proportional to the product of \(e_{1}\) (the nutrition conversion rate) and \(\alpha _{1}\) (the capture rate). From (i), (ii), (iii) and (iv) of Theorem 4.1, one can see that a small noise (\(\sigma _{i}\)) and a large growth rate (\(\rho _{i}\)) lead to the persistence of phytoplankton populations. Meanwhile, a high nutrient conversion rate (\(e_{1}\)) from P to Z, a high predation rate (\(\alpha _{1}\)) of Z to P, a small death rate (μ) and a small noise (\(\sigma _{1}\) and \(\sigma _{3}\)) contribute to the persistence of the zooplankton population.
5 Existence of an ergodic stationary distribution
In the study of a zooplankton and phytoplankton deterministic model, the stability of each equilibrium is our main concern. For a stochastic model, we concentrate on the existence of the unique stationary distribution. For the plankton system, one of the most important things is to investigate the persistence of the population. Meanwhile, the existence of stationary distribution implies that the populations are persistent. Therefore, it is very meaningful to obtain the unique ergodic stationary distribution. In the following, based on the theory of Has’minskii [33], we will prove that the system (1.3) has a stationary distribution which is ergodic when the white noises are not particularly large. Let \(X(t)\) be a homogeneous Markov process in \(R^{d}\) of the stochastic differential equation \(dX(t)=b(X)\,dt+\sum_{r=1}^{k}g_{r}(X)\,dB_{r}(t)\), then the diffusion matrix is defined as \(A(x)=(a_{ij}(x))\), \(a_{ij}(x)=\sum_{r=1}^{k}g^{i} _{r}(x)g^{j}_{r}(x)\).
Lemma 5.1
([33])
The Markov process \(X(t)\) has a unique ergodic stationary distribution \(\mu (\cdot )\) if there exists a bounded open domain \(U\subset R^{n}\) with regular boundary Γ, having the following properties:
- \(A_{1}\)::
-
the diffusion matrix \(A(x)\) is strictly positive definite for all \(x\in U\);
- \(A_{2}\)::
-
there exists a nonnegative \(C^{2}\)-function V such that LV is negative for any \(R^{d}\backslash U\).
Assumption 5.1
Assume that
where \(M=r_{1}-\frac{\sigma _{1}^{2}}{2}+r_{2}- \frac{\sigma _{2}^{2}}{2}-\frac{1}{2}-m-\frac{\sigma _{3}^{2}}{2}\), \(M_{1}=\frac{H(r_{2}+a+\frac{r_{2}}{H})^{2}}{4r_{2}}\), \(M_{2}=\frac{( \frac{ec+2e+cm}{cm}r_{1}+b)^{2}cm}{4(c+2)er_{1}}\).
Theorem 5.1
Under Assumption 5.1, the system (1.3) has a unique ergodic stationary distribution \(\mu (\cdot )\) for any initial value \((P(0),T(0),Z(0))\in R^{3}_{+}\).
Proof
In order to prove Theorem 5.1, one only needs to validate conditions \(A_{1}\) and \(A_{2}\) of Lemma 5.1. The diffusion matrix of the system (1.3) is given by
Clearly, the matrix A is positive definite for any compact \(R_{+}^{3}\), so the condition \(A_{1}\) of Lemma 5.1 holds.
Construct a \(C^{2}\)-function \(W:R_{+}^{3} \rightarrow R\)
where \(c_{1}\) and \(c_{2}\) are positive constants which will be determined later. Obviously, \(W(P,T,Z)\) is a nonnegative function. According to the Itô formula, then
and
Hence, we get
Choose \(c_{1}=\frac{e}{c}c_{2}\) and \(c_{2}=\frac{c+2}{m}\), then
Now, we define a closed set
where \(0<\epsilon <1\) is a sufficiently small number such that
In addition, we denote
Then \(R_{+}^{3}\setminus U_{\epsilon }=D_{\epsilon }^{1}\cup D_{ \epsilon }^{2}\cup D_{\epsilon }^{3}\cup D_{\epsilon }^{4}\cup D_{ \epsilon }^{5}\cup D_{\epsilon }^{6}\) and on each \(D_{\epsilon }^{i}\) we have the following.
Case 1. On \(D_{\epsilon }^{1}\), we have \(0< P<\epsilon \),
where \(K_{1}=\frac{1}{2}[ \frac{H(r_{2}+a+\frac{r_{2}}{H})^{2}}{4r_{2}}-M]<0\). In fact, it follows from (5.4) and Assumption 5.1 that \(K_{1}<0\).
Case 2. On \(D_{\epsilon }^{2}\), we have \(0< T<\epsilon \),
where \(K_{2}=\frac{1}{2}[\frac{(\frac{ec+2e+cm}{cm}r_{1}+b)^{2}cm}{4(c+2)er _{1}}-M]<0\). In fact, it follows from (5.5) and Assumption 5.1 that \(K_{2}<0\).
Case 3. On \(D_{\epsilon }^{3}\), we have \(0< Z<\epsilon \),
where \(K_{3}=\frac{1}{2}(M_{1}+M_{2}-M)<0\). In fact, it follows from (5.6) and Assumption 5.1 that \(K_{3}<0\).
Case 4. On \(D_{\epsilon }^{4}\), we have \(P>\frac{1}{\epsilon }\),
where \(K_{4}=\sup_{(P,T,Z)\in R_{+}^{3}}\{-\frac{ce+2e}{2cm}r_{1}P ^{2}+(\frac{ce+cm+2e}{cm}r_{1}+b)P-\frac{r_{2}}{H}T^{2}+(r_{2}+a+\frac{r _{2}}{H})T-Z-M\}\). In fact, it follows from (5.7) that \(LW\leq -1\).
Case 5. On \(D_{\epsilon }^{5}\), we have \(T>\frac{1}{\epsilon }\),
where \(K_{5}=\sup_{(P,T,Z)\in R_{+}^{3}}\{-\frac{ce+2e}{cm}r_{1}P^{2}+( \frac{ce+cm+2e}{cm}r_{1}+b)P-\frac{r_{2}}{2H}T^{2}+(r_{2}+a+\frac{r _{2}}{H})T-Z-M\}\). In fact, it follows from (5.8) that \(LW\leq -1\).
Case 6. On \(D_{\epsilon }^{5}\), we have \(Z>\frac{1}{\epsilon }\),
where \(K_{6}=M_{1}+M_{2}-M\). In fact, it follows from (5.9) that \(LW\leq -1\).
In conclusion, we can obtain that \(LW\leq \min \{K_{1},K_{2},K_{3},-1 \}\), \((P,T,Z)\in R_{+}^{3}\setminus D_{\epsilon }\). Then, the conclusion follows from \(A_{2}\) of Lemma 5.1.
Thus, according to Lemma 5.1, the system (1.3) admits a unique ergodic stationary distribution \(\mu (\cdot )\). This completes the proof. □
Remark 5.1
From the expression of Π, we can see that, as \(\sigma _{i}\) gets smaller, Π gets bigger. When \(\sigma _{i}\) (\(i=1,2,3\)) is big enough, Π is less than 0. Hence, environmental noise plays an important role in population persistence.
6 Numerical analysis and discussions
In this paper, according to the fact that the environmental fluctuation has a great effect on the aquatic ecosystem, we propose and investigate a stochastic phytoplankton-toxin phytoplankton–zooplankton model. Without the effects of environmental fluctuations, Banerjee and Venturino [13] gave a comprehensive analysis and showed that the toxic phytoplankton does not drive the zooplankton population towards extinction. With the effects of environmental fluctuations, we have proved the existence of global positive solution of the investigated model and obtain the sufficient conditions for weakly persistence in the mean and extinction of the plankton. We also investigate the existence of ergodic stationary distribution by constructing a suitable Lyapunov function. The results show that a large environmental fluctuation may lead to the extinction of the population, and small environmental fluctuation can keep population weakly persistent in the mean. We also find that the noise-induced extinction of one phytoplankton population may lead to the density increase of the other phytoplankton population in two competitive phytoplankton populations. Thus noise-induced extinction of non-toxic-phytoplankton population may lead to an outburst of toxic-phytoplankton population. In the following, we will verify our main results with the help of a numerical method which is based on the work of [34, 35].
The following example concerns the extinction and weakly persistent in the mean of the populations.
Example 6.1
Let the parameters be \(r_{1}=0.6\), \(r_{2}=0.7\), \(a=0.1\), \(b=0.9\), \(c=1.35\), \(e=1.63\), \(m=0.3\), \(H=0.33\).
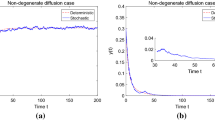
(i) Fix \(\sigma _{1}=0.1\) and \(\sigma _{3}=0.05\), let \(\sigma _{2}\) vary to see the effect of noise on the dynamics of model (1.3). We first take \(\sigma _{2}=0.1\), it is easy to compute that \(r_{1}-\frac{\sigma _{1} ^{2}}{2}=0.595>0\), \(r_{2}-\frac{\sigma _{2}^{2}}{2}=0.695>0\) and \(r_{1}(e-m)-(e\frac{\sigma _{1}^{2}}{2}+r_{1}\frac{\sigma _{3}^{2}}{2})=0.7891>0\), in view of (i) of Theorem 4.1, the populations \(P(t)\), \(T(t)\) and \(Z(t)\) are weakly persistent in the mean (see Fig. 1). Changing \(\sigma _{2}\) from \(\sigma _{2}=0.1\) to \(\sigma _{2}=1.2\), we obtain that \(r_{1}-\frac{\sigma _{1}^{2}}{2}=0.595>0\), \(r_{2}- \frac{\sigma _{2}^{2}}{2}=-0.02<0\) and \(r_{1}(e-m)-(e\frac{\sigma _{1} ^{2}}{2}+r_{1}\frac{\sigma _{3}^{2}}{2})=0.7891>0\) which satisfy the conditions (ii) of Theorem 4.1, the populations \(P(t)\) and \(Z(t)\) are weakly persistent in the mean and the population \(T(t)\) goes to extinction (see Fig. 2). From Fig. 1, we can find that phytoplankton, toxic-phytoplankton and zooplankton population reach the steady state value after some transient oscillations for the deterministic model, while all populations fluctuate around the steady state values of the corresponding deterministic models for a stochastic model. Figures 1 and 2 show that, under small noise, all populations preserve some stability and large noise may lead to the extinction of the toxic-phytoplankton population. The results also reflect that if the reproduction rate of the population is dominated by the environmental noise, the population will go to extinction. Otherwise, the population will be weakly persistent in the mean.
Next, we focus on Figs. 1 and 5, the populations \(P(t)\), \(T(t)\) and \(Z(t)\) are persistent for corresponding deterministic model of model (1.3). From Fig. 1, we can see that the populations \(P(t)\), \(T(t)\) and \(Z(t)\) are weakly persistent for stochastic model (1.3). However, if we only increase the values of \(\sigma _{i}\) (\(i=1,2,3\)) from 0.1, 0.1, 0.05 to 1.1, 1.2, 1, respectively, all the other parameters being the same as for Fig. 1 (see Fig. 5), we can find that all the populations \(P(t)\), \(T(t)\) and \(Z(t)\) go extinct, which furthermore indicates that a large fluctuation plus conditions that ensure the persistence of the deterministic model allow extinction for the solutions of the stochastic model.
(ii) Fix \(\sigma _{2}=0.1\) and \(\sigma _{3}=0.05\), letting \(\sigma _{1}\) vary from \(\sigma _{1}=0.1\) to \(\sigma _{1}=1.1\), when \(\sigma _{1}=0.1\), we check that \(r_{1}-\frac{\sigma _{1}^{2}}{2}=-0.005<0\), \(r_{2}-\frac{ \sigma _{2}^{2}}{2}=0.695>0\) and by (iii) of Theorem 4.1, both the populations \(P(t)\) and \(Z(t)\) are in extinction, the population \(T(t)\) is weakly persistent in the mean (see Fig. 3). The results imply that if zooplankton feeds enough on the toxin phytoplankton, it is driven to extinction. Figure 3 also shows that the noise-induced extinction of \(P(t)\) contributes the density increase of \(T(t)\), which fluctuates around a much higher density level than that of the deterministic counterpart. Thus a noise-induced extinction of nontoxic phytoplankton may lead to more serious outbreaks of the toxic phytoplankton. From Figs. 2 and 3, we also find the interesting phenomenon that the noise-induced extinction of one phytoplankton population may lead to a density increase of the other phytoplankton population in two competitive phytoplankton populations. Furthermore, if we fix \(\sigma _{1}=1.1\) and \(\sigma _{3}=0.05\) and change \(\sigma _{2}\) from \(\sigma _{2}=0.1\) to \(\sigma _{2}=1.2\), we can easily derive that \(r_{1}-\frac{\sigma _{1} ^{2}}{2}=-0.005<0\), \(r_{2}-\frac{\sigma _{2}^{2}}{2}=-0.02<0\); according to (iv) of Theorem 4.1, the populations \(P(t)\), \(T(t)\) and \(Z(t)\) are in extinction, which is shown in Fig. 4.
To further illustrate the existence of a stationary distribution, we consider the following example.
Example 6.2
We choose the parameters as \(r_{1}=0.6\), \(r_{2}=0.7\), \(a=0.1\), \(b=0.9\), \(c=1.35\), \(e=1.63\), \(m=0.3\), \(H=0.33\), \(\sigma _{1}=0.1\), \(\sigma _{2}=0.1\), \(\sigma _{3}=0.05\). By a simple computation, we obtain \(M=0.4887\), \(M_{1}=0.1626\), and \(M_{2}= 0.0874\). Furthermore, \(\varPi = 0.2387>0\). That is to say, the condition of Theorem 5.1 holds, for the system (1.3) exists a unique ergodic stationary distribution \(\mu (\cdot )\) (see Fig. 5).
The figure shows the frequency histogram of \(P(t)\), \(T(t)\) and \(Z(t)\) for model (1.3) with the initial value \((P(0),T(0),Z(0))=(0.2,0.1,0.4)\), and \(\sigma_{1}=0.1\), \(\sigma_{2}=0.1\), \(\sigma_{3}=0.05\)
References
Caraballo, T., Colucci, R., Han, X.: Non-autonomous dynamics of a semi-Kolmogorov population model with periodic forcing. Nonlinear Anal., Real World Appl. 31, 661–680 (2016)
Wen, X., Yin, H., Wei, Y.: Dynamics of stochastic non-autonomous plankton-allelopathy system. Adv. Differ. Equ. 2015, 327 (2015)
Seliger, H.: Toxic phytoplankton blooms in the sea. Limnology Oceanography 39(1), 210–211 (1994)
Wells, M.L., Trainer, V.L., Smayda, T.J., Karlson, B.S.O., Trick, C.G., Kudela, R.M., Ishikawa, A., Bernard, S., Wulff, A., Anderson, D.M., Cochlan, W.P.: Harmful algal blooms and climate change: learning from the past and present to forecast the future. Harmful Algae 49, 68–93 (2015)
Rafuse, C., Cembella, A., Laycock, M., Jellett, J.: Rapid monitoring of toxic phytoplankton and zooplankton with a lateral-flow immunochromatographic assay for asp and psp toxins. In: Harmful Algae 2002 (2004)
Chattopadhayay, J., Sarkar, R.R., Mandal, S.: Toxin-producing plankton may act as a biological control for planktonic blooms-field study and mathematical modelling. J. Theor. Biol. 3, 333–344 (2002)
Turner, J.T., Tester, P.A.: Toxic marine phytoplankton, zooplankton grazers, and pelagic food webs. Limnol. Oceanogr. 5, 1203–1214 (1997)
Bandyopadhyay, M., Saha, T., Pal, R.: Deterministic and stochastic analysis of a delayed allelopathic phytoplankton model within fluctuating environment. Nonlinear Anal. 3, 958–970 (2008)
Jang, S.R.-J., Allen, E.J.: Deterministic and stochastic nutrient–phytoplankton–zooplankton models with periodic toxin producing phytoplankton. Appl. Math. Comput. 271, 52–67 (2015)
Ruan, S.: Persistence and coexistence in zooplankton–phytoplankton–nutrient models with instantaneous nutrient recycling. J. Math. Biol. 6, 633–654 (1993)
Mukhopadhyay, B., Bhattacharyya, R.: Modelling phytoplankton allelopathy in a nutrient-plankton model with spatial heterogeneity. Ecol. Model. 1–2, 163–173 (2006)
Zhen, J., Ma, Z.: Periodic solutions for delay differential equations model of plankton allelopathy. Comput. Math. Appl. 44, 491–500 (2002)
Banerjee, M., Venturino, E.: A phytoplankton-toxic phytoplankton–zooplankton model. Ecol. Complex. 3, 239–248 (2011)
Pal, R., Basu, D., Banerjee, M.: Modelling of phytoplankton allelopathy with Monod–Haldane-type functional response a mathematical study. Biosystems 3, 243–253 (2009)
Liu, Q., Jiang, D., Hayat, T., Alsaedi, A.: Stationary distribution of a stochastic delayed sveir epidemic model with vaccination and saturation incidence. Physica A 512, 849–863 (2018)
Caraballo, T., Colucci, R., Han, X.: Predation with indirect effects in fluctuating environments. Nonlinear Dyn. 1, 115–126 (2016)
Wei, C., Liu, J., Zhang, S.: Analysis of a stochastic eco-epidemiological model with modified Leslie–Gower functional response. Adv. Differ. Equ. 2018, 119 (2018)
Wang, W., Cai, Y., Ding, Z., Gui, Z.: A stochastic differential equation sis epidemic model incorporating Ornstein–Uhlenbeck process. Physica A 509, 921–936 (2018)
Yu, X., Yuan, S., Zhang, T.: The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms. Nonlinear Dyn. 3, 1653–1668 (2018)
Caraballo, T., Colucci, R., Han, X.: Semi-Kolmogorov models for predation with indirect effects in random environments. Discrete Contin. Dyn. Syst., Ser. B 7, 2129–2143 (2016)
Lu, R., Wei, F.: Persistence and extinction for an age-structured stochastic svir epidemic model with generalized nonlinear incidence rate. Physica A 513, 572–587 (2019)
Liu, J., Chen, L., Wei, F.: The persistence and extinction of a stochastic sis epidemic model with logistic growth. Adv. Differ. Equ. 2018, 28 (2018)
Liu, M., Du, C., Deng, M.: Persistence and extinction of a modified Leslie–Gower Holling-type ii stochastic predator–prey model with impulsive toxicant input in polluted environments. Nonlinear Anal. 27, 177–190 (2018)
Meng, X., Li, F., Gao, S.: Global analysis and numerical simulations of a novel stochastic eco-epidemiological model with time delay. Appl. Math. Comput. 339, 701–726 (2018)
Zhang, S., Meng, X., Feng, T., Zhang, T.: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. 26, 19–37 (2017)
Ji, C., Jiang, D.: The extinction and persistence of a stochastic sir model. Adv. Differ. Equ. 2017, 3 (2017)
Lv, X., Wang, L., Meng, X.: Global analysis of a new nonlinear stochastic differential competition system with impulsive effect. Adv. Differ. Equ. 2017, 296 (2017)
Wang, W., Ma, Z.: Permanence of populations in a polluted environment. Math. Biosci. 122, 235–248 (1994)
Liu, M., Wang, K.: Survival analysis of stochastic single-species population models in polluted environments. Ecol. Model. 9–10, 1347–1357 (2009)
Liu, M., Wang, K., Wu, Q.: Survival analysis of stochastic competitive models in a polluted environment and stochastic competitive exclusion principle. Bull. Math. Biol. 9, 1969–2012 (2011)
Liu, Y., Liu, Q., Liu, Z.: Dynamical behaviors of a stochastic delay logistic system with impulsive toxicant input in a polluted environment. J. Theor. Biol. 329, 1–5 (2013)
Ji, C., Jiang, D., Shi, N.: Analysis of a predator–prey model with modified Leslie–Gower and Holling-type ii schemes with stochastic perturbation. J. Math. Anal. Appl. 2, 482–498 (2009)
Khasminskii, R.: Stochastic Stability of Differential Equations. Sijthoff & Noordhoff, Rockville (1980)
Higham, D.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43, 525–546 (2001)
Mao, X., Yuan, C., Yin, G.: Numerical method for stationary distribution of stochastic differential equations with Markovian switching. J. Comput. Appl. Math. 1, 1–27 (2005)
Funding
This work is supported by Fujian Provincial Natural Science of China (2018J01418) and the Natural Science Foundation of China (11301216).
Author information
Authors and Affiliations
Contributions
The authors have contributed to the manuscript on an equal basis. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, Z., Zhang, S. & Wei, C. Dynamics of a stochastic phytoplankton-toxin phytoplankton–zooplankton model. Adv Differ Equ 2019, 347 (2019). https://doi.org/10.1186/s13662-019-2251-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2251-9