1 Introduction

Fractional differential equations (FDEs) refer to a class of differential equations which use derivatives of non-integer order [1, 2]. Fractional equations have proved to be very reliable models for many scientific and engineering problems [3, 4]. Because it is difficult to solve complex fractional problems analytically, more and more work focuses on numerical solutions [5, 6].

Recently, there has been great interest in FDEs [7–12]. Ahmad et al. [7] discussed the existence of the solution of a Caputo fractional reaction-diffusion equation with various boundary conditions. Rida et al. [8] applied the generalized differential transform method to solve nonlinear fractional reaction-diffusion partial differential equations. Chen et al. used the explicit finite-difference approximation [9] and implicit difference approximation [10] to solve the Riesz space fractional reaction-dispersion equation.

The numerical methods for FDEs include finite-difference methods [13, 14], finite element methods [15] and spectral methods [16–20]. Fractional reaction-diffusion equations are related to spatial and time coordinates, so the numerical solutions are often time-consuming. Large scale applications and algorithms in science and engineering such as neutron transport [21–23], computational fluid dynamics [24–26], large sparse systems [27] rely on parallel computing [24, 28, 29]. In order to overcome the difficulty, parallel computing has been introduced into the numerical solutions for fractional equations [30–32]. Kai Diethelm [31] parallelized the fractional Adams-Bashforth-Moulton algorithm for the first time and the execution time of the algorithm was efficiently reduced. Gong et al. [33] presented a parallel solution for time fractional reaction-diffusion equation with explicit difference method. In the parallel solver, the technology named pre-computing fractional operator was used to optimize performance.

In this paper, we address an efficient parallel algorithm for time fractional reaction-diffusion equation with an implicit finite-difference method. In this parallel algorithm, the system of linear tridiagonal equations, vector-vector additions and constant-vector multiplications are efficiently processed in parallel. The linear tridiagonal system is parallelized with a new elimination method, which is effective and has simplicity in computer programming. The results indicate there is no significant difference between the implementation and the exact solution. The parallel algorithm with 16 parallel processes on two eight-core Intel Xeon E5-2670 CPUs runs 14.55 times faster than the serial algorithm.

This paper focuses on the Caputo fractional reaction-diffusion equation:

$$ \left \{ \textstyle\begin{array}{l} {}{}_{0}^{\mathrm{C}}D_{t}^{\alpha}u(x,t) +\mu u(x,t) =\frac{\partial^{2} u(x,t)}{\partial x^{2}} +K f(x,t) \quad (0< \alpha< 1), \\ u(x,0) =\phi(x),\quad x \in[0,x_{R}], \\ u(0,t) =u(x_{R},t)=0,\quad x \in[0,T], \end{array}\displaystyle \right . $$
(1)

on a finite domain \(0\le x\le x_{R}\) and \(0\le t \le T\), where μ and K are constants. If α equals 1, equation (1) is the classical reaction-diffusion equation. The fractional derivative is in the Caputo form.

2 Background

2.1 Numerical solution with implicit finite difference

The fractional derivative of \(f(t)\) in the Caputo sense is defined as [1]

$$ {}_{0}^{\mathrm{C}} D_{t}^{\alpha}f(t)= \frac{1}{\Gamma(1-\alpha)} \int_{0} ^{t} \frac{f'(\xi )}{(t-\xi)^{\alpha}}\,d\xi \quad (0< \alpha< 1). $$
(2)

If \(f'(t)\) is continuous bounded derivatives in \([0,T]\) for every \(T>0\), we can get

$$\begin{aligned} {}_{0}^{\mathrm{C}} D_{t}^{\alpha}f(t) &=\lim_{\xi\rightarrow0,n\xi=t} \xi^{\alpha}\sum _{i=0}^{n} (-1)^{i} {\alpha\choose i} \\ &= \frac{f(0)t^{-\alpha}}{\Gamma(1-\alpha)} + \frac{1}{\Gamma(1-\alpha )} \int_{0}^{t} \frac{f'(\xi)}{(t-\xi)^{\alpha}} \,d\xi. \end{aligned}$$
(3)

Define \(\tau= \frac{T}{N}\), \(h=\frac{x_{R}}{M}\), \(t_{n}=n\tau\), \(x_{i}=0+ih\) for \(0\le n \le N\), \(0\le i \le M\). Define \(u_{i}^{n}\), \(\varphi_{i}^{n}\), and \(\phi_{i}\) as the numerical approximations to \(u(x_{i},t_{n})\), \(f(x_{i},t_{n})\), and \(\phi(x_{i})\). We can get [11]

$$ {}_{0}^{\mathrm{C}} D_{t}^{\alpha}u(x,t)|_{x_{i}}^{t_{n}}= \frac{1}{\tau\Gamma(1-\alpha)} \Biggl[b_{0} u_{i}^{n} -\sum_{k=1}^{n-1}(b_{n-k-1}-b_{n-k})u_{i}^{k} -b_{n-1}u_{i}^{0} \Biggr] + \bigcirc \bigl( \tau^{2-\alpha}\bigr), $$
(4)

where \(1\le i \le M-1\), \(n \ge1\), and

$$ b_{l}=\frac{\tau^{1-\alpha}}{1-\alpha} \bigl[(l+1)^{1-\alpha}-l^{1-\alpha} \bigr], \quad l \ge0. $$
(5)

Using implicit center difference scheme for \(\frac{\partial^{2} u(x,t)}{\partial x^{2}}\), we can get

$$ \frac{\partial^{2} u(x,t)}{\partial x^{2}}\bigg|_{x_{i}}^{t_{n}}= \frac{1}{h^{2}}\bigl(u^{n}_{i+1}-2u^{n}_{i}+u^{n}_{i-1} \bigr) + \bigcirc\bigl(h^{2}\bigr). $$
(6)

The implicit finite difference approximation [11] for equation (1) is

$$\begin{aligned}& \frac{1}{\tau\Gamma(1-\alpha)} \Biggl[b_{0} u_{i}^{n} -\sum_{k=1}^{n-1}(b_{n-k-1}-b_{n-k})u_{i}^{k} -b_{n-1}u_{i}^{0} \Biggr] +\mu u_{i}^{n} \\& \quad =\frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{h^{2}} +K\varphi_{i}^{n}. \end{aligned}$$
(7)

Define \(w=\tau\Gamma(1-\alpha)\), \(\lambda_{0}=b_{0}+\mu w+ 2w/h^{2}\), \(\lambda_{1}=-w/h^{2}\), \(\sigma=Kw\), \(U^{n}=(u^{n}_{1},u^{n}_{2}, \ldots, u^{n}_{M-1})^{T}\), \(F^{n}=(\varphi_{1}^{n}, \varphi_{2}^{n}, \ldots, \varphi _{M-1}^{n})^{T}\), and \(r_{l}=b_{l}-b_{l+1}\). Equation (7) evolves as

$$ AU^{n}=\sum_{k=1}^{n-1}r_{n-1-k}U^{k} + b_{n-1}U^{0} + \sigma F^{n}, $$
(8)

where the matrix A is a tridiagonal matrix, defined as

$$ A_{(M-1)\times(M-1)} = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \lambda_{0}&\lambda_{1} & & &\\ \lambda_{1} & \lambda_{0}& \lambda_{1} & &\\ & \ddots& \ddots& \ddots&\\ & & \lambda_{1} & \lambda_{0} & \lambda_{1}\\ & & & \lambda_{1} & \lambda_{0} \end{array}\displaystyle \right ). $$
(9)

3 Parallel algorithm

3.1 Analysis

In order to get \(U^{n}\) from equation (8), two steps need to be processed. One step performs the right-sided computation of equation (8). Set \(V^{n}=\sum_{k=1}^{n-1}r_{n-1-k}U^{k} + b_{n-1}U^{0} + \sigma F^{n}\). The calculation of \(V^{n}\) mainly involves the constant-vector multiplications and vector-vector additions. The other step solves the tridiagonal linear equations \(AU^{n}=V^{n}\). The constant-vector multiplications and vector-vector additions can easily be parallelized. So we only analyze the parallel implementation of solving the tridiagonal linear equations.

As \(2|\lambda_{1}| < |\lambda_{0}|\), the tridiagonal matrix A is strictly diagonally dominant by rows. The dominance factor ϵ can be got by

$$ \epsilon=\frac{|2\lambda_{1}|}{|\lambda_{0}|}=\frac{1}{\frac {Nx_{R}^{2}b_{0}}{2M^{2}T\Gamma(1-\alpha)} +\frac{x_{R}^{2}\mu}{2M^{2}}+1}. $$
(10)

For strictly diagonally dominant linear systems, one parallel approximation algorithm has been proposed [34]. For given α and N, the dominance factor would be very close to one with big M. The approximation algorithm would decrease the precision of the solution and even exacerbate the convergence. In other words, applying the algorithm to this solution of tridiagonal linear equations with fixed M will obviously increase the number of time steps in order to keep the same precision. Thus, it is necessary to solve tridiagonal linear equations accurately. Moreover, each iteration on time step involves one system of tridiagonal linear equations. The right-hand side \(V^{n}\) varies while the tridiagonal matrix A keeps constant in all time iterations. In order to avoid the repeated calculations, the transformation of the tridiagonal matrix is recorded in the parallel solution of tridiagonal linear equations.

3.2 Parallel solution of tridiagonal linear equations

Based on the analysis above, a parallel implementation of solving the tridiagonal linear equations is shown in Algorithm 1. The implementation is based on the divide-and-conquer principle. The number of parallel processes is p. Set \(M-1=pk\) and \(q=\frac{p}{2}\). The matrix A is divided into p blocks as follows:

$$ A_{(M-1)\times(M-1)} = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} D_{1}&C_{1} & & & \\ G_{2} & D_{2}& C_{2} & &\\ & \ddots& \ddots& \ddots&\\ & &G_{p-1} &D_{p-1} & C_{p-1}\\ & & & G_{p} & D_{p} \end{array}\displaystyle \right ), $$
(11)

where

$$ D_{i} = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} d_{(i-1)k+1}&c_{(i-1)k+1} & & & \\ g_{(i-1)k+2} & d_{(i-1)k+2} & c_{(i-1)k+2} & &\\ & \ddots& \ddots& \ddots&\\ & &g_{ik-1} &d_{ik-1} & c_{ik-1}\\ & & & g_{ik} & d_{ik} \end{array}\displaystyle \right ),\quad i=1,2,\ldots,p, $$
(12)

\(G_{i}=g_{(i-1)k+1}e_{1}e_{k}^{T}\), \(i=2,3,\ldots,p\), \(C_{j}=c_{jk}e_{k}e_{1}^{T}\), \(j = 1,2, \ldots, p-1\). \(e_{1}\) and \(e_{k}\) are k-dimensional unit vectors in which the first and last elements are one, respectively. Similarly, U and V can also have corresponding partitions. \(U^{n}=(U_{1}, U_{2}, \ldots, U_{P})^{T}\), \(U_{i}=(u_{(i-1)k+1},\ldots,u_{ik})^{T}\), and \(V^{n}=(V_{1}, V_{2}, \ldots, V_{P})^{T}\), \(V_{i}=(v_{(i-1)k+1},\ldots,v_{ik})^{T}\).

Algorithm 1
figure a

Parallel solution for tridiagonal linear equations

Full size image

Line 3 allocates \(D_{i}\), \(g_{(i-1)k+1}\), \(c_{jk}\), \(V_{i}\) to the ith process, \(i=1, \ldots, p\).

Lines 4-11 eliminate the lower and upper diagonal elements of sub-matrix \(D_{i}\) and transform diagonal elements to one. For the downward elimination, \(P_{1}\) and \(P_{p}\) begin with the first row of \(D_{i}\) in line 9 while \(P_{i}\) (\(1 < i < p\)) begins with the second row of \(D_{i}\) in line 5. After the downward elimination, the equations in all processes can be transformed to

$$\begin{aligned}& P_{i}\ (i=1)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 &c_{1} & & & \\ &1 &c_{2} & &\\ & &\ddots& \ddots&\\ & & &1 & c_{k-1}\\ & & & & 1&c_{k} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u_{1}\\ u_{2}\\ \vdots\\ u_{k-1} \\ u_{k} \\ u_{k+1} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{1}\\ v_{2}\\ \vdots\\ v_{k-1} \\ v_{k} \end{array}\displaystyle \right ), \end{aligned}$$
(13)
$$\begin{aligned}& P_{i}\ (1< i< p)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} g_{(i-1)k+1}& d_{(i-1)k+1} &c_{(i-1)k+1} & & & \\ &g_{(i-1)k+2} &1 &c_{(i-1)k+2} & &\\ &\vdots & &\ddots& \ddots&\\ &g_{ik-1} & & &1 & c_{ik-1}\\ &g_{ik} & & & & d_{ik}&c_{ik} \end{array}\displaystyle \right ) \\& \hphantom{P_{i}\ (1< i< p)\mbox{:}\quad }\quad {}\times \left ( \textstyle\begin{array}{@{}c@{}} u_{(i-1)k}\\ u_{(i-1)k+1}\\ u_{(i-1)k+2}\\ \vdots\\ u_{ik-1} \\ u_{ik} \\ u_{ik+1} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{(i-1)k+1}\\ v_{(i-1)k+2}\\ \vdots\\ v_{ik-1} \\ v_{ik} \end{array}\displaystyle \right ), \end{aligned}$$
(14)
$$\begin{aligned}& P_{i}\ (i=p)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} g_{(p-1)k+1}&1 &c_{(p-1)k+1} & & & \\ g_{(p-1)k+2}& &1 &c_{(p-1)k+2} & &\\ \vdots& & &\ddots& \ddots&\\ g_{pk-1}& & & &1 & c_{pk-1}\\ g_{pk}& & & & & 1 \end{array}\displaystyle \right ) \\& \hphantom{P_{i}\ (i=p)\mbox{:}\quad }\quad {}\times \left ( \textstyle\begin{array}{@{}c@{}} u_{(p-1)k}\\ u_{(p-1)k+1}\\ u_{(p-1)k+2}\\ \vdots\\ u_{pk-1} \\ u_{pk} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{(p-1)k+1}\\ v_{(p-1)k+2}\\ \vdots\\ v_{pk-1} \\ v_{pk} \end{array}\displaystyle \right ). \end{aligned}$$
(15)

For the upward elimination, \(P_{1}\) and \(P_{p}\) begin with the last row of \(D_{i}\) in line 10 while \(P_{i}\) (\(1 < i < p\)) begins with the penultimate row of \(D_{i}\) in line 6. The upward elimination makes the equations in all processes become

$$\begin{aligned}& P_{i}\ (i=1)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & & & & & c_{1} \\ &1 & & &&c_{2}\\ & &\ddots& &&\vdots\\ & & &1 && c_{k-1}\\ & & & & 1&c_{k} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u_{1}\\ u_{2}\\ \vdots\\ u_{k-1} \\ u_{k} \\ u_{k+1} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{1}\\ v_{2}\\ \vdots\\ v_{k-1} \\ v_{k} \end{array}\displaystyle \right ), \end{aligned}$$
(16)
$$\begin{aligned}& P_{i}\ (1< i< p)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} g_{(i-1)k+1}& d_{(i-1)k+1} & & & & c_{(i-1)k+1} \\ &g_{(i-1)k+2} &1 & & &c_{(i-1)k+2} \\ &\vdots & &\ddots& &\vdots\\ &g_{ik-1} & & &1 & c_{ik-1}\\ &g_{ik} & & & & d_{ik}&c_{ik} \end{array}\displaystyle \right ) \\& \hphantom{P_{i}\ (1< i< p)\mbox{:}\quad}\quad {}\times \left ( \textstyle\begin{array}{@{}c@{}} u_{(i-1)k}\\ u_{(i-1)k+1}\\ u_{(i-1)k+2}\\ \vdots\\ u_{ik-1} \\ u_{ik} \\ u_{ik+1} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{(i-1)k+1}\\ v_{(i-1)k+2}\\ \vdots\\ v_{ik-1} \\ v_{ik} \end{array}\displaystyle \right ), \end{aligned}$$
(17)
$$\begin{aligned}& P_{i}\ (i=p)\mbox{:}\quad \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} g_{(p-1)k+1}&1 & & & & \\ g_{(p-1)k+2}& &1 & & &\\ \vdots& & &\ddots& &\\ g_{(p-1)k-1}& & & &1 & \\ g_{pk}& & & & & 1 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u_{(p-1)k}\\ u_{(p-1)k+1}\\ u_{(p-1)k+2}\\ \vdots\\ u_{pk-1} \\ u_{pk} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{(p-1)k+1}\\ v_{(p-1)k+2}\\ \vdots\\ v_{pk-1} \\ v_{pk} \end{array}\displaystyle \right ). \end{aligned}$$
(18)

In the elimination, the tridiagonal matrix and the right-hand-side vector are processed separately.

Line 12 means that \(P_{i}\) (\(1< i\le q\)) and \(P_{i}\) (\(q+1\le i < p\)), respectively, sends the first and last equations to \(P_{1}\) and \(P_{p}\). Those equations, the last one in \(P_{1}\) and the first one in \(P_{p}\) can form the reduced system of equations as follows:

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1&c_{k} & & & & \\ g_{k+1}& d_{k+1} &c_{k+1} & & &\\ & g_{2k} & d_{2k} &c_{2k} & &\\ & & \ddots & \ddots &\ddots& \\ & & & g_{(p-2)k+1} & d_{(p-2)k+1} & c_{(p-2)k+1} \\ & & & g_{(p-1)k} &d_{(p-1)k} & c_{(p-1)k}\\ & & & & g_{(p-1)k+1}& 1 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u_{k}\\ u_{k+1}\\ u_{2k}\\ \vdots\\ u_{(p-2)k+1} \\ u_{(p-1)k} \\ u_{(p-1)k+1} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{}} v_{k}\\ v_{k+1}\\ v_{2k}\\ \vdots\\ v_{(p-2)k+1} \\ v_{(p-1)k} \\ v_{(p-1)k+1} \end{array}\displaystyle \right ). $$
(19)

We can find the coefficient matrix in equation (19) is still a tridiagonal matrix. Line 13 means the reduced system of equations is solved only with processes \(P_{1}\) and \(P_{p}\). \(P_{1}\) and \(P_{p}\) deal with the reduced system of equations using the functions in lines 9-11 as well. \(P_{1}\) and \(P_{p}\) exchange the qkth and \(qk+1\)th equations after elimination, and both can obtain \(u_{(q+1)k}\) and \(u_{(q+1)k+1}\). In process \(P_{1}\), \(u_{(i-1)k+1}\) and \(u_{ik}\) are acquired and sent to \(P_{i}\) (\(1 < i \le q\)). In process \(P_{p}\), \(u_{(i-1)k+1}\) and \(u_{ik}\) are got and dispatched to \(P_{i}\) (\(q+1 \le i < p\)). After \(P_{i}\) (\(1 < i < p\)) receives \(u_{(i-1)k+1}\) and \(u_{ik}\) from \(P_{1}\) or \(P_{p}\), \(U_{i}\) can be solved using equation (17). \(U_{1}\) and \(U_{p}\) can also be figured out by equation (16) and equation (18), respectively.

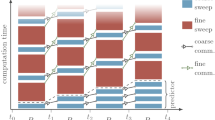
For the parallel implementation of solving tridiagonal linear equations, there are totally three communications shown in Figure 1. The first communication means that \(P_{i}\) (\(1< i< p\)) sends the first and last equations to \(P_{1}\) or \(P_{p}\) after the elimination. The second communication indicates that \(P_{1}\) and \(P_{p}\) exchange the qkth and \(qk+1\)th equations in order to acquire \(u_{(q+1)k}\) and \(u_{(q+1)k+1}\) simultaneously in the solution of the reduced system. The third communication is that \(P_{i}\) (\(1< i< p\)) receives \(u_{(i-1)k+1}\) and \(u_{ik}\) from \(P_{1}\) or \(P_{p}\) after the reduced system is solved.

Figure 1
figure 1

Communication in the parallel implementation of tridiagonal linear equations. The number of parallel processes is four.

Full size image

3.3 Implementation

The parallel algorithm for Caputo fractional reaction-diffusion equation with implicit finite-difference method is proposed as shown in Algorithm 2. \(F(,)\), \(U(,)\), \(V()\), \(A(,)\) are evenly distributed among all processes in order to void the load imbalance. Line 6 computes \(F(,)\), \(A()\), \(r()\) and initializes \(U(,)\), \(V()\). Vector \(r()\) is stored in all processes and calculated simultaneously. Lines 9-13 solve the tridiagonal linear equations \(AU^{0}=V\) for the first time. The loop of line 14 represents iterations on time steps. Since there are dependence between the solutions of adjacent time steps, the parallelization of the solution could be carried out only on space steps. In each iteration on time steps, line 16 solves \(V^{n}=\sum_{k=1}^{n-1}r_{n-1-k}U^{k} + b_{n-1}U^{0} + \sigma F^{n}\) in parallel, and mainly includes parallel constant-vector multiplications and vector-vector additions. Lines 18-22 solve the tridiagonal linear equations \(AU^{n}=V^{n}\) for the \((n+1)\)th time. As the tridiagonal matrix keeps constant in all time iterations, the solution of lines 18-22 does not deal with the tridiagonal matrix and only processes \(V^{n}\) with transform_mid_v() and transform_edg_v(). Particularly, the coefficient matrix of the reduced system also does not vary with time iterations. The elimination in line 22 simply involves the right-sided vector of the reduced system as well. Therefore, the communications in lines 18-22 only transfer the right-hand side of the corresponding equations rather than the entire ones.

Algorithm 2
figure b

Parallel solution for Caputo fractional reaction-diffusion equation with implicit finite-difference method

Full size image

4 Experimental results and discussion

The experiment platform is a service node containing two eight-core Intel Xeon E5-2670 CPUs with 128 GB of memory. All codes are compiled with Intel C compiler with level-three optimization and run in double-precision floating-point. The specifications are listed in Table 1.

Table 1 The specifications of the experiment’s platform
Full size table

The following Caputo fractional reaction-diffusion equation [11] is considered, shown in equation (20):

$$ \left \{ \textstyle\begin{array}{l} {}_{0}D_{t}^{\alpha}u(x,t) +\mu u(x,t) =\frac{\partial^{2} u(x,t)}{\partial x^{2}} +K f(x,t), \\ u(x,0) =0,\quad x \in(0,2), \\ u(0,t) =u(2,t)=0, \end{array}\displaystyle \right . $$
(20)

with \(\mu=1\), \(K=1\), \(\alpha=0.7\), and

$$ f(x,t)=\frac{2}{\Gamma(2.3)} x(2-x) t^{1.3}+x(2-x)t^{2}+2t^{2}. $$
(21)

The exact solution of equation (20) is

$$ u(x,t)=x(2-x)t^{2}. $$
(22)

4.1 Accuracy of parallel solution

For the example in equation (20), the parallel solution compares well with the exact analytic solution to the fractional partial differential equation shown in Figure 2. Δt and h are \(\frac{1.0}{65}\) and \(\frac{2.0}{65}\). The maximum absolute error is \(7.47 \times10^{-4}\). The difference between serial and parallel solution is only \(4.22 \times10^{-15}\). When different Δt and h are applied, the maximum errors between the exact analytic solution and the parallel solution are shown in Table 2. The maximum error gradually decreases with the increasing number of time and space steps. Altogether, our proposed parallel solution and the exact analytic solution have no noticeable artifacts.

Figure 2
figure 2

Result comparison between exact analytic solution with parallel solution at time \(\pmb{t = 1.0}\) and \(\pmb{p=16}\) , \(\pmb{M=N=65}\) .

Full size image
Table 2 Result comparison between the exact analytic solution and the parallel solution at time \(\pmb{t = 1.0}\) and \(\pmb{p=8}\) , where different M and N are applied
Full size table

4.2 Performance improvement

The performance comparison between serial solution (SS) and parallel solution (PS) is shown in Table 3 when different M and N are applied. In PS, 16 processes run in parallel. With \(M=N=65\), PS is a little slower than SS. When M and N are greater than or equal to 129, PS is faster than SS. Compared with SS, the speedup of PS increases gradually with increasing M and N. When M and N increase to 2,049, the runtime of SS reaches 4.03 seconds and that of PS is only \(2.77 \times 10^{-1}\) seconds. Therefore, the speedup between PS and SS rises to 14.55.

Table 3 Performance comparison between serial solution (SS) and parallel solution (PS) when different M and N are applied
Full size table

4.3 Scalability

With fixed \(M=N=2\text{,}049\), the performance comparison among the parallel solutions with a different number of processes is shown in Table 4. When two parallel processes are used, the speedup is 2.22. When four processes run in parallel, the speedup reaches 4.24. When more than one process is adopted, the total communication cost will increase with the number of parallel processes. However, the speedups in the two situations above outperform the corresponding perfect speedups. The main reason is that the solution of Caputo fractional reaction-diffusion equation with implicit finite-difference method is memory-intensive, and the decrease of memory overhead by the improvement of data locality is more than the increase of communication cost in the parallelization of two or four processes. When the number of processes grows to 16, the speedup is about 14.55 times and the scaling efficiency reaches 91%. Altogether, our proposed parallel solution has good scalability in performance.

Table 4 Performance of parallel solution with \(\pmb{M = N = 2\text{,}049}\) when different numbers of processes are applied
Full size table

5 Conclusions and future work

In this article, we propose a parallel algorithm for time fractional reaction-diffusion equation using the implicit finite-difference method. The algorithm includes a parallel solver for linear tridiagonal equations and parallel vector arithmetic operations. The solver is based on the divide-and-conquer principle and introduces a new tridiagonal reduced system with an elimination method. The experimental results shows the proposed parallel algorithm is valid and runs much more rapidly than the serial solution. The results also demonstrate the algorithm exhibits good scalability in performance. In addition, the introduced tridiagonal reduced system can be regarded as a general method for tridiagonal systems and applied on more applications. In the future, we would like to accelerate the solution of time fractional reaction-diffusion equation on heterogeneous architectures [35].