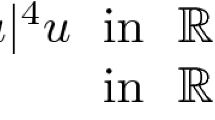Multi-peak solutions for a nonlinear Schrödinger-Poisson system including critical growth in $\mathbb{R}^{3}$

Abstract

We consider the semiclassical states of the Schrödinger-Poisson system: $-\varepsilon^{2}\Delta u+V(x)u+\phi(x)u=f(u)$, $-\Delta\phi=u^{2}$ in $\mathbb{R}^{3}$. By the variational method, we construct a multi-peak solution $(u_{\varepsilon},\phi_{\varepsilon})$ around several given isolated positive local minimum components of V as $\varepsilon\rightarrow0$. The nonlinearity f is of critical growth. Moreover, the monotonicity of $f(s)/s^{3}$ and the so-called Ambrosetti-Rabinowitz condition are not required.

1 Introduction and main result

We are concerned with the nonlinear Schrödinger-Poisson system

$$ \left \{ \textstyle\begin{array}{l} -\varepsilon^{2}\Delta v+V(x)v+\lambda\phi(x)v=f(v) \quad \mbox{in } \mathbb{R} ^{3}, \\ -\Delta\phi=v^{2}, \qquad \lim_{|x|\rightarrow\infty}\phi(x)=0 \quad \mbox{in } \mathbb{R}^{3}, \end{array}\displaystyle \right . $$

(1.1)

where $\lambda>0$ and $\varepsilon>0$. The system arose in the interaction of a charged particle with the electrostatic field and the term $\lambda\phi v$ concerns the interaction with the electric field. For more background, we refer to [1–4]. One of the most interesting classes of solutions to (1.1) is the class of solutions with the finite energy for $\varepsilon>0$ small. In the view of quantum mechanics, these solutions are called bound states; they are referred to as semiclassical states.

In this paper, we are concerned with the existence and concentration of bound states of (1.1) as $\varepsilon \rightarrow0$. If $\lambda =0$, system (1.1) reduces to the Schrödinger equation

$$ -\varepsilon^{2}\Delta v+V(x)v=f(v), \quad v\in H^{1}\bigl(\mathbb{R}^{3}\bigr). $$

(1.2)

In the past decades, there has been considerable attention to solutions of (1.2). Based a Lyapunov-Schmidt reduction argument, around any given non-degenerate critical point of V, Floer and Weinstein [5] constructed a single-peak solutions of (1.2) for $N=1$ and $f(s)=s^{3}$. By using a similar argument, Oh [6] extended the result in [5] to the higher dimension case. Initiated by Rabinowitz [7], the variational approaches have become an important tool to deal with more general classes of the nonlinearity f. By using the mountain pass argument, Wang [8] obtained spike solutions of (1.2) around the global minimum points of V for ε small. Later, del Pino and Felmer [9] gave a development of the variational approach in [7, 8] and constructed a single-peak solution around the local minimum points of V. But in [7–9], there are more restrictions on f involved, such as (H): $f(s)/s$ is nondecreasing in $(0,\infty)$ and (AR): the Ambrosetti-Rabinowitz condition. To remove or eliminate (H) or (AR), Byeon and Jeanjean [10] developed the penalized argument in [9] to explore what the essential features are to guarantee the existence of spike solutions to (1.2). In [10] the authors showed that the Berestycki-Lions conditions are almost optimal if f is of subcritical growth.

If $\lambda\neq0$, the Schrödinger-Poisson system (1.1) is nonlocal. For $V(x)\equiv$ constant and $f(v)=|v|^{p-2}v$, $p\in (1,\frac{11}{7})$, D’Aprile and Wei [11] constructed positive solutions of (1.1) which concentrate around a sphere in $\mathbb{R}^{3}$ as $\varepsilon\rightarrow0$. For $f(v)=v^{p}$, $p\in(1,5)$, Ruiz and Vaira [12] constructed multi-bump solutions around the local minimum of the potential V. Here, we also would like to cite [13–17]. In [18] He and Zou considered ground state solutions of Schrödinger-Poisson system (1.1) in the critical case. By the Nehari manifold method, the authors obtained the existence of ground solutions concentrating around the global minimal points of V. But in the work above, the nonlinearity f usually satisfies the monotonicity condition: $f(s)/s^{3}$ is nondecreasing in $(0,\infty)$, (AR) or other restrictions. Recently, Seok [19] considered the spike solutions of (1.1) for a more general nonlinear term. With a penalization argument introduced in [10], the author constructed multi-peak solutions of (1.1) for any several given isolated local minimum components of V. Precisely, assume that V satisfies:

• (V1) $V\in C(\mathbb{R}^{3},\mathbb{R})$ and $0< V_{0}=\inf_{x\in \mathbb{R}^{3}}V(x)$.

• (V2) There are bounded disjoint open sets $O^{i}\subset\mathbb{R}^{3}$, $i=1,2,\ldots,k$ such that for any $i\in\{1,2,\ldots,k\}$,

  $$0< m_{i}\equiv\inf_{x\in O^{i}}V(x)< \min _{x\in\partial O^{i}}V(x), $$

  and f satisfies the Berestycki-Lions conditions:

  (f₁):

  $f\in C(\mathbb{R}, \mathbb{R})$ such that $f(t)=0$ for $t\leq0$ and $\lim_{t\to0}f(t)/t=0$;

  (f₂):

  there exists $p\in(1,5)$ such that $\lim\sup_{t\to \infty}f(t)/t^{p}<\infty$;

  (f₃):

  there exists $T>0$ such that $\frac{m}{2}T^{2}< F(T) :\equiv\int_{0}^{T}f(t) \, \mathrm{d}t$.

For any $k>1$ and any $i\in\{1,2,\ldots,k\}$, let

$$\mathcal{M}^{i}\equiv\bigl\{ x\in O^{i}: V(x)=m_{i} \bigr\} . $$

Theorem A

(see [19])

Assume that (V1)-(V2) and (f₁)-(f₃), then for sufficiently small $\varepsilon>0$, (1.1) admits a positive solution $(v_{\varepsilon},\phi_{\varepsilon})\in H^{1}(\mathbb{R}^{3})\times D^{1,2}(\mathbb{R}^{3})$, which satisfies:

• (i) there exist k local maximum points $x_{\varepsilon}^{i}\in O^{i}$ of $v_{\varepsilon}$ such that

  $$\lim_{\varepsilon\rightarrow0}\max_{1\le i\le k}\operatorname {dist} \bigl(x_{\varepsilon}^{i},\mathcal{M}^{i}\bigr)=0, $$

  and $w_{\varepsilon}(x)\equiv v_{\varepsilon}(\varepsilon x+x_{\varepsilon}^{i})$ converges (up to a subsequence) locally uniformly to a least energy solution of

  $$ -\Delta u+m_{i}u=f(u), \quad u>0, u\in H^{1} \bigl(\mathbb{R}^{3}\bigr); $$

  (1.3)

• (ii) $v_{\varepsilon}(x)\le C\exp(-\frac{c}{\varepsilon}\min_{1\le i\le k}|x-x_{\varepsilon}^{i}|)$ for some $c,C>0$.

By (f₂) the problem in [19] is of subcritical growth. More recently, Zhang [20] considered the single-peak solutions of (1.1) in the critical case. Assume that f satisfies:

• (F1) $\lim_{t\rightarrow0}\frac{f(t)}{t}=0$.

• (F2) $\lim_{t\rightarrow\infty}\frac{f(t)}{t^{5}}=\kappa>0$.

• (F3) There exist $C>0$ and $p<6$ such that $f(t)\ge\kappa t^{5}+Ct^{p-1}$ for $t\ge0$.

By using a similar argument to [21], in [20] the author obtained a single-spike solution of (1.1) around the local minimal point of V. Motivated by the work above, we are interested in the multi-peak solutions of (1.1) with a general nonlinear term in the critical case. Now, we state our main result of the present paper as follows.

Theorem 1.1

Let $p>4$ and suppose that (V1)-(V2) and (F1)-(F3). Then for any $\lambda>0$ and sufficiently small $\varepsilon>0$, (1.1) admits a positive solution $(v_{\varepsilon},\phi_{\varepsilon})\in H^{1}(\mathbb{R}^{3})\times D^{1,2}(\mathbb{R}^{3})$, which satisfies:

• (i) there exist k local maximum points $x_{\varepsilon}^{i}\in O^{i}$ of $v_{\varepsilon}$ such that

  $$\lim_{\varepsilon\rightarrow0}\max_{1\le i\le k}\operatorname{dist} \bigl(x_{\varepsilon}^{i},\mathcal{M}^{i}\bigr)=0, $$

  and $w_{\varepsilon}(x)\equiv v_{\varepsilon}(\varepsilon x+x_{\varepsilon}^{i})$ converges (up to a subsequence) locally uniformly to a least energy solution of

  $$ -\Delta u+m_{i}u=f(u),\quad u>0, u\in H^{1} \bigl(\mathbb{R}^{3}\bigr); $$

  (1.4)

• (ii) $v_{\varepsilon}(x)\le C\exp(-\frac{c}{\varepsilon}\min_{1\le i\le k}|x-x_{\varepsilon}^{i}|)$ for some $c,C>0$.

Remark 1.1

Without loss of generality, in the present paper we can assume that $V_{0}=\kappa=\lambda=1$.

Notations

• $\|u\|_{p}:= (\int_{\mathbb{R}^{3}}|u|^{p} \, \mathrm {d}x )^{1/p}$ for $p\in[2,\infty)$.

• $\|u\|:= (\|u\|^{2}_{2}+\|\nabla u\|^{2}_{2} )^{1/2}$ for $u\in H^{1}(\mathbb{R}^{3})$.

• C, c are positive constants, which may change from line to line.

2 Proof of Theorem 1.1

First, we introduce some results about the solutions of the limit problem (1.4). For each $1\le i\le k$, as we can see in [22], with the same assumptions in Theorem 1.1, (1.4) admits a least energy solution U for any $m_{i}>0$ and U satisfies Pohozaev’s identity

$$ \int_{\mathbb{R}^{3}}|\nabla U|^{2}\, \mathrm {d}x=6 \int_{\mathbb{R}^{3}} \biggl(F(U)-\frac {a}{2}U^{2} \biggr) \, \mathrm {d}x, $$

and so $\int_{\mathbb{R}^{3}}| \nabla U|^{2}\, \mathrm{d}x=3E_{i}$. Moreover, the least energy $E_{i}$ is corresponding to a mountain path value. Let $S_{i}$ be the set of least energy solutions U of (1.4) satisfying $U(0)=\max_{x\in\mathbb{R}^{3}}U(x)$. For each $i\in\{ 1,2,\ldots ,k\}$, we have the following proposition.

Proposition 2.1

(see Proposition 2.1 in [23])

• (1) $S_{i}$ is compact in $H^{1}(\mathbb{R}^{3})$.

• (2) $0<\inf\{\|U\|_{\infty}:U\in S_{i}\}\le\sup\{\|U\| _{\infty}:U\in S_{a}\}:=\kappa_{i}<\infty$.

• (3) There exist $C,c>0$ (independent of $U\in S_{i}$) such that $|D^{\alpha}U(x)|\le C\exp(-c|x|)$, $x\in\mathbb{R}^{3}$ for $|\alpha|=0,1$.

By the Lax-Milgram theorem, for any $v\in H^{1}(\mathbb{R}^{3})$, there exists a unique $\phi_{v}\in D^{1,2}(\mathbb{R}^{3})$ such that $-\Delta\phi_{v}=v^{2}$ with

$$ \phi_{v}(x)= \int_{\mathbb{R}^{3}}\frac {v^{2}(y)}{4\pi|x-y|} \, \mathrm{d}y. $$

(2.1)

Then the system (1.1) is equivalent to

$$ -\varepsilon^{2}\Delta v+V(x)v+\phi _{v}(x)v=f(v), \quad v\in H^{1}\bigl(\mathbb{R}^{3}\bigr). $$

(2.2)

Let $u(x)=v(\varepsilon x)$ and $V_{\varepsilon}(x)=V(\varepsilon x)$, then

$$ -\Delta u+V_{\varepsilon}(x)u+\varepsilon ^{2} \phi_{u}(x)u=f(u), \quad u\in H^{1}\bigl( \mathbb{R}^{3}\bigr). $$

(2.3)

In the following, we consider (2.3) instead of (1.1). Let $H_{\varepsilon}$ be the completion of $C_{0}^{\infty}(\mathbb{R}^{3})$ with respect to the norm

$$\|u\|_{\varepsilon}= \biggl( \int_{\mathbb{R}^{3}} \bigl[|\nabla u|^{2}+V_{\varepsilon}u^{2}\bigr]\, \mathrm{d}x \biggr)^{\frac{1}{2}}. $$

For $u\in H^{1}(\mathbb{R}^{3})$, let $T(u)=\frac{1}{4}\int_{\mathbb{R}^{3}}\phi_{u}u^{2}\, \mathrm{d}x$. Now, we summarize some properties of $\phi_{u}$.

Proposition 2.2

([24, 25])

For any $u\in H^{1}(\mathbb{R}^{3})$, we have

• (1) $\phi_{u}:H^{1}(\mathbb{R}^{3})\mapsto D^{1,2}(\mathbb{R}^{3})$ is continuous, and maps bounded sets into bounded sets.

• (2) $\phi_{u}\ge0$, $\|\nabla\phi_{u}\|_{2}\le c\|u\|^{2}$, and $T(u)\le c\|u\|^{4}$ for some $c>0$.

In the following, we use the truncation argument to prove Theorem 1.1. A similar argument can be found in [26]. Since we are concerned with the positive solutions of (2.2), from now on, we assume that $f(s)=0$ for all $s\le0$. By the maximum principle, any nontrivial solution of (2.2) is positive. Let $\kappa=\max_{1\le i\le k}\{\kappa_{i}\}$, define

$$f_{j}(t)=\min\bigl\{ f(t),j\bigr\} , \quad t\in\mathbb{R} $$

for any fixed $j>\max_{t\in[0,\kappa]}f(t)$. Consider the following truncated problem:

$$ -\Delta u+V_{\varepsilon}(x)u+\varepsilon ^{2} \phi_{u}(x)u=f_{j}(u),\quad u\in H_{\varepsilon}. $$

(2.4)

In the following, we prove that (2.4) has a solution $u_{\varepsilon}$ satisfying $\|u_{\varepsilon}\|_{\infty}\le\kappa$ for ε small. So we can show that $u_{\varepsilon}$ is the solution of the original problem (2.3).

Now, for each $1\le i\le k$, we consider the limit equation of (2.4),

$$ -\Delta u+m_{i}u=f_{j}(u),\quad u\in H^{1}\bigl(\mathbb{R}^{3}\bigr). $$

(2.5)

Lemma 2.1

Assume that (F1)-(F3), then (2.5) admits a positive ground state solution.

Proof

By [27], it suffices to verify that $f_{j}$ satisfies the Berestycki-Lions conditions: (f₁)-(f₃). (f₁) and (f₂) are obvious. For any $U\in S_{i}$, as we can see in [22],

$$6 \int_{\mathbb{R}^{3}}\biggl(F(U)-\frac{m_{i}}{2}U^{2}\biggr)\, \mathrm{d}x= \int _{\mathbb{R}^{3}}|\nabla U|^{2} \, \mathrm{d}x, $$

which implies that

$$F\bigl(U(x_{0})\bigr)>\frac{m}{2}U^{2}(x_{0}) $$

for some $x_{0}\in\mathbb{R}^{3}$. Let $T=U(x_{0})>0$, $F_{j}(T)=F(T)>\frac {m}{2}T^{2}$, where $F_{j}(t)=\int_{0}^{t}f_{j}(s) \, \mathrm{d}s$. The proof is completed. □

For each $i\in\{1,2,\ldots,k\}$, let $S_{i}^{j}$ be the set of positive ground state solutions U of (2.5) satisfying $U(0)=\max_{x\in\mathbb{R}^{3}}U(x)$. Then by [10] we know $S_{i}^{j}$ is compact in $H^{1}(\mathbb{R}^{3})$. Denote by $E_{i}^{j}$ the least energy of (2.5), then $E_{i}^{j}\le E_{i}$ due to $S_{i}\subset S_{i}^{j}$. Since $f_{j}(t)\le f(t)$ for any $t\ge0$, $E_{i}^{j}\ge E_{i}$. Thus, $E_{i}^{j}=E_{i}$.

Lemma 2.2

For $j>\max_{t\in[0,\kappa]}f(t)$ and each $i\in\{1,2,\ldots,k\}$, we have

$$S_{i}^{j}=S_{i}. $$

Proof

The proof is similar to [26, 28]. For completeness, we give the details here. Obviously, $S_{i}\subset S_{i}^{j}$. In the following, we prove $S_{i}^{j}\subset S_{i}$. Take any $u_{j}\in S_{i}^{j}$ and consider the constraint minimization problem

$$ M_{j}:=\inf \bigl\{ W(u):\Upsilon_{j}(u)=1,u \in H^{1}\bigl(\mathbb{R}^{2}\bigr) \bigr\} , $$

(2.6)

where

$$W(u)=\frac{1}{2} \int_{\mathbb{R}^{3}}|\nabla u|^{2} \, \mathrm{d}x,\qquad \Upsilon_{j}(u)= \int _{\mathbb{R}^{3}}G_{j}(u)\, \mathrm{d}x, \qquad G_{j}(s)=F_{j}(s)-\frac{m_{i}}{2}s^{2}. $$

By Lemma 1 in [29], $u_{j}$ is a minimizer of $W(v)$ on $\{v\in H^{1}(\mathbb{R}^{3}): \Upsilon_{j}(v)=\lambda_{j}\}$, where $\lambda_{j}= (M_{j}/3 )^{\frac{3}{2}}$. By Pohozaev’s identity, we get $\|\nabla u_{j}\| _{2}^{2}=3E_{i}^{j}$. Let $v_{j}=u_{j}(\lambda_{j}^{1/3}\cdot)$, we have $\|\nabla v_{j}\|_{2}^{2}=2W(v_{j})=2M_{j}$. So by the scaling, we have

$$E_{i}^{j}=2\cdot3^{-3/2}M_{j}^{\frac{3}{2}}. $$

Similarly, we consider the problem

$$ M:=\inf \bigl\{ W(u):\Upsilon(u)=1,u\in H^{1}\bigl( \mathbb{R}^{2}\bigr) \bigr\} , $$

(2.7)

where

$$\Upsilon(u)= \int_{\mathbb{R}^{3}}G(u)\, \mathrm{d}x, \qquad G(s)=F(s)- \frac{m_{i}}{2}s^{2}. $$

Then we can get

$$E_{i}=2\cdot3^{-3/2}M^{\frac{3}{2}}. $$

Then $M_{j}=M$ since $E_{i}^{j}=E_{i}$.

Obviously, $\Upsilon_{j}(v_{j})=1$, so $\Upsilon(v_{j})\ge1$. Now, we claim that $\Upsilon(v_{j})=1$. If not, by a scaling, we have

$$W(v_{j})\ge M\bigl(\Upsilon(v_{j})\bigr)^{1/3}>M=M_{j}, $$

which is in contradiction with $W(v_{j})=M_{j}$. Thus, $\Upsilon(v_{j})=1$ and $v_{j}$ is a minimizer of (2.7). By Lemma 1 in[29] again, we get $u_{j}\in S_{m}$. The proof is completed. □

Completion of the proof for Theorem 1.1:

Proof

For some fixed $j>\max_{t\in[0,\kappa]}f(t)$, we adopt some ideas in [30] to construct the multi-bump solutions of the truncation problem (2.4).

For any set $B\subset\mathbb{R}^{3}$ and $\varepsilon>0$, set $B_{\varepsilon}\equiv\{ x\in\mathbb{R}^{3}: \varepsilon x\in B\}$ and $B^{\delta}\equiv\{x\in \mathbb{R}^{3}: \operatorname {dist}(x,B)\le\delta\}$. Let $\mathcal{M}=\bigcup_{i=1}^{k}\mathcal {M}^{i}$ and $O=\bigcup_{i=1}^{k} O^{i}$. Fixing an arbitrary $\mu>0$, we define

$$ \chi_{\varepsilon}(x)= \left \{ \textstyle\begin{array}{l@{\quad}l} 0, & \mbox{if } x\in O_{\varepsilon}, \\ \varepsilon^{-\mu}, & \mbox{if } x\in\mathbb{R}^{3}\setminus O_{\varepsilon}, \end{array}\displaystyle \right .\qquad Q_{\varepsilon}(u)= \biggl( \int_{\mathbb{R}^{3}}\chi_{\varepsilon}u^{2}\, \mathrm{d}x-1 \biggr)_{+}^{2}. $$

Now, we construct a set of approximate solutions of (2.4). Let

$$\delta=\frac{1}{10}\min\Bigl\{ \operatorname{dist}\bigl( \mathcal{M},O^{c}\bigr),\min_{i\neq j}\operatorname{dist} \bigl(O^{i},O^{j}\bigr)\Bigr\} . $$

We fix a $\beta\in(0,\delta)$ and a cut-off $\varphi\in C_{0}^{\infty}(\mathbb{R} ^{3})$ such that $0\le\varphi\le1$, $\varphi(x)=1$ for $|x|\le\beta$ and $\varphi (x)=0$ for $|x|\ge2\beta$. Let $\varphi_{\varepsilon}(y)=\varphi (\varepsilon y)$, $y\in\mathbb{R} ^{3}$. For each $i\in\{1,2,\ldots,k\}$ and some $x_{i}\in(\mathcal {M}^{i})^{\beta}$, $1\le i\le k$, and $U_{i}\in S_{i}$, we define

$$U_{\varepsilon}^{x_{1},x_{2},\ldots,x_{k}}(y)=\sum_{i=1}^{k} \varphi _{\varepsilon} \biggl(y-\frac {x_{i}}{\varepsilon} \biggr)U_{i} \biggl(y-\frac{x_{i}}{\varepsilon} \biggr). $$

Here, we recall that $S_{i}^{j}=S_{i}$ ($1\le i\le k$) by Lemma 2.2. As in [30], we will find a solution of (2.4) in a small neighborhood of

$$X_{\varepsilon}=\bigl\{ U_{\varepsilon}^{x_{1},x_{2},\ldots,x_{k}} \mid x_{i}\in \bigl(\mathcal {M}^{i}\bigr)^{\beta}, U_{i}\in S_{i},i=1,2,\ldots,k\bigr\} $$

for sufficiently small $\varepsilon>0$. Let $\Gamma_{\varepsilon}^{j}(u)=P_{\varepsilon}^{j}(u)+Q_{\varepsilon}(u)$ for any $u\in H_{\varepsilon}$, where

$$P_{\varepsilon}^{j}(u)=\frac{1}{2} \int_{\mathbb{R}^{3}}\bigl(|\nabla u|^{2}+V_{\varepsilon}u^{2}\bigr) \, \mathrm{d}x- \int _{\mathbb{R}^{3}} F_{j}(u) \, \mathrm{d}x. $$

By Proposition 2.2, it is easy to see that $\Gamma_{\varepsilon}^{j}\in C^{1}(H_{\varepsilon})$. The set $X_{\varepsilon}^{d}$ is bounded in $H^{1}(\mathbb{R}^{3})$ for any $d>0$. By Proposition 2.2 $\varepsilon^{2}T(u)=O(\varepsilon ^{2})$ uniformly for $u\in X_{\varepsilon}^{d}$. Then, as we can see in [19, 30], for some small $d>0$, there exists $\varepsilon_{0}>0$ such that for $\varepsilon\in (0,\varepsilon_{0})$, $\Gamma_{\varepsilon}^{j}$ admits a critical point $u_{\varepsilon}\in X_{\varepsilon}^{d}$ with the following properties:

• (i) there exist $\{y_{\varepsilon}^{i}\}_{i=1}^{k}\subset\mathbb{R}^{3}$, $x^{i}\in \mathcal{M}^{i}$, $U_{i}\in S_{i}$ such that for any $1\le i\le k$,

  $$\lim_{\varepsilon\rightarrow0}\bigl\vert \varepsilon y_{\varepsilon}^{i}-x^{i} \bigr\vert =0 \quad \mbox{and}\quad \lim_{\varepsilon\rightarrow0}\Biggl\Vert u_{\varepsilon}-\sum_{i=1}^{k}U_{i} \bigl(\cdot-y_{\varepsilon}^{i}\bigr)\Biggr\Vert _{\varepsilon}=0; $$

• (ii) there exist $C,c>0$ (independent of ε, i), such that

  $$ 0< c\le u_{\varepsilon}(y)\le C\exp \biggl(-\frac{1}{2}\min _{1\le i\le k}\bigl\vert y-y_{\varepsilon}^{i}\bigr\vert \biggr)\quad \mbox{for } y\in\mathbb{R}^{3}, \varepsilon\in(0, \varepsilon_{0}). $$

  (2.8)

It follows from the decay (2.8) that $Q_{\varepsilon}(u_{\varepsilon})=0$ for small $\varepsilon >0$, i.e., $u_{\varepsilon}$ is a solution of (2.4). Let $w_{\varepsilon}^{i}(\cdot)=u_{\varepsilon}(\cdot+y_{\varepsilon}^{i})$, by the elliptic estimates, $w_{\varepsilon}^{i}\in C^{1,\alpha}(\mathbb{R}^{3})$ for some $\alpha\in(0,1)$ and each $1\le i\le k$. By (2.8) there exists $z_{\varepsilon}^{i}\in\mathbb{R}^{3}$ such that

$$\bigl\Vert w_{\varepsilon}^{i}\bigr\Vert _{\infty}=w_{\varepsilon}^{i} \bigl(z_{\varepsilon}^{i}\bigr)=u_{\varepsilon}\bigl(z_{\varepsilon}^{i}+y_{\varepsilon}^{i} \bigr). $$

Moreover, $\{z_{\varepsilon}^{i}\}_{i=1}^{k}\subset\mathbb{R}^{3}$ is uniformly bounded for ε. Assume that $z_{\varepsilon}^{i}\rightarrow z^{i}$ as $\varepsilon\rightarrow0$, let $u_{\varepsilon}(\cdot )=v_{\varepsilon}(\varepsilon\cdot)$ and $x_{\varepsilon}^{i}=\varepsilon y_{\varepsilon}^{i}+\varepsilon z_{\varepsilon}^{i}$, then $\max_{x\in\mathbb{R}^{3}}v_{\varepsilon}(x)=v_{\varepsilon}(x_{\varepsilon}^{i})$, $\lim_{\varepsilon\rightarrow0}\operatorname {dist}(x_{\varepsilon}^{i},\mathcal{M}^{i})=0$ and $\|v_{\varepsilon}(\varepsilon\cdot+x_{\varepsilon}^{i})- U_{i}(\cdot +z^{i})\|_{\varepsilon}\rightarrow0$ as $\varepsilon\rightarrow 0$ for each $1\le i\le k$.

In the following, we prove that $\|u_{\varepsilon}\|_{\infty}\le\kappa$ uniformly holds for sufficiently small $\varepsilon>0$, which implies that $v_{\varepsilon}$ is a solution of the original problem (2.2). For each $1\le i\le k$, let $\tilde{w}_{\varepsilon}^{i}(\cdot)=u_{\varepsilon}(\cdot +x_{\varepsilon}^{i}/\varepsilon)$, then $\| \tilde{w}_{\varepsilon}^{i}\|_{\infty}=\tilde{w}_{\varepsilon}^{i}(0)$ and

$$-\Delta\tilde{w}_{\varepsilon}^{i}+V\bigl(\varepsilon x+x_{\varepsilon}^{i}\bigr)\tilde{w}_{\varepsilon}^{i}+ \varepsilon^{2}\phi_{\tilde {w}_{\varepsilon}^{i}}\tilde{w}_{\varepsilon}^{i}=f_{j} \bigl(\tilde{w}_{\varepsilon}^{i}\bigr), \quad \tilde {w}_{\varepsilon}^{i}\in H_{\varepsilon}. $$

Since that $f_{j}(t)\le j$ for all $t\in\mathbb{R}$, it follows from the elliptic estimate (see [31]) that $\tilde{w}_{\varepsilon}^{i}\rightarrow U_{i}(\cdot +z^{i})$ uniformly in $B_{1}(0)$. So we have $\tilde{w}_{\varepsilon}^{i}(0)\le\kappa$ uniformly holds for sufficiently small $\varepsilon>0$. The proof is completed. □