1 Introduction

Mathematical models have been an important tool in analyzing the spread and control of infectious diseases since the pioneer work of Kermack and McKendrick [1]. Most of the research literature on these types of models assumes that the disease incubation is negligible so that, once infected, each susceptible individual (in the class S) instantaneously becomes infectious (in the class I) and later recovers (in the class R) with a permanent or temporary acquired immunity [2]. A compartmental model based on these assumptions is customarily called a SIR or SIRS model. Regarding research on the SIR or SIRS models and its generalizations, the reader can refer to [3–5].

Some diseases, however, incubate inside the hosts for a period of time before the hosts become infectious. In the case of assuming that the susceptible individual first goes through a latent period after infection before becoming infectious, the resulting models are of SEI, SEIR or SEIRS type, respectively, depending on whether the acquired immunity is permanent or otherwise. There has been a great deal of work on these types of models in the literature [6–9]. Some scholars simply considered the therapy of the active patients and neglected the importance of remedying the latent patients. However, it is very important to cure the latent patients because if some diseases such as the tuberculosis (see [10]) miss the best treatment time in latent period, the diseases will be fatal. Especially, Meng et al. [11] discussed an SEIS epidemic model in a population that is compartmentalized into three classes: the susceptible, exposed, and infectious classes, with sizes denoted by \(S(t)\), \(E(t)\), \(I(t)\), respectively. The system has the following form:

$$ \textstyle\begin{cases} \dot{S}=\Lambda-\mu S-\alpha SI+\gamma_{1} E+\gamma_{2} I,\\ \dot{E}=(1-p)\alpha SI-\beta E-\gamma_{1}E-\mu E,\\ \dot{I}=p\alpha SI+\beta E-\gamma_{2} I-\mu I, \end{cases} $$
(1)

where μ is the death rate for physical disease, Λ the influx or recruitment of the susceptible and the exposed, \(\gamma_{1}\) and \(\gamma_{2}\) the treatment cure rate of latent and active disease, respectively, β the breakdown rate from latent to active condition, \(\alpha S(t)I(t)\) the bilinear incidence, p the proportion of infection instantaneously degenerating in active condition, the dynamics of latently infected population depends on the proportion of the infection that results in latent infection \((1-p)\alpha I(t)S(t)\). The basic reproduction number of model (1) is

$$\mathcal{R}_{0}=\frac{\alpha\beta(1-p) \Lambda}{(\beta+\gamma _{1}+\mu) (\mu\gamma_{2}+\mu^{2}-\alpha p\Lambda)}, $$

which determines the extinction and persistence of the epidemic. According to the results in [11], one can see that

  1. (a)

    if \(0<\mathcal{R}_{0}<1\), the disease-free equilibrium \((\Lambda /\mu, 0, 0)\) is globally asymptotically stable, and it is unstable when \(\mathcal{R}_{0}>1\);

  2. (b)

    if \(\mathcal{R}_{0}>1\), the endemic equilibrium \((S^{*}, E^{*}, I^{*})\) of model (1) is globally asymptotically stable, where

    $$ \begin{aligned} &S^{*}=\frac{(\beta+\gamma_{1}+\mu)(\gamma_{2}+\mu)}{\alpha(\beta +\gamma_{1}p+\mu p)}, \\ &E^{*}=\frac{\beta\Lambda\alpha(1-p)^{2}(\gamma_{2}+\mu)}{ \alpha\mu(\beta+\gamma_{1}p+\mu p)(\beta+\mu+\gamma_{1}p+\gamma_{2}(1-p))} \biggl(1-\frac{1}{\mathcal{R}_{0}} \biggr), \\ &I^{*}=\frac{(\beta+\gamma_{1}p+\mu p)E^{*} }{(1-p)(\gamma_{2}+\mu)}. \end{aligned} $$
    (2)

However, the deterministic approach has some limitations in the mathematical modeling transmission of an infectious disease. Stochastic differential equation (SDE) models play a significant role in various branches of applied sciences including infectious dynamics, as they provide some additional degree of realism compared to their deterministic counterpart [12]. Recently, many authors have introduced parameter perturbation into epidemic models and have studied their dynamics [13–20].

In this paper, taking account of the effect of randomly fluctuating environment, we incorporate white noise in each equation of model (1). We assume that fluctuations in the environment will manifest themselves mainly as fluctuations in parameters \(\gamma_{1}\), \(\gamma_{2}\) as follows:

$$\gamma_{i}\rightarrow\gamma_{i}+\sigma_{i} \dot{B}_{i}(t), \quad i=1,2, $$

where \(B_{i}(t)\) (\(i=1,2\)) is for the mutually independent standard Brownian motions with \(B_{i}(0)=0\), and \(\sigma_{i}^{2}\) (\(i = 1, 2\)), the intensities of white noise. The stochastic version corresponding to the deterministic model (1) takes the following form:

$$ \textstyle\begin{cases} d{S}= [\Lambda-\mu S -\alpha SI+\gamma_{1} E+\gamma_{2} I ]\,dt +\sigma_{1} E\,dB_{1}(t)+\sigma_{2}I\,dB_{2}(t),\\ d{E}= [(1-p)\alpha SI-\beta E-\gamma_{1}E-\mu E ]\,dt-\sigma_{1} E\,dB_{1}(t),\\ d{I}= [p\alpha SI+\beta E-\gamma_{2} I-\mu I ]\,dt-\sigma_{2}I\,dB_{2}(t). \end{cases} $$
(3)

The equation for the total population \(N(t)=S(t)+ E(t) + I(t)\) size is obtained from (3) as

$$dN=(\Lambda-\mu N)\,dt. $$

It follows that

$$ \lim_{t\rightarrow\infty}\bigl(S(t)+E(t)+I(t)\bigr)= \frac {\Lambda}{\mu}. $$
(4)

By (4), we take \(S(t)=\frac{\Lambda}{\mu}-E(t)-I(t)\), and substitute it into the second and the third equations of model (3), and we can easily obtain the following limit system:

$$ \textstyle\begin{cases} d{E}= [(1-p)\alpha (\frac{\Lambda}{\mu}-I-E )I-\beta E-\gamma_{1}E-\mu E ]\,dt-\sigma_{1} E\,dB_{1}(t),\\ d{I}= [p\alpha (\frac{\Lambda}{\mu}-I-E )I+\beta E-\gamma_{2} I- \mu I ]\,dt-\sigma_{2}I\,dB_{2}(t), \end{cases} $$
(5)

with any given initial value \((E(0), I(0)\in\mathbb{R}_{+}^{2}\). It is easy, by simple computations, to conclude that model (5) has a unique disease-free equilibrium, \(E_{0}=(0,0)\).

This paper is organized as follows. In Section 2, we give some preliminaries. In Section 3, we deduce the conditions which will cause the disease to die out. The condition for the disease to be persistent (i.e., endemic) is given in Section 4. In Section 5, we provide some numerical examples to support our analytic results. In the last section, Section 6, we provide a brief discussion and summary of main results.

2 Preliminaries

Throughout this paper, let \((\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\in\mathbb{R}_{+}} \mathbb{P})\) be a complete probability space with a filtration \(\{\mathcal{F}_{t}\}_{t\in\mathbb{R}_{+}}\) satisfying the usual conditions (i.e., it is right continuous and increasing while \(\mathcal{F}_{0}\) contains all \(\mathbb{P}\)-null sets). Let

$$\Gamma= \biggl\{ (E,I)\in\mathbb{R}_{+}^{2}:0< E(t)+I(t)< \frac{\Lambda }{\mu} \biggr\} . $$

Consider the general n-dimensional stochastic differential equation

$$ {d}x(t)=f\bigl(x(t),t\bigr)\,{d}t+\varphi\bigl(x(t),t\bigr) \,{d}B(t) $$
(6)

on \(t\geq0\) with initial value \(x(0)=x_{0}\), the solution is denoted by \(x(t, x_{0})\). Assume that \(f(0,t) =0\) and \(\varphi(0, t) = 0\) for all \(t\geq0\), and equation (6) has the solution \(x(t)= 0\), which is called the trivial solution.

Definition 2.1

[21]

The trivial solution \(x(t)= 0\) of equation (6) is said to be almost surely exponentially stable if for all \(x_{0}\in \mathbb{R}^{n}\),

$$\limsup_{t\rightarrow\infty} \frac{1}{t} \log\bigl\vert x(t,x_{0})\bigr\vert < 0 \quad \textit{a.s.} $$

Definition 2.2

[22]

The population \(x(t)\) is said to be strongly persistent in the mean if \(\liminf_{t\rightarrow\infty} \frac{1}{t} \int_{0}^{t}x(s)\,ds>0\).

The differential operator \(\mathcal{L}\) associated with the function displayed in equation (6) is defined for a function \(V(t,x)\in C^{1,2}(\mathbb{R}\times\mathbb{R}^{n})\) by the formula

$$ \mathcal{L}V=\frac{\partial V}{\partial t} +f^{\mathrm{trp}}\frac{\partial V}{\partial x} +\frac{1}{2} \operatorname {Trc}\biggl[g^{\mathrm{trp}} \frac{\partial^{2} V}{\partial x^{2}} \biggr], $$
(7)

where Trc means trace and trp denotes the transpose of a matrix.

The following lemma is quoted from [16, 23] where it was proved and applied. It plays a similar role in this paper.

Lemma 2.3

Let \(x\in C[\Omega\times[0,\infty),(0,\infty)]\). If there exist positive constants λ, μ such that

$$\log x(t)\geq\lambda t-\mu \int_{0}^{t}x(s)\,ds+F(t),\quad \textit{a.s.} $$

for all \(t\geq0\), where \(F \in C[\Omega\times[0,\infty),\mathbb {R}]\) and \(\lim_{t\rightarrow\infty}\frac{F(t)}{t}=0\), then

$$\liminf_{t\rightarrow\infty} \frac{1}{t} \int_{0}^{t}x(s)\,ds\geq\frac{\lambda }{\mu}, \quad \textit{a.s.} $$

To investigate the dynamical behavior of a population model, the first concern is whether the solution of the model is positive and global. Motivated by [14], we can prove the global existence of a solution to model (5). One can obtain the following results.

Lemma 2.4

Let \((E(0),I(0))\in\Gamma\), and model (5) admits a unique solution \((E(t),I(t))\) on \(t\geq0\), which remains in Γ with probability 1. That is, the set Γ is almost surely positively invariant of model (5).

3 Stochastic disease-free dynamics

Now we present the following theorem, which gives conditions for the almost surely exponential stability of the equilibrium of model (5), which is motivated by [21, 24]. Denote \(\sigma:=\min\{\sigma_{1},\sigma_{2}\}\) and \(X(t):=(E(t),I(t))\). First of all, we give the property of the disease-free (i.e., \(I=0\)) dynamics.

Theorem 3.1

If

$$ R_{0}^{s}:=\frac{\alpha\beta(1-p) \Lambda}{(\beta+\gamma_{1}+\mu +\sigma^{2}/4) (\mu\gamma_{2}+\mu^{2}+\mu\sigma^{2}/4-\alpha p\Lambda)}< 1, $$
(8)

then the disease-free equilibrium \((0,0)\) of model (5) is almost surely exponentially stable. In other words, the disease will die out with probability one.

Proof

Let us fix any positive real number \(a_{1}\). We define the following stochastic process:

$$ z\bigl(X(t)\bigr)=a_{1} E+I. $$
(9)

Since \(z(X(t)>0)\) for all \(t>0\), we can define a \(C^{2}\)-function \(V:\mathbb{R}_{+}^{2}\rightarrow\mathbb{R}_{+}\) by

$$V\bigl(X(t)\bigr)=\ln z\bigl(X(t)\bigr). $$

By Itô’s formula, we can express the stochastic process \(V(X(x))\) as

$$ V(X(t)=V\bigl(X(0)\bigr)+ \int_{0}^{t}\mathcal{L}V\bigl(X(\tau)\bigr)d \tau+G(t), $$
(10)

where

$$G(t)= \int_{0}^{t}\frac{-a_{1}\sigma_{1}E(\tau)}{z(X(\tau ))}\,dB_{1}( \tau) + \int_{0}^{t}\frac{-\sigma_{1}I(\tau)}{z(X(\tau ))}\,dB_{2}(\tau) $$

and

$$\begin{aligned} \mathcal{L}V\bigl(X(t)\bigr) =&\frac{1}{z} \bigl(a_{1} \bigl((1-p)\alpha ({\Lambda}/{\mu}-E-I )I- \beta E-\gamma_{1}E-\mu E \bigr) \\ &{} +p\alpha ({\Lambda}/{\mu}-E-I )I+\beta E-\gamma_{2} I-\mu I \bigr)-\frac{1}{z^{2}} \biggl(\frac{a_{1}^{2}\sigma_{1}^{2}E^{2}}{2}+\frac{\sigma_{2}^{2}I^{2}}{2} \biggr). \end{aligned}$$

Regarding the quadratic variations of the stochastic integral \(G(t)\) we have

$$\int_{0}^{t} \biggl(\frac{-a_{1}\sigma_{1}E(\tau)}{z(X(\tau ))} \biggr)^{2}\,d\tau\leq \sigma_{1}^{2}t,\quad \quad \int_{0}^{t} \biggl(\frac{-\sigma_{1}I(\tau)}{z(X(\tau ))} \biggr)^{2}\,d\tau \leq{\sigma_{2}^{2}t}. $$

By the strong law of large numbers for martingales [25], we have

$$\lim_{t\rightarrow\infty} \frac{G(t)}{t} =0 \quad \textit{a.s.} $$

Now we prove that

$$ \mathcal{L}V\bigl(x(t)\bigr)< 0 \quad \textit{a.s.} $$
(11)

To this end, we set

$$ v(t)=z^{-1} E, \quad\quad w(t)=z^{-1}I. $$
(12)

It follows that

$$0< v(t)< \frac{1}{a_{1}}, \quad\quad 0< w(t)< 1 \quad \text{for every } t>0, $$

that is, the stochastic processes \(v(t)\), \(w(t)\) are bounded above by \(\max\{1/a_{1},1\}\), and non-negative. By virtue of (9) we have

$$ a_{1}v(t)+w(t)=1 \quad \text{for every } t>0. $$
(13)

This enables us to write down the expression for \(\mathcal{L}V(X(t))\) as

$$ \begin{aligned}[b] \mathcal{L}V(X) &=a_{1} \bigl((1-p)\alpha(\Lambda/\mu-I-E)w-\beta v-\gamma_{1}v-\mu v\bigr) \\ &\hphantom{=}{} +p\alpha(\Lambda/\mu-I-E)w+\beta v-\gamma_{2} w-\mu w -\frac{a_{1}^{2}\sigma_{1}^{2}v^{2}}{2}-\frac{\sigma_{2}^{2}w^{2}}{2} \\ &\leq\bigl(a_{1}(1-p)\alpha\Lambda/\mu+p\alpha\Lambda/\mu- \gamma_{2}-\mu \bigr) w -\bigl(a_{1}(\beta+ \gamma_{1}+\mu)-\beta\bigr)v \\ &\hphantom{=}{} -\frac{\sigma^{2}}{2} \bigl(a_{1}^{2}v^{2}+w^{2} \bigr). \end{aligned} $$
(14)

In view of \(a_{1}v+w=1\), we have

$$-\frac{\sigma^{2}}{2} \bigl(a_{1}^{2}v^{2}+w^{2} \bigr)\leq-\frac{\sigma^{2}}{4}(a_{1}v+w)^{2} = - \frac{\sigma^{2}}{4}(a_{1}v+w). $$

It follows that

$$ \mathcal{L}V(X)\leq A_{1}v+A_{2}w, $$
(15)

where

$$\begin{aligned}& A_{1}=\beta-a_{1} \biggl(\beta+\gamma_{1}+\mu+ \frac{\sigma^{2}}{4} \biggr), \\& A_{2}=\frac{1}{\mu}\biggl(a_{1}(1-p)\alpha\Lambda+p \alpha\Lambda-\gamma _{2}\mu-\mu^{2}-\frac{\sigma^{2}\mu}{4} \biggr). \end{aligned}$$

Let \(a_{1}=\frac{\beta}{\beta+\gamma_{1}+\mu+{\sigma^{2}}/{4}}\), then \(A_{1}=0\). The condition \(R_{0}^{s} < 1\) is equivalent to the following inequality:

$$\frac{\alpha\beta(1-p) \Lambda}{\beta+\gamma_{1}+\mu+\sigma^{2}/4}< \mu\gamma_{2}+\mu^{2}+\mu \sigma^{2}/4-\alpha p\Lambda, $$

which implies \(A_{2}<0\). It follows from \(0< w<1\) that \(\mathcal{L}V(X(t))<0\). It finally follows from (10) by dividing t on both sides and then letting \(t\rightarrow\infty\) that

$$ \limsup_{t\rightarrow\infty} \frac{1}{t}\ln z\bigl(X(t) \bigr)= \limsup_{t\rightarrow\infty} \frac {1}{t} \int_{0}^{t} \mathcal{L}V\bigl(X(\tau)\bigr)\,d\tau< 0\quad \textit{a.s.}, $$
(16)

which is the required assertion. □

Remark 3.2

It is noted that \(R_{0}^{s}=\frac{\alpha\beta(1-p) \Lambda}{(\beta +\gamma_{1}+\mu+\sigma^{2}/4) (\mu\gamma_{2}+\mu^{2}+\mu\sigma^{2}/4-\alpha p\Lambda)}< R_{0}\). Therefore, if \(R_{0}<1\), no matter how the noise intensities change, we have the disease-free equilibrium to be almost surely exponentially stable. However, if \(R_{0}>1\), by increasing the values of noise intensities such that \(R_{0}^{s}<1\), the disease-free equilibrium will still be almost surely exponentially stable. That is to say, in this situation, for the deterministic model, there is an endemic equilibrium which is globally stable, but for the stochastic model, there is a stable disease-free equilibrium which means that the disease goes extinct exponentially a.s.

4 Stochastic endemic dynamics

In this section we intend to prove the stochastic endemic dynamics (i.e., persistence of E and I) of model (5) under certain parametric restrictions.

Theorem 4.1

If

$$ R_{0}^{*}:=\frac{\alpha\beta(1-p) \Lambda}{(\beta+\gamma_{1}+\mu +\sigma_{1}^{2}/2) (\mu\gamma_{2}+\mu^{2}+\mu\sigma^{2}_{2}/2-\alpha p\Lambda)}>1, $$
(17)

then for any initial value \((E(0), I(0))\in\Gamma\), the solution \((E(t), I(t))\) of model (5) has the following property:

$$\liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} E(s)\,ds\geq\frac{\alpha(1-p)\Lambda(\gamma_{2}\mu+\mu^{2}+\mu\sigma _{2}^{2}/2-\alpha p\Lambda)}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} \bigl(R_{0}^{*}-1\bigr) $$

and

$$\liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} I(s)\,ds\geq \bigl(\gamma_{2} \mu+\mu^{2}+\mu\sigma_{2}^{2}/2-\alpha p\Lambda \bigr) \bigl(R_{0}^{*}-1\bigr). $$

That is the solutions of model (5) are strongly persistent in the mean.

Proof

An integration of the first equation of model (5) yields

$$\begin{aligned}& \frac{\alpha(1-p)\Lambda}{\mu} \bigl\langle I(t) \bigr\rangle - \alpha(1-p) \bigl( \bigl\langle I(t)^{2} \bigr\rangle + \bigl\langle E(t)I(t) \bigr\rangle \bigr)- (\beta+\gamma_{1}+\mu ) \bigl\langle E(t) \bigr\rangle \\& \quad =\frac{E(t)-E(0)}{t}+\frac{\sigma_{1}}{t} \int_{0}^{t}E(s)\,dB_{1}(s). \end{aligned}$$

We compute that

$$ \begin{aligned}[b] \bigl\langle E(t) \bigr\rangle &= \frac{{\alpha(1-p)\Lambda}}{ \mu(\beta+\gamma_{1}+\mu)} \bigl\langle I(t) \bigr\rangle - \frac{\alpha(1-p) }{\beta+\gamma_{1}+\mu} \bigl( \bigl\langle I(t)^{2} \bigr\rangle + \bigl\langle E(t)I(t) \bigr\rangle \bigr)-\varphi(t) \\ &\leq\frac{{\alpha(1-p)\Lambda}}{ \mu(\beta+\gamma_{1}+\mu)} \bigl\langle I(t) \bigr\rangle -\varphi(t), \end{aligned} $$
(18)

where

$$\varphi(t)=\frac{1}{\beta+\gamma_{1}+\mu} \biggl(\frac{E(t)-E(0)}{t}+\frac{\sigma_{1}}{t} \int _{0}^{t}E(s)\,dB_{1}(s) \biggr). $$

Since \(E(t),I(t)<\Lambda/\mu\), by the strong law of large numbers for martingales [25], we have

$$\lim_{t\rightarrow\infty} \frac{E(t)}{t} =0, \quad\quad \lim_{t\rightarrow\infty} \frac{1}{t} \int_{0}^{t}E(s)\,dB_{1}(s)=0 \quad \textit{a.s.} $$

Obviously, \(\lim_{t\rightarrow\infty} \varphi(t)=0\) a.s.

Applying Itô’s formula to the first equation of model (5) leads to

$$\begin{aligned} d\bigl(\ln(\mu/\Lambda E)\bigr) =&\frac{\alpha(1-p)\Lambda}{\mu} \frac{I}{E}- \frac{\alpha(1-p) I^{2}}{E}- \alpha(1-p) I- \biggl(\beta+ \gamma_{1}+\mu+\frac{1}{2}\sigma_{1}^{2} \biggr) \\ &{}-\sigma_{1}\,dB_{1}(t). \end{aligned}$$
(19)

An integration of (19) yields

$$\begin{aligned} \frac{\alpha(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} \biggl\langle \frac{I}{E} \biggr\rangle =&1+ \frac{1}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} \biggl(\alpha(1-p) \biggl( \biggl\langle \frac{I^{2}}{E} \biggr\rangle + \langle I \rangle \biggr) \\ &{} +\frac{\sigma_{1}\,dB_{1}(t)}{t}+\frac{\ln(\mu/\Lambda (E(t)-E(0))}{t} \biggr). \end{aligned}$$

Noting that \(-\infty<\ln(\mu/\Lambda(E(t))<0\) (as \(0< E(t)<\Lambda /\mu\)), then for arbitrary \(0<\varepsilon<1\), there exist \(T=T(\omega)>0\) and a set \(\Omega_{\varepsilon}\), such that \(P(\Omega_{\varepsilon})\geq1-\varepsilon\). For all \(t\geq T(\omega)\), \(\omega\in \Omega_{\varepsilon}\),

$$\frac{\alpha(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} \biggl\langle \frac{I}{E} \biggr\rangle < 1, $$

which is equivalent to

$$\frac{\alpha(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} \int_{0}^{t}\frac{I(s)}{E(s)}\,ds< t. $$

It follows from \(0< E(t),I(t)<\Lambda/\mu\) that

$$ \frac{\alpha(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)} I(t)< E(t). $$
(20)

Hence, applying Itô’s formula to the second equation of model (5) leads to

$$ d( \ln I)=\frac{\alpha p\Lambda}{\mu}-\gamma_{2}-\mu- \frac {1}{2}\sigma_{2}^{2}+ \frac{E}{I}- \alpha p E- \alpha(1-p) I-\sigma_{2}\,dB_{2}(t). $$
(21)

Integrating this from 0 to t, we have

$$ \begin{aligned}[b] \frac{\ln I(t)}{t}&\geq \biggl( \frac{\alpha\beta(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu +\sigma_{1}^{2}/2)}+ \frac{\alpha p\Lambda}{\mu}-\gamma_{2}-\mu- \sigma_{2}^{2}/2 \biggr) \\ &\hphantom{\geq}{} - \biggl(\frac{{\alpha^{2}p(1-p)\Lambda}}{ \mu(\beta+\gamma_{1}+\mu)}+\alpha(1-p) \biggr) \bigl\langle I(t) \bigr\rangle +\varphi(t))-\frac{\sigma _{2}B_{2}(t)}{t}+\frac{\ln I(0)}{t}. \end{aligned} $$
(22)

Since

$$\lim_{t\rightarrow\infty} \bigl(\varphi(t)\bigr)-\frac {\sigma_{2}B_{2}(t)}{t} + \frac{\ln I(0)}{t} )=0, $$

it follows from Lemma 2.3 that

$$\begin{aligned} \liminf_{t\rightarrow\infty}\bigl\langle I(t)\bigr\rangle \geq& \frac{\alpha\beta(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma_{1}^{2}/2)}+ \frac{\alpha p\Lambda}{\mu}-\gamma_{2}-\mu- \sigma_{2}^{2}/2 \\ =&\bigl(\gamma_{2}\mu+\mu^{2}+\mu\sigma_{2}^{2}/2- \alpha p\Lambda\bigr) \bigl(R_{0}^{*}-1\bigr)>0. \end{aligned}$$

Finally, according to the last equality of (20), we get

$$\liminf_{t\rightarrow\infty}\bigl\langle E(t)\bigr\rangle > \frac{\alpha(1-p)\Lambda}{\mu(\beta+\gamma_{1}+\mu+\sigma _{1}^{2}/2)},\qquad \liminf_{t\rightarrow\infty}\bigl\langle I(t)\bigr\rangle >0\quad \textit{a.s.} $$

This finishes the proof. □

Remark 4.2

It is noted that \(R_{0}^{*}< R_{0}^{s}< R_{0}\). Therefore, if \(R_{0}^{*}>1\), then \(R_{0}>1\). That is to say, if for stochastic model the disease will be prevalent, for a deterministic model the disease also must be prevalent.

5 Numerical simulations

In this section, we give some numerical simulations to show the effect of noise on the dynamics of model (5) by using the Milstein method mentioned in Higham [26].

For model (5), the parameters are taken as follows:

$$ \begin{aligned} & \Lambda= 0.6,\quad\quad \mu= 0.5,\quad\quad \alpha= 0.8,\quad\quad \gamma_{{1}}= 0.1,\quad\quad \gamma_{{2}}= 0.1 ,\\ & \beta=1,\quad\quad p= 0.4, \end{aligned} $$
(23)

with initial values

$$ \bigl(E(0), I(0)\bigr)=(0.10,0.25)\in\Gamma. $$
(24)
  1. 1.

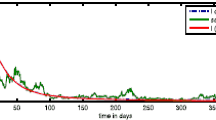
    Now we note that these parameters give a value of \({R}_{0} =1.667\) to the basic reproduction number in the deterministic case (i.e., with \(\sigma_{1}=\sigma_{2}=0\)). Consequently the system eventually approaches an endemic equilibrium point \(( 0.0523, 0.18)\) (see Figure 1).

    Figure 1
    figure 1

    The paths of \(\pmb{E(t)}\) , \(\pmb{I(t)}\) for model ( 5 ) with initial values ( 24 ). The parameters are taken as (23), \(\sigma_{1}=\sigma_{2}=0\) (\({R}_{0} =1.667\)).

    Full size image
  2. 2.

    Choose \(\sigma_{1}=0.75\), \(\sigma_{2}=0.8\), then we obtain \({R}_{0}^{s}=0.9279\). Theorem 3.1 asserts that the disease-free equilibrium is almost surely exponentially stable, and the disease will die out with probability one (see Figure 2).

    Figure 2
    figure 2

    The paths of \(\pmb{E(t)}\) , \(\pmb{I(t)}\) for model ( 5 ) with initial values ( 24 ). The parameters are taken as (23), \(\sigma_{1}=0.75\), \(\sigma_{2}=0.8\) (\({R}_{0}^{s}=0.9279\), \({R}_{0}^{*}=0.5712\)).

    Full size image
  3. 3.

    Choose \(\sigma_{1}=0.1\), \(\sigma_{2}=0.2\), then we obtain \({R}_{0}^{s}=1.6450\) and \({R}_{0}^{*}=1.5207\). Theorem 4.1 asserts that the solutions of model (5) are strongly persistent in mean (see Figure 3).

    Figure 3
    figure 3

    The paths of \(\pmb{E(t)}\) , \(\pmb{I(t)}\) for model ( 5 ) with initial values ( 24 ). The parameters are taken as (23), \(\sigma_{1}=0.1\), \(\sigma_{2}=0.2\) (\({R}_{0}^{s}=1.6450\), \({R}_{0}^{*}=1.5207\)).

    Full size image
  4. 4.

    Now change \(\sigma_{1}=0.1\), \(\sigma_{2}=0.6\), then we obtain \({R}_{0}^{s}=1.6450\) and \({R}_{0}^{*}=0.9063\). Therefore, the conditions of Theorems 3.1 and 4.1 are not satisfied. In this case, our simulations suggest that the disease will die out with probability one (see Figure 4).

    Figure 4
    figure 4

    The paths of \(\pmb{E(t)}\) , \(\pmb{I(t)}\) for model ( 5 ) with initial values ( 24 ). The parameters are taken as (23), \(\sigma_{1}=0.1\), \(\sigma_{2}=0.6\) (\(\mathcal{R}_{0}^{s}=1.6450\), \(\mathcal{R}_{0}^{*}=0.9063\)).

    Full size image

6 Discussions

In this paper, we mainly focus on the SDE version of an SEIS epidemic model with latent patients and active patients. We show that the SDE model has a unique positive global solution and establish some conditions for determining the disease outbreak or extinct. The key parameters are \(R_{0}^{s}\) and \(R_{0}^{*}\), which are all less than the corresponding deterministic version of the basic reproduction number \(R_{0}\).

Theorem 3.1 shows that if \(R_{0}^{S}<1\), the disease will die out (cf. Figure 2). Theorem 4.1 shows that if \(R_{0}^{*}>1\), then the disease will persist (cf. Figure 3). By numerical simulations, we also show that if \(R_{0}^{*}<1<R_{0}^{S}\), the disease will die out (cf. Figure 4). Hence, we can make a conjecture that the behavior of the disease is determined by \(R_{0}^{*}\). It is well known that for deterministic epidemic models, the basic reproduction number \(R_{0}\) determines the prevalence or extinction of the disease. In this paper, we consider the threshold \(R_{0}^{*}\) as the basic reproduction number of model (5). Notice that \(R_{0}^{*}< R_{0}\), and it is possible that \(R_{0}^{*}<1<R_{0}\). This is the case when the deterministic model has an endemic (see Figure 1), while the stochastic model has disease extinction with probability one (see Figure 4). That is to say, in this case, noise can suppress the disease outbreak.