1 Introduction

The SIR (susceptible, infectious, recovered) epidemic model is one of the most popular epidemic models in epidemiology; it was initially proposed by Kermack and Mckendrick [1–4]. Since then, the SIR models have been considered by many researchers [5–16]. They have made a wealth of research achievements. In 1980s, Hethcote [17] considered the initial value problem (IVP) for the SIR model of an endemic disease with vital dynamics as follows:

$$\begin{aligned} \textstyle\begin{cases} (NS(t))'=-\lambda SNI+\mu N-\mu NS, \\ (NI(t))'=\lambda SNI-\gamma NI -\mu NI, \\ (NR(t))'=\gamma NI-\mu NR, \\ NS(0)=NS_{0}>0, \qquad NI(0)=NI_{0}\geq0, \\ NR(0)=NR_{0}\geq0, \\ NS(t)+NI(t)+NR(t)=N, \end{cases}\displaystyle \end{aligned}$$

where the contact rate λ, the removal rate constant γ and the death rate constant μ are positive constants. For more details of a simple SIR model, we can refer to the books of Hethcote [17] and Anderson and May [18].

In addition, Gao et al. [7] have investigated a delayed SIR epidemic model with pulse vaccination. They conclude that the infection-free periodic solution is globally attractive and the system is permanent. Meng and Chen [9] studied the SIR epidemic model with both vertical and horizontal transmission, analyzed some dynamical behaviors, such as the infection-free equilibrium, the positive equilibrium, the permanence, global asymptotic behavior and so on, and one obtained some important qualitative properties.

Recently, pulse vaccination strategy, a new vaccination strategy against measles, has been proposed. Its theoretical study was started by Agur et al. in [19]. As for pulse vaccination strategy, a lot of original work has been done in [5–9, 19–21].

In the real world, individual members of many species experience two stages of life, immature and mature ones. Stage-structured population models have received great attention, and many stage-structured models have been studied in recent years [22–28].

Theories of impulsive differential equations have been introduced into population dynamics lately [29–32]. Impulsive equations are found in almost every domain of applied science and have been studied in many investigations [30, 31, 33–35]. They generally describe phenomena which are subject to steep or instantaneous changes.

Motivated by the above studies, our study is to investigate transmission dynamics of an SIR epidemic model with stage structure and pulse vaccination. We assume that the matured population approaches a steady state, if there is no disease infection and all matured individuals are susceptible. We assume full immunity of recovered individuals; that is to say, those individuals are no longer susceptible after they have recovered.

The present paper is to introduce birth pulse of the population, state structure and pulse vaccination into SIR epidemic model and obtain some important qualitative properties for the investigated system. As a matter of fact, pulse birth is used in an epidemic model. To the best of our knowledge, no such research has been conducted.

2 The model

In this work, we consider an SIR epidemic model with stage structure and pulse vaccination:

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{1}(t)}{dt}=-(c+d_{1})S_{1}(t),\\ \frac{dS_{2}(t)}{dt}=cS_{1}(t)-d_{2}S_{2}(t)-\beta S_{2}(t)I(t), \\ \frac{dI(t)}{dt}=\beta S_{2}(t)I(t)-(r+d_{3})I(t), \\ \frac{dR(t)}{dt}=rI(t)-d_{4}R(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=S_{2}(t)(a-bS_{2}(t)), \\ \Delta S_{2}(t)=0,\\ \Delta I(t)=0, \\ \Delta R(t)=0, \end{array}\displaystyle \right \}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=0,\\ \Delta S_{2}(t)=-\mu S_{2}(t),\\ \Delta I(t)=0,\\ \Delta R(t)=\mu S_{2}(t), \end{array}\displaystyle \right\}\quad t=(n+l)\tau, n=1,2,\ldots, \end{cases} $$
(1)

where \(S_{1}(t)\), \(S_{2}(t)\) represent the numbers of the immature and the mature of the susceptible. \(I(t)\), \(R(t)\) represent the numbers of the infectious, and the recovered, respectively. c is called the rate of the immature susceptible turning into the mature susceptible. \(d_{1}\), \(d_{2}\), \(d_{3}\), \(d_{4}\), respectively denote the natural death rate of the immature susceptible, the mature susceptible, the infectious and the recovered. β is the average number of adequate contacts of a mature infectious individual per unit time. r stands for the recovery rate of the mature infectious individual. The mature susceptible is birth pulse with intrinsic rate of natural increase and density dependence rate of the mature susceptible denoted by a, b, respectively. The pulse birth and pulse vaccination occurs every τ period (τ is a positive constant). \(\Delta S_{2}(t)=S_{2}(t^{+})-S_{2}(t)\). μ (\(0< \mu < 1\)) is the proportion of the successful vaccination which is called pulse vaccination rate, at \(t=(n+l)\tau\), \(0< l<1\), \(n\in Z_{+}\). \(\Delta S_{1}(t)=S_{1}(t^{+})-S_{1}(t)\), and \(S_{2}(t)(a-bS_{2}(t))\) represents the birth effort of the mature susceptible at \(t=n\tau\), \(n\in Z_{+}\).

In this paper, we assume:

  1. (i)

    The susceptible is infertile after being infected; that is to say, the infectious and the recovered have no ability to reproduce.

  2. (ii)

    The immature susceptible is immune to the disease for taking from their parent population; that is to say, the immature susceptible achieves temporary immunity.

As the first, second, and third equations do not comprise \(R(t)\), we can simplify system (1) as follows:

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{1}(t)}{dt}=-(c+d_{1})S_{1}(t),\\ \frac{dS_{2}(t)}{dt}=cS_{1}(t)-d_{2}S_{2}(t)-\beta S_{2}(t)I(t), \\ \frac{dI(t)}{dt}=\beta S_{2}(t)I(t)-(r+d_{3})I(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=S_{2}(t)(a-bS_{2}(t)), \\ \Delta S_{2}(t)=0,\\ \Delta I(t)=0, \end{array}\displaystyle \right\}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=0,\\ \Delta S_{2}(t)=-\mu S_{2}(t),\\ \Delta I(t)=0, \end{array}\displaystyle \right \}\quad t=(n+l) \tau, n=1,2,\ldots. \end{cases} $$
(2)

This is equivalent to system (1).

3 Some lemmas

Before discussing the main results, we will introduce some definitions, notations, and lemmas. Denote by \(f=(f_{1},f_{2},f_{3},f_{4})\) the map defined by the right-hand side of system (1), the solution of (1), denoted by \(z(t)=(S_{1}(t), S_{2}(t), I(t), R(t))^{T}\), is a piecewise continuous function \(z: R_{+}\rightarrow R_{+}^{4}\), where \(R_{+}=[0, \infty)\), \(R_{+}^{4}=\{z\in R^{4}: z>0 \}\). \(z(t)\) is continuous on \((n\tau, (n+l)\tau]\times R_{+}^{4}\) and \(((n+l)\tau, (n+1)\tau]\times R_{+}^{4}\) (\(n\in Z_{+}\), \(0< l< 1\)). According to [30, 31], the global existence and uniqueness of solutions of system (1) is guaranteed by the smoothness properties of f, the mapping defined by the right-hand side of system (1).

Let \(V: R_{+}\times R_{+}^{4}\rightarrow R_{+}\). Then V is said to be belonged to class \(V_{0}\) if:

  1. (i)

    V is continuous in \((n\tau, (n+l)\tau]\times R_{+}^{4}\) and \(((n+l)\tau, (n+1)\tau]\times R^{4}\), for all \(z\in R^{4}_{+}\), \(n\in Z_{+}\), and \(\lim_{(t,y)\rightarrow ((n+l)\tau^{+},z)}V(t,y)=V((n+l)\tau^{+}, z)\) and \(\lim_{(t,y)\rightarrow ((n+1)\tau^{+},z)}V(t,y)=V((n+1)\tau^{+}, z)\) exist.

  2. (ii)

    V is locally Lipschitzian in z.

Definition 3.1

If \(V\in V_{0}\), then, for \((t,z)\in(n\tau, (n+l)\tau]\times R_{+}^{4}\) and \(((n+l)\tau, (n+1)\tau)\times R_{+}^{4}\), the upper right derivative of \(V(t,z)\) with respect to the impulsive differential system (1) is defined as

$$D^{+}V(t,z)=\lim_{h\rightarrow0}\sup\frac{1}{h} \bigl[V \bigl(t+h, z+hf(t,z) \bigr)-V(t,z) \bigr]. $$

Lemma 3.2

(see [30], Theorem 1.4.1)

Let the function \(m\in PC'[R_{+}, R]\) satisfy the inequalities

$$ \textstyle\begin{cases} m'(t) \leq p(t)m(t)+q(t), \quad t\neq t_{k}, k=1,2,\ldots,\\ m(t_{k}^{+}) \leq d_{k}m(t_{k})+b_{k}, \quad t=t_{k}, t\geq t_{0}, \end{cases} $$
(3)

where \(p,q\in C[R_{+}, R]\) and \(d_{k}\geq0\) and \(b_{k}\) are constants. Then

$$\begin{aligned} m(t) \leq& m(t_{0})\prod_{t_{0}< t_{k}< t}d_{k} \exp \biggl( \int _{t_{0}}^{t}p(s)\,ds \biggr)+\sum _{t_{0}< t_{k}< t} \biggl(\prod_{t_{k}< t_{j}< t}d_{j} \exp \biggl( \int_{t_{k}}^{t}p(s)\,ds \biggr) \biggr)b_{k} \\ &{}+ \int_{t_{0}}^{t}\prod_{s< t_{k}< t}d_{k} \exp \biggl( \int_{s}^{t}p(\sigma )\,d\sigma \biggr)q(s)\,ds,\quad t \geq t_{0}. \end{aligned}$$

Lemma 3.3

There exists a constant \(M>0\) such that \(S_{1}(t)\leq M\), \(S_{2}(t)\leq M\), \(I(t)\leq M\), \(R(t)\leq M\) for each solution \((S_{1}(t), S_{2}(t), I(t), R(t))\) of system (1) with t large enough.

Proof

Define \(V(t)=S_{1}(t)+S_{2}(t)+I(t)+R(t)\), \(d=\min\{ d_{1}, d_{2}, d_{3}, d_{4}\}\). When \(t\neq(n+l)\tau\), \(t\neq(n+1)\tau\), we have

$$\begin{aligned} D^{+}V(t)+dV(t) =& -cS_{1}(t)-d_{1}S_{1}(t)+cS_{1}(t)-d_{2}S_{2}(t)- \beta S_{2}(t)I(t) \\ &{}+\beta S_{2}(t)I(t)-(r+d_{3})I(t)+rI(t)-d_{4}R(t) \\ &{}+dS_{1}(t)+dS_{2}(t)+dI(t)+dR(t) \\ =& -(d_{1}-d)S_{1}(t)-(d_{2}-d)S_{2}(t) \\ &{}-(d_{3}-d)I(t)-(d_{4}-d)R(t)\leq\delta\leq0. \end{aligned}$$

When \(t=(n+l)\tau\), we have

$$\begin{aligned} V \bigl((n+l)\tau^{+} \bigr) =& S_{1} \bigl((n+l) \tau^{+} \bigr)+S_{2} \bigl((n+l)\tau^{+} \bigr)+I \bigl((n+l)\tau^{+} \bigr)+R \bigl((n+l)\tau ^{+} \bigr) \\ =& S_{1} \bigl((n+l)\tau \bigr)+(1-\mu)S_{2} \bigl((n+l) \tau \bigr)+I \bigl((n+l)\tau \bigr) \\ &{}+R \bigl((n+l)\tau \bigr)+\mu S_{2} \bigl((n+l)\tau \bigr) \\ =& S_{1} \bigl((n+l)\tau \bigr)+S_{2} \bigl((n+l)\tau \bigr)+I \bigl((n+l)\tau \bigr)+R \bigl((n+l)\tau \bigr) \\ =& V \bigl((n+l)\tau \bigr). \end{aligned}$$

When \(t=(n+1)\tau\), we have

$$\begin{aligned} V \bigl((n+1)\tau^{+} \bigr) =& S_{1} \bigl((n+1) \tau^{+} \bigr)+S_{2} \bigl((n+1)\tau^{+} \bigr)+I \bigl((n+1)\tau^{+} \bigr)+R \bigl((n+1)\tau ^{+} \bigr) \\ =& \bigl[S_{1} \bigl((n+1)\tau \bigr)+S_{2} \bigl((n+1) \tau \bigr) \bigl(a-bS_{2} \bigl((n+1)\tau \bigr) \bigr) \bigr]+S_{2} \bigl((n+1)\tau \bigr) \\ &{}+I \bigl((n+1)\tau \bigr)+R \bigl((n+1)\tau \bigr) \\ =& S_{1} \bigl((n+1)\tau \bigr)+S_{2} \bigl((n+1)\tau \bigr) \bigl(a-bS_{2} \bigl((n+1)\tau \bigr)\bigr)+S_{2} \bigl((n+1)\tau \bigr) \\ &{}+I \bigl((n+1)\tau \bigr)+R \bigl((n+1)\tau \bigr) \\ =& V \bigl((n+1)\tau \bigr)+S_{2} \bigl((n+1)\tau \bigr) \bigl(a-bS_{2} \bigl((n+1)\tau \bigr)\bigr) \\ \leq& V \bigl((n+1)\tau \bigr)+\frac{a^{2}}{4b}. \end{aligned}$$

We make a notation as \(\xi=\frac{a^{2}}{4b}>0\). Then by Lemma 3.2, for \(t\in(n\tau, (n+1)\tau]\), we have

$$\begin{aligned} V(t) \leq& V(0)\exp(-d t)+ \int^{t}_{0}\delta\exp \bigl(-d(t-s) \bigr)\,ds+\sum _{0< n\tau< t}\xi\exp \bigl(-d(t-n\tau) \bigr) \\ =& V(0)\exp(-d t)+\frac{\delta}{d} \bigl(1-\exp(-d t) \bigr)+\xi \frac{\exp (-d(t-\tau))-\exp(-d(t-(n+1)\tau))}{1-\exp(d\tau)} \\ < & V(0)\exp(-d t)+\frac{\delta}{d} \bigl(1-\exp(-d t) \bigr)+ \frac{\xi\exp(-d(t-\tau))}{1-\exp(d\tau)}+ \frac{\xi\exp(d\tau)}{\exp (d\tau)-1} \\ \rightarrow& \frac{\delta}{d}+\frac{\xi\exp(d\tau)}{\exp(d\tau)-1} \quad\mbox{as } t\rightarrow\infty. \end{aligned}$$

So \(V(t)\) is uniformly ultimately bounded. Hence, by the definition of \(V(t)\) we see that there exists a constant \(M>0\), such that \(S_{1}(t)\leq M\), \(S_{2}(t)\leq M\), \(I(t)\leq M\), \(R(t)\leq M\) for t large enough.

We choose the following notation:

$$\begin{aligned} \Omega^{*} = \frac{(c+d_{1}-d_{2})[1+e^{-(c+d_{1}-d_{2})\tau}-e^{-(c+d_{1})\tau }-e^{d_{2}\tau}]+ac[1-e^{-(c+d_{1}-d_{2})\tau}]}{ (c+d_{1}-d_{2})[1-e^{-(c+d_{1})\tau}]+ac [1-e^{-(c+d_{1}-d_{2})l\tau}]}. \end{aligned}$$

If \(I(t)=0\), then we have the following subsystem of (2):

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{1}(t)}{dt}=-(c+d_{1})S_{1}(t),\\ \frac{dS_{2}(t)}{dt}=cS_{1}(t)-d_{2}S_{2}(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=S_{2}(t)(a-bS_{2}(t)), \\ \Delta S_{2}(t)=0, \end{array}\displaystyle \right\}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{1}(t)=0,\\ \Delta S_{2}(t)=-\mu S_{2}(t), \end{array}\displaystyle \right\}\quad t=(n+l)\tau, n=1,2,\ldots. \end{cases} $$
(4)

We easily obtain the analytic solution of system (4) between pulses as follows:

$$\begin{aligned} \textstyle\begin{cases} S_{1}(t)=S_{1}(n\tau^{+})e^{-(c+d_{1})(t-n\tau)},\quad t\in(n\tau, (n+1)\tau ], \\ S_{2}(t)= \textstyle\begin{cases} e^{-d_{2}(t-n\tau)} [ S_{2}(n\tau^{+}) +\frac{c S_{1}(n\tau^{+})(1-e^{-(c+d_{1}-d_{2})(t-n\tau)})}{c+d_{1}-d_{2}} ],\quad t\in(n\tau, (n+l)\tau], \\ e^{-d_{2}(t-(n+l)\tau)} [ S_{2}((n+l)\tau^{+}) + \frac{c S_{1}((n+l)\tau^{+})(1-e^{-(c+d_{1}-d_{2})(t-(n+l)\tau)})}{c+d_{1}-d_{2}} ],\\ \quad t\in((n+l)\tau, (n+1)\tau]. \end{cases}\displaystyle \end{cases}\displaystyle \end{aligned}$$
(5)

Considering the fourth, fifth, seventh, and eighth equations of system (2), we have the stroboscopic map of (2)

$$\begin{aligned} \textstyle\begin{cases} S_{1}((n+1)\tau^{+})= [ e^{-(c+d_{1})\tau}+\frac{a c\zeta}{c+d_{1}-d_{2}} ] S_{1}(n\tau^{+})+a(1-\mu)e^{-d_{2}\tau}S_{2}(n\tau^{+})\\ \hphantom{S_{1}((n+1)\tau^{+})= }{}-b [ \frac{c\zeta }{c+d_{1}-d_{2}}S_{1}(n\tau^{+})+(1-\mu)e^{-d_{2}\tau}S_{2}(n\tau^{+}) ]^{2},\\ S_{2}((n+1)\tau^{+})=\frac{c\zeta}{c+d_{1}-d_{2}} S_{1}(n\tau^{+})+(1-\mu)e^{-d_{2}\tau}S_{2}(n\tau^{+}), \end{cases}\displaystyle \end{aligned}$$
(6)

where \(\zeta= e^{-d_{2}\tau}[(1-\mu)(1-e^{-(c+d_{1}-d_{2})l\tau })+e^{-(c+d_{1}-d_{2})l\tau}-e^{-(c+d_{1}-d_{2})\tau}]>0\). If we choose \(A=e^{-(c+d_{1})\tau}+\frac{a c\zeta }{c+d_{1}-d_{2}}> 0\), \(B=a(1-\mu)e^{-d_{2}\tau}>0\), \(C=\frac{c\zeta}{c+d_{1}-d_{2}}\), \(D=(1-\mu)e^{-d_{2}\tau}\), \(A<1\), and \(0< D<1\), the following two equivalence relations are found by calculation:

$$\begin{aligned} &\mu< \Omega^{*} \Leftrightarrow 1-A-D+AD-BC< 0, \\ &\mu> \Omega^{*} \Leftrightarrow 1-A-D+AD-BC>0. \end{aligned}$$

The two fixed points of (6) are obtained as \(G_{1}(0,0)\) and \(G_{2}(S_{1}^{*}, S_{2}^{*})\), where

$$ \textstyle\begin{cases} S_{1}^{*}=\frac{(1-D-A+AD-BC)(-1+D)}{bC^{2}}, \quad \mu< \Omega^{*},\\ S_{2}^{*}=\frac{-(1-D-A+AD-BC)}{bC},\quad \mu< \Omega^{*}. \end{cases} $$
(7)

 □

Lemma 3.4

(i) If \(\mu>\Omega^{*}\), then the fixed point \(G_{1}(0,0)\) is globally asymptotically stable. (ii) If \(\mu<\Omega^{*}\), then the fixed point \(G_{2}(S_{1}^{*}, S_{2}^{*})\) is globally asymptotically stable.

Proof

This proof is similar to Lemma 3.3 of [36]. For convenience, denote \((S_{1}^{n}, S_{2}^{n})=(S_{1}(n\tau^{+}), S_{2}(n\tau^{+}))\). The linear form of (6) can be written as

$$ \begin{pmatrix} S_{1}^{n+1}\\ S_{2}^{n+1} \end{pmatrix} = M \begin{pmatrix} S_{1}^{n}\\ S_{2}^{n} \end{pmatrix}. $$
(8)

Obviously, the near dynamics of \(G_{1}(0,0)\) and \(G_{2}(S_{1}^{*}, S_{2}^{*})\) are determined by linear system (8). The stabilities of \(G_{1}(0,0)\) and \(G_{2}(S_{1}^{*}, S_{2}^{*})\) are determined by the eigenvalue of M less than 1. If M satisfies the Jury criterion [37], we know that the eigenvalue of M is less than 1,

$$ 1-\operatorname{tr} M+\det M>0. $$
(9)

(i) If \(\mu>\Omega^{*}\), namely \(1-D-A+AD-BC>0\), \(G_{1}(0,0)\) is the unique fixed point of system of (6), we have

$$ M= \begin{pmatrix} A&B\\ C&D \end{pmatrix}. $$
(10)

Calculating \(1-\operatorname{tr} M+\det M=1-(A+D)+(AD-BC)>0\), and from the Jury criterion, \(G_{1}(0,0)\) is locally stable, and then it is globally asymptotically stable.

(ii) If \(\mu<\Omega^{*}\), say \(1-A-D+AD-BC<0\), \(G_{1}(0,0)\) is unstable. For \(1-A-D+AD-BC<0\), \(G_{2}(S_{1}^{*}, S_{2}^{*})\) exists, and

$$ M= \begin{pmatrix} A-2b(CS_{1}^{*}+DS_{2}^{*})C & B-2b(CS_{1}^{*}+DS_{2}^{*})D\\ C & D \end{pmatrix} . $$
(11)

Also

$$\begin{aligned} &1-\operatorname{tr} M+\det M \\ &\quad= 1- \bigl\{ \bigl[A-2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)C \bigr]+D \bigr\} \\ &\qquad{}+ \bigl\{ \bigl[A-2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)C \bigr]\times D- \bigl[B-2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)D \bigr]\times C \bigr\} \\ &\quad= 1-A+2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)C-D \\ &\qquad{}+ \bigl[AD-2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)CD-BC+2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)DC \bigr] \\ &\quad= 1-A-D+2b \bigl(CS_{1}^{*}+DS_{2}^{*} \bigr)C+AD-BC \\ &\quad= (1-A-D+AD-BC)+2b \\ &\qquad{} \times\biggl( C\frac{(1-D-A+AD-BC)(-1+D)}{bC^{2}}+D\frac{-(1-D-A+AD-BC)}{bC} \biggr)C \\ &\quad=(1-A-D+AD-BC) \\ &\qquad{}+2 \bigl( (1-D-A+AD-BC) (-1+D)-D(1-D-A+AD-BC) \bigr) \\ &\quad= (1-A-D+AD-BC)-2(1-A-D+AD-BC) \\ &\quad=-(1-A-D+AD-BC)>0. \end{aligned}$$

From the Jury criterion, \(G_{2}(S_{1}^{*}, S_{2}^{*})\) is locally stable, and then it is globally asymptotically stable. This completes the proof. □

Lemma 3.5

(i) If \(\mu>\Omega^{*}\), then the trivial periodic solution \((0,0)\) of system (4) is globally asymptotically stable.

(ii) If \(\mu<\Omega^{*}\), then the periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)})\) of system (4) is globally asymptotically stable, where

$$\begin{aligned} \textstyle\begin{cases} \widetilde{S_{1}(t)}=S_{1}^{*}e^{-(c+d_{1})(t-n\tau)},\quad t\in(n\tau, (n+1)\tau],\\ \widetilde{S_{2}(t)}= \textstyle\begin{cases} e^{-d_{2}(t-n\tau)} [ S_{2}^{*} +\frac{c S_{1}^{*}(1-e^{-(c+d_{1}-d_{2})(t-n\tau)})}{c+d_{1}-d_{2}} ],\quad t\in(n\tau, (n+l)\tau], \\ e^{-d_{2}(t-(n+l)\tau)} [ (1-\mu) e^{-d_{2}l\tau}(S_{2}^{*}+\frac{cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})l\tau })}{c+d_{1}-d_{2}}) \\ \quad{}+ \frac{c S_{1}^{*}e^{-(c+d_{1})l\tau}(1-e^{-(c+d_{1}-d_{2})(t-(n+l)\tau )})}{c+d_{1}-d_{2}} ],\quad t\in((n+l)\tau, (n+1)\tau], \end{cases}\displaystyle \end{cases}\displaystyle \end{aligned}$$
(12)

in which \(S_{1}^{*}\), \(S_{2}^{*}\) are determined as in (7).

4 The dynamics

In this section, for system (2) there obviously exists an infection-free periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\). First, we prove that the infection-free periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\) of system (2) is globally asymptotically stable. After that, we prove that system (2) is permanent.

Theorem 4.1

If

$$\begin{aligned} &\mu< \Omega^{*}, \\ &\tau>\frac{1}{c+d_{1}}\ln(1+a) \end{aligned}$$

and

$$\begin{aligned} \mu > &\biggl[ \frac{S_{2}^{*} (1-e^{-d_{2}\tau}) }{d_{2}} +\frac{cS_{1}^{*} (1-e^{-d_{2}\tau}) }{d_{2}(c+d_{1}-d_{2})} -\frac{cS_{1}^{*} (1-e^{-(c+d_{1})\tau })}{(c+d_{1})(c+d_{1}-d_{2})}- \frac{(r+d_{3})\tau}{\beta} \biggr] \\ &{}\times \biggl[ \bigl(e^{-d_{2}l\tau}-e^{-d_{2}\tau} \bigr) \biggl( \frac{S_{2}^{*}}{d_{2}} +\frac{cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})l\tau})}{d_{2}(c+d_{1}-d_{2})} \biggr) \biggr]^{-1}, \end{aligned}$$

then the infection-free periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\) of system (2) is globally asymptotically stable, where \(S_{1}^{*}\), \(S_{2}^{*}\) are defined by (7).

Proof

First of all, we prove the local stability. Defining \(Z_{1}(t)=S_{1}(t)-\widetilde{S_{1}(t)}\), \(Z_{2}(t)=S_{2}(t)-\widetilde{S_{2}(t)}\), \(I(t)=I(t)\), we have the following linearly similar system for (2):

$$\begin{pmatrix} \frac{dZ_{1}(t)}{dt}\\ \frac{dZ_{2}(t)}{dt}\\ \frac{dI(t)}{dt} \end{pmatrix} = \begin{pmatrix} -(c+d_{1}) & 0 & 0\\ c & -d_{2} & -\beta\widetilde{S_{2}(t)} \\ 0 & 0 & \beta\widetilde{S_{2}(t)}-(r+d_{3}) \end{pmatrix} \begin{pmatrix} Z_{1}(t)\\ Z_{2}(t)\\ I(t) \end{pmatrix}. $$

It is easy to obtain the fundamental matrix

$$\Phi(t)= \begin{pmatrix} \exp[-(c+d_{1})t] & 0 & 0 \\ * & \exp(-d_{2}t) & \dagger\\ 0 & 0 & \exp[\int_{0}^{t}(\beta\widetilde{S_{2}(s)}-(r+d_{3}))\,ds] \end{pmatrix}. $$

There is no need to calculate the exact forms of ∗, †, as they are not required in the analysis that follows. The linearization of the fourth, fifth, and sixth equations of system (2) is

$$\begin{pmatrix} Z_{1}((n+1)\tau^{+})\\ Z_{2}((n+1)\tau^{+})\\ I((n+1)\tau^{+}) \end{pmatrix} = \begin{pmatrix} 1+a&0 &0\\ 0&1&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} Z_{1}((n+1)\tau)\\ Z_{2}((n+1)\tau)\\ I((n+1)\tau) \end{pmatrix}. $$

The linearization of the seventh, eighth, and ninth equations of system (2) is

$$\begin{pmatrix} Z_{1}((n+l)\tau^{+})\\ Z_{2}((n+l)\tau^{+})\\ I((n+l)\tau^{+}) \end{pmatrix} = \begin{pmatrix} 1&0 &0\\ 0&1-\mu&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} Z_{1}((n+l)\tau)\\ Z_{2}((n+l)\tau)\\ I((n+l)\tau) \end{pmatrix}. $$

The stability of the infection-free periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\) is determined by the eigenvalues of

$$M= \begin{pmatrix} 1&0 &0\\ 0&1-\mu&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} 1+a&0 &0\\ 0&1&0\\ 0&0&1 \end{pmatrix} \Phi(\tau), $$

which are

$$\begin{aligned} \lambda_{1} =& (1+a)\exp \bigl[-(c+d_{1})\tau \bigr], \\ \lambda_{2} =& (1-\mu)e^{-d_{2}\tau}< 1 \end{aligned}$$

and

$$\lambda_{3}=\exp \biggl[ \int_{0}^{\tau} \bigl(\beta \widetilde{S_{2}(s)}-(r+d_{3}) \bigr)\,ds \biggr]. $$

According to the conditions of this theorem, we easily know that \((1+a)\exp[-(c+d_{1})\tau]<1\), and \(\exp [\int_{0}^{\tau}(\beta \widetilde{S_{2}(s)}-(r+d_{3}))\,ds ]<1\), then \(\lambda_{1}<1\), and \(\lambda_{3}<1\). From the Floquet theory [38], the infection-free \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\) of system (2) is locally stable.

The following task is to prove the global attractivity; choose \(\varepsilon>0 \) such that

$$\rho=\exp \biggl[ \int_{0}^{\tau} \bigl(\beta \bigl( \widetilde{S_{2}(s)}+\varepsilon \bigr)-(r+d_{3}) \bigr)\,ds \biggr]< 1. $$

From the second of system (2), we notice that \(\frac{dS_{2}(t)}{dt}\leq cS_{1}(t)-d_{2}S_{2}(t)\), so we consider the following impulsive differential equation:

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{11}(t)}{dt}=-cS_{11}(t)-d_{1}S_{11}(t),\\ \frac{dS_{12}(t)}{dt}=cS_{11}(t)-d_{2}S_{12}(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{11}(t)=S_{12}(t)(a-bS_{12}(t)), \\ \Delta S_{12}(t)=0, \end{array}\displaystyle \right\}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{11}(t)=0,\\ \Delta S_{12}(t)=-\mu S_{12}(t), \end{array}\displaystyle \right \}\quad t=(n+l)\tau, n=1,2,\ldots. \end{cases} $$
(13)

From Lemma 3.5 and the comparison theorem of impulsive equations (see [30], Theorem 3.1.1), we have \(S_{1}(t)\leq S_{11}(t)\), \(S_{2}(t)\leq S_{12}(t)\), and \(S_{11}(t)\rightarrow\widetilde{S_{1}(t)}\), \(S_{12}(t)\rightarrow\widetilde{S_{2}(t)}\) as \(t\rightarrow\infty\); that is,

$$ \textstyle\begin{cases} S_{1}(t) \leq S_{11}(t)\leq\widetilde{S_{1}(t)}+\varepsilon,\\ S_{2}(t) \leq S_{12}(t)\leq\widetilde{S_{2}(t)}+\varepsilon, \end{cases} $$
(14)

for t large enough. For convenience, we may assume that (14) holds for all \(t\geq0\). From (2) and (14), we get

$$ \textstyle\begin{cases} \frac{dI(t)}{dt}\leq[\beta(\widetilde{S_{2}(t)}+\varepsilon )-(r+d_{3})]I(t),\quad t\neq n\tau, t\neq(n+l)\tau, \\ \Delta I(t)=0, \quad t=n\tau, t=(n+l)\tau. \end{cases} $$
(15)

So \(I(t)\leq I(0^{+})\exp[\int_{0}^{t}(\beta( \widetilde{S_{2}(t)}+\varepsilon)-(r+d_{3}))\,ds]\), thus \(I((n+1)\tau)\leq I(n\tau^{+})\times \exp[\int_{n\tau}^{(n+1)\tau}(\beta( \widetilde{S_{2}(t)}+\varepsilon)-(r+d_{3}))\,ds]\), hence \(I(n\tau)\leq I(0^{+}) \rho^{n}\) and \(I(n\tau)\rightarrow0\) as \(n\rightarrow\infty\). Therefore, \(I(t)\rightarrow0\) as \(t\rightarrow\infty\).

Next we prove that \(S_{1}(t)\rightarrow\widetilde{S_{1}(t)}\), \(S_{2}(t)\rightarrow\widetilde{S_{2}(t)}\) as \(t\rightarrow\infty\). Since \(\forall\varepsilon>0\), we have \(0< I(t)<\varepsilon\) for all \(t\geq0\), then, for system (2), we have

$$ cS_{1}(t)-(d_{2}+\beta\varepsilon)S_{2}(t)\leq \frac{dS_{2}(t)}{dt}\leq cS_{1}(t)-d_{2}S_{2}(t), $$
(16)

then we have \(S_{21}(t)\leq S_{1}(t)\leq S_{31}(t)\), \(S_{22}(t) \leq S_{2}(t) \leq S_{32}(t)\), and \(S_{21}(t)\rightarrow \widetilde{S_{21}(t)}\), \(S_{22}(t)\rightarrow\widetilde{S_{22}(t)}\), \(S_{31}(t)\rightarrow\widetilde{S_{1}(t)}\), \(S_{32}(t)\rightarrow \widetilde{S_{2}(t)}\), as \(t\rightarrow\infty\). Meanwhile \((S_{21}(t), S_{22}(t))\) and \((S_{31}(t), S_{32}(t))\) are the solutions to

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{21}(t)}{dt}=-cS_{21}(t)-d_{1}S_{21}(t),\\ \frac{dS_{22}(t)}{dt}=cS_{21}(t)-(d_{2}+\beta \varepsilon)S_{22}(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{21}(t)=S_{22}(t)(a-bS_{22}(t)), \\ \Delta S_{22}(t)=0, \end{array}\displaystyle \right \}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{21}(t)=0,\\ \Delta S_{22}(t)=-\mu S_{22}(t), \end{array}\displaystyle \right\}\quad t=(n+l)\tau, n=1,2\ldots, \end{cases} $$
(17)

and

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{31}(t)}{dt}=-cS_{31}(t)-d_{1}S_{31}(t),\\ \frac{dS_{32}(t)}{dt}=cS_{31}(t)-d_{2}S_{32}(t), \end{array}\displaystyle \right \}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{31}(t)=S_{32}(t)(a-bS_{32}(t)), \\ \Delta S_{32}(t)=0, \end{array}\displaystyle \right\}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{31}(t)=0,\\ \Delta S_{32}(t)=-\mu S_{32}(t), \end{array}\displaystyle \right \}\quad t=(n+l)\tau, n=1,2,\ldots, \end{cases} $$
(18)

respectively. Here \((\widetilde{S_{21}(t)}, \widetilde{S_{22}(t)})\) can be expressed as

$$\begin{aligned} \textstyle\begin{cases} \widetilde{S_{21}(t)}=S_{21}^{*}e^{-(c+d_{1})(t-n\tau)},\quad t\in(n\tau, (n+1)\tau], \\ \widetilde{S_{22}(t)}= \textstyle\begin{cases} e^{-(d_{2}+\beta\varepsilon)(t-n\tau)} [ S_{22}^{*} +\frac{c S_{21}^{*}(1-e^{-(c+d_{1}-d_{2}-\beta \varepsilon)(t-n\tau)})}{c+d_{1}-d_{2}-\beta\varepsilon} ],\quad t\in(n\tau, (n+l)\tau], \\ e^{-(d_{2}+\beta\varepsilon)(t-(n+l)\tau)} [ (1-\mu) e^{-(d_{2}+\beta \varepsilon)l\tau}(S_{22}^{*}+\frac {cS_{21}^{*}(1-e^{-(c+d_{1}-d_{2}-\beta \varepsilon)l\tau})}{c+d_{1}-d_{2}-\beta\varepsilon}) \\ \quad{}+ \frac{c S_{21}^{*}e^{-(c+d_{1})l\tau}(1-e^{-(c+d_{1}-d_{2}-\beta \varepsilon)(t-(n+l)\tau)})}{c+d_{1}-d_{2}-\beta\varepsilon} ],\quad t\in((n+l)\tau, (n+1)\tau], \end{cases}\displaystyle \end{cases}\displaystyle \end{aligned}$$
(19)

where

$$ \textstyle\begin{cases} S_{21}^{*}=\frac{(1-D_{1}-A_{1}+A_{1}D_{1}-B_{1}C_{1})(-1+D_{1})}{bC_{1}^{2}},\quad \mu< \widetilde{\Omega^{*}}, \\ S_{22}^{*}=\frac{-(1-D_{1}-A_{1}+A_{1}D_{1}-B_{1}C_{1})}{bC_{1}},\quad \mu< \widetilde{\Omega^{*}}, \end{cases} $$
(20)

and \(\zeta_{1}= e^{-(d_{2}+\beta \varepsilon)\tau}[(1-\mu)(1-e^{-(c+d_{1}-d_{2}-\beta \varepsilon)l\tau})+e^{-(c+d_{1}-d_{2}-\beta \varepsilon)l\tau}-e^{-(c+d_{1}-d_{2}-\beta\varepsilon)\tau}]>0\). \(A_{1}=e^{-(c+d_{1})\tau}+\frac{a c\zeta_{1} }{c+d_{1}-d_{2}-\beta\varepsilon}> 0\), \(B_{1}=a(1-\mu)e^{-(d_{2}+\beta\varepsilon)\tau}>0\), \(C_{1}=\frac{c\zeta_{1} }{c+d_{1}-d_{2}-\beta\varepsilon}\), \(D_{1}=(1-\mu)e^{-(d_{2}+\beta\varepsilon)\tau}\), \(A_{1}<1\), \(0< D_{1}<1\), and

$$\widetilde{\Omega^{*} }= \frac{(c+d_{1}-d_{2}-\beta \varepsilon)[1+e^{-(c+d_{1}-d_{2}-\beta \varepsilon)\tau}-e^{-(c+d_{1})\tau}-e^{(d_{2}+\beta \varepsilon)\tau}]+ac[1-e^{-(c+d_{1}-d_{2}-\beta\varepsilon)\tau}]}{ (c+d_{1}-d_{2}-\beta \varepsilon)[1-e^{-(c+d_{1})\tau}]+ac[1-e^{-(c+d_{1}-d_{2}-\beta \varepsilon)l\tau}]}. $$

Therefore, for any \(\varepsilon_{1}>0\), there exists \(t_{1}\), \(t>t_{1}\), such that

$$\widetilde{S_{21}(t)}-\varepsilon_{1}< S_{1}(t)< \widetilde {S_{1}(t)}+\varepsilon_{1} $$

and

$$\widetilde{S_{22}(t)}-\varepsilon_{1}< S_{2}(t)< \widetilde {S_{2}(t)}+\varepsilon_{1}. $$

Letting \(\varepsilon\rightarrow0\), we have

$$\widetilde{S_{1}(t)}-\varepsilon_{1}< S_{1}(t)< \widetilde {S_{1}(t)}+\varepsilon_{1} $$

and

$$\widetilde{S_{2}(t)}-\varepsilon_{1}< S_{2}(t)< \widetilde {S_{2}(t)}+\varepsilon_{1} $$

for t large enough, which implies that \(S_{1}(t)\rightarrow \widetilde{S_{1}(t)}\), \(S_{2}(t)\rightarrow\widetilde{S_{2}(t)}\) as \(t\rightarrow\infty\). This completes the proof. □

The next work is to investigate the permanence of system (2). Before starting this work, we should give the following definition.

Definition 4.2

System (2) is said to be permanent if there are constants \(m, M>0\) (independent of initial value) and a finite time \(T_{0}\), such that for all solutions \((S_{1}(t), S_{2}(t), I(t))\) with any initial values \(S_{1}(0^{+})>0\), \(S_{2}(0^{+})>0\), \(I(0^{+})>0\), we have \(m\leq S_{1}(t)\leq M\), \(m\leq S_{2}(t)\leq M\), \(m\leq I(t)\leq M\) for all \(t\geq T_{0}\). Here \(T_{0}\) may depend on the initial values \((S_{1}(0^{+}), S_{2}(0^{+}), I(0^{+}))\).

Theorem 4.3

If

$$\begin{aligned} &\mu< \Omega^{*}, \\ &\tau< \frac{1}{c+d_{1}}\ln(1+a), \end{aligned}$$

and

$$\begin{aligned}& \mu< \biggl[ \frac{S_{2}^{*} (1-e^{-d_{2}\tau}) }{d_{2}} +\frac{cS_{1}^{*} (1-e^{-d_{2}\tau}) }{d_{2}(c+d_{1}-d_{2})} - \frac{cS_{1}^{*} (1-e^{-(c+d_{1})\tau })}{(c+d_{1})(c+d_{1}-d_{2})}-\frac{(r+d_{3})\tau}{\beta} \biggr] \\& \hphantom{\mu< }{}\times \biggl[ \bigl(e^{-d_{2}l\tau}-e^{-d_{2}\tau} \bigr) \biggl( \frac{S_{2}^{*}}{d_{2}} +\frac{cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})l\tau})}{d_{2}(c+d_{1}-d_{2})} \biggr) \biggr]^{-1}, \end{aligned}$$
(21)

then system (2) is permanent, where \(S_{1}^{*}\), \(S_{2}^{*}\) are defined by (7).

Proof

Let \((S_{1}(t), S_{2}(t), I(t))\) be a solution of (2) with \(S_{1}(0)>0\), \(S_{2}(0)>0\), \(I(0)>0\). By Lemma 3.3, we have proved there exists a constant \(M>0\), such that \(S_{1}(t)\leq M\), \(S_{2}(t)\leq M\), \(I(t)\leq M\) for t large enough.

From the proof of Theorem 4.1, we know that \(S_{1}(t)> \widetilde{S_{1}(t)}-\varepsilon_{1}\), \(S_{2}(t)>\widetilde{S_{2}(t)}-\varepsilon_{1}\) for t large enough, and \(\varepsilon_{1}>0\). So, \(S_{1}(t)\geq S_{1}^{*}e^{-(c+d_{1})\tau}-\varepsilon_{1}=m_{2}\), and

$$\begin{aligned} S_{2}(t) \geq& e^{-d_{2}l\tau}\biggl[S_{2}^{*}+ \frac{cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})\tau })}{c+d_{1}-d_{2}} \biggr] \\ &{}+e^{-d_{2}(1-l)\tau}\biggl[ (1-\mu)e^{-d_{2}\tau}\biggl(S_{2}^{*}+ \frac {cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})l\tau})}{c+d_{1}-d_{2}}\biggr) \\ &{}+\frac{cS_{1}^{*}e^{-(c+d_{1})l\tau}(1-e^{-(c+d_{1}-d_{2})(1-l)\tau })}{c+d_{1}-d_{2}}\biggr] \\ \geq& e^{-d_{2}l\tau}\biggl[S_{2}^{*}+\frac{cS_{1}^{*}(1-e^{-(c+d_{1}-d_{2})\tau })}{c+d_{1}-d_{2}} \biggr]+e^{-d_{2}(1-l)\tau} \\ &{}\times\biggl[(1-\mu)e^{-d_{2}\tau}S_{2}^{*}+\frac{cS_{1}^{*}[(1-\mu)e^{-d_{2}\tau }+e^{-(c+d_{1})\tau}](1-e^{-(c+d_{1}-d_{2})(1-l)\tau})}{c+d_{1}-d_{2}} \biggr] -\varepsilon_{1}\\ =&m'_{2}, \end{aligned}$$

for t large enough, where \(S_{1}^{*}\) and \(S_{2}^{*}\) are defined by (7). Thus, we only need to find \(m_{1}>0\) such that \(I(t)\geq m_{1}\) for t large enough. We will do it in the following two steps.

1∘ Prove that \(I(t)\geq m_{1}\), for t large enough. Otherwise, we can select \(m_{3}>0\) small enough, and prove \(I(t)< m_{3}\) cannot hold for \(t\geq0\). By condition (21), we can obtain

$$\begin{aligned} \sigma =& \frac{S_{42}^{*}}{d_{2}+\beta m_{3}} \bigl(1-e^{-(d_{2}+\beta m_{3})l\tau} \bigr) \\ &{}+\frac{cS_{41}^{*}}{(d_{2}+\beta m_{3})(c+d_{1}-d_{2}-\beta m_{3})} \bigl(1-e^{-(d_{2}+\beta m_{3})l\tau} \bigr) \\ &{}-\frac{cS_{41}^{*}}{(c+d_{1})(c+d_{1}-d_{2}-\beta m_{3})} \bigl(1-e^{-(c+d_{1})l\tau} \bigr) \\ &{}+(1-\mu) \bigl(e^{-(d_{2}+\beta m_{3})l\tau}-e^{-(d_{2}+\beta m_{3})\tau} \bigr) \biggl( \frac{S_{42}^{*}}{d_{2}+\beta m_{3}}+\frac {cS_{41}^{*}(1-e^{-(c+d_{1}-d_{2}-\beta m_{3})l\tau})}{(d_{2}+\beta m_{3})(c+d_{1}-d_{2}-\beta m_{3})} \biggr) \\ &{} +\frac{cS_{41}^{*}e^{-(c+d_{1})l\tau}}{(d_{2}+\beta m_{2})(c+d_{1}-d_{2}-\beta m_{3})} \bigl(1-e^{-(d_{2}+\beta m_{3})(1-l)\tau } \bigr) \\ &{} +\frac{cS_{41}^{*}}{(c+d_{1})(c+d_{1}-d_{2}-\beta m_{3})} \bigl(e^{-(c+d_{1})\tau}-e^{-(c+d_{1})l\tau} \bigr) - \frac{(r+d_{3})\tau}{\beta} \\ >&0. \end{aligned}$$

By Lemma 3.5, we have \(S_{1}(t)\geq S_{41}(t)\), \(S_{2}(t)\geq S_{42}(t)\), and \(S_{41}(t)\rightarrow\widetilde{S_{41}(t)}\), \(S_{42}(t)\rightarrow \widetilde{S_{42}(t)}\), \(t\rightarrow\infty\), where \((S_{41}(t), S_{42}(t))\) is the solution to

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \frac{dS_{41}(t)}{dt}=-cS_{41}(t)-d_{1}S_{41}(t),\\ \frac{dS_{42}(t)}{dt}=cS_{41}(t)-(d_{2}+\beta m_{3})S_{42}(t), \end{array}\displaystyle \right\}\quad t\neq n\tau, t \neq(n+l) \tau, \\ \left.\textstyle\begin{array}{l} \Delta S_{41}(t)=S_{42}(t)(a-bS_{42}(t)), \\ \Delta S_{42}(t)=0, \end{array}\displaystyle \right\}\quad t=n\tau, n=1,2,\ldots, \\ \left.\textstyle\begin{array}{l} \Delta S_{41}(t)=0,\\ \Delta S_{42}(t)=-\mu S_{42}(t), \end{array}\displaystyle \right \}\quad t=(n+l)\tau, n=1,2,\ldots, \end{cases} $$
(22)

with

$$\begin{aligned} \textstyle\begin{cases} \widetilde{S_{41}(t)}=S_{41}^{*}e^{-(c+d_{1})(t-n\tau)},\quad t\in(n\tau, (n+1)\tau], \\ \widetilde{S_{42}(t)}= \textstyle\begin{cases} e^{-(d_{2}+\beta m_{3})(t-n\tau)} [ S_{42}^{*} +\frac{c S_{41}^{*}(1-e^{-(c+d_{1}-d_{2}-\beta m_{3})(t-n\tau)})}{c+d_{1}-d_{2}-\beta m_{3}} ],\quad t\in(n\tau, (n+l)\tau], \\ e^{-(d_{2}+\beta m_{3})(t-(n+l)\tau)} [ (1-\mu) e^{-(d_{2}+\beta m_{3})l\tau}(S_{42}^{*}+\frac{cS_{41}^{*}(1-e^{-(c+d_{1}-d_{2}-\beta m_{3})l\tau})}{c+d_{1}-d_{2}-\beta m_{3}}) \\ \quad{}+ \frac{c S_{41}^{*}e^{-(c+d_{1})l\tau}(1-e^{-(c+d_{1}-d_{2}-\beta m_{3})(t-(n+l)\tau)})}{c+d_{1}-d_{2}-\beta m_{3}} ],\quad t\in((n+l)\tau, (n+1)\tau]. \end{cases}\displaystyle \end{cases}\displaystyle \end{aligned}$$
(23)

Here \(S_{41}^{*}\) and \(S_{42}^{*}\) are determined as

$$ \textstyle\begin{cases} S_{41}^{*}=\frac{(1-D_{2}-A_{2}+A_{2}D_{2}-B_{2}C_{2})(-1+D_{2})}{bC_{2}^{2}}, \quad\mu< \Omega^{**}\\ S_{42}^{*}=\frac{-(1-D_{2}-A_{2}+A_{2}D_{2}-B_{2}C_{2})}{bC_{2}}, \quad \mu< \Omega^{**}, \end{cases} $$
(24)

and \(\zeta_{2}= e^{-(d_{2}+\beta m_{3})\tau}[(1-\mu)(1-e^{-(c+d_{1}-d_{2}-\beta m_{3})l\tau})+e^{-(c+d_{1}-d_{2}-\beta m_{3})l\tau}-e^{-(c+d_{1}-d_{2}-\beta m_{3})\tau}]>0\). \(A_{2}=e^{-(c+d_{1})\tau}+\frac{a c\zeta_{2} }{c+d_{1}-d_{2}-\beta m_{3}}> 0\), \(B_{2}=a(1-\mu)e^{-(d_{2}+\beta m_{3})\tau}>0\), \(C_{2}=\frac{c\zeta_{2} }{c+d_{1}-d_{2}-\beta m_{3}}\), \(D_{2}=(1-\mu)e^{-(d_{2}+\beta m_{3})\tau}\), \(A_{2}<1\), \(0< D_{2}<1\), and

$$\Omega^{**} = \frac{(c+d_{1}-d_{2}-\beta m_{3})[1+e^{-(c+d_{1}-d_{2}-\beta m_{3})\tau}-e^{-(c+d_{1})\tau}-e^{(d_{2}+\beta m_{3})\tau}]+ac[1-e^{-(c+d_{1}-d_{2}-\beta m_{3})\tau}]}{ (c+d_{1}-d_{2}-\beta m_{3})[1-e^{-(c+d_{1})\tau}]+ac[1-e^{-(c+d_{1}-d_{2}-\beta m_{3})l\tau}]}.$$

Therefore, there exist \(T_{1}>0\) and \(\varepsilon_{3}>0\), such that

$$S_{1}(t) \geq S_{41}(t)\geq\widetilde{S_{41}(t)}- \varepsilon_{3} $$

and

$$S_{2}(t) \geq S_{42}(t)\geq\widetilde{S_{42}(t)}- \varepsilon_{3}. $$

Then

$$ \frac{dI(t)}{dt}\geq \bigl[\beta \bigl(\widetilde{S_{42}(t)}- \varepsilon _{3} \bigr)-(r+d_{3}) \bigr]I(t), $$
(25)

for \(t\geq T_{1}\). Let \(N_{1}\in N\) and \(N_{1}\tau>T_{1}\). Integrating (25) on \((n\tau, (n+1)\tau]\), \(n\geq N_{1}\), we have

$$I \bigl((n+1)\tau \bigr) \geq I \bigl(n\tau^{+} \bigr)\exp \biggl( \int_{n\tau}^{(n+1)\tau} \bigl[\beta \bigl( \widetilde{S_{42}(t)}-\varepsilon_{3} \bigr)-(r+d_{3}) \bigr]\,dt \biggr) =I(n\tau)e^{\sigma}, $$

then \(I((N_{1}+k)\tau)\geq I(N_{1}\tau^{+})e^{k\sigma}\rightarrow\infty\), as \(k\rightarrow\infty\), which is a contradiction to the boundedness of \(I(t)\). Hence, there exists a \(t_{1}>0\), such that \(I(t_{1})\geq m_{3}\).

2∘ If \(I(t)\geq m_{3}\) for all \(t\geq t_{1}\), and let \(m_{1}=m_{3}\) then our aim is obtained. Otherwise, let \(t^{\ast}=\inf_{t\geq t_{1}}\{ I(t)< m_{3}\}\), there are two possible cases for \(t^{*}\). In the following, we will apply the ideas in Meng and Chen [9] to complete the remaining proof.

Case (I): \(t^{*}=n_{1}\tau\), \(n_{1}\in N\). Then \(I(t)\geq m_{3}\) for \(t\in[t_{1}, t^{*})\) and \(x(t^{*})=m_{3}\). Select \(n_{2},n_{3}\in N\), such that

$$n_{2}\tau >T_{1},\qquad e^{(n_{2}+1)\sigma_{1}\tau}e^{n_{3}\sigma}>1, $$

where \(\sigma_{1}=\beta m_{2}^{\prime}-(r+d_{3})<0\). Let \(T=n_{2}\tau+n_{3}\tau\), we claim that there must be a \(t_{2}\in (t^{*}, t^{*}+T]\), such that \(I(t_{2})>m_{3}\). Otherwise, i.e., (\(\forall t\in(t^{*}, t^{*}+T]\), \(I(t)\leq m_{3}\)) consider (22) with \(S_{41}(n_{1}\tau^{+})=S_{1}(n_{1}\tau^{+})\), \(S_{42}(n_{1}\tau^{+})=S_{2}(n_{1}\tau^{+})\), for \(t\in(n\tau, (n+1)\tau)\) and \(n_{1}\leq n\leq n_{1}+n_{2}+n_{3}\), we have

$$S_{1}(t) \geq S_{41}(t)\geq\widetilde{S_{41}(t)}- \varepsilon_{3} $$

and

$$S_{2}(t) \geq S_{42}(t)\geq\widetilde{S_{42}(t)}- \varepsilon_{3}, $$

for \(t^{*}+n_{2}\tau\leq t \leq t^{*}+T\). This implies (25) holds for \(t^{*}+n_{2}\tau\leq t \leq t^{*}+T\). As in step 1, we have

$$I \bigl(t^{*}+T \bigr)\geq I \bigl(t^{*}+n_{2}\tau \bigr)e^{n_{3}\sigma}. $$

The third equation of (2) gives

$$ \frac{dI(t)}{dt}\geq I(t) \bigl[\beta m_{2}^{\prime}-(r+d_{3}) \bigr]=\sigma_{1}I(t), $$
(26)

for \(t\in[t^{*}, t^{*}+n_{2}\tau]\).

Integrating on \([t^{*}, t^{*}+n_{2}\tau]\), we have

$$I \bigl(t^{*}+n_{2}\tau \bigr)\geq m_{3}e^{\sigma_{1} n_{2}\tau}. $$

Then

$$\begin{aligned} I \bigl(t^{*}+T \bigr) \geq& I \bigl(t^{*}+n_{2} \tau \bigr)e^{n_{3}\sigma}\geq m_{3}e^{\sigma _{1} n_{2}\tau} e^{n_{3}\sigma} \\ \geq& m_{3}e^{\sigma_{1} (n_{2}+1)\tau} e^{n_{3}\sigma}> m_{3}, \end{aligned}$$

which is a contradiction.

Let \(\overline{t}=\inf_{t\geq t^{*}}\{ I(t)>m_{3}\}\), thus \(I(t)\leq m_{3}\) for \(t\in[t^{*}, \overline{t}]\), \(I(\overline{t})=m_{3}\), since \(I(t)\) is continuous and \(I(t)\) is not affected by the impulsive effect. For \(t\in(t^{*}, \overline{t}]\), suppose \(t\in(t^{*}+(p-1)\tau, t^{*}+p\tau]\), \(p\in N\), and \(p\leq n_{2}+n_{3}\), by (26) we have

$$\begin{aligned} I(t) \geq& I \bigl(t^{*}+(p-1)\tau \bigr) e^{\sigma_{1}(t-(t^{*}+(p-1)\tau))} \\ \geq& I \bigl(t^{*} \bigr) e^{(p-1)\sigma_{1}\tau} e^{\sigma_{1}\tau} = I \bigl(t^{*} \bigr) e^{p\sigma_{1}\tau} \\ \geq& m_{3} e^{p\sigma_{1}\tau} \geq m_{3} e^{(n_{2}+n_{3})\sigma _{1}\tau}=m'_{1} \quad \bigl(\mbox{clearly}, m_{3}>m'_{1} \bigr), \end{aligned}$$

hence, we have \(I(t)\geq m'_{1}\) for \(t\in(t^{*}, \overline{t})\). For \(t>\overline{t}\), the same arguments can be presented, since \(I(\overline{t})\geq m_{3}\).

Case (II): \(t^{*}\neq n\tau\), \(n\in N\). Then \(I(t)\geq m_{3}\) for \(t\in[t_{1}, t^{*}]\) and \(I(t^{*})=m_{3}\), suppose \(t^{*}\in(n_{4}\tau, (n_{4}+1)\tau)\), \(n_{4}\in N\). There are two possible cases for \(t\in(t^{*}, (n_{4}+1)\tau)\).

Case (IIa): \(I(t)\leq m_{3}\) for all \(t\in(t^{*}, (n_{4}+1)\tau)\). We claim that there must be a \(t'_{2}\in[(n_{4}+1)\tau, (n_{4}+1)\tau+T]\), such that \(I(t'_{2})>m_{3}\). Otherwise, i.e., \(\forall t\in [(n_{4}+1)\tau, (n_{4}+1)\tau+T]\), we have \(I(t)\leq m_{3}\). Consider (22) with \(S_{41}((n_{4}+1)\tau^{+})=S_{1}((n_{4}+1)\tau^{+})\), \(S_{42}((n_{4}+1)\tau^{+})=S_{2}((n_{4}+1)\tau^{+})\), one can get

$$S_{1}(t)\geq S_{41}(t) \geq \widetilde{S_{41}}(t)- \varepsilon_{3},\qquad S_{2}(t)\geq S_{42}(t) \geq \widetilde{S_{42}}(t)-\varepsilon_{3}, $$

for \(t\in(n\tau, (n+1)\tau]\) and \(n_{4}+1\leq n \leq n_{4}+1+n_{2}+n_{3}\). Similarly, we have

$$I \bigl((n_{4}+1+n_{2}+n_{3})\tau \bigr)\geq I \bigl((n_{4}+1+n_{2})\tau \bigr) e^{n_{3}\sigma}. $$

Since \(I(t)\leq m_{3}\) for \(t\in(t^{*}, (n_{4}+1)\tau)\), (26) holds on \([t^{*}, (n_{4}+1+n_{2})\tau]\), so we have

$$I \bigl((n_{4}+1+n_{2})\tau \bigr)\geq m_{3} e^{(n_{2}+1)\sigma_{1} \tau}. $$

In fact, since \(t\leq(n_{4}+1+n_{2})\tau\), \(n_{4}\tau\leq t^{*}\leq (n_{4}+1)\tau\), \(\sigma_{1}<0\), then \(n_{2}\tau\leq t-t^{*} \leq(n_{2}+1)\tau\), \(e^{(t-t^{*})\sigma _{1}\tau} \geq e^{(n_{2}+1)\sigma_{1}\tau}\). Thus,

$$I \bigl((n_{4}+1+n_{2})\tau \bigr)\geq I \bigl(t^{*} \bigr) e^{(t-t^{*})\sigma_{1}\tau} \geq m_{3} e^{(n_{2}+1)\sigma_{1}\tau}. $$

Therefore,

$$\begin{aligned} I \bigl((n_{4}+1+n_{2}+n_{3})\tau \bigr) \geq& I \bigl((n_{4}+1+n_{2})\tau \bigr) e^{n_{3}\sigma} \\ \geq& m_{3} e^{(n_{2}+1)\sigma_{1}\tau} e^{n_{3}\sigma} > m_{3}, \end{aligned}$$

which is a contradiction. Let \(\overline{t}=\inf_{t>t^{*}} \{ I(t)>m_{3}\}\), then \(I(t)\leq m_{3}\) for \(t\in(t^{*}, \overline{t})\) and \(I(\overline{t})=m_{3}\). For \(t\in(t^{*}, \overline{t})\), suppose \(t\in(n_{4}\tau+(p'-1)\tau, n_{4}\tau+p'\tau]\), \(p'\in N\), \(p'\leq 1+n_{2}+n_{3}\), we have

$$\begin{aligned} I(t) \geq& I \bigl(t^{*} \bigr)e^{(t-t^{*})\sigma_{1} } \geq I \bigl(t^{*} \bigr) e^{\sigma _{1} \tau} \geq I \bigl(t^{*} \bigr) e^{p' \sigma_{1} \tau} \\ \geq& I \bigl(t^{*} \bigr) e^{(1+n_{2}+n_{3})\sigma_{1} \tau}\geq m_{3} e^{(1+n_{2}+n_{3})\sigma_{1} \tau}. \end{aligned}$$

Let \(m_{1}=m_{3} e^{(1+n_{2}+n_{3})\sigma_{1} \tau}< m_{3} e^{(n_{2}+n_{3})\sigma_{1} \tau}=m'_{1}\) (clearly, \(m_{3}>m_{1}\)), hence, \(I(t)\geq m_{1}\) for \(t\in(t^{*}, \overline{t})\). For \(t>\overline{t}\), the same arguments can be presented, since \(I(\overline{t})\geq m_{1}\).

Case (IIb): Suppose that there exists a \(t\in(t^{*}, (n_{4}+1)\tau)\), such that \(I(t)>m_{3}\). Let \(t^{**}=\inf_{t>t^{*}} \{I(t)>m_{3}\}\), then \(I(t)\leq m_{3}\) for \(t\in(t^{*}, t^{**})\) and \(x(t^{**})=m_{3}\). For \(t\in(t^{*}, t^{**})\), (26) holds true, integrating (26) over \((t^{*}, t^{**})\), we have

$$I(t)\geq I \bigl(t^{*} \bigr) e^{\sigma_{1}(t-t^{*})} \geq m_{3} e^{\sigma_{1}\tau} >m_{3} e^{(1+n_{2}+n_{3})\sigma_{1}\tau} =m_{1}. $$

Since \(I(t^{**})\geq m_{3}\), for \(t>t^{**}\), the same arguments can be presented. Hence \(I(t)\geq m_{1}\) for all \(t\geq t_{1}\). This completes the proof. □

5 Discussion

In this work, we consider an SIR epidemic model with state structure and pulse vaccination at different fixed moments. We prove that all solutions of system (2) are uniformly ultimately bounded. The conditions for the global asymptotic stability of the infection-free periodic solution of system (2) are given, and the permanence of system (2) is also obtained.

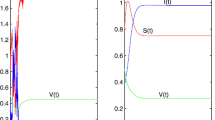
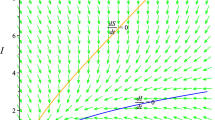
From the conditions of Theorems 4.1 and 4.3, we know that there exists a threshold \(\tau_{0}\). If \(\tau> \tau_{0}\), the infection-free periodic solution \((\widetilde{S_{1}(t)}, \widetilde{S_{2}(t)}, 0)\) of system (2) is globally asymptotically stable. If \(\tau< \tau_{0}\), system (2) is permanent. That is, improving the proportion of immune vaccination and enlarging the period of birth pulse, the disease will die out. If the period of pulse vaccinate is suitable, system (2) will be permanent. This means after some period of time the disease will come to be endemic. The results obtained provide a reliable tactic basis for preventing the disease from spreading.