1 Introduction

Mathematical models have been become the important tools in investigating transmission and control of infectious diseases. To better understand the transmission pattern of infectious disease, a great many epidemic models have been formulated (see [1–21] and references therein). Recently, Takeuchi et al. [12] developed a delayed SIR epidemic model with bilinear incidence rate in order to investigate the spread of vector diseases, and McCluskey [9] discussed the global stability of equilibria for the system. In 2009, Wang et al. [13] analyzed the following SIR vector disease model with incubation time delay and logistic growth rate with carrying capacity K:

$$\begin{aligned}& \frac{dS(t)}{dt}=rS(t) \biggl(1-\frac{S(t)}{K} \biggr)-{ \beta}S(t)I(t-\tau), \\& \frac{dI(t)}{dt}={\beta}S(t)I(t-\tau)-(\mu_{1}+\gamma)I(t), \\& \frac{dR(t)}{dt}={\gamma}I(t)-\mu_{2}R(t). \end{aligned}$$
(1)

\(S(t)\), \(I(t)\), and \(R(t)\) are the numbers of susceptible, infective and recovered host individuals at time t, respectively. r denotes the intrinsic birth rate. β denotes the average number of contacts per infective per unit time. τ is the incubation time. \(\mu_{1}\) and \(\mu_{2}\) represent the death rate of infective and recovered, respectively. γ is the recovered rate of infective individuals. It is reasonable to assume that all the parameters are positive constants. Wang et al. [13] presented the dynamic properties of system (1). The global stability of the disease-free equilibrium is derived when the basic reproduction number \(R_{0}\) is less than unity. The unique endemic equilibrium is absolutely stable when \(1< R_{0}<3\), and it is conditionally stable when \(R_{0}>3\). Moreover, the existence of a Hopf bifurcation is given.

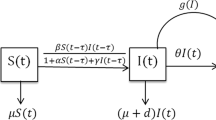
Because of considering the behavioral changes of susceptible individuals, Zhang et al. [19] extended system (1) and proposed the following vector disease model with saturated incidence rate:

$$\begin{aligned}& \frac{dS(t)}{dt}=rS(t) \biggl(1-\frac{S(t)}{K} \biggr)-{\beta} \frac {S(t)}{1+{\alpha}S(t)}I(t-\tau), \\& \frac{dI(t)}{dt}={\beta}\frac{S(t)}{1+{\alpha}S(t)}I(t-\tau)-(\mu _{1}+ \gamma)I(t), \\& \frac{dR(t)}{dt}={\gamma}I(t)-\mu_{2}R(t), \end{aligned}$$
(2)

where the parameters r, β, τ, \(\mu_{1}\), \(\mu_{2}\), and γ are the same meanings as that defined in model (1), and \(\alpha\geq0\) is a constant in order to represent the saturation effect. The global dynamics for model (2) was investigated. If \(R_{0}\) is less than one, the disease-free equilibrium is globally asymptotically stable; while the unique endemic equilibrium may be stable or unstable under some conditions if \(R_{0}\) is greater than one. Furthermore, the Hopf bifurcation emerges if other conditions are satisfied when \(R_{0}\) is greater than one.

Although the bilinear incidence rate was frequently used in the literature of mathematical modeling, there are plenty of reasons why this bilinear incidence rate may require modification [5, 22]. For example, the saturated incidence rate of the form \(\frac{{\beta}S(t)I(t)}{1+{\alpha}I(t)}\) or \(\frac{{\beta}S(t)I(t)}{1+{\alpha}S(t)}\) was formulated as crowding effects of infective or behavioral changes of susceptible individuals were considered [2, 10, 18, 19, 23–25]. Moreover, other forms of nonlinear incidence rates are often developed in many papers (for details one can refer to [4, 5, 14–17, 22]). Motivated by those works, in the present paper, we attempt to extend system (1) or (2) to a more general incidence rate of the form \({\beta}F(S(t))I(t-\tau)\). It is assumed that function F is continuous on \([0,\infty)\) and continuously differentiable on \((0,\infty)\), which satisfies the following hypothesis. Furthermore, it is assumed \(F(S)\) is strictly monotonically increasing on \([0,+\infty)\) with \(F(0)=0\).

Then the delayed SIR vector disease model can be written as

$$\begin{aligned}& \frac{dS(t)}{dt}=rS(t) \biggl(1-\frac{S(t)}{K} \biggr)-{\beta }F\bigl(S(t)\bigr)I(t-\tau), \\& \frac{dI(t)}{dt}={\beta}F\bigl(S(t)\bigr)I(t-\tau)-(\mu_{1}+ \gamma)I(t), \\& \frac{dR(t)}{dt}={\gamma}I(t)-\mu_{2}R(t). \end{aligned}$$
(3)

It should be noted that the general nonlinear incidence rate in system (3) includes some special cases. If \(F(S)=S\), then it becomes the classical bilinear incidence rate, which has been investigated by Wang et al. [13]. If \(F(S)=S^{q}\) (\(q>0\)), then the incidence rate is used in [20]. If \(F(S)=\frac{S}{1+{\alpha}S}\), it becomes the saturated one, which has been discussed in [18, 19].

For simplicity, we make system (3) non-dimensional by writing

$$\tilde{S}(\tilde{t})=\frac{S(t)}{K},\qquad \tilde{I}(\tilde{t})= \frac{I(t)}{K},\qquad \tilde{R}(\tilde{t})=\frac{R(t)}{K} $$

and

$$\begin{aligned}& \tilde{t}={\beta}Kt,\qquad \tilde{F}\bigl(\tilde{S}(\tilde{t})\bigr)= \frac{F(S(t))}{K},\qquad \tilde{\mu}_{1}=\frac{\mu_{1}}{{\beta}K}, \\& \tilde{\gamma}=\frac{\gamma}{{\beta}K},\qquad \tilde{\mu}_{2}= \frac{\mu_{2}}{{\beta}K},\qquad \tilde{\tau}=\frac{\tau}{{\beta}K}. \end{aligned}$$

It is clear that F̃ is also strictly monotonically increasing on \([0,+\infty)\) with \(F(0)=0\). For notational simplicity, dropping the \(\tilde{\hphantom{a}}\), system (3) can be turned into

$$\begin{aligned}& \frac{dS(t)}{dt}=rS(t) \bigl(1-S(t)\bigr)-F\bigl(S(t)\bigr)I(t- \tau), \\& \frac{dI(t)}{dt}=F\bigl(S(t)\bigr)I(t-\tau)-(\mu_{1}+\gamma)I(t), \\& \frac{dR(t)}{dt}={\gamma}I(t)-\mu_{2}R(t). \end{aligned}$$
(4)

The rest of the paper is structured as follows. In Section 2, the nonnegativity and boundedness of the solutions are discussed. In Section 3, the stabilities of the trivial equilibrium and the disease-free equilibrium are described. Section 4 deals with the existence and stability of the endemic equilibrium and the existence of a Hopf bifurcation. In Section 5, the numerical simulations are performed, followed by a brief conclusion in Section 6.

2 Nonnegativity and boundedness of solutions

The initial conditions for system (4) take the form

$$ \begin{aligned} &S(\theta)=\phi_{1}(\theta),\qquad I( \theta)=\phi_{2}(\theta), \qquad R(\theta)=\phi _{3}(\theta), \\ &\phi_{i}(\theta)\geq0,\qquad \phi_{i}(0)>0, \quad i=1,2,3, \end{aligned} $$
(5)

where \((\phi_{1}(\theta),\phi_{2}(\theta),\phi_{3}(\theta))\in C([-\tau ,0],\mathbb{R}^{3}_{+})\), here \(\mathbb{R}^{3}_{+}=\{(x_{1},x_{2},x_{3}); x_{i}\geq0, i=1,2,3\}\). The fundamental theory of functional differential equations [26] implies for any initial conditions (5), system (4) has a unique solution \((S(t),I(t),R(t))\). The following theorem shows that the solution is nonnegative and bounded for a positive initial value (5).

Theorem 2.1

System (4) has a nonnegative and bounded solution with the initial value \((\phi_{1}(\theta),\phi_{2}(\theta),\phi_{3}(\theta))\in C([-\tau ,0],\mathbb{R}^{3}_{+})\) and \(\phi_{i}(\theta)\geq0\), \(\phi_{i}(0)>0\), \(i=1,2,3\).

Proof

First we show that \(S(t)\) is nonnegative for all \(t\geq0\). On the contrary, it is assumed that there exists \(t_{1}>0\) such that \(S(t_{1})=0\) and \(S'(t_{1})<0\). Then the first equation of system (4) implies \(S'(t_{1})=0\), which is a contradiction. Therefore, it follows that \(S(t) \geq 0\) for all \(t \geq 0\).

By using the variation-of-constant formula and the step-by-step integration method, integrating the second equation of system (4) from 0 to t for \(0< t \leq \tau\), we obtain

$$I(t)=e^{-(\mu_{1}+\gamma)t} \biggl(\phi_{2}(0)+\int^{t}_{0}F \bigl(S(\xi)\phi _{2}(\xi-\tau)e^{(\mu_{1}+\gamma)\xi}\, d\xi\bigr) \biggr). $$

It is easy to see that \(I(t)>0\) for all \(0 \leq t \leq \tau\). Then integrating the second equation of system (4) from τ to t for \(\tau< t \leq 2\tau\) gives

$$I(t)=e^{-(\mu_{1}+\gamma)t} \biggl(I(\tau)+\int^{t}_{\tau}F \bigl(S(\xi)I(\xi-\tau )e^{(\mu_{1}+\gamma)\xi}\, d\xi\bigr) \biggr). $$

Note that \(I(t)>0\) for all \(\tau \leq t \leq 2\tau\) and this process can easily be carried on. It implies that for all \(t>0\), we have \(I(t)>0\).

From the third equation of system (4), we obtain

$$R(t)=e^{-\mu_{2}t} \biggl(\phi_{3}(0)+\int^{t}_{0}{ \gamma}I(\xi)e^{\mu _{2}\xi}\, d\xi \biggr), $$

which shows \(R(t)\) is nonnegative for all \(t>0\).

Next we prove that the solutions of system (4) are ultimately uniformly bounded for all \(t \geq 0\). It follows from the first equation of system (4) that \(S'(t) \leq rS(t)(1-S(t))\), which implies \(\limsup_{t\rightarrow\infty}S(t) \leq 1\). Then for sufficiently large t, adding the equations of system (4) yields

$$\begin{aligned} \frac{d(S(t)+I(t)+R(t))}{dt}&=rS(t) \bigl(1-S(t)\bigr)-{\mu_{1}}I(t)-{ \mu_{2}}R(t) \\ &\leq rS(t)-{\mu_{1}}I(t)-{\mu_{2}}R(t) \\ &=(r+1)S(t)-S(t)-{\mu_{1}}I(t)-{\mu_{2}}R(t) \\ &\leq (r+1)S(t)-{\mu_{m}}\bigl(S(t)+I(t)+R(t)\bigr) \\ &\leq (r+1)-{\mu_{m}}\bigl(S(t)+I(t)+R(t)\bigr), \end{aligned}$$

where \({\mu_{m}}=\min\{1,\mu_{1},\mu_{2}\}\). Then we have \(\limsup_{t{\rightarrow}\infty}(S(t)+I(t)+R(t)) \leq \frac{r+1}{\mu_{m}}\). Therefore, \(S(t)\), \(I(t)\), \(R(t)\) are ultimately uniformly bounded. The proof is completed. □

3 Stabilities of the trivial equilibrium and the disease-free equilibrium

In this section, we restrict our attention to the stability of the trivial equilibrium and the disease-free equilibrium. Let

$$ \sigma_{0}=\frac{F(1)}{\mu_{1}+\gamma}. $$
(6)

It will be a threshold parameter.

Before the main results are established, the following lemma will be given first.

Lemma 3.1

(see [27])

Consider the equation

$$ u'(t)=au(t-\tau)-bu(t), $$
(7)

where \(a, b, \tau>0\), and \(u(t)>0\) for \(-\tau \leq t \leq 0\). We have

  1. (i)

    if \(a< b\), then \(\lim_{t\rightarrow\infty}u(t)=0\);

  2. (ii)

    if \(a>b\), then \(\lim_{t\rightarrow\infty}u(t)=+\infty\).

The characteristic equation at an arbitrary equilibrium \((\bar{S},\bar{I},\bar{R})\) is given by

$$ (\lambda+\mu_{2})\bigl[\bigl(\lambda+F'( \bar{S})\bar{I}-r(1-2\bar{S})\bigr) \bigl(\lambda+\mu_{1}+\gamma-F( \bar{S})e^{-\lambda\tau}\bigr) +F(\bar{S})F'(\bar{S}) \bar{I}e^{-\lambda\tau}\bigr]=0. $$
(8)

Theorem 3.1

The trivial equilibrium \(E_{0}\) of system (4) is always unstable.

Proof

At the equilibrium \(E_{0}(0,0,0)\), the characteristic equation (8) reduces to

$$ (\lambda+\mu_{2}) (\lambda-r) (\lambda+ \mu_{1}+\gamma)=0. $$
(9)

It is obvious that (9) has a positive root \(\lambda=r\), therefore \(E_{0}\) is unstable. □

Theorem 3.2

If \(\sigma_{0}<1\), the disease-free equilibrium \(E_{1}\) for system (4) is globally asymptotically stable; and if \(\sigma_{0}>1\), the disease-free equilibrium \(E_{1}\) for system (4) is unstable.

Proof

The characteristic equation (8) at \(E_{1}=(1,0,0)\) becomes

$$ (\lambda+\mu_{2}) (\lambda+r) \bigl(\lambda+ \mu_{1}+\gamma-F(1)e^{-\lambda\tau}\bigr)=0. $$
(10)

Assume that \(\sigma_{0}<1\). Equation (10) has roots \(-\mu_{2}<0\), \(-r<0\), and the root of the equation \(\lambda+\mu_{1}+\gamma-F(1)e^{-\lambda\tau}=0\). Let \(G(\lambda)=\lambda+\mu_{1}+\gamma-F(1)e^{-\lambda\tau}\). Suppose \(\operatorname{Re}(\lambda) \geq 0\), then \(G(\lambda)=0\) implies

$$\begin{aligned} \operatorname{Re}(\lambda) =&-(\mu_{1}+\gamma)+F(1)e^{-\operatorname{Re}(\lambda)\tau} \cos{\operatorname{Im}(\lambda )\tau} \\ =&(\mu_{1}+\gamma)\bigl[\sigma_{0}e^{-\operatorname{Re}(\lambda)\tau}\cos{ \operatorname{Im}(\lambda)\tau }-1\bigr] \\ \leq &(\mu_{1}+\gamma) \bigl(\sigma_{0}e^{-\operatorname{Re}(\lambda)\tau}-1 \bigr) \\ \leq &(\mu_{1}+\gamma) (\sigma_{0}-1)< 0, \end{aligned}$$

which is a contradiction. Then it follows that \(E_{1}\) is locally asymptotically stable.

Now it is sufficient to prove \(E_{1}\) is globally attractive if \(\sigma_{0}<1\). From the first equation for system (4), it follows that

$$ \frac{dS(t)}{dt} \leq rS(t) \bigl(1-S(t)\bigr), $$
(11)

which implies \(\limsup_{t\rightarrow\infty}S(t) \leq 1\). It indicates that for sufficiently large t, there exists a small \(\varepsilon>0\) such that \(S(t)<1+\varepsilon\) and \(F(1+\varepsilon)<\mu_{1}+\gamma\) because of \(\sigma_{0}=\frac{F(1)}{\mu_{1}+\gamma}<1\). Then for sufficiently large t, because of the monotonicity of the function \(F(S)\), the second equation for system (4) can be rewritten as

$$ \frac{dI(t)}{dt} \leq F(1+\varepsilon)I(t-\tau)-( \mu_{1}+\gamma)I(t). $$
(12)

By \(F(1+\varepsilon)<\mu_{1}+\gamma\) and Lemma 3.1, we get \(\limsup_{t\rightarrow\infty}I(t) \leq 0\), which implies \(I(t)\rightarrow0\) as \(t\rightarrow\infty\). By the theory of asymptotic autonomous systems [28], it then follows that \(S(t)\rightarrow1\) and \(R(t)\rightarrow0\) as \(t\rightarrow\infty\). The first part of the proof is completed.

If \(\sigma_{0}>1\), then \(G(0)=(\mu_{1}+\gamma)(1-\sigma_{0})<0\). When \(\lambda\rightarrow{+\infty}\), \(G(\lambda)\rightarrow{+\infty}\). Then \(G(\lambda)=0\) has at least one positive root. Therefore \(E_{1}\) is unstable. □

4 The stability of endemic equilibrium and Hopf bifurcation

In this section, we pay attention to the stability of the endemic equilibrium and Hopf bifurcation when \(\sigma_{0}>1\).

Theorem 4.1

If \(\sigma_{0}>1\), system (4) admits exactly one endemic equilibrium \(E_{*}=(S^{*}, I^{*}, R^{*})\), where

$$F\bigl(S^{*}\bigr)=\mu_{1}+\gamma,\quad 0< S^{*}< 1, \qquad I^{*}=\frac{rS^{*}(1-S^{*})}{F(S^{*})},\qquad R^{*}=\frac{\gamma}{\mu_{2}}I^{*}. $$

Proof

At the endemic equilibrium \(E_{*}\), it follows from the second equation of system (4) that \(F(S^{*})=\mu_{1}+\gamma\). Let \(H(S)=F(S)-(\mu_{1}+\gamma)\). It is obvious that \(H(0)=F(0)-(\mu_{1}+\gamma)=-(\mu_{1}+\gamma)<0\). For all \(S \geq 1\), \(H(S) \geq H(1)=F(1)-(\mu_{1}+\gamma)=(\mu_{1}+\gamma)(\sigma_{0}-1)>0\) because \(H(S)\) is monotonically increasing on the interval \([0,+\infty)\) and \(\sigma_{0}>1\). Therefore \(H(S)=0\) has exactly one root \(S^{*}\in(0,1)\). It is not difficult to compute the expressions \(I^{*}\) and \(R^{*}\) from system (4) at the endemic equilibrium \(E_{*}\). □

By using (8), the characteristic equation at endemic equilibrium \(E_{*}=(S^{*},I^{*},R^{*})\) can be turned into

$$ (\lambda+\mu_{2})\bigl[\lambda^{2}+a{ \lambda}+b-e^{-\lambda\tau}(c{\lambda}+d)\bigr]=0, $$
(13)

where

$$\begin{aligned}& a=\mu_{1}+\gamma+F'\bigl(S^{*} \bigr)I^{*}-r\bigl(1-2S^{*}\bigr), \\& b=(\mu_{1}+\gamma)\bigl[F'\bigl(S^{*} \bigr)I^{*}-r\bigl(1-2S^{*}\bigr)\bigr], \\& c=F\bigl(S^{*}\bigr), \qquad d=-r\bigl(1-2S^{*}\bigr)F \bigl(S^{*}\bigr). \end{aligned}$$
(14)

Then the characteristic roots at \(E_{*}\) are \(-\mu_{2}\) and the roots of the following equation:

$$ \lambda^{2}+a{\lambda}+b-e^{-\lambda\tau}(c{ \lambda}+d)=0. $$
(15)

Proposition 4.1

Assume \(\sigma_{0}>1\) and \(I^{*}F'(S^{*})>r(1-2S^{*})\), then all the roots of (15) have a negative real part for \(\tau=0\).

Proof

If the incubation time delay \(\tau=0\), (15) yields

$$ \lambda^{2}+(a-c){\lambda}+(b-d)=0. $$
(16)

It follows from the fact \((\mu_{1}+\gamma)=F(S^{*})\) and from (14) that

$$\begin{aligned}& b-d=(\mu_{1}+\gamma)F'\bigl(S^{*} \bigr)I^{*}>0, \\& a-c=F'\bigl(S^{*}\bigr)I^{*}-r \bigl(1-2S^{*}\bigr). \end{aligned}$$

Since \(I^{*}F'(S^{*})>r(1-2S^{*})\), it is obvious that \(a-c>0\), which completes the theorem. □

Proposition 4.2

Assume \(\sigma_{0}>1\), then the following statements hold.

  1. (i)

    If \(I^{*}F'(S^{*})\geq2r(1-2S^{*})\), then all the roots of (19) have a negative real part for \(\tau>0\).

  2. (ii)

    If \(I^{*}F'(S^{*})<2r(1-2S^{*})\), then there exists a monotone increasing sequence \(\{\tau_{n}\}^{\infty}_{n=0}\) with \(\tau_{0}>0\) such that (15) has a pair of imaginary roots for \(\tau=\tau_{n}\) (\(n=0,1,2,\ldots\)).

Proof

Suppose that \(\lambda=i{\omega}\), \(\omega>0\) is a root of (15). We substitute \(\lambda=i{\omega}\) into (15) to derive

$$ -{\omega}^{2}+ia{\omega}+b-(\cos\omega\tau-i\sin\omega \tau) (ic{\omega}+d)=0. $$
(17)

Separating the real and imaginary parts gives

$$ \begin{aligned} &-{\omega}^{2}+b=d\cos\omega \tau+c\omega\sin\omega\tau, \\ &a\omega=c\omega\cos\omega\tau-d\sin\omega\tau. \end{aligned} $$
(18)

Squaring and adding both equations in (18), we obtain

$$ {\omega}^{4}+\bigl(a^{2}-2b-c^{2} \bigr){\omega}^{2}+b^{2}-d^{2}=0. $$
(19)

By applying (14), we get

$$a^{2}-2b-c^{2}=\bigl[F'\bigl(S^{*} \bigr)I^{*}-r\bigl(1-2S^{*}\bigr)\bigr]^{2}\geq0, \quad b-d>0 $$

and

$$b+d=(\mu_{1}+\gamma)\bigl[F'\bigl(S^{*} \bigr)I^{*}-2r\bigl(1-2S^{*}\bigr)\bigr]. $$

Firstly assume that \(I^{*}F'(S^{*})\geq2r(1-2S^{*})\). Then we arrive at \(a^{2}-2b-c^{2}>0\) and \(b+d\geq0\). That is to say, (19) has no positive real root ω, which is a contradiction. Therefore, all the roots of (15) have negative real part for \(\tau>0\). The first part of the proof is completed.

Secondly suppose \(I^{*}F'(S^{*})<2r(1-2S^{*})\), which indicates \(b+d<0\). Therefore, there exists a unique positive real \(\omega_{0}\) satisfying (19), where

$$ {\omega_{0}}=\sqrt{\frac{\sqrt {(a^{2}-2b-c^{2})^{2}-4(b-d)(b+d)}-(a^{2}-2b-c^{2})}{2}}. $$
(20)

It should be noted that \(\lambda=-i{\omega_{0}}\) is also a root of (15). Then (15) has a single pair of purely imaginary roots \(\pm{i}\omega_{0}\). Then using (18), we obtain

$$(ac-d)\omega^{2}_{0}+bd=\bigl(c^{2} \omega^{2}_{0}+d^{2}\bigr)\cos{ \omega_{0}}\tau, $$

and it follows that

$$ \tau_{n}={\frac{1}{\omega_{0}}}\arccos{ \frac{(ac-d)\omega ^{2}_{0}+bd}{c^{2}\omega^{2}_{0}+d^{2}}}+{\frac{2n{\pi}}{\omega_{0}}},\quad n=0,1,2,\ldots. $$
(21)

This completes the proof of the theorem. □

We give the following proposition without any proof, since the proof is similar to that of [6].

Proposition 4.3

If \(\sigma_{0}>1\) and \(I^{*}F'(S^{*})<2r(1-2S^{*})\), then we have the transversality condition

$${\biggl.\frac{d\operatorname{Re}(\lambda(\tau))}{d\tau}\biggr|_{\lambda=i\omega_{0}}}>0. $$

Summarizing the above propositions, we obtain the following theorem.

Theorem 4.2

Assume \(\sigma_{0}>1\), then the following statements hold.

  1. (i)

    If \(I^{*}F'(S^{*})\geq2r(1-2S^{*})\), then the endemic equilibrium of system (4) is locally asymptotically stable for \(\tau\geq0\).

  2. (ii)

    If \(I^{*}F'(S^{*})<2r(1-2S^{*})\), then the endemic equilibrium of system (4) is locally asymptotically stable for \(0\leq\tau<\tau_{0}\) and it is unstable for \(\tau>\tau_{0}\).

Remark 4.1

If both \(\sigma_{0}>1\) and \(I^{*}F'(S^{*})<2r(1-2S^{*})\) hold true, system (4) undergoes a Hopf bifurcation at the endemic equilibrium \(E_{*}\) when τ crosses \(\tau_{n}\) (\(n=0,1,\ldots\)).

5 Numerical results

In this section, we consider the numerical results of system (4) with the saturated incidence rate of the form \(F(S)=\frac{S}{1+{\alpha}S}\). That is to say, we give the numerical simulations of system (2). In system (2), we set \(\beta=0.01\), \(K=100\), \(r=\mu_{1}=\mu_{2}=0.1\), and \(\alpha=0.01\). Then we get the non-dimensional quantities \(\tilde{r}=\tilde{\mu}_{1}=\tilde{\mu}_{2}=0.1\), \(\tilde{\alpha}=0.01\), and \(\tilde{t}={\beta}Kt=t\). Dropping the \(\tilde{\hphantom{a}}\) for convenience, we obtain the following non-dimensional system corresponding to system (2):

$$\begin{aligned}& \frac{dS(t)}{dt}=rS(t) \bigl(1-S(t)\bigr)-\frac{S(t)}{1+{\alpha}S(t)}I(t- \tau), \\& \frac{dI(t)}{dt}=\frac{S(t)}{1+{\alpha}S(t)}I(t-\tau)-(\mu_{1}+\gamma )I(t), \\& \frac{dR(t)}{dt}={\gamma}I(t)-\mu_{2}R(t). \end{aligned}$$
(22)

Therefore, we have \(r=\mu_{1}=\mu_{2}=0.1\) and \(\alpha=0.01\). If we choose \(\gamma=0.1\), the endemic equilibrium of system (22) is \(E_{*}=(0.2004, 0.0798, 0.0798)\), \(\sigma_{0}=4.9505\), and \(\tau_{0}=2.0288\) by applying (17). It should also be noted that \(I^{*}F'(S^{*})=0.0795\) and \(2r(1-2S^{*})=0.1198\), which imply the endemic equilibrium \(E_{*}\) is conditionally stable. Furthermore, we can see that the endemic equilibrium \(E_{*}\) is asymptotical stable if the time delay \(\tau=1<\tau_{0}=2.0288\) (see Figure 1), while the endemic equilibrium \(E_{*}\) loses its stability, Hopf bifurcation occurs, and system (22) exhibits a stable period solution if \(\tau=2.5>\tau_{0}\) (see Figure 2).

Figure 1
figure 1

Temporal behavior of the infective individuals and corresponding three-dimensional phase for system ( 22 ) with \(\pmb{\sigma_{0}=4.9505}\) and \(\pmb{I^{*}F'(S^{*})=0.0795<2r(1-2S^{*})=0.1198}\) . The initial value is set to be \((0.9, 0.3, 0.2)\) and \(\tau=1<\tau_{0}=2.0288\).

Full size image
Figure 2
figure 2

Temporal behavior of the infective individuals and corresponding three-dimensional phase for system ( 22 ) with \(\pmb{\sigma_{0}=4.9505}\) and \(\pmb{I^{*}F'(S^{*})=0.0795<2r(1-2S^{*})=0.1198}\) . The initial value is set to be \((0.35, 0.3, 0.2)\) and \(\tau=2.5>\tau_{0}=2.0288\).

Full size image

If γ is chosen as 0.35 and other parameters are set as in Figure 1, then the endemic equilibrium is \(E_{*}=(0.4520, 0.0546, 0.1909)\), \(\sigma_{0}=2.2002\), and \(I^{*}F'(S^{*})=0.0541>2r(1-2S^{*})=0.0192\), which imply the condition (i) of Theorem 4.2 is satisfied. Moreover, from Figure 3, we can see the endemic equilibrium \(E_{*}\) is globally asymptotically stable although \(\tau=2.5>\tau_{0}\).

Figure 3
figure 3

Plots of the infective individuals and corresponding three-dimensional phase for system ( 22 ) with \(\pmb{\sigma_{0}=2.2002}\) and \(\pmb{I^{*}F'(S^{*})=0.0541>2r(1-2S^{*})=0.0192}\) . The initial value is set to be \((0.4, 0.3, 0.25)\) and \(\tau=2.5>\tau_{0}=2.0288\). The values of parameters are as in Figure 1 but \(\gamma=0.35\).

Full size image

6 Conclusion

In this paper, a delayed SIR vector disease model with incubation time delay is established, in which the growth of susceptible individuals follows the logistic function in the absence of disease and the more general form of the nonlinear incidence rate is considered. The stability of the equilibria has been discussed by analyzing the roots of characteristic equations and applying the theory of asymptotic autonomous systems. It is shown that the trivial equilibrium is always unstable. The stability of the disease-free equilibrium is completely determined by the threshold parameter \(\sigma_{0}\): the disease-free equilibrium is globally asymptotically stable if \(\sigma_{0}<1\) while it is unstable if \(\sigma_{0}>1\). Moreover, if \(\sigma_{0}>1\), there exists a unique endemic equilibrium. It is found that \(I^{*}F'(S^{*})=2r(1-2S^{*})\) is the condition which determines the absolute stability or conditional stability of the endemic equilibrium. To be specific, the endemic equilibrium is absolutely stable if \(I^{*}F'(S^{*})\geq2r(1-2S^{*})\) holds true, while it is conditionally stable if \(I^{*}F'(S^{*})<2r(1-2S^{*})\) is satisfied. Furthermore, there is a certain threshold time value \(\tau_{0}\) such that the endemic equilibrium is locally asymptotically stable when \(0<\tau<\tau_{0}\), whereas it is unstable when \(\tau>\tau_{0}\). It is worth noting that, if \(\sigma_{0}>1\) and \(I^{*}F'(S^{*})<2r(1-2S^{*})\), the system exhibits a Hopf bifurcation when the time delay τ crosses \(\tau_{n}\) (\(n=0,1,\ldots\)).

References [4, 5, 8, 10, 11] have discussed the delayed SIR vector disease models with nonlinear incidence functions. But the growth of the number of susceptible individuals is governed by a constant rate rather than the logistic function. They have proved that the endemic equilibrium is globally asymptotically stable for any delay and the model does not exhibit a Hopf bifurcation, which implies that the incubation delay does not cause any periodic oscillations. On the other hand, [6, 13, 19] have also investigated the delayed SIR vector disease models with the logistic growth of susceptible individuals. They have found that the endemic equilibrium is unstable and a Hopf bifurcation occurs under some conditions for some delays. For example, Wang et al. [13] investigated system (1) with the incidence function \(F(S)=S\). They have proved if \(R_{0}>3\), the endemic equilibrium is stable when the delay \(\tau<\tau_{0}\) is satisfied, while the endemic equilibrium is unstable and the model undergoes Hopf bifurcation when \(\tau=\tau_{n}\), \(n=0, 1, 2, \ldots \) . Therefore, the logistic growth of susceptible individuals should be more responsible for the instability of the endemic equilibrium, and Hopf bifurcation may be the result of the logistic growth of susceptible individuals.

Wang et al. [13] analyzed system (1) for the incidence function \(F(S)=S\). Zhang et al. [19] also formulated system (2) for the incidence function \(F(S)=\frac{S}{1+{\alpha}S}\). As a matter of fact, two systems in the above-mentioned papers could be studied as special cases for system (3). It should be pointed out here that the threshold parameter \(\sigma_{0}\) defined in the present paper is the same as \(R_{0}\) derived in [13] and is equivalent to \(R_{0}\) given in [19]. Furthermore, our results for the stability of equilibria extend the results in [13] and [19]. The numerical simulations performed further illustrate the theoretical results.