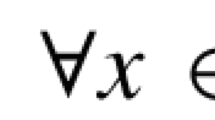1 Introduction: backward-shifting matrices of sequences

Let \(\mathbf{a}=\{a(k)\}_{k=0}^{\infty}=(a(0),a(1),a(2),\ldots,a(k),\ldots)\) be an infinite sequence. We also regard the sequence as a (\(1\times \infty\)) row vector. Two special sequences are the unit sequence \(\mathbf{e}=\{e(k)\}_{k=0}^{\infty}=\{\delta_{k,0}\}_{k=0}^{\infty}\) (\(\delta_{k,0}\) is the Kronecker delta) and the null sequence \(\mathbf{o}=\{0\}_{k=0}^{\infty}\).

For any sequence a, we always assume \(a(k)=0\) if \(k<0\). Thus, we may express all of the backward-shifting (namely right-shifting) sequences of a as \(\mathbf{a}_{(-1)}=\{a(k-1)\}_{k=0}^{\infty}=(0,a(0),a(1),a(2), \ldots)\), \(\mathbf{a}_{(-2)}=\{a(k-2)\}_{k=0}^{\infty}=(0,0,a(0),a(1),a(2),\ldots)\), \(\mathbf{a}_{(-3)}=\{a(k-3)\}_{k=0}^{\infty}=(0,0,0,a(0),a(1),a(2),\ldots)\), and so on.

In this section, we give mainly attention to the convolution (Cauchy multiplication) of two sequences. As we know, if the sequence c is a convolution of two sequences a and b, expressed as \(\mathbf{a}\ast\mathbf {b}=\mathbf{b}\ast\mathbf{a}=\mathbf{c}\), then the general term \(c(k)\) of the sequence c is [1]

$$ c(k)=\sum_{i=0}^{k} a(i)b(k-i)=\sum_{i=0}^{k} a(k-i)b(i), \quad k\in \mathbb {N}_{0}. $$
(1)

For any sequence a, we have \(\mathbf{a}\ast\mathbf{e}=\mathbf {e}\ast\mathbf{a}=\mathbf{a}\), and \(\mathbf{a}\ast\mathbf{o}=\mathbf{o}\ast\mathbf{a}=\mathbf{o}\).

We may construct (define) a matrix A associated with any sequence a, each row vector of which is corresponding backward-shifting sequence of a, as

$$ \mathbf{A}= \begin{pmatrix} \mathbf{a}\\ \mathbf{a}_{(-1)} \\ \mathbf{a}_{(-2)} \\ \mathbf{a}_{(-3)} \\ \vdots \end{pmatrix} = \begin{pmatrix} a(0) & a(1) & a(2) & a(3) & \cdots\\ & a(0) & a(1) & a(2) & \cdots \\ & & a(0) & a(1) &\cdots \\ & & & a(0) & \cdots \\ & & & & \ddots \end{pmatrix}, $$
(2)

and call the infinite dimensional, upper triangular Toeplitz matrix the backward-shifting matrix of the sequence a, or simply, the BS-matrix of a [2]. Obviously, for a given sequence, there exists one and only one BS-matrix corresponding to the sequence.

We may see from (1) and (2) that, if \(\mathbf{a}\ast\mathbf{b}=\mathbf{b}\ast\mathbf{a}=\mathbf{c}\), then \(\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{C}\), where A, B, and C are the corresponding BS-matrices; and vice versa.

In the case that the first term \(a(0)\) of the sequence a is not zero, then the corresponding BS-matrix A is reversible, that is, there exists an inverse matrix \(\mathbf {A}^{-1}\) of A making \(\mathbf{A}\mathbf{A}^{-1}=\mathbf{A}^{-1}\mathbf{A}=\mathbf{E}\), where E is the \(\infty\times\infty\) unit matrix. Of course, E also is the BS-matrix of the unit sequence e. Furthermore, we may see that \(\mathbf{A}_{k}\mathbf{A}_{k}^{-1}=\mathbf {A}_{k}^{-1}\mathbf{A}_{k}=\mathbf{E}_{k}\), where \(\mathbf{A}_{k}\) and \(\mathbf{A}_{k}^{-1}\) (\(k\in \mathbb {N}_{0}\)) both are the \((k+1)\times (k+1)\) upper-left sub-matrices of the matrices A and \(\mathbf{A}^{-1}\), respectively, and \(\mathbf {E}_{k}\) (\(k\in \mathbb {N}_{0}\)) is the \((k+1)\times(k+1)\) unit matrix. The matrices \(\mathbf{A}_{k}\), \(\mathbf {A}_{k}^{-1}\) (\(k\in \mathbb {N}_{0}\)) are all upper triangular Toeplitz matrices.

We denote the sequence, the BS-matrix of which is \(\mathbf{A}^{-1}\), \(\tilde{\mathbf{a}}\), and we call \(\tilde{\mathbf{a}}\) the convolution inverse of a. The general term \(\tilde{a}(k)\) of the sequence \(\tilde{\mathbf{a}}\) (e.g., see [1]) is the (\(0,k\))th entry of the matrix \(\mathbf{A}^{-1}\) or \(\mathbf{A}_{k}^{-1}\). Hence, from the matrix theory we know that \(\tilde{a}(k)\) is the (\(0,k\))th entry of the adjoint matrix of \(\mathbf{A}_{k}\), which is the algebraic cofactor of the (\(k,0\))th entry of \(\mathbf {A}_{k}\), divided by the determinant of \(\mathbf{A}_{k}\). Thus, \(\tilde{a}(0)=1/a(0)\), and for \(k>0\),

$$ \tilde{a}(k)=(-1)^{k}\bigl(a(0)\bigr)^{-(k+1)} \begin{vmatrix} a(1) & a(2) &\cdots& a(k-1) & a(k) \\ a(0) & a(1) & \ddots& a(k-2) & a(k-1) \\ & \ddots& \ddots& \ddots& \vdots \\ & & \ddots& a(1) & a(2) \\ & & & a(0) & a(1) \end{vmatrix}. $$
(3)

If the three BS-matrices A, B, and C satisfy \(\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{C}\) and A is reversible (\(a(0)\neq0\)), then \(\mathbf{B}=\mathbf{A}^{-1}\mathbf{C}=\mathbf{C}\mathbf{A}^{-1}\), at the same time we have \(\mathbf{b}=\tilde{\mathbf{a}}\ast\mathbf{c}=\mathbf{c}\ast\tilde{\mathbf{a}}\).

In the second section of this paper, based on these relationships between sequences and their BS-matrices as mentioned above, we develop a direct method used to solve the initial value problem of a linear, time-invariant, non-homogeneous difference equation. In this method, the general term of solution sequence has an explicit formula, which includes coefficients and initial values of the solved equation only. In the third section of this paper, the authors point out that the solution sequence of the initial value problem surely satisfies two adjoint linear recursive equations, which may give the solution sequence several new features.

2 Direct solutions of linear non-homogeneous difference equations

Linear difference equations are ubiquitous in many engineering theories and mathematical branches. For example, they appear in the theory of discrete systems and control theory of discrete systems as basic models of the discrete systems [3–5], and discrete-time signal processing as basic recurrence relations of sampled signals [6]. In algebraic combinatorics, they are also one of main study topics, tying different special sequences in with their generating functions [1, 7]. For more details, the reader may refer to [8].

In this section, by means of the BS-matrices of sequences we give a direct computational method used to solve the initial value problem of a linear, time-invariant, non-homogeneous difference equation.

Let \(\mathbf{a}=\{a(k)\}_{k=0}^{\infty}\) be the solution sequence of a non-homogeneous linear difference equation of order p (\(p\in \mathbb {N}\)),

$$ a(k)+b_{1}a(k-1)+b_{2}a(k-2)+ \cdots+b_{p}a(k-p)=d_{k},\quad k\geq p, $$
(4)

which has p given initial values:

$$ a(0)=a_{0}, \qquad a(1)=a_{1}, \qquad a(2)=a_{2},\qquad \ldots, \qquad a(p-1)=a_{p-1}, $$
(5)

where \(b_{0}\) (=1) and \(b_{k}\) (\(p\geq k\geq1\)) are time-invariant coefficients of the equation; \(d_{k}\) (\(k\geq p\)) are infinite given (known) numbers.

Theorem 2.1

Let \(\mathbf{a}=\{a(k)\}_{k=0}^{\infty}\) be a solution sequence of the linear difference equation (4) with p initial values \(a(k)=a_{k}\) (\(p>k\geq0\)). Let \(\mathbf{b}=\{b(k)\}_{k=0}^{\infty}\) be a coefficient sequence of the equation, where

$$ b(k)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 1, & k=0; \\ b_{k}, & p\geq k>0;\\ 0, & k> p. \end{array}\displaystyle \right . $$
(6)

Let \(\mathbf{c}=\{c(k)\}_{k=0}^{\infty}\) be the right-side term sequence of the equation, where

$$ c(k)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \sum_{i=0}^{k} a_{i}b_{k-i}, & p>k\geq0; \\ d_{k}, & k\geq p. \end{array}\displaystyle \right . $$
(7)

Then the general term \(a(k)\) of a is

$$ a(k)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} a_{k}, & p>k\geq0; \\ \sum_{i=0}^{k} \tilde{b}(i)c(k-i)=\sum_{i=0}^{k} \tilde{b}(k-i)c(i), & k\geq p, \end{array}\displaystyle \right . $$
(8)

where \(\tilde{b}(0)=1\), and for \(k\geq1\)

$$ \tilde{b}(k)=(-1)^{k} \begin{vmatrix} b(1) & b(2) & \cdots & b(k-1) & b(k) \\ 1 & b(1) & \ddots& b(k-2) & b(k-1) \\ &\ddots& \ddots& \ddots& \vdots \\ & & \ddots& b(1) & b(2) \\ & & & 1 & b(1) \end{vmatrix}. $$
(9)

Proof

We can rewrite equation (4) as a form of sequence convolution: \(\mathbf{a}\ast\mathbf{b}=\mathbf{c}\), where the general terms of the sequences b and c are shown in (6) and (7). Therefore, denoting the BS-matrices of a, b, and c by A, B and C, respectively, we have \(\mathbf{A}\mathbf{B}=\mathbf {C}\). For \(b(0)=1\), B is reversible and thus \(\mathbf{A}=\mathbf{C}\mathbf{B}^{-1}\). Hence, \(\mathbf{a}=\mathbf{c}\ast\tilde{\mathbf{b}}\), that is, equation (8) holds. □

Next, let us see several simple but enlightening examples, in which p is 1 or 2 only.

Example 2.2

The Fibonacci sequence f (OEIS A000045) [9] is the solution sequence of a linear difference equation of order two: \(f(k)-f(k-1)-f(k-2)=0\) (\(k\geq2\)) with two initial values \(f(0)=0\) and \(f(1)=1\). We may rewrite it as \(\mathbf{b}\ast\mathbf{f}=\mathbf{c}\), where \(\mathbf{b}=(1,-1,-1,0,0,\ldots)\) and \(\mathbf{c}=(0,1,0,0,0,\ldots)\). Thus, according to equation (8), we have \(f(k)=\sum_{i+j=k}\tilde{b}(i)c(j)=\tilde{b}(k-1)c(1)=\tilde{b}(k-1)\). Hence the general term \(f(k)\) of the Fibonacci sequence when \(k\geq2\) has a determinant form:

$$ f(k)=(-1)^{k-1} \begin{vmatrix} -1 & -1 & & & \\ 1 & -1 & -1 & & \\ & 1 & -1 & -1 & \\ & & \ddots& \ddots& \\ & & & 1 & -1 \end{vmatrix}_{(k-1)\times(k-1)}. $$
(10)

For example, the sixth term and seventh term of the Fibonacci sequence are, respectively,

$$f(5)= \begin{vmatrix} -1 & -1 & 0 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 1 & -1 \end{vmatrix} =5,\qquad f(6)= - \begin{vmatrix} -1 & -1 & 0 & 0 & 0 \\ 1 & -1 & -1 & 0 & 0 \\ 0 & 1 & -1 & -1 & 0 \\ 0 & 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 1 & -1 \end{vmatrix}=8. $$

Example 2.3

The sequences of Chebyshev polynomials, \(\mathbf{t}(x)=\{T_{k}(x)\}_{k=0}^{\infty}\) and \(\mathbf{u}(x)=\{U_{k}(x)\}_{k=0}^{\infty}\), are solution sequences of two identical linear time-invariant difference equations of order 2: \(T_{k}(x)-2xT_{k-1}(x)+T_{k-2}(x)=0\) and \(U_{k}(x)-2xU_{k-1}(x)+U_{k-2}(x)=0\) (\(k\geq2\)) with different initial values \(T_{0}(x)=1\), \(T_{1}(x)=x\), and \(U_{0}(x)=1\), \(U_{1}(x)=2x\), respectively (see [10]). Thus, we may rewrite them as \(\mathbf{t}\ast\mathbf{b}=\mathbf{c}_{t}\) and \(\mathbf{u}\ast\mathbf{b}=\mathbf{c}_{u}\), where \(\mathbf{b}=(1,-2x,1,0,0,\ldots)\), \(\mathbf{c}_{t}=(1,-x,0,0,\ldots)\), and \(\mathbf{c}_{u}=(1,0,0,0,\ldots)=\mathbf{e}\). According to (8), we obtain \(U_{0}(x)=1\), \(U_{1}(x)=2x\), and for \(k\geq2\),

$$ U_{k}(x)=(-1)^{k} \begin{vmatrix} -2x & 1 & \cdots& 0 & 0 \\ 1 & -2x & \ddots& 0 & 0 \\ & \ddots& \ddots & \ddots& \vdots \\ & & 1 & -2x & 1 \\ & & & 1 & -2x \end{vmatrix} _{k\times k}, $$
(11)

and \(T_{0}(x)=1\), \(T_{1}(x)=x\), and for \(k\geq2\),

$$\begin{aligned} T_{k}(x)={}&(-1)^{k} \begin{vmatrix} -2x & 1 & \cdots& 0 & 0 \\ 1 & -2x & \ddots& 0 & 0 \\ & \ddots& \ddots & \ddots& \vdots \\ & & 1 & -2x & 1 \\ & & & 1 & -2x \end{vmatrix} _{k\times k} \\ &{}+x(-1)^{k} \begin{vmatrix} -2x & 1 & \cdots& 0 & 0 \\ 1 & -2x & \ddots& 0 & 0 \\ & \ddots& \ddots & \ddots& \vdots \\ & & 1 & -2x & 1 \\ & & & 1 & -2x \end{vmatrix} _{(k-1)\times(k-1)}. \end{aligned}$$
(12)

Example 2.4

The tower of Hanoi puzzle (see [7]) is an initial value problem of a linear non-homogeneous difference equation of order 1: \(a(k)-2a(k-1)=1\) for \(k\geq1\) and \(a(0)=0\). The corresponding sequences \(\mathbf{b}=(1,-2,0,0,\ldots)\) and \(\mathbf{c}=(0,1,1,1,\ldots)\). By using (8)-(6), we obtain \(a(0)=0\) and for \(k\geq1\),

$$\begin{aligned} a(k)&=\sum_{i=0}^{k}\tilde{b}(k-i)c(i)=\sum _{i=1}^{k}(-1)^{k-i} \begin{vmatrix} -2 & & & & \\ 1 & -2 & & & \\ & 1 & -2 & & \\ & & \ddots& \ddots& \\ & & & 1 & -2 \end{vmatrix} _{(k-i)\times(k-i)} \\ &=\sum_{i=1}^{k}2^{k-i}=2^{k}-1. \end{aligned}$$

Example 2.5

Let us solve the non-homogeneous Fibonacci-type linear difference equation \(r(k)-r(k-1)-r(k-2)=d_{k}\) (\(k\geq2\)) with two initial values \(r(0)=0\) and \(r(1)=1\), where \(d_{k}\) (\(k\geq2\)) are infinite given numbers. We may express this equation as a convolution form: \(\mathbf{b}\ast\mathbf{r}=\mathbf{c}\), where \(\mathbf{b}=(1,-1,-1,0,0,0,\ldots)\) and \(\mathbf{c}=(0,1,d_{2},d_{3},d_{4},d_{5},\ldots)\). Hence, according to (8) we have \(\mathbf{r}=\mathbf{c}\ast\tilde{\mathbf{b}}\). We see from Example 2.2 that \(\tilde{b}(k)=f(k+1)\), the \((k+1)\)th Fibonacci number. Thus, the general term of the solution sequence r is that \(r(0)=0\), \(r(1)=1\), and for \(k\geq2\),

$$r(k)=\sum_{i=0}^{k} c(i)\tilde{b}(k-i)=\sum _{i=0}^{k} c(i)f(k+1-i)=f(k)+d_{2}f(k-1)+ \cdots+d_{k}f(1). $$

Remark 1

As we know, traditional methods used for solving linear non-homogeneous difference equations face several difficulties in practical applications. Here, the traditional methods include the classical method (the discrete analogue of the technique of solving linear differential equations, namely the solution of a non-homogeneous equation is the sum of the general solution of corresponding homogeneous equation and a particular solution of the non-homogeneous equation) [1], and the generating function method [1] or similar Z-transform method [5, 6] (usually, the former is used in mathematics, and the latter in engineering theories). Summarily, these methods are all unable to give explicit expressions of the general term of solution sequences by using coefficients and the non-homogeneous right-side terms. This is because they always need to find all complex roots of a polynomial (the characteristic polynomial of the equation). In general and higher order cases, that is very difficult. Besides, finding particular solutions of the non-homogeneous equations as in the classical method, or expanding rational fraction functions as a sum of simple fractions, or finding power series expansions or finding inverse Z-transforms as in the generating function method and Z-transform method, are also very difficult in general cases.

However, by using the direct method developed in this paper, we can directly solve the initial value problems of linear non-homogeneous difference equations (recursive relation). We can explicitly express the general term of the solution sequence by using the coefficients, initial values, and non-homogeneous right-side terms of the solved equation only. This is a distinct difference of the direct method.

Remark 2

Recently, Birmajer et al. gave another direct expression of the solution sequence for the homogeneous case [11], as for \(k\geq p\),

$$a(k) = \sum_{i=0}^{p-1} c(i)\sum _{j=0}^{k-i} \frac{j!}{(k-i)!} B_{k-i,j}(1!b_{1}, 2!b_{2}, \dots), $$

where \(c(k)=\sum_{i=0}^{k} a_{i}b_{k-i}\) for \(p>k\geq0\), and \(B_{n,k}(x_{1},x_{2},\dots)\) is the \((n,k)\)th partial Bell polynomial in the variables \(x_{1},x_{2},\dots,x_{n-k+1}\) (see (1) of [12]). Readers may compare it with equation (8) in the homogeneous case (\(d_{k}=0\) when \(k\geq p\)).

3 Adjoint linear recursive equations

Let a be the solution sequence of the initial value problem of linear non-homogeneous difference equation (4). We may find that the sequence a satisfies an adjoint linear recursive relation, as shown in the following theorem.

Theorem 3.1

Let a be the solution sequence of linear non-homogeneous difference equation (4) with initial values shown in (5), in which \(a_{0}\neq0\). Then the sequence a satisfies the following so-called adjoint linear recursive equation of the first kind:

$$ \tilde{\mathbf{c}}\ast\mathbf{a}=\tilde{\mathbf{b}}, $$
(13)

that is,

$$ \tilde{c}(0)a(k)+\tilde{c}(1)a(k-1)+\tilde{c}(2)a(k-2)+ \cdots+ \tilde{c}(k)a(0)=\tilde{b}(k), \quad k\in \mathbb {N}_{0}, $$
(14)

where the sequences b and c are shown in (6) and (7), respectively; \(\tilde{\mathbf{b}}\) and \(\tilde{\mathbf{c}}\) are the first row vectors of the BS-matrices \(\mathbf{B}^{-1}\) and \(\mathbf{C}^{-1}\), respectively, that is, \(\tilde{b}(0)=1\), \(\tilde{c}(0)=\frac{1}{c(0)}=\frac{1}{a_{0}}\), and for \(k\geq1\),

$$ \tilde{b}(k)=(-1)^{k} \begin{vmatrix} b(1) & b(2) & \cdots & b(k-1) & b(k) \\ 1 & b(1) & \ddots& b(k-2) & b(k-1) \\ & \ddots& \ddots& \ddots& \vdots \\ & & \ddots& b(1) & b(2) \\ & & & 1 & b(1) \end{vmatrix} $$
(15)

and

$$ \tilde{c}(k)=\frac{(-1)^{k}}{a_{0}^{k+1}} \begin{vmatrix} c(1) & c(2) & \cdots& c(k-1) & c(k) \\ a_{0} & c(1) & \ddots& c(k-2) & c(k-1) \\ & \ddots& \ddots& \ddots& \vdots \\ & & \ddots& c(1) & c(2) \\ & & & a_{0} & c(1) \end{vmatrix}. $$
(16)

Proof

For the initial value problem (4) and (5), we have \(\mathbf{A}\mathbf{B}=\mathbf{C}\), where A, B, and C are BS-matrices of three sequences a, b, and c. The general terms of sequences b and c are shown in (6) and (7). Because \(b(0)=1\) and \(c(0)=a_{0}\neq0\), the matrices B and C both are reversible. Hence, we have \(\mathbf{C}^{-1}\mathbf{A}=\mathbf{B}^{-1}\), that is, \(\tilde{\mathbf{c}}\ast\mathbf{a}=\tilde{\mathbf{b}}\). □

Example 3.2

The Lucas sequence l (OEIS A000032) [9] is the solution sequence of a Fibonacci-type linear difference equation: \(l(k)-l(k-1)-l(k-2)=0\) (\(k\geq2\)), with \(l(0)=2\) and \(l(1)=1\). In this case, \(\mathbf{b}=(1,-1,-1,0,0,0,\ldots)\) and \(\mathbf{c}=(2,-1,0,0,0,0,\ldots)\). Thus, \(\tilde{b}(0)=1\) and \(\tilde{c}(0)=\frac{1}{2}\), and for \(k\geq 1 \),

$$\tilde{b}(k)=(-1)^{k} \begin{vmatrix} -1 & -1 & & & \\ 1 & -1 & -1 & & \\ & 1 & -1 & -1 & \\ & & \ddots& \ddots& \\ & & & 1 & -1 \end{vmatrix} _{k\times k} $$

and

$$\tilde{c}(k)=\frac{(-1)^{k}}{2^{k+1}} \begin{vmatrix} -1 & 0 & \cdots& 0 & 0 \\ 2 & -1 & \ddots& 0 & 0 \\ & \ddots& \ddots& \ddots& \vdots \\ & & 2 & -1 & 0 \\ & & & 2 & -1 \end{vmatrix} _{k\times k}=\frac{1}{2^{k+1}}. $$

We see from Example 2.2 that \(\tilde{b}(k)=f(k+1)\), the \((k+1)\)th Fibonacci number. Hence, the Lucas sequence satisfies the following linear recursive relation:

$$l (0)+2l (1)+2^{2}l (2)+\cdots+2^{k-1} l (k-1)+2^{k}l (k)= 2^{k+1}f(k+1),\quad k\in \mathbb {N}_{0}. $$

This is a well-known identity for the Lucas numbers.

Example 3.3

The sequence \(\mathbf{t}(x)\) of the Chebyshev polynomials \(T_{k}(x)\) (\(k\in \mathbb {N}_{0}\)) of the first kind is the solution of linear homogeneous difference equation of order two: \(T_{k}(x)-2xT_{k-1}(x)+T_{k-2}(x)=0\) (\(k\geq2\)) with \(T_{0}(x)=1\) and \(T_{1}(x)=x\). Hence \(\mathbf{b}=(1,-2x,1,0,0,0,\ldots)\) and \(\mathbf{c}=(1,-x,0,0,0,0,\ldots)\). We see from Example 2.3 that \(\tilde{b}(k)=U_{k}(x)\), the kth Chebyshev polynomial of the second kind. \(\tilde{c}(0)=1\), and for \(k\geq1 \),

$$\tilde{c}(k)=(-1)^{k} \begin{vmatrix} -x & 0 & \cdots& 0 & 0 \\ 1 & -x & 0 & \cdots& 0 \\ & \ddots& \ddots& \ddots& \vdots \\ & & 1 & -x & 0 \\ & & & 1 & -x \end{vmatrix} _{k\times k}=x^{k}. $$

Hence, the adjoint linear recursive relation of the Chebyshev polynomials \(T_{k}(x)\) of the first kind is

$$T_{k}(x)+xT_{k-1}(x)+x^{2}T_{k-2}(x)+ \cdots+x^{k-1}T_{1}(x)+x^{k}T_{0}(x)= U_{k}(x), \quad k\in \mathbb {N}_{0}. $$

Thus, we get a new identity for the Chebyshev polynomials of the first kind.

We may give another adjoint linear recursive equation in a similar way, as follows.

Theorem 3.4

Let a be the solution sequence of the non-homogeneous linear difference equation (4) with initial values shown in (5), in which \(a_{0}\neq0\). Then the sequence a satisfies the following so-called adjoint linear recursive equation of the second kind:

$$ \tilde{\mathbf{c}}\ast\mathbf{b}\ast\mathbf{a}=\mathbf{e}, $$
(17)

that is,

$$ \sum_{i=0}^{k}\sum _{j=0}^{i}\tilde{c}(j)b(i-j)a(k-i)=0, \quad k>0, $$
(18)

where the sequences b and c are shown in (6) and (7), respectively; and \(\tilde{\mathbf{c}}\) is shown in (16).

Proof

For the initial value problem (4) and (5), we have \(\mathbf{A}\mathbf{B}=\mathbf{B}\mathbf{A}=\mathbf{C}\), where A, B and C are the BS-matrices of the three sequences a, b, and c. The general terms of sequences b and c are shown in (6) and (7). Because \(c(0)=a_{0}\neq0\), the matrix C is reversible. Hence, we have \(\mathbf{C}^{-1}\mathbf{B}\mathbf{A}=\mathbf{E}\), that is, \(\tilde{\mathbf{c}}\ast\mathbf{b}\ast\mathbf{a}=\mathbf{e}\). □

Example 3.5

For the Lucas sequence l shown in Example 3.2, \(l (0)=2\) and \(l (1)=1\). We have the coefficient sequences \(\mathbf {b}=(1,-1,-1,0,0,0,\ldots)\) and \(\mathbf{c}=(2,-1,0,0,0,0,\ldots)\). Hence, \(\tilde{c}(0)=\frac{1}{2}\), and for \(k\geq1\),

$$\tilde{c}(k)=\frac{(-1)^{k}}{2^{k+1}} \begin{vmatrix} -1 & 0 & \cdots& 0 & 0 \\ 2 & -1 & \ddots& 0 & 0 \\ & \ddots& \ddots& \ddots& \vdots \\ & & 2 & -1 & 0 \\ & & & 2 & -1 \end{vmatrix} _{k\times k}=\frac{1}{2^{k+1}}. $$

Thus, according to equation (18) the Lucas sequence satisfies the following linear recursive relation: for \(k>1\),

$$5\bigl[l (0)+2l (1)+2^{2}l (2)+\cdots+2^{k-2}l(k-2)\bigr]+2^{k-1}l (k-1)-2^{k}l (k)=0. $$

This is a new identity for the Lucas numbers.

Example 3.6

For the sequence \(\mathbf{t}(x)\) of the Chebyshev polynomials of the first kind shown in Example 3.3, \(T_{0}(x)=1\), \(T_{1}(x)=x\), and we have the coefficient sequences \(\mathbf{b}=(1,-2x,1,0,0,0,\ldots)\) and \(\mathbf{c}=(1,-x,0,0,0,0,\ldots)\). We also see from Example 3.3 that \(\tilde{c}(0)=1\), and for \(k\geq1 \), \(\tilde{c}(k)=x^{k}\). Hence, denoting by \(\tilde {\mathbf{t}}(x)=\tilde{\mathbf{c}}\ast\mathbf{b}\), we have \(\tilde{t}_{0}(x)=1\), \(\tilde{t}_{1}(x)=-x\), and for \(k>1\), \(\tilde{t}_{k}(x)=\sum_{i=0}^{k} b(i)\tilde{c}(k-i)=x^{k-2}(1-x^{2})\). Thus, the adjoint linear recursive equation of the second kind of the Chebyshev polynomials \(T_{k}(x)\) of the first kind is that for \(k>0\)

$$T_{k}(x)-xT_{k-1}(x)+\bigl(1-x^{2} \bigr)T_{k-2}(x)+\cdots +x^{k-3}\bigl(1-x^{2} \bigr)T_{1}(x)+x^{k-2}\bigl(1-x^{2} \bigr)T_{0}(x)=0. $$

Here, we get another new identity for the Chebyshev polynomials \(T_{k}(x)\) of the first kind.

4 Conclusions

In this paper, the authors develop a direct method used to solve the initial value problems of a linear non-homogeneous time-invariant difference equation. In this method, the obtained general term of the solution sequence has an explicit formula, which includes coefficients, initial values, and right-side terms of the solved equation only. Furthermore, when the solution sequence has a nonzero first term, it satisfies two adjoint linear recursive equations; this usually shows several new features of the solution sequence.