A geometric approach for solving the density-dependent diffusion Nagumo equation

Abstract

In this paper, some solutions of the density-dependent diffusion Nagumo equation are obtained by using a new approach, the Lie symmetry group-preserving scheme (LSGPS). The effects of various model parameters on the solution are investigated graphically using LSGPS. Finally, a different reduction method of PDEs is applied to construct two new analytical solutions and a first integral of the Nagumo equation.

1 Introduction

A systematic and powerful method to derive the exact solutions of nonlinear differential equations is the Lie symmetry method which has some important properties such as conservation laws, can successfully be obtained using the symmetries [1–5]. Among the existing numerical algorithms, the group preserving scheme (GPS) provided by Liu [6] is a numerical method based upon Lie group solvers that preserves the Lie group structure under discretization. This method uses the Cayley transformation and the Padé approximations in the augmented Minkowski space $\mathbb{M}^{n+1}$. One of the major benefits of GPS in the $\mathbb{M}^{n+1}$ is that it can avoid ghost fixed points and spurious solutions. We refer the reader to the following papers about GPS, e.g. [7–16].

The density-dependent diffusion Nagumo equation [17]

$$ \frac{\partial u}{\partial t}=\frac{\partial}{\partial x} \biggl(u^{m} \frac{\partial u}{\partial x} \biggr)+u(1-u) (u-\alpha),\quad \alpha\in\mathbb{R}, m\geq1, $$

(1)

with its diffusion coefficient being a simple power function and the nonlinearity assumed to be singular at zero, has various biological applications, such as population genetics, nuclear reactor theory, chemical reactions, and it is used in the modeling of electrical pulse propagation of nerve axons. The existence of one-dimensional traveling wave solutions of (1) has been studied in [18] by Sánchez-Garduño and Maini. Mansour in [19] has computed the traveling wave solutions of (1) with the wave speed c and the special case $m=2$. The minimum speed and the corresponding trajectory for the sharp traveling waves have been determined in the mentioned paper. An approximation to the wave speed is considered by Pedersen in [20] and he claimed that the wave speed does not depend on the parameter $g_{K,AT P}$, mimicking the glucose concentration in the islet. The δ-expansion method in [21] has been applied to obtain traveling wave solutions of (1) on the real line, subject to conditions at infinity. Masemola et al. in [22] have recently applied the Lie symmetry method to construct the conservation laws and the exact solutions of the underlying equation for the special cases $m=2$ and $\alpha=-1$.

2 Group-preserving schemes

Most of the physical systems are formulated in terms of a system of k ordinary differential equations,

$$ \frac{d\mathbf{W}}{d\xi}=\mathbf{f}(\xi,\mathbf{W}),\quad \xi\in \mathbb{R}, \mathbf{W}\in\mathbb{R}^{k}, $$

(2)

such that equation (2) is a differential equation on the manifold $\mathfrak{M}\subset\mathbb{R}^{k}$, if

$$ \mathbf{W}_{0}\in\mathfrak{M}\quad \text{implies}\quad \mathbf{W}(\xi) \in\mathfrak {M} \quad \text{for all } \xi. $$

(3)

Many numerical approaches have been proposed to approximate the solution of equation (2). Almost all methods discretize the system of differential equations to produce related difference equations. Obviously, from the same differential equations, the methods obtain different difference equations, but they have the same aim in that the dynamics of the difference equation must correspond closely to the dynamics of the differential equations.

This section gives an introduction to GPS from the class of the relatively new area of numerical analysis called geometric integration. The name ‘geometric integration’ is utilized to a series of numerical approaches that aim to preserve the qualitative and geometrical features of a differential equation when it is discretized [23–25]. Hairer in [26] illustrated a procedure to modify classical methods for solving differential equations on manifolds in order to preserve certain geometric properties of the exact flow. The concept of geometric numerical integration by the important example of the Störmer/Verlet method is given by Hairer et al. in [27].

2.1 A Lie algebra formulation

In the formulation of GPS, for a k-dimensional ordinary differential equations system (2), it is possible embed them into the $k+1$-dimensional augmented dynamical systems:

$$ \frac{d}{d\xi} \left [ \textstyle\begin{array}{@{}c@{}} \mathbf{W} \\ \|\mathbf{W}\| \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \mathbf{0}_{k\times k} & \frac{\mathbf{f}(\xi,\mathbf{W})}{\|\mathbf {W}\|} \\ \frac{\mathbf{f}^{\mathrm{T}}(\xi,\mathbf{W})}{\|\mathbf{W}\|} & 0 \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{@{}c@{}} \mathbf{W} \\ \|\mathbf{W}\| \end{array}\displaystyle \right ]. $$

(4)

Clearly, the first equation in equation (4) is the same as the dynamical system (2), whereas the second equation imposes a Minkowskian structure of the augmented state variables of $X:=(\mathbf{W}^{\mathrm{T}},\|\mathbf{W}\|)^{\mathrm{T}}$, satisfying the cone condition:

$$ X^{\mathrm{T}}gX=0, $$

(5)

where

$$ g=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} I_{k} & \mathbf{0}_{k\times1} \\ \mathbf{0}_{1\times k} & -1 \end{array}\displaystyle \right ] $$

(6)

is a Minkowski metric. Hence equation (5) in terms of X becomes

$$ X^{\mathrm{T}}gX=\mathbf{W}\cdot\mathbf{W}-\|\mathbf{W}\|^{2}=\| \mathbf{W}\| ^{2}-\|\mathbf{W}\|^{2}=0. $$

(7)

Thus, we imposed a natural constraint (cone condition) on the augmented dynamical system and, consequently, we have an $k+1$-dimensional augmented system:

$$ X'=\mathcal{A}X, $$

(8)

with constraint (5) and

$$ \mathcal{A}:=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \mathbf{0}_{k\times k} & \frac{\mathbf{f}(\xi,\mathbf{W})}{\|\mathbf {W}\|} \\ \frac{\mathbf{f}^{\mathrm{T}}(\xi,\mathbf{W})}{\|\mathbf{W}\|} & 0 \end{array}\displaystyle \right ], $$

(9)

satisfying¹

$$ \mathcal{A}^{\mathrm{T}}g+g\mathcal{A}=0. $$

(10)

The discretized mapping $\mathcal{G}\in \mathit{SO}_{0}(k, 1)$, corresponding to $\mathcal{A}$, preserves the following properties:

$$ \mathcal{G}^{\mathrm{T}}g\mathcal{G}=g, \qquad \operatorname{det}( \mathcal{G})=1,\qquad \mathcal{G}_{0}^{0}>0, $$

(11)

where $\mathcal{G}_{0}^{0}$ is the 00th component of $\mathcal{G}$. Now, we are ready to develop the group-preserving numerical scheme as follows:

$$ X_{n+1}=\mathcal{G}(n)X_{n}, $$

(12)

where $X_{n}$ denotes the numerical value of X at $\xi_{n}$, and

$$ \mathcal{G}(n)=\exp\bigl[\Delta\xi\mathcal{A}(n)\bigr]= \left [\textstyle\begin{array}{@{}c@{\quad}c@{}} I_{k}+\frac{(\alpha_{n}-1)}{\|\mathbf{f}_{n}\|^{2}}\mathbf{f}_{n} \mathbf {f}_{n}^{\mathrm{T}} & \frac{\beta_{n} \mathbf{f}_{n}}{\|\mathbf{f}_{n}\|} \\ \frac{\beta_{n} \mathbf{f}_{n}^{\mathrm{T}}}{\|\mathbf{f}_{n}\|} & \alpha_{n} \end{array}\displaystyle \right ], $$

(13)

where

$$ \alpha_{n}=\cosh \biggl(\frac{\Delta\xi \|\mathbf{f}_{n}\|}{\|\mathbf{W}_{n}\|} \biggr), \qquad \beta_{n}=\sinh \biggl(\frac {\Delta\xi \|\mathbf{f}_{n}\|}{\|\mathbf{W}_{n}\|} \biggr)\quad \mbox{and}\quad \mathbf{f}_{n}=\mathbf{f}(\xi _{n},\mathbf{W}_{n}). $$

(14)

Substituting $\exp[\Delta\xi\mathcal{A}(n)]$ for $\mathcal{G}(n)$ into equation (12) yields

$$ \mathbf{W}_{n+1}=\mathbf{W}_{n}+ \frac{(\alpha_{n}-1)\mathbf{f}_{n}\cdot\mathbf {W}_{n}+\beta_{n}\|\mathbf{W}_{n}\|\|\mathbf{f}_{n}\|}{\|\mathbf{f}_{n}\| ^{2}}\mathbf{f}_{n} =\mathbf{W}_{n}+ \eta_{n} \mathbf{f}_{n}. $$

(15)

Since $\mathbf{f}_{n}\cdot\mathbf{W}_{n}\geq -\|\mathbf{f}_{n}\|\|\mathbf{W}_{n}\|$ one can prove that

$$ \eta_{n}\geq \biggl[1-\exp \biggl(-\frac{\Delta\xi \|\mathbf{f}_{n}\|}{\|\mathbf{W}_{n}\|} \biggr) \biggr] \frac{\|\mathbf{W}_{n}\| }{\|\mathbf{f}_{n}\|}>0,\quad \forall\Delta\xi>0. $$

(16)

The group properties are preserved for all $\Delta\xi>0$.

2.2 Lie symmetry group preserving scheme

The LSGPS is actually a new combination of Lie symmetries and GPS. By using this procedure first the given PDE reduces to some ODEs by Lie symmetries and then we approximate the solution of reduced ODE by GPS. Generally, we call the combination of Lie symmetries and GPS LSGPS. To discuss LSGPS, let be a PDE as follows:

$$ \Pi u=f\quad \text{in } \Omega\subset\mathbb{R}^{2}, $$

(17)

where Π is a nonlinear operator, and $u=u(t,x)$ is an unknown dependent variable.

Suppose that the spatial (time) derivatives of (17) are discretized by some methods - finite differences, finite elements, finite volumes, or any other method. Then, this semi-discretization generates a system of ordinary differential equations that can be solved by GPS, but some problems may occur during this procedure. Semi-discretization is very sensitive to the choice of the discretization step size Δx (Δt), i.e. many criteria should be considered, e.g. consistency, stability, the Courant-Friedrichs-Levi (CFL) condition, and so on. Thus, if the choice of Δx (Δt) were either too little or too big then either the consistency or the stability of the discretization may be missed and thus the final solution of (17) could not be trusted. It may happen that Δx (Δt) has to be very small, e.g. $\Delta x=0.0001$, in order to achieve a good result with semi-discretization, thus leading to a huge number of ODEs, e.g. $\Delta x=10^{-n}$ means a system of n ODEs, for which the traditional GPS or Lie group shooting method will require a large number of operations and computations.

Instead the benefits of the LSGPS are several, mainly one needs just one ODE, while in the traditional GPS a large number of ODEs are necessary. Also since discretization reduces the accuracy and imposes the error, solutions obtained by LSGPS are more accurate than by GPS, because LSGPS uses the discretization in one dimension, while GPS uses the discretization in two dimensions.

3 Lie group analysis and LSGPS of density-dependent diffusion Nagumo equation

Let us assume that equation (1), with independent variables t, x and dependent variable u, is invariant under one parameter continuous transformations:

$$\begin{aligned}& \breve{t}=t+\epsilon\xi^{1}(t,x,u)+ O\bigl(\epsilon^{2} \bigr), \\& \breve{x}=x+\epsilon\xi^{2}(t,x,u)+ O\bigl(\epsilon^{2} \bigr), \\& \breve{u}=u+\epsilon\phi(t,x,u)+ O\bigl(\epsilon^{2}\bigr), \end{aligned}$$

where ϵ is the group parameter. The associated Lie algebra of infinitesimal symmetries is the set of vector fields of the form

$$ V=\xi^{1}(t,x,u)\frac{\partial}{\partial t}+\xi^{2}(t,x,u) \frac{\partial}{\partial{x}} +\phi(t,x,u)\frac{\partial}{\partial{u}}. $$

(18)

If the above vector field generates a symmetry of equation (1), then

$$ \operatorname{Pr}^{(2)}V(F)\vert_{F=0}=0,\quad F:= \frac{\partial u}{\partial t}-\frac{\partial}{\partial x} \biggl(u^{m}\frac{\partial u}{\partial x} \biggr)-u(1-u) (u-\alpha), $$

(19)

where $\operatorname{Pr}^{(2)}X$ denotes the second prolongation of V and it concludes determining the equations containing an overdetermined system of linear PDEs in $\xi^{1}$, $\xi^{2}$, and ϕ.

These determining equations can easily be integrated to show that the symmetry group of equation (1) is spanned by the vector fields:

$$ V_{1}=\frac{\partial}{\partial t},\qquad V_{2}=\frac{\partial}{\partial x} $$

(20)

for arbitrary m and α,

$$ V_{1}=\frac{\partial}{\partial t}, \qquad V_{2}=\frac{\partial}{\partial x}, \qquad V_{3}=e^{-2t}\frac{\partial}{\partial t}+e^{-2t}u \frac{\partial}{\partial u} $$

(21)

for $\alpha=-1$ and $m=2$. However, it is important that the ambient concentration α should be in $(0,1)$. Thus, the last case $\alpha=-1$ has no physical interpretation and we consider it just from the mathematical viewpoint. Here, we consider two nonzero conjugacy classes of one-dimensional subalgebras as follows:

$$ \mathcal{L}_{1,1}=\langle V_{1}+cV_{2} \rangle, \qquad \mathcal{L}_{2,1}=\langle V_{1}+cV_{3} \rangle. $$

(22)

Below, we list the corresponding similarity variables and similarity solutions as well as the reduced ODEs obtained from the generators of optimal system.

Reduction 1

Using the subalgebra $\mathcal{L}_{1,1}$, we obtain the similarity variables and similarity solutions $u(t,x)=F(\xi)$, $\xi=x-ct$, and the reduced ODE is

$$ \bigl(\bigl(F(\xi)^{m}F'(\xi)\bigr) \bigr)'+cF'(\xi)+F(\xi) \bigl(1-F(\xi) \bigr) \bigl(F( \xi)-\alpha \bigr)=0, $$

(23)

where $c\in\mathbb{R}$ is the wave speed. Solutions of equation (23) are indeed traveling wave solutions of (1), which previously were discussed in the literature [17–21]. The solutions of equation (23) are indeed traveling wave solutions of (1) which previously were discussed in the literature [17–21]. Now, if we solve (23) by GPS, then the obtained results are indeed the solutions of (1) achieved by LSGPS. The natural conditions

$$ \lim_{\xi\rightarrow-\infty}F(\xi)=A,\qquad \lim_{\xi\rightarrow \infty}F( \xi)=B, $$

(24)

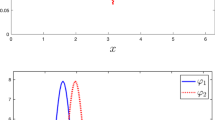
where $A,B\in\{0,1,\alpha\}$ are taken into account for dealing with (23). Also, the initial conditions $F(0)=0.5$ and $F'(0)=\lambda$ ($\lambda\in\mathbb{R}$ and specially $\lambda=0$), which are determined by the application at hand are applied in our computations. As can be seen from the figures of this paper, it tries to achieve the equilibrium $\lim_{\xi\rightarrow +\infty}F(\xi)=\alpha$. To illustrate the behavior of traveling wave solutions with different parameters m, c and α, we provide several numerical plots obtained from GPS. Figures 1 and 2 show the solutions with varying initial conditions $F'(0)$ with respect to $\alpha=0.6$ and $\alpha=0.2$, respectively. Because of the singularity for large values of $\|F'(0)\|$, small values are singled out. Equilibriums $F(\xi)\rightarrow0.6$ as $\xi\rightarrow+\infty$ in Figure 1 and $F(\xi)\rightarrow0.2$ as $\xi\rightarrow+\infty$ in Figure 2 are depicted. Now, in Figures 3-12, we take the pragmatic convection $F'(0)=0$.

Figure 1

Plot of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{c=0.3}$ , $\pmb{\alpha=0.6}$ , $\pmb{F(0)=0.5}$ for varying $\pmb{F'(0)}$ .

Figure 2

Plot of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{c=0.3}$ , $\pmb{\alpha=0.2}$ , $\pmb{F(0)=0.5}$ for varying $\pmb{F'(0)}$ .

Figure 3

Plots of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{\alpha=0.6}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ for varying c .

Traveling waves, by varying wave speeds c, are demonstrated in Figure 3. A high smoothness of the solutions by varying c from 0.1 to 4 is reported. Similar to the two previous figures, by increasing the c, a smooth tending of the solutions to $\alpha=0.2$ is reported in Figure 4.

Figure 4

Plots of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{\alpha=0.2}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ for varying c .

As mentioned in [17], the power m appearing in the nonlinear density dependence serves to smooth out the solutions of the density-dependent diffusion Nagumo equation. Indeed, the oscillations diminish while m is increasing, and Figures 5 and 6 exhibit that there are more oscillations for the standard Nagumo equation ($m=0$) than $m>0$ and monotone solutions for $m\geq2$ are reported.

Figure 5

Plots of $\pmb{F(\xi)}$ when $\pmb{c=0.3}$ , $\pmb{\alpha=0.6}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ for varying m .

Figure 6

Plots of $\pmb{F(\xi)}$ when $\pmb{c=0.3}$ , $\pmb{\alpha=0.2}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ for varying m .

Now, we present the obtained traveling wave solutions for variable density parameter $\alpha\in(0,1)$, with respect to $c=1$ and $c=0.3$. Comparison of Figures 7, 9, and 11 with their related Figures 8, 10, and 12 shows that the solutions with respect to $c=1$ tend directly to α in a more streamlined manner than the solutions with respect to $c=0.3$.

Figure 7

Plots of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=0.3}$ for varying α .

Figure 8

Plots of $\pmb{F(\xi)}$ when $\pmb{m=1}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=1}$ for varying α .

Figure 9

Plots of $\pmb{F(\xi)}$ when $\pmb{m=2}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=0.3}$ for varying α .

Figure 10

Plots of $\pmb{F(\xi)}$ when $\pmb{m=2}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=1}$ for varying α .

Figure 11

Plots of $\pmb{F(\xi)}$ when $\pmb{m=3}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=0.3}$ for varying α .

Figure 12

Plots of $\pmb{F(\xi)}$ when $\pmb{m=3}$ , $\pmb{F(0)=0.5}$ , $\pmb{F'(0)=0}$ , $\pmb{c=1}$ for varying α .

Reduction 2

Using the subalgebra $\mathcal{L}_{2,1}$, we obtain the similarity variables and similarity solutions $u(t,x)=\frac{e^{t}\Psi(\xi)}{\sqrt{e^{2t}+c}}$, $\xi=x$, and the reduced ODE is

$$ \Psi^{2}(\xi)\Psi''(\xi)+2 \Psi(\xi) \bigl(\Psi'(\xi) \bigr)^{2}+\Psi(\xi )- \Psi^{3}(\xi)=0. $$

(25)

Now, we utilize the reduction method [11, 28–32], instead of using the usual method based on invariants. Obtaining the first integrals of ODEs is often sophisticated work, however, using the mentioned reduction method, the first integral of the reduced ODE (25) is easily obtained. Equation (25) can be written as an autonomous system of two ODEs of first order, i.e.:

$$ \left \{ \textstyle\begin{array}{l} w_{1}'= w_{2}, \\ w_{2}'= \frac{w_{1}^{2}-1-2w_{2}^{2}}{w_{1}}, \end{array}\displaystyle \right . $$

(26)

using the obvious change of dependent variables

$$ w_{1}(\xi)=\Psi(\xi),\qquad w_{2}(\xi)=\Psi'( \xi). $$

(27)

It is possible to choose $w_{1}$ as a new independent variable, because (26) is autonomous. In this way, a first-order nonautonomous ODE can be extracted from system (26) as follows:

$$ \frac{dw_{2}}{dw_{1}}=\frac{w_{1}^{2}-1-2w_{2}^{2}}{w_{1}w_{2}}, $$

(28)

of which its integration leads to

$$ w_{2}=\sqrt{\frac{6a_{1}+2w_{1}^{6}-3w_{1}^{4}}{6w_{1}^{4}}}, $$

(29)

with $a_{1}$ an arbitrary constant. Clearly, corresponding first integral of equation (25) is

$$ \bigl(\Psi'(\xi) \bigr)^{2}\Psi^{4}(\xi)- \frac{1}{3}\Psi^{6}(\xi)+\frac {1}{2}\Psi^{4}( \xi)=a_{1}. $$

(30)

Lastly we replace (29) from (26) into the first equation of system (26) from which one concludes to a first-order separable as follows:

$$ w_{1}'=\sqrt{\frac{6a_{1}+2w_{1}^{6}-3w_{1}^{4}}{6w_{1}^{4}}}. $$

(31)

The exact solution of equation (31) can be implicitly expressed by

$$ \int\frac{6w_{1}^{2}}{\sqrt{36a_{1}+12w_{1}^{6}-18w_{1}^{4}}}\, dw_{1}=\xi+a_{2}, $$

(32)

and replacing $w_{1}$ with $\Psi(\xi)$ yields the exact solution of (25). Assuming $a_{1}=0$ yields the following explicit solutions:

$$ \Psi_{\pm}(\xi)=\frac{\sqrt{2}}{4} \biggl( \frac{3+e^{\pm\frac{2(\xi +a_{2})}{\sqrt{3}}}}{e^{\pm\frac{\xi+a_{2}}{\sqrt{3}}}} \biggr), $$

(33)

and therefore

$$ u_{\pm}(t,x)=\frac{\sqrt{2}e^{t}}{4\sqrt{e^{2t}+c}} \biggl(\frac{3+e^{\pm\frac {2(x+a_{2})}{\sqrt{3}}}}{e^{\pm\frac{x+a_{2}}{\sqrt{3}}}} \biggr). $$

(34)

The solution of $u_{+}(t,x)$ in three dimensions is plotted in Figure 13 with respect to $c=a_{2}=1$.

Figure 13

Plot of obtained solution of ( 1 ) from Reduction 2 with respect to $\pmb{m=2}$ and $\pmb{\alpha=-1}$ .

4 Final remarks

In this paper, we considered the density-dependent diffusion Nagumo equation within a new geometric method, LSGPS. Three dimensional Lie algebra and optimal system of Lie algebras related to equation (1) were obtained. After the reduction of this equation by utilizing the Lie symmetries, the traveling wave solutions are first discussed in Reduction 1. Another reduction of the Nagumo equation, by using Lie symmetries and Nucci’s method (Reduction 2), leads to a first integral and two new analytical solutions of equation (1).