Dynamics of a delayed SEIRS-V model on the transmission of worms in a wireless sensor network

Abstract

A delayed SEIRS-V model on the transmission of worms in a wireless sensor network is considered. Choosing delay as a bifurcation parameter, the existence of the Hopf bifurcation of the model is investigated. Furthermore, we use the normal form method and the center manifold theorem to determine the direction of the Hopf bifurcation and the stability of the bifurcated periodic solutions. Finally, some numerical simulations are presented to verify the theoretical results.

1 Introduction

In past several decades, many authors have studied different mathematical models which illustrate the dynamical behavior of the transmission of computer viruses based on the classical epidemic models due to the lots of similarities between biological viruses and computer viruses [1–12]. In [3], Yuan and Chen investigated the behavior of virus propagation in a network by proposing an e-SEIR model. In [7], Mishra and Pandey proposed an SEIRS model to investigate the transmission of worms in a network. As wireless sensor networks are unfolding their vast potential in a plethora of application environments, security still remains one of the most critical challenges yet to be fully addressed [13, 14]. In order to study the attacking behavior of possible worms in a wireless sensor network and considering that there is a basic similarity between the software viruses spread among wireless devices and the transmission of epidemic diseases in a population, Mishra and Keshri [14] proposed the following SEIRS-V model:

$$\{\begin{array}{l}\frac{dS(t)}{dt}=A-\beta S(t)I(t)-(\mu +p)S(t)+\delta R(t)+\eta V(t),\\ \frac{dE(t)}{dt}=\beta S(t)I(t)-(\mu +\alpha )E(t),\\ \frac{dI(t)}{dt}=\alpha E(t)-(\mu +\epsilon +\gamma )I(t),\\ \frac{dR(t)}{dt}=\gamma I(t)-(\mu +\delta )R(t),\\ \frac{dV(t)}{dt}=pS(t)-(\mu +\eta )V(t),\end{array}$$

(1)

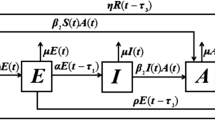
where $S(t)$, $E(t)$, $I(t)$, $R(t)$ and $V(t)$ represent the numbers of sensor nodes at time t in states susceptible, exposed, infectious, recovered and vaccinated, respectively. A is the inclusion of new nodes to the wireless sensor network, β is the transmission coefficient. α, γ, δ, η and p are state transition rates. ε and μ are the crashing rates of the sensor nodes due to the attack of worms and the reason other than the attack of worms, respectively. Mishra and Keshri [14] studied the stability of system (1).

As is known, computer virus models with time delay have been investigated by many authors [15–18]. In [15], Feng et al. investigated a viral infection model in computer networks with time delay due to the temporary immunity period of the recovered computers. In [17], Dong et al. proposed a computer virus model with time delay due to the time that the computers in a network use antivirus software to clean the viruses and investigated the Hopf bifurcation of the model by choosing the delay as a bifurcation parameter. Motivated by the work above, and considering that the sensor nodes need some time to clean the worms in a wireless sensor network by using antivirus software and the recovered and the vaccinated sensor nodes have a temporary immunity period after which they may be infected again because of antivirus software, we incorporate two delays into system (1) and get the following delayed SEIRS-V system on the transmission of worms in a wireless sensor network:

$$\{\begin{array}{l}\frac{dS(t)}{dt}=A-\beta S(t)I(t)-(\mu +p)S(t)+\delta R(t-{\tau }_2)+\eta V(t-{\tau }_2),\\ \frac{dE(t)}{dt}=\beta S(t)I(t)-(\mu +\alpha )E(t),\\ \frac{dI(t)}{dt}=\alpha E(t)-(\mu +\epsilon )I(t)-\gamma I(t-{\tau }_1),\\ \frac{dR(t)}{dt}=\gamma I(t-{\tau }_1)-\mu R(t)-\delta R(t-{\tau }_2),\\ \frac{dV(t)}{dt}=pS(t)-\mu V(t)-\eta V(t-{\tau }_2),\end{array}$$

(2)

where ${\tau }_1$ is the time that the sensor nodes need to clean the worms by using antivirus software and ${\tau }_2$ is the temporary immunity period after which they may be infected again because of antivirus software. For the convenience of analysis, we assume that ${\tau }_1={\tau }_2$. Let ${\tau }_1={\tau }_2$, then system (2) becomes

$$\{\begin{array}{l}\frac{dS(t)}{dt}=A-\beta S(t)I(t)-(\mu +p)S(t)+\delta R(t-\tau )+\eta V(t-\tau ),\\ \frac{dE(t)}{dt}=\beta S(t)I(t)-(\mu +\alpha )E(t),\\ \frac{dI(t)}{dt}=\alpha E(t)-(\mu +\epsilon )I(t)-\gamma I(t-\tau ),\\ \frac{dR(t)}{dt}=\gamma I(t-\tau )-\mu R(t)-\delta R(t-\tau ),\\ \frac{dV(t)}{dt}=pS(t)-\mu V(t)-\eta V(t-\tau ).\end{array}$$

(3)

This paper is organized as follows. In Section 2, we investigate local stability of the positive equilibrium and obtain sufficient conditions for the existence of local Hopf bifurcation. In Section 3, we determine direction and stability of the Hopf bifurcation by using the normal form theory and the center manifold theorem. In order to testify the theoretical analysis, a numerical example is presented in Section 4. Section 5 concludes the paper and indicates future directions for research.

2 Local stability of positive equilibrium and existence of local Hopf bifurcation

It is not difficult to verify that if $R_0=\frac{\alpha \beta A(\mu +\eta )+p\eta (\mu +\alpha )(\mu +\epsilon +\gamma )}{(\mu +p)(\mu +\alpha )(\mu +\eta )(\mu +\epsilon +\gamma )}>1$, then system (3) has the unique positive equilibrium $D_{\ast }(S_{\ast },E_{\ast },I_{\ast },R_{\ast },V_{\ast })$, where

$$\begin{array}{c}{S}^{\ast }=\frac{(\mu +\alpha )(\mu +\epsilon +\gamma )}{\alpha \beta },E_{\ast }=\frac{\mu +\epsilon +\gamma }{\alpha }{I}_{\ast },\hfill \\ R_{\ast }=\frac{\gamma }{\mu +\delta }{I}_{\ast },V_{=}\frac{p(\mu +\alpha )(\mu +\epsilon +\gamma )}{\alpha \beta (\mu +\eta )},\hfill \\ I_{\ast }=\frac{\alpha \beta A(\mu +\delta )(\mu +\eta )+p\eta (\mu +\alpha )(\mu +\delta )(\mu +\epsilon +\gamma )-(\mu +p)(\mu +\alpha )(\mu +\delta )(\mu +\eta )(\mu +\epsilon +\gamma )}{\beta (\mu +\alpha )(\mu +\delta )(\mu +\eta )(\mu +\epsilon +\gamma )-\alpha \beta \delta \gamma (\mu +\eta )}.\hfill \end{array}$$

The Jacobian matrix of system (3) about the positive equilibrium $D_{\ast }$ is

$$J(D_{\ast })=\left(\begin{array}{ccccc}\lambda -a_{11}& 0& -a_{13}& -b_{14}{e}^{-\lambda \tau }& -b_{15}{e}^{-\lambda \tau }\\ -a_{21}& \lambda -a_{22}& -a_{23}& 0& 0\\ 0& -a_{32}& \lambda -a_{33}-b_{33}{e}^{-\lambda \tau }& 0& 0\\ 0& 0& -b_{43}{e}^{-\lambda \tau }& \lambda -a_{44}-b_{44}{e}^{-\lambda \tau }& 0\\ -a_{51}& 0& 0& 0& \lambda -a_{55}-b_{55}{e}^{-\lambda \tau }\end{array}\right),$$

where

$$\begin{array}{c}{a}_{11}=-(\beta I_{\ast }+\mu +p),a_{13}=-\beta S_{\ast },a_{21}=\beta I_{\ast },\hfill \\ a_{22}=-(\mu +\alpha ),a_{23}=\beta S_{\ast },a_{32}=\alpha ,\hfill \\ a_{33}=-(\mu +\epsilon ),a_{44}=-\mu ,a_{51}=p,a_{55}=-\mu ,\hfill \\ b_{14}=\delta ,b_{15}=\eta ,b_{33}=-\gamma ,\hfill \\ b_{43}=\gamma ,b_{44}=-\delta ,b_{55}=-\eta .\hfill \end{array}$$

Thus, the characteristic equation of system (3) at $D^{\ast }$ is

$$\begin{array}{c}{\lambda }^5+A_4{\lambda }^4+A_3{\lambda }^3+A_2{\lambda }^2+A_1\lambda +A_0+(B_4{\lambda }^4+B_3{\lambda }^3+B_2{\lambda }^2+B_1\lambda +B_0)e^{-\lambda \tau }\hfill \\ +(C_3{\lambda }^3+C_2{\lambda }^2+C_1\lambda +C_0)e^{-2\lambda \tau }+(D_2{\lambda }^2+D_1\lambda +D_0)e^{-3\lambda \tau }=0,\hfill \end{array}$$

(4)

where

$$\begin{array}{c}{A}_0=-a_{44}{a}_{55}(a_{11}{a}_{22}{a}_{33}+a_{13}{a}_{21}{a}_{32}),\hfill \\ A_1=a_{33}{a}_{44}{a}_{55}(a_{11}+a_{22})+a_{11}{a}_{22}{a}_{55}(a_{33}+a_{44})\hfill \\ \phantom{A_1=}+a_{11}{a}_{22}{a}_{33}{a}_{44}+a_{13}{a}_{21}{a}_{32}(a_{44}+a_{55}),\hfill \\ A_2=-a_{55}(a_{11}{a}_{22}+a_{33}{a}_{44}+(a_{11}+a_{22})(a_{33}+a_{44}))\hfill \\ \phantom{A_2=}-a_{13}{a}_{21}{a}_{32}-a_{11}{a}_{22}(a_{33}+a_{44})-a_{33}{a}_{44}(a_{11}+a_{22}),\hfill \\ A_3=a_{11}{a}_{22}+a_{33}{a}_{44}+(a_{11}+a_{22})(a_{33}+a_{44})\hfill \\ \phantom{A_3=}+a_{55}(a_{11}+a_{22}+a_{33}+a_{44}),\hfill \\ A_4=-(a_{11}+a_{22}+a_{33}+a_{44}+a_{55}),\hfill \\ B_0=a_{44}{a}_{51}{b}_{15}(a_{22}{a}_{33}-a_{23}{a}_{32})-a_{13}{a}_{21}{a}_{32}(a_{44}{b}_{55}+a_{55}{b}_{44})\hfill \\ \phantom{B_0=}-a_{11}{a}_{22}(a_{33}{a}_{44}{b}_{55}+a_{44}{a}_{55}{b}_{33}+a_{33}{a}_{55}{b}_{44}),\hfill \\ B_1=b_{33}(a_{11}{a}_{22}(a_{44}+a_{55})+a_{44}{a}_{55}(a_{11}+a_{22}))+a_{13}{a}_{21}{a}_{32}(b_{44}+b_{55})\hfill \\ \phantom{B_1=}+b_{44}(a_{11}{a}_{22}(a_{33}+a_{55})+a_{33}{a}_{55}(a_{11}+a_{22}))\hfill \\ \phantom{B_1=}+b_{55}(a_{11}{a}_{22}(a_{33}+a_{44})+a_{33}{a}_{44}(a_{11}+a_{22}))\hfill \\ \phantom{B_1=}+a_{51}{b}_{15}(a_{23}{a}_{32}-a_{22}{a}_{33}-a_{22}{a}_{44}-a_{33}{a}_{44}),\hfill \\ B_2=a_{51}{b}_{15}(a_{22}+a_{33}+a_{44})-b_{33}(a_{11}{a}_{22}+a_{44}{a}_{55}+(a_{11}+a_{22})(a_{44}+a_{55}))\hfill \\ \phantom{B_2=}-b_{44}(a_{11}{a}_{22}+a_{33}{a}_{55}+(a_{11}+a_{22})(a_{33}+a_{55}))\hfill \\ \phantom{B_2=}-b_{55}(a_{11}{a}_{22}+a_{33}{a}_{44}+(a_{11}+a_{22})(a_{33}+a_{44})),\hfill \\ B_3=b_{33}(a_{11}+a_{22}+a_{44}+a_{55})+b_{44}(a_{11}+a_{22}+a_{33}+a_{55})\hfill \\ \phantom{B_3=}+b_{55}(a_{11}+a_{22}+a_{33}+a_{44})-a_{51}{b}_{15},\hfill \\ B_4=-(b_{33}+b_{44}+b_{55}),C_3=b_{33}{b}_{44}+b_{33}{b}_{55}+b_{44}{b}_{55},\hfill \\ C_2=a_{51}{b}_{15}(b_{33}+b_{44})-b_{33}{b}_{44}(a_{11}+a_{22}+a_{33})-b_{33}{b}_{55}(a_{11}+a_{22}+a_{44})\hfill \\ \phantom{C_2=}-b_{44}{b}_{55}(a_{11}+a_{22}+a_{33}),\hfill \\ C_1=b_{44}{b}_{55}(a_{11}{a}_{22}+a_{33}(a_{11}+a_{22}))-a_{21}{a}_{32}{b}_{14}{b}_{43}+b_{33}{b}_{44}(a_{11}{a}_{22}+a_{55}(a_{11}+a_{22}))\hfill \\ \phantom{C_1=}+b_{33}{b}_{55}(a_{11}{a}_{22}+a_{44}(a_{11}+a_{22}))-a_{51}{b}_{15}(b_{33}(a_{22}+a_{44})+b_{44}(a_{22}+a_{33})),\hfill \\ C_0=a_{51}{b}_{15}(a_{22}{a}_{44}{b}_{33}+a_{22}{a}_{33}{b}_{44}-a_{23}{a}_{32}{b}_{44})+a_{21}{a}_{32}(a_{55}{b}_{14}{b}_{43}-a_{13}{b}_{44}{b}_{55})\hfill \\ \phantom{C_0=}-a_{11}{a}_{22}(a_{55}{b}_{33}{b}_{44}+a_{44}{b}_{33}{b}_{55}+a_{33}{b}_{44}{b}_{55}),\hfill \\ D_2=-b_{33}{b}_{44}{b}_{55},D_1=b_{33}{b}_{44}{b}_{55}(a_{11}+a_{22})-a_{51}{b}_{15}{b}_{33}{b}_{44},\hfill \\ D_0=a_{21}{a}_{32}{b}_{14}{b}_{43}{b}_{55}+a_{22}{a}_{51}{b}_{15}{b}_{33}{b}_{44}-a_{11}{a}_{22}{a}_{33}{b}_{44}{b}_{55}.\hfill \end{array}$$

Multiplying $e^{\lambda \tau }$ on both sides of Eq. (4), it is easy to obtain

$$\begin{array}{c}{B}_4{\lambda }^4+B_3{\lambda }^3+B_2{\lambda }^2+B_1\lambda +B_0+({\lambda }^5+A_4{\lambda }^4+A_3{\lambda }^3+A_2{\lambda }^2+A_1\lambda +A_0)e^{\lambda \tau }\hfill \\ +(C_3{\lambda }^3+C_2{\lambda }^2+C_1\lambda +C_0)e^{-\lambda \tau }+(D_2{\lambda }^2+D_1\lambda +D_0)e^{-2\lambda \tau }=0.\hfill \end{array}$$

(5)

When $\tau =0$, Eq. (5) reduces to

$${\lambda }^5+m_4{\lambda }^4+m_3{\lambda }^3+m_2{\lambda }^2+m_1\lambda +m_0=0,$$

(6)

where

$$\begin{array}{c}{m}_0=A_0+B_0+C_0+D_0,m_1=A_1+B_1+C_1+D_1,\hfill \\ m_2=A_2+B_2+C_2+D_2,m_3=A_3+B_3+C_3,\hfill \\ m_4=A_4+B_4=p+\alpha +\delta +\epsilon +\gamma +\eta +\beta I_{\ast }+5\mu .\hfill \end{array}$$

Obviously, $m_4>0$. By the Routh-Hurwitz criterion, sufficient conditions for all roots of Eq. (6) to have a negative real part are given in the following form:

$$D_2=det\left(\begin{array}{cc}{m}_4& 1\\ m_2& m_3\end{array}\right)>0,$$

(7)

$$D_3=det\left(\begin{array}{ccc}{m}_4& 1& 0\\ m_2& m_3& m_4\\ 0& m_1& m_2\end{array}\right)>0,$$

(8)

$$D_4=det\left(\begin{array}{cccc}{m}_4& 1& 0& 0\\ m_2& m_3& m_4& 1\\ m_0& m_1& m_2& m_3\\ 0& 0& m_0& m_1\end{array}\right)>0,$$

(9)

$$D_5=det\left(\begin{array}{ccccc}{m}_4& 1& 0& 0& 0\\ m_2& m_3& m_4& 1& 0\\ m_0& m_1& m_2& m_3& m_4\\ 0& 0& m_0& m_1& m_2\\ 0& 0& 0& 0& m_0\end{array}\right)>0.$$

(10)

Thus, if condition (H₁) Eq. (7)-Eq. (10) holds, $D_{\ast }$ is locally asymptotically stable in the absence of delay.

For $\tau >0$, let $\lambda =i\omega$ ($\omega >0$) be the root of Eq. (5). Then we can get

$$\{\begin{array}{l}{g}_{1}cos\tau \omega -g_{2}sin\tau \omega +g_3=h_{1}sin2\tau \omega +h_{2}cos2\tau \omega ,\\ g_{4}sin\tau \omega +g_{5}cos\tau \omega +g_6=h_{1}cos2\tau \omega -h_{2}sin2\tau \omega ,\end{array}$$

where

$$\begin{array}{c}{g}_1=A_4{\omega }^4-(A_2+C_2){\omega }^2+A_0+C_0,\hfill \\ g_2={\omega }^5-(A_3-C_3){\omega }^3+(A_1-C_1)\omega ,\hfill \\ g_3=B_4{\omega }^4-B_2{\omega }^2+B_0,\hfill \\ g_4=A_4{\omega }^4-(A_2-C_2){\omega }^2+A_0-C_0,\hfill \\ g_5={\omega }^5-(A_3+C_3){\omega }^3+(A_1+C_1)\omega ,\hfill \\ g_6=B_1\omega -B_3{\omega }^3,h_1=-D_1\omega ,h_2=D_2{\omega }^2-D_0.\hfill \end{array}$$

Then we can get

$${(g_{1}cos\tau \omega -g_{2}sin\tau \omega +g_3)}^2+{(g_{4}sin\tau \omega +g_{5}cos\tau \omega +g_6)}^2=h_1^2+h_2^2.$$

(11)

According to $sin\tau \omega =\pm \sqrt{1-{cos}^2\tau \omega }$, we consider the following two cases.

Case 1. $sin\tau \omega =\sqrt{1-{cos}^2\tau \omega }$, then Eq. (11) becomes

$$\begin{array}{c}{(g_{1}cos\tau \omega -g_2\sqrt{1-{cos}^2\tau \omega }+g_3)}^2+{(g_4\sqrt{1-{cos}^2\tau \omega }+g_{5}cos\tau \omega +g_6)}^2\hfill \\ =h_1^2+h_2^2,\hfill \end{array}$$

(12)

which is equivalent to

$$e_4{cos}^4\tau \omega +e_3{cos}^3\tau \omega +e_2{cos}^2\tau \omega +e_{1}cos\tau \omega +e_0=0,$$

(13)

where

$$\begin{array}{c}{e}_0={(g_2^2+g_3^2+g_4^2+g_6^2-h_1^2-h_2^2)}^2-4{(g_4{g}_6-g_2{g}_3)}^2,\hfill \\ e_1=4{(g_2^2+g_3^2+g_4^2+g_6^2-h_1^2-h_2^2)}^2(g_1{g}_3+g_5{g}_6)\hfill \\ \phantom{e_1=}-8(g_4{g}_5-g_1{g}_2)(g_4{g}_6-g_2{g}_3),\hfill \\ e_2=4{(g_1{g}_3+g_5{g}_6)}^2-4{(g_4{g}_5-g_1{g}_2)}^2+4{(g_4{g}_6-g_2{g}_3)}^2\hfill \\ \phantom{e_2=}+2(g_1^2+g_5^2-g_2^2-g_4^2)(g_2^2+g_3^2+g_4^2+g_6^2-h_1^2-h_2^2),\hfill \\ e_3=(g_1{g}_3+g_5{g}_6)(g_1^2+g_5^2-g_2^2-g_4^2)+8(g_4{g}_5-g_1{g}_2)(g_4{g}_6-g_2{g}_3),\hfill \\ e_4={(g_1^2+g_5^2-g_2^2-g_4^2)}^2+4{(g_4{g}_5-g_1{g}_2)}^2.\hfill \end{array}$$

Let $cos\tau \omega =r$ and denote

$$f(r)=r^4+\frac{e_3}{e_4}{r}^3+\frac{e_2}{e_4}{r}^2+\frac{e_1}{e_4}r+\frac{e_0}{e_4}.$$

Thus,

$$f^{\prime }(r)=4r^3+\frac{3e_3}{e_4}{r}^2+\frac{2e_2}{e_4}r+\frac{e_1}{e_4}.$$

Set

$$4r^3+\frac{3e_3}{e_4}{r}^2+\frac{2e_2}{e_4}r+\frac{e_1}{e_4}=0.$$

(14)

Let $y=r+\frac{e_3}{4e_4}$. Then Eq. (14) becomes

$$y^3+{\gamma }_{1}y+{\gamma }_0=0,$$

where

$${\gamma }_1=\frac{e_1}{2e_4}-\frac{3e_3^2}{16e_4^2},{\gamma }_0=\frac{e_3^3}{32e_4^3}-\frac{e_2{e}_3}{8e_4^2}+\frac{e_1}{e_4}.$$

Define

$$\begin{array}{c}{\beta }_1={\left(\frac{{\gamma }_0}{2}\right)}^2+{\left(\frac{{\gamma }_1}{3}\right)}^3,{\beta }_2=\frac{-1+\sqrt{3}i}{2},\hfill \\ y_1=\sqrt[3]{-\frac{{\gamma }_0}{2}+\sqrt{{\beta }_1}}+\sqrt[3]{-\frac{{\gamma }_0}{2}-\sqrt{{\beta }_1}},\hfill \\ y_2=\sqrt[3]{-\frac{{\gamma }_0}{2}+\sqrt{{\beta }_1}}{\beta }_2+\sqrt[3]{-\frac{{\gamma }_0}{2}-\sqrt{{\beta }_1}}{\beta }_2^2,\hfill \\ y_3=\sqrt[3]{-\frac{{\gamma }_0}{2}+\sqrt{{\beta }_1}}{\beta }_2^2+\sqrt[3]{-\frac{{\gamma }_0}{2}-\sqrt{{\beta }_1}}{\beta }_2.\hfill \end{array}$$

Then we can get the expression of $cos\tau \omega$, and we denote $f_1(\omega )=cos\tau \omega$. Substitute $f_1(\omega )=cos\tau \omega$ into Eq. (11), we can get the expression of $sin\tau \omega$, and we denote $f_2(\omega )=sin\tau \omega$. Thus, a function with respect to ω can be established by

$$f_1^2(\omega )+f_2^2(\omega )=1.$$

(15)

If all the parameters of system (3) are given, we can calculate the roots of Eq. (15) by Matlab software package. Therefore, we make the following assumption in order to give the main results in this paper.

(H₂) Eq. (15) has finite positive roots which are denoted by ${\omega }_1,{\omega }_2,\dots ,{\omega }_k$, respectively. For every fixed ${\omega }_i$ ($1\le i\le k$), the corresponding critical value of time delay is

$${\tau }_i^{(j)}=\frac{1}{{\omega }_i}arccos{f}_1({\omega }_i)+\frac{2j\pi }{{\omega }_i},i=1,2,\dots ,k,j=0,1,2,\dots .$$

Case 2. $sin\tau \omega =-\sqrt{1-{cos}^2\tau \omega }$, then Eq. (11) becomes

$$\begin{array}{c}{(g_{1}cos\tau \omega +g_2\sqrt{1-{cos}^2\tau \omega }+g_3)}^2+{(g_{5}cos\tau \omega -g_4\sqrt{1-{cos}^2\tau \omega }+g_6)}^2\hfill \\ =h_1^2+h_2^2.\hfill \end{array}$$

(16)

Similar as in Case 1, we can get the expression of $cos\tau \omega$ denoted as $f_{1\ast }(\omega )$ and the expression of $sin\tau \omega$ denoted by $f_{2\ast }(\omega )$, and further we get a function with respect to ω that can be established by

$$f_{1\ast }^2(\omega )+f_{2\ast }^2(\omega )=1.$$

(17)

We assume that Eq. (17) has finite positive roots denoted by ${\omega }_1^{\prime },{\omega }_2^{\prime },\dots ,{\omega }_k^{\prime }$, respectively. Then we can get the critical value of time delay corresponding to every fixed positive root ${\omega }_i^{\prime }$ of Eq. (17):

$${\tau }_i^{\prime (j)}=\frac{1}{{\omega }_i^{\prime }}arccos{f}_{1\ast }\left({\omega }_i^{\prime }\right)+\frac{2j\pi }{{\omega }_i^{\prime }},i=1,2,\dots ,k,j=0,1,2,\dots .$$

Let

$${\tau }_0=min\{{\tau }_i^{(0)},{\tau }_i^{\prime (0)}\},i=1,2,\dots ,k.$$

Then, when $\tau ={\tau }_0$, Eq. (5) has a pair of purely imaginary roots $\pm i{\omega }_0$.

Next, we verify the transversality condition. Taking the derivative of λ with respect to τ in Eq. (5), it is easy to obtain

$${\left[\frac{d\lambda }{d\tau }\right]}^{-1}=\frac{g_1(\lambda )+g_2(\lambda )e^{\lambda \tau }+g_3(\lambda )e^{-\lambda \tau }+g_4(\lambda )e^{-2\lambda \tau }}{h_1(\lambda )-h_2(\lambda )e^{\lambda \tau }}-\frac{\tau }{\lambda },$$

with

$$\begin{array}{c}{g}_1(\lambda )=4B_4{\lambda }^3+3B_3{\lambda }^2+2B_2\lambda +B_1,\hfill \\ g_2(\lambda )=5{\lambda }^4+4A_4{\lambda }^3+3A_3{\lambda }^2+2A_2\lambda +A_1,\hfill \\ g_3(\lambda )=3C_3{\lambda }^2+2C_2\lambda +C_1,\hfill \\ g_4(\lambda )=2D_2\lambda +D_1,\hfill \\ h_1(\lambda )=C_3{\lambda }^4+(C_2+2D_2){\lambda }^3+(C_1+2D_1){\lambda }^2+(C_0+2D_0)\lambda ,\hfill \\ h_2(\lambda )={\lambda }^6+A_4{\lambda }^5+A_3{\lambda }^4+A_2{\lambda }^3+A_1{\lambda }^2+A_0\lambda .\hfill \end{array}$$

Thus,

$${\left[\frac{d\lambda }{d\tau }\right]}_{\lambda =i{\omega }_0}^{-1}=\frac{P_R+P_{I}i}{Q_R+Q_{I}i},$$

where

$$\begin{array}{c}{P}_R=(5{\omega }_0^4-(3A_3+3C_3){\omega }_0^2+A_1+C_1)cos{\tau }_0{\omega }_0\hfill \\ \phantom{P_R=}+(4A_4{\omega }_0^3+(2C_2-2A_2){\omega }_0)sin{\tau }_0{\omega }_0\hfill \\ \phantom{P_R=}+D_{1}cos2{\tau }_0{\omega }_0+2D_2{\omega }_{0}sin2{\tau }_0{\omega }_0+B_1-3B_3{\omega }_0^2,\hfill \\ P_I=(5{\omega }_0^4-(3A_3-3C_3){\omega }_0^2+A_1+C_1)sin{\tau }_0{\omega }_0\hfill \\ \phantom{P_I=}-(4A_4{\omega }_0^3-(2C_2+2A_2){\omega }_0)cos{\tau }_0{\omega }_0\hfill \\ \phantom{P_I=}-D_{1}sin2{\tau }_0{\omega }_0+2D_2{\omega }_{0}cos2{\tau }_0{\omega }_0+2B_2{\omega }_0-4B_4{\omega }_0^3,\hfill \\ Q_R=({\omega }_0^6-A_3{\omega }_0^4+A_1{\omega }_0^2)cos{\tau }_0{\omega }_0+(A_4{\omega }_0^5-A_2{\omega }_0^3+A_0{\omega }_0)sin{\tau }_0{\omega }_0\hfill \\ \phantom{Q_R=}+C_3{\omega }_0^4-(C_1+2D_1){\omega }_0^2,\hfill \\ P_I=({\omega }_0^6-A_3{\omega }_0^4+A_1{\omega }_0^2)sin{\tau }_0{\omega }_0-(A_4{\omega }_0^5-A_2{\omega }_0^3+A_0{\omega }_0)cos{\tau }_0{\omega }_0\hfill \\ \phantom{P_I=}+(C_0+2D_0){\omega }_0-(C_2+2D_2){\omega }_0^3.\hfill \end{array}$$

Obviously, if condition (H₃) $P_R{Q}_R+P_I{Q}_I\ne 0$ holds, then $Re{[\frac{d\lambda }{d\tau }]}_{\lambda =i{\omega }_0}^{-1}\ne 0$. Therefore, by the Hopf bifurcation theorem in [18], we have the following results.

Theorem 1 For system (3), if conditions (H₁)-(H₃) hold, then the positive equilibrium $D^{\ast }(S_{\ast },E_{\ast },I_{\ast },R_{\ast },V_{\ast })$ of system (3) is asymptotically stable for $\tau \in [0,{\tau }_0)$, and system (3) undergoes a Hopf bifurcation at the positive equilibrium $D^{\ast }(S_{\ast },E_{\ast },I_{\ast },R_{\ast },V_{\ast })$ when $\tau ={\tau }_0$.

3 Direction and stability of the Hopf bifurcation

Let $\tau =\tau +\mu$, $\mu \in R$ so that $\mu =0$ is the Hopf bifurcation value of system (2) and normalize the time delay by $t\to (t/\tau )$. Let $u_1(t)=S(t)-S_{\ast }$, $u_2(t)=E(t)-E_{\ast }$, $u_3(t)=I(t)-I_{\ast }$, $u_4(t)=R(t)-R_{\ast }$, $u_5(t)=V(t)-V_{\ast }$, then system (3) can be transformed into the following form:

$$\dot{u}(t)=L_{\mu }{u}_t+F(\mu ,u_t),$$

(18)

where $u_t={(u_1(t),u_2(t),u_3(t),u_4(t),u_5(t))}^T\in C=C([-1,0],R^5)$,

$$L_{\mu }\varphi =({\tau }_0+\mu )(A^{\prime }\varphi (0)+B^{\prime }\varphi (-1))$$

and

$$F(\mu ,\varphi )=({\tau }_0+\mu )\left(\begin{array}{c}-\beta {\varphi }_1(0){\varphi }_3(0)\\ \beta {\varphi }_1(0){\varphi }_3(0)\\ 0\\ 0\\ 0\end{array}\right),$$

where

$$\begin{array}{c}{A}^{\prime }=\left(\begin{array}{ccccc}{a}_{11}& 0& a_{13}& 0& 0\\ a_{21}& a_{22}& a_{23}& 0& 0\\ 0& a_{32}& a_{33}& 0& 0\\ 0& 0& 0& a_{44}& 0\\ a_{51}& 0& 0& 0& a_{55}\end{array}\right),\hfill \\ B^{\prime }=\left(\begin{array}{ccccc}0& 0& 0& b_{14}& b_{15}\\ 0& 0& 0& 0& 0\\ 0& 0& b_{33}& 0& 0\\ 0& 0& b_{43}& b_{44}& 0\\ 0& 0& 0& 0& b_{55}\end{array}\right).\hfill \end{array}$$

By the Riesz representation theorem, there exists a $5\times 5$ matrix function $\eta (\theta ,\mu ):[-1,0]\to R^{5\times 5}$ whose elements are of bounded variation such that

$$L_{\mu }\varphi ={\int }_{-1}^{0}d\eta (\theta ,\mu )\varphi (\theta ),\varphi \in C.$$

In fact, we choose

$$\eta (\theta ,\mu )=({\tau }_0+\mu )(A^{\prime }\delta (\theta )+B^{\prime }\delta (\theta +1)),$$

where δ is the Dirac delta function.

For $\varphi \in C([-1,0],R^5)$, we define

$$A(\mu )\varphi =\{\begin{array}{ll}\frac{d\varphi (\theta )}{d\theta },& -1\le \theta <0,\\ {\int }_{-1}^{0}d\eta (\theta ,\mu )\varphi (\theta ),& \theta =0\end{array}$$

and

$$R(\mu )\varphi =\{\begin{array}{ll}0,& -1\le \theta <0,\\ F(\mu ,\varphi ),& \theta =0.\end{array}$$

Then system (18) is equivalent to the following operator equation:

$$\dot{u}(t)=A(\mu )u_t+R(\mu )u_t.$$

The adjoint operator $A^{\ast }$ of A is defined by

$$A^{\ast }(\phi )=\{\begin{array}{ll}-\frac{d\phi (s)}{ds},& 0<s\le 1,\\ {\int }_{-1}^{0}d{\eta }^T(s,0)\phi (-s),& s=0,\end{array}$$

associated with a bilinear form

$$〈\phi (s),\varphi (\theta )〉=\overline{\phi }(0)\varphi (0)-{\int }_{\theta =-1}^0{\int }_{\xi =0}^{\theta }\overline{\phi }(\xi -\theta )d\eta (\theta )\varphi (\xi )d\xi ,$$

(19)

where $\eta (\theta )=\eta (\theta ,0)$.

Let $q(\theta )={(1,q_2,q_3,q_4,q_5)}^T{e}^{i{\omega }_0{\tau }_0\theta }$ be the eigenvector of $A(0)$ corresponding to $+i{\omega }_0{\tau }_0$ and $q^{\ast }(s)=D(1,q_2^{\ast },q_3^{\ast },q_4^{\ast },q_5^{\ast })e^{i{\omega }_0{\tau }_{0}s}$ be the eigenvector of $A^{\ast }(0)$ corresponding to $-i{\omega }_0{\tau }_0$. From the definition of $A(0)$ and $A^{\ast }(0)$ and by a simple computation, we obtain

$$\begin{array}{c}{q}_2=\frac{i{\omega }_0-a_{33}-b_{33}{e}^{-i{\tau }_0{\omega }_0}}{a_{32}}{q}_3,\hfill \\ q_3=\frac{1}{a_{13}}(i{\omega }_0-a_{11}-\frac{b_{14}{b}_{33}{e}^{-i{\tau }_0{\omega }_0}}{i{\omega }_0-a_{44}-b_{44}{e}^{-i{\tau }_0{\omega }_0}}-\frac{a_{51}{b}_{15}{e}^{-i{\tau }_0{\omega }_0}}{i{\omega }_0-a_{55}-b_{55}{e}^{-i{\tau }_0{\omega }_0}}),\hfill \\ q_4=\frac{b_{43}{e}^{-i{\tau }_0{\omega }_0}}{i{\omega }_0-a_{44}-b_{44}{e}^{-i{\tau }_0{\omega }_0}}{q}_3,q_5=\frac{a_{51}}{i{\omega }_0-a_{55}-b_{55}{e}^{-i{\tau }_0{\omega }_0}},\hfill \\ q_2^{\ast }=-\frac{i{\omega }_0+a_{11}}{a_{21}}+\frac{a_{51}{b}_{15}{e}^{i{\tau }_0{\omega }_0}}{a_{21}(i{\omega }_0+a_{55}+b_{55}{e}^{i{\tau }_0{\omega }_0})},\hfill \\ q_3^{\ast }=\frac{(i{\omega }_0+a_{11})(i{\omega }_0+a_{22})}{a_{21}{a}_{32}}-\frac{a_{51}{b}_{15}(i{\omega }_0+a_{22})e^{i{\tau }_0{\omega }_0}}{a_{21}{a}_{32}(i{\omega }_0+a_{55}+b_{55}{e}^{i{\tau }_0{\omega }_0})},\hfill \\ q_4^{\ast }=-\frac{b_{14}{e}^{i{\tau }_0{\omega }_0}}{i{\omega }_0+a_{44}+b_{44}{e}^{i{\tau }_0{\omega }_0}},q_5^{\ast }=-\frac{b_{15}{e}^{i{\tau }_0{\omega }_0}}{i{\omega }_0+a_{55}+b_{55}{e}^{i{\tau }_0{\omega }_0}}.\hfill \end{array}$$

From Eq. (19), we have

$$\begin{array}{rcl}〈q^{\ast }(s),q(\theta )〉& =& \overline{D}[1+q_2{\overline{q}}_2^{\ast }+q_3{\overline{q}}_3^{\ast }+q_4{\overline{q}}_4^{\ast }+q_5{\overline{q}}_5^{\ast }+{\tau }_0{e}^{-i{\tau }_0{\omega }_0}(q_3(b_{33}{\overline{q}}_3^{\ast }+b_{43}{\overline{q}}_4^{\ast })\\ +q_4(b_{14}+b_{44}{\overline{q}}_4^{\ast })+q_5(b_{15}+b_{55}{\overline{q}}_5^{\ast })\left)\right].\end{array}$$

Then we choose

$$\begin{array}{rcl}\overline{D}& =& [1+q_2{\overline{q}}_2^{\ast }+q_3{\overline{q}}_3^{\ast }+q_4{\overline{q}}_4^{\ast }+q_5{\overline{q}}_5^{\ast }+{\tau }_0{e}^{-i{\tau }_0{\omega }_0}(q_3(b_{33}{\overline{q}}_3^{\ast }+b_{43}{\overline{q}}_4^{\ast })\\ {+q_4(b_{14}+b_{44}{\overline{q}}_4^{\ast })+q_5(b_{15}+b_{55}{\overline{q}}_5^{\ast }))]}^{-1}\end{array}$$

such that $〈q^{\ast },q〉=1$, $〈q^{\ast },\overline{q}〉=0$.

Next, we can obtain the coefficients which will be used to determine the properties of the Hopf bifurcation by using a computation process similar as in [19]:

$$\begin{array}{c}{g}_{20}=2\beta {\tau }_0\overline{D}{q}_3({\overline{q}}_2^{\ast }-1),\hfill \\ g_{11}=\beta {\tau }_0\overline{D}(q_3+{\overline{q}}_3)({\overline{q}}_2^{\ast }-1),\hfill \\ g_{02}=2\beta {\tau }_0\overline{D}{\overline{q}}_3({\overline{q}}_2^{\ast }-1),\hfill \\ g_{21}=2\beta {\tau }_0\overline{D}({\overline{q}}_2^{\ast }-1)(W_{11}^{(1)}(0)q_3+\frac{1}{2}{W}_{20}^{(1)}(0){\overline{q}}_3+W_{11}^{(3)}(0)+\frac{1}{2}{W}_{20}^{(3)}(0)),\hfill \end{array}$$

with

$$\begin{array}{c}{W}_{20}(\theta )=\frac{i{g}_{20}q(0)}{{\tau }_0{\omega }_0}{e}^{i{\tau }_0{\omega }_0\theta }+\frac{i{\overline{g}}_{02}\overline{q}(0)}{3{\tau }_0{\omega }_0}{e}^{-i{\tau }_0{\omega }_0\theta }+E_1{e}^{2i{\tau }_0{\omega }_0\theta },\hfill \\ W_{11}(\theta )=-\frac{i{g}_{11}q(0)}{{\tau }_0{\omega }_0}{e}^{i{\tau }_0{\omega }_0\theta }+\frac{i{\overline{g}}_{11}\overline{q}(0)}{{\tau }_0{\omega }_0}{e}^{-i{\tau }_0{\omega }_0\theta }+E_2,\hfill \end{array}$$

where $E_1$ and $E_2$ can be determined by the following equations respectively:

$$\begin{array}{c}{E}_1=2{\left(\begin{array}{ccccc}2i{\omega }_0-a_{11}& 0& -a_{13}& -b_{14}{e}^{-2i{\tau }_0{\omega }_0}& -b_{15}{e}^{-2i{\tau }_0{\omega }_0}\\ -a_{21}& 2i{\omega }_0-a_{22}& -a_{23}& 0& 0\\ 0& -a_{32}& a_{33}^{\prime }& 0& 0\\ 0& 0& -b_{43}{e}^{-2i{\tau }_0{\omega }_0}& a_{44}^{\prime }& 0\\ -a_{51}& 0& 0& 0& a_{55}^{\prime }\end{array}\right)}^{-1}\left(\begin{array}{c}{E}_1^{(1)}\\ E_1^{(2)}\\ 0\\ 0\\ 0\end{array}\right),\hfill \\ E_2=-{\left(\begin{array}{ccccc}{a}_{11}& 0& a_{13}& b_{14}& b_{15}\\ a_{21}& a_{22}& a_{23}& 0& 0\\ 0& a_{32}& a_{33}+b_{33}& 0& 0\\ 0& 0& b_{43}& a_{44}+b_{44}& 0\\ a_{51}& 0& 0& 0& a_{55}+b_{55}\end{array}\right)}^{-1}\left(\begin{array}{c}{E}_2^{(1)}\\ E_2^{(2)}\\ 0\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

with

$$\begin{array}{c}{a}_{33}^{\prime }=2i{\omega }_0-a_{33}-b_{33}{e}^{-2i{\tau }_0{\omega }_0},\hfill \\ a_{44}^{\prime }=2i{\omega }_0-a_{44}-b_{44}{e}^{-2i{\tau }_0{\omega }_0},\hfill \\ a_{55}^{\prime }=2i{\omega }_0-a_{55}-b_{55}{e}^{-2i{\tau }_0{\omega }_0},\hfill \\ E_1^{(1)}=-\beta q_3,E_1^{(2)}=\beta q_3,\hfill \\ E_2^{(1)}=-\beta (q_3+{\overline{q}}_3),E_2^{(2)}=\beta (q_3+{\overline{q}}_3).\hfill \end{array}$$

Then we can get the following coefficients:

$$\begin{array}{c}{C}_1(0)=\frac{i}{2{\tau }_0{\omega }_0}(g_{11}{g}_{20}-2{|g_{11}|}^2-\frac{{|g_{02}|}^2}{3})+\frac{g_{21}}{2},\hfill \\ {\mu }_2=-\frac{Re\{C_1(0)\}}{Re\{{\lambda }^{\prime }({\tau }_0)\}},{\beta }_2=2Re\{C_1(0)\},\hfill \\ T_2=-\frac{Im\{C_1(0)\}+{\mu }_{2}Im\{{\lambda }^{\prime }({\tau }_0)\}}{{\tau }_0{\omega }_0}.\hfill \end{array}$$

(20)

In conclusion, we have the following results.

Theorem 2 For system (3), if ${\mu }_2>0$ (${\mu }_2<0$), then the Hopf bifurcation is supercritical (subcritical). If ${\beta }_2<0$ (${\beta }_2>0$), then the bifurcating periodic solutions are stable (unstable). If $T_2>0$ ($T_2<0$), then the bifurcating periodic solutions increase (decrease).

4 Numerical simulation

In this section, we present a numerical example to verify the theoretical analysis in Section 2 and Section 3. Let $A=2$, $p=0.32$, $\alpha =0.25$, $\beta =0.3$, $\mu =0.003$, $\delta =0.3$, $\eta =0.06$, $\epsilon =0.07$, $\gamma =0.4$. Then we get a particular case of system (3):

$$\{\begin{array}{l}\frac{dS(t)}{dt}=2-0.3S(t)I(t)-0.323S(t)+0.3R(t-\tau )+0.06V(t-\tau ),\\ \frac{dE(t)}{dt}=0.3S(t)I(t)-0.253E(t),\\ \frac{dI(t)}{dt}=0.25E(t)-0.073I(t)-0.4I(t-\tau ),\\ \frac{dR(t)}{dt}=0.4I(t-\tau )-0.003R(t)-0.3R(t-\tau ),\\ \frac{dV(t)}{dt}=0.32S(t)-0.003V(t)-0.06V(t-\tau ).\end{array}$$

(21)

It is easy to verify that $R_0=4.8750>1$ and system (21) has the unique positive equilibrium $D_{\ast }(1.5956,44.7772,23.6666,31.2430,8.1046)$. Further, we have ${\omega }_0=0.4883$, ${\tau }_0=2.4273$. First, we choose $\tau =2.365<{\tau }_0$, the corresponding phase plots are shown in Figures 1 and 2; it is easy to see that system (21) is asymptotically stable from Figures 1 and 2. Then we choose $\tau =2.595>{\tau }_0$. The corresponding phase plots are illustrated by Figures 3 and 4. We can see that system (21) undergoes a Hopf bifurcation in this case. This property can also be seen from the bifurcation diagram in Figure 5. In addition, we obtain ${\lambda }^{\prime }({\tau }_0)=0.0540+0.0774i$, $C_1(0)=-1.2390+0.9658i$. Thus, we have ${\mu }_2=22.9444>0$, ${\beta }_2=-2.4780<0$, $T_2=-2.1690<0$. From Theorem 2, we can conclude that the Hopf bifurcation is supercritical and the bifurcating periodic solutions are stable, and the period of the periodic solutions decreases.

Figure 1

The phase plot of the states S , E , R for $\mathit{\tau }\mathbf{=}\mathbf{2.365}\mathbf{<}\mathbf{2.4273}\mathbf{=}{\mathit{\tau }}_{\mathbf{0}}$ .

Figure 2

The phase plot of the states S , I , V for $\mathit{\tau }\mathbf{=}\mathbf{2.365}\mathbf{<}\mathbf{2.4273}\mathbf{=}{\mathit{\tau }}_{\mathbf{0}}$ .

Figure 3

The phase plot of the states S , E , R for $\mathit{\tau }\mathbf{=}\mathbf{2.595}\mathbf{>}\mathbf{2.4273}\mathbf{=}{\mathit{\tau }}_{\mathbf{0}}$ .

Figure 4

The phase plot of the states S , I , V for $\mathit{\tau }\mathbf{=}\mathbf{2.595}\mathbf{>}\mathbf{2.4273}\mathbf{=}{\mathit{\tau }}_{\mathbf{0}}$ .

Figure 5

The bifurcation diagram with respect to τ .

5 Conclusions

This paper is concerned with a delayed SEIRS-V model on the transmission of worms in a wireless sensor network. The main results are given in terms of local stability and local Hopf bifurcation. By choosing the delay as a bifurcation parameter, sufficient conditions for local stability of the positive equilibrium and existence of the Hopf bifurcation of system (3) are obtained. We have proven that when the conditions are satisfied, there exists a critical value ${\tau }_0$ of the delay below which system (3) is stable and above which system (3) is unstable. Especially, system (3) undergoes a Hopf bifurcation at the positive equilibrium when $\tau ={\tau }_0$. The occurrence of Hopf bifurcation means that the state of worms prevalence in a wireless sensor network changes from a positive equilibrium to a limit cycle, which is not welcomed in a wireless sensor network. Hence, we should control the occurrence of Hopf bifurcation by combining some bifurcation control strategies, and we leave this as the future work. Further, the properties of Hopf bifurcation are studied by using the normal form method and the center manifold theorem. Finally, a numerical example is given to support our theoretical results.