Dynamic behaviors of a modified predator-prey model with state-dependent impulsive effects

Abstract

In this paper, we formulate a two-dimensional autonomous predator-prey model with state-dependent impulsive effects and square root response function. The square root response function indicates that the prey population gather together for self-defense purposes. Firstly, we prove that the system has semitrivial periodic solution under some conditions. Furthermore, by the Poincaré map and the theory of impulsive differential equations, the existence and stability of positive order-1 or order-2 periodic solution of the system are investigated in detail. The validity of all results is illustrated by numerical simulations.

1 Introduction

Many evolutionary processes in nature are subjected to short temporary perturbations and experience abrupt changes at certain moments of time. The duration of the changes is very short and negligible in comparison with the duration of the process considered. These short-time perturbations are often assumed to be momentary changes or impulses. Therefore, it is realistic that impulsive differential equations model such processes. In the recent ten years, the theory of impulsive differential equations has been extensively used to model many real processes in biology, physics, chemistry, engineering, and other sciences. Particularly, some impulsive differential equations have been introduced successfully in population dynamics (such as fishing or agriculture) and epidemic dynamics; see [1–9] and references therein. In most of the cases, scholars investigate the population dynamical systems with impulsive perturbation at fixed times. However, in practical ecological systems, the implementations of some control strategy (by catching, poisoning or releasing the natural enemy, etc.) depend on the state of target species, which is a more realistic project. This is known as impulsive state feedback control strategy, which is widely used in many biological systems. Recently, a few studies on state-dependent impulse effects were made in [10–18]. In particular, Jiang et al. [10, 11], Nie et al. [12–14] and Zhang et al. [18] investigated some predator-prey systems by using the Poincaré map and theory of impulsive differential equations, the sufficient conditions of existence and stability of semitrivial solution and positive periodic solution were obtained. Guo and Chen [16] and Tian et al. [17] studied the existence and stability of the positive period-1 solution of the system with impulsive state feedback control. The abundant dynamic behaviors of the systems were obtained.

These predator-prey systems with prey group defense ability have more abundant and interesting dynamic characteristics and attract attention of many scholars. A recent novel contribution models the fact that it is the individuals at the edge of the herd that generally suffer the heaviest consequences of the predators’ attacks. Recently, some predator-prey models [19–23] in which the prey exhibits herd behavior were considered. In these models, the predator interacts with the prey along the outer corridor of the herd of prey. As a mathematical consequence of the herd behavior, the interaction terms in systems use the square root of the prey population rather than simply the prey population. The use of the square root properly accounts for the assumption that the interactions occur along the boundary of the population. For example, for drifting herbivores in the savannas, moving in very large herds and subject to individual attacks of predators, the likelihood that they are hunted in the way we describe here is evident [23].

Braza [19] analyzed the following predator-prey model with square root functional responses:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t)(1-x(t))-\sqrt {x(t)}y(t),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=-sy(t)+c\sqrt {x(t)}y(t), \end{array}\displaystyle \right . $$

(1.1)

where the prey is denoted by $x(t)$, and the predator by $y(t)$, s is the death rate of the predator, and c is the biomass conversion or consumption rate.

Basing on these reasons mentioned, we will consider the dynamic behaviors for system (1.1) with state-dependent impulse effects; in other words, when the amount of the herbivores reaches a threshold value, we will release predators and capture some herbivores, helping this way to preserve natural balance. The system is modeled by the following equations:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \left . \textstyle\begin{array}{l@{}} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t)(1-x(t))-\sqrt {x(t)}y(t),\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=-sy(t)+c\sqrt {x(t)}y(t), \end{array}\displaystyle \right \}&x \neq h, \\ \left . \textstyle\begin{array}{l@{}} \Delta x(t)=x(t^{+})-x(t)=-px(t),\\ \Delta y(t)=y(t^{+})-y(t)=qy(t)+\alpha, \end{array}\displaystyle \right \}&x=h, \end{array}\displaystyle \right . $$

(1.2)

where $h>0$, $\alpha\geq0$, $p\in(0, 1)$, and $q\in(-1, \infty)$, and $(x^{*}, y^{*})$ is the positive equilibrium of system (1.1). When the amount of the prey reaches the threshold h at time $t_{h}$, a control strategy is taken, and the amount of prey and predator abruptly turn to $(1-p)h$ and $(1+q)y(t_{h})+\alpha$, respectively.

2 Preliminaries

The dynamic behaviors for system (1.1) are studied by many investigators. Throughout this paper, we assume that system (1.1) has a unique positive equilibrium point $(x^{*}, y^{*})$ under the following condition:

• (H) $c>s$, where

  $$ \left \{ \textstyle\begin{array}{@{}l} x^{*}=\frac{s^{2}}{c^{2}},\\ y^{*}=\frac{s(c^{2}-s^{2})}{c^{3}}. \end{array}\displaystyle \right . $$

  (2.1)

By the biological background of system (1.2) we only consider system (1.2) in the region $D=R^{2}_{+}$. Obviously, the global existence and uniqueness of solutions of system (1.2) are guaranteed by the smoothness properties of f, which is the mapping defined by the right-hand side of system (1.1); for details, see [24, 25].

Denote $R=(-\infty, \infty)$. First, we give the notion of the distance between a point and a set. Let $S\subset R^{2}=\{(x, y): x\in R, y\in R\}$ be an arbitrary set, and $P\in R^{2}$ be an arbitrary point. Then the distance between the point P and the set S is denoted by

$$\mathrm{d}(P, S)=\inf_{P_{0}\in S}\| P-P_{0}\|, $$

where $\|P-P_{0}\|=\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}}$ for points $P(x, y)\in R^{2}$ and $P_{0}(x_{0}, y_{0})\in S$.

Let $z(t)=(x(t), y(t))$ be a solution of (1.2), and let $z(t; t_{0}, z_{0})$ denote the solution of (1.2) for which $z(t_{0}^{+}; t_{0}, z_{0})=z_{0}$. Next, we define the positive orbit through the point $z_{0}\in R^{2}_{+}=\{(x, y): x\geq0, y\geq0 \}$ for $t\geq t_{0}$ as

$$O^{+}(z_{0}, t_{0})=\bigl\{ z\in R_{+}^{2}: z=z(t), t\geq t_{0}, z(t_{0})=z_{0}\bigr\} . $$

In the rest of this paper, we will use the following definitions.

Definition 2.1

[25]

The solution $z(t)$ of system (1.2) is said to be:

• (1) Orbitally stable if $\forall\varepsilon>0$, $\exists \delta>0$ such that for any $z^{*}(t_{0})=(x_{0}^{*}, y_{0}^{*})\,\bar{\in}\,\{h\} \times[y^{*}, +\infty)$ satisfying $\| z^{*}(t_{0})-z(t_{0})\|<\delta$, we have $\mathrm{d}(z(t; t_{0}, z^{*}(t_{0})), O^{+}(z_{0}, t_{0}))<\varepsilon$ for $t>t_{0}$.

• (2) Orbitally attractive if $\forall\varepsilon>0$, $\exists\delta >0$ and $\tilde{T}>0$ such that for any $z^{*}(t_{0})=(x_{0}^{*}, y_{0}^{*})\,\bar{\in}\, \{h\}\times[y^{*}, +\infty)$ satisfying $\| z^{*}(t_{0})-z(t_{0})\|<\delta$, we have $\mathrm{d}(z(t; t_{0},z^{*}(t_{0})), O^{+}(z_{0}, t_{0}))<\varepsilon$ for any $t>t_{0}+\tilde{T}$.

To discuss the dynamics of system (1.2), we define two cross-sections of the vector field (1.2) by $\sum^{p}=\{(x,y): x=(1-p)h, y>0\}$ and $\sum^{h}=\{(x,y): x=h, y>0\}$. Denote by $P_{t}$ the point representing the state of the system at time t. Suppose that the point $S_{n}(h, y_{n})$ is on the section $\sum^{h}$; then the point $P_{t}$ jumps from the position $S_{n}(h, y_{n})$ to the point $S^{+}_{n}((1-p)h, (1+q)y_{n}+\alpha)$ on the section $\sum^{p}$ due to the impulse effects. The point $P_{t}$ continues its motion along the solution curve of system (1.2) and reaches the point $S_{n+1}(h, y_{n+1})$ on the section $\sum^{h}$ again, where $y_{n+1}$ is decided by $y_{n}$ and the parameters q and α. Therefore, we defined the Poincaré map of $\sum^{h}$ as follows:

$$ y_{n+1}=P_{2}(q, \alpha, y_{n}). $$

(2.2)

Next, we consider the autonomous system with impulse effects

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{\mathrm{d}x}{\mathrm{d}t}=P(x, y),\qquad \frac{\mathrm{d}y}{\mathrm {d}t}=Q(x, y), \qquad\varphi(x, y)\neq0,\\ \Delta x=\xi(x, y),\qquad \Delta y=\eta(x, y),\qquad \varphi(x, y)=0, \end{array}\displaystyle \right . $$

(2.3)

where $P(x, y)$ and $Q(x, y)$ are continuous differential functions defined on $R^{2}$, and $\varphi(x, y)$ is a sufficiently smooth function with grad$\varphi(x, y)\neq0$. Let system (2.3) have a positive T-periodic solution $(u(t), v(t))$ with moments of an impulse effect $\tau_{j}: \tau_{j+m}=\tau_{j}+T$ ($j\in N$), m is a positive integer. By Corollary 2 of Theorem 1 given in Simeonov and Bainov [3] we have the following lemma.

Lemma 2.1

(Analogue of Poincaré’s criterion)

If the Floquet multiplier μ satisfies the condition $|\mu|<1$, where

$$\mu=\prod^{m}_{j=1}K_{j}\exp \biggl[ \int_{0}^{T}\biggl(\frac{\partial P(u(t), v(t))}{ \partial x}+ \frac{\partial Q(u(t), v(t))}{\partial y}\biggr)\,\mathrm{d}t\biggr] $$

with

$$K_{j}=\frac{(\frac{\partial\eta}{\partial y}\frac{\partial\varphi }{\partial x}-\frac{\partial\eta}{\partial x} \frac{\partial\varphi}{\partial y}+\frac{\partial\varphi}{\partial x})P_{+} + (\frac{\partial \xi}{\partial x}\frac{\partial\varphi}{\partial y}-\frac{\partial \xi}{\partial y} \frac{\partial\varphi}{\partial x}+\frac{\partial \varphi}{\partial y})Q_{+}}{\frac{\partial\varphi}{\partial x}P + \frac{\partial\varphi}{\partial y}Q}, $$

and P, Q, $\frac{\partial\xi}{\partial x}$, $\frac{\partial\xi}{\partial y}$, $\frac{\partial\eta}{\partial x}$, $\frac{\partial\eta}{\partial y}$, $\frac{\partial\varphi}{\partial x}$, and $\frac{\partial \varphi}{\partial y}$ are calculated at the point $(u(\tau_{j}), v(\tau_{j}))$, $P_{+}=P(u(\tau_{j}^{+}), v(\tau_{j}^{+}))$, $Q_{+}=Q(u(\tau_{j}^{+}), v(\tau_{j}^{+}))$, and $\tau_{j}$ ($j\in N$) is the time of the jth jump. Then, $(u(t), v(t))$ is orbitally asymptotically stable.

Now, let $z(t)=(x(t), y(t))$ be a solution of system (1.2) with initial conditions $z_{0}=z(t_{0})=((1-p)h, y_{0})\in R_{+}^{2}$. This trajectory $O^{+}(z_{0},t_{0})$ begins from the point $E_{0}((1-p)h, y_{0})$ and moves along the solution curve $z(t)$, then it first intersects the section $\sum^{h}$ at the point $F_{0}(h, \widetilde{y}_{0})$, and, next, the point $F_{0}$ is transferred to the point $E_{1}((1-p)h, y_{1})$ on the section $\sum^{p}$ due to the impulse effects, then reaches the point $F_{1}(h, \widetilde{y}_{1})$ on the section $\sum^{h}$ again, etc. So, we have two-point sequences $\{E_{k}((1-p)h, y_{k})\}$ and $\{F_{k}(h, \widetilde{y}_{k})\}$ ($k=0,1,2,\ldots$). In addition, notice that the coordinates satisfy the relation $y_{k}=(1+q)\widetilde{y}_{k-1}+\alpha$ ($k=1,2,\ldots$).

Definition 2.2

A trajectory $O^{+}(z_{0},t_{0})$ of system (1.2) is said to be order-k periodic if there exists a positive integer $k\geq1$ such that k is the smallest integer for $y_{0}=y_{k}$.

3 Main results

3.1 Existence of semitrivial periodic solution with $\alpha=0$

Let $y(t)=0$ for $t\in[0,\infty)$. Then from system (1.2) we have

$$\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{\mathrm{d} x(t)}{\mathrm{d} t}=x(t)(1-x(t)),& x\neq h,\\ \Delta x=x(t^{+})-x(t) = -p x,& x=h. \end{array}\displaystyle \right . $$

Set $x_{0}=x(0^{+}) = (1-p)h$. Then the solution of the equation

$$\frac{\mathrm{d} x(t)}{\mathrm{d} t}=x(t) \bigl(1-x(t)\bigr) $$

is $x(t)=\frac{1}{1+\bar{c}\mathrm{e^{-t}}}$, where $\bar{c}=\frac {1}{(1-p)h}-1$.

By the periodic condition, let $x(T)=h$ and $x(T^{+})=x_{0}$. Then

$$T =\ln\bigl\{ \bigl[1-(1-p)h\bigr]/\bigl[(1-p) (1-h)\bigr]\bigr\} , $$

where $0< h<1$ ensures that $T>0$.

This means that system (1.2) with $\alpha=0$ has the following semitrivial periodic solution

$$ \left \{ \textstyle\begin{array}{@{}l} \bar{x}(t)=\frac{(1-p)h}{(1-p)h+[1-(1-p)h]\exp (-(t-(k-1)T))},\\ \bar{y}(t)=0. \end{array}\displaystyle \right . $$

(3.1)

for $(k-1)T < t \leq kT$ ($k=1,2,\ldots$).

3.2 Existence and stability of positive periodic solutions

In this subsection, we give sufficient conditions for the existence and stability of positive periodic solutions in the cases $h \leq x^{*}$ and $h > x^{*}$, respectively.

Case I: $h\leq x^{*}$.

On the existence of positive periodic solution of system (1.2), we have the following theorem.

Theorem 3.1

For any $q>-1$ and $\alpha> 0$, system (1.2) has a positive order-1 periodic solution.

Proof

Let the point $M_{1}((1-p)h, \beta_{0})$ be on the section $\sum^{p}$, where $\beta_{0}$ is small enough, and $\beta_{0} < \alpha$. The trajectory $O^{+}(M_{1}, t_{0})$ of system (1.2) begins from the point $M_{1}$ and moves along the solution curve of system (1.2), then intersects the section $\sum^{h}$ at the point $N_{1}(h,\beta_{1})$. At the point $N_{1}$, the trajectory $O^{+}(M_{1}, t_{0})$ instantly jumps to the point $M_{2}((1-p)h, (1+q)\beta_{1}+\alpha)$ on the section $\sum^{p}$ by impulse effect and then reaches the point $N_{2}(h, \beta_{2})$ on the section $\sum^{h}$ again. Since $(1+q)\beta_{1}+\alpha > \beta_{0}$, the point $M_{2}$ is above the point $M_{1}$. Without doubt, the point $N_{2}$ is above the point $N_{1}$, and $\beta_{2} > \beta_{1}$. So, from (2.2) we have $\beta_{2}=P_{2}(q, \alpha, \beta_{1})$ and

$$ \beta_{1}- P_{2}(q, \alpha, \beta_{1}) = \beta_{1}- \beta_{2} < 0. $$

(3.2)

On the other hand, suppose that the vertical isocline $L: 1 - x - \frac{y}{\sqrt{x}}=0$ intersects the section $\sum^{p}$ at the point $E_{0}((1- p)h, (1 -(1-p)h)\sqrt{(1-p)h})$. The trajectory $O^{+}(E_{0}, t_{0})$ from the initial point $E_{0}$ intersects the section $\sum^{h}$ at the point $F_{1}(h, y_{1})$ with $y_{1}< y^{*}$, then suddenly jumps to the point $F_{1}^{+}((1-p)h, (1+q)y_{1}+ \alpha)$ on the section $\sum^{p}$, and finally reaches the point $F_{2}(h, y_{2})$ on the section $\sum^{h}$ again. Suppose that there is a positive constant $q^{*}$ such that $(1+q)y_{1}+ \alpha=(1-(1-p)h)\sqrt{(1-p)h}$. Then, the point $F_{1}^{+}$ coincides with the point $E_{0}$ for $q=q^{*}$, the point $F_{1}^{+}$ is above the point $E_{0}$ for $q>q^{*}$, and $F_{1}^{+}$ is under the point $E_{0}$ for $q< q^{*}$. However, on account of the point $E_{0}$ on the isocline L and the phase portrait of system (1.2), we find that the point $F_{2}$ is under the point $F_{1}$ for any $q \in (- 1, q^{*}) \cup (q^{*}, \infty)$.

From this analysis we have that

• (i) if $y_{1} = y_{2}$, then system (1.2) has a positive order-1 periodic solution;

• (ii) if $y_{1} > y_{2}$, then

  $$ y_{1} -P_{2}(q, \alpha, y_{1}) = y_{1} - y_{2} > 0. $$

  (3.3)

By (3.2) and (3.3) it follows that the Poincaré map (2.2) has a fixed point, that is, system (1.2) has a positive order-1 periodic solution. This completes the proof. □

Next, we state and prove the stability of the positive order-1 periodic solutions of system (1.2).

Theorem 3.2

Let $(\phi(t), \psi(t))$ be a positive order-1 T-periodic solution of system (1.2) that starts from the point $(h, \gamma)$. Suppose that

$$ |\mu| =\biggl| k \exp \int_{0}^{T}\biggl[1-2\phi(t)-\frac{\psi(t)}{2\sqrt {\phi(t)}}-s+c \sqrt{\phi(t)}\biggr]\,\mathrm{d}t \biggr|< 1, $$

(3.4)

where

$$\gamma>0,\quad k=\frac{(1-p)(1+q)[1-(1- p)h- \frac{(1+q)\gamma+\alpha}{\sqrt {(1-p)h}}]}{1-h-\frac{\gamma}{\sqrt{h}}}. $$

Then $(\phi(t), \psi(t))$ is orbitally asymptotically stable.

Proof

Suppose that the periodic solution $(\phi(t), \psi(t))$ intersects the sections $\sum^{p}$ and $\sum^{h}$ at the points $E^{+}((1 - p)h, (1 + q)\gamma + \alpha)$ and $E(h, \gamma)$, respectively. Comparing with system (2.3), we have

$$\left \{ \textstyle\begin{array}{@{}l} P(x, y) =(1-x- \frac{y}{\sqrt{x}})x,\\ Q(x, y) =(-s + c\sqrt{x})y, \end{array}\displaystyle \right . $$

and $\xi(x, y)=-px$, $\eta(x, y)=qy+\alpha$, $\varphi(x, y)=x-h$, $(\phi(T), \psi(T))=(h, \gamma)$, and $(\phi(T^{+}), \psi(T^{+}))=((1-p)h, (1+q)\gamma+ \alpha)$.

Thus,

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{\partial P}{\partial x}=1 - 2x - \frac{y}{2\sqrt{x}},\\ \frac{\partial Q}{\partial y}=-s + c\sqrt{x}, \end{array}\displaystyle \right . $$

(3.5)

and

$$ \frac{\partial\xi}{\partial x}=-p,\qquad \frac{\partial\eta}{\partial y}=q, \qquad\frac{\partial\varphi}{\partial x}=1,\qquad \frac{\partial\xi}{\partial y}=\frac{\partial\eta}{\partial x}=\frac {\partial\varphi}{\partial y}=0. $$

(3.6)

It follows from (3.5), (3.6), and Lemma 2.1 that

$$\begin{aligned} k = & \frac{(1+q)P(\phi(T^{+}), \psi(T^{+}))}{P(\phi(T), \psi(T))}\\ = & \frac{(1-p)(1+q)[1-(1- p)h- \frac{(1+q)\gamma+\alpha}{\sqrt {(1-p)h}}]}{1-h-\frac{\gamma}{\sqrt{h}}} \end{aligned}$$

and

$$\mu=k \exp \int_{0}^{T}\biggl[1 -2\phi(t)- \frac{\psi(t)}{2\sqrt{\phi (t)}}-s+c\sqrt{\phi(t)}\biggr]\,\mathrm{d}t. $$

Therefore, by Lemma 2.1, provided that condition (3.4) is satisfied, the order-1 periodic solution $(\phi(t), \psi(t))$ of system (1.2) is orbitally asymptotically stable. This completes the proof. □

Case II: $h>x^{*}$.

On the existence and stability of positive periodic solution of system (1.2), we have the following theorem.

Theorem 3.3

For $h>x^{*}$, there is a positive constant $\alpha^{*}=\alpha (h)>0$ such that for any $q>-1$ and $\alpha>\alpha^{*}$, system (1.2) only has a orbitally asymptotically stable positive order-1 or order-2 periodic solution.

Proof

In view of the phase portrait of system (1.2), there is a trajectory Γ that begins from the point $D_{1}((1-p)h, \tilde{y}_{1})$, crosses $\sum^{p}$ at the point $D_{2}((1-p)h, \tilde{ y}_{2})$ ($\tilde{y}_{2}< \tilde{y}_{1}$), and then tangents to the section $\sum^{h}$ at the point $D_{3}(h,(1-h)\sqrt{h})$. So, the trajectory of system (1.2) that starts from the point $((1-p)h, y)$ with $y\in(\tilde{y}_{1}, \tilde{y}_{2})$ will not meet $\sum^{h}$, and tends to the equilibrium point $(x^{*}, y^{*})$. (See Figure 1.)

Figure 1

Geometrical construction. The phase portrait of the phase space of the system (1.2).

Let $\alpha^{*}=\tilde{y}_{1}+(1-h)\sqrt{h}$. The trajectory of system (1.2) that starts from the point $E((1-p)h, \tilde{y})$ ($\tilde{y}\in(0,\tilde{y}_{2})\cup(\tilde{y}_{1},+\infty)$) will intersect with $\sum^{h}$ infinitely many times due to the impulse effects with $\alpha>\alpha^{*}$ and $h>x^{*}$. Suppose that the orbit $O^{+}(E,t_{0})$ intersects $\sum^{h}$ at the point $(h,y_{0})$; then $y_{0}\in(0,(1-h)\sqrt{h})$. Further, from the Poincaré map (2.2) of the section $\sum^{h}$ it follows that $y_{1}=P_{2}(q,\alpha,y_{0})$ and $y_{2}=P_{2}(q,\alpha,y_{1})$. Repeating this process, we have $y_{n+1}=P_{2}(q,\alpha,y_{n})$ ($n=1,2,\ldots$). On the other hand, for any two points $A_{i}(h,y_{i})$ and $A_{j}(h,y_{j})$ on $\sum^{h}$, where $y_{i},y_{j}\in(0,(1-h)\sqrt{h})$ and $y_{i}< y_{j}$, the points $A_{i}^{+}((1-p)h, (1+q)y_{i}+\alpha)$ and $A_{j}^{+}((1-p)h, (1+q)y_{j}+\alpha)$ are above the point $D_{1}$ for the impulse effects. Therefore, from the phase portrait of the system (1.2) we have

$$ 0< y_{j+1}< y_{i+1}< (1-h)\sqrt{h} $$

(3.7)

for $\alpha>\alpha^{*}$.

Now, suppose that the trajectory of system (1.2) that starts from the point $E_{1}((1-p)h,y)$ ($y\in[\tilde{y}_{1}, \infty)$) intersects with $\sum^{h}$ at the point $E_{2}(h, y_{0})$ for the fist time; then $y_{0}\in(0, (1-h)\sqrt{h}]$. If $y_{0}=(1-h)\sqrt{h}$ and $y=(1+q)y_{0}+\alpha$, then system (1.2) has a positive order-1 periodic solution. Otherwise, from the Poincaré map (2.2) of the section $\sum^{h}$ it follows that $y_{1}=P_{2}(q, \alpha,y_{0})$ and $y_{2}=P_{2}(q, \alpha, y_{1})$; and so forth, we have $y_{n+1}=P_{2}(q,\alpha,y_{n})$ ($n=2,3,\ldots$). In particular, if $y_{0}=y_{1}$, then system (1.2) has a positive order-1 periodic solution, and if $y_{0}\neq y_{1}$ and $y_{0}=y_{2}$, then system (1.2) has a positive order-2 periodic solution.

Next, similarly to [12, 13, 16], we discuss the general circumstance, that is, $y_{0}\neq y_{1} \neq y_{2}\neq\cdots\neq y_{n}$ ($n>2$).

(a) If $y_{0}< y_{1}$, then from (3.7) we obtain that $y_{1}>y_{2}$. Consequently, the relation of $y_{0}$, $y_{1}$, and $y_{2}$ is one of the following cases:

• (i) $y_{2}< y_{0}< y_{1}$.

  If $y_{2}< y_{0}< y_{1}$, then $y_{3}>y_{1}>y_{0}>y_{2}$ by (3.7). Repeating the process, we have

  $$0< \cdots< y_{2n} < \cdots< y_{2} < y_{0} < y_{1} < \cdots< y_{2n+1} < \cdots< (1-h)\sqrt{h}. $$

• (ii) $y_{0}< y_{2}< y_{1}$.

  If $y_{0}< y_{2}< y_{1}$, then similarly to (i) we have

  $$y_{0}< y_{2} < \cdots< y_{2n} < \cdots< y_{2n+1} < \cdots< y_{3}< y_{1} < (1-h) \sqrt{h}. $$

(b) If $y_{0}> y_{1}$, from (3.7) we obtain that $y_{1}< y_{2}$. Consequently, the relation of $y_{0}$, $y_{1}$, and $y_{2}$ is one of the following cases:

• (i) $y_{1}< y_{0}< y_{2}$.

  If $y_{1}< y_{0}< y_{2}$, then $y_{2}> y_{0}> y_{1}> y_{3}$ by (3.7). Repeating the process, we have

  $$0< \cdots< y_{2n+1}< \cdots< y_{1}< y_{0}< y_{2}< \cdots< y_{2n}< \cdots< (1-h)\sqrt{h}. $$

• (ii) $y_{1}< y_{2}< y_{0}$.

  If $y_{1}< y_{2}< y_{0}$, then similarly to (i) we have

  $$0< y_{1}< \cdots< y_{2n+1}< \cdots< y_{2n}< \cdots< y_{2}< y_{0}< (1-h)\sqrt{h}. $$

From this analysis, in case (i) of (a), it follows from the monotone bounded theorem that $\lim_{n\rightarrow\infty} y_{2n}=\theta_{2}$ and $\lim_{n\rightarrow\infty} y_{2n+1}=\theta_{1}$; in addition, $0< \theta_{2}< y_{0}< \theta_{1}< (r-h)\sqrt{h}$. Thus, we get $\theta_{2}=P_{2}(q, \alpha, \theta_{1})$ and $\theta_{1}=P_{2}(q, \alpha, \theta_{2})$. This means that system (1.2) has an orbitally asymptotically stable positive order-2 periodic solution. Similarly, in case (i) of (b), system (1.2) has also an orbitally asymptotically stable positive order-2 periodic solution. In cases (ii) of (a) and (ii) of (b), it follows from the Poincaré map and the closed interval theorem that system (1.2) has an orbitally asymptotically stable positive order-1 periodic solution. The proof is completed. □

Remark

From the proof of Theorem 3.3 we note that the trajectory of system (1.2) passing through the point $((1-p)h, y)$ ($y\in(\tilde{y}_{2}, \tilde{y}_{1})$) will not intersect with $\sum^{h}$ as time increases and will tend to the focus $(x^{*}, y^{*})$. Therefore, $\alpha>\widetilde{y_{1}}+ (1-h)\sqrt{h}$ is a sufficient condition ensuring that the trajectory of system (1.2) intersects with $\sum^{h}$ infinitely many times in view of the impulse effects.

4 Numerical simulation

We have obtained analytical results on dynamical behaviors of a predator-prey model with state-dependent impulse effects in front sections. Now we will illustrate the validity of these results through numerical simulation.

In system (1.1), let $s=0.5$ and $c=0.6$. Then the positive equilibrium point $(x^{*}, y^{*})=(0.6945, 0.2546)$ is globally asymptotically stable.

For the semitrivial periodic solution (3.1) of system (1.2), we set the parameters as follows:

• (1) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0$, $h=0.6< x^{*}$, $q=0.001$.

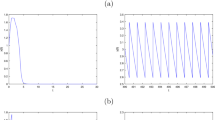
Under this choice of parameters, we find that the trajectory of system (1.2) intersects the section $\sum^{h}$ infinitely many times and tends to the semitrivial T-periodic solution (3.1), where $T=0.4855$, so the semitrivial T-periodic solution (3.1) is stable (see Figure 2).

• (2) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0$, $h=0.6< x^{*}$, $q=0.1$.

Figure 2

A stable semitrivial periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

Under this choice of parameters, we find that the trajectory of system (1.2) intersects the section $\sum^{h}$ infinitely many times and is away from the semitrivial T-periodic solution (3.1), where $T=0.4855$, so the semitrivial T-periodic solution (3.1) is unstable (see Figure 3).

• (3) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0$, $h=0.72> x^{*}$, $q=0.1$.

Figure 3

A unstable semitrivial periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

Under this choice of parameters, we find that the trajectory of system (1.2) intersects the section $\sum^{h}$ finitely many times and tends to the positive equilibrium point $(x^{*}, y^{*})$, so the semitrivial T-periodic solution (3.1), where $T=0.6381$, is unstable (see Figure 4).

Figure 4

A unstable semitrivial periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

For the positive periodic solution of system (1.2), we set the parameters as follows:

• (1) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0.2$, $h=0.6< x^{*}$, $q=0.1$.

Under this choice of parameters, the conditions of Theorem 3.1 are established, so we get a stable order-1 positive periodic solution (see Figure 5).

• (2) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0.45$, $h=0.72> x^{*}$, $q=0.1$.

Figure 5

A stable order-1 positive periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

Under this choice of parameters, the conditions of Theorem 3.2 are established, so we also get a stable order-1 positive periodic solution (see Figure 6).

• (3) $s=0.5$, $c=0.6$, $p=0.2$, $\alpha=0.6$, $h=0.72> x^{*}$, $q=0.1$.

Figure 6

A stable order-1 positive periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

Under this choice of parameters, the conditions of Theorem 3.2 are established, so we obtain a stable order-2 positive periodic solution (see Figure 7).

Figure 7

A stable order-2 positive periodic solution. $x(0)=0.5$, $y(0)=0.6$. (a) Time series graph for prey $x(t)$; (b) Time series graph for predator $y(t)$; (c) Phase space graph for prey $x(t)$ and predator $y(t)$.

5 Conclusion

On the basis of the predator-prey model (1.1) with square root functional responses, we formulate a new model (1.2) with state impulsive control strategy. In spite of the simplicity of the model, which is composed of two ordinary differential equations together with relations defining the impulsive condition, it is very significant and has interesting dynamical behaviors.

For the predator-prey model (1.1), the prey exhibits strong herd structure implying that the predator generally interacts with the prey along the outer corridor of the herd, and this behavior makes their predators difficult to get food (such as lions on the vast grassland). If this situation continues for a long time in this way, then the predator will be in peril of extinction (see Figure 2). In order to prevent the predator from dying out, we must take some control strategy to ensure that this result does not happen. In this paper, we investigate theoretically the state impulsive control strategy of protecting the predator. Furthermore, we have obtained some interesting results (see Figures 3, 4, 5, 6), which show that h, q, and α are important control parameters. Unfortunately, we cannot currently prove the stability of the semitrivial periodic solution (3.1).