1 Introduction

In the past few years, synchronization of dynamical systems has shown interesting behaviors which have received increasing attention in various fields of industry and various sciences [1–3]. Meanwhile, many kinds of synchronization have been proposed [4–13] and various control methods have been reported to achieve the different kinds of synchronization for complex networks [14–20].

In many practical situations, time delay may cause undesirable dynamic behaviors such as oscillation, instability, and poor performance. Therefore, the development of synchronization of complex dynamical networks with time delays is very important.

In [21] Guo studied lag synchronization of complex networks with non-delay coupling by proposing pinning control. On the basis of adaptive control, Ji et al. [22] proposed a method with lag synchronization between uncertain complex dynamical networks CDNs with constant delay coupling. Wang et al. [23] proposed function projective synchronization (FPS)in CDNs having constant delay coupling and non-identical reference nodes and both network nodes and reference have unknown parameters and bounded external disturbances. Zhang and Zhao [24] investigated both projective and lag synchronization between general complex networks via impulsive control. Based on an adaptive feedback controller, projective lag synchronization of the general complex dynamical networks was proposed with non-delay coupling and different nodes [25]. In [26] Rui-Jin et al. proposed several nonlinear controllers to realize the problem of projective synchronization with non-delayed and constant delayed coupling in drive-response dynamical networks consisting of identical nodes and different nodes.

Motivated by the above discussion, the aim of this paper is to deal with the problem of a projective lag synchronization (PLS) scheme in drive-response dynamical networks (DRDNs) model with coupling delayed consisting of identical and different nodes. Both the drive and the network nodes have uncertain parameters and disturbance. Based on Lyapunov stability theory, an adaptive control method is designed to achieve the projective lag synchronization in DRDNs with constant and time-varying coupling delay. Adopting adaptive gains laws, the unknown parameters are estimated. In addition, the controller is designed to overcome the unknown bounded disturbance. In conclusion, the network is asymptotically synchronized with the proposed method. Moreover, numerical simulations are performed to verify the effectiveness of the theoretical results.

The rest of this paper is organized as follows: the DRDNs model with delay coupling is introduced in Section 2. A general method of PLS in a drive-response dynamical networks (DRDNs) model with constant coupling delayed by an adaptive control method is discussed in Section 3. Section 4 deals with a further investigation of PLS in a drive-response dynamical networks (DRDNs) model with time-varying coupling delayed by using the proposed method. Examples and their simulations are shown in Section 5. Finally, the conclusions are presented in Section 6.

2 Model description

Consider a controlled complex dynamical network with delay coupling consisting of N linearly and diffusively different nodes with both uncertain parameters and disturbance, described as follows:

$$\begin{aligned} \dot{x^{r}_{i}}(t) =&g_{i} \bigl(x^{r}_{i}(t)\bigr)+ G_{i} \bigl(x^{r}_{i}(t)\bigr)\theta _{i}+ c\sum ^{N}_{j=1}a_{ij}\Gamma x^{r}_{j}(t-d_{i}) +\Delta_{i}(t)+u_{i}(t), \quad i= 1,2,\ldots,N, \end{aligned}$$
(1)

where \(x^{r}_{i}=(x^{r}_{i1},x^{r}_{i2},\ldots,x^{r}_{in})^{T}\in\mathbf {R}^{n}\) denotes the state vector of the ith node, \(g_{i}:\mathbf {R}^{n}\longrightarrow\mathbf{R}^{n}\) and \(G_{i}:\mathbf {R}^{n}\longrightarrow\mathbf{R}^{n\times m_{i}}\) are the known continuous nonlinear function matrices determining the dynamic behavior of the node, \({\theta_{i}}\) is the unknown constant parameter vector, \(u_{i}\in\mathbf{R}^{n}\) is the control input, c is the coupling strength, and \(d_{i}\geq0\) is an unknown coupling delay. Here \(\Gamma= \operatorname{diag}(\gamma_{1}, \gamma_{2}, \ldots, \gamma_{n})\) is the inner coupling matrix with \(\gamma_{i}=1 \) for the ith state variable, i.e. matrix Γ determines the variables with which the nodes in system are coupled. \(A=(a_{ij})_{N\times N}\in\mathbf{R}^{N\times N}\) is the coupling configuration matrix representing the topological structure of the networks, where \(a_{ij}\) is defined as follows: if there exists a connection between node i and node j (\(j\neq i\)), then \(a_{ij} > 0\), otherwise \(a_{ij}=0\), and the diagonal elements of matrix A are defined by

$$ a_{ii}= -\sum_{j=1,j\neq i}^{N}a_{ij}, \quad i= 1,2,\ldots,N. $$
(2)

The reference node is described as follows:

$$ \dot{x}^{d}(t)=f\bigl(x^{d}(t)\bigr)+F \bigl(x^{d}(t)\bigr)\Phi+\Delta_{d}(t), $$
(3)

where the superscripts d stand for the drive system; \(x^{d}=(x^{d}_{1},x^{d}_{2},\ldots,x^{d}_{n})^{T}\in\mathbf{R}^{n}\) denotes the state vector of the drive system, \(f:\mathbf {R}^{n}\longrightarrow\mathbf{R}^{n}\) and \(F_{i}:\mathbf {R}^{n}\longrightarrow\mathbf{R}^{n\times m_{i}}\) are the known continuous nonlinear function matrices determining the dynamic behavior of the node; Φ is the unknown constant parameter vector, and \(\Delta_{d}\) contains the mismatched terms.

The projective lag synchronization error is defined as

$$e_{i}(t)=x_{i}^{r}(t)-\alpha x^{d}(t-\tau), \quad i=1,\ldots,N, $$
(4)

where α is the nonzero a scaling factor, \(\tau>0\) is a constant representing time delay or lag. Then the objective of this paper is to design a controller \(u_{i}(t)\) such that the reference nodes (1) and dynamical networks (3) are asymptotically synchronized such that

$$ \lim_{t\longrightarrow\infty}\bigl\| x_{i}^{r}(t)- \alpha x^{d}(t-\tau)\bigr\| =0,\quad i=1,\ldots,N, $$
(5)

which means that the network (1) is projective lag synchronized with reference node (3).

The error dynamics is obtained:

$$\begin{aligned} \dot{e}_{i} =&g_{i} \bigl(x^{r}_{i}(t)\bigr)+ G_{i} \bigl(x^{r}_{i}(t)\bigr)\theta_{i}(t)+ c\sum ^{N}_{j=1}a_{ij}\Gamma e_{j}(t-d_{i})+u_{i}(t)+\Delta _{i}(t) \\ &{}-\alpha \bigl(f\bigl(x^{d}(t-\tau)\bigr)+F\bigl(x^{d}(t-\tau)\bigr) \Phi(t)+ \Delta _{d}(t) \bigr), \quad i=1,\ldots,N. \end{aligned}$$
(6)

Assumption 2.1

[22]

For any positive constant \(\varepsilon_{i}\) the time-varying disturbance \(\Delta_{i}(t)\) is bounded i.e. \(\|\Delta _{i}(t)\|\leq\varepsilon_{i}\).

3 PLS in DRDNs with constant delay

In this section, we design an adaptive control method to realize projective lag synchronization for uncertain complex dynamical networks with constant delay coupling.

Theorem 3.1

The projective lag synchronization error (6) is asymptotically stable with a given time delay τ and scaling factor α, by using the following control input and adaptive laws:

$$\begin{aligned}& \begin{aligned}[b] u_{i}(t) ={}&{-}q_{i}e_{i}(t)- \beta_{i}\operatorname{sgn}\bigl(e_{i}(t)\bigr)-g_{i} \bigl(x^{r}_{i}(t)\bigr)- G_{i} \bigl(x^{r}_{i}(t)\bigr)\hat{\theta}_{i}(t) \\ &{} +\alpha \bigl(f\bigl(x^{d}(t-\tau)\bigr)+F\bigl(x^{d}(t- \tau)\bigr)\hat{\Phi}(t) \bigr),\quad i=1,\ldots,N, \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}& \dot{\hat{\theta}}_{i}(t)=k_{1}G_{i}^{T} \bigl(x^{r}_{i}(t)\bigr)e_{i}(t), \end{aligned}$$
(8)
$$\begin{aligned}& \dot{\hat{\Phi}}(t)=-k_{2}F_{i}^{T} \bigl(x^{d}_{i}(t-\tau)\bigr)e_{i}(t), \end{aligned}$$
(9)
$$\begin{aligned}& \dot{q}_{i}(t)=k_{3}e_{i}(t)^{T}e_{i}(t), \end{aligned}$$
(10)
$$\begin{aligned}& \dot{\beta}_{i}(t)=k_{4}e_{i}(t)^{T}\operatorname{sgn} \bigl(e_{i}(t)\bigr), \end{aligned}$$
(11)

where \(k_{1}\), \(k_{2}\), \(k_{3}\), and \(k_{4}\) are positive constants and \(\hat{\Phi}(t)\) and \(\hat{\theta}_{i}(t)\) are the estimated parameters for the reference node (1) and network (3), respectively.

Proof

Construct the Lyapunov function candidate as follows:

$$\begin{aligned} V(t) =&\frac{1}{2}\sum ^{N}_{i=1}e_{i}(t)^{T}e_{i}(t)+ \frac {1}{2k_{1}}\sum^{N}_{i=1}\tilde{ \theta}^{T}_{i}(t)\tilde{\theta}_{i}(t) + \frac{1}{2k_{2}}\sum^{N}_{i=1}\tilde{ \Phi}_{i}^{T}(t)\tilde{\Phi }_{i}(t) \\ &{}+\frac{1}{2k_{3}}\sum^{N}_{i=1} \tilde{q}^{2}_{i}(t)+\frac {1}{2k_{4}}\sum ^{N}_{i=1}\tilde{\beta}^{2}_{i}(t)+ \frac{1}{2}\int_{t-d_{i}}^{t} \sum ^{N}_{i=1} e_{i}(s)^{T}e_{i}(s) \,\mathrm{d}s, \end{aligned}$$
(12)

where \(\tilde{\Phi}_{i}(t)=\hat{\Phi}_{i}(t)-\Phi\), \(\tilde{\theta}_{i}(t)=\hat {\theta}_{i}(t)-\theta_{i}\), \(\tilde{q}_{i}(t)=q_{i}(t)-q^{*}_{i}\), \(\tilde {\beta}_{i}(t)=\beta_{i}(t)-\beta^{*}_{i}\), where \(q^{*}_{i}\) and \(\beta^{*}_{i}\) are positive constants.

The time derivative of \(V(t)\) along the error dynamics (6) is

$$\begin{aligned} \dot{V} =&\sum_{i=1}^{N} \biggl[e^{T}_{i}(t)\dot{e}_{i}(t)+ \frac {1}{k_{1}}\dot{\hat{\theta_{i}}}^{T}(t)\tilde{ \theta}_{i}(t)+ \frac {1}{k_{2}}\dot{\hat{\Phi_{i}}}^{T}(t) \tilde{\Phi}_{i}(t)+ \frac {1}{k_{3}} \dot{q}_{i} \tilde{q}_{i}(t)+ \frac{1}{k_{4}} \dot{\beta }_{i}\tilde{ \beta}_{i}(t) \biggr] \\ &{}+\frac{1}{2} \sum^{N}_{i=1} e_{i}(t)^{T}e_{i}(t)-\frac{1}{2} \sum ^{N}_{i=1} e_{i}(t-d_{i})^{T}e_{i}(t-d_{i}). \end{aligned}$$
(13)

By application of the control input (7) to the error dynamics \(\dot{e}_{i}(t)\) we have

$$\begin{aligned} \dot{V} =& \sum_{i=1}^{N} \bigl[e^{T}_{i}(t) \bigl(-q_{i}e_{i}(t)- \beta _{i}(t)\operatorname{sgn}\bigl(e_{i}(t)\bigr)-G_{i} \bigl(x^{r}_{i}(t)\bigr)\tilde{\theta}_{i}(t) \bigr) \bigr] \\ &{}+ \sum_{i=1}^{N} \Biggl[e^{T}_{i}(t) \Biggl(\alpha F\bigl(x^{d}(t-\tau)\bigr)\tilde {\Phi}(t)+c\sum ^{N}_{j=1}a_{ij}\Gamma e_{j}(t-d_{i})+ \Delta _{i}(t)-\alpha\Delta_{d}(t) \Biggr) \Biggr] \\ &{}+\sum_{i=1}^{N} \biggl[ \frac{1}{k_{1}}\dot{\hat{\theta _{i}}}^{T}(t)\tilde{ \theta}_{i}(t)+ \frac{1}{k_{2}}\dot{\hat{\Phi _{i}}}^{T}(t) \tilde{\Phi}_{i}(t)+ \frac{1}{k_{3}} \dot{q}_{i}\tilde {q}_{i}(t)+\frac{1}{k_{4}} \dot{\beta}_{i}\tilde{ \beta}_{i}(t) \biggr] \\ &{}+\frac{1}{2} \sum^{N}_{i=1} e_{i}(t)^{T}e_{i}(t)-\frac{1}{2} \sum ^{N}_{i=1} e_{i}(t-d_{i})^{T}e_{i}(t-d_{i}). \end{aligned}$$
(14)

From the adaptation laws (8)-(11), V̇ is inferred as follows:

$$\begin{aligned} \dot{V} =&-\sum_{i=1}^{N}q^{*}e^{T}_{i}(t)e_{i}(t)- \sum_{i=1}^{N}\beta ^{*}e^{T}_{i}(t)\operatorname{sgn} \bigl(e_{i}(t)\bigr)+ \sum^{N}_{i=1}e^{T}_{i}(t) \bigl(\Delta _{i}(t)-\alpha\Delta_{d}(t) \bigr) \\ &{}+c\sum^{N}_{i=1}e^{T}_{i}(t) \sum^{N}_{j=1}a_{ij}\Gamma e_{j}(t-d_{i})+\frac{1}{2} \sum ^{N}_{i=1} e_{i}(t)^{T}e_{i}(t) -\frac{1}{2} \sum^{N}_{i=1} e_{i}(t-d_{i})^{T}e_{i}(t-d_{i}). \end{aligned}$$
(15)

Let \(e(t)=(e^{T}_{1}(t),e^{T}_{2}(t),\ldots,e^{T}_{N}(t))^{T}\in\mathbf {R}^{nN}\), \(P=(A \otimes\Gamma)\) where ⊗ represents the Kronecker product. Then we have

$$\begin{aligned} \dot{V} =& c e^{T}(t)P e(t-d)-\sum _{i=1}^{N}q^{*}e^{T}_{i}(t)e_{i}(t)- \sum_{i=1}^{N}\beta ^{*}e^{T}_{i}(t)\operatorname{sgn} \bigl(e_{i}(t)\bigr) \\ &{}+ \sum^{N}_{i=1}e^{T}_{i}(t) \bigl(\Delta_{i}(t)-\alpha\Delta_{d}(t) \bigr)+ \frac{1}{2} \sum^{N}_{i=1} e_{i}(t)^{T}e_{i}(t) -\frac{1}{2} \sum^{N}_{i=1} e_{i}(t-d_{i})^{T}e_{i}(t-d_{i}). \end{aligned}$$

We use the fact \(2x^{T}y\leq x^{T}Sx+y^{T}S^{-1}y\) for any vector \(x,y\in\mathbf{R}^{m}\), and a positive definite matrix \(S\in\mathbf {R}^{m\times m}\). From the assumption 1, the following inequality is inferred:

$$\Delta_{i}(t)-\alpha\Delta_{d}(t)\leq\bigl\| \bigl( \Delta_{i}(t)-\alpha \Delta_{d}(t)\bigr)\bigr\| \leq \bigl\| \Delta_{i}(t)\bigr\| +\alpha \bigl\| \Delta_{d}(t) \bigr\| \leq\varepsilon_{i}, $$

where \(\varepsilon_{i}\) is a positive constant. We have

$$\begin{aligned} \dot{V} \leq& \frac{1}{2}c^{2} e^{T}(t)P^{T}Pe(t)+ \frac {1}{2}e^{T}(t-d_{i})e(t-d_{i})-q^{*}e^{T}(t)e(t) \\ &{}+\sum^{N}_{i=1} \bigl( \varepsilon_{i}-\beta^{*} \bigr)\bigl\| e_{i}(t)\bigr\| +\frac{1}{2} e(t)^{T}e(t)- \frac{1}{2} e(t-d_{i})^{T}e(t-d_{i}) \\ \leq&e^{T}(t) \biggl(\frac{1}{2}c^{2} P^{T}P-q^{*}+\frac{1}{2}I \biggr)e(t)+\sum ^{N}_{i=1} \bigl(\varepsilon_{i}- \beta^{*} \bigr)\bigl\| e_{i}(t)\bigr\| \\ \leq&\bigl(\lambda- q^{*}\bigr)e(t)^{T}e(t)+\sum ^{N}_{i=1} \bigl(\varepsilon _{i}- \beta^{*} \bigr)\bigl\| e_{i}(t)\bigr\| , \end{aligned}$$

where \(\textstyle\lambda=\lambda_{\max} (\frac{c^{2} P^{T}P+I}{2} )\). Therefore, by taking appropriate \(q^{*}\) and \(\beta^{*}\) such that

$$\begin{aligned}& \bigl(\lambda-q^{*}\bigr)< 0, \\& \varepsilon_{i}-\beta^{*}< 0,\quad i=1,2,\ldots, N, \end{aligned}$$

we obtain

$$\dot{V}\leq-e(t)^{T}e(t). $$

Since V is positive definite and V̇ is negative definite, the error \(e_{i}(t)\) is asymptotically stable in the sense of Lyapunov stability theory and the networks (3) projective lag synchronizes the drive system (1) asymptotically by the control (7) and the update laws (8)-(11). This completes the proof. □

4 PLS in DRDNs with time-varying delayed coupling

The adaptive control method is designed to realize projective lag synchronization for uncertain complex dynamical networks with time-varying delay coupling.

Theorem 4.1

We assume a given synchronization scaling factor α and propagation delay \(\tau(t)\). The projective lag synchronization with time-varying delayed coupling in the drive-response dynamical networks can be realized if the control input and adaptive lows are chosen as

$$\begin{aligned}& \begin{aligned}[b] u_{i}(t) ={}&{-}q_{i}e_{i}(t)- \beta_{i}\operatorname{sgn}\bigl(e_{i}(t)\bigr)-g_{i} \bigl(x^{r}_{i}(t)\bigr)- G_{i} \bigl(x^{r}_{i}(t)\bigr)\hat{\theta}_{i}(t) \\ &{} +\alpha \bigl(f\bigl(x^{d}(t-\tau)\bigr)+F\bigl(x^{d}(t- \tau)\bigr)\hat{\Phi}(t) \bigr), \quad i=1,\ldots,N,\end{aligned} \end{aligned}$$
(16)
$$\begin{aligned}& \dot{\hat{\theta}}_{i}(t)=k_{1}G_{i}^{T} \bigl(x^{r}_{i}(t)\bigr)e_{i}(t), \end{aligned}$$
(17)
$$\begin{aligned}& \dot{\hat{\Phi}}(t)=-k_{2}F_{i}^{T} \bigl(x^{d}_{i}(t-\tau)\bigr)e_{i}(t), \end{aligned}$$
(18)
$$\begin{aligned}& \dot{q}_{i}(t)=k_{3}e_{i}(t)^{T}e_{i}(t), \end{aligned}$$
(19)
$$\begin{aligned}& \dot{\beta}_{i}(t)=k_{4}e_{i}(t)^{T}\operatorname{sgn} \bigl(e_{i}(t)\bigr), \end{aligned}$$
(20)

where \(k_{1}\), \(k_{2}\), \(k_{3}\), and \(k_{4}\) are positive constants and \(\hat{\Phi}(t)\) and \(\hat{\theta}_{i}(t)\) are the estimated parameters for the reference node(1) and network (3), respectively.

Proof

Choose the Lyapunov function candidate as follows:

$$\begin{aligned} V(t) =&\frac{1}{2}\sum^{N}_{i=1}e_{i}(t)^{T}e_{i}(t)+ \frac {1}{2k_{1}}\sum^{N}_{i=1}\tilde{ \theta}^{T}_{i}(t)\tilde{\theta}_{i}(t) + \frac{1}{2k_{2}}\sum^{N}_{i=1}\tilde{ \Phi}_{i}^{T}(t)\tilde{\Phi }_{i}(t) \\ &{}+\frac{1}{2k_{3}}\sum^{N}_{i=1} \tilde{q}^{2}_{i}(t)+\frac {1}{2k_{4}}\sum ^{N}_{i=1}\tilde{\beta}^{2}_{i}(t) \\ &{}+\frac{1}{2(1-\eta)}\int_{t-\tau_{1}}^{t} \sum ^{N}_{i=1} e_{i}(s)^{T}e_{i}(s) \,\mathrm{d}s. \end{aligned}$$
(21)

The rest of the proof is similar to Theorem 3.1 According to the Lyapunov stability theory, the error system is asymptotically stable. This completes the proof. □

5 Illustrative example

This section presents the drive-response dynamical networks with three identical, different nodes systems, unknown parameters, and disturbance, which are used to show the effectiveness of the proposed schemes obtained in the previous sections. We use the Lorenz system as drive system, which is described as follows:

$$ \begin{pmatrix} \dot{x}_{1}^{d} \\ \dot{x}_{2}^{d} \\ \dot{x}_{3}^{d} \end{pmatrix} = \begin{pmatrix} 0 \\ -x_{1}^{d}x_{3}^{d}-x_{2}^{d} \\ x_{1}^{d}x_{2}^{d} \end{pmatrix} + \begin{pmatrix} x_{2}^{d}-x_{1}^{d}& 0 & 0 \\ 0 & x_{1}^{d} & 0 \\ 0 & 0 & -x_{3}^{d} \end{pmatrix} \begin{pmatrix} \Phi_{1} \\ \Phi_{2} \\ \Phi_{3} \end{pmatrix} +\Delta_{d}(t), $$
(22)

where the unknown parameters vector and mismatch terms are chosen as \(\Phi= [\Phi_{1}\ \Phi_{2}\ \Phi_{3}]=[10\ 28\ \frac {8}{3}]\), \(\Delta_{d}(t)=[ 2\cos(t)\ 3\sin(t)\ \sin(t)]\).

The inner coupling matrix \(\Gamma=I_{3\times3}\) and the coupling configuration matrix \(A=(a_{ij})\) is chosen to be

$$\begin{aligned} A= \begin{bmatrix} -2 & 1 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{bmatrix}. \end{aligned}$$

5.1 Synchronization with constant delay

We discuss the problem of PLS in drive-response dynamical networks with identical and different nodes consisting of fully unknown parameters, mismatch terms, and disturbance with constant delay coupling.

5.1.1 Synchronization with identical nodes

We take a chaotic Chen system as the ith networks nodes with unknown parameters and disturbance to realize PLS in DRDNs and verify the effectiveness of the proposed scheme which can be described as follows:

$$\begin{aligned} \begin{pmatrix} \dot{x}_{i1}^{r} \\ \dot{x}_{i2}^{r} \\ \dot{x}_{i3}^{r} \end{pmatrix} =& \begin{pmatrix} 0 \\ -x_{i1}^{r}x_{i3}^{r} \\ x_{i1}^{r}x_{i2}^{r} \end{pmatrix} + \begin{pmatrix} x_{i2}^{r}-x_{i1}^{r}& 0 & 0 \\ -x_{i1}^{r} & x_{i1}^{r}+x_{i2}^{r} & 0 \\ 0 & 0 & -x_{i3}^{r} \end{pmatrix} \begin{pmatrix} \theta_{i1} \\ \theta_{i2} \\ \theta_{i3} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{ij} \Gamma x^{r}_{j}(t-d_{i})+\Delta_{i}(t)+u_{i}. \end{aligned}$$
(23)

Here the unknown parameters vector is \(\theta_{1}= [35\ 28\ 3]^{T}\). The disturbance signals are chosen as \(\Delta_{i}= [0.3\cos(t)\sin(t)\ 0.1\sin(t)\ 0.5\cos(t)]\).

In these numerical simulations, we assume that \(c=0.2\), \(\alpha=2\), \(d_{i}=0.2\), and \(\tau=1\). The gains of the adaptive laws (8)-(11) are \(k_{1}= 9\), \(k_{2}= 8\), \(k_{3}=1\), \(k_{4}=0.8 \). We take the initial states as \(x^{d}(0)= [ 1\ {-}1\ {-}1]^{T} \), \(x^{r}_{i}(0)\) are chosen in \([-5, 5 ]\) randomly, and \(\hat{\Phi}_{0} = \hat{\theta}_{i0}= q_{i0} =\beta_{i0}=0\).

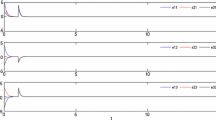
The numerical results are presented in Figures 1 and 2. The time evolution of the synchronization errors is illustrated in Figure 1, which displays \(e\longrightarrow0 \) with \(t \longrightarrow\infty\). The identified parameters of the reference node and network nodes are depicted in Figure 2(a) and Figure 2(b), which converge to their real values. These results verify that the proposed control (7) with adaptive laws (8)-(11) makes the network (3) projective lag synchronized, even if the network and the reference node (1) have fully unknown parameters, mismatch terms, and disturbances.

Figure 1
figure 1

The synchronization error \(\pmb{e_{i}(t)=x_{i}^{r}(t)- \alpha x^{d}(t-\tau)}\) .

Full size image
Figure 2
figure 2

The estimated parameters \(\pmb{\hat{\phi_{i}}}\) (a) and \(\pmb{\hat{\theta_{i}}}\) (b).

Full size image

5.1.2 Synchronization with different nodes

The Chen system, the Lu system, and the Rossler system as the response networks with constant delayed coupling, respectively, are described as follows:

$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{11}^{r} \\ \dot{x}_{12}^{r} \\ \dot{x}_{13}^{r} \end{pmatrix} ={}& \begin{pmatrix} 0 \\ -x_{11}^{r}x_{13}^{r} \\ x_{11}^{r}x_{12}^{r} \end{pmatrix} + \begin{pmatrix} x_{12}^{r}-x_{11}^{r}& 0 & 0 \\ -x_{11}^{r} & x_{11}^{r}+x_{12}^{r} & 0 \\ 0 & 0 & -x_{13}^{r} \end{pmatrix} \begin{pmatrix} \theta_{11} \\ \theta_{12} \\ \theta_{13} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{1j}\Gamma x^{r}_{j}(t-d_{1})+u_{1}(t), \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{21}^{r} \\ \dot{x}_{22}^{r} \\ \dot{x}_{23}^{r} \end{pmatrix} ={}& \begin{pmatrix} 0 \\ -x_{21}^{r}x_{23}^{r} \\ x_{21}^{r}x_{22}^{r} \end{pmatrix} + \begin{pmatrix} x_{22}^{r}-x_{21}^{r}& 0 & 0 \\ 0 & x_{22}^{r} & 0 \\ 0 & 0 & -x_{23}^{r} \end{pmatrix} \begin{pmatrix} \theta_{21} \\ \theta_{22} \\ \theta_{23} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{2j}\Gamma x^{r}_{j}(t-d_{2})+u_{2}(t),\end{aligned} \end{aligned}$$
(25)
$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{31}^{r} \\ \dot{x}_{32}^{r} \\ \dot{x}_{33}^{r} \end{pmatrix} ={}& \begin{pmatrix} -x_{32}^{r}-x_{33}^{r} \\ x_{31}^{r} \\ x_{31}^{r}x_{32}^{r}+0.2 \end{pmatrix} + \begin{pmatrix} 0 & 0 \\ x_{32}^{r} & 0 \\ 0 & -x_{33}^{r} \end{pmatrix} \begin{pmatrix} \theta_{31} \\ \theta_{32} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{3j}\Gamma x^{r}_{j}(t-d_{3})+u_{3}(t).\end{aligned} \end{aligned}$$
(26)

In these numerical simulations, we assume that \(c=0.2\), \(\alpha=2\), \(d_{i}=0.2\), and \(\tau=1\). The gains of the adaptive laws (8)-(11) are \(k_{1}= 9\), \(k_{2}= 9\), \(k_{3}=1\), \(k_{4}=2 \), and \(q_{i}=0 \). We take the initial states as \(x^{d}(0)= [1\ 2\ 3]^{T} \), \(x^{r}_{i}(0)\) are chosen in \([-5 , 5 ]\) randomly, and \(\hat {\Phi}_{0} = \hat{\theta}_{i0}= q_{i0} =\beta_{i0}=0\).

The time evolution of the synchronization errors is illustrated in Figure 3, which displays \(e\longrightarrow0 \) with \(t \longrightarrow \infty\). The estimated parameters of the reference node and network nodes are depicted in Figure 4(a) and Figure 4(b), respectively, which converge to their real values. These results prove that the proposed control (7) with adaptive laws (8)-(10) makes the network (3) projective lag synchronized if the drive system and the network have unknown parameters.

Figure 3
figure 3

The synchronization error of different nodes.

Full size image
Figure 4
figure 4

The estimated parameters \(\pmb{\hat{\phi_{i}}}\) (a) and \(\pmb{\hat{\theta_{i}}}\) (b) with constant coupling delay.

Full size image

5.2 Synchronization with varying coupling delay coupling

In this subsection, a drive-response dynamical networks with three identical, different node systems, fully unknown parameters, mismatch, and disturbance terms are used to show the effectiveness of the proposed schemes obtained in the previous sections.

5.2.1 Synchronization with identical nodes

The chaotic Chen system is chosen as three nodes of complex dynamical networks; the complex dynamical networks with time-varying coupling delay can be described as follows:

$$ \begin{aligned}[b] \begin{pmatrix} \dot{x}_{i1}^{r} \\ \dot{x}_{i2}^{r} \\ \dot{x}_{i3}^{r} \end{pmatrix}={}& \begin{pmatrix} 0 \\ -x_{i1}^{r}x_{i3}^{r} \\ x_{i1}^{r}x_{i2}^{r} \end{pmatrix} + \begin{pmatrix} x_{i2}^{r}-x_{i1}^{r}& 0 & 0 \\ -x_{i1}^{r} & x_{i1}^{r}+x_{i2}^{r} & 0 \\ 0 & 0 & -x_{i3}^{r} \end{pmatrix} \begin{pmatrix} \theta_{i1} \\ \theta_{i2} \\ \theta_{i3} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{ij} \Gamma x^{r}_{j}\bigl(t-\tilde{d}_{i}(t)\bigr)+ \Delta _{i}(t)+u_{i}. \end{aligned} $$
(27)

The propagation delay \(d_{i}(t)=1+0.2\sin(t)\) and \(\tau=1\). The gains of the adaptive laws (17)-(20) are \(k_{1}= 15\), \(k_{2}= 10\), \(k_{3}=1\), \(k_{4}=0.9 \). We take the initial states as \(x^{d}(0)= [0.2\ 0.1\ 0.3]^{T} \), \(x^{r}_{i}(0)\) are chosen in \([-5 , 5 ]\) randomly, and \(\hat{\Phi}_{0} = \hat{\theta}_{i0}= q_{i0} =\beta _{i0}=0\).

The time evolution of the synchronization errors is depicted in Figure 5, which displays \(e\longrightarrow0 \) with \(t \longrightarrow\infty\). The estimated parameters of the reference node and network nodes are depicted in Figure 6(a) and Figure 6(b), which converge to their real values. These results verify that the proposed control (21) with adaptive laws (17)-(20) makes the network (3) projective lag synchronized.

Figure 5
figure 5

The synchronization error of identical nodes with time-varying delay.

Full size image
Figure 6
figure 6

The estimated parameters \(\pmb{\hat{\phi_{i}}}\) (a) and \(\pmb{\hat{\theta_{i}}}\) (b) with time-varying coupling delay.

Full size image

5.2.2 Synchronization with different nodes

The chaotic Chen system, the Lu system, and the Rossler system are chosen as nodes of complex dynamical networks; complex dynamical networks with time-varying coupling delay can be described as follows:

$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{11}^{r} \\ \dot{x}_{12}^{r} \\ \dot{x}_{13}^{r} \end{pmatrix} ={}& \begin{pmatrix} 0 \\ -x_{11}^{r}x_{13}^{r} \\ x_{11}^{r}x_{12}^{r} \end{pmatrix} + \begin{pmatrix} x_{12}^{r}-x_{11}^{r}& 0 & 0 \\ -x_{11}^{r} & x_{11}^{r}+x_{12}^{r} & 0 \\ 0 & 0 & -x_{13}^{r} \end{pmatrix} \begin{pmatrix} \theta_{11} \\ \theta_{12} \\ \theta_{13} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{1j}\Gamma x^{r}_{j}\bigl(t-\tilde{d}_{1}(t) \bigr)+u_{1}(t), \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{21}^{r} \\ \dot{x}_{22}^{r} \\ \dot{x}_{23}^{r} \end{pmatrix} ={}& \begin{pmatrix} 0 \\ -x_{21}^{r}x_{23}^{r} \\ x_{21}^{r}x_{22}^{r} \end{pmatrix} + \begin{pmatrix} x_{22}^{r}-x_{21}^{r}& 0 & 0 \\ 0 & x_{22}^{r} & 0 \\ 0 & 0 & -x_{23}^{r} \end{pmatrix} \begin{pmatrix} \theta_{21} \\ \theta_{22} \\ \theta_{23} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{2j}\Gamma x^{r}_{j}\bigl(t-\tilde{d}_{2}(t) \bigr)+u_{2}(t), \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}& \begin{aligned}[b] \begin{pmatrix} \dot{x}_{31}^{r} \\ \dot{x}_{32}^{r} \\ \dot{x}_{33}^{r} \end{pmatrix} ={}& \begin{pmatrix} -x_{32}^{r}-x_{33}^{r} \\ x_{31}^{r} \\ x_{31}^{r}x_{32}^{r}+0.2 \end{pmatrix} + \begin{pmatrix} 0 & 0 \\ x_{32}^{r} & 0 \\ 0 & -x_{33}^{r} \end{pmatrix} \begin{pmatrix} \theta_{31} \\ \theta_{32} \end{pmatrix} \\ &{}+ c\sum^{3}_{j=1}a_{3j}\Gamma x^{r}_{j}\bigl(t-\tilde{d}_{3}(t) \bigr)+u_{3}(t). \end{aligned} \end{aligned}$$
(30)

In these numerical simulations, we assume the time delay \(d_{i}(t)=1+0.2\sin(t)\) and \(\tau=1\). The gain of the adaptive laws (17)-(20) are \(k_{1}= 7\), \(k_{2}= 9\), \(k_{3}=1\), \(k_{4}=2.5 \). We take the initial states as \(x^{d}(0)= [3\ 2\ 1]^{T} \), \(x^{r}_{i}(0)\) are chosen in \([-5 , 5 ]\) randomly and \(\hat{\Phi}_{0} = \hat{\theta}_{i0}= q_{i0} =\beta_{i0}=0\).

In Figure 7 shows the time evolution of the synchronization errors. The estimated parameters of the reference node and network nodes are depicted in Figure 8(a) and Figure 8(b), respectively, which converge to their real values. These results verify that the proposed control (21) with adaptive laws (17)-(19) makes the network (3) projective lag synchronized, even though the drive system and the network have unknown parameters.

Figure 7
figure 7

The synchronization error of different nodes with time-varying delay.

Full size image
Figure 8
figure 8

The estimated parameters \(\pmb{\hat{\phi_{i}}}\) (a) and \(\pmb{\hat{\theta_{i}}}\) (b) with time-varying coupling delay.

Full size image

6 Conclusion

An adaptive projective lag synchronization (PLS) scheme was proposed in drive-response dynamical networks with delayed coupling consisting of identical and different nodes. Both of the reference node and network nodes have fully unknown parameters and disturbances. Adaptive control and update laws were designed to achieve the PLS with constant time delay and with time-varying coupling delay. Based on the Lyapunov stability theory and adaptive laws the unknown parameters were estimated. Furthermore, the unknown bounded disturbances were also overcome by the proposed control. The numerical results showed the effectiveness of the proposed approach.