Abstract
In this paper, the exact spatiotemporal soliton solutions of the generalized \((3+1)\)-dimensional nonlinear Schrödinger equation with varying coefficients in optical fiber communication are obtained explicitly by using the similarity transformation. In addition, the propagation characteristics of the spatiotemporal optical solitons which can be dramatically affected by the complicated group velocity dispersion and self-phase modulation are discussed in detail.
Similar content being viewed by others
1 Introduction
The nonlinear Schrödinger (NLS) equation is one of the important mathematical models in many fields of physics, which has been widely applied in Bose-Einstein condensates [1–3], nonlinear optical fiber communication [4, 5], plasma physics [6, 7], hydrodynamics [8], and so on. Recently more and more people have been devoted to solving the exact solutions of the generalized NLS models [9–11]. Today, the temporal optical solitons of the NLS equation have been the objects of theoretical and experimental studies in optical fiber communication, and optical solitons are regarded as an important alternative to the next generation of ultrafast optical telecommunication systems. The study of optical solitons has reached the stage of a real-life application. The propagation of optical pulse in monomode optical fiber is governed by the NLS equation.
As is known to all, there are many kinds of powerful methods to obtain the exact solutions of various nonlinear wave equations such as the NLS-type equations. For example, inverse scattering method [12], Bäcklund transformation [13, 14], Darboux transformation [15], Hirota bilinear method [16, 17], Lie symmetry method [18, 19], Riemann-Hilbert formulation [20], generalized sine-cosine method [21], similarity transformation [22–24], multiple exp-function method [25], and other efficient techniques [26–30]. Among all these methods, the similarity transformation is a powerful approach to solve high-dimensional and variable-coefficient NLS-type equations. In the framework of similarity transformation, the high-dimensional and variable-coefficient NLS-type equations can be transformed into ordinary differential equations with constant coefficient, which are easy to be solved. Thus in this paper, with the aid of the symbolic computation, we use the similarity transformation and construct the analytical spatiotemporal soliton solutions to the generalized \((3+1)\)-dimensional nonlinear Schrödinger equation with varying coefficients in nonlinear optics
where \(u\equiv u(z,\mathbf{r})\) with \(\mathbf{r}=(x,y,t)\in\mathbf {R}^{3}\), denotes the normalized slowly varying complex wave packet envelope in a diffractive nonlinear Kerr medium with anomalous dispersion, and \(|u|^{2}\) is the optical power. Notation \(\nabla\equiv (\partial_{x}, \partial_{y}, \partial_{t})\) is a gradient operator, and \(\nabla^{2}=\partial_{x}^{2}+\partial_{y}^{2}+\partial_{t}^{2}\) represents the 3D Laplacian. Here z is the normalized propagation distance, and t is the normalized retarded time, i.e., time in the frame of reference moving with the wave packet. All coordinates are made dimensionless by the choice of coefficients. The real function \(\alpha(z,\mathbf{r})=\mathbf{r}\mathbf {A}(z)\mathbf{r}\) stands for the linear potential, where \(\mathbf {A}(z)=\operatorname{diag}(a_{1}(z), a_{2}(z), a_{3}(z))\) is a diagonal z-dependent \(3\times3\) matrix. The real functions \(\beta(z)\), \(\chi(z)\) and \(\gamma (z)\) stand for the group velocity dispersion (GVD), self-phase modulation (SPM) and linear gain (\(\gamma>0\)) or loss (\(\gamma<0\)), respectively. Strong interference of the effects of nonlinearity and varying dispersion can lead to a rich variety of possible configurations for dispersion management.
The generalized \((3+1)\)-dimensional nonlinear Schrödinger equation Eq. (1) is of considerable importance in optical fiber communication as it describes the amplification or absorption of pulses propagating in a monomode optical fiber with distributed dispersion and nonlinearity. In practical applications, the model is of primary interest not only for the amplification and compression of optical solitons in inhomogeneous systems, but also for the stable transmission of soliton control.
The paper is organized as follows. In Section 2, the similarity transformation is described, which converts a partial differential equation with variable coefficients into a family of first-order ordinary differential equations. In Section 3, several periodic traveling wave solutions are derived and some examples, which demonstrate the propagation characteristics of the spatiotemporal solitons, are given. Finally, a short conclusion is presented.
2 Similarity transformation
Our goal is to search for a transformation connecting solutions of Eq. (1) with those of the stationary NLS equation with constant coefficients
Here, \(F\equiv F(\xi)\) is a function of the only variable \(\xi\equiv\xi (z,\mathbf{r})\) whose relation to the original variables \((z,\mathbf {r})\) is to be determined. Table 1 shows a part of the Jacobi elliptic functions (JEFs) solutions of Eq. (2). The constants \(q_{2}\) and \(q_{4}\) appearing in Eq. (2) are related to the square of the elliptic modulus M of JEFs (see Table 1) [27, 28]. The parameter M of JEFs varies between 0 and 1. When \(M\rightarrow0\), JEFs degenerate into trigonometric functions, i.e., \(\mathrm{sn}(x)\rightarrow\sin(x)\), \(\mathrm{cn}(x)\rightarrow\cos(x)\), \(\mathrm{dn}(x)\rightarrow1\), etc., and the periodic traveling wave solutions become the periodic trigonometric solutions. When \(M\rightarrow1\), JEFs degenerate into hyperbolic functions, i.e., \(\mathrm{sn}(x)\rightarrow \tanh(x), \mathrm{cn}(x)\rightarrow \operatorname{sech}(x)\), \(\mathrm{dn}(x)\rightarrow \operatorname{sech}(x)\), etc., and the periodic traveling wave solutions become the soliton solutions.
We consider the general similarity transformation
where \(f(z,\mathbf{r})\), \(B(z,\mathbf{r})\) and \(\xi(z,\mathbf{r})\) are all real-valued functions to be determined.
Requiring \(F(\xi)\) to satisfy Eq. (2) and \(u(z,\mathbf{r})\) to be a solution of Eq. (1), we substitute the ansatz (3) into Eq. (1) and after simple algebra obtain the set of equations
To solve Eqs. (4)-(8) explicitly, we first consider the special case of \(f(z,\mathbf{r})\) depending only on the propagation coordinate z, i.e., \(f(z,\mathbf{r})\equiv f(z)\). Then Eqs. (4)-(8) are simplified
We consider ξ parameterizing moving plains
where \(\mathbf{k}(z)=[k_{1}(z),k_{2}(z),k_{3}(z)]\). The nontrivial phase now reads
where
Substituting Eq. (14), Eq. (15) into Eqs. (9)-(13) and requiring that \(x^{n}\), \(y^{n}\), \(t^{n}\) (\(n=0,1,2\)) of each term be separately equal to zero, we obtain a system of algebraic and first-order ordinary differential equations that the parameters must satisfy:
where \(j=1,2,3\).
By solving Eqs. (16)-(22) self-consistently, one obtains a set of conditions on the coefficients and parameters, necessary for Eq. (1) to have exact periodic wave solutions.
3 Analytical solutions and the propagation characteristics of the spatiotemporal solitons
As it is clear, Eq. (16) which is critical of Eqs. (16)-(22) is a standard Riccati equation with varying coefficients. The case of \(\beta \equiv \mathrm{const}\) has been studied in many papers (see, for example, [28, 29] and the references therein). In this paper, we concentrate on the case of \(\beta=e^{mz}\), \(a_{j}=s_{j}e^{-mz}\), \(j=1,2,3\), where m, \(s_{j}\) (\(j=1,2,3\)) are arbitrary nonzero constants, and the following set of exact solutions is found:
Here, \(b_{j}^{0}\), \(k_{j}^{0}\) (\(j=1,2,3\)), \(\omega_{0}\), \(c_{0}\), \(f_{0}\) are all arbitrary constants, and \(h_{j}\), \(\theta_{j}\), \(\rho_{j}\) are as follows.
I. When \(16s_{j}+m^{2}>0\), we have
II. When \(16s_{j}+m^{2}=0\), we have
where \(h_{j}^{0}\) is an arbitrary nonzero constant. However, if we take \(h_{j}^{0}\rightarrow0\), then \(h_{j}\), \(\theta_{j}\), \(\rho_{j}\) are as follows:
Incorporating these solutions back into Eq. (3), we can obtain the general periodic traveling wave solutions to the generalized NLSE
As long as one chooses the constants according to the relations listed in Table 1 and substitutes the appropriate \(F(\xi)\) into Eq. (37), one obtains the exact periodic traveling wave solutions to the generalized \((3+1)\)-dimensional NLSE.
As an example, we select the solutions 1, 2, 13, 14 in Table 1 and the parameters \(b_{j}^{0}=k_{j}^{0}=f_{0}=1\) (\(j=1,2,3\)), \(\omega_{0}=c_{0}=0\), \(\gamma=\cos (z)\). According to the value of parameter \(h_{j}^{0}\), we list two classes.
3.1 The parameter \(h_{j}^{0}=1\) (\(j=1,2,3\))
Family 1
Taking parameters \(m=0.03\), \(s_{j}=0.0001\), we can obtain the periodic wave solution
and the nonlinearity coefficient
where
Family 2
Taking parameters \(m=-0.03\), \(s_{j}=0.0001\), we can obtain the periodic wave solution
and the nonlinearity coefficient
where
Family 3
Taking parameters \(m=0.04\), \(s_{j}=-0.0001\), we can obtain the periodic wave solution
where
The nonlinearity coefficient is of the form
The function f is of the form
Family 4
Taking parameters \(m=-0.04\), \(s_{j}=-0.0001\), we can obtain the periodic wave solution
where
The nonlinearity coefficient is of the form
The function f is of the form
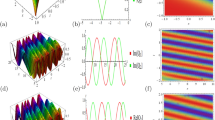
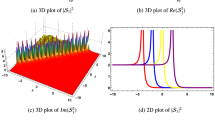
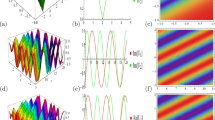
Figures 1 and 2 show the profiles of the nonlinear parameter χ and the function f as a function of z given by Eqs. (39)-(40), (42)-(43), (45)-(46), (48)-(49). The function f has an important effect on modulating the amplitude of the solution u. It is seen in this situation that χ and f are periodically oscillating along the z-axis. It can also be seen that the amplitude of χ increases along the z-axis in Figure 1(a) and Figure 2(a), and the amplitude of f decreases along the z-axis in Figure 1(b) and Figure 2(b). However, the amplitude of χ decreases along the z-axis in Figure 1(c) and Figure 2(c), and the amplitude of f increases along the z-axis in Figure 1(d) and Figure 2(d). Figure 3(a) and (b) presents the evolution plots of the dark and bright exact one-soliton solutions \(u_{1}\) given by Eq. (38) respectively under the strict integrable condition Eq. (39). Figure 3(c) and (d) presents the periodic evolution plot described by the Jacobian elliptic sine and cosine functions, respectively. It can also be seen from Figure 3 that the soliton maintains its shape when traveling down the fiber, in spite of the velocity and the background being fluctuant due to the fluctuation of the fiber parameters. Figure 4 shows the evolution plots of optical power \(|u_{2}|^{2}\) given by Eq. (41) under the strict integrable condition Eq. (42). Figure 5 shows the evolution plots of optical power \(|u_{3}|^{2}\) given by Eq. (44) under the strict integrable condition Eq. (45). Figures 6 and 7 show the evolution plots of optical power \(|u_{4}|^{2}\) given by Eq. (47) under the strict integrable condition Eq. (48). Note that \(F(\xi )\) in Figure 7 is the solutions 13, 14 in Table 1.
Density \(\pmb{|u_{1}|^{2}}\) as a function of propagation distance \(\pmb{L\equiv x+y+t}\) and z given by Eq. ( 38 ), with (a) \(\pmb{F(\xi)=\tanh(\xi)}\) , (b) \(\pmb{F(\xi)=\operatorname{sech}(\xi)}\) , (c) \(\pmb{F(\xi)=\mathrm{sn}(\xi)}\) , \(\pmb{M=0.5}\) and (d) \(\pmb{F(\xi )=\mathrm{cn}(\xi)}\) , \(\pmb{M=0.5}\) .
Density \(\pmb{|u_{2}|^{2}}\) as a function of propagation distance \(\pmb{L\equiv x+y+t}\) and z given by Eq. ( 41 ), with (a) \(\pmb{F(\xi)=\tanh(\xi)}\) , (b) \(\pmb{F(\xi)=\operatorname{sech}(\xi)}\) , (c) \(\pmb{F(\xi)=\mathrm{sn}(\xi)}\) , \(\pmb{M=0.5}\) and (d) \(\pmb{F(\xi )=\mathrm{cn}(\xi)}\) , \(\pmb{M=0.5}\) .
Density \(\pmb{|u_{3}|^{2}}\) as a function of propagation distance \(\pmb{L\equiv x+y+t}\) and z given by Eq. ( 44 ), with (a) \(\pmb{F(\xi)=\tanh(\xi)}\) , (b) \(\pmb{F(\xi)=\operatorname{sech}(\xi)}\) , (c) \(\pmb{F(\xi)=\mathrm{sn}(\xi)}\) , \(\pmb{M=0.5}\) and (d) \(\pmb{F(\xi )=\mathrm{cn}(\xi)}\) , \(\pmb{M=0.5}\) .
Density \(\pmb{|u_{4}|^{2}}\) as a function of propagation distance \(\pmb{L\equiv x+y+t}\) and z given by Eq. ( 47 ), with (a) \(\pmb{F(\xi)=\tanh(\xi)}\) , (b) \(\pmb{F(\xi)=\operatorname{sech}(\xi)}\) , (c) \(\pmb{F(\xi)=\mathrm{sn}(\xi)}\) , \(\pmb{M=0.5}\) and (d) \(\pmb{F(\xi )=\mathrm{cn}(\xi)}\) , \(\pmb{M=0.5}\) .
Density \(\pmb{|u_{4}|^{2}}\) as a function of propagation distance \(\pmb{L\equiv x+y+t}\) and z given by Eq. ( 47 ), with (a) \(\pmb{F(\xi)=\mathrm{sn}/(1+\mathrm{dn})}\) , \(\pmb{M=0.9999}\) , (b) \(\pmb{F(\xi)=\mathrm{cn}/(\sqrt{1-M^{2}}+\mathrm{dn})}\) , \(\pmb{M=0.9999}\) , (c) \(\pmb{F(\xi )=\mathrm{sn}/(1+\mathrm{dn})}\) , \(\pmb{M=0.5}\) and (d) \(\pmb{F(\xi)=\mathrm{cn}/(\sqrt{1-M^{2}}+\mathrm{dn})}\) , \(\pmb{M=0.5}\) .
3.2 The parameter \(h_{j}^{0}=0\) (\(j=1,2,3\))
Family 5
Taking parameters \(m=0.03\), \(s_{j}=0.0001\), we can obtain the periodic wave solution as follows.
Case 1.
where
The nonlinearity coefficient is of the form
Case 2.
where
The nonlinearity coefficient is of the form
Family 6
Taking parameters \(m=-0.03\), \(s_{j}=0.0001\), we can obtain the periodic wave solution as follows.
Case 1.
where
The nonlinearity coefficient is of the form
Case 2.
where
The nonlinearity coefficient is of the form
Family 7
Taking parameters \(m=0.04\), \(s_{j}=-0.0001\), we can obtain the periodic wave solution
where
The nonlinearity coefficient is of the form
Family 8
Taking parameters \(m=-0.04\), \(s_{j}=-0.0001\), we can obtain the periodic wave solution
where
The nonlinearity coefficient is of the form
The evolution plots of solutions u in Families 5-8 are very close to the evolution plots in [28], and we omit the corresponding discussion for the limit of the length.
4 Conclusions
In conclusion, we have used similarity transformation to construct analytical spatiotemporal soliton solutions of the generalized \((3+1)\)-dimensional NLS equation with varying coefficients, and also investigated the propagation characteristics of the spatiotemporal solitons which can be dramatically affected by the complicated potential.
References
Bradley, CC, Sackett, CA, Tollett, JJ, Hulet, RG: Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett. 27, 1687-1690 (1995)
Saito, H, Ueda, M: Dynamically stabilized bright solitons in a two-dimensional Bose-Einstein condensate. Phys. Rev. Lett. 90, 040403 (2003)
Wang, DS, Hu, XH, Hu, J, Liu, WM: Quantized quasi-two-dimensional Bose-Einstein condensates with spatially modulated nonlinearity. Phys. Rev. A 81, 025604 (2010)
Porsezian, K, Hasegawa, A, Serkin, VN, Belyaeva, TL, Ganapathy, R: Dispersion and nonlinear management for femtosecond optical solitons. Phys. Lett. A 361, 504-508 (2007)
Calvo, GF, Belmonte-Beitia, J, Pérez-García, VM: Exact bright and dark spatial soliton solutions in saturable nonlinear media. Chaos Solitons Fractals 41, 1791-1798 (2009)
Rose, HA, Weinstein, MI: On the bound states of the nonlinear Schrödinger equation with a linear potential. Physica D 30, 207-218 (1988)
Oelza, D, Trabelsi, S: Analysis of a relaxation scheme for a nonlinear Schrödinger equation occurring in plasma physics. Math. Model. Anal. 19, 257-274 (2014)
Nore, C, Brachet, ME, Fauve, S: Numerical study of hydrodynamics using the nonlinear Schrödinger equation. Physica D 65, 154-162 (1993)
Wang, DS, Hu, XH, Liu, WM: Localized nonlinear matter waves in two-component Bose-Einstein condensates with time-and space-modulated nonlinearities. Phys. Rev. A 82, 023612 (2010)
Yan, ZY: Exact analytical solutions for the generalized non-integrable nonlinear Schrödinger equation with varying coefficients. Phys. Lett. A 374, 4838-4843 (2010)
Wang, DS, Song, SW, Xiong, B, Liu, WM: Vortex states in rotating Bose-Einstein condensate with spatiotemporally modulated interaction. Phys. Rev. A 84, 053607 (2011)
Ablowitz, MJ, Segur, H: Soliton and the Inverse Scattering Transformation. SIAM, Philadelphia (1981)
Rogers, C, Schief, WK: Backlund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory. Cambridge University Press, Cambridge (2002)
Wang, DS, Wei, XQ: Integrability and exact solutions of a two-component Korteweg de Vries system. Appl. Math. Lett. 51, 60-67 (2016)
Matveev, VB, Salle, MA: Darboux Transformation and Solitons. Springer, Berlin (1991)
Hirota, R: Exact solution of the Korteweg de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27, 1192-1194 (1971)
Ma, WX: Generalized bilinear differential equations. Stud. Nonlinear Sci. 2, 140-144 (2011)
Belmonte-Beitia, J, Pérez-García, VM, Vekslerchik, V: Lie symmetries and solitons in nonlinear systems with spatially inhomogeneous nonlinearities. Phys. Rev. Lett. 98, 064102 (2007)
Ma, WX, Chen, M: Direct search for exact solutions to the nonlinear Schrödinger equation. Appl. Math. Comput. 215, 2835-2842 (2009)
Wang, DS, Zhang, DJ, Yang, J: Integrable properties of the general coupled nonlinear Schrödinger equations. J. Math. Phys. 51, 023510 (2010)
Yan, ZY: Envelope compactons and solitary patterns. Phys. Lett. A 355, 212-215 (2006)
Belmonte-Beitia, J, Pérez-García, VM, Vekslerchik, V, Konotop, VV: Localized nonlinear waves in systems with time- and space-modulated nonlinearities. Phys. Rev. Lett. 100, 164102 (2008)
Wang, DS, Shi, YR, Chow, KW, Yu, ZX, Li, XG: Matter-wave solitons in a spin-1 Bose-Einstein condensate with time-modulated external potential and scattering lengths. Eur. Phys. J. D 67, 242 (2013)
Wang, DS, Ma, YQ, Li, XG: Prolongation structures and matter-wave solitons in \(F=1\) spinor Bose-Einstein condensate with time-dependent atomic scattering lengths in an expulsive harmonic potential. Commun. Nonlinear Sci. Numer. Simul. 19, 3556-3569 (2014)
Ma, WX, Zhu, ZN: Solving the \((3 + 1)\)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 218, 11871-11879 (2012)
Ma, WX, Wu, HY, He, JS: Partial differential equations possessing Frobenius integrable decompositions. Phys. Lett. A 364, 29-32 (2007)
Yan, ZY: The new tri-function method to multiple exact solutions of nonlinear wave equations. Phys. Scr. 78, 035001 (2008)
Wang, XL, Wu, ZH: New exact solutions and dynamics in \((3+1)\)-dimensional Gross-Pitaevskii equation with repulsive harmonic potential. Commun. Theor. Phys. 61, 583-589 (2014)
Ma, WX, Fuchssteiner, B: Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. Non-Linear Mech. 31, 329-338 (1996)
Ma, WX: Trilinear equations, Bell polynomials, and resonant solutions. Front. Math. China 8, 1139-1156 (2013)
Acknowledgements
This work is supported by the Science and Technology Project of Beijing Municipal Commission of Education (Grant No. KM201311232021).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors completed the paper together. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, X., Yang, J. Exact spatiotemporal soliton solutions to the generalized three-dimensional nonlinear Schrödinger equation in optical fiber communication. Adv Differ Equ 2015, 347 (2015). https://doi.org/10.1186/s13662-015-0683-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0683-4