1 Introduction

Dispersal is a ubiquitous phenomenon in the natural world. It is important for us to understand the ecological and evolutionary dynamics of populations mirrored by the large number of mathematical models devoting to it in the scientific literature [1–5]. In recent years, the analysis of these models focus on the coexistence of population and local (or global) stability of equilibria [6, 7]. Spatial factors play a fundamental role on the persistence and stability of the population, and the complete results have not yet been obtained even in the simplest one-species case. Most previous papers focused on the population dynamical system modeled by the ordinary differential equations. But in practice, it is often the case that diffusion occurs in regular pulses. For example, when winter comes, birds will migrate between patches in search for a better environment, whereas they do not diffuse in other seasons, and the excursion of foliage seeds to occur at fixed periods of time every year, thus impulsive diffusion provides a more natural description. Jiao et al. [8] presented a delayed predator-prey model with impulsive diffusion between two patches. They obtained the permanent condition of the system by the theory of impulsive delay differential equation.

The most threatening problem to society is the change in both terrestrial and aquatic environment caused by the different kinds of stresses (temperature, toxicants/pollutants, etc.) affecting the long term survival of species, human life, and biodiversity of the habitat [9–11]. The presence of a toxicant in the environments decreases the growth rate of species and its carrying capacity. In recent years, some investigations have been carried out to study the effect of toxicant on a single species population [12–15], and a lot of scholars have adopted a mathematical modeling approach to study the influence of environmental pollution on the surviving of a biological population [16, 17]. Most of the previous work assumed that input of toxicant was continuous. The toxicants, however, are often emitted to the environment with regular pulse [18]. A lot of data have indicated that the use of agriculture chemicals may cause potential harm to the health of both human beings and other living beings. If the spraying of agriculture chemicals can be regarded as time pulse discharge, modeling by the continuous input of toxin can be regarded as obsolete and should be replaced by impulsive perturbations. In this case, though the discharge of toxin is transient, the influence of the toxin will last long. Therefore, it is very important how to control the pulse input cycle of toxin to protect the population’s persistent existence.

Theories of impulsive differential equations have been introduced into population dynamics lately [19–24]. Impulsive equations are found in almost every domain of applied science and have been studied in many investigations [19–33], they generally describe phenomena which are subject to steep or instantaneous changes. Especially, Jiao et al. [24] suggested releasing pesticides is combined with transmitting infective pests into an SI model. This may be accomplished by avoiding periods when the infective pests would be exposed or placing the pesticides in a location where the transmitting infective pests would not contact it. So we address an impulsive differential equation modeling the process of releasing infective pests and spraying pesticides at different fixed moments.

The organization of this paper is as follows. In the next section, we introduce the model and background concepts. In Section 3, some important lemmas are presented. In Section 4, we give the globally asymptotically stable condition of population-extinction solution of system (2.1) and the population permanent condition of system (2.1). In Section 5, a numerical analysis and a brief discussion are given.

2 The model

In this work, we consider a single population system with impulsively unilateral diffusion and impulsive input toxins in a polluted environment,

$$ \textstyle\begin{cases} \left . \begin{aligned} & \tfrac{dx(t)}{dt}=x(t)(a-bx(t))-\beta c_{o}(t)x(t), \\ & \tfrac{dy(t)}{dt}=-dy(t),\\ & \tfrac{dc_{o}(t)}{dt}=fc_{e}(t)-(g+m)c_{o}(t),\\ & \tfrac{dc_{e}(t)}{dt}=-hc_{e}(t), \end{aligned} \right \}\quad t\neq n\tau, t\neq(n+l)\tau, \\ \left . \begin{aligned} & \triangle x(t)=0,\\ & \triangle y(t)=0,\\ & \triangle c_{o}(t)=0,\\ & \triangle c_{e}(t)=\mu, \end{aligned} \right \}\quad t= n\tau, n= 1,2,\ldots,\\ \left . \begin{aligned} & \triangle x(t)=-Dx(t),\\ & \triangle y(t)=Dx(t),\\ & \triangle c_{o}(t)=0,\\ & \triangle c_{e}(t)=0, \end{aligned} \right \}\quad t= (n+l)\tau, n= 1,2,\ldots,\\ x(0^{+})>0,\qquad y(0^{+})>0,\qquad c_{o}(0^{+})>0,\qquad c_{e}(0^{+})>0, \end{cases} $$
(2.1)

where we suppose that system (2.1) is composed of two patches connected by diffusion. Patch 1 is occupied by population \(x(t)\). Patch 2 is occupied by population \(y(t)\). \(x(t)\) represents the density of the population at patch 1, and \(y(t)\) represents the density of the population at patch 2. Patch 1 is polluted periodically. There is no pollution in patch 2. \(c_{o}(t)\) represents the concentration of toxicant in the organism of the population at time t in patch 1. \(c_{e}(t)\) represents the concentration of the toxicant in the system environment of patch 1. The intrinsic rate of natural increase and density dependence rate of the population in the first habitat are denoted by a, b, respectively. \(a/b\) denotes the carrying capacity of population in the patch 1. \(d>0\) represents the death rate of the population in patch 2. \(fc_{e}(t)\) is the organism’s net uptake of toxicant from the system environment at time t in patch 1. \(-g c_{0}(t)\) and \(-mc_{0}(t)\) represent the elimination and depuration rates of toxicant in the organism at time t in patch 1, respectively. \(-h c_{e}(t)\) represents the totality of losses from the system environment including processes such as biological transformation, chemical hydrolysis, volatilization, microbial degradation, and photosynthetic degradation at time t in patch 1, and \(h>f\) is assumed in this paper. \(\beta>0\) represents the depletion rate coefficient of the normal population during to the environment pollutant concentration of patch 1. The impulsive inputting toxicant occurs every τ period (τ is a positive constant)in patch 1. \(\triangle c_{e}(t)=c_{e}(t^{+})-c_{e}(t)\). \(\mu\geq0 \) represents the amount of the pulse input of toxicant concentration at \(t=(n+l)\tau\), \(0< l<1\), \(n\in Z_{+}\) in patch 1. D is the dispersal rate between the two patches. It is assumed that the net exchange from patch 1 to patch 2 is proportional to the pollution degree of patch 1. The pulse diffusion occurs every τ period (τ is a positive constant), the system evolves from its initial state without being further affected by diffusion until the next pulse appears, where \(\triangle x(n\tau)=x(n\tau^{+})-x(n\tau)\). \(x(n\tau^{+})\) represents the density of the population in patch 1 immediately after the nth diffusion pulse at time \(t = n\tau\), while \(x(n\tau)\) represents the density of the population in patch 1 before the nth diffusion pulse at time \(t = n\tau\), \(n = 0, 1, 2,\ldots\) .

In this paper, we always assume that

  1. (A1)

    the population diffuses periodically from patch 1 to patch 2 for dodging polluted environment in patch 1;

  2. (A2)

    the toxicants are emitted to the environment with regular pulse in patch 1, and patch 2 has no pollution.

3 Preliminary lemmas

Before discussing the main results, we will give some definitions, notations, and lemmas. Denote by \(f=(f_{1},f_{2},f_{3},f_{4})\) the map defined by the right hand of system (2.1). The solution of system (2.1), denoted by \(z(t)=(x(t),y(t),c_{o}(t), c_{e}(t))^{T}\), is a piecewise continuous function z: \(R_{+}\rightarrow R_{+}^{4}\), where \(R_{+}=[0,\infty)\), \(R_{+}^{4}=\{z\in R^{4}:z>0\}\). \(z(t)\) is continuous on \((n\tau, (n+l)\tau]\) and \(((n+l)\tau, (n+1)\tau]\) (\(n \in Z_{+}\), \(0 \leq l \leq1\)). According to [21], the global existence and uniqueness of solutions of system (2.1) is guaranteed by the smoothness properties of f, which denotes the mapping defined by the right-hand side of system (2.1).

Let \(V:R_{+}\times R_{+}^{4} \rightarrow R_{+}\), then V is said to belong to class \(V_{0}\), if

  1. (i)

    V is continuous in \((n\tau, (n+l)\tau]\times R^{4}_{+}\) and \(((n+l)\tau, (n+1)\tau]\times R^{4}_{+}\), for each \(z\in R^{4}_{+}\), \(n \in Z_{+}\). \(\lim_{(t, u)\rightarrow((n+l)\tau^{+}, z)}V(t,u)=V((n+l)\tau^{+}, z)\), and \(\lim_{(t,u)\rightarrow ((n+1)\tau^{+}, z)}V(t, u)=V((n+1)\tau^{+}, z)\) exist;

  2. (ii)

    V is locally \(Lipschitzian\) in z.

Definition 3.1

If \(V \in V_{0} \), then for \((t, z) \in(n \tau, (n+l)\tau]\times R^{4}_{+}\) and \(((n+l)\tau, (n+1)\tau]\times R^{4}_{+}\), the upper right derivative of \(V(t,z)\) with respect to the impulsive differential system (2.1) is defined as

$$D^{+}V(t,z)= \lim_{h \rightarrow 0} \sup\frac{1}{h} \bigl[V\bigl(t+h, z+hf(t,z)\bigr)-V(t,z)\bigr]. $$

Now, we show that all solutions of system (2.1) are uniformly ultimately bounded.

Lemma 3.2

There exists a constant \(M>0\) such that \(x(t)\leq M\), \(y(t)\leq M\) and \(c_{o}(t)\leq M\), \(c_{e}(t)\leq M\) for each solution \((x(t),y(t),c_{o}(t),c_{e}(t) )\) of system (2.1) with all t large enough.

Proof

Define \(V(t)=x(t)+y(t)+c_{o}(t)+c_{e}(t)\), and choose \(\lambda =\min\{d,g+m,h-f\}\), then \(t\neq n\tau\), we have

$$\begin{aligned} &D^{+}V(t)+ \lambda V(t) \\ &\quad \leq x(t)\bigl[(a+\lambda)-bx(t)\bigr]-(d-\lambda )y(t)-(g+m- \lambda)c_{o}(t)-(h-f-\lambda)c_{e}(t) \\ &\quad < -b\biggl(x(t)-\frac{a+\lambda}{2b}\biggr)^{2}+ \frac{(a+\lambda)^{2}}{4b}< \frac {(a+\lambda)^{2}}{4b}. \end{aligned} $$

For convenience, we denote \(\zeta=\frac{(a+\lambda)^{2}}{4b}\).

When \(t=(n+l)\tau\),

$$V\bigl((n+l)\tau^{+}\bigr)= x\bigl((n+l)\tau\bigr)+y\bigl((n+l)\tau \bigr)+c_{o}\bigl((n+l)\tau\bigr)+c_{e}\bigl((n+l)\tau \bigr)+\mu\leq V\bigl((n+l)\tau\bigr)+\mu. $$

When \(t=(n+1)\tau\),

$$\begin{aligned} V\bigl((n+1)\tau^{+}\bigr)&= x\bigl((n+1)\tau\bigr)+y \bigl((n+1)\tau\bigr)+c_{o}\bigl((n+1)\tau\bigr)+c_{e} \bigl((n+1)\tau\bigr)-Dx(t)+Dx(t) \\ & =V\bigl((n+1)\tau\bigr). \end{aligned} $$

From Lemma 2.2 [22], page 23, for \(t\in(n\tau,(n+l)\tau]\) and \(((n+l)\tau,(n+1)\tau]\), we have

$$V(t) \leq V\bigl(0^{+}\bigr)e^{-dt}+\frac{\zeta}{d} \bigl(1-e^{-dt}\bigr) +\mu\frac {e^{-d(t-\tau)}}{1-e^{-d\tau}}+\xi\frac{e^{d\tau}}{e^{d\tau}-1} \rightarrow \frac{\zeta}{d}+\mu\frac{e^{d\tau}}{e^{d\tau}-1}, \quad \mbox{as } t \rightarrow\infty. $$

So \(V(t)\) is uniformly ultimately bounded. Hence, by the definition of \(V(t)\), there exists a constant \(M>0\) such that \(x(t)\leq M\), \(y(t)\leq M\), \(c_{o}(t)\leq M\), and \(c_{e}(t)\leq M\) for t large enough. The proof is complete. □

The subsystem of (2.1) is

$$ \textstyle\begin{cases} \left . \begin{aligned} &\tfrac{dc_{o}(t)}{dt}=fc_{e}(t)-(g+m)c_{o}(t),\\ &\tfrac{dc_{e}(t)}{dt}=-hc_{e}(t), \end{aligned} \right \} \quad t\neq n\tau, n\in Z_{+}, \\ \left . \begin{aligned} & \triangle c_{o}(t)=0,\\ & \triangle c_{e}(t)=\mu, \end{aligned} \right \}\quad t= n\tau, n\in Z_{+}. \end{cases} $$
(3.1)

Then we give an important property of system (3.1) as follows.

Lemma 3.3

[33]

System (3.1) has a unique positive τ-periodic solution \((\widetilde{c_{o}(t)},\widetilde{c_{e}(t)})\), which is globally asymptotically stable, where

$$ \textstyle\begin{cases} \widetilde{c_{o}(t)}=\widetilde{c_{o}(0)}e^{-(g+m)(t-n\tau)} +\frac{\mu f(e^{-(g+m)(t-n\tau)}-e^{-h(t-n\tau)})}{(h-g-m)(1-e^{-h\tau })},\\ \widetilde{c_{e}(t)}=\frac{\mu e^{-h(t-n\tau)}}{1-e^{-h\tau}},\\ \widetilde{c_{o}(0)}=\frac{\mu f(e^{-(g+m)\tau}-e^{-h\tau })}{(h-g-m)(1-e^{-(g+m)\tau})(1-e^{-h\tau})},\\ \widetilde{c_{e}(0)}=\frac{\mu}{1-e^{-h\tau}}. \end{cases} $$
(3.2)

Remark 3.4

From Lemma 3.3, we can obtain \(m_{o}-\varepsilon\leq c_{o}(t)\leq M_{o}+\varepsilon\) and \(m_{e}-\varepsilon\leq c_{e}(t)\leq M_{e}+\varepsilon\) for t large enough, where \(m_{o}=\frac{\mu f(e^{-(g+m)\tau}-e^{-h\tau})}{(h-g-m)(e^{(g+m)\tau}-1)(1-e^{-h\tau})}>0\), \(M_{o}=\frac{\mu f(e^{-(g+m)\tau}-e^{-h\tau})}{(h-g-m)(1-e^{-(g+m)\tau})(1-e^{-h\tau })}+\frac{\mu f}{\vert h-g-m\vert (1-e^{-h\tau})}>0\), \(m_{e}=\frac{\mu e^{-h\tau}}{1-e^{-h\tau}}>0\) and \(M_{e}=\frac{\mu}{1-e^{-h\tau}}>0\) for a sufficiently small \(\varepsilon>0\).

4 The dynamics

In this section, we firstly prove that system (2.1) is permanent. For system (2.1) obviously exists a population-extinction boundary periodic solution \((0,0,\widetilde {c_{o}(t)},\widetilde{c_{e}(t)})\). Then we prove that the population-extinction boundary periodic solution \((0,0,\widetilde{c_{o}(t)}, \widetilde{c_{e}(t)})\) of system (2.1) is globally asymptotically stable.

4.1 The permanence of (2.1)

The subsystem of system (2.1) is obtained as follows:

$$ \textstyle\begin{cases} \left . \begin{aligned} &\tfrac{dx(t)}{dt}=x(t)(a-bx(t))-\beta c_{o}(t)x(t), \\ &\tfrac{dy(t)}{dt}=-dy(t), \end{aligned} \right \}\quad t\neq(n+1)\tau, \\ \left . \begin{aligned} &\triangle x(t)=-Dx(t),\\ &\triangle y(t)=D x(t), \end{aligned} \right \}\quad t= (n+1)\tau, n= 1,2,\ldots. \end{cases} $$
(4.1)

Considering the first equation of system (4.1) and Remark 3.4, we have

$$ x(t)\bigl[a-\beta(M_{o}+\varepsilon)-bx(t)\bigr]\leq \frac{dx(t)}{dt}\leq x(t)\bigl[a-\beta(m_{o}-\varepsilon)-bx(t) \bigr].$$
(4.2)

Then we can obtain two comparative systems, referring to system (4.1),

$$ \textstyle\begin{cases} \left . \begin{aligned} &\tfrac{dx_{1}(t)}{dt}=x_{1}(t)[a-\beta(M_{o}+\varepsilon)-bx_{1}(t)], \\ &\tfrac{dy_{1}(t)}{dt}=-dy_{1}(t), \end{aligned} \right \}\quad t\neq(n+1)\tau, \\ \left . \begin{aligned} &\triangle x_{1}(t)=-Dx_{1}(t),\\ &\triangle y_{1}(t)=Dx_{1}(t), \end{aligned} \right \} \quad t= (n+1)\tau, n= 1,2,\ldots, \end{cases} $$
(4.3)

and

$$ \textstyle\begin{cases} \left . \begin{aligned} &\tfrac{dx_{2}(t)}{dt}=x_{2}(t)[a-\beta(m_{o}-\varepsilon)-bx_{2}(t)], \\ &\tfrac{dy_{2}(t)}{dt}=-dy_{2}(t), \end{aligned} \right \}\quad t\neq(n+1)\tau, \\ \left . \begin{aligned} &\triangle x_{2}(t)=-Dx_{2}(t),\\ &\triangle y_{2}(t)=Dx_{2}(t), \end{aligned} \right \}\quad t= (n+1)\tau, n= 1,2,\ldots. \end{cases} $$
(4.4)

It is clear that

$$ \textstyle\begin{cases} x_{1}(t)\leq x(t)\leq x_{2}(t),\\ y_{1}(t)\leq y(t)\leq y_{2}(t). \end{cases} $$
(4.5)

We can easily obtain the analytic solution of system (4.3) between pulses, i.e.

$$ \textstyle\begin{cases} x_{1}(t)=\frac{ae^{(a-\beta(M_{o}+\varepsilon))(t-(n+l)\tau )}x_{1}((n+l)\tau^{+})}{(a-\beta(M_{o}+\varepsilon)) +b[e^{(a-\beta(M_{o}+\varepsilon))(t-(n+l)\tau)}-1]x_{1}((n+l)\tau ^{+})},& (n+l)\tau< t\leq(n+l+1)\tau,\\ y_{1}(t)=y_{1}((n+l)\tau^{+})e^{-d(t-(n+l)\tau)},& (n+l)\tau< t\leq (n+l+1)\tau. \end{cases} $$
(4.6)

Considering the third and fourth equations of system (4.3), we have the stroboscopic map of system (4.3),

$$ \textstyle\begin{cases} x_{1}((n+l+1)\tau^{+})=(1-D)\frac{ae^{(a-\beta(M_{o}+\varepsilon))\tau }x_{1}((n+l)\tau^{+})}{(a-\beta(M_{o}+\varepsilon)) +b[e^{(a-\beta(M_{o}+\varepsilon))\tau}-1]x_{1}((n+l)\tau^{+})} ,\\ y_{1}((n+l+1)\tau^{+})=D\frac{ae^{(a-\beta(M_{o}+\varepsilon))\tau }x_{1}((n+l)\tau^{+})}{(a-\beta(M_{o}+\varepsilon)) +b[e^{(a-\beta(M_{o}+\varepsilon))\tau}-1]x_{1}((n+l)\tau ^{+})}+e^{-d\tau}y_{1}((n+l)\tau^{+}). \end{cases} $$
(4.7)

The two fixed points of (4.7) are obtained as \(G_{1}(0,0)\) and \(G_{2}(x_{1}^{\ast},y_{1}^{\ast})\), where

$$ \textstyle\begin{cases} x_{1}^{\ast}=\frac{(1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}-[a-\beta (M_{o}+\varepsilon)]}{b(e^{(a-\beta(M_{o}+\varepsilon))\tau}-1)}, \\ \quad (1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}>a-\beta(M_{o}+\varepsilon ),\\ y_{1}^{\ast}=\frac{De^{(a-\beta(M_{o}+\varepsilon))\tau }[(1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}-(a-\beta(M_{o}+\varepsilon))]}{(1-D)be^{(a-\beta(M_{o}+\varepsilon))\tau}(e^{(a-\beta (M_{o}+\varepsilon))\tau}-1)(1-e^{-d\tau})}, \\ \quad (1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}>a-\beta(M_{o}+\varepsilon). \end{cases} $$
(4.8)

Theorem 4.1

  1. (i)

    If \((1-D)ae^{(a-\beta M_{o})\tau}< a-\beta M_{o}\), the fixed point \(G_{1}(0,0)\) of (4.7) is globally asymptotically stable.

  2. (ii)

    If \((1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}\), the fixed point \(G_{2}(x_{1}^{\ast}, y_{1}^{\ast})\) of (4.7) is globally asymptotically stable.

Proof

For convenience, we denote \((x_{1}^{n+l},y_{1}^{n+l})=(x_{1}((n+l)\tau^{+}),y_{1}((n+l)\tau^{+}))\). The linear form of (4.7) can be written as

( x n + l + 1 y n + l + 1 ) =M ( x n + l y n + l ) .
(4.9)

Obviously, the near dynamics of \(G_{1}(0,0)\) and \(G_{2}(x_{1}^{\ast}, y_{1}^{\ast})\) are determined by the linear system (4.7). The stabilities of \(G_{1}(0,0)\) and \(G_{2}(x_{1}^{\ast}, y_{1}^{\ast})\) of (4.7) are determined by the eigenvalue of M being less than 1. If M satisfies the \(Jury\) criteria [30], we can know the eigenvalue of M less than 1, we have

$$ 1- \operatorname {tr}M+ \det M>0. $$
(4.10)

(i) If \((1-D)ae^{(a-\beta M_{o})\tau}< a-\beta M_{o}\), there must exist a sufficiently small \(\varepsilon>0\) such that \((1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}< a-\beta (M_{o}+\varepsilon)\), and \(\varepsilon<\frac{a-\beta M_{o}}{\beta}\). Then \(G_{1}(0,0)\) is the unique fixed point of system (4.7), we have

M= ( ( 1 − D ) a e ( a − β ( M o + ε ) ) τ a − β ( M o + ε ) 0 D a e ( a − β ( M o + ε ) ) τ a − β ( M o + ε ) e − d τ ) .
(4.11)

Then

$$\begin{aligned} 1- \operatorname {tr}M+ \det M&=1-\biggl[\frac{(1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}}{a-\beta (M_{o}+\varepsilon)}+e^{-d_{2}\tau} \biggr]+\biggl[\frac{(1-D)ae^{(a-\beta (M_{o}+\varepsilon))\tau}}{a-\beta(M_{o}+\varepsilon)}\times e^{-d\tau}\biggr] \\ &=\biggl[\frac{(1-D)e^{(a-\beta M_{o})\tau}}{a-\beta(M_{o}+\varepsilon )}-1\biggr]\times\bigl(e^{-d\tau}-1 \bigr) \\ &=\biggl[\frac{(1-D)e^{(a-\beta M_{o})\tau}-(a-\beta(M_{o}+\varepsilon ))}{a-\beta(M_{o}+\varepsilon)}\biggr]\times\bigl(e^{-d\tau}-1 \bigr)>0. \end{aligned} $$

From the \(Jury\) criteria, \(G_{1}(0,0)\) is locally stable, then it is globally asymptotically stable.

(ii) If \((1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}\), there must exist a sufficiently small \(\varepsilon>0\) such that \((1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}>a-\beta (M_{o}+\varepsilon)\), Then \(G_{1}(0,0)\) is unstable. \(G_{2}(x_{1}^{\ast},y_{1}^{\ast})\) exists, and

M= ( ( 1 − D ) A B ( B + C x ∗ ) 2 0 D A B ( B + C x ∗ ) 2 E ) ,
(4.12)

where \(A=ae^{(a-\beta(M_{o}+\varepsilon))\tau}\), \(B=a-\beta(M_{o}+\varepsilon)\), \(C=b[e^{(a-\beta(M_{o}+\varepsilon))\tau}-1]\), \(E=e^{-d\tau}\), and \(1< E<1\).

Then

$$\begin{aligned} 1- \operatorname {tr}M+ \det M&=1-\biggl[\frac{(1-D)AB}{(B+Cx^{\ast})^{2}}+E\biggr]+ \frac {(1-D)AB}{(B+Cx^{\ast})^{2}}\times E \\ &=\biggl[\frac{(1-D)AB}{(B+Cx^{\ast})^{2}}-1\biggr]\times(E-1) \\ & =\frac{a-\beta(M_{o}+\varepsilon)-(1-D)ae^{(a-\beta(M_{o}+\varepsilon ))\tau}}{(1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}}\times(E-1)>0 \end{aligned} $$

and from the \(Jury\) criteria, \(G_{2}(x_{1}^{\ast}, y_{1}^{\ast})\) is locally stable, and then it is globally asymptotically stable. This completes the proof. □

Similarly to the methods in [32], the following lemma can easily be proved.

Theorem 4.2

  1. (i)

    If

    $$(1-D)ae^{(a-\beta M_{o})\tau}< a-\beta M_{o}, $$

    the triviality periodic solution \((0,0)\) of system (4.3) is globally asymptotically stable.

  2. (ii)

    If

    $$(1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}, $$

    the periodic solution \((\widetilde{x_{1}(t)},\widetilde{y_{1}(t)} )\) of system (4.3) is globally asymptotically stable, where

    $$ \textstyle\begin{cases} \widetilde{x_{1}(t)}=\frac{ae^{(a-\beta(M_{o}+\varepsilon))(t-(n+l)\tau )}x_{1}^{\ast}}{(a-\beta(M_{o}+\varepsilon)) +b[e^{(a-\beta(M_{o}+\varepsilon))(t-(n+l)\tau)}-1]x_{1}^{\ast}}, &(n+l)\tau< t\leq(n+l+1)\tau,\\ \widetilde{ y_{1}(t)}=y_{1}^{\ast}e^{-d(t-(n+l)\tau)}, &(n+l)\tau< t\leq(n+l+1)\tau, \end{cases} $$
    (4.13)

    where \(x_{1}^{\ast}\) and \(y_{1}^{\ast}\) are determined as in (4.8).

From Theorem 4.2, we can obtain the following.

Remark 4.3

If \((1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}\), for any sufficiently small \(\varepsilon_{1}>0\), there exists a \(T_{1}\) such that \(x_{1}(t)\geq \widetilde{x_{1}(t)}-\varepsilon_{1}\) and \(y_{1}(t)\geq \widetilde{y_{1}(t)}-\varepsilon_{1}\) for \(t>T_{1}\).

We can also obtain the analytic solution of system (4.4) between pulses, i.e.

$$ \textstyle\begin{cases} x_{2}(t)=\frac{ae^{(a-\beta(m_{o}-\varepsilon))(t-(n+l)\tau )}x_{2}((n+l)\tau^{+})}{(a-\beta(m_{o}-\varepsilon)) +b[e^{(a-\beta(m_{o}-\varepsilon))(t-(n+l)\tau)}-1]x_{2}((n+l)\tau ^{+})},& (n+l)\tau< t\leq(n+l+1)\tau,\\ y_{2}(t)=y_{2}((n+l)\tau^{+})e^{-d(t-(n+l)\tau)}, & (n+l)\tau< t\leq (n+l+1)\tau. \end{cases} $$
(4.14)

Considering the third and fourth equations of system (4.3), we have the stroboscopic map of system (4.3),

$$ \textstyle\begin{cases} x_{2}((n+l+1)\tau^{+})=(1-D)\frac{ae^{(a-\beta(m_{o}-\varepsilon))\tau }x_{2}((n+l)\tau^{+})}{(a-\beta(m_{o}-\varepsilon)) +b[e^{(a-\beta(m_{o}-\varepsilon))\tau}-1]x_{2}((n+l)\tau^{+})} ,\\ y_{2}((n+l+1)\tau^{+})=D\frac{ae^{(a-\beta(m_{o}-\varepsilon))\tau }x_{2}((n+l)\tau^{+})}{(a-\beta(m_{o}-\varepsilon)) +b[e^{(a-\beta(m_{o}-\varepsilon))\tau}-1]x_{2}((n+l)\tau ^{+})}+e^{-d\tau}y_{2}((n+l)\tau^{+}). \end{cases} $$
(4.15)

The two fixed points of (4.7) are obtained as \(G_{1}(0,0)\) and \(G_{2}(x_{1}^{\ast},y_{1}^{\ast})\), where

$$ \textstyle\begin{cases} x_{2}^{\ast}=\frac{(1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}-[a-\beta (m_{o}-\varepsilon)]}{b(e^{(a-\beta(m_{o}-\varepsilon))\tau}-1)}, \\ \quad (1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}>a-\beta(m_{o}-\varepsilon ),\\ y_{2}^{\ast}=\frac{De^{(a-\beta(m_{o}-\varepsilon))\tau }[(1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}-(a-\beta(m_{o}-\varepsilon))]}{(1-D)be^{(a-\beta(m_{o}-\varepsilon))\tau}(e^{(a-\beta (m_{o}-\varepsilon))\tau}-1)(1-e^{-d\tau})}, \\ \quad (1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}>a-\beta(m_{o}-\varepsilon). \end{cases} $$
(4.16)

Similarly to system (4.3), we have some theorems as regards system (4.4).

Theorem 4.4

  1. (i)

    If

    $$(1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}< a-\beta(m_{o}-\varepsilon), $$

    the fixed point \(G'_{1}(0,0)\) of (4.15) is globally asymptotically stable.

  2. (ii)

    If

    $$(1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}>a-\beta(m_{o}-\varepsilon), $$

    the fixed point \(G'_{2}(x_{2}^{\ast}, y_{2}^{\ast})\) of (4.15) is globally asymptotically stable.

Theorem 4.5

  1. (i)

    If \((1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}< a-\beta(m_{o}-\varepsilon )\), the triviality periodic solution \((0,0)\) of system (4.4) is globally asymptotically stable.

  2. (ii)

    If \((1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}>a-\beta (m_{o}-\varepsilon)\) the periodic solution \((\widetilde{x_{2}(t)},\widetilde{y_{2}(t)} )\) of system (4.4) is globally asymptotically stable, where

    $$ \textstyle\begin{cases} \widetilde{x_{2}(t)}=\frac{ae^{(a-\beta(m_{o}-\varepsilon))(t-(n+l)\tau )}x_{2}^{\ast}}{(a-\beta(m_{o}-\varepsilon)) +b[e^{(a-\beta(m_{o}-\varepsilon))(t-(n+l)\tau)}-1]x_{2}^{\ast}},& (n+l)\tau< t\leq(n+l+1)\tau,\\ \widetilde{y_{2}(t)}=y_{2}^{\ast}e^{-d(t-(n+l)\tau)}, &(n+l)\tau< t\leq(n+l+1)\tau. \end{cases} $$
    (4.17)

    Here \(x_{2}^{\ast}\) and \(y_{2}^{\ast}\) are determined as in (4.16).

Remark 4.6

If \((1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}< a-\beta (m_{o}-\varepsilon)\), for any sufficiently small \(\varepsilon_{2}>0\), there exists a \(T_{2}\) such that \(x_{2}(t)\leq \varepsilon_{2}\) and \(y_{2}(t)\leq \varepsilon_{2}\) for \(t>T_{2}\).

From Theorem 4.2, Remark 4.3, Theorem 4.5, and Remark 4.6, we present an important theorem in this paper.

Theorem 4.7

  1. (i)

    If

    $$(1-D)ae^{(a-\beta m_{o})\tau}< a-\beta m_{o} $$

    holds, the population of system (2.1) will go extinct.

  2. (ii)

    If

    $$(1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o} $$

    holds, the population of system (2.1) is permanent.

Proof

(i) According to the impulsive comparative theorem [18] and the condition \((1-D)ae^{(a-\beta m_{o})\tau}< a-\beta m_{o}\), there exists a sufficiently small \(\varepsilon>0\) such that \((1-D)ae^{(a-\beta(m_{o}-\varepsilon))\tau}< a-\beta(m_{o}-\varepsilon )\), and, from Remark 4.6, for any sufficiently small \(\varepsilon_{2}>0\), there exists a \(T_{2}>0\) such that \(x(t)\leq x_{2}(t)\leq\varepsilon_{2}\) and \(y(t)\leq y_{2}(t)\leq \varepsilon_{2}\) for \(t>T_{2}\). That is to say, for any sufficiently small \(\varepsilon_{2}>0\), there exists a \(T_{2}>0\) such that \(x(t)\leq\varepsilon_{2}\) and \(y(t)\leq\varepsilon_{2}\) for \(t>T_{2}\). These show that the population of system (2.1) will go extinct.

(ii) According to the impulsive comparative theorem [18] and the condition \((1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}\), there exists a sufficiently small \(\varepsilon>0\) such that \((1-D)ae^{(a-\beta(M_{o}+\varepsilon))\tau}>a-\beta(M_{o}+\varepsilon )\), and from Remark 4.3, for any sufficiently small \(\varepsilon_{1}>0\), there exists a \(T_{1}>0\) such that \(x(t)\geq x_{1}(t)\geq\widetilde{x_{1}(t)}-\varepsilon_{1}\geq x_{1}^{\ast}e^{-(d_{1}+M_{o}+\varepsilon)\tau}-\varepsilon_{1}\stackrel {\Delta}{=}m_{1}\) and \(y(t)\geq y_{1}(t)\geq\widetilde{y_{1}(t)}-\varepsilon_{1}\geq y_{1}^{\ast}e^{-d_{2}\tau}-\varepsilon_{1}\stackrel{\Delta}{=}m_{2}\) for \(t>T_{1}\), where \(x^{\ast}_{1}\) and \(y^{\ast}_{1}\) are determined as (4.8). From Lemma 3.2, there exist \(M>0\) and \(T>0\) such that \(x(t)< M\) and \(y(t)< M\) for \(t>T\). From the above discussion, we know \(m_{1}< x(t)< M\) and \(m_{2}< y(t)< M\) for \(t>\max\{T,T_{1}\}\). That is to say, the population of system (2.1) is permanent. □

From Lemma 3.2, Remark 3.4, and Theorem 4.7, we have the following.

Theorem 4.8

If

$$(1-D)ae^{(a-\beta M_{o})\tau}>a-\beta M_{o}, $$

system (2.1) is permanent.

4.2 The globally asymptotical stability of population-extinction boundary periodic solution of (2.1)

Theorem 4.9

If

$$(1-D)ae^{(a-\beta m_{o})\tau}< a-\beta m_{o}, $$

holds, the population-extinction boundary periodic solution \((0,0,\widetilde{c_{o}(t)}, \widetilde{c_{e}(t)})\) of system (2.1) is globally asymptotically stable, where \(m_{o}\) is defined as Remark  3.4.

Proof

Firstly, we prove the local stability. Define \(x(t)=x(t)\), \(y(t)=y(t)\), \(z_{1}(t)=c_{o}(t)-\widetilde{c_{o}(t)}\), \(z_{2}(t)=c_{e}(t)-\widetilde {c_{e}(t)}\), we have the following linearly similar system of system (2.1):

( d x ( t ) d t d y ( t ) d t d z 1 ( t ) d t d z 2 ( t ) d t ) = ( a − β c o ( t ) ˜ 0 0 0 0 − d 0 0 0 0 − ( g + m ) f 0 0 0 − h ) ( x ( t ) y ( t ) z 1 ( t ) z 2 ( t ) ) .

It is easy to obtain the fundamental solution matrix

Φ(t)= ( exp ( ∫ 0 t ( a − β c o ( s ) ˜ ) d s ) 0 0 0 0 exp [ − d t ] 0 0 0 0 exp [ − ( g + m ) t ] † 0 0 0 exp ( − h t ) ) .

There is no need to calculate the exact form of † as it is not required in the analysis that follows. The linearization of the 5th, 6th, 18th, and 9th equations of system (2.1) is

( x ( n τ + ) y ( n τ + ) z 1 ( n τ + ) z 2 ( n τ + ) ) = ( 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ) ( x ( n τ ) y ( n τ ) z 1 ( n τ ) z 2 ( n τ ) ) .

The linearization of the 9th, 10th, 11th, and 12th equations of system (2.1) is

( x ( ( n + l ) τ + ) y ( ( n + l ) τ + ) z 1 ( ( n + l ) τ + ) z 2 ( ( n + l ) τ + ) ) = ( 1 − D 0 0 0 D 1 0 0 0 0 1 0 0 0 0 1 ) ( x ( ( n + l ) τ ) y ( ( n + l ) τ ) z 1 ( ( n + l ) τ ) z 2 ( ( n + l ) τ ) ) .

The stability of the population-extinction periodic solution \((0,0,\widetilde{c_{o}(t)},\widetilde{c_{e}(t)})\) is determined by the eigenvalues of

M= ( 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ) ( 1 − D 0 0 0 D 1 0 0 0 0 1 0 0 0 0 1 ) Φ(τ),

which are

$$\begin{aligned}& \lambda_{1}=(1-D)\exp\biggl[\int^{\tau}_{0} \bigl(a-\beta\widetilde{c_{0}(s)}\bigr)\,ds\biggr], \\& \lambda_{2}=e^{-d\tau}< 1, \\& \lambda_{3}= \exp\bigl[-(g+m)\tau\bigr]< 1, \end{aligned}$$

and

$$\lambda_{4}=e^{-h\tau}< 1. $$

According the condition, we easily find \((1-D)e^{(a-\beta m_{o})\tau }<1\). Then, from Remark 3.4, we have \((1-D)\exp(\int^{\tau }_{0}(a-\beta\widetilde{c_{o}(s)})\,ds)<1\), then \(\lambda_{1}<1\). From the Floquet theory [18], the population-extinction \((0,0,\widetilde{c_{o}(t)},\widetilde{c_{e}(t)})\) is locally stable.

The following task is to prove the global attraction. Then we have subsystem (3.1) of system (2.1). From Lemma 3.3, we know that the τ-periodic solution \((\widetilde{c_{o}(t)},\widetilde{c_{e}(t)})\) of system (2.1) has globally asymptotical stability, and

$$ \textstyle\begin{cases} c_{o}(t) \geq\widetilde{c_{o}(t)}-\varepsilon\geq m_{o}-\varepsilon,\\ c_{e}(t) \geq\widetilde{c_{e}(t)}-\varepsilon, \end{cases} $$
(4.18)

for all t large enough. For convenience, we may assume (4.2) holds for all \(t\geq0\). From (2.1) and (4.2), we get

$$ \textstyle\begin{cases} \left . \begin{aligned} &\tfrac{dx(t)}{dt}< x(t)[a-\beta(m_{o}-\varepsilon)-bx(t)], \\ &\tfrac{dy(t)}{dt}=-dy(t), \end{aligned} \right \}\quad t\neq(n+1)\tau, \\ \left . \begin{aligned} &\triangle x(t)=-Dx(t),\\ &\triangle y(t)=Dx(t), \end{aligned} \right \}\quad t= (n+1)\tau, n= 1,2,\ldots, \end{cases} $$
(4.19)

and its comparable equation is system (4.4). From Remark 4.6, for any sufficiently small \(\varepsilon_{2}>0\), there exists a \(T_{2}\) such that \(x(t)\leq x_{2}(t)\leq \varepsilon_{2}\) and \(y(t)\leq y_{2}(t)\leq \varepsilon_{2}\) for \(t>T_{2}\). That is, as \(t\rightarrow\infty\), we have

$$ \textstyle\begin{cases} x(t) \rightarrow0,\\ y(t) \rightarrow0. \end{cases} $$
(4.20)

This completes the proof. □

5 Discussion

In this work, we consider a single population system with impulsively unilateral diffusion and impulsive input toxins in a polluted environment. We prove that all solutions of system (2.1) are uniformly ultimately bounded. The condition of the globally asymptotically stable population-extinction solution of system (2.1) is obtained, and the condition of the population permanence of system (2.1) is also obtained.

5.1 The simulation of system (2.1) affected by parameter μ

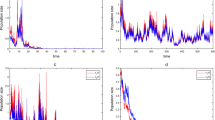
If it is assumed that \(x(0)=1\), \(y(0)=0.5\), \(c_{o}(0)=0.5\), \(c_{e}(0)=0.5\), \(a=0.4\), \(b=1\), \(d=0.1\), \(\beta=0.05\), \(\mu=2\), \(f=0.1\), \(m=0.1\), \(g=0.1\), \(l=0.25\), \(D=0.1\), \(\tau=1\), then the population-extinction periodic solution of system (2.1) is globally asymptotically stable (see Figure 1). If it is also assumed that \(x(0)=1\), \(y(0)=0.5\), \(c_{o}(0)=0.5\), \(c_{e}(0)=0.5\), \(a=0.4\), \(b=1\), \(d=0.1\), \(\beta =0.05\), \(\mu=1\), \(f=0.1\), \(m=0.1\), \(g=0.1\), \(l=0.25\), \(D=0.1\), \(\tau=1\), then system (2.1) is permanent (see Figure 2).

Figure 1
figure 1

Globally asymptotically stable population-extinction periodic solution of system ( 2.1 ) with \(\pmb{x(0)=1}\) , \(\pmb{y(0)=0.5}\) , \(\pmb{c_{o}(0)=0.5}\) , \(\pmb{c_{e}(0)=0.5}\) , \(\pmb{a=0.4}\) , \(\pmb{b=1}\) , \(\pmb{d=0.1}\) , \(\pmb{\beta=0.05}\) , \(\pmb{\mu=2}\) , \(\pmb{f=0.1}\) , \(\pmb{m=0.1}\) , \(\pmb{g=0.1}\) , \(\pmb{l=0.25}\) , \(\pmb{D=0.1}\) , \(\pmb{\tau=1}\) . (a) Time-series of \(x(t)\); (b) time-series of \(y(t)\); (c) time-series of \(c_{o}(t)\); (d) time-series of \(c_{e}(t)\).

Full size image
Figure 2
figure 2

The permanence of system ( 2.1 ) with \(\pmb{x(0)=1}\) , \(\pmb{y(0)=0.5}\) , \(\pmb{c_{o}(0)=0.5}\) , \(\pmb{c_{e}(0)=0.5}\) , \(\pmb{a=0.4}\) , \(\pmb{b=1}\) , \(\pmb{d=0.1}\) , \(\pmb{\beta=0.05}\) , \(\pmb{\mu=1}\) , \(\pmb{f=0.1}\) , \(\pmb{m=0.1}\) , \(\pmb{g=0.1}\) , \(\pmb{l=0.25}\) , \(\pmb{D=0.1}\) , \(\pmb{\tau=1}\) . (e) Time-series of \(x(t)\); (f) time-series of \(y(t)\); (g) time-series of \(c_{o}(t)\); (h) time-series of \(c_{e}(t)\).

Full size image

From the simulation experiments, the parameters μ obviously affect the dynamical behaviors of system (2.1). If all parameters of system (2.1) are fixed, when \(\mu=2\), the population of system (2.1) will go extinct, when \(\mu=1\), system (2.1) is permanent. From Theorem 4.7, we can easily deduce that there must exist a threshold \(\mu^{\ast}\). If \(\mu >\mu^{\ast}\), the population-extinction periodic solution of system (2.1) is globally asymptotically stable. If \(\mu<\mu^{\ast}\), system (2.1) is permanent.

5.2 The simulation of system (2.1) affected by parameter D

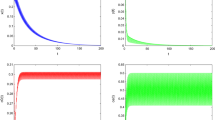
If it is assumed that \(x(0)=1\), \(y(0)=0.5\), \(c_{o}(0)=0.5\), \(c_{e}(0)=0.5\), \(a=0.4\), \(b=1\), \(d=0.1\), \(\beta=0.05\), \(\mu=1\), \(f=0.1\), \(m=0.1\), \(g=0.1\), \(l=0.25\), \(D=0.95\), \(\tau=1\), then the population-extinction periodic solution of system (2.1) is globally asymptotically stable (see Figure 3). If it is also assumed that \(x(0)=1\), \(y(0)=0.5\), \(c_{o}(0)=0.5\), \(c_{e}(0)=0.5\), \(a=0.4\), \(b=1\), \(d=0.1\), \(\beta =0.05\), \(\mu=1\), \(f=0.1\), \(m=0.1\), \(g=0.1\), \(l=0.25\), \(D=0.1\), \(\tau=1\), then system (2.1) is permanent (see Figure 4).

Figure 3
figure 3

Globally asymptotically stable population-extinction periodic solution of system ( 2.1 ) with \(\pmb{x(0)=1}\) , \(\pmb{y(0)=0.5}\) , \(\pmb{c_{o}(0)=0.5}\) , \(\pmb{c_{e}(0)=0.5}\) , \(\pmb{a=0.4}\) , \(\pmb{b=1}\) , \(\pmb{d=0.1}\) , \(\pmb{\beta=0.05}\) , \(\pmb{\mu=1}\) , \(\pmb{f=0.1}\) , \(\pmb{m=0.1}\) , \(\pmb{g=0.1}\) , \(\pmb{l=0.25}\) , \(\pmb{D=0.95}\) , \(\pmb{\tau=1}\) . (a \(\boldsymbol{'}\) ) Time-series of \(x(t)\); (b \(\boldsymbol{'}\) ) time-series of \(y(t)\); (c \(\boldsymbol{'}\) ) time-series of \(c_{o}(t)\); (d \(\boldsymbol{'}\) ) time-series of \(c_{e}(t)\).

Full size image
Figure 4
figure 4

The permanence of system ( 2.1 ) with \(\pmb{x(0)=1}\) , \(\pmb{y(0)=0.5}\) , \(\pmb{c_{o}(0)=0.5}\) , \(\pmb{c_{e}(0)=0.5}\) , \(\pmb{a=0.4}\) , \(\pmb{b=1}\) , \(\pmb{d=0.1}\) , \(\pmb{\beta=0.05}\) , \(\pmb{\mu=1}\) , \(\pmb{f=0.1}\) , \(\pmb{m=0.1}\) , \(\pmb{g=0.1}\) , \(\pmb{l=0.25}\) , \(\pmb{D=0.1}\) , \(\pmb{\tau=1}\) . (e \(\boldsymbol{'}\) ) Time-series of \(x(t)\); (f \(\boldsymbol{'}\) ) time-series of \(y(t)\); (g \(\boldsymbol{'}\) ) time-series of \(c_{o}(t)\); (h \(\boldsymbol{'}\) ) time-series of \(c_{e}(t)\).

Full size image

From the simulation experiments, the parameters D obviously affect the dynamical behaviors of system (2.1). If all parameters of system (2.1) are fixed, when \(D=0.95\), the population of system (2.1) will go extinct, when \(D=0.1\), system (2.1) is permanent. From Theorem 4.7, we can easily deduce that there must exist a threshold \(D^{\ast}\). If \(D >D^{\ast}\), the population-extinction periodic solution of system (2.1) is globally asymptotically stable. If \(D < D^{\ast}\), system (2.1) is permanent.

From the simulations of system (2.1), the diffusing parameter D of the population plays an important role in system (2.1). The environmental pollution will also reduce the biological diversity of the nature world. Our results also provide a reliable tactic basis for practical biological resource management.