1 Introduction

A heterogeneous host population can be divided into several homogeneous groups according to models of transmission, contact patterns, or geographic distributions. Multi-group epidemic models have been proposed in the literature of mathematical epidemiology to describe the transmission dynamics of infectious diseases in heterogeneous host populations, such as measles, mumps, gonorrhea, HIV/AIDS, West-Nile virus and vector-borne diseases such as malaria. Various forms of multi-group epidemic models have subsequently been studied to understand the mechanism of disease transmission. One of the most important subjects in this field is to obtain a threshold that determines the persistence or extinction of a disease. Guo et al. in [1] developed a graph-theoretic approach to prove the global asymptotic stability of a unique endemic equilibrium of a multi-group epidemic model. By applying the idea, global stability of endemic equilibrium for several classes of multi-group epidemic models was investigated in [1–10].

In the real world, some epidemics, such as malaria, dengue, fever, gonorrhea and bacterial infections, may have a different ability to transmit the infections in different ages. For example, measles and varicella always occur in juveniles, while it is reasonable to consider the transmission of diseases such as typhus, diphtheria in adult population. In recent years, epidemic models with stage structure have been studied in many papers [11–17]. For some disease (for example, tuberculosis, influenza, measles), on adequate contact with an infective, a susceptible individual becomes exposed, that is, infected but not infective. This individual remains in the exposed class for a certain period before becoming infective (see, for example, [18–22]).

In this paper, we formulate an epidemic model with latency spreading in a heterogeneous host population. Let \(S^{(1)}_{k}\), \(S^{(2)}_{k}\), \(E_{k}\), \(I_{k}\) and \(R_{k}\) denote the immature susceptible, mature susceptible, infected but non-infectious, infectious and recovered population in the kth group, respectively. The disease incidence in the kth group can be calculated as

$$\sum_{i=1}^{2} S^{(i)}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}(I_{j}), $$

where the sum takes into account cross-infections from all groups and \(\beta^{(i)}_{kj}\) is the transmission coefficient between compartments \(S^{(i)}_{k}\) and \(I_{j}\). \(G_{j}(I_{j})\) includes some special incidence functions in the literature. For instance, \(G_{j}(I_{j}) =\frac{I_{j}}{1+\alpha_{j}I_{j}}\) (saturation effect). Let \(d^{(1)}_{k}\) and \(d^{(2)}_{k}\) represent death rates of \(S^{(1)}_{k}\) and \(S^{(2)}_{k}\) populations, respectively. Then we obtain the following model for a disease with latency:

$$ \left \{ \textstyle\begin{array}{@{}l} \dot{S}^{(1)}_{k}=\varphi_{k}(S^{(1)}_{k})-\sum^{n}_{j=1}\beta ^{(1)}_{kj}S^{(1)}_{k} G_{j}(I_{j}) -a_{k}S^{(1)}_{k},\\ \dot{S}^{(2)}_{k}=a_{k}S^{(1)}_{k}-\sum^{n}_{j=1}\beta ^{(2)}_{kj}S^{(2)}_{k} G_{j}(I_{j}) -d^{(2)}_{k}S^{(2)}_{k},\\ \dot{E_{k}}=\sum^{2}_{i=1}\sum^{n}_{j=1}\beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j})-(d_{k}+\eta_{k})E_{k},\\ \dot{I_{k}}=\eta_{k}E_{k}-(d_{k}+\mu_{k}+\gamma_{k})I_{k},\\ \dot{R_{k}}=\gamma_{k} I_{k}-d_{k}R_{k}, \quad k=1,2,\ldots,n, \end{array}\displaystyle \right . $$
(1)

where \(\varphi_{k}(S^{(1)}_{k})\) denotes the net growth rate of the immature susceptible class in the kth group (a typical form of \(\varphi_{k}(S^{(1)}_{k})\) is \(\varphi_{k}(S^{(1)}_{k})=b_{k}-d^{(1)}_{k}S^{(1)}_{k}\) with \(b_{k}\) the recruitment constant and \(d^{(1)}_{k}\) the natural death rate). \(a_{k}\) is the conversion rate from an immature individual to a mature individual in group k. \(\eta _{k}\) represents the rate of becoming infectious after a latent period in the kth group. \(d_{k}\), \(\mu_{k}\) and \(\gamma_{k}\) are the natural death rate, the disease-related death rate and the recovery rate in the kth group, respectively. All parameter values are assumed to be nonnegative and \(a_{k}, \eta_{k}, d^{(i)}_{k}, d_{k}>0\).

Remark

The model (1) can be regarded as an SVEIR model such that \(S_{k}^{(1)}\) is unvaccinated and \(S_{k}^{(2)}\) is vaccinated with vaccination rate \(a_{k}\). References studied on the SVEIR model can be seen in [23, 24] and so on.

Since the variable \(R_{k}\) does not appear in the remaining four equations of (1), if we denote \(m_{k}:=d_{k}+\mu_{k}+\gamma_{k}\), then we can obtain the following reduced system:

$$ \left \{ \textstyle\begin{array}{@{}l} \dot{S}^{(1)}_{k}=\varphi_{k}(S^{(1)}_{k})-\sum^{n}_{j=1}\beta ^{(1)}_{kj}S^{(1)}_{k} G_{j}(I_{j}) -a_{k}S^{(1)}_{k},\\ \dot{S}^{(2)}_{k}=a_{k}S^{(1)}_{k}-\sum^{n}_{j=1}\beta ^{(2)}_{kj}S^{(2)}_{k} G_{j}(I_{j}) -d^{(2)}_{k}S^{(2)}_{k},\\ \dot{E_{k}}=\sum^{2}_{i=1}\sum^{n}_{j=1}\beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j})-(d_{k}+\eta_{k})E_{k},\\ \dot{I_{k}}=\eta_{k}E_{k}-m_{k}I_{k},\quad k=1,2,\ldots,n. \end{array}\displaystyle \right . $$
(2)

The initial conditions for system (2) are

$$ S^{(1)}_{k}(0)>0,\qquad S^{(2)}_{k}(0)>0, \qquad E_{k}(0)>0, \qquad I_{k}(0)>0, \quad k=1,2,\ldots,n. $$
(3)

The organization of this paper is as follows. In the next section, we prove some preliminary results for system (2). In Section 3, the main theorem of this paper is stated and proved. In the last section, a brief discussion and numerical simulations which support our theoretical analysis are given.

2 Preliminaries

We assume:

  1. (A1)

    \(\varphi_{k}\) and \(G_{k}\) are Lipschitz on \([0,+\infty)\);

  2. (A2)

    \(\varphi_{k}\) is strictly decreasing on \([0,+\infty)\), and there exists \(S^{(1)}_{k 0}>0\) such that

    $$\varphi_{k}\bigl(S^{(1)}_{k 0}\bigr) -a_{k}S^{(1)}_{k0}=0; $$
  3. (A3)

    \(\frac{G_{k}(x)}{x}\) is nonincreasing on \((0,+\infty)\) and

    $$\delta_{k}=\lim_{x\rightarrow0} \frac{G_{k}(x)}{x} >0\mbox{ exists},\quad k=1,2,\ldots,n. $$

From our assumptions, it is clear that system (2) has a unique solution for any given initial conditions (3) and the solution remains nonnegative. If (A2) holds, then we see that system (2) has a disease-free equilibrium

$$P_{0}=\bigl(S_{10}^{(1)}, S_{10}^{(2)}, \ldots, S_{n0}^{(1)}, S_{n0}^{(2)}, 0 ,0, \ldots,0\bigr), $$

where

$$ \varphi_{k}\bigl(S_{k0}^{(1)}\bigr)=d^{(2)}_{k}S_{k0}^{(2)}, \qquad a_{k}S_{k0}^{(1)}=d^{(2)}_{k}S_{k0}^{(2)},\quad k=1,2,\ldots,n. $$
(4)

For two nonnegative n-square matrices \(\mathbf{A}=(a_{kj})\) and \(\mathbf{B}=(a_{kj})\), we write \(\mathbf{A}\leq\mathbf{B}\) if \(a_{kj}\leq b_{kj}\) for all k and j, and \(\mathbf{A}<\mathbf{B}\) if \(\mathbf{A}\leq\mathbf{B}\) and \(\mathbf{A}\neq\mathbf{B}\). Following [25], we set matrices

$$\begin{aligned}& \mathbf{F}:= \Biggl(\sum_{i=1}^{2} \beta^{(i)}_{kj} S_{k0}^{(i)} \delta _{j} \Biggr)_{n \times n}, \qquad \mathbf{V}:=\operatorname{diag} \biggl( \frac{ m_{1}(d_{1}+\eta_{1})}{\eta_{1}}, \frac{ m_{2} (d_{2}+\eta_{2})}{\eta_{2}},\ldots, \frac{m_{n} (d_{n}+\eta_{n})}{\eta_{n}} \biggr) . \end{aligned}$$

The next generation matrix for system (2) is

$$\begin{aligned} \mathbf{Q}&:=\mathbf{FV^{-1}} = \biggl( \frac{ \eta_{k} \sum_{i=1}^{2} \beta^{(i)}_{kj} S_{k0}^{(i)} \delta_{j}}{m_{k}( d_{k}+\eta_{k} ) } \biggr)_{n \times n}\\ &= \begin{bmatrix} \frac{\eta_{1} \sum_{i=1}^{2} \beta^{(i)}_{11} S_{10}^{(i)} \delta_{1}}{m_{1}( d_{1}+\eta_{1} ) } & \cdots& \frac{ \eta_{1} \sum_{i=1}^{2} \beta ^{(i)}_{1n} S_{10}^{(i)} \delta_{n}}{m_{1}( d_{1}+\eta_{1} ) } \\ \vdots &\ddots & \vdots\\ \frac{ \eta_{n} \sum_{i=1}^{2} \beta^{(i)}_{n1} S_{n0}^{(i)} \delta_{1}}{m_{n}( d_{n}+\eta_{n} ) } & \cdots& \frac{ \eta_{n} \sum_{i=1}^{2} \beta ^{(i)}_{nn} S_{n0}^{(i)} \delta_{n}}{m_{n}( d_{n}+\eta_{n} ) } \end{bmatrix}. \end{aligned}$$

Thus, we obtain the basic reproduction number \(R_{0}\) for system (2) as

$$R_{0}=\rho(\mathbf{Q}), $$

where ρ denotes the spectral radius.

Let \(N_{k}=S^{(1)}_{k}+S^{(2)}_{k}+E_{k}+I_{k}\), \(\underline{d}_{k}=\min\{ d^{(1)}_{k}, d^{(2)}_{k}, d_{k}, m_{k} \}\), \(k=1,2,\ldots,n\). Then from (2) we have

$$ \dot{N_{k}}\leq\varphi _{k}\bigl(S^{(1)}_{k} \bigr)+d^{(1)}_{k}S^{(1)}_{k}- \underline{d}_{k}N_{k}. $$
(5)

We derive from (5) that the region

$$\begin{aligned} \Gamma =& \biggl\{ \bigl(S^{(1)}_{1}, S^{(2)}_{1}, \ldots, S^{(1)}_{n}, S^{(2)}_{n}, E_{1},\ldots, E_{n} , I_{1}, \ldots, I_{n} \bigr) \in \mathbb{R}_{+}^{4n}: S^{(1)}_{k}\leq S_{k0}^{(1)},\\ &{} S^{(2)}_{k}\leq S_{k0}^{(2)}, S^{(1)}_{k}+S^{(2)}_{k}+E_{k}+I_{k} \leq \frac{\varphi_{k}(0)+d^{(1)}_{k} S_{k0}^{(1)}}{\underline{d}_{k}}, k=1,2,\ldots,n \biggr\} \end{aligned}$$

is positively invariant with respect to (2). Let \(\Gamma^{\circ}\) denote the interior of Γ.

3 Main results

In the section, we study the global stability of equilibria of system (2).

Theorem 3.1

Assume that (A1)-(A3) hold and \(\mathbf{B}=(\sum_{i=1}^{2}\beta ^{(i)}_{kj})\) is irreducible.

  1. (1)

    If \(R_{0}\leq1\), then \(P_{0}\) is globally asymptotically stable in Γ;

  2. (2)

    If \(R_{0}>1\), then \(P_{0}\) is unstable and system (2) admits at least one endemic equilibrium in \(\Gamma^{\circ}\).

Proof

Let

$$\begin{aligned}& \mathbf{S}=\bigl(S^{(1)}_{1}, S^{(2)}_{1}, \ldots,S^{(1)}_{n},S^{(2)}_{n}\bigr), \qquad \mathbf{S^{0}}=\bigl(S^{(1)}_{10}, S^{(2)}_{10}, \ldots ,S^{(1)}_{n0},S^{(2)}_{n0} \bigr), \\& \mathbf{I}=(I_{1}, I_{2}, \ldots, I_{n}),\qquad \mathbf{Q(S,I)}= \biggl( \frac{ \sum^{2}_{i=1}\sum^{n}_{j=1} \eta_{k} \beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j}) }{m_{k} ( d_{k}+\eta _{k} )I_{j} } \biggr)_{n \times n} . \end{aligned}$$

Notice that B is irreducible, then \(\mathbf{Q(S,I)}\) and Q are irreducible. By (A3), we have \(\mathbf{0}\leq\mathbf{Q(S,I)}\leq\mathbf{Q}\). Hence \(\mathbf{Q(S,I)}+ \mathbf{Q}\) is also irreducible. That is, \(0 \leq\mathbf{Q(S,I)}<\mathbf{Q}\) and \(\mathbf{Q(S,I)}+ \mathbf{Q}\) is irreducible provided that \(\mathbf{S} \neq\mathbf{S^{0}}\). Thus, by [26], Corollary 1.5, p.27, \(\rho(\mathbf{Q(S,I)})<\rho(\mathbf{Q})\) if \(\mathbf{S} \neq \mathbf{S^{0}}\). Since Q is irreducible, there exist \(\omega_{k}>0\), \(k=1,2,\ldots,n\), such that

$$(\omega_{1}, \omega_{2}, \ldots, \omega_{n}) \rho(\mathbf{Q})= (\omega _{1}, \omega_{2}, \ldots, \omega_{n})\mathbf{Q} . $$

Consider a Lyapunov functional

$$L =\sum_{k=1}^{n}\frac{\omega_{k} \eta_{k}}{m_{k} (d_{k}+\eta_{k} )} \biggl[ E_{k} + \frac{d_{k}+\eta_{k}}{\eta_{k}}I_{k} \biggr]. $$

Differentiating L along the solution of system (2), we obtain

$$\begin{aligned} \dot{L} =& \sum_{k=1}^{n} \frac{\omega_{k} \eta_{k}}{m_{k} (d_{k}+\eta_{k} ) } \Biggl[ \sum^{2}_{i=1}\sum ^{n}_{j=1}\beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j}) - \frac{m_{k} ( d_{k}+\eta_{k} ) }{ \eta_{k} } I_{k} \Biggr] \\ =& \sum_{k=1}^{n}\omega_{k} \biggl[ \frac{ \sum^{2}_{i=1}\sum^{n}_{j=1} \eta_{k} \beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j}) }{m_{k} ( d_{k}+\eta_{k} ) } - I_{k} \biggr] \\ =&(\omega_{1}, \omega_{2}, \ldots, \omega_{n}) \bigl(\mathbf{Q(S,I)}\mathbf {I}^{T}-\mathbf{I}^{T}\bigr) \\ \leq&(\omega_{1}, \omega_{2}, \ldots, \omega_{n}) \bigl(\mathbf{Q}\mathbf{I}^{T}- \mathbf{I}^{T}\bigr) \\ =&\bigl[\rho(\mathbf{Q})-1\bigr] (\omega_{1}, \omega_{2}, \ldots, \omega_{n})\mathbf{I}^{T}\leq0. \end{aligned}$$

If \(R_{0}<1\), then \(\dot{L}=0\) if and only if \(\mathbf {I}^{T}=\mathbf{0}\). If \(R_{0}=1\), then \(\dot{L}=0\) implies

$$(\omega_{1}, \omega_{2}, \ldots, \omega_{n}) \bigl(\mathbf{Q(S,I)}\mathbf {I}^{T}-\mathbf{I}^{T}\bigr) =0. $$

Therefore, \(\dot{L}=0\) if and only if \(\mathbf{I}=\mathbf{0}\), or \(\mathbf{S}=\mathbf{S^{0}}\). On the other hand, from the last equation in system (2), we see that \(\mathbf{I}=\mathbf{0}\) implies that \(E_{k}=0\) for \(k=1,2,\ldots,n\). Hence, the largest invariant subset of the set, where \(\dot{L}=0\), is the singleton \(\{P_{0}\}\). By LaSalle’s invariance principle, \(P_{0}\) is globally asymptotically stable for \(R_{0}\leq1\).

If \(R_{0}>1\) and \(\mathbf{I}\neq\mathbf{0}\), then

$$\bigl[\rho(\mathbf{Q})-1\bigr] (\omega_{1}, \omega_{2}, \ldots, \omega_{n})\mathbf {I}^{T} >0. $$

Thus, by continuity, we have \(\dot{L}= (\omega_{1}, \omega_{2}, \ldots, \omega_{n})(\mathbf{Q(S,I)}\mathbf{I}^{T}-\mathbf{I}^{T}) >0\) in a neighborhood of \(P_{0}\) in \(\Gamma^{\circ}\). This implies that \(P_{0}\) is unstable. From a uniform persistence result of [27] and a similar argument as in the proof of Proposition 3.3 of [28], we can deduce that the instability of \(P_{0}\) implies the uniform persistence of system (2) in \(\Gamma^{\circ}\). This together with the uniform boundedness of solutions of system (2) in \(\Gamma^{\circ}\) implies that system (2) has an endemic equilibrium in \(\Gamma^{\circ}\) (see Theorem 2.8.6 of [29] or Theorem D.3 of [30]). The proof is completed. □

By Theorem 3.1, we have that if \(\mathbf{B}=(\sum_{i=1}^{2}\beta^{(i)}_{kj})\) is irreducible, (A1)-(A3) hold and \(R_{0}>1\), then system (2) has an endemic equilibrium \(P^{*}\) in \(\Gamma^{\circ}\). Let

$$P^{*}=\bigl(S_{1}^{(1)*}, S_{1}^{(2)*}, \ldots, S_{n}^{(1)*},S_{n}^{(2)*}, E_{1}^{*},\ldots, E_{n}^{*}, I_{1}^{*}, \ldots, I_{n}^{*}\bigr), $$

then the components of \(P^{*}\) satisfy

$$\begin{aligned}& \varphi_{k}\bigl(S^{(1)*}_{k}\bigr)= \sum _{i=1}^{2}S^{(i)*}_{k}\sum _{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr)+d^{(2)}_{k}S_{k}^{(2)*}, \end{aligned}$$
(6)
$$\begin{aligned}& a_{k}\bigl(S^{(1)*}_{k}\bigr)= S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr)+d^{(2)}_{k}S_{k}^{(2)*}, \end{aligned}$$
(7)
$$\begin{aligned}& \sum_{i=1}^{2}S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr)=(d_{k}+ \eta_{k})E^{*}_{k}=\frac{m_{k}(d_{k}+\eta _{k})}{\eta_{k}}I^{*}_{k},\quad k=1,2,\ldots,n. \end{aligned}$$
(8)

Since \(\varphi_{k}\) is strictly decreasing on \([0,+\infty)\), we have

$$ \bigl[\varphi_{k}\bigl(S^{(1)}_{k}\bigr)- \varphi_{k}\bigl(S^{(1)*}_{k}\bigr) \bigr] \biggl( 1- \frac{ S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) \leq0, $$
(9)

where equality holds if and only if \(S^{(1)}_{k}=S_{k}^{(1)*}\), \(k=1,2,\ldots,n\).

We further make the following assumption:

  1. (A4)

    \(G_{k}\) is strictly increasing on \([0,+\infty)\), and

    $$ \frac{G_{k}(x_{k})I_{k}}{G_{k}(I_{k} )x_{k} } + \frac{G_{k}(I_{k})}{G_{k}(x_{k})}-\frac{I_{k}}{x_{k}} -1\leq0,\quad k=1,2, \ldots,n, $$
    (10)

    where \(x_{k}>0\) is chosen in an arbitrary way and equality holds if \(I_{k}=x_{k}\).

Theorem 3.2

Assume that \(\mathbf{B}=[\sum_{i=1}^{2}\beta^{(i)}_{kj}]\) is irreducible. If \(R_{0}>1\), then \(P^{*}\) is globally asymptotically stable.

Proof

Set \(\overline{\beta}_{kj}=\sum_{i=1}^{2} \beta^{(i)}_{kj}S_{k}^{(i)*}G_{j}(I_{j}^{*})\), \(1\leq k,j\leq n\), and

$$\overline{B} = \begin{bmatrix} \sum_{l \neq1} \overline{\beta}_{1l} & -\overline{\beta}_{21}& \ldots& -\overline{\beta}_{n1}\\ -\overline{\beta}_{12} & \sum_{l \neq2} \overline{\beta}_{2l} & \ldots& -\overline{\beta}_{n1} \\ \vdots& \vdots& \ddots& \vdots\\ -\overline{\beta}_{1n} & -\overline{\beta}_{2n} & \ldots& \sum_{l \neq n} \overline{\beta}_{nl} \end{bmatrix}. $$

Then \(\overline{B}\) is also irreducible. It follows from Lemma 2.1 of [1] that the solution space of the linear system

$$ \overline{B}\mathbf{v}=0 $$
(11)

has dimension 1 with a basis

$$ \mathbf{v}:=(v_{1}, v_{2}, \ldots, v_{n})^{T}=( \xi_{1}, \xi_{2}, \ldots, \xi_{n})^{T}, $$
(12)

where \(\xi_{k}\) denotes the cofactor of the kth diagonal entry of \(\overline{B}\). Note that from (11) we have

$$ \sum_{j=1}^{n}\overline{B}_{kj}v_{k}= \sum_{j=1}^{n}\overline{B}_{jk}v_{j},\quad k=1, 2, \ldots, n. $$
(13)

From (13), we have

$$\begin{aligned} & \sum_{k=1}^{n}v_{k}\sum _{j=1}^{n} \sum_{i=1}^{2} \beta^{(i)}_{kj}S^{(i)*}_{k}G_{j}(I_{j}) \\ &\quad=\sum_{k,j=1}^{n}\sum _{i=1}^{2}\beta ^{(i)}_{jk}S^{(i)*}_{j}v_{j}G_{k}(I_{k})= \sum_{k=1}^{n} \Biggl[ \sum _{j=1}^{n}\sum_{i=1}^{2} \beta^{(i)}_{jk} S^{(i)*}_{j}G_{k} \bigl(I_{k}^{*}\bigr)v_{j} \Biggr] \frac{G_{k}(I_{k})}{G_{k}(I_{k}^{*})} \\ &\quad=\sum_{k=1}^{n} \Biggl[ \sum _{j=1}^{n}(\overline{\beta}_{jk} v_{j}) \Biggr]\frac{G_{k}(I_{k})}{G_{k}(I_{k}^{*})}=\sum_{k=1}^{n} \Biggl[ \sum_{j=1}^{n}(\overline{ \beta}_{kj} v_{k}) \Biggr]\frac{G_{k}(I_{k})}{G_{k}(I_{k}^{*})} \\ &\quad=\sum_{k=1}^{n}v_{k}\sum _{j=1}^{n} \sum_{i=1}^{2} \beta^{(i)}_{kj}S^{(i)*}_{k}G_{j} \bigl(I^{*}_{j}\bigr)\frac {G_{k}(I_{k})}{G_{k}(I^{*}_{k})}. \end{aligned}$$
(14)

Consider a Lyapunov functional

$$\begin{aligned} V =&\sum_{k=1}^{n}v_{k} \Biggl[ \sum_{i=1}^{2} \biggl(S^{(i)}_{k}-S^{(i)*}_{k} -S^{(i)*}_{k}\ln\frac{ S^{(i)}_{k}}{S^{(i)*}_{k}} \biggr) +E_{k}- E^{*}_{k} \\ &{} - E^{*}_{k}\ln\frac{E_{k}}{E^{*}_{k}}+ \frac{d_{k}+\eta_{k}}{\eta_{k}} \int_{I^{*}_{k}}^{I_{k}} \frac{G_{k}(x)-G_{k}(I^{*}_{k})}{G_{k}(x)}\,dx \Biggr]. \end{aligned}$$

Differentiating V along the solution of system (2), we obtain

$$\begin{aligned} \dot{V} =&\sum_{k=1}^{n} v_{k} \Biggl\{ \varphi_{k}\bigl(S^{(1)}_{k} \bigr)-d^{(2)}_{k}S^{(2)}_{k}- \frac{m_{k}(d_{k}+\eta_{k})}{\eta_{k}} I_{k} \\ &{}-\frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \Biggl[ \varphi_{k}\bigl(S^{(1)}_{k} \bigr)-S^{(1)}_{k}\sum_{j=1}^{n} \beta^{(1)}_{kj} G_{j}(I_{j}) -a_{k}S^{(1)}_{k} \Biggr] \\ &{}-\frac{S^{(2)*}_{k}}{S^{(2)}_{k}} \Biggl[ a_{k}S^{(1)}_{k}-S^{(2)}_{k} \sum_{j=1}^{n}\beta^{(2)}_{kj} G_{j}(I_{j}) -d^{(2)}_{k}S^{(2)}_{k} \Biggr] \\ &{}-\frac{E^{*}_{k}}{E_{k}} \Biggl[ \sum^{2}_{i=1} \sum^{n}_{j=1}\beta^{(i)}_{kj}S^{(i)}_{k} G_{j} (I_{j})-(d_{k}+\eta_{k})E_{k} \Biggr] \\ &{}-\frac{G_{k}(I^{*}_{k})}{G_{k}(I_{k}) } \biggl[ (d_{k}+\eta_{k} )E_{k} - \frac{m_{k}(d_{k}+\eta_{k})}{\eta_{k}} I_{k} \biggr] \Biggr\} \\ =& \sum_{k=1}^{n}v_{k} \Biggl\{ \varphi_{k}\bigl(S^{(1)}_{k}\bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) +d^{(2)}_{k}S^{(2)*}_{k} \biggl( 1- \frac{S^{(2)}_{k}}{S^{(2)*}_{k}} \biggr) \\ &{}+a_{k}S^{(1)*}_{k} \biggl( 1-\frac{S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \biggr)+\sum_{i=1}^{2} S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}(I_{j}) \\ &{}-\frac{E^{*}_{k}}{E_{k}}\sum_{i=1}^{2}-S^{(i)}_{k} \sum_{j=1}^{n}\beta ^{(i)}_{kj} G_{j}(I_{j}) +(d_{k}+\eta_{k} )E^{*}_{k} \biggl(1-\frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k}G_{k}(I_{k}) } \biggr) \\ &{}+\frac{m_{k}(d_{k}+\eta_{k})}{\eta_{k}} I^{*}_{k} \frac{ I_{k}G_{k}(I^{*}_{k})}{I^{*}_{k}G_{k}(I_{k})}- \frac{m_{k}(d_{k}+\eta _{k})}{\eta_{k}} I^{*}_{k} \frac{ I_{k} }{ I^{*}_{k}} \Biggr\} . \end{aligned}$$

From (7) and (8), we have

$$\begin{aligned} \dot{V} = &\sum_{k=1}^{n}v_{k} \Biggl\{ \varphi_{k}\bigl(S^{(1)}_{k}\bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) +d^{(2)}_{k}S^{(2)*}_{k} \biggl( 1- \frac{S^{(2)}_{k}}{S^{(2)*}_{k}} \biggr) \\ &{}-\frac{E^{*}_{k}}{E_{k}} \sum_{i=1}^{2} S^{(i)}_{k} \sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}(I_{j})\\ &{}+ \Biggl[S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) +d^{(2)}_{k}S^{(2)*}_{k} \Biggr] \biggl( 1-\frac{S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \biggr)\\ &{}+ \sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j} \bigl(I^{*}_{j} \bigr) \biggl[ 1 - \frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } +\frac{G_{j}(I_{j})}{G_{j}(I^{*}_{j})} +\frac{ I_{k} G_{k}(I^{*}_{k})}{ I^{*}_{k} G_{k}(I_{k}) } - \frac{I_{k}}{I^{*}_{k}} \biggr] \Biggr\} . \end{aligned}$$

By (10) and (14), we obtain

$$\begin{aligned} \dot{V} \leq& \sum_{k=1}^{n}v_{k} \Biggl\{ \varphi_{k}\bigl(S^{(1)}_{k}\bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) +d^{(2)}_{k}S^{(2)*}_{k} \biggl( 1- \frac{S^{(2)}_{k}}{S^{(2)*}_{k}} \biggr) \\ &{}-\frac{E^{*}_{k}}{E_{k}}\sum_{i=1}^{2} S^{(i)}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}(I_{j})+ \Biggl[S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr)+d^{(2)}_{k}S^{(2)*}_{k} \Biggr] \\ &{}\times \biggl( 1-\frac{S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \biggr) +\sum _{i=1}^{2} S^{(i)*}_{k}\sum _{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \biggl[ 2- \frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \Biggr\} =:B_{1}. \end{aligned}$$
(15)

From (6), we know that

$$ \varphi_{k}\bigl(S^{(1)*}_{k}\bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) = \Biggl(\sum_{i=1}^{2}S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr)+d^{(2)}_{k}S_{k}^{(2)*} \Biggr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr). $$
(16)

By (16), we can rewrite \(B_{1}\) as

$$\begin{aligned} \dot{V} =&\sum_{k=1}^{n}v_{k} \Biggl\{ \bigl[ \varphi_{k}\bigl(S^{(1)}_{k}\bigr)- \varphi_{k}\bigl(S^{(1)*}_{k}\bigr) \bigr] \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) \\ &{}+d^{(2)}_{k}S^{(2)*}_{k} \biggl( 3- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}}-\frac {S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} -\frac{S^{(2)}_{k}}{S^{(2)*}_{k}} \biggr) \\ &{}-\frac{E^{*}_{k}}{E_{k}} \sum_{i=1}^{2} S^{(i)}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}(I_{j}) +S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \\ &{}\times \biggl(2-\frac{S^{(1)*}_{k}}{S^{(1)}_{k}}-\frac {S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \biggr)+ S^{(1)*}_{k}\sum_{j=1}^{n} \beta^{(1)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) \\ &{}+\sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 2 - \frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \Biggr\} . \end{aligned}$$

By (9) and the arithmetic-geometric mean, we easily see that

$$\begin{aligned} B_{1} \leq& \sum_{k=1}^{n}v_{k} \Biggl\{ -\frac{E^{*}_{k}}{E_{k}} \sum_{i=1}^{2} S^{(i)}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}(I_{j}) \\ &{}+S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl( 2-\frac{S^{(1)*}_{k}}{S^{(1)}_{k}}-\frac {S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \biggr) \\ &{}+S^{(1)*}_{k}\sum_{j=1}^{n} \beta^{(1)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl( 1- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \biggr) \\ &{}+\sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 2 - \frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \Biggr\} =:B_{2}. \end{aligned}$$
(17)

We can rewrite \(B_{2}\) as

$$\begin{aligned} B_{2} =&\sum_{k=1}^{n}v_{k} \Biggl\{ S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 3- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}}-\frac {S^{(1)}_{k}S^{(2)*}_{k}}{S^{(1)*}_{k}S^{(2)}_{k}} \\ &{}-\frac{S^{(2)}_{k} E^{*}_{k} G_{j}(I_{j}) }{S^{(2)*}_{k}E_{k}G_{j}(I^{*}_{j})} \biggr] +S^{(1)*}_{k}\sum _{j=1}^{n}\beta^{(1)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \biggl[ 2- \frac{S^{(1)*}_{k}}{S^{(1)}_{k}} \\ &{}-\frac{S^{(1)}_{k} E^{*}_{k} G_{j}(I_{j}) }{S^{(1)*}_{k}E_{k}G_{j}(I^{*}_{j}) } \biggr]+\sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 1- \frac{ E_{k}G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \Biggr\} . \end{aligned}$$

By the arithmetic-geometric mean, we have that

$$\begin{aligned} B_{2} \leq& \sum_{k=1}^{n}v_{k} \Biggl\{ 3S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[1 - \biggl(\frac{E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j})} \biggr)^{\frac{1}{3}} \biggr] \\ &{}+2S^{(1)*}_{k}\sum_{j=1}^{n} \beta^{(1)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[1 - \biggl( \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \biggr)^{\frac{1}{2} } \biggr] \\ &{}+\sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 1- \frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \Biggr\} =:B_{3}. \end{aligned}$$
(18)

We can rewrite \(B_{3}\) as

$$\begin{aligned} B_{3} =& \sum_{k=1}^{n}v_{k} \Biggl\{ 3S^{(2)*}_{k}\sum_{j=1}^{n} \beta^{(2)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 1 - \biggl[ \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \biggr]^{\frac{1}{3} } +\ln \biggl[ \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \biggr]^{\frac{1}{3} } \biggr] \\ &{}+2S^{(1)*}_{k}\sum_{j=1}^{n} \beta^{(1)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \biggl[ 1 - \biggl[ \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \biggr]^{\frac{1}{2} } +\ln \biggl[ \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \biggr]^{\frac{1}{2} } \biggr] \\ &{}-\sum_{i=1}^{2} S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \ln\frac{E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } \\ &{}+\sum_{i=1}^{2} S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \biggl[ 1- \frac{ E_{k}G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } +\ln\frac{ E_{k} G_{k}(I^{*}_{k})}{ E^{*}_{k} G_{k}(I_{k}) } \biggr] \\ &{}-\sum_{i=1}^{2} S^{(i)*}_{k}\sum_{j=1}^{n} \beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j} \bigr) \ln\frac{ E_{k} G_{k}(I^{*}_{k}) }{E^{*}_{k}G_{k}(I_{k}) } \Biggr\} . \end{aligned}$$

Using the fact that \(1-x+\ln x \leq0\), where equality holds if and only if \(x=1\), we obtain

$$\begin{aligned} B_{3} \leq& \sum_{k=1}^{n}v_{k} \sum_{i=1}^{2} S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \biggl[ -\ln \frac{ E^{*}_{k} G_{j}(I_{j}) }{E_{k}G_{j}(I^{*}_{j}) } -\ln \frac{ E_{k} G_{k}(I^{*}_{k}) }{E^{*}_{k}G_{k}(I_{k}) } \biggr] \\ =& \sum_{k=1}^{n}v_{k}\sum _{i=1}^{2} S^{(i)*}_{k} \sum_{j=1}^{n}\beta^{(i)}_{kj} G_{j}\bigl(I^{*}_{j}\bigr) \ln \frac{ G_{k}(I_{k}) G_{j}(I^{*}_{j}) }{G_{k}(I^{*}_{k})G_{j}(I_{j}) } \\ =& \sum_{k=1}^{n}v_{k}\sum ^{n}_{j=1} \overline{\beta}_{kj} \ln \frac{G_{k}(I_{k} )G_{j}(I^{*}_{j}) }{G_{k}(I^{*}_{k})G_{j}(I_{j})}. \end{aligned}$$
(19)

In the following, we will show that

$$ H_{n} := \sum_{k=1}^{n}v_{k} \sum^{n}_{j=1} \overline{ \beta}_{kj} \ln\frac{G_{k}(I_{k} )G_{j}(I^{*}_{j}) }{G_{k}(I^{*}_{k})G_{j}(I_{j})} \equiv0. $$
(20)

We first give the proof of (20) for \(n=2\), which would give a reader the basic yet clear ideas without being hidden by the complexity of terms caused by larger values of n. When \(n=2\), we have

$$\begin{aligned} {H}_{2} = \sum_{k=1}^{2}v_{k} \sum^{2}_{j=1} \overline{ \beta}_{kj} \ln\frac{G_{k}(I_{k} )G_{j}(I^{*}_{j}) }{G_{k}(I^{*}_{k})G_{j}(I_{j})}. \end{aligned}$$

Formula (12) gives \(v_{1}=\overline{\beta}_{21}\) and \(v_{2}=\overline{\beta}_{12}\) in this case. Expanding \(H_{2}\) yields

$$\begin{aligned} H_{2} =&\overline{\beta}_{21} \overline{ \beta}_{11} \ln \frac{G_{1}(I_{1} )G_{1}(I^{*}_{1}) }{G_{1}(I^{*}_{1})G_{1}(I_{1})} + \overline{\beta}_{12} \overline{\beta}_{22} \ln\frac{G_{2}(I_{2} )G_{2}(I^{*}_{2}) }{G_{2}(I^{*}_{2})G_{2}(I_{2})} \\ &{}+\overline{\beta}_{21}\overline{\beta}_{12} \ln \frac{G_{1}(I_{1} )G_{2}(I^{*}_{2}) }{G_{1}(I^{*}_{1})G_{2}(I_{2})}+\overline{\beta}_{12}\overline{\beta}_{21} \ln\frac{G_{2}(I_{2} )G_{1}(I^{*}_{1}) }{G_{2}(I^{*}_{2})G_{1}(I_{1})} \\ =&\overline{\beta}_{12}\overline{\beta}_{21} \biggl[ \ln \frac{G_{1}(I_{1} )G_{2}(I^{*}_{2}) }{G_{1}(I^{*}_{1})G_{2}(I_{2})} + \ln\frac{G_{2}(I_{2} )G_{1}(I^{*}_{1}) }{G_{2}(I^{*}_{2})G_{1}(I_{1})} \biggr]=0. \end{aligned}$$

For more general n, by a similar argument as in the proof of \(\sum_{k, j=1}^{n}v_{k} \overline{\beta}_{kj} \ln \frac{E^{*}_{k}E_{j} }{E_{k}E^{*}_{j}}\equiv0\) in [7], we obtain that

$$\sum_{k=1}^{n}v_{k} \sum ^{n}_{j=1} \overline{\beta}_{kj} \ln\frac{G_{k}(I_{k} )G_{j}(I^{*}_{j}) }{G_{k}(I^{*}_{k})G_{j}(I_{j})} =- \sum_{k,j=1}^{n}v_{k} \overline{\beta}_{kj} \ln\frac{G_{k}(I^{*}_{k} )G_{j}(I_{j}) }{G_{k}(I_{k})G_{j}(I^{*}_{j})}\equiv0. $$

From (17)-(19), we see that if \(\dot{V}=0\), then

$$\begin{aligned} S^{(i)}_{k}=S^{(i)*}_{k},\quad i=1,2, k=1,2, \ldots,n. \end{aligned}$$
(21)

If (21) holds, it follows from (2) that

$$\left \{ \textstyle\begin{array}{@{}l} 0=\varphi_{k}(S^{(1)*}_{k})- \sum^{n}_{j=1}\beta ^{(1)}_{kj}S^{(1)*}_{k} G_{j}(I_{j}) -a_{k}S^{(1)*}_{k},\\ 0=a_{k}S^{(1)*}_{k}- \sum^{n}_{j=1}\beta ^{(2)}_{kj}S^{(2)*}_{k}G_{j}(I_{j})-d^{(2)}_{k}S^{(2)*}_{k}. \end{array}\displaystyle \right . $$

Then we obtain that

$$\dot{E_{k}}= \bigl( \varphi_{k}\bigl(S^{(1)*}_{k} \bigr)-a_{k}S^{(1)*}_{k} \bigr) + \bigl( a_{k}S^{(1)*}_{k}-d^{(2)}_{k}S^{(2)*}_{k} \bigr) -(d_{k}+\eta_{k})E_{k}. $$

This implies that

$$ \lim_{t\rightarrow+\infty}E_{k}=\frac{ ( \varphi_{k}(S^{(1)*}_{k})-a_{k}S^{(1)*}_{k} ) + ( a_{k}S^{(1)*}_{k}-d^{(2)}_{k}S^{(2)*}_{k} )}{(d_{k}+\eta_{k})}=E^{*}_{k}. $$
(22)

By (22) and the fourth equation of system (2), we have

$$ \lim_{t\rightarrow+\infty}I_{k}= \frac{ \eta_{k}E^{*}_{k}}{m_{k}} = I^{*}_{k}. $$
(23)

From (21)-(23) and the characteristics of V, we obtain that the largest invariant subset of the set, where \(\dot{V}=0\), is the singleton \(\{P^{*}\}\). By LaSalle’s invariance principle, \(P^{*}\) is globally asymptotically stable for \(R_{0}>1 \). □

4 Numerical examples

For certain sexually transmitted diseases, AIDS/HIV for example, it is natural to consider two groups of people: a group of males and a group of females. Further, it is always assumed that there are two important age stages for the susceptible, a group of immature susceptible \(S^{(1)}_{k}\) who are less than 18 years old, and a group of mature susceptible \(S^{(2)}_{k}\) who are more than 18 years old. Thus, we consider the following model:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \dot{S}^{(1)}_{k}=\varphi_{k}(S^{(1)}_{k})-\sum^{2}_{j=1}\beta ^{(1)}_{kj}S^{(1)}_{k} G_{j}(I_{j}) -a_{k}S^{(1)}_{k},\\ \dot{S}^{(2)}_{k}=a_{k}S^{(1)}_{k}-\sum^{2}_{j=1}\beta ^{(2)}_{kj}S^{(2)}_{k} G_{j}(I_{j}) -d^{(2)}_{k}S^{(2)}_{k},\\ \dot{E_{k}}=\sum^{2}_{i=1}\sum^{2}_{j=1}\beta^{(i)}_{kj}S^{(i)}_{k} G_{j}(I_{j})-(d_{k}+\eta_{k})E_{k},\\ \dot{I_{k}}=\eta_{k}E_{k}-m_{k}I_{k}, \quad k=1,2, \end{array}\displaystyle \right . \end{aligned}$$
(24)

where \(\varphi_{k}(S^{(1)}_{k})=b_{k}-d^{(1)}_{k}S^{(1)}_{k}\), \(G_{j}(I_{j})=\frac{I_{j}}{1+\alpha_{j}I_{j}}\).

Clearly, (A1)-(A4) hold. We fix the parameters as follows:

$$\begin{aligned} &b_{1}=50,\qquad b_{2}=30,\qquad d^{(1)}_{1}=0.001,\qquad d^{(2)}_{1}=0.2,\qquad d^{(1)}_{2}=0.002, \\ &d^{(2)}_{2}=0.3,\qquad d_{1}=0.1,\qquad d_{2}=0.2,\qquad \eta_{1}=0.1, \qquad\eta_{2}=0.2, \\ &m_{1}=0.5,\qquad m_{2}=0.6, \qquad a_{1}=0.6,\qquad a_{2}=0.5,\qquad \alpha_{1}=\alpha_{2}=0.1. \end{aligned}$$
(25)

Then we have \(P_{0}\approx( 83.1947, 249.5840, 59.7610, 99.6016 , 0 , 0, 0 , 0)\).

Case 1. If \(\beta^{(1)}_{1j}=\beta^{(2)}_{k1} =0.002\), \(\beta^{(1)}_{2j}=\beta^{(2)}_{k2} =0.002\), \(k=1,2\), \(j=1,2\), then we obtain

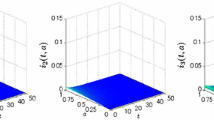
$$\mathbf{Q}\approx \begin{pmatrix} 0.6656& 0.5546 \\ 0.3187& 0.2656 \end{pmatrix},\qquad R_{0}\approx0.9312. $$

By Theorem 3.1, the disease dies out in both groups. Numerical simulation illustrates this fact (see Figure 1).

Figure 1
figure 1

Dynamic behavior of system ( 24 ) with parameter values in ( 25 ) and Case 1. \(R_{0}\approx0.9312\). The initial conditions are: \(S^{(1)}_{1}(0)=70\), \(S^{(2)}_{1}(0)=200\), \(S^{(1)}_{2}(0)=80\), \(S^{(2)}_{2}(0)=240\), \(E_{1}(0)=1\), \(E_{2}(0)=9\), \(I_{1}(0)=3\), \(I_{2}(0)=6\).

Full size image

Case 2. If \(\beta^{(1)}_{1j}=\beta^{(2)}_{k1} =0.0025\), \(\beta^{(1)}_{2j}=\beta^{(2)}_{k2} =0.002\), \(k=1,2\), \(j=1,2\), then we have \(P^{*}\approx(82.7845, 244.9127, 59.4787, 98.2113, 4.6734, 1.0441, 0.9347, 0.3480)\) and \(R_{0}\approx 1.0941\).

By Theorem 3.2, the disease persists in both groups. Numerical simulation illustrates this fact (see Figure 2).

Figure 2
figure 2

Dynamic behavior of system ( 24 ) with parameter values in ( 25 ) and Case 2. \(R_{0}\approx1.0941\). The initial conditions are: \(S^{(1)}_{1}(0)=70\), \(S^{(2)}_{1}(0)=200\), \(S^{(1)}_{2}(0)=80\), \(S^{(2)}_{2}(0)=240\), \(E_{1}(0)=1\), \(E_{2}(0)=9\), \(I_{1}(0)=3\), \(I_{2}(0)=6\).

Full size image