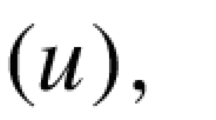Abstract
In this paper, we consider some problems of normal families for solutions of certain Laplace with their derivatives that share a constant. We prove some results which are improvements of some earlier related theorems. Meanwhile, asymptotic behaviors of them are also obtained.
Similar content being viewed by others
1 Introduction and results
Let D be a domain in \(\mathbb{C}\). Let \(\mathscr{F}\) be a solution of certain Laplace equations defined in the domain D. \(\mathscr{F}\) is said to be normal in D, in the sense of Montel, if for any sequence \(\{f_{n}\}\subset\mathscr{F}\), there exists a subsequence \(\{f_{n_{j}}\}\) such that \(f_{n_{j}}\) converges spherically locally uniformly in D to a meromorphic function or ∞.
Let \(g(z)\) be a solution of certain Laplace equations and a be a finite complex number. If \(f(z)\) and \(g(z)\) have the same zeros, then we say that they share a IM (ignoring multiplicity) (see [1, 2]).
In 2009, Schiff [3] proved the following result.
Theorem A
Letfbe a transcendental meromorphic function in the complex plane. Letn, kbe two positive integers such that \(n\geq k+1\), then \((f^{n})^{(k)}\)assumes every finite non-zero value infinitely often.
Corresponding to Theorem A, there are the following theorems about normal families in [4].
Theorem B
Let \(\mathscr{F}\)be a family of meromorphic functions inD. Letn, kbe two positive integers such that \(n\geq k+3\). If \((f^{n})^{(k)}\neq1\)for each function \(f\in\mathscr{F}\), then \(\mathscr{F}\)is normal inD.
Recently, corresponding to Theorem B, Xue [5] proved the following result.
Theorem C
Let \(\mathscr{F}\)be a family of meromorphic functions inD. Letn, kbe two positive integers such that \(n\geq k+2\). Let \(a\neq0\)be a finite complex number. If \((f^{n})^{(k)}\)and \((g^{n})^{(k)}\)shareainDfor each pair of functionsfandgin \(\mathscr{F}\), then \(\mathscr{F}\)is normal inD.
Lei, Yang and Fang [6] proved the following theorem.
Theorem D
Letfbe a transcendental meromorphic function in the complex plane. Letkbe a positive integer. Let \(L[f]=a_{k}f^{(k)}+a_{k-1}f^{(k-1)}+\cdots+a_{0}f\), where \(a_{0}, a_{1},\ldots, a_{k}\)are small functions and \(a_{j}\) (≢0) (\(j=1,2,\ldots,k\)). For \(c\neq0, \infty\), let \(F=f^{n}L[f]-c\), wherenis a positive integer. Then, for \(n\geq2\), \(F=f^{n}L[f]-c\)has infinitely many zeros.
From Theorem D, we immediately obtain the following result.
Corollary D
Letfbe a transcendental meromorphic function in the complex plane. Letcbe a finite complex number such that \(c\neq0\). Letn, kbe two positive integers. Then, for \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), \(f^{n}f^{(k)}-c\)has infinitely many zeros.
From Corollary D, it is natural to ask whether Corollary D can be improved by the idea of sharing values similarly with Theorem C? In this paper we investigate the problem and obtain the following result.
Theorem 1
Let \(\mathscr{F}\)be a family of meromorphic functions inD. Letn, kbe two positive integers such that \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\). Letabe a finite complex number such that \(a\neq0\). If, for each \(f\in\mathscr{F}\), fhas only zeros of multiplicity at leastk. If \(f^{n}f^{(k)}\)and \(g^{n}g^{(k)}\)shareainDfor every pair of functions \(f, g\in\mathscr{F}\), then \(\mathscr{F}\)is normal inD.
Remark 1
From Theorem 1, it is easy to see \(\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\geq2\) for any positive integer k.
Example 1
Let \(D=\{z:|z|<1\}\), \(n, k\in N\) with \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\) and n be a positive integer, for \(k=2\), let
For any \(f_{m}\) and \(g_{m}\) in \(\mathscr{F}\), we have \(f_{m}^{n}f^{(k)}_{m}=0\), obviously \(f_{m}^{n}f^{(k)}_{m}\) and \(g_{m}^{n}g^{(k)}_{m}\) share any \(a\neq0\) in D. But \(\mathscr{F}\) is not normal in D.
Example 2
Let \(D=\{z:|z|<1\}\), \(n, k\in N\) with \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\) and n be a positive integer, and let
For any \(f_{m}\) and \(g_{m}\) in \(\mathscr{F}\), we have \(f_{m}^{n}f^{(k)}_{m}=m^{k}e^{(mn+m)z}\), obviously \(f_{m}^{n}f^{(k)}_{m}\) and \(g_{m}^{n}g^{(k)}_{m}\) share 0 in D. But \(\mathscr{F}\) is not normal in D.
Example 3
Let \(D=\{z:|z|<1\}\), \(n, k\in N\) with \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), and n be a positive integer, let
For any \(f_{m}\) and \(g_{m}\) in \(\mathscr{F}\), we have \(f_{m}f'_{m}=mz+1\). Obviously \(f_{m}f'_{m}\) and \(g_{m}g'_{m}\) share 1 in D. But \(\mathscr{F}\) is not normal in D.
Remark 2
Example 1 shows that f has only zeros of multiplicity at least k is necessary in Theorem 1. Example 2 shows that \(a\neq0\) in Theorem 1 is inevitable. Example 3 shows that Theorem 1 is not true for \(n=1\).
2 Lemmas
In order to prove our theorem, we need the following lemmas.
Lemma 2.1
Let \(\mathscr{F}\)be a family of meromorphic functions inDwith the property that for each \(f\in\mathscr{F}\), all zeros are of multiplicity at leastk. Suppose that there exists a number \(A\geq1\)such that \(|f^{(k)}(z)|\leq A\)whenever \(f\in\mathscr{F}\)and \(f=0\). If \(\mathscr{F}\)is not normal inD, then for \(0\leq\alpha\leq k\), there exist
-
(1)
a number \(r\in(0,1)\);
-
(2)
a sequence of complex numbers \(z_{n}\), \(|z_{n}|< r\);
-
(3)
a sequence of functions \(f_{n}\in\mathscr{F}\);
-
(4)
a sequence of positive numbers \(\rho_{n}\rightarrow0^{+}\);
such that \(g_{n}(\xi)=\rho_{n}^{-\alpha}f_{n}(z_{n}+\rho_{n}\xi)\)locally uniformly (with respect to the spherical metric) converges to a non-constant meromorphic function \(g(\xi)\)on \(\mathbb{C}\), and moreover, the zeros of \(g(\xi)\)are of multiplicity at leastk, \(g^{\sharp}(\xi)\leq g^{\sharp}(0)=kA+1\), where \(g^{\sharp}(z)=\frac{|g'(z)|}{1+|g(z)|^{2}}\). In particular, ghas order at most 2.
Lemma 2.2
Letn, kbe two positive integers such that \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), and let \(a\neq0\)be a finite complex number. Iffis a rational but not a polynomial meromorphic function andfhas only zeros of multiplicity at leastk, then \(f^{n}f^{(k)}-a\)has at least two distinct zeros.
Proof
If \(f^{n}f^{(k)}-a\) has zeros and has exactly one zero.
We set
where A is a non-zero constant. Because the zeros of f are at least k, we obtain \(m_{i}\geq k\) (\(i=1,2,\ldots,s\)), \(n_{j}\geq 1\) (\(j=1,2,\ldots,t\)).
For simplicity, we denote
and
From (2.1), we obtain
where g is a polynomial of degree at most \(k(s+t-1)\).
From (2.1) and (2.4), we obtain
where p and q are polynomials of degree M and N, respectively. Also p and q have no common factor, where \(M_{i}=(n+1)m_{i}-k\) and \(N_{j}=(n+1)n_{j}+k\). By (2.2) and (2.3), we deduce \(M_{i}=(n+1)m_{i}-k\geq k(n+1)-k=nk\) and \(N_{j}=(n+1)n_{j}+k\geq n+k+1\). For simplicity, we denote
and
Since \(f^{n}f^{(k)}-a=0\) has just a unique zero \(z_{0}\), from (2.5) we obtain
By \(a\neq0\), we obtain \(z_{0}\neq\alpha_{i} \) (\(i=1,\ldots,s\)), where B is a non-zero constant.
From (2.5), we obtain
where \(g_{1}(z)\) is a polynomial of degree at most \((k+1)(s+t-1)\).
From (2.8), we obtain
where \(g_{2}(z)=B(l-N)z^{t}+B_{1}z^{t-1}+\cdots+B_{t}\) is a polynomial (\(B_{1},\ldots, B_{t}\) are constants).
Now we distinguish two cases.
Case 1. If \(l\neq N\), by (2.8), then we obtain \(\deg p\geq\deg q\). So \(M\geq N\). By (2.9) and (2.10), we obtain \(\sum_{i=1}^{s}(M_{i}-1)\leq\deg g_{2}=t\). So \(M-s-\deg(g)\leq t\) and \(M\leq s+t+\deg(g)\leq(k+1)(s+t)-k<(k+1)(s+t)\). By (2.6) and (2.7), we obtain
By \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), we deduce \(M< M\), which is impossible.
Case 2. If \(l= N\), then we distinguish two subcases.
Subcase 2.1. If \(M\geq N\), by (2.9) and (2.10), we obtain \(\sum_{i=1}^{s}(M_{i}-1)\leq\deg g_{2}=t\). So \(M-s-\deg(g)\leq t\) and \(M\leq s+t+\deg(g)\leq(k+1)(s+t)-k<(k+1)(s+t)\), then this is impossible, which is similar to Case 1.
Subcase 2.2. If \(M< N\), by (2.9) and (2.10), we obtain \(l-1\leq\deg g_{1}\leq(s+t-1)(k+1)\), then
By \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), we deduce \(N< N\), which is impossible.
If \(f^{n}f^{(k)}-a\neq0\). We know f is rational but not a polynomial, then \(f^{n}f^{(k)}\) is rational but not a polynomial. At this moment, \(l=0\) for (2.8), proceeding as above in Case 1, we have a contradiction. □
3 Proof of Theorem 1
We may assume that \(D=\{|z|<1\}\). Suppose that \(\mathscr{F}\) is not normal in D. Without loss of generality, we assume that \(\mathscr{F}\) is not normal at \(z_{0}=0\). Then, by Lemma 2.1, there exist
-
(1)
a number \(r\in(0,1)\);
-
(2)
a sequence of complex numbers \(z_{j}\), \(z_{j}\rightarrow0\) (\(j\rightarrow\infty\));
-
(3)
a sequence of functions \(f_{j}\in\mathscr{F}\);
-
(4)
a sequence of positive numbers \(\rho_{j}\rightarrow0^{+}\)
such that \(g_{j}(\xi)=\rho_{j}^{-\frac{k}{n+1}}f_{j}(z_{j}+\rho_{j}\xi)\) converges uniformly with respect to the spherical metric to a non-constant meromorphic function \(g(\xi)\) in \(\mathbb {C}\). Moreover, \(g(\xi)\) is of order at most 2.
By Hurwitz’s theorem, the zeros of \(g(\xi)\) are at least k multiple.
On every compact subset of \(\mathbb{C}\) which contains no poles of g, we have
which converges uniformly with respect to the spherical metric to \(g^{n}(\xi)(g^{(k)}(\xi))-a\).
If \(g^{n}(\xi)(g^{(k)}(\xi))\equiv a\) (≠0) and g has only zeros of multiplicity at least k, then g has no zeros. From \(g^{n}g^{(k)}\) having no zeros and \(g^{n}(\xi)(g^{(k)}(\xi))\equiv a\), we know that g has no poles. Because \(g(\xi)\) is a non-constant meromorphic function in \(\mathbb{C}\) and g has order at most 2, we obtain \(g(\xi)=e^{d\xi^{2}+h\xi+c}\), where d, h, c are constants and \(dh\neq0\). So \(g^{n}(\xi)(g^{(k)}(\xi))\not\equiv a\), which is a contradiction.
When \(g^{n}(\xi)(g^{(k)}(\xi))-a\neq0\), (\(a\neq0\)), we distinguish three cases.
Case 1. If g is a transcendental meromorphic function, by Corollary D, this is a contradiction.
Case 2. If g is a polynomial, the zeros of \(g(\xi)\) are at least k multiple and \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), then \(g^{n}(\xi)(g^{(k)}(\xi))-a=0\) must have zeros, which is a contradiction.
Case 3. If g is a non-polynomial rational function, by Lemma 2.2, which is a contradiction.
Next we will prove that \(g^{n}g^{(k)}-a\) has just a unique zero. To the contrary, let \(\xi_{0}\) and \(\xi_{0}^{\ast}\) be two distinct solutions of \(g^{n}g^{(k)}-a\), and choose δ (>0) small enough such that \(D(\xi_{0}, \delta)\cap D(\xi_{0}^{\ast}, \delta)=\emptyset\), where \(D(\xi_{0}, \delta)=\{\xi:|\xi-\xi_{0}|<\delta\}\) and \(D(\xi_{0}^{\ast}, \delta)=\{\xi:|\xi-\xi_{0}^{*}|<\delta\}\). From (3.1), by Hurwitz’s theorem, there exist points \(\xi_{j}\in D(\xi_{0}, \delta)\), \(\xi_{j}^{*}\in D(\xi_{0}^{*}, \delta)\) such that for sufficiently large j,
and
By the hypothesis that for each pair of functions f and g in \(\mathscr{F}\), \(f^{n}f^{(k)}\) and \(g^{n}g^{(k)}\) share a in D, we know for any positive integer m
and
Fix m, take \(j\rightarrow\infty\) and note \(z_{j}+\rho_{j}\xi_{j}\rightarrow0\), \(z_{j}+\rho_{j}\xi_{j}^{*}\rightarrow0\), then we have
Since the zeros of \(f_{m}^{n}(0)(f^{(k)}_{m}(0))-a\) have no accumulation point, we have \(z_{j}+\rho_{j}\xi_{j}= 0\) and \(z_{j}+\rho_{j}\xi_{j}^{*}= 0\).
Hence
This contradicts with \(\xi_{j}\in D(\xi_{0},\delta)\), \(\xi_{j}^{*}\in D(\xi_{0}^{*},\delta)\) and \(D(\xi_{0},\delta)\cap D(\xi_{0}^{*},\delta)=\emptyset\). So \(g^{n}g^{(k)}-a\) has just a unique zero, which can be denoted by \(\xi_{0}\).
From the above, we know \(g^{n}g^{(k)}-a\) has just a unique zero. If g is a transcendental meromorphic function, by Corollary D, then \(g^{n}g^{(k)}-a= 0\) has infinitely many solutions, which is a contradiction.
From the above, we know \(g^{n}g^{(k)}-a\) has just a unique zero. If g is a polynomial, then we set \(g^{n}g^{(k)}-a=K(z-z_{0})^{l}\), where K is a non-zero constant and l is a positive integer. Because the zeros of \(g(\xi)\) are at least k multiple and \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\), then we obtain \(l\geq3\). Then \([g^{n}g^{(k)}]'=Kl(z-z_{0})^{l-1}\) (\(l-1\geq2\)). But \([g^{n}g^{(k)}]'\) has exactly one zero, so \(g^{n}g^{(k)}\) has the same zero \(z_{0}\) too. Hence \(g^{n}g^{(k)}(z_{0})=0\), which redcontradicts with \(g^{n}g^{(k)}(z_{0})=a\neq0\).
If g is a rational function but not a polynomial, by Lemma 2.2, then \(g^{n}g^{(k)}-a=0\) at least has two distinct zeros, which is a contradiction.
4 Discussion
In 2013, Ren [9] proved the following theorem.
Theorem E
Let \(\mathscr{F}\)be a family of meromorphic functions inD, nbe a positive integer anda, bbe two constants such that \(a\neq0,\infty\)and \(b\neq\infty\). If \(n\geq3\)and for each function \(f\in\mathscr{F}\), \(f'-af^{n}\neq b\), then \(\mathscr{F}\)is normal inD.
Recently, Ren and Yang [4] improved Theorem E by the idea of shared values. Meanwhile, Yang and Ren [10] also proved the following theorem with some new ideas.
Theorem F
Let \(\mathscr{F}\)be a family of meromorphic functions inD, nbe a positive integer anda, bbe two constants such that \(a\neq0,\infty\)and \(b\neq\infty\). If \(n\geq4\)and for each pair of functionsfandgin \(\mathscr{F}\), \(f'-af^{n}\)and \(g'-ag^{n}\)share the valueb, then \(\mathscr{F}\)is normal inD.
By Theorem 1, we immediately obtain the following result.
Corollary 1
Let \(\mathscr{F}\)be a family of meromorphic functions in a domainDand eachfhas only zeros of multiplicity at least \(k+1\). Letn, kbe positive integers and \(n\geq\frac{1+\sqrt{1+4k(k+1)^{2}}}{2k}\)and let \(a\neq0, \infty\)be a complex number. If \(f^{(k)}-af^{-n}\)and \(g^{(k)}-ag^{-n}\)share 0 for each pair of functionsfandgin \(\mathscr {F}\), then \(\mathscr{F}\)is normal inD.
Remark 3
Obviously, for \(k=1\) and \(b=0\), Corollary 1 occasionally investigates the situation when the power of f is negative in Theorem F.
Recently, Yang and Ren [10] proved the following result.
Theorem G
Let \(\mathscr{F}\)be a family of meromorphic functions in the plane domain D. Letnbe a positive integer such that \(n\geq2\). Letabe a finite complex number such that \(a\neq0\). If \(f^{n}f'\)and \(g^{n}g'\)shareainDfor every pair of functions \(f, g\in\mathscr{F}\), then \(\mathscr{F}\)is normal inD.
Remark 4
Obviously, our result which has the more extensive form improves Theorems C and G in some sense.
Remark 5
For further study, we pose a question.
Question 1
Does the conclusion of Theorem 1 still hold for \(n\geq2\)?
Change history
04 February 2020
The Editors-in-Chief have retracted this article [1] because it shows significant overlap with an article by different authors that was simultaneously under consideration with another journal [2] and with a previously published article by another group of different authors [3]. In addition, the identity of the corresponding author could not be verified: Roskilde University confirmed that Beatriz Ychussie was never affiliated to this institution. The authors have not responded to any correspondence about this retraction.
References
Drasin, D: Normal families and Nevanlinna theory. Acta Math. 122, 231-263 (1969)
Schwick, W: Sharing values and normality. Arch. Math. 59, 50-54 (1992)
Schiff, J: Normal Families. Springer, Berlin (1993)
Ren, YD, Yang, P: Growth estimates for modified Neumann integrals in a half space. J. Inequal. Appl. 2013, Article ID 572 (2013)
Xue, GX: Rarefied sets at infinity associated with the Schrödinger operator. J. Inequal. Appl. 2014, Article ID 247 (2014)
Lei, CL, Yang, DG, Fang, ML: Normal families and shared values of meromorphic functions. J. Math. Anal. Appl. 364, 143-150 (2010)
Xue, GX: A remark on the a-minimally thin sets associated with the Schrödinger operator. Bound. Value Probl. 2014, Article ID 133 (2014)
Zalcman, L: Normal families: new perspectives. Bull. Am. Math. Soc. 35, 215-230 (1998)
Ren, YD: Solving integral representations problems for the stationary Schrödinger equation. Abstr. Appl. Anal. 2013, Article ID 715252 (2013)
Yang, DW, Ren, YD: Dirichlet problem on the upper half space. Proc. Indian Acad. Sci. Math. Sci. 124(2), 175-178 (2014)
Acknowledgements
This work was completed while the corresponding author was visiting the Department of Mathematical Sciences at the Columbia University, and he is grateful for the kind hospitality of the Department.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
Both authors contributed equally to the writing of this paper. Both authors read and approved the final manuscript.
The Editors-in-Chief have retracted this article [1] because it shows significant overlap with an article by different authors that was simultaneously under consideration with another journal [2] and a previously published article by another group of different authors [2]. In addition, the identity of the corresponding author could not be verified: Roskilde University confirmed that Beatriz Ychussie was never affiliated to this institution. The authors have not responded to any correspondence about this retraction.
[1] Yan, Z. and Ychussie, B. Normal families and asymptotic behaviors for solutions of certain Laplace equations. Advances in Difference Equations __ 2015: 226. https://doi.org/10.1186/s13662-015-0564-x
[2] Sun, J., He, B. and Peixoto-de-Büyükkurt, C. Growth properties at infinity for solutions of modified Laplace equations. J Inequal Appl 2015, 256 (2015) https://doi.org/10.1186/s13660-015-0777-2
[3] Jianming Qi and Taiying Zhu, Some Normal Criteria about Shared Values with Their Multiplicity Zeros, Abstract and Applied Analysis, vol. 2010, Article ID 147878, 14 pages, 2010. https://doi.org/10.1155/2010/147878.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yan, Z., Ychussie, B. RETRACTED ARTICLE: Normal families and asymptotic behaviors for solutions of certain Laplace equations. Adv Differ Equ 2015, 226 (2015). https://doi.org/10.1186/s13662-015-0564-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0564-x