1 Introduction

In general, complex networks consist of a large number of nodes, in which every node is a fundamental cell with specific activity. In the past two decades, complex networks have attracted scholars’ increasing attention. Several famous network models, such as scale-free model [1], small-world model [2, 3], which accurately characterize some important natural structures, have been presented. Synchronization is a universal phenomenon in various fields of science and society, and many significant works have been obtained in [4–8]; Wu et al. investigate synchronization of an array of linearly coupled identical systems in [9–11]; research in [12, 13] shows that the structure of networks must have an inevitable effect on the ability and speed of synchronization. It is well known that time-delays widely exist in a large number of concrete systems, and coupled dynamical networks are often associated with time-delays due to the finite speeds of transmission and spreading as well as traffic congestion. A lot of efforts have been made to study the synchronization of dynamical coupled systems with time-delays in [14–18].

At the same time, we notice that a large number of practical networks, such as economic networks, power networks and so on, are singular differential systems which are also named differential-algebraic systems or descriptor systems. Singular systems have some particular complex properties which need not be considered in normal systems. In singular systems, impulse behavior may appear (if the index is greater than one) and initial value problem may also be unsolvable or have more than one solution, regularity is closely related to the solution behavior of the corresponding singular systems [19]. In order to make a singular system solvable with no impulse behavior and unique solution, the system must be regular and the initial condition must be compatible, which can be acquired similarly to the method presented in [20]. Due to the effect of time-delays, coupled correlative terms will inevitably appear if the system is divided into two subsystems including a differential subsystem and an algebraic subsystem, which makes the problems become more complicated. Recently, Xiong et al. [21] have investigated synchronization of singular hybrid coupled networks without time-delays, the original system is divided into two subsystems including a differential subsystem and an algebraic subsystem, the authors present a sufficient condition of global synchronization, but the presented method cannot be applied to singular delayed networks. Koo et al. [22] and Li et al. [23] investigate synchronization of singular complex dynamical networks with time-varying bounded delays. Sufficient conditions for synchronization in terms of LMIs (linear matrix inequalities) are obtained, respectively. Motivated by this research, in this paper we study synchronization problem of singular dynamical networks with non-delay coupling and unbounded time-delay coupling simultaneously. Based on the Lyapunov-Krasovskii functional method, a simple sufficient condition of synchronization is derived by using matrix analysis and matrix inequality technique. Our presented method can also be applied to more general dynamical networks including the networks presented in [21–23]. Finally, a numerical example shows that our presented method is simple and convenient in computation.

Notation: The notation used throughout this paper is fairly standard. \(R^{n}\) denotes an n-dimensional Euclidean space, \(R^{n\times n}\) is the set of all \(n\times n\) real matrices, \(I_{n}\) stands for the identity matrix of order n, \(U^{T}\) means the transpose of a real matrix or vector U, \(\|x\|\) denotes the Euclidean norm of a real vector x. For a real matrix A, \(\lambda_{\mathrm{max}}(A)\) and \(\lambda_{\mathrm{min}}(A)\) denote the maximal and minimal eigenvalue respectively. \(\|A\|=\sqrt{\lambda_{\mathrm{max}}(A^{T}A)}\) denotes the spectral norm of matrix A, \(A>B\) (or \(A\ge B\)) means the symmetric matrix \(A-B\) is positive definite (or positive semi-definite) and \(A\otimes B\) denotes the Kronecker product between matrix A and B.

2 Preliminaries

In this section, we now introduce some notations and preliminaries. Consider the singular delayed network consisting of N linearly and diffusively coupled identical nodes, with full diagonal coupling, and each node is an n-dimensional dynamical oscillator which can be chaotic. The state equations of the network are described as

$$\begin{aligned} E\dot{x}_{i}(t) =&Ax_{i}(t)+f\bigl(x_{i}(t),t \bigr) +c_{1}\sum_{j=1}^{N}b_{ij} \Gamma x_{j}(t) \\ &{}+c_{2}\sum_{j=1}^{N} \hat{b}_{ij}\hat{\Gamma} x_{j}\bigl(t-\tau_{i}(t) \bigr),\quad i=1,2,\ldots,N, \end{aligned}$$
(1)

where matrix E may be singular and \(0<\operatorname{rank}(E)=p<n\), \(A\in R^{n\times n}\) is a constant matrix. \(x_{i}=(x_{i1},x_{i2},\ldots,x_{in})^{T} \in R^{n}\) is the state vector of node i, \(f:R^{n}\times R\rightarrow R^{n}\) is a continuously differentiable vector-valued function describing the dynamics of the nodes, \(c_{i}>0\) (\(i=1,2\)) represent the coupling strength, the inner coupling link matrices are diagonal matrices, \(\Gamma=\operatorname{diag}\{r_{1},r_{2},\ldots,r_{n}\}\) with \(r_{i}>0\), \(\hat{\Gamma}=\operatorname{diag}\{\hat{r}_{1},\hat{r}_{2},\ldots,\hat{r}_{n}\}\) with \(\hat{r}_{i}>0\). The coupling time-delays \(\tau_{i}(t)> 0\) are differentiable and \(\dot{\tau}_{i}(t)\le d_{i} <1\), \(i=1,2,\ldots,N\). The coupling configuration matrices \(B=(b_{ij})_{N\times N}\) and \(\hat{B}=(\hat{b}_{ij})_{N\times N}\) describe the topological structure of the network, in which \(b_{ij}\) (the entries \(\hat{b}_{ij}\) are defined similarly) is defined as follows: if there is a connection from node i to node j (\(i\neq j\)), then \(b_{ij}>0\); else \(b_{ij}=0\), the diagonal entries of matrix B are defined by

$$b_{ii}=-\sum_{j=1,j\neq i}^{N} b_{ij}=-\sum_{j=1,j\neq i}^{N} b_{ji},\quad i=1,2,\ldots, N. $$

We assume that network (1) is connected in the sense that there are no isolated clusters, i.e., matrices B and \(\hat{B}\) are irreducible, hence the zero is an eigenvalue of B and \(\hat{B}\) with multiplicity 1 (see [18]). Furthermore, the eigenvalues can be arranged respectively as

$$\begin{aligned}& 0=\lambda_{1} > \lambda_{2}\geq\lambda_{3}\geq \cdots\geq\lambda_{N}, \\& 0=\mu_{1} > \mu_{2}\geq\mu_{3}\geq\cdots\geq \mu_{N}. \end{aligned}$$

In virtue of the Kronecker product, system (1) can be written as

$$\begin{aligned} (I_{N}\otimes E)\dot{x}(t) =&(I_{N}\otimes A)x(t)+I_{N}\otimes f\bigl(x(t),t\bigr) \\ &{}+c_{1}(B\otimes \Gamma)x(t)+c_{2}(\hat{B}\otimes \hat{\Gamma})x\bigl(t-\tau(t) \bigr), \end{aligned}$$
(2)

where \(x(t)=(x_{1}^{T}(t),x_{2}^{T}(t),\ldots,x_{N}^{T}(t))^{T}\), \(x(t-\tau(t))=(x_{1}^{T}(t-\tau_{1}(t)),x_{2}^{T}(t-\tau_{2}(t)),\ldots,x_{N}^{T}(t-\tau _{N}(t)))^{T}\), \(I_{N}\otimes f(x(t),t)=(f^{T}(x_{1}(t),t),f^{T}(x_{2}(t),t),\ldots,f^{T}(x_{N}(t),t))^{T}\).

To obtain our main results, the following lemmas will be used later.

Lemma 2.1

([20])

For any vectors \(x,y\in R^{n}\) and \(\varepsilon> 0\), the inequality \(2x^{T}y\leq\varepsilon x^{T}x+\frac{1}{\varepsilon} y^{T}y\) holds.

Lemma 2.2

([24])

Suppose that U and V are real symmetric matrices and \(U >0\), \(V\ge0\), α is a positive number. Then

$$\alpha U>V\quad \Leftrightarrow\quad \lambda_{\mathrm{max}}\bigl(VU^{-1} \bigr)< \alpha \quad \Leftrightarrow\quad \lambda_{\mathrm{max}} \bigl(U^{-\frac{1}{2}}VU^{-\frac{1}{2}}\bigr)< \alpha. $$

3 Main results

In this section, the main results of this paper on asymptotical synchronization of singular delayed network (1) are derived. We first introduce the following definition.

Definition 3.1

([21])

The singular delayed network (1) is said to achieve asymptotical synchronization if

$$ x_{i}(t)=s(t),\quad i=1,2,\ldots,N, \mbox{as }t\rightarrow\infty, $$
(3)

where \(s(t)\in R^{n}\) is a synchronous solution of an isolated cell such that \(E\dot{s}(t)=As(t)+f(s(t),t)\).

Remark 3.1

In [25], the authors presented a sufficient condition on the existence and uniqueness of solution of the system \(E\dot{x}(t)=Ax(t)+f(x(t),t)\).

Theorem 3.1

Suppose that matrix \(B\hat{B}\) is symmetric, then the synchronization state \(s(t)\) of the singular delayed network (1) is asymptotically stable if the linear time-varying singular delayed systems

$$ E\dot{y}_{i}=(A+J+c_{1}\lambda_{i} \Gamma)y_{i}(t) +c_{2}\mu_{i}\hat{\Gamma} y_{i}\bigl(t-\tau_{i}(t)\bigr),\quad i=1,2,\ldots,N, $$
(4)

are asymptotically stable about their zero solutions, where \(s(t)\) is an asymptotical stable solution of an isolated cell, J is the Jacobian matrix of \(f(x(t),t)\) at \(s(t)\).

Proof

To investigate the stability of the synchronous solution \(s(t)\), let

$$ e_{i}(t)=x_{i}(t)-s(t),\quad i=1,2,\ldots,N. $$
(5)

Then we obtain an error system in a compact form

$$ (I_{N}\otimes E)\dot{e}(t)=\bigl(I_{N}\otimes(A+J)\bigr)e(t) +c_{1}(B\otimes\Gamma)e(t)+c_{2}(\hat{B}\otimes \hat{\Gamma})e \bigl(t-\tau(t)\bigr), $$
(6)

where \(e(t)=(e_{1}^{T}(t),e_{2}^{T}(t),\ldots,e_{N}^{T}(t))^{T}\), \(e(t-\tau(t))=(e_{1}^{T}(t-\tau_{1}(t)),e_{2}^{T}(t-\tau_{2}(t)),\ldots,e_{N}^{T}(t-\tau _{N}(t)))^{T}\).

Obviously, the dynamical network (2) will achieve asymptotical synchronization if the error system (6) is asymptotically stable about the zero solution.

Since matrix \(B\hat{B}\) is symmetric, there exists an orthogonal matrix \(U\in R^{N\times N}\) such that

$$ UBU^{T}=\Lambda_{1},\qquad U\hat{B} U^{T}= \Lambda_{2}, $$
(7)

where \(\Lambda_{1}=\operatorname{diag}\{\lambda_{1},\lambda_{2},\ldots,\lambda_{N}\}\), \(\Lambda_{2}=\operatorname{diag}\{\mu_{1},\mu_{2},\ldots,\mu_{N}\}\) are both diagonal matrices.

Let \(y(t)=(U^{T}\otimes I_{n})e(t)=(y_{1}^{T}(t),y_{2}^{T}(t),\ldots,y_{N}^{T}(t))^{T}\), we have

$$ (I_{N}\otimes E)\dot{y}(t)=\bigl(I_{N}\otimes(A+J)\bigr)y(t) +c_{1}(\Lambda_{1}\otimes\Gamma)y(t)+c_{2}( \Lambda_{2}\otimes \hat{\Gamma})y\bigl(t-\tau(t)\bigr). $$
(8)

Namely,

$$ E\dot{y}_{i}(t)=(A+J+c_{1}\lambda_{i} \Gamma)y_{i}(t) +c_{2}\mu_{i}\hat{\Gamma} y_{i}\bigl(t-\tau_{i}(t)\bigr),\quad i=1,2,\ldots,N. $$
(9)

The proof is completed. □

In order to make singular system (1) or (4) solvable with no impulse, we suppose that the following assumption holds.

Assumption 1

There exist matrices \(P_{i}\) and positive-define matrices \(Q_{i}\) such that the following inequalities hold:

$$\begin{aligned}& E^{T}P_{i}=P_{i}^{T}E\ge0,\quad i=1,2, \ldots,N, \end{aligned}$$
(10)
$$\begin{aligned}& \begin{aligned} &(A+J)^{T}P_{1}+P_{1}^{T}(A+J)< 0, \\ &P_{i}^{T}(A+J+c_{1}\lambda_{i} \Gamma)+ (A+J+c_{1}\lambda_{i} \Gamma)^{T}P_{i}+2 \beta_{i}Q_{i}\le0,\quad i=2,3,\ldots,N \end{aligned} \end{aligned}$$
(11)

and

$$ \|P_{i}\|< \sqrt{1-d_{i}}\lambda_{\mathrm{min}}Q_{i}, \quad i=2,3,\ldots,N, $$
(12)

where \(\beta_{i}=c_{2}\hat{r}|\mu_{i}|\) (\(i=2,3,\ldots,N\)), \(\hat{r}= \max_{1\le i\le n} \hat{r}_{i}\).

Remark 3.2

The initial function space of differential systems with unbounded delays is not completed. Let \(\mathit{BC}:=\{\phi| \phi:(-\infty ,0] \rightarrow R^{n} , \phi \mbox{ is bounded and continuous}\}\), then \((\mathit{BC},\|\cdot\|)\) is a Banach space. We also may define a new complete initial function space.

Let \(x: [a,b]\rightarrow R^{n}\), with the norm \(\|x\|:=\sup_{s\in[a,b]}|x(s)|\). Denote \(C := \{\phi| \phi: (-\infty,0] \rightarrow R^{n} , \phi\mbox{ is continuous}\}\), then C and BC are both linear spaces.

Let \(h\in C\), \(h\geq0\), and \(0<\int^{0}_{-\infty}h(s)\, ds<\infty\). Denote \(C^{n}_{h}:= \{\phi| \int^{0}_{-\infty}h(s)\|\phi\|\, ds< \infty, \phi\in C \}\), the norm of \(\phi\in C^{n}_{h}\) is defined as \(\|\phi\|_{h}:= \int^{0}_{-\infty}h(s)\|\phi\|\, ds\), hence \(C^{n}_{h}\) is a linear subspace of C and \(\mathit{BC} \sqsubset C^{n}_{h}\).

Lemma 3.1

([26])

\((C^{n}_{h}, \|\cdot\|_{h})\) is a Banach space.

Under condition (11), it follows from [27] that the pair \((E, A+J+c_{1}\lambda_{i} \Gamma)\) is regular and impulse free, hence the solution of Eq. (4) exists and is impulse free and unique on \([t_{0},\infty)\) for any admissible initial condition \(\phi \in C^{n}_{h} \).

Theorem 3.2

Suppose that matrix \(B\hat{B}\) is symmetric and Assumption  1 holds, then the singular networks with unbounded coupled delays (4) will asymptotically synchronize in the sense of (3).

Proof

Construct the Lyapunov-Krasovskii functionals as:

$$ V_{i}(t)= y_{i}^{T}(t)E^{T}P_{i}y_{i}(t)+ \beta_{i}\int_{t-\tau_{i}(t)}^{t}y_{i}^{T}(s)Q_{i}y_{i}(s) \, ds. $$
(13)

We get the derivatives of \(V_{i}(t)\) along the trajectories of the ith equation (4) as follows:

$$\begin{aligned} \dot{V}_{i}(t) =& y_{i}^{T}(t)P_{i}^{T} \bigl((A+J+c_{1}\lambda_{i} \Gamma)y_{i}(t) +c_{2}\mu_{i} \hat{\Gamma}y_{i}\bigl(t- \tau_{i}(t)\bigr)\bigr) \\ &{}+\bigl((A+J+c_{1} \lambda_{i} \Gamma)y_{i} +c_{2}\mu_{i} \hat{\Gamma}y_{i}\bigl(t-\tau_{i}(t)\bigr) \bigr)^{T} \\ &{}\times P_{i}y_{i}(t)+\beta_{i}y_{i}^{T}(t)Q_{i}y_{i}(t)- \beta_{i}\bigl(1-\dot{\tau}_{i}(t)\bigr) y_{i}^{T}\bigl(t-\tau_{i}(t)\bigr)Q_{i}y_{i} \bigl(t-\tau_{i}(t)\bigr) \\ =&y_{i}^{T}(t) \bigl(P_{i}^{T}(A+J+c_{1} \lambda_{i} \Gamma)+(A+J+c_{1}\lambda_{i} \Gamma)^{T}P_{i}+\beta_{i} Q_{i} \bigr)y_{i}(t) \\ &{} +2c_{2}\mu_{i}y_{i}^{T}(t)P_{i}^{T} \hat{\Gamma}y_{i}\bigl(t-\tau_{i}(t)\bigr) - \beta_{i}\bigl(1-\dot{\tau}_{i}(t)\bigr) y_{i}^{T}\bigl(t-\tau_{i}(t)\bigr)Q_{i}y_{i} \bigl(t-\tau_{i}(t)\bigr) \\ \le&-\beta_{i}y_{i}^{T}(t)Q_{i}y_{i}(t)+2c_{2} \mu_{i}y_{i}^{T}(t)P_{i}^{T} \hat{\Gamma}y_{i}\bigl(t-\tau_{i}(t)\bigr) \\ &{}- \beta_{i}(1-d_{i})y_{i}^{T}\bigl(t- \tau_{i}(t)\bigr)Q_{i}y_{i}\bigl(t- \tau_{i}(t)\bigr). \end{aligned}$$

From Lemma 2.1, we obtain

$$\begin{aligned}& 2c_{2}\mu_{i} y_{i}^{T}(t)P_{i}^{T} \hat{\Gamma}y_{i}\bigl(t-\tau_{i}(t)\bigr) \\& \quad = 2c_{2}\mu_{i}y_{i}^{T}(t)P_{i}^{T} \hat{\Gamma}^{\frac{1}{2}}Q_{i}^{-\frac{1}{2}} Q_{i}^{\frac{1}{2}} \hat{\Gamma}^{\frac{1}{2}}y_{i}\bigl(t-\tau_{i}(t)\bigr) \\& \quad \leq\frac{c_{2}\hat{r}}{\alpha_{i}(1-d_{i})}|\mu_{i}|y_{i}^{T}(t)P_{i}^{T}Q_{i}^{-1}P_{i}y_{i}(t) +\alpha_{i} c_{2}\hat{r} |\mu_{i}|(1-d_{i}) y_{i}^{T}\bigl(t-\tau_{i}(t)\bigr)Q_{i}y_{i} \bigl(t-\tau _{i}(t)\bigr) \\& \quad =\frac{\beta_{i}}{\alpha_{i}(1-d_{i})}y_{i}^{T}(t)P_{i}^{T}Q_{i}^{-1}P_{i}y_{i}(t)+ \alpha_{i} \beta_{i}(1-d_{i})y_{i}^{T} \bigl(t-\tau_{i}(t)\bigr)Q_{i}y_{i}\bigl(t- \tau_{i}(t)\bigr). \end{aligned}$$

Then we get

$$\begin{aligned} \dot{V}_{i}(t) \le& \beta_{i}y_{i}^{T}(t) \biggl(\frac{1}{\alpha_{i}(1-d_{i})}P_{i}^{T}Q_{i}^{-1}P_{i} -Q_{i}\biggr)y_{i}(t) \\ &{}+\beta_{i}(1-d_{i}) (\alpha_{i}-1) y_{i}^{T}\bigl(t- \tau_{i}(t)\bigr)Q_{i}y_{i}\bigl(t- \tau_{i}(t)\bigr). \end{aligned}$$

From the definition of spectral norm, we know

$$\begin{aligned}& \biggl(\lambda_{\mathrm {max}} \biggl(Q_{i}^{-\frac{1}{2}}\biggl( \frac{1}{1-d_{i}}P_{i}^{T}Q_{i}^{-1}P_{i} \biggr)Q_{i}^{-\frac{1}{2}}\biggr)\biggr) ^{\frac{1}{2}} \\& \quad =\frac{1}{\sqrt{1-d_{i}}}\bigl(\lambda_{\mathrm{ max}}\bigl(Q_{i}^{-\frac{1}{2}}P_{i}^{T}Q_{i}^{-1}P_{i}Q_{i}^{-\frac{1}{2}} \bigr)\bigr) ^{\frac{1}{2}} \\& \quad =\frac{1}{\sqrt{1-d_{i}}}\bigl\Vert Q_{i}^{-\frac{1}{2}}P_{i}Q_{i}^{-\frac{1}{2}} \bigr\Vert \\& \quad \le\frac{1}{\sqrt{1-d_{i}}}\bigl\Vert Q_{i}^{-\frac{1}{2}}\bigr\Vert ^{2}\|P_{i}\| \\& \quad =\frac{1}{\sqrt{1-d_{i}}\lambda_{\mathrm{min}}(Q_{i})}\|P_{i}\|. \end{aligned}$$

Since \(P_{i}^{T}Q_{i}^{-1}P_{i}\geq0\), from (12) we get

$$\lambda_{\mathrm{max}}\biggl(Q_{i}^{-\frac{1}{2}}\biggl( \frac {1}{1-d_{i}}P_{i}^{T}Q_{i}^{-1}P_{i} \biggr)Q_{i}^{-\frac{1}{2}}\biggr)< 1. $$

Hence, there exist \(\eta_{i}>0\) (\(i=1,2,\ldots,N\)) such that

$$\lambda_{\mathrm{max}}\biggl(Q_{i}^{-\frac{1}{2}}\biggl( \frac {1}{1-d_{i}}P_{i}^{T}Q_{i}^{-1}P_{i} \biggr)Q_{i}^{-\frac{1}{2}}\biggr) < \eta_{i}< 1. $$

Since \(P_{i}^{T}Q_{i}^{-1}P_{i}\ge0\), from Lemma 2.2 we obtain

$$\frac{1}{1-d_{i}}P_{i}^{T}Q_{i}^{-1}P_{i}< \eta_{i} Q_{i}. $$

Choose \(\alpha_{i}<1\) such that \(0<\frac{\eta_{i}}{\alpha_{i}}<1\). Then

$$ M_{i}:=\beta_{i}\biggl(\frac{1}{\alpha_{i}(1-d_{i})}P_{i}^{T}Q_{i}^{-1}P_{i}- Q_{i}\biggr) < \beta_{i}\biggl(\frac{ \eta_{i}}{\alpha_{i}}-1\biggr) Q_{i}< 0 $$
(14)

and

$$ N_{i}:=\beta_{i}(1-d_{i}) ( \alpha_{i}-1)Q_{i}< 0. $$
(15)

Hence we obtain

$$\dot{V}_{i}(t)\le y_{i}^{T}(t)M_{i}y_{i}(t)+y_{i}^{T} \bigl(t-\tau_{i}(t)\bigr)N_{i}y_{i}\bigl(t- \tau_{i}(t)\bigr). $$

From (14) and (15), we know \(\dot{V}_{i}(t)\) (\(i=1,2,\ldots,N\)) are negative definite. Therefore Eq. (4) is asymptotically stable about zero solution via the Lyapunov stability theory, then the singular delayed network (1) will achieve asymptotical synchronization. □

Remark 3.3

  1. (1)

    If \(b_{ij}=0\) (i.e., \(B=0\)) and \(\tau_{i}(t)=\tau (t)\) is bounded, Eq. (1) is reduced to

    $$ E\dot{x}_{i}(t)=Ax_{i}(t)+f\bigl(x_{i}(t),t \bigr) +c_{2}\sum_{j=1}^{N} \hat{b}_{ij}\hat{\Gamma} x_{j}\bigl(t-\tau(t)\bigr),\quad i=1,2,\ldots ,N, $$
    (16)

    which is the network model presented in [22, 23].

  2. (2)

    If \(\hat{b}_{ij}=0\) (i.e., \(\hat{B}=0\)), Eq. (1) is reduced to

    $$ E\dot{x}_{i}(t)=Ax_{i}(t)+f\bigl(x_{i}(t),t \bigr) +c_{1}\sum_{j=1}^{N}b_{ij} \Gamma x_{j}(t) ,\quad i=1,2,\ldots,N, $$
    (17)

    which is the network model presented in [21].

Hence, the model investigated in this paper may characterize many natural dynamical networks and our proposed method can also be applied to more general dynamical networks.

Remark 3.4

In reality, it is difficult to compute matrices \(P_{i}\) (\(i =1, 2, \ldots , N\)) and \(Q_{i}\) (\(i=2, 3,\ldots , N\)) for a general complex model with a large number N of nodes or with a large dimension from conditions (10) and (11). It should be pointed out that (10) and (11) cannot be solved directly by the LMI toolbox of Matlab. However, if matrix E is positive semi-definite and matrix A is negative definite, one can easily choose positive definite matrices \(P_{i}\) and \(Q_{i}\) satisfying conditions (10)-(12) (see the following numerical example). Comparing with [21–23], our proposed method is simple and convenient in computation.

4 An illustrative example

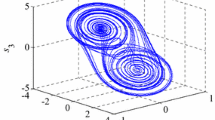
In this section, a simple example is given to illustrate theoretical results and the presented conditions in Theorem 3.2 can be easily obtained. We consider the following singular complex network with six nodes (see Figure 1) in which each node is connected to other nodes and which is described as

$$\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} \dot{x}_{i1}\\ \dot{x}_{i2}\\ \dot{x}_{i3} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -1 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 1 & -2 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} x_{i1}\\ x_{i2}\\ x_{i3} \end{array}\displaystyle \right ) + \left ( \textstyle\begin{array}{@{}c@{}} -x_{i1}+2x_{i2}^{2}\\ - x_{i2}\\ x_{i2}-2 x_{i3} \end{array}\displaystyle \right ) ,\quad i=1,2,3,4,5,6, $$

and the solution of the state equation can be written as

$$\left \{ \textstyle\begin{array}{l} x_{i1}=k_{1}e^{-t}-\frac{k_{2}^{2}}{4}e^{-5t}, \\ x_{i2}=k_{2}e^{-\frac{5}{2}t}, \\ x_{i3}=\frac{k_{2}}{2}e^{-\frac{5}{2}t}, \end{array}\displaystyle \right . $$

which is asymptotically stable at \(s(t)=0\), where \(k_{1}\), \(k_{2}\) are both constants. And the Jacobian is \(J=\operatorname{diag}\{-1,-1,-2\}\). For convenience, we assume coupled time-delays \(\tau_{i}(t)=0.4t\), the coupling strength \(c_{1}=c_{2}=1\) and the inner coupling matrices \(\Gamma=\hat{\Gamma}=I_{3}\), the coupling configuration matrices are

$$B=\hat{B}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} -5 & 1 & 1 & 1 & 1 & 1 \\ 1 & -5 & 1 & 1 & 1 & 1\\ 1 & 1 & -5 & 1 & 1 & 1 \\ 1 & 1 & 1 & -5 & 1 & 1 \\ 1 & 1 & 1 & 1 & -5 & 1 \\ 1 & 1 & 1 & 1 & 1 & -5 \end{array}\displaystyle \right ) , $$

and the eigenvalues are 0, −6, −6, −6, −6, −6.

Figure 1
figure 1

Structure of the network.

Full size image

One can choose \(P_{i}=I_{3}\) (\(i=1,2,3,4,5,6\)), hence condition (10) holds. Matrices \(Q_{i}\) can be chosen as

$$Q_{i}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \frac{4}{3} & 0 & 0 \\ 0 & \frac{3}{2} & -\frac{1}{6} \\ 0& -\frac{1}{6} & \frac{5}{3} \end{array}\displaystyle \right ),\quad i=2,3,4,5,6, $$

and the minimal eigenvalue of \(Q_{i}\) is \(\frac{4}{3}\), which shows that condition (11) is satisfied. Noting that \(d_{i}=0.4\), hence condition (12) holds. Therefore the singular delayed network (1) will achieve asymptotical synchronization by Theorem 3.2.

5 Conclusions

This paper investigates singular complex networks with non-delay coupling and unbounded time-delay coupling simultaneously. Based on the Lyapunov stability theory and matrix inequalities and singular system theory, a simple sufficient condition of synchronization is derived, which can be easily realized and is simple and convenient in computation. The proposed method also can be applied to more general complex networks comparing with [21–23]. Finally, a simple example is given to illustrate the effectiveness of our theoretical results.