1 Introduction and preliminaries

The time stability analysis of reaction-diffusion time-delays neural networks has attached more and more interests ([1–5] and the references therein) due to the practical importance and successful applications of neural networks in many areas, such as image processing, combinatorial optimization, signal processing, pattern recognition. Generally, an important precondition of the above applications is that the equilibrium of the neural networks should be stable. Hence, the stability analysis of neural networks has always been an important research topic. Many methods have been proposed to reduce the conservatism of the stability criteria, such as the model transformation method, the free-weighting-matrix approach, constructing novel Lyapunov functionals method, the delay decomposition technique, and the weighting-matrix decomposition method. For example, by using a Lyapunov functional, a modified stability condition for neural networks with discrete and distributed delays has been obtained in [6]; by constructing a general Lyapunov functional and convex combination approach, the stability criterion for neural networks with mixed delays has been obtained in [7]; by partitioning the time delay and using the Jensen integral inequalities, the stability condition on delayed neural networks with both discrete and distributed delays has been obtained in [8], by employing homomorphic mapping theory and M-matrix theory, the stability criterion for neural networks with discrete and distributed time-delays has been derived in [9]. However, the above methods seem to become less effective in studying the stability of reaction-diffusion integro-differential equations. Some variational methods should be added (see, e.g., [1, 3, 4]). In the actual operations, diffusion effects cannot be avoided in neural networks when electrons are moving in asymmetric electromagnetic fields. Strictly speaking, all the neural networks models should have been reaction-diffusion partial differential equations. Recently, Lyapunov functionals method and the Poincaré inequality were employed to investigate the stability of discrete and distributed time-delays reaction-diffusion integro-differential equations in [1]. But it should be noted that parameter uncertainties cannot be inevitable as usual. Besides, the neural networks are often disturbed by environmental noise in the real world. The noise may influence the stability of the equilibrium and vary some structure parameters, which usually correspond to the Markov process. Systems with Markovian jumping parameters are frequently dominated by discrete-state homogeneous Markov processes, and each state of the parameters represents a mode of the system. During the recent decade, bidirectional associative memory (BAM) neural networks, neural networks with Markovian jumping parameters, have been extensively studied ([10–14] and the references therein) due to the fact that systems with Markovian jumping parameters are useful in modeling abrupt phenomena, such as random failures, changing in the interconnections of subsystems, and operating in different points of a nonlinear plant. So, in this paper, we are to employ Lyapunov stability theory and the M-matrix, H-matrix, and linear matrix equality (LMI) techniques and variational methods to investigate the stochastically robust exponential stability of a class of discrete and distributed time-delays Markovian jumping reaction-diffusion uncertain parameter integro-differential equations (BAM neural networks) as follows:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{\partial u}{\partial t} = \nabla\cdot(\Theta\circ\nabla u) -A(r(t)) u +(C(r(t))+\Delta C(r(t))) f(v) +(E(r(t))\\ \hphantom{\frac{\partial u}{\partial t} =}{}+\Delta E(r(t))) f(v (t-\tau(t),x))+(L(r(t))+\Delta L(r(t)))\int_{t-\varrho}^{t}f(v(s,x))\,ds,\\ \hphantom{\frac{\partial u}{\partial t} =}{} t\geqslant0, x\in\Omega, \\ \frac{\partial v }{\partial t} = \nabla\cdot(\Lambda\circ\nabla v) - B(r(t)) v + (D(r(t))+\Delta D(r(t))) g (u) +(H(r(t)) \\ \hphantom{\frac{\partial v }{\partial t} =}{}+\Delta H(r(t))) g (u(t-\gamma(t),x))+(W(r(t))+\Delta W(r(t)))\int_{t-\rho}^{t}g(u(s,x))\,ds,\\ \hphantom{\frac{\partial v }{\partial t} =}{} t\geqslant0, x\in\Omega,\\ u(s,x)=\phi(s,x), \qquad v(s,x)=\psi(s,x), \quad (s,x)\in[-\tau ,0]\times\Omega,\\ u(t,x)=v(t,x)=0\in R^{n},\quad (t,x)\in[0,+\infty)\times\partial\Omega, \end{array}\displaystyle \right . $$
(1.1)

where \(x\in\Omega\), and Ω is a bounded domain in \(R^{m}\) with a smooth boundary ∂Ω of class \(\mathcal{C}^{2}\) by Ω (see, e.g., [15]). \(u=u(t,x)=(u_{1}(t,x),u_{2}(t,x),\ldots ,u_{n}(t,x))^{T}\), \(v=v(t,x)=(v_{1}(t,x),v_{2}(t,x),\ldots,v_{n}(t,x))^{T}\in R^{n}\), and \(u_{i}(t,x)\) and \(v_{j}(t,x)\) are state variables of the ith neuron and the jth neuron at time t and in space variable x. \(f(v)=f(v(t,x))=(f_{1}(v_{1}(t,x)),\ldots, f_{n}(v_{n}(t,x)))^{T}\), \(g(u)=g(u(t,x))=(g_{1}(u_{1}(t,x)),\ldots,g_{n}(u_{n}(t,x)))^{T}\), and \(f_{j}(u_{j}(t,x))\), \(g_{j}(u_{j}(t,x))\) are neuron activation functions of the jth unit at time t and in space variable x. \(f(v(t-\tau(t),x))=(f_{1}(v_{1}(t-\tau_{1}(t),x)),\ldots,f_{j}(v_{j}(t-\tau _{j}(t),x)),\ldots,f_{n}(v_{n}(t-\tau_{n}(t),x)))^{T}\), \(g(u(t-\gamma(t),x))=(g_{1}(u_{1}(t-\gamma_{1}(t),x)),\ldots,g_{j}(u_{j}(t-\gamma _{j}(t),x)),\ldots,g_{n}(u_{n}(t-\gamma_{n}(t),x)))^{T}\), \(\tau_{j}(t)\) and \(\gamma_{j}(t)\) are discrete delays, and ϱ and ρ are distributed time-delays. τ is the constant, satisfying \(0\leqslant\max\{\tau_{j}(t),\gamma_{j}(t), \varrho,\rho\}\leqslant\tau\) for all \(j=1,2,\ldots,n\). \(\Theta=\Theta(t,x,u)\), \(\Lambda=\Lambda(t,x,v) \), and \(\Theta\circ \nabla u=(\Theta_{ik} \frac{\partial u_{i}}{\partial x_{k}})_{n\times m}\), \(\Lambda\circ\nabla u=(\Lambda_{ik} \frac{\partial u_{i}}{\partial x_{k}})_{n\times m}\) are the Hadamard products of matrix \(\Theta=(\Theta_{ik})_{n\times m}\) and ∇u, and of matrix \(\Lambda=(\Lambda_{ik})_{n\times m}\) and ∇u, respectively (see [16]). The smooth functions \(\Theta _{ik} = \Theta_{ik}(t,x,u)\geqslant0\) and \(\Lambda_{ik} = \Lambda_{ik}(t,x,v)\geqslant0\) are diffusion operators. \((\Omega_{*}, \Upsilon, \mathbb{P})\) is the given probability space where \(\Omega_{*}\) is the sample space, ϒ is the σ-algebra of the subset of the sample space, and \(\mathbb{P}\) is the probability measure defined on ϒ. Let \(S=\{1, 2, \ldots, N\}\) and the random form process \(\{r(t): [0, +\infty)\to S\}\) be a homogeneous, finite-state Markovian process with right continuous trajectories with generator \(\Pi=(\pi_{ij})_{N\times N}\) and transition probability from mode i at time t to mode j at time \(t +\Delta t\), \(i, j \in S\),

$$\mathbb{P }\bigl(r(t+\delta)=j\mid r(t)=i\bigr)= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \pi_{ij}\delta+o(\delta) , & j\neq i,\\ 1+ \pi_{ij}\delta+o(\delta) , & j=i, \end{array}\displaystyle \right . $$

where \(\pi_{ij}\geqslant0\) is the transition probability rate from i to j (\(j\neq i\)) and \(\pi_{ii}=-\sum_{j=1, j\neq i}^{N}\pi_{ij}\), \(\delta>0\), and \(\lim_{\delta\to0}o(\delta)/\delta=0\).

Define the norm \(\|\cdot\|\) for vector \(u\in R^{n}\) and matrix \(C=(c_{ij})_{n\times n}\) as follows:

$$\|u\|=\sqrt{\sum_{i=1}^{n}u_{i}^{2}} , \qquad \|C\| =\sqrt{\lambda_{\max} \bigl(CC^{T} \bigr)}. $$

Denote \(|u|=(|u_{1}|,|u_{2}|,\ldots,|u_{n}|)^{T}\) for the vector \(u=(u_{1},\ldots ,u_{n})^{T}\in R^{n}\), and \(|C|=(|c_{ij}|)_{n\times n}\) for the matrix \(C=(c_{ij})_{n\times n}\).

Definition 1.1

For symmetric matrices A, B, we denote \(A< B\) or \(B>A\) if matrix \(B-A\) is a positive definite matrix. Particularly, \(A>0\) if a symmetric matrix A is a positive definite matrix.

In this paper, we denote by \(\lambda_{\max} C\) and \(\lambda_{\min} C\) the maximum and minimum eigenvalue of matrix C. For any mode \(r(t)=r\in S\), we denote \(A_{r}=A(r(t))\) for convenience. So do \(B_{r}\), \(C_{r}\), \(D_{r}\), \(E_{r}\), \(H_{r}\), \(L_{r}\), and \(W_{r}\). In the real world, the parameter uncertainties are inevitable. We assume that

$$ \begin{aligned} &\Delta C_{r} \in\bigl[-C^{*}_{r}, C^{*}_{r}\bigr], \qquad \Delta D_{r} \in\bigl[-D^{*}_{r}, D^{*}_{r}\bigr], \qquad\Delta E_{r} \in\bigl[-E^{*}_{r}, E^{*}_{r}\bigr], \\ &\Delta H_{r} \in\bigl[-H^{*}_{r}, H^{*}_{r}\bigr], \qquad \Delta L_{r} \in\bigl[-L^{*}_{r}, L^{*}_{r} \bigr],\qquad \Delta W_{r} \in\bigl[-W^{*}_{r}, W^{*}_{r}\bigr], \end{aligned} $$
(1.2)

where \(C^{*}_{r}\), \(D^{*}_{r}\), \(E^{*}_{r}\), \(H^{*}_{r}\), \(L^{*}_{r}\), \(W^{*}_{r}\) are nonnegative matrices. \(A_{r}\), \(B_{r}\) are diagonal matrices.

There are positive definite diagonal matrices \(\underline {A}_{r}\), \(\underline{B}_{r}\), \(\overline{A}_{r}\), and \(\overline{B}_{r}\) such that

$$ 0< \underline{A}_{r}\leqslant A_{r}\leqslant \overline{A}_{r},\qquad 0< \underline{B}_{r}\leqslant B_{r}\leqslant\overline{B}_{r},\quad r\in S. $$
(1.3)

There exist positive definite diagonal matrices F and G such that

$$ \bigl|f(u)-f(v)\bigr|\leqslant F|u-v|, \qquad \bigl|g(u)-g(v)\bigr|\leqslant G|u-v|,\quad \forall u,v\in R^{n}. $$
(1.4)

Throughout this paper, we assume that \(f(0)=g(0)=0\in R^{n}\). Then \(u=0\), \(v=0\) is the null solution for the system (1.1).

Let \(u(t,x ;\phi,\psi,i_{0})\), \(v(t,x ;\phi,\psi,i_{0})\) denote the state trajectory from the initial condition \(r(0)=i_{0}\), \(u(t_{0}+\theta,x ; \phi,\psi,i_{0})=\phi(\theta,x)\), \(v(t_{0}+\theta,x ; \phi,\psi,i_{0})=\psi(\theta,x)\) on \(-\tau\leqslant\theta\leqslant0\) in \(L_{\mathcal{F}_{0}}^{2}([-\tau ,0]\times\Omega; R^{n})\). (Remark: \(t_{0}=0\).) Here, \(L_{\mathcal{F}_{0}}^{2}([-\tau,0]\times \Omega; R^{n})\) denotes the family of all \(\mathcal{F}_{0}\)-measurable \(\mathcal{C}([-\tau,0]\times\Omega; R^{n})\)-value random variables \(\xi=\{\xi(\theta,x): -\tau\leqslant\theta\leqslant0, x\in\Omega\}\) such that \(\sup_{-\tau\leqslant\theta\leqslant0}\mathbb{E}\|\xi(\theta)\| _{2}^{2}<\infty\), where \(\mathbb{E}\{\cdot\}\) stands for the mathematical expectation operator with respect to the given probability measure \(\mathbb{P}\).

Definition 1.2

The system (1.1) is said to be globally stochastically exponentially robust stability if for every initial condition \(\phi, \psi\in L_{\mathcal{F}_{0}}^{2}([-\tau,0]\times\Omega; R^{n})\), \(r(0)=i_{0}\), there exist scalars \(c_{1}>0\), \(c_{2}>0\), \(\beta>0\), and \(\gamma>0\) such that for any solution \(u(t,x ;\phi,\psi,i_{0})\), \(v(t,x ;\phi,\psi,i_{0})\),

$$\begin{aligned} &\mathbb{E}\bigl(\bigl\| u(t,x ;\phi,\psi,i_{0})\bigr\| _{2}^{2} \bigr)+\mathbb{E}\bigl(\bigl\| v(t,x ;\phi ,\psi,i_{0})\bigr\| _{2}^{2} \bigr)\\ &\quad\leqslant\gamma e^{-\beta t} \Bigl[ c_{1}\sup _{-\tau\leqslant\theta\leqslant0}\mathbb{E}\bigl( \bigl\| \phi(\theta,x)\bigr\| _{2}^{2} \bigr) +c_{2}\sup_{-\tau\leqslant \theta\leqslant0}\mathbb{E}\bigl(\bigl\| \psi( \theta,x)\bigr\| _{2}^{2}\bigr) \Bigr], \end{aligned}$$

\(t\geqslant t_{0}\), for all admissible uncertainties satisfying (1.1), where the norm \(\|u\| _{2}= (\sum_{i=1}^{n}\int_{\Omega}u_{i}^{2}(t, x)\,dx )^{\frac{1}{2}}\) for \(u=(u_{1}(t,x),\ldots, u_{n}(t,x))^{T}\in R^{n}\).

Definition 1.3

[17]

A matrix \(A=(a_{ij})_{n\times n}\) is an H-matrix if its comparison matrix \(M(A)=(m_{ij})_{n\times n}\) is an M-matrix, where

$$m_{ij}= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} |a_{ii}|, & i=j, \\ -|a_{ij}|, & i\neq j. \end{array}\displaystyle \right . $$

Lemma 1.4

[17]

\(A,B\in z_{n}\triangleq\{ A=(a_{ij})_{n\times n}\in R^{n\times n}: a_{ij}\leqslant0, i\neq j\}\), if A is a M-matrix, A, B satisfy \(a_{ij}\leqslant b_{ij}\), \(i,j=1,2,\ldots,n\), then B is a M-matrix.

Lemma 1.5

[18]

For given constants \(k_{1}\) and \(k_{2}\) satisfying \(k_{1} >k_{2} >0\), \(V(t)\) is a nonnegative continuous function on \([t_{0}-\tau , t_{0}]\), if the following inequality holds:

$$D^{+}V(t)\leqslant k_{1}V(t)+ k_{2}\overline{V}(t), $$

where

$$\begin{aligned}& D^{+}V(t)=\limsup_{\Delta t\to0^{+}}\frac{V(t+\Delta t)-V(t)}{\Delta t}, \\& \overline{V}(t)=\limsup_{t-\tau\leqslant s\leqslant t}V(s), \end{aligned}$$

\(\tau>0\) is a constant. Then, as \(t \geqslant t_{0}\), we have

$$V(t)\leqslant\overline{V}(t_{0})e^{-\lambda(t-t_{0})}, $$

where λ is the unique positive solution of the following equation:

$$\lambda=k_{1}-k_{2}e^{\lambda\tau}. $$

Lemma 1.6

(Schur complement [19])

Given matrices \(\mathcal{Q}(t)\), \(\mathcal{S}(t)\), and \(\mathcal{R}(t)\) with appropriate dimensions, where \(\mathcal{Q}(t)=\mathcal{Q}(t)^{T}\), \(\mathcal{R}(t)=\mathcal{R}(t)^{T}\), then

$$ \begin{pmatrix} \mathcal{Q}(t)& \mathcal{S}(t) \\ \mathcal{S}^{T}(t) & \mathcal{R}(t) \end{pmatrix}>0, $$

if and only if

$$\mathcal{R}(t)>0, \quad \mathcal{Q}(t)-\mathcal{S}(t)\mathcal {R}^{-1}(t)\mathcal{S}^{T}(t)>0; $$

or

$$\mathcal{Q}(t)>0, \quad \mathcal{R}(t)-\mathcal{S}^{T}(t)\mathcal {Q}^{-1}(t)\mathcal{S}^{T}(t)>0, $$

where \(\mathcal{Q}(t)\), \(\mathcal{S}(t)\), and \(\mathcal{R}(t)\) are dependent on t.

2 Main result

Denote by \(\lambda_{1}\) the first eigenvalue of −Δ in Sobolev space \(W_{0}^{1,2}(\Omega) \), where

$$\lambda_{1} = \min\biggl\{ \int_{\Omega}\bigl|\nabla\eta(x)\bigr|^{2}\,dx: \eta(x)\in W_{0}^{1, 2}(\Omega), \int_{\Omega}\bigl|\eta(x)\bigr|^{2}\,dx=1\biggr\} $$

(see [20, 21] for details).

Lemma 2.1

Let \(P_{r}=\operatorname{diag}(p_{r1} ,p_{r2} ,\ldots ,p_{rn})\) be a positive definite matrix, \(\alpha_{r}>0\) with \(\alpha _{r}I\leqslant P_{r}\), and u, v be a solution of system (1.1). Then we have

$$\left \{ \textstyle\begin{array}{@{}l} \int_{\Omega}u^{T} P_{r} \nabla\cdot (\Theta\circ\nabla u )\,dx\leqslant-\lambda_{1}\alpha_{r}\Theta_{*}\|u\|_{2}^{2},\\ \int_{\Omega}v^{T} P_{r} \nabla\cdot (\Lambda\circ\nabla v )\,dx\leqslant-\lambda_{1}\alpha_{r}\Lambda_{*}\|v\|_{2}^{2} , \end{array}\displaystyle \right . $$

where I denotes the identity matrix, \(\Theta_{*}=\min_{ik}\inf_{t,x,u}\Theta(t,x,u)_{ik}\geqslant0\), \(\Lambda_{*}=\min_{ik}\inf_{t,x,v}\Lambda (t, x,v)_{ik}\geqslant0\).

Proof

Since u, v is a solution of system (1.1), it follows by the Gauss formula and the Dirichlet boundary condition that

$$\begin{aligned} &\int_{\Omega}u^{T} P_{r} \bigl(\nabla \cdot(\Theta\circ\nabla u) \bigr)\,dx \\ &\quad=\int_{\Omega}u^{T}P_{r} \Biggl(\sum _{k=1}^{m}\frac{\partial}{\partial x_{k}}\biggl( \Theta_{1k} \frac{\partial u_{1}}{\partial x_{k}}\biggr),\ldots,\sum _{k=1}^{m}\frac{\partial}{\partial x_{k}}\biggl( \Theta_{nk} \frac{\partial u_{n}}{\partial x_{k}}\biggr) \Biggr)^{T}\,dx \\ &\quad=-\sum_{k=1}^{m} \sum _{j=1}^{n}\int_{\Omega}p_{rj} \Theta_{jk}\biggl(\frac{\partial u_{j}}{\partial x_{k}} \biggr)^{2}\,dx\leqslant-\lambda_{1}\alpha_{r} \Theta_{*} \|u\|_{2}^{2}. \end{aligned}$$

Similarly, we can prove that \(\int_{\Omega}v^{T} P_{r} \nabla\cdot (\Lambda\circ\nabla v )\,dx\leqslant-\lambda_{1}\alpha_{r}\Lambda_{*}\|v\|_{2}^{2}\). Thus, the proof is completed. □

Throughout this paper, we define Φ, Ψ, \(\widetilde{\Phi}\), and \(\widetilde{\Psi}\) as follows:

$$\begin{aligned}& \begin{aligned}[b] \Phi={}&\frac{1}{\alpha} \Biggl[2\lambda_{1} \alpha_{r}\Theta _{*}I+2P_{r}\underline{A}_{r} - \beta \| C_{r}\| (\lambda_{\max}F)I-P_{r}\Delta C_{r}\Delta C_{r}^{T}P_{r}-G^{2}\\ &{}-\beta \| D_{r}\| (\lambda_{\max}G)I -\beta \bigl\| |E_{r}|\bigr\| ^{2}I \\ &{}-P_{r}\Delta E_{r} \Delta E_{r}^{T}P_{r}- \varrho\beta \bigl\| |L_{r}|\bigr\| ^{2}I-\varrho P_{r}\Delta L_{r} \Delta L_{r}^{T}P_{r}-\sum _{j=1}^{N}\pi_{rj}P_{j} \Biggr], \end{aligned} \\& \begin{aligned}[b] \Psi={}&\frac{1}{\alpha} \Biggl[ 2\lambda_{1} \alpha_{r}\Lambda_{*}I +2P_{r}\underline{B}_{r}-F^{2}- \beta \| C_{r}\| (\lambda_{\max}F)I\\ &{}-\beta \| D_{r}\| (\lambda_{\max}G)I-P_{r}\Delta D_{r}\Delta D_{r}^{T}P_{r}-\beta \bigl\| |H_{r}|\bigr\| ^{2}I \\ &{}-P_{r}\Delta H_{r} \Delta H_{r}^{T}P_{r} -\rho\beta \bigl\| |W_{r}|\bigr\| ^{2}I-\rho P_{r}\Delta W_{r} \Delta W_{r}^{T}P_{r}-\sum _{j=1}^{N}\pi_{rj}P_{j} \Biggr], \end{aligned} \\& \begin{aligned}[b] \widetilde{\Phi}={}&\frac{1}{\alpha} \Biggl[ 2 \lambda_{1}\alpha _{r}\Theta_{*}I+2P_{r} \underline{A}_{r} -\beta \| C_{r}\| (\lambda_{\max}F)I-P_{r}{C_{r}^{*}} {C_{r}^{*}}^{T}P_{r}-G^{2}-\beta \| D_{r}\| (\lambda_{\max}G)I \\ &{}-\beta \bigl\| |E_{r}|\bigr\| ^{2}I-P_{r}{E_{r}^{*}} {E_{r}^{*}}^{T}P_{r}-\varrho\beta \bigl\| |L_{r}| \bigr\| ^{2}I-\varrho P_{r}{L_{r}^{*}} {L_{r}^{*}}^{T}P_{r}-\sum _{j=1}^{N}\pi_{rj}P_{j} \Biggr], \end{aligned} \\& \begin{aligned}[b] \widetilde{\Psi}={}&\frac{1}{\alpha} \Biggl[ 2 \lambda_{1}\alpha _{r}\Lambda_{*}I +2P_{r} \underline{B}_{r}-F^{2}-\beta \| C_{r}\| ( \lambda_{\max}F)I \\ &{}-\beta \| D_{r}\| (\lambda_{\max}G)I-P_{r}{D_{r}^{*}} {D_{r}^{*}}^{T}P_{r}-\beta \bigl\| |H_{r}| \bigr\| ^{2}I \\ &{}-P_{r}{H_{r}^{*}} {H_{r}^{*}}^{T}P_{r}- \rho\beta \bigl\| |W_{r}| \bigr\| ^{2}I-\rho P_{r}{W_{r}^{*}} {W_{r}^{*}}^{T}P_{r}-\sum _{j=1}^{N}\pi_{rj}P_{j} \Biggr]. \end{aligned} \end{aligned}$$

Lemma 2.2

If the following two inequalities hold:

$$ \widetilde{\Phi}- \frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max }F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I>0,\quad \forall r\in S, $$
(2.1)

and

$$ \widetilde{\Psi}-\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max }F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I>0,\quad \forall r\in S, $$
(2.2)

we have

$$ \Phi- \frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha}I>0, \quad\forall r\in S, $$
(2.3)

and

$$ \Psi-\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha}I>0, \quad \forall r\in S, $$
(2.4)

where I denotes the identity matrix, and \(\alpha_{r}, \beta , \alpha>0\).

Proof

Let

$$ U=\frac{1}{\alpha} \bigl( P_{r}{C_{r}^{*}} {C_{r}^{*}}^{T}P_{r} +P_{r}{E_{r}^{*}} {E_{r}^{*}}^{T}P_{r} +\varrho P_{r}{L_{r}^{*}} {L_{r}^{*}}^{T}P_{r} \bigr). $$
(2.5)

Since \(C^{*}\), \(E^{*}\), \(L^{*}\) all are nonnegative matrices, U is also a nonnegative matrix.

Then \((\widetilde{\Phi}+U-\frac{(1+\beta )(\tau+1)\max\{(\lambda _{\max}F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I )\) is a positive diagonal matrix, and \((\widetilde{\Phi}-\frac{(1+\beta )(\tau+1)\max\{(\lambda _{\max}F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I )\) is a M-matrix.

Let

$$ Q=\frac{1}{\alpha} \bigl[ P_{r}\Delta C_{r}\Delta C_{r}^{T}P_{r} +P_{r}\Delta E_{r} \Delta E_{r}^{T}P_{r} +\varrho P_{r}\Delta L_{r} \Delta L_{r}^{T}P_{r} \bigr]. $$
(2.6)

It follows by (1.2) that \(|Q_{ij}|\leqslant U_{ij}\) for all \(i,j=1,2,\ldots,n\). Here, we denote matrices \(Q=(Q_{ij})_{n\times n}\) and \(U=(U_{ij})_{n\times n}\). For convenience, we denote

$$\begin{aligned}& \widehat{\Phi} =\widetilde{\Phi}-\frac{(1+\beta )(\tau+1)\max\{(\lambda _{\max}F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I, \\& \underline{\Phi}=\Phi- \frac{(1+\beta )(\tau+1)\max\{(\lambda _{\max}F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I. \end{aligned}$$

Denote, in addition, \(\widetilde{Q}= \frac{1}{\alpha} [2\lambda _{1}\alpha_{r}\Theta_{*}I+2P_{r}\underline{A}_{r} -\beta \| C_{r}\| (\lambda_{\max}F)I-G^{2}-\beta \| D_{r}\| (\lambda_{\max }G)I -\beta \| |E_{r}|\|^{2}I -\varrho\beta \| |L_{r}|\|^{2}I-\sum_{j=1}^{N}\pi_{rj}P_{j} ]-\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max }F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I\), and \(\widetilde{Q}=\operatorname{diag}(\widetilde{Q}_{1},\widetilde{Q}_{2}, \ldots ,\widetilde{Q}_{n})\) is a diagonal matrix. So the comparison matrix \(M(\underline{\Phi})=(\mu_{ij})\) of \(\underline {\Phi}\) is

$$\mu_{ij}=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} -|Q_{ij}|, & i\neq j,\\ \widetilde{Q}_{i} -Q_{ii}, & i= j. \end{array}\displaystyle \right . $$

It is obvious that \(\mu_{ij}\geqslant\widehat{\Phi}_{ij}\) for all \(i,j=1,2,\ldots,n\). From Lemma 1.4, we know that \(M(\underline{\Phi})\) is an M-matrix. According to Definition 1.3, \(\underline{\Phi}\) is a H-matrix with positive diagonal elements, it is to say \(\underline{\Phi}>0\). Hence we have proved (2.3) by way of (2.1). Similarly, we can also derive (2.4) from the condition (2.2). The proof is completed. □

Theorem 2.3

Assume that (1.2)-(1.4) hold. If, in addition, there exist a sequence of positive definite diagonal matrices \(P_{r}\) (\(r\in S\)) and positive scalars β, \(\alpha_{r}\) (\(r\in S\)) such that the following LMIs conditions hold:

$$\begin{aligned}& \begin{pmatrix} \mathcal{Q}_{r}& \frac{1}{\sqrt{\alpha}} P_{r}C_{r}^{*}& \frac{1}{\sqrt{\alpha }} P_{r}E_{r}^{*}& \sqrt{\frac{\varrho}{\alpha}}P_{r}L_{r}^{*} \\ \frac{1}{\sqrt{\alpha}}(C_{r}^{*})^{T} P_{r}& I& 0& 0 \\ \frac{1}{\sqrt{\alpha}}(E_{r}^{*})^{T} P_{r}& 0 & I& 0\\ \sqrt{\frac{\varrho}{\alpha}}(L_{r}^{*})^{T}P_{r} & 0 & 0& I&\ \end{pmatrix}>0, \quad r \in S, \end{aligned}$$
(2.7)
$$\begin{aligned}& \begin{pmatrix} \mathfrak{Q}_{r}& \frac{1}{\sqrt{\alpha}} P_{r}D_{r}^{*}& \frac{1}{\sqrt{\alpha }}P_{r}H_{r}^{*}& \sqrt{\frac{\rho}{\alpha}}P_{r}W_{r}^{*} \\ \frac{1}{\sqrt{\alpha}}(D_{r}^{*})^{T}P_{r}& I& 0& 0 \\ \frac{1}{\sqrt{\alpha}}(H_{r}^{*})^{T}P_{r} & 0 & I& 0\\ \sqrt{\frac{\rho}{\alpha}}(W_{r}^{*})^{T}P_{r} & 0& 0 & I&\ \end{pmatrix}>0, \quad r \in S, \end{aligned}$$
(2.8)
$$\begin{aligned}& \alpha_{r}I \leqslant P_{r},\quad r \in S, \end{aligned}$$
(2.9)
$$\begin{aligned}& P_{r}\leqslant\beta I,\quad r \in S, \end{aligned}$$
(2.10)

then the system (1.1) is stochastically global exponential robust stability, where

$$\begin{aligned} \mathcal{Q}_{r}\triangleq{}&\frac{1}{ \alpha} \Biggl[2 \lambda_{1}\alpha _{r}\Theta_{*}I+2P_{r} \underline{A}_{r} -\beta \| C_{r}\| (\lambda_{\max}F)I-G^{2}- \beta \| D_{r}\| (\lambda_{\max }G)I\\ &{} -\beta \bigl\| |E_{r}|\bigr\| ^{2}I -\varrho\beta \bigl\| |L_{r}| \bigr\| ^{2}I-\sum_{j=1}^{N}\pi_{rj}P_{j} \Biggr] \\ &{} -\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha}I, \\ \mathfrak{Q}_{r}\triangleq{}&\frac{1}{ \alpha} \Biggl[2 \lambda_{1}\alpha _{r}\Lambda_{*}I+2P_{r} \underline{B}_{r} -\beta \| C_{r}\| (\lambda_{\max}F)I-F^{2}- \beta \| D_{r}\| (\lambda_{\max }G)I -\beta \bigl\| |H_{r}|\bigr\| ^{2}I \\ &{}-\varrho\beta \bigl\| |W_{r}|\bigr\| ^{2}I-\sum_{j=1}^{N}\pi_{rj}P_{j} \Biggr] \\ &{} -\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max }F)^{2},(\lambda_{\max}G)^{2}\}}{\alpha}I, \end{aligned}$$

and α is a positive scalar with \(\alpha<\alpha_{r}\) for all \(r\in S\).

Proof

Let \(P_{r}=\operatorname{diag}(p_{r1},\ldots,p_{rn})\) be a positive definite matrix for mode \(r\in S\), we consider the following Lyapunov-Krasovskii functional:

$$V(t)=\int_{\Omega}\bigl( u^{T}(t,x)P_{r}u(t,x)+v^{T}(t,x)P_{r}v(t,x) \bigr)\,dx,\quad r\in S. $$

It follows from Lemma 2.1 that

$$ \begin{aligned} &\int_{\Omega}2u^{T}P_{r}\nabla\cdot(\Theta \circ\nabla u)\,dx \leqslant-2\lambda_{1}\int_{\Omega}u^{T}\alpha_{r}\Theta_{*}I u\,dx, \quad\mbox{and}\\ &\int _{\Omega}2v^{T}P_{r}\nabla\cdot(\Lambda\circ \nabla v)\,dx \leqslant-2\lambda_{1}\int_{\Omega}v^{T}\alpha_{r}\Lambda_{*}I v\,dx. \end{aligned} $$
(2.11)

Obviously, we can get by (1.3)

$$ \begin{aligned} &\int_{\Omega}-2u^{T}P_{r}A_{r}u\,dx \leqslant\int_{\Omega}-2u^{T}P_{r} \underline{A}_{r}u\,dx, \quad\mbox{and}\\ &\int_{\Omega}-2v^{T}P_{r}B_{r}v\,dx \leqslant\int_{\Omega}-2v^{T}P_{r} \underline{B}_{r}v\,dx. \end{aligned} $$
(2.12)

Besides, we can derive the following inequalities by the assumptions on f, g, β, and \(C_{r}\), \(D_{r}\), \(E_{r}\), \(H_{r}\), \(L_{r}\), \(W_{r}\):

$$\begin{aligned} &\int_{\Omega}2u^{T}P_{r}(C_{r}+ \Delta C_{r})f(v)\,dx \\ &\quad\leqslant 2\int_{\Omega}\bigl(\|u\|\cdot \|P_{r}\|\cdot\| C_{r}\|\cdot\bigl\| f(v)\bigr\| + u^{T}P_{r}\Delta C_{r} f(v) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl(2\|u\|\cdot\beta \| C_{r}\|\cdot\bigl\| f(v)\bigr\| +2 u^{T}P_{r}\Delta C_{r} f(v) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl[ u^{T} \bigl(\beta \| C_{r}\| (\lambda_{\max }F)I+P_{r}\Delta C_{r}\Delta C_{r}^{T}P_{r} \bigr)u \\ &\qquad{}+v^{T} \bigl(F^{2}+\beta \| C_{r}\| ( \lambda_{\max}F)I \bigr)v \bigr]\,dx, \end{aligned}$$
(2.13)
$$\begin{aligned} &\int_{\Omega}2v^{T}P_{r}(D_{r}+ \Delta D_{r})g(u)\,dx \\ &\quad\leqslant2\int_{\Omega}\bigl(\|v\|\cdot\beta \| D_{r}\|\cdot\bigl\| g(u)\bigr\| + v^{T}P_{r}\Delta D_{r} g(u) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl[ u^{T} \bigl(G^{2}+\beta \| D_{r}\| (\lambda_{\max }G)I \bigr)u \\ &\qquad{}+v^{T} \bigl(\beta \| D_{r}\| (\lambda_{\max}G)I+P_{r} \Delta D_{r}\Delta D_{r}^{T}P_{r} \bigr)v \bigr]\,dx, \end{aligned}$$
(2.14)
$$\begin{aligned} &\int_{\Omega}2u^{T}P_{r}(E_{r}+ \Delta E_{r})f\bigl(v\bigl(t-\tau(t),x\bigr)\bigr)\,dx \\ &\quad=\int _{\Omega}\bigl(2u^{T}P_{r} E_{r}f \bigl(v\bigl(t-\tau(t),x\bigr)\bigr)+2u^{T}P_{r}\Delta E_{r} f\bigl(v\bigl(t-\tau (t),x\bigr)\bigr) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl(2|u|^{T}\beta |E_{r}|\bigl|f\bigl(v\bigl(t-\tau (t),x\bigr)\bigr)\bigr|+2u^{T}P_{r} \Delta E_{r} f\bigl(v\bigl(t-\tau(t),x\bigr)\bigr) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl( \beta \bigl( |u|^{T} |E_{r}|\bigl|E_{r}^{T}\bigr||u|+ f^{T}\bigl(v \bigl(t-\tau (t),x\bigr)\bigr)f\bigl(v\bigl(t-\tau(t),x\bigr)\bigr)\bigr) \\ &\qquad{}+ u^{T}P_{r}\Delta E_{r} \Delta E_{r}^{T}P_{r}u+f^{T}\bigl(v\bigl(t- \tau(t),x\bigr)\bigr)f\bigl(v\bigl(t-\tau(t),x\bigr)\bigr) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl[ u^{T} \bigl(\beta \bigl\| |E_{r}|\bigr\| ^{2}I+P_{r}\Delta E_{r} \Delta E_{r}^{T}P_{r} \bigr)u \\ &\qquad{}+v^{T} \bigl(t-\tau(t),x\bigr) (1+\beta )F^{2} v\bigl(t-\tau(t),x\bigr) \bigr]\,dx, \end{aligned}$$
(2.15)
$$\begin{aligned} &\int_{\Omega}2v^{T}P_{r}(H_{r}+ \Delta H_{r})g\bigl(u\bigl(t-\gamma(t),x\bigr)\bigr)\,dx \\ &\quad=\int_{\Omega}\bigl(2v^{T}P_{r} H_{r}g\bigl(u\bigl(t-\gamma(t),x\bigr)\bigr)+2v^{T}P_{r} \Delta H_{r} g\bigl(u\bigl(t-\gamma(t),x\bigr)\bigr) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl( \beta \bigl(|v|^{T} |H_{r}||H_{r}|^{T} |v|+g^{T}\bigl(u \bigl(t-\gamma (t),x\bigr)\bigr) g\bigl(u\bigl(t-\gamma(t),x\bigr)\bigr)\bigr) \\ &\qquad{}+ v^{T}P_{r}\Delta H_{r} \Delta H_{r}^{T}P_{r}v+g^{T}\bigl(u\bigl(t- \gamma(t),x\bigr)\bigr)g\bigl(u\bigl(t-\gamma(t),x\bigr)\bigr) \bigr)\,dx \\ &\quad\leqslant\int_{\Omega}\bigl[ u^{T}\bigl(t- \gamma(t),x\bigr) (1+\beta )G^{2} u\bigl(t-\gamma (t),x \bigr) \\ &\qquad{}+v^{T} \bigl(\beta \bigl\| |H_{r}|\bigr\| ^{2}I+P_{r} \Delta H_{r} \Delta H_{r}^{T}P_{r} \bigr)v \bigr]\,dx, \end{aligned}$$
(2.16)
$$\begin{aligned} &\int_{\Omega}\biggl(2u^{T}P_{r}(L_{r}+ \Delta L_{r})\int_{t-\varrho }^{t}f\bigl(v(s,x) \bigr)\,ds \biggr)\,dx \\ &\quad=\int_{\Omega}\biggl(\int_{t-\varrho}^{t}2u^{T}P_{r} L_{r} f\bigl(v(s,x)\bigr)\,ds + \int_{t-\varrho}^{t}2u^{T}P_{r} \Delta L_{r}f\bigl(v(s,x)\bigr)\,ds \biggr)\,dx \\ &\quad\leqslant\int_{\Omega}\biggl[\int_{t-\varrho}^{t} \bigl(\beta \bigl(|u|^{T} |L_{r}|| L_{r}|^{T} |u|+f^{T}\bigl(v(s,x)\bigr)f\bigl(v(s,x)\bigr)\bigr) \bigr)\,ds \\ &\qquad{}+\int_{t-\varrho}^{t} \bigl(u^{T}P_{r} \Delta L_{r} \Delta L_{r}^{T}P_{r}u+f^{T} \bigl(v(s,x)\bigr)f\bigl(v(s,x)\bigr) \bigr)\,ds \biggr]\,dx \\ &\quad\leqslant\int_{\Omega}\biggl[ u^{T} \bigl( \varrho\beta \bigl\| |L_{r}|\bigr\| ^{2}I+\varrho P_{r} \Delta L_{r} \Delta L_{r}^{T}P_{r} \bigr)u \\ &\qquad{}+\int_{t-\varrho}^{t} v^{T}(s,x) (1+\beta ) F^{2}v(s,x)\,ds \biggr]\,dx, \end{aligned}$$
(2.17)
$$\begin{aligned} &\int_{\Omega}\biggl(2v^{T}P_{r}(W_{r}+ \Delta W_{r})\int_{t-\rho }^{t}g\bigl(u(s,x) \bigr)\,ds \biggr)\,dx \\ &\quad=\int_{\Omega}\biggl(\int_{t-\rho}^{t}2v^{T}P_{r} W_{r} g\bigl(u(s,x)\bigr)\,ds + \int_{t-\rho }^{t}2v^{T}P_{r} \Delta W_{r}g\bigl(u(s,x)\bigr)\,ds \biggr)\,dx \\ &\quad\leqslant\int_{\Omega}\biggl[\int_{t-\rho}^{t} \beta \bigl(|v|^{T} | W_{r} ||W_{r}|^{T} |v|+g^{T}\bigl(u(s,x)\bigr)g\bigl(u(s,x)\bigr) \bigr)\,ds \\ &\qquad{}+\int_{t-\rho}^{t} \bigl(v^{T}P_{r} \Delta W_{r} \Delta W_{r}^{T}P_{r}v+g^{T} \bigl(u(s,x)\bigr)g\bigl(u(s,x)\bigr) \bigr)\,ds \biggr]\,dx \\ &\quad\leqslant\int_{\Omega}\biggl[ v^{T} \bigl(\rho \beta \bigl\| |W_{r}|\bigr\| ^{2}I+\rho P_{r}\Delta W_{r} \Delta W_{r}^{T}P_{r} \bigr)v \\ &\qquad{}+ \int_{t-\rho}^{t} u^{T}(s,x) (1+\beta ) G^{2}u(s,x)\,ds \biggr]\,dx. \end{aligned}$$
(2.18)

Moreover, we can conclude from the restrictions of α, β that

$$\begin{aligned} &\int_{\Omega}\biggl(\int_{t-\rho}^{t} u^{T}(s,x) (1+\beta )G^{2}u(s,x)\,ds+\int_{t-\varrho}^{t} v^{T}(s,x) (1+\beta )F^{2}v(s,x)\,ds \biggr)\,dx \\ &\quad\leqslant(1+\beta )\int_{\Omega}\biggl[\int _{t-\tau}^{t} \bigl(u^{T}(s,x) G^{2}u(s,x) + v^{T}(s,x) F^{2}v(s,x)\,ds \bigr) \biggr]\,dx \\ &\quad\leqslant\frac{(1+\beta )\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha_{r}} \\ &\qquad{}\times\int_{\Omega}\biggl[\int _{t-\tau}^{t} \bigl(u^{T}(s,x)P_{r} u(s,x) + v^{T}(s,x)P_{r} v(s,x)\,ds \bigr) \biggr]\,dx \\ &\quad\leqslant\frac{(1+\beta )\tau\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha_{r}}\sup_{t-\tau\leqslant s\leqslant t}V(s), \end{aligned}$$
(2.19)

and

$$\begin{aligned} &\int_{\Omega}\bigl[u^{T}\bigl(t- \gamma(t),x\bigr) (1+\beta )G^{2} u\bigl(t-\gamma(t),x\bigr) +v^{T}\bigl(t-\tau(t),x\bigr) (1+\beta )F^{2} v\bigl(t- \tau(t),x\bigr) \bigr]\,dx \\ &\quad\leqslant\frac{(1+\beta )\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha_{r}}\sup_{t-\tau\leqslant s\leqslant t}V(s). \end{aligned}$$
(2.20)

Then we can conclude from (2.9)-(2.20) and the weak infinitesimal operator \(\mathcal{L}\) that

$$\begin{aligned} \mathcal{L}V(t)={}&\lim_{\delta\to0^{+}} \frac{1}{\delta}\biggl\{ \mathbb{E} \biggl[\int_{\Omega}\bigl(u^{T}(t+\delta,x)P\bigl(r(t+\delta)\bigr)u(t+\delta ,x) \\ &{}+v^{T}(t+\delta,x)P\bigl(r(t+\delta)\bigr)v(t+\delta,x) \bigr)\,dx \Big| r(t)=r \biggr] \\ &{}-\int_{\Omega}\bigl(u^{T}(t,x)P_{r}u(t,x)+v^{T}(t,x)P_{r}v(t,x) \bigr)\,dx \biggr\} \\ ={}&\lim_{\delta\to0^{+}}\frac{\mathbb{E} [\int_{\Omega}u^{T}(t+\delta,x) (P_{r}+\sum_{j=1}^{N}\pi_{rj}P_{j} )u(t+\delta ,x)\,dx-\int_{\Omega}u^{T}(t,x)P_{r}u(t,x)\,dx ]}{\delta} \\ &{}+\lim_{\delta\to0^{+}} \frac{\mathbb{E} [\int_{\Omega}v^{T}(t+\delta,x) (P_{r}+\sum_{j=1}^{N}\pi_{rj}P_{j} )v(t+\delta ,x)\,dx-\int_{\Omega}v^{T}(t,x)P_{r}v(t,x)\,dx ]}{\delta} \\ \leqslant{}&-\mathbb{E}\int_{\Omega}\Biggl[u^{T} \Biggl(2\lambda_{1}\alpha_{r}\Theta _{*}I+2P_{r} \underline{A}_{r} -\beta \| C_{r}\| (\lambda_{\max}F)I-P_{r} \Delta C_{r}\Delta C_{r}^{T}P_{r}-G^{2} \\ &{}-\beta \| D_{r}\| (\lambda_{\max}G)I-\beta \bigl\| |E_{r}|\bigr\| ^{2}I-P_{r}\Delta E_{r} \Delta E_{r}^{T}P_{r}-\varrho\beta \bigl\| |L_{r}|\bigr\| ^{2}I \\ &{}-\varrho P_{r}\Delta L_{r} \Delta L_{r}^{T}P_{r}-\sum _{j=1}^{N}\pi_{rj}P_{j} \Biggr)u \\ &{}+ v^{T} \Biggl(2\lambda_{1}\alpha_{r} \Lambda_{*}I+2P_{r}\underline{B}_{r}-F^{2}-\beta \| C_{r}\| (\lambda_{\max}F)I \\ &{}-\beta \| D_{r}\| ( \lambda_{\max}G)I-P_{r}\Delta D_{r}\Delta D_{r}^{T}P_{r}-\beta \bigl\| |H_{r}|\bigr\| ^{2}I \\ &{}-P_{r}\Delta H_{r} \Delta H_{r}^{T}P_{r}-\rho\beta \bigl\| |W_{r}|\bigr\| ^{2}I-\rho P_{r}\Delta W_{r} \Delta W_{r}^{T}P_{r}-\sum _{j=1}^{N}\pi _{rj}P_{j} \Biggr)v \\ &{}+ (1+\beta ) \biggl(u^{T}\bigl(t-\gamma(t),x\bigr) G^{2} u\bigl(t-\gamma(t),x\bigr) +v^{T}\bigl(t-\tau (t),x\bigr) F^{2} v\bigl(t-\tau(t),x\bigr) \\ &{}+\int_{t-\rho}^{t} u^{T}(s,x) G^{2}u(s,x)\,ds+\int_{t-\varrho}^{t} v^{T}(s,x) F^{2}v(s,x)\,ds \biggr) \Biggr]\,dx \\ \leqslant{}&-\min_{r\in S}\{\lambda_{\min}\Phi, \lambda_{\min}\Psi \}\mathbb{E}V(t) \\ &{}+ \frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{ \alpha } \sup _{t-\tau\leqslant s\leqslant t}\mathbb{E}V(s). \end{aligned}$$
(2.21)

Let \(\Delta t>0\) be small enough, we can integrate (2.21) from t to \(t+\Delta t\) as follows:

$$\begin{aligned} &\mathbb{E}V(t+\Delta t)-\mathbb{E}V(t) \\ &\quad\leqslant \int _{t}^{t+\Delta t} \biggl(-\min_{r\in S}\{ \lambda_{\min}\Phi,\lambda _{\min}\Psi\}\mathbb{E}V(\theta) \\ &\qquad{} + \frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha} \sup_{\theta-\tau\leqslant s\leqslant\theta}\mathbb{E}V(s) \biggr)\,d\theta. \end{aligned}$$
(2.22)

Hence,

$$\begin{aligned} D^{+}\mathbb{E}V(t)\leqslant{}&{-}\min_{r\in S}\{\lambda_{\min} \Phi ,\lambda_{\min}\Psi\}\mathbb{E}V(t) \\ &{}+ \frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda_{\max }G)^{2}\}}{\alpha} \sup _{t-\tau\leqslant s\leqslant t}\mathbb{E}V(s). \end{aligned}$$
(2.23)

Let \(k_{1}=\min_{r\in S}\{\lambda_{\min}\Phi,\lambda_{\min}\Psi\} \), and \(k_{2}=\frac{(1+\beta )(\tau+1)\max\{(\lambda_{\max}F)^{2},(\lambda _{\max}G)^{2}\}}{\alpha}\). Moreover, the conditions (2.1) and (2.2) are satisfied owing to (2.7)-(2.10) and Schur complement theorem (Lemma 1.6), and we can conclude from Lemma 2.2 that \(k_{1}\) and \(k_{2}\) satisfy all the conditions in Lemma 1.5. Since \(k_{1}\) and \(k_{2}\) are independent of mode \(r\in S\), it follows by Lemma 1.5 that

$$ \mathbb{E}V(t)\leqslant\mathbb{E} \overline{V}(0)e^{-\lambda t}, $$
(2.24)

where λ is the unique positive solution of the equation \(\lambda =k_{1}-k_{2}e^{\lambda\tau}\), and

$$ \mathbb{E}\overline{V}(0)=\limsup_{-\tau\leqslant s\leqslant 0}\mathbb{E}V(s) \leqslant\beta \Bigl[\sup_{-\tau\leqslant \theta\leqslant0}\mathbb{E}\bigl( \bigl\| \phi(\theta,x) \bigr\| _{2}^{2}\bigr) + \sup_{-\tau\leqslant \theta\leqslant0}\mathbb{E} \bigl(\bigl\| \psi(\theta,x)\bigr\| _{2}^{2}\bigr) \Bigr], $$
(2.25)

where \(\beta=\max_{r\in S} (\lambda_{\max}P_{r} )\).

Moreover, (2.24) and (2.25) yield

$$\begin{aligned} \Bigl(\min_{r\in S}\alpha_{r} \Bigr)\mathbb{E}\int _{\Omega}\bigl(u^{T}u+v^{T}v\bigr)\,dx&\leqslant \mathbb{E}V(t)\\ &\leqslant \beta \Bigl[\sup_{-\tau\leqslant \theta\leqslant0}\mathbb{E}\bigl( \bigl\| \phi(\theta,x)\bigr\| _{2}^{2}\bigr) + \sup_{-\tau\leqslant \theta\leqslant0} \mathbb{E}\bigl(\bigl\| \psi(\theta,x)\bigr\| _{2}^{2}\bigr) \Bigr]e^{-\lambda t}, \end{aligned}$$

from which one derives

$$\begin{aligned} &\mathbb{E}\|u\|_{2}^{2}+\mathbb{E}\|v\|_{2}^{2} \leqslant \frac{\beta }{\min_{r\in S}\alpha_{r}} e^{-\lambda t} \Bigl[\sup_{-\tau \leqslant \theta\leqslant0} \mathbb{E}\bigl( \bigl\| \phi(\theta,x)\bigr\| _{2}^{2}\bigr) + \sup _{-\tau\leqslant \theta\leqslant0}\mathbb{E}\bigl(\bigl\| \psi(\theta,x)\bigr\| _{2}^{2} \bigr) \Bigr],\\ &\quad t\geqslant0. \end{aligned}$$

According to Definition 1.2, we know that the system (1.1) is stochastically global exponential robust stability. The proof is completed. □

Remark 2.1

In 2015, [9], Theorem 3.3 offered a stability criterion for the following neural networks ([9], (22)) with discrete and distributed time-delays by way of M-matrix and H-matrix methods:

$$\dot{z}(t)=-Cz(t)+Ag\bigl(z(t)\bigr)+Bg\bigl(z\bigl(t-\tau(t)\bigr)\bigr)+D\int _{t-\sigma}^{t}g\bigl(z(s)\bigr)\,ds. $$

However, using the M-matrix and H-matrix methods is not easy in obtaining the LMI criterion conditions. Motivated by some methods of [9], we employ the Schur complement technique to derive the LMI-based stability criterion - Theorem 2.3.

3 Example

Consider two modes for the Markovian jumping system (1.1).

For Mode 1,

$$\begin{aligned}& \underline{A}_{1}= \begin{pmatrix} 2.9& 0\\ 0 & 2.1 \end{pmatrix},\qquad\underline{B}_{1}= \begin{pmatrix} 2.7& 0\\ 0 & 1.9 \end{pmatrix},\\& C_{1}= \begin{pmatrix} 0.5& 0.01\\ 0.01 & 0.6 \end{pmatrix} =D_{1}=E_{1}=H_{1}=L_{1}=W_{1}, \\& C_{1}^{*}= E_{1}^{*}=L_{1}^{*}= \begin{pmatrix} 0.05& 0.01\\ 0.01 & 0.06 \end{pmatrix}, \qquad D_{1}^{*}= H_{1}^{*}=W_{1}^{*}= \begin{pmatrix} 0.07& 0.03\\ 0.03 & 0.06 \end{pmatrix}. \end{aligned}$$

For Mode 2,

$$\begin{aligned}& \underline{A}_{2}= \begin{pmatrix} 2.8& 0\\ 0 & 2 \end{pmatrix},\qquad\underline{B}_{2}= \begin{pmatrix} 2.1& 0\\ 0 & 2.8 \end{pmatrix},\\& C_{2}= \begin{pmatrix} 0.7& 0.01\\ 0.01 & 0.5 \end{pmatrix} =D_{2}=E_{2}=H_{2}=L_{2}=W_{2}, \\& C_{2}^{*}= E_{2}^{*}=L_{2}^{*}= \begin{pmatrix} 0.06& 0.02\\ 0.02 & 0.05 \end{pmatrix}, \qquad D_{2}^{*}= H_{2}^{*}=W_{2}^{*}= \begin{pmatrix} 0.07& 0.03\\ 0.03 & 0.06 \end{pmatrix}. \end{aligned}$$

Let \(u=(u_{1},u_{2})^{T}\), \(v=(v_{1},v_{2})^{T}\in R^{2}\), \(x=(x_{1},x_{2})\in(0,10)\times (0,10)\subset R^{2}\), and then \(\lambda_{1}=0.02\pi^{2}=0.1974\) (see [22], Remark 2.5). Assume that \(\varrho=0.8\), \(\rho=0.7\), \(\tau=1.2\), and

$$\begin{aligned}& F= \begin{pmatrix} 0.3& 0\\ 0 & 0.2 \end{pmatrix},\qquad G= \begin{pmatrix} 0.2& 0 \\ 0 & 0.3 \end{pmatrix},\\& \Theta= \begin{pmatrix} 0.005& 0.009 \\ 0.006 & 0.008 \end{pmatrix},\qquad\Lambda= \begin{pmatrix} 0.007& 0.009 \\ 0.006 & 0.004 \end{pmatrix}. \end{aligned}$$

So \(\Lambda_{*}=0.004\), \(\Theta_{*}=0.005\). Let \(\pi_{11}=-0.6\), \(\pi_{12}=0.6\); \(\pi_{21}=0.2\), \(\pi_{22}=-0.2\). Let \(\alpha=5\), then we use the Matlab LMI toolbox to solve the linear matrices inequalities (2.7)-(2.10), and then the feasibility data follows:

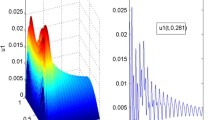
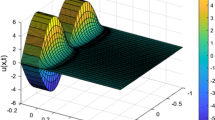
$$P_{1}= \begin{pmatrix} 5.5763& 0\\ 0& 5.7127 \end{pmatrix},\qquad P_{2}= \begin{pmatrix} 5.9111 & 0\\ 0& 5.8758 \end{pmatrix}, $$

and \(\alpha_{1}=5.2048\), \(\alpha_{2}=5.3765\), \(\beta=6.1317\). Hence, \(\alpha=5<\alpha_{1}\) and \(\alpha=5<\alpha_{2}\). According to Theorem 2.3, we know that the system (1.1) is stochastically global exponential robust stability (see Figures 1-4).

Figure 1
figure 1

Computer simulations of the state \(\pmb{u_{1}(t, x)}\) .

Full size image
Figure 2
figure 2

Computer simulations of the state \(\pmb{u_{2}(t, x)}\) .

Full size image
Figure 3
figure 3

Computer simulations of the state \(\pmb{v_{1}(t, x)}\) .

Full size image
Figure 4
figure 4

Computer simulations of the state \(\pmb{v_{2}(t, x)}\) .

Full size image

4 Conclusions

LMI-based stability criterion can easily be computed by the Matlab toolbox which has a high efficiency and other advantages in large-scale engineering calculations. In this paper, we employ Lyapunov stability theory, the M-matrix, H-matrix and linear matrix equality (LMI) techniques and variational methods to obtain the LMI-based stochastically exponential robust stability criterion for discrete and distributed time-delays Markovian jumping reaction-diffusion integro-differential equations with uncertain parameters, whose background of physics and engineering is BAM neural networks. Since using the M-matrix and H-matrix methods is not easy in obtaining the LMI criterion conditions, the methods employed in this paper improve those of previous related literature to some extent. Moreover, a numerical example in Section 3 is presented to illustrate the effectiveness of the proposed methods.