Delay-dependent exponential stability for Markovian jumping stochastic Cohen-Grossberg neural networks with p-Laplace diffusion and partially known transition rates via a differential inequality

Abstract

In this paper, new stochastic global exponential stability criteria for delayed impulsive Markovian jumping p-Laplace diffusion Cohen-Grossberg neural networks (CGNNs) with partially unknown transition rates are derived based on a novel Lyapunov-Krasovskii functional approach, a differential inequality lemma and the linear matrix inequality (LMI) technique. The employed methods are different from those of previous related literature to some extent. Moreover, a numerical example is given to illustrate the effectiveness and less conservatism of the proposed method due to the significant improvement in the allowable upper bounds of time delays.

1 Introduction

It is well known that Cohen-Grossberg in [1] proposed originally the Cohen-Grossberg neural networks (CGNNs). Since then the CGNNs have found their extensive applications in pattern recognition, image and signal processing, quadratic optimization, and artificial intelligence [2–6]. However, these successful applications are greatly dependent on the stability of the neural networks, which is also a crucial feature in the design of the neural networks. In practice, both time delays and impulse may cause undesirable dynamic network behaviors such as oscillation and instability [2–12]. Therefore, the stability analysis for delayed impulsive CGNNs has become a topic of great theoretic and practical importance in recent years [2–6]. Recently, CGNNs with Markovian jumping parameters have been extensively studied due to the fact that systems with Markovian jumping parameters are useful in modeling abrupt phenomena such as random failures, operating in different points of a nonlinear plant, and changing in the interconnections of subsystems [13–18]. Noise disturbance is unavoidable in real nervous systems, which is a major source of instability and poor performances in neural networks. A neural network can be stabilized or destabilized by certain stochastic inputs. The synaptic transmission in real neural networks can be viewed as a noisy process introduced by random fluctuations from the release of neurotransmitters and other probabilistic causes. Hence, noise disturbance should be also taken into consideration in discussing the stability of neural networks [14–18]. On the other hand, diffusion phenomena cannot be unavoidable in real world. Usually diffusion phenomena were simulated by linear Laplacian diffusion for simplicity in many previous literatures [2, 19–21]. However, diffusion behavior is so complicated that the nonlinear reaction-diffusion models were considered in several papers [3, 22–25]. The nonlinear p-Laplace diffusion ($p>1$) was considered in simulating some diffusion behaviors [3]. In addition, aging of electronic component, external disturbance, and parameter perturbations always result in a side-effect of partially unknown Markovian transition rates [26, 27]. To the best of our knowledge, stochastic stability for the delayed impulsive Markovian jumping p-Laplace diffusion CGNNs has rarely been considered. Besides, the stochastic exponential stability always remains the key factor of concern owing to its importance in designing a neural network, and such a situation motivates our present study. So, in this paper, we shall investigate the stochastic global exponential stability criteria for the above-mentioned CGNN by means of the linear matrix inequalities (LMIs) approach.

2 Model description and preliminaries

The stability of the following Cohen-Grossberg neural networks was studied in some previous literature via the differential inequality (see, e.g., [2]).

$$\{\begin{array}{l}\frac{\partial u}{\partial t}=\mathrm{\nabla }\cdot (\mathcal{D}\circ \mathrm{\nabla }u(t,x))-\tilde{A}(u(x,t))\\ \phantom{\frac{\partial u}{\partial t}=}\times [\tilde{B}(u(t,x))-C\tilde{f}(u(t,x))-D\tilde{g}(u(t-\tau (t),x))+J],\\ \text{for all }t⩾t_0,t\ne t_k,x\in \mathrm{\Omega },\\ u(t_k,x)=M_{k}u(t_k^{-},x)+N\tilde{h}(u(t_k^{-}-\tau (t),x)),k=1,2,\dots ,\end{array}$$

(2.1)

where $u=u(t,x)={(u_1(t,x),u_2(t,x),\dots ,u_n(t,x))}^T$, $\tilde{f}(u)={({\tilde{f}}_1(u_1),{\tilde{f}}_2(u_2),\dots ,{\tilde{f}}_n(u_n))}^T$, $\tilde{g}(u)={({\tilde{g}}_1(u_1),{\tilde{g}}_2(u_2),\dots ,{\tilde{g}}_n(u_n))}^T$.

In this paper, we always assume $\tilde{h}\equiv 0$ for some rational reason (see [3]). According to [[2], Definition 2.1], a constant vector $u^{\ast }\in R^n$ is said to be an equilibrium point of system (2.1) if

$$\tilde{B}\left(u^{\ast }\right)-C\tilde{f}\left(u^{\ast }\right)+D\tilde{g}\left(u^{\ast }\right)+J=0,\text{and}(M_k-I)u^{\ast }+N\tilde{h}\left(u^{\ast }\right)=0.$$

(2.2)

Let $v=u-u^{\ast }$, then system (2.1) with $\tilde{h}\equiv 0$ can be transformed into

$$\{\begin{array}{l}\frac{\partial v}{\partial t}=\mathrm{\nabla }\cdot (\mathcal{D}\circ \mathrm{\nabla }v(t,x))-A(v(t,x))[B(v(t,x))-Cf(v(t,x))-Dg(v(t-\tau (t),x))],\\ \text{for all }t⩾t_0,t\ne t_k,x\in \mathrm{\Omega },\\ v(t_k,x)=M_{k}v(t_k^{-},x),k=1,2,\dots ,\end{array}$$

(2.3)

where $v=v(t,x)={(v_1(t,x),v_2(t,x),\dots ,v_n(t,x))}^T$, $u^{\ast }={(u_1^{\ast },u_2^{\ast },\dots ,u_n^{\ast })}^T$, $A(v(t,x))=\tilde{A}(v(t,x)+u^{\ast })=\tilde{A}(u(t,x))$,

$$\begin{array}{r}B(v(t,x))=\tilde{B}(u(t,x))-\tilde{B}\left(u^{\ast }\right),f(v(t,x))=\tilde{f}(u(t,x))-\tilde{f}\left(u^{\ast }\right),\\ g(v(t,x))=\tilde{g}(u(t,x))-\tilde{g}\left(u^{\ast }\right),\end{array}$$

(2.4)

and

$$f(v)={(f_1(v_1),f_2(v_2),\dots ,f_n(v_n))}^T,g(v)={(g_1(v_1),g_2(v_2),\dots ,g_n(v_n))}^T.$$

Then, according to [[2], Definition 2.1], $v\equiv 0$ is an equilibrium point of system (2.3). Hence, further we only need to consider the stability of the null solution of Cohen-Grossberg neural networks. Naturally, we propose the following hypotheses on system (2.3) with $h\equiv 0$.

(A1) $A(v(t,x))$ is a bounded, positive, and continuous diagonal matrix, i.e., there exist two positive diagonal matrices $\underline{A}$ and $\overline{A}$ such that $0<\underline{A}⩽A(v(t,x))⩽\overline{A}$.

(A2) $B(v(t,x))={(b_1(v_1(t,x)),b_2(v_2(t,x)),\dots ,b_n(v_n(t,x)))}^T$ such that there exists a positive definite matrix $B=diag{(B_1,B_2,\dots ,B_n)}^T\in R^n$ satisfying

$$\frac{b_j(r)}{r}⩾B_j,\mathrm{\forall }j=1,2,\dots ,n,\text{ and }r\in R.$$

(A3) There exist constant diagonal matrices $G_k=diag(G_1^{(k)},G_2^{(k)},\dots ,G_n^{(k)})$, $F_k=diag(F_1^{(k)},F_2^{(k)},\dots ,F_n^{(k)})$, $k=1,2$ with $|F_j^{(1)}|⩽F_j^{(2)}$, $|G_j^{(1)}|⩽G_j^{(2)}$, $j=1,2,\dots ,n$, such that

$$F_j^{(1)}⩽\frac{f_j(r)}{r}⩽F_j^{(2)},G_j^{(1)}⩽\frac{g_j(r)}{r}⩽G_j^{(2)},\mathrm{\forall }j=1,2,\dots ,n,\text{ and }r\in R.$$

Remark 2.1 In many previous works (see, e.g., [2, 3]), authors always assumed

$$0⩽\frac{f_j(r)}{r}⩽F_j,0⩽\frac{g_j(r)}{r}⩽G_j,\mathrm{\forall }i=1,2,\dots ,n.$$

However, $F_j^{(1)}$, $G_j^{(1)}$ in (A3) may not be positive constants, and hence the functions f, g are more generic.

Remark 2.2 It is obvious from (2.4) that $B(0)=0=f(0)=g(0)$, and then $B(0)-Cf(0)+Dg(0)=0$.

Since stochastic noise disturbance is always unavoidable in practical neural networks, it may be necessary to consider the stability of the null solution of the following Markovian jumping CGNNs:

$$\{\begin{array}{l}dv(t,x)=\{\mathrm{\nabla }\cdot (\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v(t,x))-A(v(x,t))[B(v(t,x))-C(r(t))f(v(t,x))\\ \phantom{dv(t,x)=}-D(r(t))g(v(t-\tau (t),x))]\}dt+\sigma (t,v(t,x),v(t-\tau (t),x),r(t))dw(t),\\ \text{for all }t⩾t_0,t\ne t_k,x\in \mathrm{\Omega },\\ v(t_k,x)=M_k(r(t))v(t_k^{-},x),k=1,2,\dots .\end{array}$$

(2.5)

The initial conditions and the boundary conditions are given by

$$v(\theta ,x)=\varphi (\theta ,x),(\theta ,x)\in [-\tau ,0]\times \mathrm{\Omega },$$

(2.5b)

and

$$\mathfrak{B}[v_i(t,x)]=0,(t,x)\in [-\tau ,+\mathrm{\infty })\times \partial \mathrm{\Omega },i=1,2,\dots ,n.$$

(2.5c)

Here $p>1$ is a given scalar, and $\mathrm{\Omega }\in R^m$ is a bounded domain with a smooth boundary ∂ Ω of class ${\mathcal{C}}^2$ by Ω, $v(t,x)={(v_1(t,x),v_2(t,x),\dots ,v_n(t,x))}^T\in R^n$, where $v_i(t,x)$ is the state variable of the i th neuron and the j th neuron at time t and in a space variable x. Matrix $\mathcal{D}(t,x,v)={({\mathcal{D}}_{jk}(t,x,v))}_{n\times m}$ satisfies ${\mathcal{D}}_{jk}(t,x,v)⩾0$ for all j, k, $(t,x,v)$, where the smooth functions ${\mathcal{D}}_{jk}(t,x,v)$ are diffusion operators. $\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v={({\mathcal{D}}_{jk}(t,x,v){|\mathrm{\nabla }{v}_i|}^{p-2}\frac{\partial v_i}{\partial x_k})}_{n\times m}$ denotes the Hadamard product of matrix $\mathcal{D}(t,x,v)$ and ${\mathrm{\nabla }}_{p}v$ (see [13] or [28] for details).

Denote $w(t)={(w^{(1)}(t),w^{(2)}(t),\dots ,w^{(n)}(t))}^T$, where $w^{(j)}(t)$ is scalar standard Brownian motion defined on a complete probability space $(\mathrm{\Omega }\ast ,\mathcal{F},\mathcal{P})$ with a natural filtration ${\{{\mathcal{F}}_t\}}_{t⩾0}$. Noise perturbations $\sigma :R^{+}\times R^n\times R^n\times S\to R^{n\times n}$ is a Borel measurable function. $\{r(t),t⩾0\}$ is a right-continuous Markov process on the probability space, which takes values in the finite space $S=\{1,2,\dots ,s\}$ with generator $\mathrm{\Pi }=\{{\pi }_{ij}\}$ given by

$$\mathcal{P}(r(t+\delta )=j|r(t)=i)=\{\begin{array}{ll}{\pi }_{ij}\delta +o(\delta ),& j\ne i,\\ 1+{\pi }_{ij}\delta +o(\delta ),& j=i,\end{array}$$

where ${\pi }_{ij}⩾0$ is a transition probability rate from i to j ($j\ne i$) and ${\pi }_{ii}=-{\sum }_{j=1,j\ne i}^s{\pi }_{ij}$, $\delta >0$, and ${lim}_{\delta \to 0}o(\delta )/\delta =0$. In addition, the transition rates of the Markovian chain are considered to be partially available, namely some elements in the transition rate matrix Π are time-invariant but unknown. For instance, a system with three operation modes may have the transition rate matrix Π as follows:

$$\mathrm{\Pi }=\left[\begin{array}{ccc}{\pi }_{11}& ?& ?\\ ?& {\pi }_{22}& ?\\ {\pi }_{31}& {\pi }_{32}& {\pi }_{33}\end{array}\right],$$

where ‘?’ represents the inaccessible element. For notational clarity, we denote $S_{kn}^i\triangleq \{j\text{, if }{\pi }_{ij}\text{ is known}\}$ and $S_{un}^i\triangleq \{j\text{, if }{\pi }_{ij}\text{ is unknown, and }j\ne i\}$ for a given $i\in S$. Denote ${\tilde{\alpha }}_i⩾{max}_{j\in S_{un}^i}{\pi }_{ij}$. The time-varying delay $\tau (t)$ satisfies $0<\tau (t)⩽\tau$ with $\dot{\tau }(t)⩽\kappa <1$. $A(v(t,x))=diag(a_1(v_1(t,x)),a_2(v_2(t,x)),\dots ,a_n(v_n(t,x)))$, $B(v(t,x))={(b_1(v_1(t,x)),b_2(v_2(t,x)),\dots ,b_n(v_n(t,x)))}^T$, where $a_j(v_j(t,x))$ represents an amplification function, and $b_j(v_j(t,x))$ is an appropriately behavior function. $C(r(t))$, $D(r(t))$ and $M_k(r(t))$ are denoted by $C_i$, $D_i$, $M_{ki}$ with $C_i={(c_{lk}^i)}_{n\times n}$, $D_i={(d_{lk}^i)}_{n\times n}$, respectively, and $c_{lk}^i$, $d_{lk}^i$ denote the connection strengths of the k th neuron on the l th neuron in the mode $r(t)=i$, respectively. $M_{ki}$ is a symmetrical matrix for any given k, i. Denote vector functions $f(v(t,x))={(f_1(v_1(t,x)),f_2(v_2(t,x)),\dots ,f_n(v_n(t,x)))}^T$, $g(v(t,x))={(g_1(v_1(t,x)),\dots ,g_n(v_n(t,x)))}^T$, where $f_j(v_j(t,x))$, $g_j(v_j(t,x))$ are neuron activation functions of the j th unit at time t and in a space variable x.

In addition, we always assume that $t_0=0$ and $v(t_k^{+},x)=v(t_k,x)$ for all $k=1,2,\dots$ , where $v(t_k^{-},x)$ and $v(t_k^{+},x)$ represent the left-hand and right-hand limits of $v(t,x)$ at $t_k$. And each $t_k$ ($k=1,2,\dots$) is an impulsive moment satisfying $0<t_1<t_2<\cdots <t_k<\cdots$ and ${lim}_{k\to \mathrm{\infty }}{t}_k=+\mathrm{\infty }$. The boundary condition (2.5c) is called the Dirichlet boundary condition or the Neumann boundary condition, which is defined as (6a) in [13]. Similarly as (i)-(xii) of [13], we introduce the following standard notations.

$$\begin{array}{c}{L}^2(R\times \mathrm{\Omega }),L_{{\mathcal{F}}_0}^2([-\tau ,0]\times \mathrm{\Omega };R^n),Q={(q_{ij})}_{n\times n}>0(<0),Q={(q_{ij})}_{n\times n}⩾0(⩽0),\hfill \\ Q_1⩾Q_2(Q_1⩽Q_2),Q_1>Q_2(Q_1<Q_2),{\lambda }_{max}(\mathrm{\Phi }),{\lambda }_{min}(\mathrm{\Phi }),|C_{n\times n}|,|u(t,x)|,\hfill \\ \text{the identity matrix }I\text{ and the symmetric terms}\ast .\hfill \end{array}$$

Throughout this paper, we assume (A1)-(A3) and the following conditions hold:

(A4) $\sigma (t,0,0,i)=0$ for all $i\in S$.

Remark 2.3 The condition $|H|=H$ is not too stringent for a semi-positive definite matrix $H={(h_{ij})}_{n\times n}⩾0$. Indeed, $|H|=H$ if all $h_{ij}⩾0$, $\mathrm{\forall }i,j$.

(A5) There exist symmetrical matrices $R_j⩾0$ with $|R_j|=R_j$, $j=1,2$ such that for any mode $i\in S$,

$$\begin{array}{r}trace\left[{\sigma }^T(t,v(t,x),v(t-\tau (t),x),i)\sigma (t,v(t,x),v(t-\tau (t),x),i)\right]\\ ⩽v^T(t,x)R_{1}v(t,x)+v^T(t-\tau (t),x)R_{2}v(t-\tau (t),x).\end{array}$$

Similarly as is [[2], Definition 2.1], we can see from (A4) that system (2.5) has the null solution as its equilibrium point.

Lemma 2.1 [[13], Lemma 6]

Let $P_i=diag(p_{i1},p_{i2},\dots ,p_{in})$ be a positive definite matrix for a given i, and v be a solution of system (2.5). Then we have

$$\begin{array}{rl}{\int }_{\mathrm{\Omega }}{v}^T{P}_i(\mathrm{\nabla }\cdot (\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v))dx& =-\sum _{k=1}^m\sum _{j=1}^n{\int }_{\mathrm{\Omega }}{p}_{ij}{\mathcal{D}}_{jk}(t,x,v){|\mathrm{\nabla }{v}_j|}^{p-2}{\left(\frac{\partial v_j}{\partial x_k}\right)}^{2}dx\\ ={\int }_{\mathrm{\Omega }}(\mathrm{\nabla }\cdot {(\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v)}^T{P}_{i}vdx.\end{array}$$

Lemma 2.2 (see [11])

Consider the following differential inequality:

$$\{\begin{array}{l}{D}^{+}v(t)⩽-av(t)+b{[v(t)]}_{\tau },t\ne t_k,\\ v(t_k)⩽a_{k}v(t_k^{-})+b_k{[v(t_k^{-})]}_{\tau },\end{array}$$

where $v(t)⩾0$, ${[v(t_k)]}_{\tau }={sup}_{t-\tau ⩽s⩽t}v(s)$, ${[v(t_k^{-})]}_{\tau }={sup}_{t-\tau ⩽s<t}v(s)$ and $v(t)$ is continuous except $t_k$, $k=1,2,\dots$ , where it has jump discontinuities. The sequence $t_k$ satisfies $0=t_0<t_1<t_2<\cdots <t_k<t_{k+1}<\cdots$ , and ${lim}_{k\to \mathrm{\infty }}{t}_k=\mathrm{\infty }$. Suppose that

• (1) $a>b⩾0$;

• (2) $t_k-t_{k-1}>\delta \tau$, where $\delta >1$, and there exist constants $\gamma >0$, $M>0$ such that

  $${\rho }_1{\rho }_2\cdots {\rho }_{k+1}{e}^{k\lambda \tau }⩽M{e}^{\gamma t_k},$$

where ${\rho }_i=max\{1,a_i+b_i{e}^{\lambda \tau }\}$, $\lambda >0$ is the unique solution of the equation $\lambda =a-b{e}^{\lambda \tau }$;

then

$$v(t)⩽M{[v(0)]}_{\tau }{e}^{-(\lambda -\gamma )t}.$$

In addition, if $\theta ={sup}_{k\in Z}\{1,a_k+b_k{e}^{\lambda \tau }\}$, then

$$v(t)⩽\theta {[v(0)]}_{\tau }{e}^{-(\lambda -\frac{ln(\theta e^{\lambda \tau })}{\delta \tau })t},t⩾0.$$

3 Main results

Theorem 3.1 Assume that $p>1$. If the following conditions are satisfied:

(C1) there exist a sequence of positive scalars ${\underline{\alpha }}_i$, ${\overline{\alpha }}_i$ ($i\in S$) and positive definite diagonal matrices $P_i=diag(p_{i1},p_{i2},\dots ,p_{in})$ ($i\in S$), $L_1$, $L_2$ and Q such that the following LMI conditions hold:

$${\mathrm{\Theta }}_i\triangleq -\left(\begin{array}{cccc}{\mathcal{A}}_{i1}& 0& (F_1+F_2)L_1+P_i\overline{A}|C_i|& P_i\overline{A}|D_i|\\ \ast & {\mathcal{A}}_{i2}& 0& (G_1+G_2)L_2\\ \ast & \ast & -2L_1& 0\\ \ast & \ast & \ast & -2L_2\end{array}\right)>0,\mathrm{\forall }i\in S,$$

(3.1)

$$P_i>{\underline{\alpha }}_{i}I,\mathrm{\forall }i\in S,$$

(3.2)

$$P_i<{\overline{\alpha }}_{i}I,\mathrm{\forall }i\in S,$$

(3.3)

where $\dot{\tau }(t)⩽\kappa <1$ for all t, and

$$\begin{array}{c}{\mathcal{A}}_{i1}=-2P_i\underline{A}B+{\overline{\alpha }}_i{R}_1+\sum _{j\in S_{kn}^i}{\pi }_{ij}{P}_j+{\tilde{\alpha }}_i\sum _{j\in S_{un}^i}{P}_j+Q-2F_1{L}_1{F}_2,\hfill \\ {\mathcal{A}}_{i2}=-(1-\kappa )Q-2G_1{L}_2{G}_2;\hfill \end{array}$$

(C2) ${min}_{i\in S}\{\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}{P}_i},\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}Q}\}>\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}{max}_{i\in S}{\overline{\alpha }}_i⩾0$;

(C3) there exists a constant $\delta >1$ such that ${inf}_{k\in Z}(t_k-t_{k-1})>\delta \tau$, ${\delta }^2\tau >ln(\rho e^{\lambda \tau })$ and $\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau }>0$, where $\rho ={max}_j\{1,a_j+b_j{e}^{\lambda \tau }\}$ with $a_j\equiv ({max}_{k,i}\frac{{\lambda }_{max}(M_{ki}{P}_i{M}_{ki})}{{\lambda }_{min}{P}_i})$ and $b_j\equiv 1$, and $\lambda >0$ is the unique solution of the equation $\lambda =a-b{e}^{\lambda \tau }$ with $a={min}_{i\in S}\{\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}{P}_i},\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}Q}\}$ and $b=\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}{max}_{i\in S}{\overline{\alpha }}_i$,

then the null solution of system (2.5) is stochastically exponentially stable with the convergence rate $\frac{1}{2}(\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau })$.

Proof Consider the Lyapunov-Krasovskii functional

$$V(t,v(t,x),i)=V_{1i}+V_{2i},\mathrm{\forall }i\in S,$$

where

$$\begin{array}{r}{V}_{1i}={\int }_{\mathrm{\Omega }}{v}^T(t,x)P_{i}v(t,x)dx={\int }_{\mathrm{\Omega }}|v^T(t,x)|P_i|v(t,x)|dx,\\ V_{2i}={\int }_{\mathrm{\Omega }}{\int }_{-\tau (t)}^0{v}^T(t+\theta ,x)Qv(t+\theta ,x)d\theta dx\\ \phantom{V_{2i}}={\int }_{\mathrm{\Omega }}{\int }_{-\tau (t)}^0|v^T(t+\theta ,x)|Q|v(t+\theta ,x)|d\theta dx.\end{array}$$

(3.4)

From (A3), we have

$$\begin{array}{r}2\left|f^T(v(t,x))\right|L_1\left|f(v(t,x))\right|-2|v^T(t,x)|(F_1+F_2)L_1\left|f(v(t,x))\right|\\ +2|v^T(t,x)|F_1{L}_1{F}_2|v(t,x)|⩽0,\end{array}$$

(3.5)

$$\begin{array}{r}2\left|g^T\left(v(t-\tau (t),x)\right)\right|L_2\left|g\left(v(t-\tau (t),x)\right)\right|\\ -2\left|v^T(t-\tau (t),x)\right|(G_1+G_2)L_2\left|g\left(v(t-\tau (t),x)\right)\right|\\ +2\left|v^T(t-\tau (t),x)\right|G_1{L}_2{G}_2\left|v(t-\tau (t),x)\right|⩽0.\end{array}$$

(3.6)

Denote $\zeta (t,x)={(|v^T(t,x)|,|v^T(t-\tau (t),x)|,|f^T(v(t,x))|,|g^T(v(t-\tau (t),x))|)}^T$. Let ℒ be the weak infinitesimal operator such that $\mathcal{L}V(t,v(t,x),i)=\mathcal{L}{V}_{1i}+\mathcal{L}{V}_{2i}$ for any given $i\in S$. Next, it follows by Lemma 2.1, (A1)-(A5), (3.5) and (3.6) that for $t\ne t_k$,

$$\mathcal{L}V(t)⩽-{\int }_{\mathrm{\Omega }}{\zeta }^T(t,x){\mathrm{\Theta }}_i\zeta (t,x)dx+{\int }_{\mathrm{\Omega }}\left|v^T(t-\tau (t),x)\right|{\overline{\alpha }}_i{R}_2\left|v(t-\tau (t),x)\right|dx,$$

(3.7)

where $v=v(t,x)$ is a solution for system (2.5). □

Remark 3.1 Here, we employ some new methods different from those of [[3], (2.4)-(2.6)] in the proof of [[3], Theorem 2.1] and [[2], Theorem 3.1]. Hence, our LMI condition (3.1) is more effective than the LMI condition (2.1) in [[3], Theorem 2.1] even when system (2.5) is reduced to system (3.11) (see Remark 3.3 below).

It is not difficult to conclude from the Itô formula that for $t\in [t_k,t_{k+1})$,

$$D^{+}EV(t)⩽-\underset{i\in S}{min}\{\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}{P}_i},\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}Q}\}EV(t)+\left(\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}\underset{i\in S}{max}{\overline{\alpha }}_i\right){[EV(t)]}_{\tau }.$$

(3.8)

Owing to $t_k-t_{k-1}>\delta \tau >\tau$, we can derive

$$V(t_k)⩽\left(\underset{k,i}{max}\frac{{\lambda }_{max}(M_{ki}{P}_i{M}_{ki})}{{\lambda }_{min}{P}_i}\right)V\left(t_k^{-}\right)+{\left[V\left(t_k^{-}\right)\right]}_{\tau }.$$

(3.9)

It follows from (C3) that ${\rho }^{k+1}{e}^{k\lambda \tau }⩽e^{({\delta }^2-\lambda )\tau }{e}^{\delta t_k}$, where $\rho ={max}_j\{1,a_j+b_j{e}^{\lambda \tau }\}$ with $a_j\equiv ({max}_{k,i}\frac{{\lambda }_{max}(M_{ki}{P}_i{M}_{ki})}{{\lambda }_{min}{P}_i})$ and $b_j\equiv 1$, and $\lambda >0$ is the unique solution of the equation $\lambda =a-b{e}^{\lambda \tau }$, satisfying $\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau }>0$. Moreover, combining (3.8), (3.9), (C2), (C3) and Lemma 2.2 results in

$$E{\parallel v(t,x)\parallel }_2^2⩽\left[\frac{{max}_{i\in S}({\lambda }_{max}{P}_i+{\lambda }_{max}Q)}{{min}_{i\in S}({\lambda }_{min}{P}_i)}\rho \underset{-\tau ⩽s⩽0}{sup}E{\parallel \varphi (s)\parallel }_2^2\right]e^{-(\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau })t}.$$

(3.10)

Therefore, we can see by [[13], Definition 2.1] that the null solution of system (2.5) is globally stochastically exponentially stable in the mean square with the convergence rate $\frac{1}{2}(\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau })$.

Remark 3.2 Although the employed Lyapunov-Krasovskii functional is simple, together with the condition (A3) it simplifies the proof process. Moreover, the obtained LMI-based criterion is more effective and less conservative than [[3], Theorem 2.1], which will be shown in a numerical example of Remark 3.3.

Moreover, if Markovian jumping phenomena are ignored, system (2.5) is reduced to the following system:

$$\{\begin{array}{l}dv(t,x)=\{\mathrm{\nabla }\cdot (\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v(t,x))-A(v(x,t))[B(v(t,x))-Cf(v(t,x))\\ \phantom{dv(t,x)=}-Dg(v(t-\tau (t),x))]\}dt+\sigma (t,v(t,x),v(t-\tau (t),x),r(t))dw(t),\\ \text{for all }t⩾t_0,t\ne t_k,x\in \mathrm{\Omega },\\ v(t_k,x)=Mv(t_k^{-},x),k=1,2,\dots ,\end{array}$$

(3.11)

where M is a symmetrical matrix.

In order to compare with the main result of [3], we may as well educe the following corollary based on Theorem 3.1.

Corollary 3.2 If the following conditions are satisfied:

(C1*) there exist positive scalars $\underline{\alpha }$, $\overline{\alpha }$ and positive definite diagonal matrices P, $L_1$, $L_2$ and Q such that the following LMI conditions hold :

where

$$A_1^{\ast }=-2P\underline{A}B+\overline{\alpha }{R}_1+Q-2F_1{L}_1{F}_2,A_2^{\ast }=-(1-\kappa )Q-2G_1{L}_2{G}_2;$$

(3.12)

(C2*) $min\{\frac{{\lambda }_{min}\tilde{\mathrm{\Theta }}}{{\lambda }_{max}P},\frac{{\lambda }_{min}\tilde{\mathrm{\Theta }}}{{\lambda }_{max}Q}\}>\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}\overline{\alpha }⩾0$;

(C3*) there exists a constant $\delta >1$ such that ${inf}_{k\in Z}(t_k-t_{k-1})>\delta \tau$, ${\delta }^2\tau >ln(\rho e^{\lambda \tau })$ and $\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau }>0$, where $\rho =max\{1,a_j+b_j{e}^{\lambda \tau }\}$ with $a_j\equiv \frac{{\lambda }_{max}(MPM)}{{\lambda }_{min}P}$ and $b_j\equiv 1$, and $\lambda >0$ is the unique solution of the equation $\lambda =\tilde{a}-\tilde{b}{e}^{\lambda \tau }$ with $\tilde{a}=min\{\frac{{\lambda }_{min}\tilde{\mathrm{\Theta }}}{{\lambda }_{max}P},\frac{{\lambda }_{min}\tilde{\mathrm{\Theta }}}{{\lambda }_{max}Q}\}$ and $\tilde{b}=\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}\overline{\alpha }$,

then the null solution of system (3.11) is stochastically globally exponential stable in the mean square with the convergence rate $\frac{1}{2}(\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau })$.

Remark 3.3 In [[3], Theorem 2.1], $R_2$ in (A5) is assumed to be 0. In addition, $F_1=G_1$ are also assumed to be 0. In [[3], Theorem 2.1], if there exist positive definite diagonal matrices $P_1$, $P_2$ such that the following LMI holds:

and other two conditions similar as (C2*) and (C3*) hold, then the null solution of system (3.11) is stochastically globally exponential stable in the mean square.

Note that $F_2^2$ in ($\tilde{\mathrm{C}}1$) exercises a malign influence on the negative definite possibility of matrix when ${\lambda }_{min}{F}_2>1$.

Indeed, we may consider system (3.11) with the following parameter:

$$\begin{array}{c}\underline{A}=\left(\begin{array}{cc}1.3& 0\\ 0& 1.4\end{array}\right),\overline{A}=\left(\begin{array}{cc}2& 0\\ 0& 2\end{array}\right),B=\left(\begin{array}{cc}1.8& 0\\ 0& 1.88\end{array}\right),\hfill \\ F_1=G_1=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right),G_2=\left(\begin{array}{cc}2& 0\\ 0& 3\end{array}\right),\hfill \\ F_2=\left(\begin{array}{cc}7.38& 0\\ 0& 7.48\end{array}\right),C=D=\left(\begin{array}{cc}0.11& -0.003\\ -0.003& 0.12\end{array}\right),\hfill \\ R_1=\left(\begin{array}{cc}0.01& 0.0012\\ 0.0012& 0.01\end{array}\right),\hfill \end{array}$$

and $\tau =0.65$, $k=0$.

Now we use matlab LMI toolbox to solve the LMI (C1*), and the result is $\mathit{tmin}=0.0050>0$, which implies the LMI ($\tilde{\mathrm{C}}1$) is found infeasible, let alone other two conditions (i.e., (C2) and (C3) in [[3], Theorem 2.1]). However, by solving LMIs, Equation (3.3*) can be seen in Page 8, one can obtain $\mathit{tmin}=-0.0056<0$ and $\underline{\alpha }=2.0198$, $\overline{\alpha }=7.5439$,

$$\begin{array}{c}P=\left(\begin{array}{cc}4.1989& 0\\ 0& 3.9019\end{array}\right),L_1=\left(\begin{array}{cc}0.1515& 0\\ 0& 0.1398\end{array}\right),\hfill \\ L_2=\left(\begin{array}{cc}0.8018& 0\\ 0& 0.4173\end{array}\right),Q=\left(\begin{array}{cc}3.5352& 0\\ 0& 3.7619\end{array}\right).\hfill \end{array}$$

As pointed out in Remark 3.1 and Remark 3.2, our Theorem 3.1 and its Corollary 3.2 are more feasible and less conservative than [[3], Theorem 2.1] as a result of our new methods employed in this paper.

Remark 3.4 Both the conclusion and the proof methods of Theorem 3.1 are different from those previous related results in the literature (see, e.g., [2, 3]). Below, we shall give a numerical example to show that Theorem 3.1 is more effective and less conservative than some existing results due to significant improvement in the allowable upper bounds of delays.

4 A numerical example

Example 1 Consider the following CGNN under the Neumann boundary condition:

$$\{\begin{array}{l}dv=[\mathrm{\nabla }\cdot (\mathcal{D}(t,x,v)\circ {\mathrm{\nabla }}_{p}v(t,x))]dt\\ \phantom{dv=}-\left(\begin{array}{cc}{a}_1(v_1)& 0\\ 0& a_2(v_2)\end{array}\right)[\left(\begin{array}{c}{b}_1(v_1)\\ b_2(v_2)\end{array}\right)-C_{i}f(v(t,x))-D_{i}g(v(t-\tau ,x))]dt\\ \phantom{dv=}+\sigma (t,v(t,x),v(t-\tau ,x),i)dw(t),i\in S=\{1,2,3\},t⩾t_0,t\ne t_k,x\in \mathrm{\Omega },\\ v(t_k,x)=M_{ki}v(t_k^{-},x),i\in S=\{1,2,3\},k=1,2,\dots \end{array}$$

(4.1)

with the initial condition

$$\varphi (s,x)=\left(\begin{array}{c}{x}^2(1-cos(5\pi x^2)){cos}^{189}(x^2-0.25)e^{-100s}\\ (1-x){sin}^2(4\pi x^2){cos}^{201}(x^2-0.55)e^{-100s}\end{array}\right),-7.75⩽s⩽0,$$

(4.2)

and the Neumann boundary condition (or the Dirichlet boundary condition), where $\tau (t)\equiv \tau =7.75$, $p=2.011$, $v={(v_1(t,x),v_2(t,x))}^T\in R^2$, $x={(x_1,x_2)}^T\in \mathrm{\Omega }=\{{(x_1,x_2)}^T\in R^2:|x_j|<\sqrt{2},j=1,2\}$, $a_1(v_1)=2.3+0.6{sin}^2(t{x}^2)$, $a_2(v_2)=2.4+0.5{cos}^2(t{x}^2)$, $b_1(v_1)=2.8v_1+2v_1{sin}^2(t^2+x^2)$, $b_2(v_2)=2.88v_2+v_2{cos}^2(t^2+x^2)$, $f(v)=g(v)={(0.1v_1,0.1v_2+0.1v_2{sin}^2(t{x}^2))}^T$, and

$$\begin{array}{r}\mathcal{D}(t,x,v)=\left(\begin{array}{cc}0.003& 0.005\\ 0.004& 0.0006\end{array}\right),\underline{A}=\left(\begin{array}{cc}2.3& 0\\ 0& 2.4\end{array}\right),\overline{A}=\left(\begin{array}{cc}2.9& 0\\ 0& 2.9\end{array}\right),\\ B=\left(\begin{array}{cc}2.8& 0\\ 0& 2.88\end{array}\right),C_1=\left(\begin{array}{cc}0.11& -0.003\\ -0.003& 0.12\end{array}\right)=D_1,\\ C_2=\left(\begin{array}{cc}0.16& -0.003\\ -0.003& 0.18\end{array}\right)=D_2,C_3=\left(\begin{array}{cc}0.13& -0.003\\ -0.003& 0.12\end{array}\right)=D_3,\\ F_1=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)=G_1,F_2=\left(\begin{array}{cc}0.1& 0\\ 0& 0.2\end{array}\right)=G_2,R_1=\left(\begin{array}{cc}0.0003& 0\\ 0& 0.0003\end{array}\right)=R_2,\\ M_k(r(t))=M=\left(\begin{array}{cc}5.5& 0.001\\ 0.001& 5.5\end{array}\right),\mathrm{\forall }r(t)=i\in S=\{1,2,3\},k=1,2,\dots .\end{array}$$

(4.3)

The two cases of the transition rate matrices are considered as follows:

$$\text{Case (1): }\mathrm{\Pi }=\left(\begin{array}{ccc}-0.6& 0.4& 0.2\\ 0.2& -0.7& 0.5\\ 0.5& 0.3& -0.8\end{array}\right),\text{Case (2): }\mathrm{\Pi }=\left(\begin{array}{ccc}-0.6& ?& ?\\ 0.2& ?& ?\\ ?& 0.3& ?\end{array}\right).$$

(4.4)

In Case (1), $S_{kn}^i=\mathrm{\varnothing }$ (the empty set), and hence ${\tilde{\alpha }}_i{\sum }_{j\in S_{un}^i}{P}_j=0$ and ${\sum }_{j\in S_{kn}^i}{\pi }_{ij}{P}_j={\sum }_{j\in S}{\pi }_{ij}{P}_j$ for all $i\in S=\{1,2,3\}$.

Now we use the Matlab LMI toolbox to solve the LMIs (3.1)-(3.3) for Case (1), and the result shows $\mathit{tmin}=-0.1099<0$, and ${\overline{\alpha }}_1=9.2330$, ${\underline{\alpha }}_1=0.7039$, ${\overline{\alpha }}_2=9.2305$, ${\underline{\alpha }}_2=0.7014$, ${\overline{\alpha }}_3=9.2321$, ${\underline{\alpha }}_3=0.7030$,

$$\begin{array}{c}{P}_1=\left(\begin{array}{cc}1.4624& 0\\ 0& 1.3531\end{array}\right),P_2=\left(\begin{array}{cc}1.4578& 0\\ 0& 1.3476\end{array}\right),\hfill \\ P_3=\left(\begin{array}{cc}1.4599& 0\\ 0& 1.3522\end{array}\right),Q=\left(\begin{array}{cc}9.2765& 0\\ 0& 9.2212\end{array}\right),\hfill \\ L_1=\left(\begin{array}{cc}4.5455& 0\\ 0& 4.4596\end{array}\right),L_2=\left(\begin{array}{cc}4.5714& 0\\ 0& 4.5093\end{array}\right).\hfill \end{array}$$

Next, we shall prove that the above data $P_i$, ${\overline{\alpha }}_i$, ${\underline{\alpha }}_i$ and Q make the conditions (C2) and (C3) hold, respectively.

Indeed, by computing, we have ${\lambda }_{min}{\mathrm{\Theta }}_1=7.6913$, ${\lambda }_{min}{\mathrm{\Theta }}_2=7.3614$, ${\lambda }_{min}{\mathrm{\Theta }}_3=7.6864$, ${\lambda }_{max}{P}_1=1.4624$, ${\lambda }_{max}Q=9.2765$, ${\lambda }_{max}{P}_2=1.4578$, ${\lambda }_{max}{P}_3=1.4599$, and then $a={min}_{i\in S}\{\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}{P}_i},\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}Q}\}=0.7936$, $b=\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}{max}_{i\in S}{\overline{\alpha }}_i=3.0038\ast {10}^{-4}$. Then $a>b⩾0$, and hence (C2) holds.

Let $\delta =2.1215$, $\tau =7.75$, and ${inf}_{k\in Z}(t_k-t_{k-1})>\delta \tau$. Solve $\lambda =a-b{e}^{\lambda \tau }$, and hence $\lambda =0.7163$. Moreover, it follows by direct computation that $a_j\equiv ({max}_{k,i}\frac{{\lambda }_{max}(M_{ki}{P}_i{M}_{ki})}{{\lambda }_{min}{P}_i})\equiv 32.7237$. Owing to $b_j\equiv 1$, we have $\rho ={max}_j\{1,a_j+b_j{e}^{\lambda \tau }\}=290.3023$. Thereby, a direct computation can derive that ${\delta }^2\tau -ln(\rho e^{\lambda \tau })=23.6587>0$ and $\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau }=0.0337>0$.

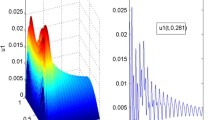
Therefore, it follows from Theorem 3.1 that the null solution of system (4.1) is stochastically exponentially stable with the convergence rate $0.0337/2=0.0169$ (see, Figures 1-3).

Figure 1

Computer simulations of the states of ${\mathit{v}}_{\mathbf{1}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{x}\mathbf{)}$ and ${\mathit{v}}_{\mathbf{2}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{x}\mathbf{)}$ .

Figure 2

Computer simulations of the state ${\mathit{v}}_{\mathbf{1}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{x}\mathbf{)}$ .

Figure 3

Computer simulations of the state ${\mathit{v}}_{\mathbf{2}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{x}\mathbf{)}$ .

In Case (2), it is obvious that ${\tilde{\alpha }}_1=0.6$, ${\tilde{\alpha }}_2=0.8$, ${\tilde{\alpha }}_3=0.7$. Solving LMIs (3.1)-(3.3) for Case (2), one can obtain $\mathit{tmin}=-0.1115<0$, and ${\overline{\alpha }}_1=9.3404$, ${\underline{\alpha }}_1=0.7464$, ${\overline{\alpha }}_2=9.3608$, ${\underline{\alpha }}_2=0.7668$, ${\overline{\alpha }}_3=9.3635$, ${\underline{\alpha }}_3=0.7695$,

$$\begin{array}{c}{P}_1=\left(\begin{array}{cc}1.5536& 0\\ 0& 1.4320\end{array}\right),P_2=\left(\begin{array}{cc}1.5984& 0\\ 0& 1.4687\end{array}\right),\hfill \\ P_3=\left(\begin{array}{cc}1.6025& 0\\ 0& 1.4754\end{array}\right),Q=\left(\begin{array}{cc}9.3823& 0\\ 0& 9.3233\end{array}\right),\hfill \\ L_1=\left(\begin{array}{cc}4.5780& 0\\ 0& 4.4899\end{array}\right),L_2=\left(\begin{array}{cc}4.6062& 0\\ 0& 4.5436\end{array}\right).\hfill \end{array}$$

Next, we shall prove that the above data $P_i$, ${\overline{\alpha }}_i$, ${\underline{\alpha }}_i$ and Q make the conditions (C2) and (C3) hold, respectively.

Indeed, we can get by direct computations that ${\lambda }_{min}{\mathrm{\Theta }}_1=7.7208$, ${\lambda }_{min}{\mathrm{\Theta }}_2=7.3554$, ${\lambda }_{min}{\mathrm{\Theta }}_3=7.7252$, ${\lambda }_{max}{P}_1=1.5536$, ${\lambda }_{max}Q=9.3823$, ${\lambda }_{max}{P}_2=1.5984$, ${\lambda }_{max}{P}_3=1.6025$, and then $a={min}_{i\in S}\{\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}{P}_i},\frac{{\lambda }_{min}{\mathrm{\Theta }}_i}{{\lambda }_{max}Q}\}=0.7840$, $b=\frac{{\lambda }_{max}{R}_2}{{\lambda }_{min}Q}{max}_{i\in S}{\overline{\alpha }}_i=33.0129\ast {10}^{-4}$, and hence $a>b⩾0$. So, the condition (C2) in Theorem 3.1 holds.

Similarly, let $\delta =2.1215$, $\tau =7.75$, and ${inf}_{k\in Z}(t_k-t_{k-1})>\delta \tau$. Solve $\lambda =a-b{e}^{\lambda \tau }$, and hence $\lambda =0.7101$. Moreover, it follows by direct computation that $a_j\equiv ({max}_{k,i}\frac{{\lambda }_{max}(M_{ki}{P}_i{M}_{ki})}{{\lambda }_{min}{P}_i})\equiv 32.9214$. Owing to $b_j\equiv 1$, we have $\rho ={max}_j\{1,a_j+b_j{e}^{\lambda \tau }\}=278.4160$. Thereby, a direct computation can derive that ${\delta }^2\tau -ln(\rho e^{\lambda \tau })=23.7485>0$ and $\lambda -\frac{ln(\rho e^{\lambda \tau })}{\delta \tau }=0.0330>0$.

Therefore, it follows from Theorem 3.1 that the null solution of system (4.1) is stochastically exponentially stable with the convergence rate $0.0330/2=0.0165$.

Table 1 shows that the convergence rate decreases when the number of unknown elements increases.

Table 1 Allowable upper bound of τ and the convergence rate for Theorem 3.1 in Case (1) and Case (2)

Remark 4.1 Table 1 shows that the null solution of system (4.1) (or (2.5)) is stochastically globally exponential stable in the mean square for the maximum allowable upper bounds $\tau =7.75$. Hence, as pointed out in Remark 3.3, the approach developed in Theorem 3.1 is more effective and less conservative than some existing results ([[3], Theorem 2.1], [29]).

5 Conclusions

In this paper, new LMI-based stochastic global exponential stability criteria for delayed impulsive Markovian jumping reaction-diffusion Cohen-Grossberg neural networks with partially unknown transition rates and the nonlinear p-Laplace diffusion are obtained, the feasibility of which can be easily checked by the Matlab LMI toolbox. Moreover, numerical example illustrates the effectiveness and less conservatism of all the proposed methods via the significant improvement in the allowable upper bounds of time delays. For further work, we are considering how to make the nonlinear p-Laplace diffusion item play a positive role in the stability criteria, which still remains an open and challenging problem.