1 Introduction

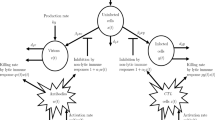
Human immunodeficiency virus (HIV) is a simple form of virus that affects the human body, and it primarily targets CD4+ T-cells. Viruses, in general, are the infectious creatures that have no reproductive ability by themselves. They depend on a host for replication to begin. HIV viruses carry a copy of their RNA that needs to first be duplicated into DNA [1]. Furthermore, once the DNA virus has been copied into these host cells, new virus particles must also be assembled at the host cell surface [2]. The maturing for these new particles might occur gradually without impacting that host cell, or it quickly erupts and destroys the host cell [3, 4]. Antiretroviral therapy (ART) would intend to inhibit that activity for different HIV viral proteins and consequently hinder the viral replication cycle [5, 6].The drug based on the inhibitor of reverse transcriptase (RTI) is an obstacle to the reverse transcription of viral DNA and prevents a productive infection of the host cell. Protease inhibitor (PI) drugs aim to suppress protease activity and prevent the development of mature viruses. The combination of reverse transcriptase inhibitor and protease inhibitor is more effective to treat HIV patients.

Mathematical modeling can contribute to the study of antiviral infection treatment and increase knowledge about the virus transmission rate [7, 8]. Numerous models of viral infections are discussed in the literature for HIV dynamics [9]. The immune system CTL plays a vital role in protecting against HIV and this ability prevents the reproduction of HIV [10]. Hence many mathematical models examine viral infection in conjunction with CTL responses [11–13]. To resist viral infection, both CTL immune response and strong antibody neutralizing are necessary for an effective vaccine [14, 15].

In [16] Wodarz suggested a model depicting the relationship between CTL and antibody immune responses. The global analysis for this model was provided by Yousfi et al. [17]. Yan and Wang included the intracellular delay in the cell infected model and analyzed the global dynamics effect of the delay [18].

The mathematical study is needed for an integrated view of the dynamics of viruses for delayed models [19–21]. Several models have been suggested with a time lag in triggering the immune reaction when the body is infected with the virus, which is called immunological delay [22–24].

In [25] Dubey et al. described the dynamics of infection by HIV involving available drug therapies, reverse transcriptase inhibitor (RTI), and protease inhibitor (PI) that includes uninfected CD4+ T-cells \(x (t)\), infected cells \(y (t)\), free virus \(v (t)\), and CTL immune response \(C(t)\), and antibody \(A(t)\). The non-linear differential equations of the first order are as follows:

$$\begin{aligned} \begin{aligned}& \mathop{x} ^{ \bullet } = \lambda + rx \biggl( 1 - \frac{x}{x_{m}} \biggr) - \lambda _{0}x - \beta ( 1 - \eta _{r} )xv, \\ &\mathop{y} ^{ \bullet } = \beta ( 1 - \eta _{r} )xv - \delta _{0}y - \omega _{1}Cy, \\ &\mathop{v} ^{ \bullet } = N\delta _{0} ( 1 - \eta _{p} )y - \delta _{1}v - \omega _{2}Av, \\ &\mathop{C} ^{ \bullet } = \alpha _{1}y + \mu _{1}Cy - \mu _{10}C, \\ &\mathop{A} ^{ \bullet } = \mu _{2}vA - \mu _{20}A, \end{aligned} \end{aligned}$$
(1)

where \(\delta _{0} = \delta _{0}^{1} + \frac{\omega _{1}\alpha _{0}}{\mu _{10}},\alpha _{1} = \alpha _{1}^{1} + \frac{\mu _{1}\alpha _{0}}{\mu _{10}} \).

Here, λ is the production level for uninfected CD4+ T-cells, \(\lambda _{0}\) is an uninfected CD4+ T-cells mortality rate, r is the maximum rate of proliferation, β is the infection rate of uninfected cells by the virus, \(x_{m} = x_{\max } \) is their carrying capacity, \(\eta _{r}\) is the rate of inhibitor reverse transcriptase therapy to destroy infected cells, and \(\eta _{p}\) is the rate at which the protease inhibitor therapy blocks the infection, \(\delta _{0}^{1}\) is the infected cell mortality rate, N is the number of particles of virus produced by the cell infected, \(\delta _{1}\) is the rate of virus removed from the body by natural factors, \(\alpha _{0}\) is the rate of produced CTL immune response, \(\mu _{10}\) is the deplete rate of CTL. \(\alpha _{1}^{1}\) is the stimulated rate of CTL, \(\mu _{1}\) is the rate at which CTL interact with the infected cells, \(\omega _{1}\) is the level of CTL interaction removed from infected cells. \(\mu _{2}\) is the rate at which antibody gets stimulated, \(\mu _{20}\) is the deplete rate of antibody due to increase in virus particles. \(\omega _{2}\) is the reduced rate of virus with antibody interaction.

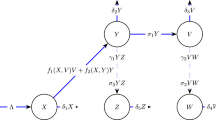
In this study, we implement a time delay to illustrate the CTL response model. The generation of CTL due to antigenic stimulation requires a period of time τ and the response to CTL in time t that depends on an antigen population in the previous time \(t - \tau \) for a time lag \(\tau > 0\). The model suggested by incorporating immune response delay in CTL is as follows:

$$\begin{aligned} \begin{aligned}& \mathop{x} ^{ \bullet } = \lambda + rx \biggl( 1 - \frac{x}{x_{m}} \biggr) - \lambda _{0}x - \beta ( 1 - \eta _{r} )xv, \\ &\mathop{y} ^{ \bullet } = \beta ( 1 - \eta _{r} )xv - \delta _{0}y - \omega _{1}Cy, \\ &\mathop{v} ^{ \bullet } = N\delta _{0} ( 1 - \eta _{p} )y - \delta _{1}v - \omega _{2}Av, \\ &\mathop{C} ^{ \bullet } = \alpha _{1}y + \mu _{1}C ( t - \tau )y ( t - \tau ) - \mu _{10}C, \\ &\mathop{A} ^{ \bullet } = \mu _{2}vA - \mu _{20}A. \end{aligned} \end{aligned}$$
(2)

The primary objective is to analyze the impact of immune reaction delay in the dynamics of (2) together with reverse transcriptase inhibitor and protease inhibitor and show the impact on the stability of the delay in the immune response.

We start with some notes that are used in the sequel to our study.

Let \(\mathbb{C} = \mathbb{C} ( [ - \tau,0 ],R_{ +}^{5} )\) be the Banach space of continuous functions mapping the interval \([ - \tau,0 ]\) in to \(R_{ +}^{5}\), where \(R_{ +}^{5} = ( x,y,v,C,A )\).

The initial conditions are given as follows:

$$\begin{aligned} &x ( \theta ) = \phi _{1} ( \theta ) \ge 0,\qquad y ( \theta ) = \phi _{2} ( \theta ) \ge 0, \qquad v ( \theta ) = \phi _{3} ( \theta ) \ge 0,\\ & C ( \theta ) = \phi _{4} ( \theta ) \ge 0,\qquad A ( \theta ) = \phi _{5} ( \theta ) \ge 0, \quad\theta \in [ - \tau, 0 ], \end{aligned}$$

where \(\phi _{i} ( \theta ) \in \zeta ^{1}\) are smooth functions for all \(i= 1, 2,3,4,5\).

The solution \(( x ( t ),y ( t ),v ( t ),C ( t ),A ( t ) )\) is easy to recognize from the basic theory of differential functions of (2) with the initial conditions as mentioned above which exist for all \(t \ge 0\) and are unique [26–28]. It can be shown that this solution exists for all \(t > 0\) and stays nonnegative. In fact, if \(x ( 0 ) > 0\), then \(x ( t ) > 0\) for all \(t > 0 \). The same argument is true for \(y,v,C\), and A components. Hence, the interior \(R_{ +}^{5}\) is invariant for system (2).

The basic reproduction ratio \(R_{0}\) of model (2) is defined by

$$ R_{0} = \frac{\beta N ( 1 - \eta _{c} )}{\delta _{1}}x_{0}, $$

where \(\eta _{c} = 1 - ( 1 - \eta _{r} ) ( 1 - \eta _{p} )\).

2 Stability of viral free steady state \(( I_{0} )\)

Theorem 2.1

If\(R_{0} < 1\)then the viral free steady state\(\mathrm{I}_{0}\)is locally asymptotically stable.

Proof

The viral free steady state of system (2) is \(\mathrm{I}_{0} ( x_{0},0,0,0,0 )\), where

$$ x_{0} = \frac{x_{m}}{2r} \biggl[ ( r - \lambda _{0} ) + \sqrt{ ( r - \lambda _{0} )^{2} + \frac{4r\lambda }{x_{m}}} \biggr]. $$

The characteristic equation of \(I_{0}\) is given by

$$ \begin{vmatrix} - h - \xi & 0 & - \beta _{1}x_{0} & 0 & 0 \\ 0 & - \delta _{0} - \xi & \beta _{1}x_{0} & 0 & 0 \\ 0 & N_{1}\delta _{0} & - \delta _{1} - \xi & 0 & 0 \\ 0 & 0 & 0 & - \mu _{10} - \xi & 0 \\ 0 & 0 & 0 & 0 & - \mu _{20} - \xi \end{vmatrix} = 0, $$

where

$$ h = \biggl( \frac{2r x_{0}}{x_{m}} - ( r - \lambda _{0} ) \biggr) = \sqrt{ ( r - \lambda _{0} )^{2} + \frac{4r\lambda }{c_{m}}} > 0,\qquad N_{1} = N ( 1 - \eta _{P} ) $$

and

$$\begin{aligned} ( \xi + h ) ( \xi + \mu _{20} ) ( \xi + \mu _{10} ) \bigl[ \varepsilon ^{2} + ( \delta _{0} + \delta _{1} )\xi + ( \delta _{0}\delta _{1} - \beta _{1}N_{1}\delta _{0}x_{0} ) \bigr] = 0. \end{aligned}$$
(3)

From (3) we get \(\xi _{1} = - h < 0,\xi _{2} = - \mu _{20} < 0,\xi _{3} = - \mu _{10}<0\); if \(R_{0} < 1\) then \(\delta _{0}\delta _{1} - \beta _{1}N_{1}\delta _{0}x_{0} > 0\).

Thus, the eigenvalues of (3) have negative real parts. Hence the viral free steady state of (2) is locally asymptotically stable. □

3 Stability analysis of infected steady state \(( I^{*} )\) and existence of Hopf bifurcation

Theorem 3.1

If\(R_{0} > 1\)then (i) the infected steady state\(I^{*}\)of system (2) is locally asymptotically stable for\(\tau = 0\);

(ii) Time delayτcrosses the critical value\(\tau _{0}\), then system (2) undergoes Hopf bifurcation at the infected steady state\(I^{*}\).

Proof

The infected steady state \(\mathrm{I}^{*} ( x^{*},y^{*},v^{*},C^{*},A^{*} )\) of (2) is given by

$$\begin{aligned} &v^{*} = \frac{\mu _{20}}{\mu _{2}}, y^{*} = \frac{\mu _{10}C^{*}}{\alpha _{1} + \mu _{1}C^{*}},\qquad A^{*} = \frac{N_{1}\delta _{0}\mu _{2}y^{*} - \delta _{1}\mu _{20}}{\mu _{20}\omega _{2}}, \\ &C^{*} = \frac{h_{2} + \sqrt{h_{2}^{2} + 4h_{1}h_{3}}}{2h_{1}}, \\ &x^{*} = \frac{x_{m}}{2r} \biggl[ f + \sqrt{f^{2} + \frac{4r\lambda }{x_{m}}} \biggr], \end{aligned}$$

where

$$\begin{aligned} &f = r - \lambda _{0} - \frac{\beta _{1}\mu _{20}}{\mu _{2}},\qquad h_{1} = \mu _{10}\mu _{2}\omega _{1},\\ & h_{2} = \beta _{1}\mu _{20}\mu _{1}x^{*} - \delta _{0}\mu _{10}\mu _{2},\qquad h_{3} = \beta _{1}\mu _{20}\alpha _{1}x^{*}. \end{aligned}$$

The uninfected CD4+ T cells \(( x^{*} )\) can achieve a steady state value by resolving the equation

$$ \frac{r}{x_{m}}x^{* 2} + \biggl( - r + \lambda _{0} + \beta _{1}\frac{\mu _{20}}{\mu _{2}} \biggr)x^{*} - \lambda = 0. $$

The immune response (\(C^{*}\)) can obtain a steady state value by solving the following equation:

$$ \omega _{1}C^{*^{2}}\mu _{10}\mu _{2} + C^{*} \bigl( \delta _{0}\mu _{10}\mu _{2} - \mu _{1}\beta ( 1 - \eta _{r} )x^{*}\mu _{20} \bigr) - \beta ( 1 - \eta _{r} )x^{*}\mu _{20}\alpha _{1} = 0. $$

The characteristic equation of \(I^{*}\) is given by

$$\begin{aligned} & \begin{vmatrix} r - \frac{2rx^{*}}{x_{m}} - \lambda _{0} - \beta _{1}v^{*} - \xi & 0 & - \beta _{1}x^{*} & 0 & 0 \\ \beta _{1}v^{*} & - \bigl( \delta _{0} + \omega _{1}C^{*} \bigr) - \xi & \beta _{1}x^{*} & - \omega _{1}y^{*} & 0 \\ 0 & N_{1}\delta _{0} & - \bigl( \delta _{1} + \omega _{2}A^{*} \bigr) - \xi & 0 & - \omega _{2}v^{*} \\ 0 & \mu _{1}C^{*}e^{ - \xi \tau } + \alpha _{1} & 0 & \mu _{1}y^{*}e^{ - \xi \tau } - \mu _{10} - \xi & 0 \\ 0 & 0 & \mu _{2}A^{*} & 0 & \mu _{2}v^{*} - \mu _{20} - \xi \end{vmatrix} \\ &\quad = 0, \end{aligned}$$

where

$$\begin{aligned} &b_{1} = r - \frac{2rx^{*}}{x_{m}} - \lambda _{0} - \beta _{1}v^{*},\qquad b_{2} = - \beta _{1}x^{*},\qquad b_{3} = \beta _{1}v^{*},\qquad b_{4} = - \bigl( \delta _{0} + \omega _{1}C^{*} \bigr), \\ &b_{5} = - \omega _{1}y^{*},\qquad b_{6} = N_{1}\delta _{0},\qquad b_{7} = - \bigl( \delta _{1} + \omega _{2}A^{*} \bigr),\qquad b_{8} = - \omega _{2}v^{*},\qquad b_{9} = \mu _{1}C^{*}, \\ &b_{10} = \alpha _{1},\qquad b_{11} = \mu _{1}y^{*},\qquad b_{12} = - \mu _{10},\qquad b_{13} = \mu _{2}A^{*},\qquad b_{14} = \mu _{2}v^{*} - \mu _{20}. \end{aligned}$$

This is equivalent to the following equation:

$$\begin{aligned} &\xi ^{5} + k_{1}\xi ^{4} + k_{2}\xi ^{3} + k_{3}\xi ^{2} + k_{4}\xi + k_{5} + e^{ - \xi \tau } \bigl( l_{1} \xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} \bigr) = 0, \\ &k_{1} = - b_{1} - b_{4} - b_{7} - b_{12} - b_{14}, \\ &k_{2} = b_{1}b_{12} + b_{4}b_{12} + b_{7}b_{12} + b_{12}b_{14} + b_{1}b_{4} + b_{1}b_{7} + b_{1}b_{14} + b_{4}b_{7} + b_{4}b_{14} \\ &\phantom{k_{2} = }{} + b{}_{7}b_{14} - b_{8}b_{13} + b_{2}b_{6} - b_{5}b_{10}, \\ &k_{3} = - b_{1}b_{4}b_{12} - b_{1}b_{7}b_{12} - b_{1}b_{12}b_{14} - b_{4}b_{7}b_{12} - b_{4}b_{12}b_{14} - b_{7}b_{12}b_{14} \\ &\phantom{k_{3} =}{}- b_{1}b_{4}b_{7} - b_{1}b_{4}b_{14} - b_{1}b{}_{7}b_{14} - b_{4}b_{7}b_{14} \\ &\phantom{k_{3} =}{}+ b_{1}b_{8}b_{13} + b_{8}b_{12}b_{13} - b_{1}b_{2}b_{6} - b_{2}b_{6}b_{14} - b_{2}b_{6}b_{12} + b_{1}b_{5}b_{10} + b_{5}b_{7}b_{10} \\ &\phantom{k_{3} =}{}+ b_{5}b_{10}b_{14} - b_{2}b_{3}b_{6} + b_{4}b_{8}b_{13}, \\ &k_{4} = b_{1}b_{4}b_{7}b_{12} + b_{1}b_{4}b_{12}b_{14} + b_{1}b_{7}b_{12}b_{14} + b_{4}b_{7}b_{12}b_{14} + b_{1}b_{4}b_{7}b_{14} - b_{1}b_{4}b_{8}b_{13} \\ &\phantom{k_{3} =}{}- b_{1}b_{12}b_{8}b_{13} - b_{4}b_{8}b_{12}b_{13} + b_{1}b{}_{2}b_{6}b_{14} \\ &\phantom{k_{4} =}{}+ b_{1}b_{2}b_{6}b_{12} + b_{2}b_{6}b_{12}b_{14} - b_{1}b_{5}b_{7}b_{10} - b_{1}b_{5}b_{10}b_{14} - b_{5}b_{7}b_{10}b_{14} \\ &\phantom{k_{3} =}{} + b_{5}b_{8}b_{10}b_{13} + b_{2}b_{3}b_{6}b_{14} + b_{2}b_{3}b_{6}b_{12}, \\ &k_{5} = - b_{1}b_{4}b_{7}b_{12}b_{14} + b_{1}b_{4}b_{8}b_{12}b_{13} - b_{1}b_{2}b_{6}b_{12}b_{14} + b_{1}b_{5}b_{7}b_{10}b_{14} \\ &\phantom{k_{3} =}{}- b_{1}b_{5}b_{8}b_{10}b_{13} - b_{2}b_{3}b_{6}b_{12}b_{14}, \\ &l_{1} = - b_{11}, \\ &l_{2} = b_{1}b_{11} + b_{4}b_{11} + b_{7}b_{11} + b_{11}b_{14} - b_{5}b_{9}, \\ &l_{3} = - b_{1}b_{4}b_{11} - b_{1}b_{7}b_{11} - b_{1}b_{11}b_{14} - b_{4}b_{7}b_{11} - b_{4}b_{11}b_{14} - b_{7}b_{11}b_{14} \\ &\phantom{l_{3} =}{}+ b_{8}b_{11}b_{13} - b_{2}b_{6}b_{11} + b_{1}b_{5}b_{9} + b_{5}b_{7}b_{9} + b_{5}b_{9}b_{14}, \\ &l_{4} = b_{1}b_{4}b_{7}b_{11} + b_{1}b_{4}b_{11}b_{14} + b_{1}b_{7}b_{11}b_{14} + b_{4}b_{7}b_{11}b_{14} - b_{1}b_{8}b_{11}b_{13} \\ &\phantom{l_{3} =}{} - b_{4}b_{8}b_{11}b_{13} + b_{1}b_{2}b_{6}b_{11} + b_{2}b_{6}b_{11}b_{14} - b_{1}b_{5}b_{7}b_{9} \\ &\phantom{l_{4} =}{}- b_{1}b_{5}b_{9}b_{14} - b_{5}b_{7}b_{9}b_{14} + b_{5}b_{8}b{}_{9}b_{13} + b_{2}b_{3}b_{6}b_{11}, \\ &l_{5} = - b_{1}b_{4}b_{7}b_{11}b_{14} + b_{1}b_{4}b_{8}b_{11}b_{13} - b_{1}b_{2}b_{6}b_{11}b_{14} + b_{1}b_{5}b_{7}b_{9}b_{14} \\ &\phantom{l_{3} =}{} - b_{1}b_{5}b_{8}b_{9}b_{13} - b_{2}b_{3}b_{6}b_{11}b_{14}. \end{aligned}$$
(4)

Case (i). If \(R_{0} > 1\) and \(\tau = 0 \).

If \(\tau = 0\) then equation (4) becomes

$$ \xi ^{5} + u_{1}\xi ^{4} + u_{2}\xi ^{3} + u_{3}\xi ^{2} + u_{4}\xi + u_{5} = 0. $$
(5)

Here, \(u_{1} = k_{1} + l_{1},u_{2} = k_{2} + l_{2},u_{3} = k_{3} + l_{3},u_{4} = k_{4} + l_{4},u_{5} = k_{5} + l_{5} \).

According to the Routh–Hurwitz condition (i) \(u_{i} > 0,i = 1,2,3,4,5\); (ii) \(u_{1}u_{2}u_{3} > u_{3}^{2} + u_{1}^{2}u_{4}\); (iii) \(( u_{1}u_{4} - u_{5} ) ( u_{1}u_{2}u_{3} - u_{3}^{2} - u_{1}^{2}u_{4} ) > u_{5} ( u_{1}u_{2} - u_{5} )^{2} + u_{1}u_{5}^{2}\); hence all the roots of (5) have negative real parts, and therefore the infected steady state \(I^{*}\) is locally asymptotically stable.

Case (ii). If \(\tau \ne 0 \).

If \(\tau \ne 0\) then the bifurcation parameter for the delay in immune response when analyzing the existence of Hopf bifurcations starting from infected steady state \(I^{*}\).

For \(\tau > 0\) and \(\xi = ip ( p > 0 )\), substituting it in to (4) and separating the real and imaginary parts, we get

$$ \left . \textstyle\begin{array}{l} ( l_{1}p^{4} - l_{3}p^{2} + l_{5} )\cos p\tau + ( - l_{2}p^{3} + l_{4}p )\sin p\tau = ( - k_{1}p^{4} + k_{3}p^{2} - k_{5} ) \\ ( - l_{2}p^{3} + l_{4}p )\cos p\tau - ( l_{1}p^{4} - l_{3}p^{2} + l_{5} )\sin p\tau = ( - p^{5} + k_{2}p^{3} - k_{4}p ) \end{array}\displaystyle \right \} $$
(6)

It follows from (6) that

$$ p^{10} + c_{1}p^{8} + c_{2}p^{6} + c_{3}p^{4} + c_{4}p^{2} + c_{5} = 0, $$
(7)

where

$$\begin{aligned} &c_{1} = k_{1}^{2} - 2k_{2} - l_{1}^{2},\qquad c_{2} = k_{2}^{2} + 2k_{4} - 2k_{1}k_{3} + 2l_{1}l_{3} - l_{2}^{2}, \\ &c_{3} = k_{3}^{2} + 2k_{1}k_{5} - 2k_{2}k_{4} + 2l_{2}l_{4} - 2l_{1}l_{5} - l_{3}^{2}, \\ &c_{4} = k_{4}^{2} - 2k_{3}k_{5} + 2l_{3}l_{5} - l_{4}^{2},\qquad c_{5} = k_{5}^{2} - l_{5}^{2}. \end{aligned}$$

Let \(m = p^{2}\), then equation (7) becomes

$$ m^{5} + c_{1}m^{4} + c_{2}m^{3} + c_{3}m^{2} + c_{4}m + c_{5} = 0. $$
(8)

Let \(\psi ( m ) = m^{5} + c_{1}m^{4} + c_{2}m^{3} + c_{3}m^{2} + c_{4}m + c_{5}\), since \(\lim_{m \to \infty } \psi ( m ) = + \infty \), we conclude that if \(c_{5} < 0\), then equation (8) has at least one positive root. Suppose that (8) has five positive roots. We have

$$ p_{1} = \sqrt{m_{1}},\qquad p_{2} = \sqrt{m_{2}},\qquad p_{3} = \sqrt{m_{3}},\qquad p_{4} = \sqrt{m_{4}},\qquad p_{5} = \sqrt{m_{5}}. $$

From (6) we have

$$\begin{aligned} &\tau _{k}^{ ( j )} = \frac{1}{p_{k}} \biggl\{ \arccos \biggl( \frac{a_{1}p_{k}^{8} + a_{2}p_{k}^{6} + a_{3}p_{k}^{4} + a_{4}p_{k}^{2} + a_{5}}{a_{6}p_{k}^{8} + a_{7}p_{k}^{6} + a_{8}p_{k}^{4} + a_{9}p_{k}^{2} + a_{10}} \biggr) + 2\pi j \biggr\} , \\ &\quad \quad k = 1,2,3,4,5, j = 0,1,2,\ldots; \end{aligned}$$
(9)

where

$$\begin{aligned} &a_{1} = l_{2} - k_{1}l_{1},\qquad a_{2} = k_{3}l_{1} + k_{1}l_{3} - k_{2}l_{2} - l_{4}, \\ &a_{3} = k_{4}l_{2} + k_{2}l_{4} - k_{5}l_{1} - k_{3}l_{3} - k_{1}l_{5},\qquad a_{4} = k_{5}l_{3} + k_{3}l_{5} - k_{4}l_{4}, \\ &a_{5} = - k_{5}l_{5},\qquad a_{6} = l_{1}^{2},\qquad a_{7} = l_{2}^{2} - 2l_{1}l_{3},\qquad a_{8} = l_{3}^{2} + 2l_{1}l_{5} - 2l_{2}l_{4}, \\ &a_{9} = l_{4}^{2} - 2l_{3}l_{5},\qquad a_{10} = l_{5}^{2}. \end{aligned}$$

\(\tau _{0}\) is chosen as \(\tau _{0} = \min ( \tau _{k}^{j} )\).We need to prove that \([ \frac{d ( \operatorname{Re} \xi )}{d\tau } ]_{\tau = \tau _{k}^{ ( j )}} \ne 0\).

By differentiating equation (4) with respect to τ, we get

$$\begin{aligned} & \biggl( \frac{d\xi }{d\tau } \biggr) = \frac{\xi e^{ - \xi \tau } ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} )}{5\xi ^{4} + 4k_{1}\xi ^{3} + 3k_{2}\xi ^{2} + 2k_{3}\xi + k_{4} + e^{ - \xi \tau } [ ( 4l_{1}\xi ^{3} + 3l_{2}\xi ^{2} + 2l_{3}\xi + l_{4} ) - \tau ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} ) ]}, \\ &\biggl( \frac{d\xi }{d\tau } \biggr)^{ - 1} = \frac{5\xi ^{4} + 4k_{1}\xi ^{3} + 3k_{2}\xi ^{2} + 2k_{3}\xi + k_{4}}{\xi e^{ - \xi \tau } ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} )} \\ &\phantom{\biggl( \frac{d\xi }{d\tau } \biggr)^{ - 1} =}{}+ \frac{4l_{1}\xi ^{3} + 3l_{2}\xi ^{2} + 2l_{3}\xi + l_{4}}{\xi ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} )} - \frac{\tau }{\xi }, \end{aligned}$$
(10)
$$\begin{aligned} &\biggl[ \frac{d ( \operatorname{Re} \xi )}{d\tau } \biggr]_{\tau = \tau _{k}^{ ( j )}}^{ - 1} = \operatorname{Re} \biggl[ \frac{ ( 5\xi ^{4} + 4k_{1}\xi ^{3} + 3k_{2}\xi ^{2} + 2k_{3}\xi + k_{4} )e^{\xi \tau }}{\xi ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} )} \biggr]_{\tau = \tau _{k}^{ ( j )}} \\ &\phantom{\biggl[ \frac{d ( \operatorname{Re} \xi )}{d\tau } \biggr]_{\tau = \tau _{k}^{ ( j )}}^{ - 1}=}{} + \operatorname{Re} \biggl[ \frac{4l_{1}\xi ^{3} + 3l_{2}\xi ^{2} + 2l_{3}\xi + l_{4}}{\xi ( l_{1}\xi ^{4} + l_{2}\xi ^{3} + l_{3}\xi ^{2} + l_{4}\xi + l_{5} )} \biggr]_{{\tau = \tau _{k}^{ ( j )}}}. \end{aligned}$$
(11)

Substituting \(\xi = ip\) to be the root of (4), we obtain

$$\begin{aligned} = {}&\frac{1}{\varLambda } \bigl\{ \bigl[ \bigl( 5p_{k}^{4} - 3k_{2}p_{k}^{2} + k_{4} \bigr)\cos ( p_{k}\tau _{k} ) - \sin ( p_{k}\tau _{k} ) \bigr] \bigl( l_{2}p_{k}^{4} - l_{4}p_{k}^{2} \bigr) \\ &{}+ \bigl[ \bigl( 5p_{k}^{4} - 3k_{2}p_{k}^{2} + k_{4} \bigr)\sin ( p_{k}\tau _{k} ) + \bigl( - 4k_{1}p_{k}^{3} + 2k_{3}p_{k} \bigr)\cos ( p_{k}\tau _{k} ) \bigr] \bigl( l_{1}p_{k}^{5} - l_{3}p_{k}^{3} + l_{5}p_{k} \bigr) \\ &{}+ \bigl( - 3l_{2}p_{k}^{2} + l_{4} \bigr) \bigl( l_{2}p_{k}^{4} - l_{4}p_{k}^{2} \bigr) + \bigl( - 4l_{1}p_{k}^{3} + 2l_{3}p_{k} \bigr) \bigl( l_{1}p_{k}^{5} - l_{3}p_{k}^{3} + l_{5}p_{k} \bigr) \bigr\} , \end{aligned}$$

where,

$$\begin{aligned} &\varLambda = \bigl( l_{2}p_{k}^{4} - l_{4}p_{k}^{2} \bigr)^{2} + \bigl( l_{1}p_{k}^{5} - l_{3}p_{k}^{3} + l_{5}p_{k}^{2} \bigr) \\ &\phantom{\varLambda }= \frac{1}{\varLambda } \bigl\{ \bigl( 5p_{k}^{4} - 3k_{2}p_{k}^{2} + k_{4} \bigr)p_{k} \bigl( \bigl( l_{1}p_{k}^{4} - l_{3}p_{k}^{2} + l_{5} \bigr)\cos ( p_{k}\tau _{k} ) - \bigl( l_{1}p_{k}^{4} - l_{3}p_{k}^{2} + l_{5} \bigr)\sin ( p_{k}\tau _{k} ) \bigr) \\ &\phantom{\varLambda =}{}+ \bigl( - 4k_{1}p_{k}^{3} + 2k_{3}p_{k} \bigr)p_{k} \bigl( \bigl( l_{1}p_{k}^{4} - l_{3}p_{k}^{2} + l_{5} \bigr)\cos ( p_{k}\tau _{k} ) - \bigl( l_{2}p_{k}^{3} - l_{4}p_{k} \bigr) \bigr) \\ &\phantom{\varLambda =}{}+ \bigl( - 3l_{2}p_{k}^{2} + l_{4} \bigr) \bigl( l_{2}p_{k}^{4} - l_{4}p_{k}^{2} \bigr) + \bigl( - 4l_{1}p_{k}^{3} + 2l_{3}p_{k} \bigr) \bigl( l_{1}p_{k}^{5} - l_{3}p_{k}^{3} + l_{5}p_{k} \bigr) \bigr\} \\ &\phantom{\varLambda }= \frac{1}{\varLambda } \bigl\{ \bigl( 5p_{k}^{4} - 3k_{2}p_{k}^{2} + k_{4} \bigr)p_{k} \bigl( - p_{k}^{5} + k_{2}p_{k}^{3} - k_{4}p_{k} \bigr) \\ &\phantom{\varLambda =}{}+ \bigl( - 4k_{1}p_{k}^{3} + 2k_{3}p_{k} \bigr)p_{k} \bigl( - k_{1}p_{k}^{4} + k_{3}p_{k}^{2} - k_{5} \bigr) \\ &\phantom{\varLambda =}{}+ \bigl( - 3l_{2}p_{k}^{2} + l_{4} \bigr) \bigl( l_{2}p_{k}^{4} - l_{4}p_{k}^{2} \bigr) + \bigl( - 4l_{1}p_{k}^{3} + 2l_{3}p_{k} \bigr) \bigl( l_{1}p_{k}^{5} - l_{3}p_{k}^{3} + l_{5}p_{k} \bigr) \bigr\} \\ &\phantom{\varLambda }= \frac{1}{\varLambda } \bigl\{ 5p_{k}^{10} + 4 \bigl( k_{1}^{2} - 2k_{2} - l_{1}^{2} \bigr)p_{k}^{8} + 3 \bigl( k_{2}^{2} + 2k_{4} - 2k_{1}k_{3} + 2l_{1}l_{3} - l_{2}^{2} \bigr)p_{k}^{6} \\ &\phantom{\varLambda =}{}+ 2 \bigl( k_{3}^{2} + 2k_{1}k_{5} - 2k_{2}k_{4} + 2l_{2}l_{4} - 2l_{1}l_{5} - l_{3}^{2} \bigr)p_{k}^{4} + \bigl( k_{4}^{2} - 2k_{3}k_{5} + 2l_{3}l_{5} - l_{4}^{2} \bigr) p_{k}^{2} \bigr\} \\ &\phantom{\varLambda }= \frac{1}{\varLambda } \bigl\{ 5p_{k}^{10} + 4c_{1}p_{k}^{8} + 3c_{2}p_{k}^{6} + 2c_{3}p_{k}^{4} + c_{4} p_{k}^{2} \bigr\} \\ &\phantom{\varLambda }=\frac{m_{k}}{\varLambda } \bigl\{ 5m_{k}^{4} + 4c_{1}m_{k}^{3} + 3c_{2}m_{k}^{2} + 2c_{3}m_{k} + c_{4} \bigr\} \\ &\phantom{\varLambda }= \frac{m_{k}}{\varLambda } \psi ^{1} ( m_{k} ), \\ &\operatorname{sign} \biggl[ \frac{d ( \operatorname{Re} \xi )}{d\tau } \biggr]_{\tau = \tau _{k}^{ ( j )}} = \operatorname{sign} \biggl[ \frac{d ( \operatorname{Re} \xi )}{d\tau } \biggr]^{ - 1}_{\tau = \tau _{k}^{ ( j )}} = \operatorname{sign} \biggl[ \frac{\psi ^{1} ( m_{K} )}{\varLambda } \biggr] \ne 0. \end{aligned}$$

Since \(m_{k},\varLambda > 0\) and \(\psi ^{1} ( m_{K} ) \ne 0\).

This completes the theorem. □

4 Estimation of length of delay to preserve stability

Lemma 4.1

(Nyquist criteria)

IfLis the arc length of a curve encircling the right half-plane, the curve\(\overline{P}_{J} ( L )\)will encircle the origin the number of times equal to the difference between the number of poles and the number of zeros of\(\overline{P}_{J} ( L )\)in the right half-plane.

In this section we shall try to estimate the length of delay to preserve the stability using Nyquist criteria [29–31].

We consider system (2) and the space of all real-valued continuous functions defined on \([ - \tau, \infty ) \). satisfying the initial conditions on \([ - \tau, 0 ] \).

Let \(X ( t ) = x ( t ) - x^{*},Y ( t ) = y ( t ) - y^{*},V ( t ) = v ( t ) - v^{*},W ( t ) = C ( t ) - C^{*},Z ( t ) = A ( t ) - A^{*}\).

Linearizing (3) about its steady state \(I^{*}\), we obtain

$$\begin{aligned} \begin{aligned}& \mathop{X} ^{ \bullet } ( t ) = \biggl[ - \lambda _{0} + r - \frac{2rx^{*}}{x_{m}} - \beta _{1}v^{*} \biggr]X ( t ) - \beta _{1}x^{*}V ( t ), \\ &\mathop{Y} ^{ \bullet } ( t ) = \beta _{1}v^{*}X ( t ) - \bigl( \delta _{0} + \omega _{1}C^{*} \bigr)Y ( t ) + \beta _{1}x^{*}V ( t ) - \omega _{1}y^{*}W ( t ), \\ &\mathop{V} ^{ \bullet } ( t ) = N_{1}\delta _{0}Y ( t ) - \bigl( \delta _{1} + \omega _{2}A^{*} \bigr)V ( t ) - \omega _{2}v^{*}Z ( t ), \\ &\mathop{W} ^{ \bullet } ( t ) = \alpha _{1}Y ( t ) - \mu _{10}W ( t ) + \mu _{1}C^{*}Y ( t - \tau ) + \mu _{1}y^{*}W ( t - \tau ), \\ &\mathop{Z} ^{ \bullet } ( t ) = \mu _{2}A^{*}V ( t ) + \bigl( \mu _{2}v^{*} - \mu _{20} \bigr)Z ( t ). \end{aligned} \end{aligned}$$
(12)

Let \(P_{1} = ( - \lambda _{0} + r - \frac{2rx^{*}}{x_{m}} - \beta _{1}v^{*} ),P_{2} = - \beta _{1}x^{*}\),

$$\begin{aligned} &Q_{1} = \beta _{1}v^{*},\qquad Q_{2} = - \bigl( \delta _{0} + \omega _{1}C^{*} \bigr),\qquad Q_{3} = \beta _{1}x^{*},\qquad Q_{4} = - \omega _{1}y^{*}, \\ &R_{1} = N_{1}\delta _{0},\qquad R_{2} = - \bigl( \delta _{1} + \omega _{2}A^{*} \bigr),\qquad R_{3} = - \omega _{2}v^{*}, \\ &T_{1} = \alpha _{1},\qquad T_{2} = - \mu _{10},\qquad T_{3} = \mu _{1}C^{*},\qquad T_{4} = \mu _{1}y^{*}, \\ &U_{1} = \mu _{2}A^{*}, \qquad U_{2} = \bigl( \mu _{2}v^{*} - \mu _{20} \bigr). \end{aligned}$$

Equation (12) becomes

$$\begin{aligned} \begin{aligned}& \mathop{X} ^{ \bullet } ( t ) = P_{1}X ( t ) + P_{2}V ( t ), \\ &\mathop{Y} ^{ \bullet } ( t ) = Q_{1}X ( t ) + Q_{2}Y ( t ) + Q_{3}V ( t ) + Q_{4}W(t), \\ &\mathop{V} ^{ \bullet } ( t ) = R_{1}Y ( t ) + R_{2}V ( t ) + R_{3}Z ( t ), \\ &\mathop{W} ^{ \bullet } ( t ) = T_{1}Y ( t ) + T_{2}W ( t ) + T_{3}Y ( t - \tau ) + T_{4}W ( t - \tau ), \\ &\mathop{Z} ^{ \bullet } ( t ) = U_{1}V ( t ) + U_{2}Z ( t ). \end{aligned} \end{aligned}$$
(13)

Taking the Laplace transform on both sides of (13), we obtain

$$\begin{aligned} &sL \bigl[ X ( t ) \bigr] - X ( 0 ) = P_{1}L \bigl[ X ( t ) \bigr] + P_{2}L \bigl[ V ( t ) \bigr], \\ &L \bigl[ Y ( t ) \bigr] - Y ( 0 ) = Q_{1}L \bigl[ X ( t ) \bigr] + Q_{2}L \bigl[ Y ( t ) \bigr] + Q_{3}L \bigl[ V ( t ) \bigr] + Q_{4} L \bigl[ W ( t ) \bigr], \\ &sL \bigl[ V ( t ) \bigr] - V ( 0 ) = R_{1}L \bigl[ Y ( t ) \bigr] + R_{2}L \bigl[ V ( t ) \bigr] + R_{3}L \bigl[ Z ( t ) \bigr], \\ &sL \bigl[ W ( t ) \bigr] - W ( 0 ) = T_{1}L \bigl[ Y ( t ) \bigr] + T_{2}L \bigl[ W ( t ) \bigr] + T_{3}e^{ - s\tau } L \bigl[ Y ( t ) \bigr] + T_{3}e^{ - s\tau } K_{1} ( s ) \\ &\phantom{sL \bigl[ W ( t ) \bigr] - W ( 0 ) =}{}+ T_{4}e^{ - s\tau } L \bigl[ W ( t ) \bigr] + T_{4}e^{ - s\tau } K_{2} ( s ), \\ &sL \bigl[ Z ( t ) \bigr] - Z ( 0 ) = U_{1}L \bigl[ V ( t ) \bigr] + U_{2}L \bigl[ Z ( t ) \bigr], \end{aligned}$$

where \(K_{1} ( s ) = \int _{ - \tau }^{0} e^{ - st}Y ( t ) \,dt, K_{2} ( s ) = \int _{ - \tau }^{0} e^{ - st}W ( t ) \,dt\).

The local asymptotic stability of the infected steady state \(I^{*}\) according to the Nyquist criterion is given by

$$\begin{aligned} &\operatorname{Im} H ( i\rho _{0} ) > 0, \end{aligned}$$
(14)
$$\begin{aligned} &\operatorname{Re} H ( i\rho _{0} ) = 0, \end{aligned}$$
(15)

where \(\rho _{0}\) is the smallest positive root of (15) and

$$ H ( s ) = s^{5} + k_{1}s^{4} + k_{2}s^{3} + k_{3}s^{2} + k_{4}s + k_{5} + e^{ - s\tau } \bigl( l_{1}s^{4} + l_{2}s^{3} + l_{3}s^{2} + l_{4}s + l_{5} \bigr). $$

From (14) and (15) we have

$$\begin{aligned} &k_{1}\rho _{0}^{4} - k_{3}\rho _{0}^{2} + k_{5} = - \bigl( l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr)\cos ( \rho _{0}\tau ) - \bigl( - l_{2}\rho _{0}^{3} + l_{4}\rho _{0} \bigr)\sin ( \rho _{0}\tau ), \end{aligned}$$
(16)
$$\begin{aligned} &\rho _{0}^{5} - k_{2}\rho _{0}^{3} + k_{4}\rho _{0} > \bigl( l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr)\sin ( \rho _{0} \tau ) - \bigl( - l_{2}\rho _{0}^{3} + l_{4}\rho _{0} \bigr) \cos ( \rho _{0}\tau ). \end{aligned}$$
(17)

Conditions (16) and (17) are the smallest conditions to ensure stability. We will use these to obtain an estimate of the length of delay. Our goal is to find an upper bound \(\rho _{ +} \) on \(\rho _{0}\), independent of τ, and we estimate τ equation (17) holds for all values of \(\rho _{0}\), \(0 < \rho _{0} < \rho _{ +} \). Maximizing the R.H.S of (16)

Subject to \(\vert \cos ( \rho _{0}\tau ) \vert \le 1\) and \(\vert \sin ( \rho _{0}\tau ) \vert \le 1\), we obtain

$$\begin{aligned} k_{1}\rho _{0}^{4} \le k_{3}\rho _{0}^{2} - k_{5} + \vert l_{1} \vert \rho _{0}^{4} + \vert l_{3} \vert \rho _{0}^{2} + \vert l_{5} \vert + \vert l_{2} \vert \rho _{0}^{3} + \vert l_{4} \vert \rho _{0}. \end{aligned}$$
(18)

It is clear that \(\rho _{0} \le \rho _{ +} \), where \(\rho _{ +} \) is the least positive root of (18).

From (17) we have

$$\begin{aligned} \rho _{0}^{4} >{}& k_{2}\rho _{0}^{2} - k_{4} + l_{1}\rho _{0}^{3}\sin ( \rho _{0}\tau ) - l_{3}\rho _{0}\sin ( \rho _{0}\tau ) + l_{5}\frac{\sin ( \rho _{0}\tau )}{\rho _{0}} \\ &{}+ l_{1}\rho _{0}^{2}\cos ( \rho _{0} \tau ) - l_{4}\cos ( \rho _{0}\tau ). \end{aligned}$$
(19)

Substituting (16) into (19) yields

$$\begin{aligned} & \bigl( k_{1}l_{1}\rho _{0}^{2} - k_{1}l_{4} + l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr) \bigl( \cos ( \rho _{0}\tau ) - 1 \bigr) \\ &\qquad{}+ \biggl( k_{1}l_{1} \rho _{0}^{3} - k_{1}l_{3}\rho _{0} + \frac{k_{1}l_{5}}{\rho _{0}} - l_{2}\rho _{0}^{3} + l_{4}\rho _{0} \biggr)\sin ( \rho _{0}\tau ) \\ &\quad < ( - l_{1} )\rho _{0}^{3} + ( k_{3} - k_{1}k_{2} - k_{1}l_{1} + l_{3} )\rho _{0}^{2} + ( k_{1}k_{4} - k_{5} - l_{5} + k_{1}l_{4} ). \end{aligned}$$
(20)

By using the bounds

$$\begin{aligned} &\mathrm{(i)}\quad \bigl( k_{1}l_{1}\rho _{0}^{2} - k_{1}l_{4} + l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr) \bigl( \cos ( \rho _{0}\tau ) - 1 \bigr) \\ &\phantom{\mathrm{(i)}\quad}\quad= \bigl( k_{1}l_{1}\rho _{0}^{2} - k_{1}l_{4} + l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr) 2 \sin ^{2} \biggl( \frac{\rho _{0}\tau }{2} \biggr) \\ &\phantom{\mathrm{(i)}\quad}\quad< 2 \bigl( k_{1}l_{1}\rho _{0}^{2} - k_{1}l_{4} + l_{1}\rho _{0}^{4} - l_{3}\rho _{0}^{2} + l_{5} \bigr) \biggl( \frac{\rho _{0}\tau }{2} \biggr)^{2} \\ &\phantom{\mathrm{(i)}\quad}\quad< \frac{1}{2} \bigl( l_{1}\rho _{0}^{6} + ( k_{1}l_{1} - l_{3} )\rho _{0}^{4} + ( l_{5} - k_{1}l_{4} )\rho _{0}^{2} \bigr)\tau ^{2}. \\ &\mathrm{(ii)}\quad \biggl( k_{1}l_{1}\rho _{0}^{3} - k_{1}l_{3}\rho _{0} + \frac{k_{1}l_{5}}{\rho _{0}} - l_{2}\rho _{0}^{3} + l_{4}\rho _{0} \biggr)\sin ( \rho _{0}\tau ) \\ &\phantom{\mathrm{(ii)}\quad}\quad < \biggl( k_{1}l_{1}\rho _{0}^{3} - k_{1}l_{3}\rho _{0} + \frac{k_{1}l_{5}}{\rho _{0}} - l_{2}\rho _{0}^{3} + l_{4}\rho _{0} \biggr)\rho _{0}\tau \\ &\phantom{\mathrm{(ii)}\quad}\quad < \bigl( ( k_{1}l_{1} - l_{2} )\rho _{0}^{4} + ( l_{4} - k_{1}l_{3} )\rho _{0}^{2} + k_{1}l_{5} \bigr)\tau. \end{aligned}$$

In (20) we obtain \(B_{1}\tau ^{2} + B_{2}\tau < B_{3}\), where

$$\begin{aligned} &B_{1} = \frac{1}{2} \bigl( l_{1}\rho _{0}^{6} + ( k_{1}l_{1} - l_{3} )\rho _{0}^{4} + ( l_{5} - k_{1}l_{4} )\rho _{0}^{2} \bigr), \\ &B_{2} = ( k_{1}l_{1} - l_{2} )\rho _{0}^{4} + ( l_{4} - k_{1}l_{3} )\rho _{0}^{2} + k_{1}l_{5}, \\ &B_{3} = - l_{1}\rho _{0}^{3} + ( k_{3} - k_{1}k_{2} - k_{1}l_{1} + l_{3} ) \rho _{0}^{2} + ( k_{1}k_{4} - k_{5} - l_{5} + k_{1}l_{4} ). \end{aligned}$$

Hence if \(\tau _{ +} = \frac{ - B_{2} + \sqrt{B_{2}^{2} + 4B_{1}B_{3}}}{2B_{1}}\), then the stability is preserved for \(0 < \tau < \tau _{ +} \). Therefore, we get Theorem 4.1.

Theorem 4.1

If there exists a delay in\(0 < \tau < \tau _{ +} \)such that\(B_{1}\tau ^{2} + B_{2}\tau < B_{3}\), then\(\tau _{ +} \)is locally asymptotically stable, the delay length for the infected steady state\(I^{*}\).

5 Results and discussion

We exhibit some numerical assumptions with respect to our hypothetical investigation which are done in MATLAB. Using the following parameter values

$$\begin{aligned} &\lambda = 10,\qquad \lambda _{0} = 0.055,\qquad \delta _{0}^{1} = 0.24,\qquad \delta _{1} = 3,\qquad \beta = 0.002,\qquad \alpha _{0} = 0.265, \\ &\alpha _{1}^{1} = 0.01,\qquad \mu _{10} = 0.755,\qquad \mu _{20} = 0.1,\qquad \mu _{1} = 0.03,\qquad \mu _{2} = 0.01, \qquad \eta _{r} = 0.57, \\ &\eta _{p} = 0.38,\qquad \omega _{1} = 0.05, \qquad \omega _{2} = 0.5,\qquad N = 100,\qquad x_{m} = 1500,\qquad r = 0.3, \end{aligned}$$

we get the infected steady state \(I^{*} ( x^{*},y^{*},v^{*},C^{*},A^{*} )=(1222.89, 21.8376, 10, 4.4869, 63.6732)\). From (8) and (9) we obtain \(\tau _{0} = 1.102\) and \(R_{0} = 21.7348 > 1\). In case that the delay moderately increases from zero, at that point the infected steady state \(I^{*}\) is locally asymptotically stable for \(\tau \in [ 0,\tau _{0} )\) (by Theorem 3.1) which is outlined in Fig. 1. In any case, the delay crosses the critical value \(\tau _{0} = 1.102\),the infected steady state \(I^{*}\) loses stability and undergoes Hopf bifurcation, which is illustrated in Fig. 2. The proposed demonstration suggests that as the response of antibody often evolves as possible in free virus response, then the level of non-infected CD4+ T-cells increases with a time delay as shown in Figs. 3 and 4.In the meantime, the level of infected CD4+ T-cells and free virus decreases as shown in Figs. 5 and 6.

Figure 1
figure 1

The phase diagrams of system (2) being asymptotically stable when \(\tau = 0.9\)

Full size image
Figure 2
figure 2

The phase diagrams of system (2) undergoing Hopf bifurcation when \(\tau = 1.2\)

Full size image
Figure 3
figure 3

The phase diagram shows that the neutralizing antibody converges to a certain extent after the regulation of free viruses and infected cells

Full size image
Figure 4
figure 4

The phase diagram shows an increased number of non-infected CD4+ T-cells, while the antibody neutralization response is increasing

Full size image
Figure 5
figure 5

The phase diagram demonstrates that the neutralization of the antibody regulates the infected cells as antibody neutralization increases

Full size image
Figure 6
figure 6

The phase diagram shows that when neutralization of antibody response increases and the free virus level converges to zero, the free virus is neutralized

Full size image

6 Conclusion

In this study, the dynamics of an HIV infection model were analyzed and described by comprising the CTL response delay according to mathematical analysis. We have shown that the reproduction ratio \(R_{0}\) plays a crucial role for inferring this model dynamics. The calculation of \(R_{0}\) in an infectious disease transmitted by blood or sex is more complicated. Several mathematical models have been proposed to explain the rate of spread of the infection. An account should be taken of the window period and HIV pathophysiology. Better integration of modeling into the decision-making process is desirable to improve the effectiveness of interventions and the knowledge of health professionals [32].

Both the viral free steady state and the infected steady state of the HIV model are ascertained. If \(R_{0} < 1\) then the viral free steady state is locally asymptotically stable, and if \(R_{0} > 1\) then infected steady state is locally asymptotically stable in absence of delay. Based on the model of differential delay, we evaluate Hopf bifurcation requirements using time delay as the bifurcation parameter. This shows that a positive steady state is locally asymptotically stable when the time delay is relatively small, whereas a Hopf bifurcation may cause a loss of stability as the delay increases. Using the Nyquist test, we also get that the maximum delay value to the infected steady State \(I^{*}\) will remain asymptomatically stable. Finally, it can be concluded that an antibody immune reaction and the combination of drug efficacy are important to reduce the potential for HIV infections through numerical simulations. Maintaining stability may be the goal to prolonging patient survival, but exposes them to transmission risk. It is interesting to know the duration of the asymptotic period for subsequent consequent clinical evaluations. Dynamic HIV transmission models can provide evidence-based guidance on optimal combination implementation strategies to treat and prevent HIV/AIDS [33].