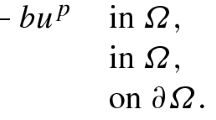1 Introduction and main results

Given \(p \in(1,\infty)\), \(s \in(0,1)\), \(\mu\in(0,N)\), \(N > sp\), we consider the problem

$$ \textstyle\begin{cases} (- \Delta)_{p}^{s} u = \lambda \vert u \vert ^{p-2} u + (\int_{\Omega}\frac{ \vert u \vert ^{p_{\mu,s}^{*}}}{ \vert x-y \vert ^{\mu}}\,dy ) \vert u \vert ^{p_{\mu,s}^{*}-2}u, & \text{in } \Omega,\\ u = 0, & \text{in } \mathbb {R}^{N} \setminus\Omega, \end{cases} $$
(1)

where \(p_{\mu,s}^{\ast}= \frac{(N-\frac{\mu}{2})p}{N-sp}\) and Ω is a bounded domain in \(\mathbb {R}^{N}\) with Lipschitz boundary. \((- \Delta)_{p}^{s}\) is the associated fractional operator which, up to a normalization constant, is defined as

$$(- \Delta)_{p}^{s} u(x) = 2 \lim_{\varepsilon \searrow0} \int_{\mathbb {R}^{N} \setminus B_{\varepsilon }(x)} \frac{ \vert u(x) - u(y) \vert ^{p-2} (u(x) - u(y))}{ \vert x - y \vert ^{N+sp}} \,dy, \quad x \in \mathbb {R}^{N}. $$

This definition is consistent with the usual definition of the linear fractional Laplacian operator \((- \Delta)^{s}\) when \(p = 2\). Recently, much attention has been paid to the problems involving nonlocal operators, and we may refer to [2, 12, 15, 18, 32, 36–38] for more details. In particular, fractional p-eigenvalue problems have been studied in [4, 6, 8, 16, 17, 19, 20, 29], and existence theories in the critical case in [1, 13, 21–25, 30, 33].

On the other hand, Equation (1) is also related to the so-called Choquard equation which is inspired by the following Hardy–Littlewood–Sobolev inequality:

$$ \int_{\mathbb {R}^{N}} \int_{\mathbb {R}^{N}}\frac{ \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}}}{ \vert x-y \vert ^{\mu}} \,dx \,dy\leq\widetilde{C}(N,\mu , s, p) \biggl( \int_{\mathbb {R}^{N}} \vert u \vert ^{p_{s}^{\ast}}\,dx \biggr)^{\frac{2p_{\mu ,s}^{\ast}}{p_{s}^{\ast}}}, $$

where \(p_{s}^{\ast}= \frac{Np}{N-sp}\). For more details about fractional Choquard equations, we refer the readers to [5, 9, 11, 24, 34, 35]. Very recently, Mukherjee and Sreenadh [24] have obtained the following multiplicity result, extending the results in [10] in the local case, for the Brezis–Nirenberg type problem of semilinear fractional Choquard equation:

$$ \textstyle\begin{cases} (- \Delta)^{s} u = (\int_{\Omega}\frac{ \vert u \vert ^{2_{\mu ,s}^{*}}}{ \vert x-y \vert ^{\mu}}\,dy ) \vert u \vert ^{2_{\mu,s}^{*}-2}u+\lambda u, & \text{in } \Omega,\\ u = 0, & \text{in } \mathbb {R}^{N} \setminus\Omega, \end{cases} $$
(2)

where Ω is a bounded domain with Lipschitz boundary in \(\mathbb {R}^{N}\), \(N>2s\), \(0< s<1\), \(2_{\mu,s}^{*}= \frac{2N-\mu}{N-2s}\), and \(\lambda >0\) is a parameter. Let \(0 < \lambda_{1} < \lambda_{2} \le\lambda_{3} \le\cdots\to+ \infty \) be the eigenvalues of the problem

$$\textstyle\begin{cases} (- \Delta)^{s} u = \lambda u, & \text{in } \Omega,\\ u = 0, & \text{in } \mathbb {R}^{N} \setminus\Omega. \end{cases} $$

There exists a constant \(\lambda^{*}\) such that if there are q number of eigenvalues lying between λ and \(\lambda+\lambda^{*}\), then problem (2) has q distinct pairs of solutions (see [24, Theorem 2.6]).

In this paper, we use a more general construction based on sublevel sets as in Perera and Szulkin [31] (see also Perera et al. [28, Proposition 3.23]) and extend the above multiplicity result to the quasilinear nonlocal problem (1). However, the standard sequence of variational eigenvalues of \((- \Delta )_{p}^{s}\) based on the genus does not provide enough information about the structure of the sublevel sets to implement the linking construction. Therefore we use a different sequence of eigenvalues as in Iannizzotto et al. [14] that is based on the \(\mathbb {Z}_{2}\)-cohomological index of Fadell and Rabinowitz [7], which is defined as follows.

Definition 1.1

Let W be a Banach space, and let \({\mathcal {A}}\) denote the class of symmetric subsets of \(W \setminus \{{0} \}\). For \(A \in {\mathcal {A}}\), let \(\overline{A} = A/\mathbb {Z}_{2}\) be the quotient space of A with each u and −u identified, let \(f : \overline{A} \to \mathbb {R}\mathrm{P}^{\infty}\) be the classifying map of A̅, and let \(f^{\ast}: H^{\ast}(\mathbb {R}\mathrm{P}^{\infty}) \to H^{\ast}(\overline{A})\) be the induced homomorphism of the Alexander–Spanier cohomology rings. The cohomological index of A is defined by

$$i(A) = \textstyle\begin{cases} \sup \{{m \ge1 : f^{\ast}(\omega^{m-1}) \ne0} \}, & A \ne \emptyset ,\\ 0, & A = \emptyset, \end{cases} $$

where \(\omega\in H^{1}(\mathbb {R}\mathrm{P}^{\infty})\) is the generator of the polynomial ring \(H^{\ast}(\mathbb {R}\mathrm{P}^{\infty}) = \mathbb {Z}_{2}[\omega]\).

For instance, the classifying map of the unit sphere \(S^{m-1}\) in \(\mathbb {R}^{m}\), \(m \ge1\) is the inclusion \(\mathbb {R}\mathrm{P}^{m-1} \subset \mathbb {R}\mathrm{P}^{\infty}\), which induces isomorphisms on \(H^{q}\) for \(q \le m - 1\), so \(i(S^{m-1}) = m\).

Define the so-called Gagliardo seminorm by

$$[u]_{s,p} = \biggl( \int_{\mathbb {R}^{2N}} \frac{ \vert u(x) - u(y) \vert ^{p}}{ \vert x - y \vert ^{N+sp}} \,dx \,dy \biggr)^{1/p}, $$

where \(u : \mathbb {R}^{N} \to \mathbb {R}\) is a measurable function, and give the fractional Sobolev space by

$$W^{s,p}\bigl(\mathbb {R}^{N}\bigr) = \bigl\{ {u \in L^{p} \bigl(\mathbb {R}^{N}\bigr) : [u]_{s,p} < \infty} \bigr\} , $$

which can be equipped with the norm

$$\Vert u \Vert _{s,p} = \bigl( \vert u \vert _{p}^{p} + [u]_{s,p}^{p} \bigr)^{1/p}, $$

where \(|\cdot|_{p}\) is the norm in \(L^{p}(\mathbb {R}^{N})\) (see Di Nezza et al. [26] for details). We work in the closed linear subspace

$$X_{p}^{s}(\Omega) = \bigl\{ {u \in W^{s,p}\bigl( \mathbb {R}^{N}\bigr) : u = 0 \text{ a.e. in } \mathbb {R}^{N} \setminus\Omega} \bigr\} , $$

equivalently renormed by setting \(\|\cdot\|_{s,p} = [\cdot]_{s,p}\) (see [26, Theorem 7.1]), which is a uniformly convex Banach space. By [26, Theorem 6.5 and Corollary 7.2], the embedding \(X_{p}^{s}(\Omega) \hookrightarrow L^{r}(\Omega)\) is continuous for \(r \in[1,p_{s}^{\ast}]\) and compact for \(r \in[1,p_{s}^{\ast})\).

The Dirichlet spectrum of \((- \Delta)_{p}^{s}\) in Ω consists of those \(\lambda\in \mathbb {R}\) for which the problem

$$ \textstyle\begin{cases} (- \Delta)_{p}^{s} u = \lambda \vert u \vert ^{p-2} u, & \text{in } \Omega ,\\ u = 0, & \text{in } \mathbb {R}^{N} \setminus\Omega, \end{cases} $$
(3)

has a nontrivial solution. We will use a suitable minimax scheme to define an incremental and unbounded sequence of variational eigenvalues. The standard scheme based on the genus is not applicable here, so we will use the following scheme based on the cohomological index introduced in Iannizzotto et al. [14] (see also Perera [27]). Let

$$\Psi(u) = \frac{1}{ \vert u \vert _{p}^{p}}, \quad u \in {\mathcal {M}}= \bigl\{ {u \in X_{p}^{s}( \Omega) : \Vert u \Vert _{s,p} = 1} \bigr\} . $$

Then eigenvalues of problem (3) are consistent with critical values of Ψ. We use the standard notation

$$\Psi^{a} = \bigl\{ {u \in {\mathcal {M}}: \Psi(u) \le a} \bigr\} , \qquad \Psi_{a} = \bigl\{ {u \in {\mathcal {M}}: \Psi(u) \ge a} \bigr\} , \quad a \in \mathbb {R}$$

for the sublevel sets and superlevel sets, respectively. Let \({\mathcal {F}}\) denote the class of symmetric subsets of \({\mathcal {M}}\), and let

$$\lambda_{k} := \inf_{M \in {\mathcal {F}}, i(M) \ge k} \sup_{u \in M} \Psi (u), \quad k \in \mathbb {N}^{+}. $$

Then \(0 < \lambda_{1} < \lambda_{2} \le\lambda_{3} \le\cdots\to+ \infty\) is a sequence of eigenvalues of problem (3), and

$$ \lambda_{k} < \lambda_{k+1}\quad \implies\quad i\bigl( \Psi^{\lambda_{k}}\bigr) = i({\mathcal {M}}\setminus\Psi_{\lambda_{k+1}}) = k $$
(4)

(see Iannizzotto et al. [14, Proposition 2.4]). Making essential use of the index information in (4), we will prove the following theorem:

Let

$$C_{H,L}:=\sup_{u \in X_{p}^{s}(\Omega) \setminus \{{0} \} }\frac { \vert u \vert _{p_{s}^{*}}}{ (\int_{\Omega}\int_{\Omega}\frac{ \vert u(x) \vert ^{p_{\mu ,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}} }{ \vert x-y \vert ^{\mu}}\,dx \,dy )^{\frac{1}{2p_{\mu,s}^{\ast}}}} \quad (\mbox{see Lemma 2.2 below}), $$

and

$$ S_{H,L}:= \inf_{u \in X_{p}^{s}(\Omega) \setminus \{{0} \}} \frac { \Vert u \Vert _{s,p}^{p}}{ (\int_{\Omega}\int_{\Omega}\frac { \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}} }{ \vert x-y \vert ^{\mu}}\,dx \,dy )^{\frac{p}{2p_{\mu,s}^{\ast}}}}. $$

Theorem 1.2

  1. (i)

    If

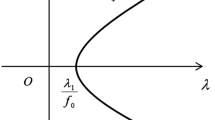
    $$\lambda_{1} - \frac{S_{H,L}}{ \vert {\Omega} \vert ^{\frac {sp}{N}}C_{H,L}^{p}}< \lambda< \lambda_{1}, $$

    then problem (1) has a pair of nontrivial solutions \(\pm u^{\lambda}\) such that \(u^{\lambda}\to0\) as \(\lambda\nearrow\lambda_{1}\).

  2. (ii)

    If \(\lambda_{k} \le\lambda< \lambda_{k+1} = \cdots= \lambda_{k+m} < \lambda_{k+m+1}\) for some \(k, m \in \mathbb {N}^{+}\) and

    $$ \lambda> \lambda_{k+1} - \frac{S_{H,L}}{ \vert {\Omega} \vert ^{\frac {sp}{N}}C_{H,L}^{p}}, $$
    (5)

    then problem (1) has m distinct pairs of nontrivial solutions \(\pm u^{\lambda}_{j}\), \(j = 1,\dots,m\), such that \(u^{\lambda}_{j} \to0\) as \(\lambda\nearrow\lambda_{k+1}\).

Corollary 1.3

Problem (1) has a nontrivial solution for all \(\lambda\in \bigcup_{k=1}^{\infty}(\lambda_{k} - \frac{S_{H,L}}{ \vert {\Omega} \vert ^{\frac{sp}{N}}C_{H,L}^{p}},\lambda_{k} )\).

We note that \(\lambda_{1} \ge\frac{S_{H,L}}{ \vert {\Omega} \vert ^{\frac {sp}{N}}C_{H,L}^{p}}\). Indeed, if \(\varphi_{1}\) is an eigenfunction associated with \(\lambda_{1}\),

$$\lambda_{1} = \frac{ \Vert \varphi_{1} \Vert _{s,p}^{p}}{ \vert \varphi_{1} \vert _{p}^{p}} \ge\frac{S_{H,L} (\int_{\Omega}\int_{\Omega}\frac { \vert \varphi_{1}(x) \vert ^{p_{\mu,s}^{\ast}} \vert \varphi_{1}(y) \vert ^{p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}}\,dx \,dy )^{\frac{p}{2p_{\mu,s}^{\ast}}}}{ \vert \varphi_{1} \vert _{p}^{p}} \ge \frac{S_{H,L}}{ \vert {\Omega} \vert ^{\frac {sp}{N}}C_{H,L}^{p}} $$

by the Hölder inequality.

2 Preliminaries and some known results

The following Hardy–Littlewood–Sobolev inequality is essential to applying the variational approach for problem (1).

Lemma 2.1

([19, Theorem 4.3])

Assume \(1< r\), \(t<\infty\), and \(0<\mu<N\) with \(\frac{1}{r}+\frac {1}{t}+\frac{\mu}{N}=2\). If \(u\in L^{r}(\mathbb {R}^{N})\) and \(v\in L^{t}(\mathbb {R}^{N})\), then there exists \(C(N,\mu,r,t)>0\) such that

$$ \int_{\mathbb {R}^{N}} \int_{\mathbb {R}^{N}}\frac{ \vert u(x) \vert \vert v(y) \vert }{ \vert x-y \vert ^{\mu}} \,dx \,dy\leq C(N,\mu,r,t) \vert u \vert _{r} \vert v \vert _{t}. $$

By the Hardy–Littlewood–Sobolev inequality, there exists \(\widetilde {C}(N,\mu, s, p)>0\) such that

$$ \int_{\mathbb {R}^{N}} \int_{\mathbb {R}^{N}}\frac{ \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}}}{ \vert x-y \vert ^{\mu}} \,dx \,dy\leq\widetilde{C}(N,\mu , s, p) \vert u \vert _{{p_{s}^{\ast}}}^{2p_{\mu,s}^{\ast}} $$
(6)

for all \(u\in X_{p}^{s}(\Omega)\). Hence, by the Sobolev embedding,

$$ \int_{\mathbb {R}^{N}} \int_{\mathbb {R}^{N}}\frac{ \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}}}{ \vert x-y \vert ^{\mu}} \,dx \,dy\leq C(N,\mu,s,p) \Vert u \Vert _{s,p}^{2p_{\mu,s}^{\ast}}, $$

for some \(C(N,\mu,s,p)>0\). Define

$$ S_{H,L} = \inf_{u \in X_{p}^{s}(\Omega) \setminus \{{0} \}} \frac { \Vert u \Vert _{s,p}^{p}}{ (\int_{\Omega}\int_{\Omega}\frac { \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast}} }{ \vert x-y \vert ^{\mu}}\,dx \,dy )^{\frac{p}{2p_{\mu,s}^{\ast}}}}. $$
(7)

Clearly, \(S_{H,L}>0\).

Now we can introduce the \(C^{1}\)- functional associated with problem (1) by

$$I_{\lambda}(u) = \frac{1}{p} \Vert u \Vert _{s,p}^{p} - \frac{\lambda}{p} \vert u \vert _{p}^{p} - \frac{1}{2p_{\mu,s}^{\ast}} \int_{\Omega}\int _{\Omega}\frac{ \vert u(x) \vert ^{p_{\mu,s}^{\ast}} \vert u(y) \vert ^{p_{\mu,s}^{\ast }} }{ \vert x-y \vert ^{\mu}}\,dx \,dy, \quad u \in X_{p}^{s}(\Omega). $$

Moreover, u is a weak solution of problem (1) if and only if u is a critical point of functional \(I_{\lambda}\).

Let

$$ \Vert u \Vert _{o}:= \biggl( \int_{\Omega} \int_{\Omega}\frac { \vert u(x) \vert ^{p_{\mu,s}^{*}} \vert u(y) \vert ^{p_{\mu,s}^{*}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{\frac{1}{2p_{\mu,s}^{\ast}}} $$

for \(u\in L^{p_{s}^{*}}(\Omega)\), we have the following lemma.

Lemma 2.2

There exists \(C_{H,L}>0\) such that \(|u|_{p_{s}^{*}}\leq C_{H,L}\|u\|_{o}\).

Proof

Let u, \(v\in L^{p_{s}^{*}}(\Omega)\), then using the Hölder inequality and the semigroup property of Riesz potential, we get

$$\begin{aligned} & \int_{\Omega} \int_{\Omega}\frac{ \vert (u+v)(x) \vert ^{p_{\mu,s}^{\ast}} \vert (u+v)(y) \vert ^{p_{\mu,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy\\ &\quad = \int_{\Omega } \int_{\Omega}\frac{ \vert (u+v)(x) \vert ^{2p_{\mu,s}^{\ast}} }{ \vert x-y \vert ^{\mu }} \,dx \,dy \\ &\quad \leq \int_{\Omega} \int_{\Omega}\frac{ \vert u(x) \vert \vert (u+v)(x) \vert ^{2p_{\mu,s}^{\ast}-1} }{ \vert x-y \vert ^{\mu}} \,dx \,dy+ \int_{\Omega } \int_{\Omega}\frac{ \vert v(x) \vert \vert (u+v)(x) \vert ^{2p_{\mu,s}^{\ast}-1} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \\ &\quad \leq \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert u(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{\frac{1}{2p_{\mu ,s}^{\ast}}} \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert (u+v)(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{1-\frac{1}{2p_{\mu ,s}^{\ast}}} \\ &\qquad {}+ \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert v(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{\frac{1}{2p_{\mu ,s}^{\ast}}} \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert (u+v)(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{1-\frac{1}{2p_{\mu ,s}^{\ast}}} \\ &\quad = \biggl( \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert u(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{\frac{1}{2p_{\mu ,s}^{\ast}}} + \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert v(x) \vert ^{2p_{\mu,s}^{\ast }} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{\frac{1}{2p_{\mu,s}^{\ast }}} \biggr) \\ &\qquad {}\times \biggl( \int_{\Omega} \int_{\Omega}\frac{ \vert (u+v)(x) \vert ^{2p_{\mu ,s}^{\ast}} }{ \vert x-y \vert ^{\mu}} \,dx \,dy \biggr)^{1-\frac{1}{2p_{\mu ,s}^{\ast}}}. \end{aligned}$$

So, we have \(\|u+v\|_{o}\leq\|u\|_{o}+\|v\|_{o}\) and other properties of the norm are also satisfied by \(\|\cdot\|_{o}\). So, \(\|\cdot\|_{o}\) is a norm on \(L^{p_{s}^{*}}(\Omega)\) and \(L^{p_{s}^{*}}(\Omega)\) is a Banach space under this norm. From (6), we have

$$ \Vert u \Vert _{o}\leq\widetilde{C}(N,\mu, s, p)^{\frac{1}{2p_{\mu ,s}^{\ast}}} \vert u \vert _{p_{s}^{*}}. $$

So, the identity map from \((L^{p_{s}^{*}}(\Omega),\|\cdot\|_{o})\) to \((L^{p_{s}^{*}}(\Omega),|\cdot|_{p_{s}^{\ast}})\) is linear and bounded. Thus, by open mapping theorem, we obtain \(\|\cdot\|_{o}\) is a norm equivalent to the standard norm \(|\cdot|_{p_{s}^{*}}\) on \(L^{p_{s}^{*}}(\Omega )\). So we have \(|u|_{p_{s}^{*}}\leq C_{H,L}\|u\|_{o}\). □

Definition 2.3

([3])

Let \({\mathcal {A}}^{\ast}\) denote the class of symmetric subsets of W, let \(r > 0\), let \(S_{r} = \{{u \in W : \|u\|_{s,p} = r} \}\), let \(0 < b \le+ \infty\), and let Γ denote the group of odd homeomorphisms of W that are the identity outside \(Ij^{-1}(0,b)\). The pseudo-index of \(M \in {\mathcal {A}}^{\ast}\) related to i, \(S_{r}\), and Γ is defined by

$$i^{\ast}(M) = \min_{\gamma\in\Gamma} i\bigl(\gamma(M) \cap S_{r}\bigr), $$

where i is in Definition 1.1.

The following is a general critical point theorem based on a pseudo-index related to the cohomological index which we apply here (see also Perera et al. [28, Proposition 3.44]).

Lemma 2.4

([30])

Let \(A_{0}\), \(B_{0}\) be symmetric subsets of \(S_{1}\) such that \(A_{0}\) is compact, \(B_{0}\) is closed, and

$$i(A_{0}) \ge k + m, \qquad i(S_{1} \setminus B_{0}) \le k $$

for some integers \(k \ge0\) and \(m \ge1\). Assume that there exists \(R > r\) such that

$$\sup I(A) \le0 < \inf I(B), \qquad\sup I(X) < b, $$

where \(A = \{{Ru : u \in A_{0}} \}\), \(B = \{{ru : u \in B_{0}} \}\), and \(X = \{{tu : u \in A, 0 \le t \le1} \}\). For \(j = k + 1,\dots,k + m\), let

$${\mathcal {A}}_{j}^{\ast}= \bigl\{ {M \in {\mathcal {A}}^{\ast}: M \textit{ is compact and } i^{\ast}(M) \ge j} \bigr\} $$

and set

$$c_{j}^{\ast}:= \inf_{M \in {\mathcal {A}}_{j}^{\ast}} \max _{u \in M} I(u). $$

Then

$$\inf I(B) \le c_{k+1}^{\ast}\le\dotsb\le c_{k+m}^{\ast}\le\sup I(X), $$

in particular, \(0 < c_{j}^{\ast}< b\). If, in addition, I satisfies the \((\mathrm{PS})_{c}\) condition for all \(c \in(0,b)\), that is, if every sequence \(\{u_{j}\} \subset W\) such that \(I(u_{j}) \to c\) and \(I'(u_{j}) \to 0\) possesses a convergent subsequence, then each \(c_{j}^{\ast}\) is a critical value of I and there are m distinct pairs of associated critical points.

3 Proof of Theorem 1.2

We only prove (ii) because the proof of (i) is similar and relatively simpler. First, \(I_{\lambda}\) satisfies the \((\mathrm{PS})_{c}\) condition for all \(c < \frac {2p_{\mu,s}^{*}-p}{2pp_{\mu,s}^{*}} S_{H,L}^{\frac{2p_{\mu ,s}^{*}}{2p_{\mu,s}^{*}-p}}\). In fact, let \(c <\frac{2p_{\mu,s}^{*}-p}{2pp_{\mu,s}^{*}} S_{H,L}^{\frac{2p_{\mu,s}^{*}}{2p_{\mu,s}^{*}-p}} \), and let \(\{u_{j}\}\) be a sequence in \(X_{p}^{s}(\Omega)\) such that

$$\begin{aligned}& I_{\lambda}(u_{j}) = \frac{1}{p} \Vert u_{j} \Vert _{s,p}^{p} - \frac{\lambda}{p} \vert u_{j} \vert _{p}^{p} - \frac{1}{2p_{\mu,s}^{\ast}} \Vert u_{j} \Vert _{o}^{2p_{\mu,s}^{\ast}} = c + \mathrm {o}(1), \end{aligned}$$
(8)
$$\begin{aligned}& \begin{aligned}[b] I_{\lambda}'(u_{j}) v &= \int_{\mathbb {R}^{2N}} \frac{ \vert u_{j}(x) - u_{j}(y) \vert ^{p-2} (u_{j}(x) - u_{j}(y)) (v(x) - v(y))}{ \vert x - y \vert ^{N+sp}} \,dx \,dy \\ & \quad {}- \lambda \int_{\Omega} \vert u_{j} \vert ^{p-2} u_{j} v \,dx - \int_{\Omega}\int _{\Omega}\frac{ \vert u_{j}(y) \vert ^{p_{\mu,s}^{\ast}} \vert u_{j}(x) \vert ^{p_{\mu,s}^{\ast}-2} u_{j}(x) v(x) }{ \vert x-y \vert ^{N+sp}} \,dx \\ &= \mathrm {o}\bigl( \Vert v \Vert _{s,p}\bigr), \quad\forall v \in X_{p}^{s}(\Omega), \end{aligned} \end{aligned}$$
(9)

as \(j \to\infty\). Then

$$\biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{*}}\biggr) \Vert u_{j} \Vert _{o}^{2p_{\mu ,s}^{\ast}} = I_{\lambda}(u_{j}) - \frac{1}{p} I_{\lambda}'(u_{j}) u_{j} = \mathrm {o}\bigl( \Vert u_{j} \Vert _{s,p} \bigr) + O(1), $$

which together with (8), Lemma 2.2, and the Hölder inequality shows that \(\{u_{j}\}\) is bounded in \(X_{p}^{s}(\Omega)\). Then there exists a subsequence of \(\{u_{j}\}\) still denoted by \(\{u_{j}\}\) and \(u\in X_{p}^{s}(\Omega)\) such that

$$u_{j}\rightharpoonup u \quad \mbox{weakly in } X_{p}^{s}( \Omega),\mbox{ and in } L^{p_{s}^{*}}(\Omega), $$

Denoting by \(p' = p/(p - 1)\) the Hölder conjugate of p, \(|u_{j}(x) - u_{j}(y)|^{p-2} (u_{j}(x) - u_{j}(y))/|x - y|^{(N+sp)/p'}\) is bounded in \(L^{p'}(\mathbb {R}^{2N})\) and converges to \(|u(x) - u(y)|^{p-2} (u(x) - u(y))/|x - y|^{(N+sp)/p'}\) a.e. in \(\mathbb {R}^{2N}\), and \((v(x) - v(y))/|x - y|^{(N+sp)/p} \in L^{p}(\mathbb {R}^{2N})\), so the first integral in (9) converges to

$$\int_{\mathbb {R}^{2N}} \frac{ \vert u(x) - u(y) \vert ^{p-2} (u(x) - u(y)) (v(x) - v(y))}{ \vert x - y \vert ^{N+sp}} \,dx \,dy $$

for a further subsequence. In addition,

$$\int_{\Omega} \vert u_{j} \vert ^{p-2} u_{j} v \,dx \to \int_{\Omega} \vert u \vert ^{p-2} uv \,dx, $$

and

$$ \begin{aligned}[b] &\int_{\Omega}\int_{\Omega}\frac{ \vert u_{j}(y) \vert ^{p_{\mu,s}^{\ast}} \vert u_{j}(x) \vert ^{p_{\mu,s}^{\ast}-2} u_{j}(x) v(x) }{ \vert x-y \vert ^{\mu}} \,dx \,dy\\ &\quad \to \int_{\Omega}\int_{\Omega}\frac{ \vert u(y) \vert ^{p_{\mu,s}^{\ast}} \vert u(x) \vert ^{p_{\mu,s}^{\ast}-2} u(x) v(x) }{ \vert x-y \vert ^{\mu}} \,dx \,dy. \end{aligned} $$
(10)

Indeed, the Riesz potential defines a linear continuous map from \(L^{\frac{2N}{2N-\mu}}(\Omega)\) to \(L^{\frac{2N}{\mu}}(\Omega)\) by the Hardy–Littlewood–Sobolev inequality. Then

$$ \frac{ \vert u_{j} \vert ^{p_{\mu,s}^{*}}}{ \vert x-y \vert ^{\mu}}\rightharpoonup\frac { \vert u \vert ^{p_{\mu,s}^{*}}}{ \vert x-y \vert ^{\mu}}\quad \mbox{in }L^{\frac{2N}{\mu}}(\Omega), $$
(11)

as \(n\rightarrow\infty\). Moreover,

$$ \vert u_{j} \vert ^{p_{\mu,s}^{*}-2}u_{j} \rightharpoonup \vert u \vert ^{p_{\mu,s}^{*}-2}u\quad \mbox{in } L^{\frac{p_{s}^{*}}{p_{\mu,s}^{*}}}(\Omega). $$
(12)

Combining (11) with (12) and \(\frac{p_{s}^{*}}{p_{\mu ,s}^{*}}=\frac{2N}{2N-\mu}\), we get the desired result (10). So passing to the limit in (9) shows that \(u \in X_{p}^{s}(\Omega)\) is a weak solution of (1).

Let \(\widetilde{u}_{j} = u_{j} - u\) and we will give the proof of \(\widetilde{u}_{j} \to0\) in \(X_{p}^{s}(\Omega)\). From [30, Lemma 3.2], we get

$$ \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} = \Vert u_{j} \Vert _{s,p}^{p} - \Vert u \Vert _{s,p}^{p} + \mathrm {o}(1). $$
(13)

We discuss as in Lemma 2.2 in [10] and have

$$ \Vert \widetilde{u}_{j} \Vert _{o}^{2p_{\mu,s}^{\ast}} = \Vert u_{j} \Vert _{o}^{2p_{\mu,s}^{\ast}} - \Vert u \Vert _{o}^{2p_{\mu,s}^{\ast}} + \mathrm {o}(1). $$
(14)

Taking \(v = u_{j}\) in (9) gives

$$ \Vert u_{j} \Vert _{s,p}^{p} = \lambda \vert u \vert _{p}^{p} + \Vert u_{j} \Vert _{o}^{2p_{\mu ,s}^{\ast}} + \mathrm {o}(1). $$
(15)

Since \(\{u_{j}\}\) is bounded in \(X_{p}^{s}(\Omega)\) and converges to u in \(L^{p}(\Omega)\), and testing (9) with \(v = u\) gives

$$ \Vert u \Vert _{s,p}^{p} = \lambda \vert u \vert _{p}^{p} + \Vert u \Vert _{o}^{2p_{\mu ,s}^{\ast}}. $$
(16)

Combining (13)–(16) and (7) gives

$$\Vert \widetilde{u}_{j} \Vert _{s,p}^{p} = \Vert \widetilde{u}_{j} \Vert _{o}^{2p_{\mu ,s}^{\ast}} + \mathrm {o}(1) \le\frac{ \Vert \widetilde{u}_{j} \Vert _{s,p}^{2p_{\mu ,s}^{\ast}}}{S_{H,L}^{2p_{\mu,s}^{\ast}/p}} + \mathrm {o}(1), $$

so

$$ \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} \bigl(S_{H,L}^{2p_{\mu,s}^{\ast}/p} - \Vert \widetilde{u}_{j} \Vert _{s,p}^{2p_{\mu,s}^{\ast}- p} \bigr) \le \mathrm {o}(1). $$
(17)

On the other hand,

$$\begin{aligned} c & = \frac{1}{p} \Vert u_{j} \Vert _{s,p}^{p} - \frac{\lambda}{p} \vert u \vert _{p}^{p} - \frac{1}{2p_{\mu,s}^{\ast}} \Vert u_{j} \Vert _{o}^{2p_{\mu ,s}^{\ast}} + \mathrm {o}(1) \quad \text{by (8)} \\ & = \biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \bigl( \Vert u_{j} \Vert _{s,p}^{p} - \lambda \vert u \vert _{p}^{p} \bigr) + \mathrm {o}(1) \quad \text{by (15)} \\ & = \biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \bigl( \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} + \Vert u \Vert _{s,p}^{p} - \lambda \vert u \vert _{p}^{p} \bigr) + \mathrm {o}(1) \quad \text{by (13)} \\ & = \biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \bigl( \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} + \Vert u \Vert _{o}^{2p_{\mu,s}^{\ast}} \bigr) + \mathrm {o}(1) \quad \text{by (16)} \\ & \ge\biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} + \mathrm {o}(1), \end{aligned}$$

so

$$ \limsup_{j \to\infty} \Vert \widetilde{u}_{j} \Vert _{s,p}^{p} \le\frac {2pp_{\mu,s}^{\ast}c}{2p_{\mu,s}^{\ast}-p} < S_{H,L}^{\frac{2p_{\mu ,s}^{\ast}}{2p_{\mu,s}^{\ast}-p}}. $$
(18)

We conclude from (17) and (18) that \(\|\widetilde{u}_{j}\|_{s,p} \to0\).

Now we can apply Lemma 2.4 with \(b = \frac{2p_{\mu,s}^{*}-p}{2pp_{\mu,s}^{*}} S_{H,L}^{\frac{2p_{\mu,s}^{*}}{2p_{\mu,s}^{*}-p}}\). By [30, Proposition 3.5], \(\Psi^{\lambda_{k+m}}\) has a compact symmetric subset \(A_{0}\) with

$$i(A_{0}) = k + m. $$

We take \(B_{0} = \Psi_{\lambda_{k+1}}\), so that

$$i(S_{1} \setminus B_{0}) = k $$

by (4). Let \(R > r > 0\) and let A, B, and X be as in Lemma 2.4. For \(u \in B_{0}\),

$$I_{\lambda}(ru) \ge\frac{r^{p}}{p} \biggl(1 - \frac{\lambda}{\lambda _{k+1}} \biggr) - \frac{r^{2p_{\mu,s}^{\ast}}}{2p_{\mu,s}^{\ast}S_{H,L}^{2p_{\mu,s}^{\ast}/p}} $$

by (7). It follows that \(\inf I_{\lambda}(B) > 0\) if r is sufficiently small since \(\lambda< \lambda_{k+1}\) and \(2p_{\mu ,s}^{\ast}> p\). For \(u \in A_{0} \subset\Psi^{\lambda_{k+1}}\),

$$I_{\lambda}(Ru) \le\frac{R^{p}}{p} \biggl(1 - \frac{\lambda}{\lambda _{k+1}} \biggr) - \frac{R^{2p_{\mu,s}^{\ast}}}{2p_{\mu,s}^{\ast}} \biggl(\frac{1}{\lambda_{k+1} \vert \Omega \vert ^{{(p_{s}^{*}-p)}/{p_{s}^{*}}}C_{H,L}^{p}} \biggr)^{\frac{2p_{\mu,s}^{*}}{p}}, $$

so there exists \(R > r\) such that \(I_{\lambda}\le0\) on A. For \(u \in X\),

$$\begin{aligned} I_{\lambda}(u) & \le\frac{\lambda_{k+1} - \lambda}{p} \vert \Omega \vert ^{\frac{p_{s}^{*}-p}{p_{s}^{*}}} \vert u \vert _{p_{s}^{*}}^{p} - \frac{ \vert u \vert _{p_{s}^{*}}^{2p_{\mu ,s}^{*}}}{2p_{\mu,s}^{\ast}(C_{H,L})^{2p_{\mu,s}^{\ast}}} \\ & \le\sup_{\rho\ge0} \biggl[\frac{ \vert \Omega \vert ^{\frac {p_{s}^{*}-p}{p_{s}^{*}}}(\lambda_{k+1} - \lambda) \rho}{p} - \frac{\rho ^{2p_{\mu,s}^{\ast}/p}}{2p_{\mu,s}^{\ast}(C_{H,L})^{2p_{\mu,s}^{\ast}}} \biggr] \\ & = \biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \vert {\Omega } \vert ^{\frac {2p_{\mu,s}^{\ast}(p_{s}^{*}-p)}{p_{s}^{*}(2p_{\mu,s}^{*}-p)}} (C_{H,L})^{\frac {2pp_{\mu,s}^{*}}{2p_{\mu,s}^{*}-p}} (\lambda_{k+1} - \lambda)^{2p_{\mu ,s}^{\ast}/({2p_{\mu,s}^{\ast}}-p)}. \end{aligned}$$

So

$$\begin{aligned} \sup I_{\lambda}(X) &\le\biggl(\frac{1}{p}-\frac{1}{2p_{\mu,s}^{\ast}}\biggr) \vert {\Omega} \vert ^{\frac{2p_{\mu,s}^{\ast}(p_{s}^{*}-p)}{p_{s}^{*}(2p_{\mu ,s}^{*}-p)}} (C_{H,L})^{\frac{2pp_{\mu,s}^{*}}{2p_{\mu,s}^{*}-p}} ( \lambda_{k+1} - \lambda)^{2p_{\mu,s}^{\ast}/{(2p_{\mu,s}^{\ast}}-p)} \\ &< \frac{2p_{\mu,s}^{\ast}-p}{2pp_{\mu,s}^{\ast}} S_{H,L}^{2p_{\mu ,s}^{\ast}/{(2p_{\mu,s}^{\ast}-p)}} \end{aligned} $$

by (5). Thus, functional \(I_{\lambda}\) has m distinct pairs of (nontrivial) critical points \(\pm u^{\lambda}_{j}\), \(j = 1,\dots,m\), such that

$$ \begin{aligned}[b] &0 < I_{\lambda}\bigl(u^{\lambda}_{j}\bigr) \le\biggl(\frac{1}{p}-\frac{1}{2p_{\mu ,s}^{\ast}}\biggr) \vert {\Omega} \vert ^{\frac{2p_{\mu,s}^{\ast}(p_{s}^{*}-p)}{p_{s}^{*}(2p_{\mu,s}^{*}-p)}} (C_{H,L})^{\frac{2pp_{\mu ,s}^{*}}{2p_{\mu,s}^{*}-p}} (\lambda_{k+1} - \lambda)^{2p_{\mu,s}^{\ast}/{(2p_{\mu,s}^{\ast}}-p)} \to0\\ &\quad \text{as } \lambda\nearrow\lambda_{k+1}. \end{aligned} $$
(19)

Then

$$\bigl\Vert u^{\lambda}_{j} \bigr\Vert _{o}^{2p_{\mu,s}^{\ast}} = \frac{2pp_{\mu,s}^{\ast}}{2p_{\mu,s}^{\ast}-p} \biggl[I_{\lambda}\bigl(u^{\lambda}_{j} \bigr) - \frac{1}{p} I_{\lambda}'\bigl(u^{\lambda}_{j} \bigr) u^{\lambda}_{j} \biggr] = \frac{2pp_{\mu ,s}^{\ast}}{2p_{\mu,s}^{\ast}-p} I_{\lambda}\bigl(u^{\lambda}_{j}\bigr) \to0 $$

and hence \(u^{\lambda}_{j} \to0\) in \(L^{p}(\Omega)\). Applying the Hölder inequality and Lemma 2.2, we deduce that

$$\bigl\Vert u^{\lambda}_{j} \bigr\Vert _{s,p}^{p} = p I_{\lambda}\bigl(u^{\lambda}_{j}\bigr) + \lambda \bigl\vert u^{\lambda}_{j} \bigr\vert _{p}^{p} + \frac{p}{2p_{\mu,s}^{\ast}} \bigl\Vert u^{\lambda}_{j} \bigr\Vert _{o}^{2p_{\mu,s}^{\ast}} \to0. $$