The error analysis of Crank-Nicolson-type difference scheme for fractional subdiffusion equation with spatially variable coefficient

Abstract

A Crank-Nicolson-type difference scheme is presented for the spatial variable coefficient subdiffusion equation with Riemann-Liouville fractional derivative. The truncation errors in temporal and spatial directions are analyzed rigorously. At each time level, it results in a linear system in which the coefficient matrix is tridiagonal and strictly diagonally dominant, so it can be solved by the Thomas algorithm. The unconditional stability and convergence of the scheme are proved in the discrete $L_{2}$ norm by the energy method. The convergence order is $\min \{2-\frac{\alpha}{2}, 1+\alpha \}$ in the temporal direction and two in the spatial one. Finally, numerical examples are presented to verify the efficiency of our method.

1 Introduction

In recent years, fractional differential equations have captured great attention of research in different domains. This facts reflect the ability of fractional calculation to describe many phenomena in different disciplines such as semiconductors, mechanics, signal processing, porous media, anomalous diffusion, and so on [1–6]. Employing fractional derivatives to describe the procedure of anomalous diffusion, we get the time fractional subdiffusion equation [2, 7, 8]:

$$ \frac{\partial u(x,t)}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[K_{r}\frac{\partial^{2}u(x,t)}{\partial x^{2}} \biggr]+f(x,t), $$

(1)

where ${}_{0} \mathcal{D}_{t}^{1-\alpha}$ ($0<\alpha<1$) denotes the Riemann-Liouville fractional derivative operator defined as

$$ {}_{0} \mathcal{D}_{t}^{1-\alpha}u(t)= \frac{1}{\varGamma (\alpha)}\frac {d}{dt} \int_{0}^{t}\frac{u(s)}{(t-s)^{1-\alpha}}\,ds. $$

(2)

Some researchers considered the similar form with Caputo derivative:

$$ {}_{0}^{C} \mathcal{D}_{t}^{\alpha}u(x,t)= \frac{\partial^{2}u(x,t)}{\partial x^{2}}+g(x,t), $$

(3)

where ${}_{0}^{C} \mathcal{D}_{t}^{\alpha}$ denotes Caputo’s derivative operator defined by

$$ {}_{0}^{C}\mathcal{D}_{t}^{\alpha}u(t)= \frac{1}{\varGamma (1-\alpha)} \int_{0}^{t}\frac {du(s)}{ds}(t-s)^{-\alpha} \,ds,\quad \alpha\in(0,1). $$

(4)

We have the following relation between the Caputo and Riemann-Liouville fractional derivatives.

Let $y(t)$ be an $(m-1)$ times continuously differentiable function in the interval $[0,T]$ with $y^{(m)}(t)$ integrable in $[0,T]$. For every p, if $0\leq m-1\leq p \leq m$, then the Riemann-Liouville fractional derivative ${}_{0} \mathcal {D}_{t}^{p} y(t)$ exists, and the following equality holds [1]:

$$\begin{aligned} {}_{0} \mathcal{D}_{t}^{p} y(t) &= \sum_{j=0}^{m-1}\frac{y^{(j)}(0)t^{j-p}}{\varGamma (1+j-p)}+{}_{0}^{C} \mathcal {D}_{t}^{p}y(t) \\ &=\sum_{j=0}^{m-1}\frac{y^{(j)}(0)t^{j-p}}{\varGamma (1+j-p)}+ \frac {1}{\varGamma (m-p)} \int_{0}^{t}\frac{y^{(m)}(s)}{(t-s)^{p-m+1}}\,ds. \end{aligned}$$

(5)

Much remarkable work has been done theoretically for diffusion and fractional problems [9–11]. Marin and Marinescu [10] studied the asymptotic partition of total energy for the solutions of the mixed initial boundary value problem within the context of the thermoelasticity of initially stressed bodies, and Hameed et al. [11] derived and analyzed a mathematical model subject to low Reynolds number and long wavelength approximations in order to study the peristaltic motion of fractional second-grade fluid in a vertical tube. In the regard of numerical work for time-fractional diffusion equations, Langlands and Henry [12] obtained an implicit numerical method for the homogeneous problem and discussed the accuracy and stability of their scheme. Zhuang et al. [13] integrated the linear and nonlinear subdiffusion equations about the time variable t and then approximated the obtained equivalent equations numerically with the idea of numerical integrals. Yuste and Acedo [14] developed an explicit scheme and gave a strict proof of the stability of the explicit scheme, and then Yuste [15] analyzed the weighted average finite difference scheme by the von Neumann method.

One main approximation approach to a discrete analog of the time-fractional derivative is an $L_{1}$ formula. Sun and Wu [16] first derived a fully discrete difference scheme employing the $L_{1}$ approximation, where the truncation error was proved to be of order $2-\alpha$ in temporal accuracy. Lin and Xu [17] constructed an effective numerical method by employing the finite difference scheme in time and using the Legendre spectral methods in space. Chen et al. [18] gave an implicit numerical scheme for the problem and proved the unconditional stability and $L_{2}$-norm convergence. Gao and Sun [19] applied the $L_{1}$ formula to approximate the Caputo time-fractional derivative and developed a compact finite difference scheme to promote the spatial accuracy for the fractional subdiffusion equation. They obtained the fourth-order convergence rate in spatial direction. Another main way to a discrete analog of the fractional derivative is the shifted Grünwald-Letnikov formula. Very recently, Deng’s group [20, 21] has presented a high-order discrete analog of the space-fractional derivative by assembling the shifted GL operator with different weights.

The Crank-Nicolson difference scheme is a classical method for difference approximation. The works employing the CN method for fractional problems constantly emerge. Zhang et al. [22] presented a Crank-Nicolson-type difference scheme for a subdiffusion equation with Riemann-Liouville fractional derivative, where the discrete $H_{1}$ norm convergence was proved rigorously, and the maximum norm error estimate was given. Based on a Crank-Nicolson-type discretization, Wang and Vong [23] proposed a second-order accuracy formula to approximate the time-fractional derivative and established a compact finite difference scheme for solving the modified anomalous fractional subdiffusion equation. For more applications of the Crank-Nicolson scheme, we refer the reader to [24–26].

The works we listed are mostly focused on the subdiffusion equation with constant coefficient. However, many practical applications involved variable diffusion coefficients [27–29]. For example, the flow of heat in a rod is constituted by composite heat-conducting materials, which means that the diffusion coefficient may vary with space variable. In view of some external heat source, Zhao [30] considered the Caputo-fractional subdiffusion equation with spatially variable coefficient:

$$ {}_{0}^{C}\mathcal{D}_{t}^{\alpha}u(x,t)= \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr)+g(x,t). $$

(6)

Employing an $L_{1}$ formula, she obtained the convergence of order $2-\alpha$ in the temporal direction and fourth-order approximation order in space. Vong et al. [31] considered the same equation under Neumann boundary conditions and obtained the global convergence of order $O(\tau^{2-\alpha}+h^{4})$. Metzler et al. [32] suggested the following fractional model equation for anomalous diffusion:

$$ {}_{0} \mathcal{D}_{t}^{\frac{2}{d_{w}}} P(r,t)= \frac{1}{r^{d_{s}-1}}\frac{\partial }{\partial r} \biggl(r^{d_{s}-1}\frac{\partial P(r,t)}{\partial r} \biggr),\quad r>0, t>0, $$

(7)

where $P(r,t)$ is the probability density of random walks on fractals, $d_{w}>2$ is the anomalous diffusion exponent, $d_{s}$ is just the spectral dimension of the fractal, and $d_{s}=\frac{2d_{f}}{d_{w}}$ with $d_{f}$ denoting fractal dimension of the underlying object. Employing (5) and neglecting the coefficient $\frac{1}{r^{d_{s}-1}}$ (which has no impact on difference approximation), (7) can be transformed into equation (6).

If $u(x,t)$ is suitably smooth in time, then we have the following relationship [1, 33]:

$$ {}_{0} \mathcal{D}_{t}^{1-\alpha} \bigl[{}_{0}^{C}\mathcal{D}_{t}^{\alpha}u(x,t) \bigr]=\frac{\partial u(x,t)}{\partial t}. $$

(8)

Therefore, implementing the operator ${}_{0} \mathcal{D}_{t}^{1-\alpha}$ on both sides of (6), we derive the following Riemann-Liouville fractional subdiffusion equation with spatially variable coefficient:

$$ \frac{\partial u(x,t)}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[ \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr]+f(x,t), $$

(9)

where $f(x,t)={}_{0} \mathcal{D}_{t}^{1-\alpha}g(x,t)$.

From the preceding discussion we see that equation (9) is a more general form. In this paper, we consider the difference scheme of (9). As far as we know, the difference scheme for this equation has not been proposed by now. In the present work, we establish a Crank-Nicolson-type difference scheme for the spatial variable coefficient problem (9) by the discrete Riemann-Liouville fractional derivative with $L_{1}$ formula. The CN-type scheme results in a linear system in which the coefficient matrix is tridiagonal and strictly diagonally dominant, so the Thomas algorithm suits.

The content of this paper is organized as follows. In Section 2, we introduce essential notation and some preliminary lemmas and then construct the Crank-Nicolson-type finite difference scheme. The unique solvability, unconditional stability, and the $L_{2}$-norm convergence are proved in Section 3 by the energy method. Some examples are listed in Section 4 to verify our theoretical analysis and testify the validation of our difference scheme. Finally, a brief conclusion ends this work.

2 Derivation of a CN-type difference scheme

Consider the following subdiffusion equation with spatially variable coefficient combined with initial boundary value conditions:

$$\begin{aligned}& \frac{\partial u(x,t)}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[\frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr]+f(x,t), \quad 0< x< L, 0< t\leq T, \end{aligned}$$

(10)

$$\begin{aligned}& u(0,t)=\varPhi _{1}(t), \qquad u(L,t)=\varPhi _{2}(t), \quad 0< t\leq T, \end{aligned}$$

(11)

$$\begin{aligned}& u(x,0)=\varPsi (x),\quad 0\leq x\leq L, \end{aligned}$$

(12)

where $0<\alpha<1$, and we suppose that $c_{1}\leq\varphi(x)\leq c_{2}$ and $\varphi(x)$, $f(x,t)$, $\varPhi _{1}(t)$, $\varPhi _{2}(t)$, $\varPsi (x)$ are sufficiently smooth functions.

For a finite difference approximation, we suppose that M and N are two positive integers and let $h=\frac{L}{M}$ and $\tau=\frac{T}{N}$ be space and temporal step lengths, respectively. Define $x_{i}=ih$, $0\leq i\leq M$, $t_{n}=n\tau$, $0\leq n\leq N$, $\varOmega _{h}=\{x_{i} \mid 0\leq i\leq M\}$, $\varOmega _{\tau}=\{t_{n} \mid 0\leq n\leq N\}$, and, in addition, $t_{k-\frac{1}{2}}=(k-\frac{1}{2})\tau$, $x_{i-\frac{1}{2}}=(i-\frac{1}{2})h$.

For any grid function $u=\{u_{i}^{n}\mid 0\leq i\leq M, 0\leq n \leq N\}$, we denote

$$\begin{aligned}& \delta_{x} u_{i-\frac{1}{2}}^{n}= \frac{1}{h}\bigl(u_{i}^{n}-u_{i-1}^{n} \bigr),\qquad \delta_{x}^{2} u_{i}^{n}= \frac{1}{h}\bigl(\delta_{x} u_{i+\frac{1}{2}}^{n}- \delta_{x} u_{i-\frac{1}{2}}^{n}\bigr), \end{aligned}$$

(13)

$$\begin{aligned}& u_{i}^{n-\frac{1}{2}}=\frac{1}{2} \bigl(u_{i}^{n}+u_{i}^{n-1}\bigr),\qquad \delta_{t} u_{i}^{n-\frac {1}{2}}=\frac{1}{\tau} \bigl(u_{i}^{n}-u_{i}^{n-1}\bigr). \end{aligned}$$

(14)

The following lemmas are needed for our error analysis.

Lemma 1

[16]

For $0<\alpha<1$ and $y\in C^{2}[0,t_{n}]$, we have:

$$\begin{aligned}& \frac{1}{\varGamma (\alpha)} \int_{0}^{t}\frac{y'(s)\,ds}{(t_{n}-s)^{\alpha}}-\frac {\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[y(t_{n})-\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k})y(t_{k})-a_{n-1}y(0) \Biggr] \\& \quad =\sum_{k=1}^{n} \int_{t_{k-1}}^{t_{k}}L_{\tau,\alpha,n}(s)y''(s) \,ds= O\bigl(\tau ^{1+\alpha}\bigr), \end{aligned}$$

(15)

where $a_{k}=(k+1)^{\alpha}-k^{\alpha}$, and for $s\in(t_{k-1},t_{k})$,

$$ L_{\tau,\alpha,n}(s) =\frac{1}{\varGamma (1+\alpha)} \biggl\{ (t_{n}-s)^{\alpha }- \biggl[\frac{s-t_{k-1}}{ \tau}(t_{n}-t_{k})^{\alpha}+ \frac{t_{k}-s}{\tau}(t_{n}-t_{k-1})^{\alpha} \biggr] \biggr\} . $$

(16)

Furthermore,

$$ \sum_{k=1}^{n} \int_{t_{k-1}}^{t_{k}}L_{\tau,\alpha,n}(s)\,ds\leq \frac {1}{\varGamma (1+\alpha)} \biggl[\frac{\alpha}{12}+ \frac{2^{1+\alpha}}{1+\alpha}- \bigl(1+2^{\alpha-1}\bigr) \biggr]\tau^{1+\alpha }. $$

(17)

Lemma 2

[34]

Let $y\in C^{3}[t_{k-1},t_{k}]$. Then

$$\begin{aligned} \frac{1}{2} \bigl[y'(t_{k})+y'(t_{k-1}) \bigr] =& \frac{1}{\tau} \bigl[y(t_{k})-y(t_{k-1}) \bigr] \\ &{}+\frac{\tau^{2}}{16} \int_{0}^{1} \biggl[y^{(3)} \biggl(t_{k-\frac{1}{2}}+\frac {s\tau}{2} \biggr)+y^{(3)} \biggl(t_{k-\frac{1}{2}} -\frac{s\tau}{2} \biggr) \biggr]\bigl(1-s^{2} \bigr)\,ds. \end{aligned}$$

(18)

Now we define the grid function $U_{i}^{n}=u(x_{i},t_{n})$, $0\leq i\leq M$, $0\leq n\leq N$, and, in addition, denote $\varphi(x_{i+\frac{1}{2}})$ by $\varphi_{i+\frac{1}{2}}$.

Lemma 3

Suppose $u\in C^{4} [x_{i},x_{i+1} ]$. Then

$$\begin{aligned}& \delta_{x} U_{i+\frac{1}{2}}=u'(x_{i+\frac{1}{2}})+ \frac{h}{4} \int _{0}^{1} \biggl[u'' \biggl(x_{i+\frac{1}{2}}+\frac{h}{2} t\biggr)-u'' \biggl(x_{i+\frac{1}{2}}-\frac {h}{2} t\biggr) \biggr](1-t)\,dt, \end{aligned}$$

(19)

$$\begin{aligned}& \delta_{x} U_{i+\frac{1}{2}}=u'(x_{i+\frac{1}{2}})+ \frac{h^{2}}{16} \int _{0}^{1} \biggl[u^{(3)} \biggl(x_{i+\frac{1}{2}}+\frac{h}{2} t\biggr)+u^{(3)} \biggl(x_{i+\frac {1}{2}}-\frac{h}{2} t\biggr) \biggr](1-t)^{2} \,dt, \end{aligned}$$

(20)

$$\begin{aligned}& \delta_{x} U_{i+\frac{1}{2}}=u'(x_{i+\frac{1}{2}})+ \frac{h^{3}}{96} \int_{0}^{1} \biggl[u^{(4)} \biggl(x_{i+\frac{1}{2}}+\frac{h}{2} t\biggr)-u^{(4)} \biggl(x_{i+\frac {1}{2}}-\frac{h}{2} t\biggr) \biggr] (1-t)^{3} \,dt \\& \hphantom{\delta_{x} U_{i+\frac{1}{2}}={}}{}+\frac{h^{2}}{24}u^{(3)}(x_{i+\frac{1}{2}}). \end{aligned}$$

(21)

Proof

Employing the Taylor expansion with integral remainder, we have:

$$\begin{aligned}& U_{i+1}=u(x_{i+\frac{1}{2}})+\frac{h}{2}u'(x_{i+\frac{1}{2}})+{ \frac {h}{2}}^{2} \int_{0}^{1} u'' \biggl(x_{i+\frac{1}{2}}+\frac{th}{2}\biggr) (1-t)\,dt, \end{aligned}$$

(22)

$$\begin{aligned}& U_{i}=u(x_{i+\frac{1}{2}})-\frac{h}{2}u'(x_{i+\frac{1}{2}})+{ \frac {h}{2}}^{2} \int_{0}^{1} u'' \biggl(x_{i+\frac{1}{2}}-\frac{th}{2}\biggr) (1-t)\,dt. \end{aligned}$$

(23)

Then subtracting these two equalities, we get the first statement. The proofs of the other two are similar by using an expansion of higher order. □

Now we analyze the truncation error of the $L_{1}$ analog for the Riemann-Liouville fractional derivative.

Lemma 4

Let $u(x,t)\in C^{4,2}([0,L]\times[0,T])$, $\varphi(x)\in C^{1}[0,L]$. Then for the truncation error, we have:

$$\begin{aligned}& {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[ \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i},t_{n}) \\& \quad =\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[\delta _{x}(\varphi \delta_{x} U)_{i}^{n}-\sum _{k=1}^{n-1} (a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k}-a_{n-1} \delta _{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr] \\& \qquad {}+\frac{t_{n}^{\alpha-1}}{\varGamma (\alpha)}\delta_{x}(\varphi\delta_{x} U)_{i}^{0}+(R_{1})_{i}^{n}, \quad 1\leq i\leq M-1, 1\leq n\leq N, \end{aligned}$$

(24)

where $(R_{1})_{i}^{n}=(R_{11})_{i}^{n}+(R_{12})_{i}^{n}$, and

$$\begin{aligned}& \begin{aligned}[b] \bigl\vert (R_{11})_{i}^{n}\bigr\vert \leq{}& \frac{1}{24}\max_{ \substack{0\leq x\leq L\\ 0\leq t\leq T} } \biggl[\biggl\vert {}_{0} \mathcal{D}_{t}^{1-\alpha}\frac{\partial^{3}}{\partial x^{3}} \biggl(\varphi\frac{\partial u}{\partial x}\biggr)\biggr\vert +\biggl\vert {}_{0} \mathcal {D}_{t}^{1-\alpha}\frac{\partial}{\partial x} \biggl(\varphi\frac{\partial^{3} u}{\partial x^{3}}\biggr)\biggr\vert \\ &{} +\frac{1}{4}\biggl\vert \varphi(x){}_{0} \mathcal{D}_{t}^{1-\alpha} \frac{\partial^{4} u}{\partial x^{4}}\biggr\vert \biggr]h^{2}, \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned}& \begin{aligned}[b] \bigl\vert (R_{12})_{i}^{n}\bigr\vert \leq{}& \frac{1}{\varGamma (1+\alpha)} \biggl[\frac{\alpha}{12}+ \frac{2^{1+\alpha}}{1+\alpha}- \bigl(1+2^{\alpha-1}\bigr) \biggr] \\ &{}\cdot\max_{ \substack{0\leq x\leq L\\ 0\leq t\leq T} } \biggl[\biggl\vert \frac{\partial^{3}}{\partial x\, \partial t^{2}}\biggl(\varphi(x) \frac{\partial u}{\partial x}\biggr)\biggr\vert + \frac{1}{2}\biggl\vert \varphi(x)\frac {\partial^{4} u}{\partial x^{2}\, \partial t^{2}}\biggr\vert \biggr] \tau^{1+\alpha}. \end{aligned} \end{aligned}$$

(26)

Proof

Let ${}_{0} \mathcal{D}_{t}^{1-\alpha}u=w$ and $W_{i}^{n}=w(x_{i},t_{n})$. Then

$$ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[ \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x}\biggr) \biggr]= \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial w}{\partial x}\biggr). $$

(27)

It follows from Lemma 3 that

$$\begin{aligned} \delta_{x}(\varphi\delta_{x} W)_{i}^{n} =&\frac{1}{h}\bigl(\varphi_{i+\frac{1}{2}}\delta_{x} W_{i+\frac{1}{2}}^{n} -\varphi_{i-\frac{1}{2}}\delta_{x} W_{i-\frac{1}{2}}^{n}\bigr) \\ =&\frac{1}{h}\bigl(\varphi_{i+\frac{1}{2}}w'_{x}(x_{i+\frac{1}{2}},t_{n})- \varphi _{i-\frac{1}{2}} w'_{x}(x_{i-\frac{1}{2}},t_{n}) \bigr) \\ &{} +\frac{h^{2}}{24}\frac{1}{h} \bigl[\varphi_{i+\frac {1}{2}}w_{x}^{(3)}(x_{i+\frac{1}{2}},t_{n}) -\varphi_{i-\frac{1}{2}} w_{x}^{(3)}(x_{i-\frac{1}{2}},t_{n}) \bigr] \\ &{} +\varphi_{i+\frac{1}{2}}\frac{h^{2}}{96} \int_{0}^{1} \biggl[w_{x}^{(4)} \biggl(x_{i+\frac{1}{2}}+\frac{t}{2}h\biggr)- w_{x}^{(4)} \biggl(x_{i+\frac{1}{2}}-\frac{t}{2}h\biggr) \biggr](1-t)^{3}\,dt \\ &{} -\varphi_{i-\frac{1}{2}}\frac{h^{2}}{96} \int_{0}^{1} \biggl[w_{x}^{(4)} \biggl(x_{i-\frac{1}{2}}+\frac{t}{2}h\biggr)- w_{x}^{(4)} \biggl(x_{i-\frac{1}{2}}-\frac{t}{2}h\biggr) \biggr](1-t)^{3}\,dt \\ =&\frac{\partial}{\partial x}\biggl(\varphi(x)\frac{\partial w}{\partial x}\biggr) (x_{i},t_{n})+\frac{h^{2}}{24}\bigl(\varphi w_{x}^{(3)}\bigr)'_{x}( \xi,t_{n}) \\ &{} +\frac{h^{2}}{16} \int_{0}^{1} \biggl[\bigl(\varphi w'_{x}\bigr)_{x}^{(3)} \biggl(x_{i}+\frac {t}{2}h,t_{n}\biggr)+\bigl(\varphi w'_{x}\bigr)_{x}^{(3)} \biggl(x_{i}-\frac{t}{2}h,t_{n}\biggr) \biggr](1-t)^{2}\,dt \\ &{} +\varphi_{i+\frac{1}{2}}\frac{h^{2}}{96} \int_{0}^{1} \biggl[w_{x}^{(4)} \biggl(x_{i+\frac{1}{2}}+\frac{t}{2}h,t_{n}\biggr)- w_{x}^{(4)}\biggl(x_{i+\frac{1}{2}}-\frac{t}{2}h,t_{n} \biggr) \biggr](1-t)^{3}\,dt \\ &{} -\varphi_{i-\frac{1}{2}}\frac{h^{2}}{96} \int_{0}^{1} \biggl[w_{x}^{(4)} \biggl(x_{i-\frac{1}{2}} +\frac{t}{2}h,t_{n}\biggr)- w_{x}^{(4)}\biggl(x_{i-\frac{1}{2}}-\frac{t}{2}h,t_{n} \biggr) \biggr] \\ &{}\cdot(1-t)^{3}\,dt, \end{aligned}$$

(28)

where $\xi\in [x_{i-1},x_{i+1} ]$. So we have

$$ \frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial w}{\partial x} \biggr) (x_{i},t_{n}) =\delta_{x}(\varphi \delta_{x} W)_{i}^{n}+(R_{11})_{i}^{n}, $$

(29)

where

$$\begin{aligned} \begin{aligned}[b] \bigl\vert (R_{11})_{i}^{n}\bigr\vert \leq{}&\frac{1}{24}\max_{ \substack{0\leq x\leq L\\ 0\leq t\leq T} } \biggl[\biggl\vert {}_{0} \mathcal{D}_{t}^{1-\alpha}\frac{\partial^{3}}{\partial x^{3}} \biggl(\varphi\frac{\partial u}{\partial x}\biggr)\biggr\vert +\biggl\vert {}_{0} \mathcal {D}_{t}^{1-\alpha}\frac{\partial}{\partial x} \biggl(\varphi\frac{\partial^{3} u}{\partial x^{3}}\biggr)\biggr\vert \\ &{} +\frac{1}{4}\biggl\vert \varphi(x){}_{0} \mathcal{D}_{t}^{1-\alpha} \frac{\partial^{4} u}{\partial x^{4}}\biggr\vert \biggr]h^{2}. \end{aligned} \end{aligned}$$

(30)

It follows from (15) and (5) that

$$\begin{aligned} \delta_{x}(\varphi\delta_{x} W)_{i}^{n} =& \bigl[{}_{0} \mathcal{D}_{t}^{1-\alpha} \delta_{x}(\varphi\delta_{x} U) \bigr](x_{i},t_{n}) \\ =&\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[\delta_{x}(\varphi\delta _{x} U)_{i}^{n}-\sum_{k=1}^{n-1} (a_{n-k-1}-a_{n-k})\delta_{x}(\varphi \delta_{x} U)_{i}^{k} -a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr] \\ &{} +\frac{t_{n}^{\alpha-1}}{\varGamma (\alpha)}\delta_{x}(\varphi\delta_{x} U)_{i}^{0}+\sum_{k=1}^{n} \int_{t_{k-1}}^{t_{k}}L_{\tau,\alpha,n}(s) \frac{\partial^{2}}{\partial t^{2}} \delta_{x}(\varphi\delta_{x} u) (x_{i},s)\,ds. \end{aligned}$$

(31)

Using similar analysis and applying Lemma 3 again, we get

$$\begin{aligned} \delta_{x}(\varphi\delta_{x} U)_{i}^{n} =& \frac{1}{2} \int_{0}^{1} \biggl[\frac {\partial}{\partial x}\biggl( \varphi(x)\frac{\partial u}{\partial x}\biggr) \biggl(x_{i}+\frac{t}{2}h,t_{n} \biggr)+\frac{\partial}{\partial x}\biggl(\varphi(x)\frac {\partial u}{\partial x}\biggr) \biggl(x_{i}-\frac{t}{2}h,t_{n}\biggr) \biggr]\,dt \\ &{} +\frac{1}{4}\varphi_{i+\frac{1}{2}} \int_{0}^{1} \biggl[\frac{\partial^{2} u}{\partial x^{2}} \biggl(x_{i+\frac{1}{2}}+\frac{t}{2}h,t_{n}\biggr)- \frac{\partial^{2} u}{\partial x^{2}}\biggl(x_{i+\frac{1}{2}}-\frac{t}{2}h,t_{n} \biggr) \biggr](1-t)\,dt \\ &{} -\frac{1}{4}\varphi_{i-\frac{1}{2}} \int_{0}^{1} \biggl[\frac{\partial^{2} u}{\partial x^{2}} \biggl(x_{i-\frac{1}{2}}+\frac{t}{2}h,t_{n}\biggr)- \frac{\partial^{2} u}{\partial x^{2}}\biggl(x_{i-\frac{1}{2}}-\frac{t}{2}h,t_{n} \biggr) \biggr](1-t)\,dt. \end{aligned}$$

(32)

Applying (17) and the last equality, it is not hard to get

$$\begin{aligned} \bigl\vert (R_{12})_{i}^{n}\bigr\vert \leq &\frac{1}{\varGamma (1+\alpha)} \biggl[\frac{\alpha}{12}+ \frac{2^{1+\alpha}}{1+\alpha}- \bigl(1+2^{\alpha-1}\bigr) \biggr] \\ &{}\cdot\max_{ \substack{0\leq x\leq L \\ 0\leq t\leq T} } \biggl[\biggl\vert \frac{\partial^{3}}{\partial x\, \partial t^{2}} \biggl(\varphi(x) \frac{\partial u}{\partial x}\biggr)\biggr\vert +\frac{1}{2}\biggl\vert \varphi(x)\frac {\partial^{4} u}{\partial x^{2}\, \partial t^{2}}\biggr\vert \biggr]\tau^{1+\alpha}. \end{aligned}$$

(33)

The proof is completed. □

We now construct a Crank-Nicolson-type scheme for problem (10)-(12). Considering equality (11) at the point $(x_{i},t_{n})$, we have

$$ \frac{\partial u(x_{i},t_{n})}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha } \biggl[\frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i},t_{n})+f(x_{i},t_{n}), \quad 1< n< N, 1< i< M-1. $$

(34)

Then

$$\begin{aligned}& \frac{1}{2} \biggl[\frac{\partial u(x_{i},t_{n})}{\partial t}+\frac {\partial u(x_{i},t_{n-1})}{\partial t} \biggr] \\& \quad =\frac{1}{2} \biggl\{ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[\frac {\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i},t_{n})+ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[\frac{\partial}{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i},t_{n-1}) \biggr\} \\& \qquad {}+\frac{1}{2}\bigl[f(x_{i},t_{n})+f(x_{i},t_{n-1}) \bigr]. \end{aligned}$$

(35)

From Lemma 2 we obtain

$$ \frac{1}{2} \biggl[\frac{\partial u(x_{i},t_{n})}{\partial t}+\frac{\partial u(x_{i},t_{n-1})}{\partial t} \biggr] =\delta_{t} U_{i}^{n-\frac{1}{2}}+ (R_{2})_{i}^{n}, $$

(36)

where

$$ (R_{2})_{i}^{n}=\frac{\tau^{2}}{16} \int_{0}^{1} \biggl[\frac{\partial^{3} u}{\partial t^{3}} \biggl(x_{i},t_{n-\frac{1}{2}}+\frac{s\tau}{2} \biggr)+ \frac {\partial^{3} u}{\partial t^{3}} \biggl(x_{i},t_{n-\frac{1}{2}}-\frac{s\tau }{2} \biggr) \biggr]\bigl(1-s^{2}\bigr)\,ds. $$

(37)

It follows from Lemma 4 that

$$\begin{aligned}& \frac{1}{2} \biggl\{ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[\frac{\partial }{\partial x} \biggl(\varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i}, t_{n})+ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl[\frac{\partial}{\partial x} \biggl( \varphi(x)\frac{\partial u}{\partial x} \biggr) \biggr](x_{i}, t_{n-1}) \biggr\} \\& \quad =\frac{t_{n}^{\alpha-1}+t_{n-1}^{\alpha-1}}{2\varGamma (\alpha)}\delta _{x}(\varphi\delta_{x} U)_{i}^{0} \\& \qquad {} +\frac{\tau^{\alpha-1}}{2\varGamma (1+\alpha)} \Biggl[\delta_{x}(\varphi\delta _{x} U)_{i}^{n}-\sum _{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k}-a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr] \\& \qquad {} +\frac{\tau^{\alpha-1}}{2\varGamma (1+\alpha)} \Biggl[\delta_{x}(\varphi\delta _{x} U)_{i}^{n-1}-\sum _{k=1}^{n-2}(a_{n-k-2}-a_{n-k-1}) \delta_{x}(\varphi \delta_{x} U)_{i}^{k}-a_{n-2} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr] \\& \qquad {} +\frac{1}{2}(R_{1})_{i}^{n}+ \frac{1}{2}(R_{1})_{i}^{n-1}. \end{aligned}$$

(38)

Denoting $U_{i}^{n-\frac{1}{2}}=\frac{1}{2}(U_{i}^{n}+U_{i}^{n-1})$ and $\delta_{x}(\varphi\delta_{x} U)_{i}^{n-\frac{1}{2}}=\frac{1}{2} [\delta _{x}(\varphi\delta_{x} U)_{i}^{n}+\delta_{x}(\varphi\delta_{x} U)_{i}^{n-1} ]$ and noticing that

$$\begin{aligned}& -\sum_{k=1}^{n-2}(a_{n-k-2}-a_{n-k-1}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k}-a_{n-2} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \\& \quad =-\sum_{l=2}^{n-1}(a_{n-l-1}-a_{n-l}) \delta_{x}(\varphi\delta_{x} U)_{i}^{l-1}-a_{n-2} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \\& \quad =-\sum_{l=1}^{n-1}(a_{n-l-1}-a_{n-l}) \delta_{x}(\varphi\delta_{x} U)_{i}^{l-1}+(a_{n-2}-a_{n-1}) \delta_{x}(\varphi\delta_{x} U)_{i}^{0}-a_{n-2} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \\& \quad =-\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k-1}-a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0}, \end{aligned}$$

(39)

we have

$$\begin{aligned}& \frac{1}{2} \biggl\{ {}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl\{ \frac {\partial}{\partial x} \biggl[\varphi(x)\frac{\partial u}{\partial x} \biggr] \biggr\} (x_{i},t_{n})+{}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl\{ \frac {\partial}{\partial x} \biggl[\varphi(x)\frac{\partial u}{\partial x} \biggr] \biggr\} (x_{i},t_{n-1}) \biggr\} \\& \quad =\frac{t_{n}^{\alpha-1}+t_{n-1}^{\alpha-1}}{2\varGamma (\alpha )}\delta_{x}(\varphi\delta_{x} U)_{i}^{0}+\frac{1}{2}(R_{1})_{i}^{n}+ \frac {1}{2}(R_{1})_{i}^{n-1}+ \frac{\tau^{\alpha-1}}{2\varGamma (1+\alpha)} \\& \qquad {}\cdot \Biggl[\delta_{x}(\varphi\delta_{x} U)_{i}^{n}-\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k}-a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr]+\frac{\tau^{\alpha-1}}{2\varGamma (1+\alpha)} \\& \qquad {}\cdot \Biggl[\delta_{x}(\varphi\delta_{x} U)_{i}^{n-1}-\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi\delta_{x} U)_{i}^{k-1}-a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr] \\& \quad =\frac{t_{n}^{\alpha-1}+t_{n-1}^{\alpha-1}}{2\varGamma (\alpha)}\delta _{x}(\varphi\delta_{x} U)_{i}^{0}+(R_{1})_{i}^{n-\frac{1}{2}}+\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \\& \qquad {} \cdot\Biggl[\delta_{x}(\varphi\delta _{x} U)_{i}^{n-\frac{1}{2}}-\sum _{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi \delta_{x} U)_{i}^{k-\frac{1}{2}}-a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr]. \end{aligned}$$

(40)

Substituting (40) and (36) into (35), we have

$$\begin{aligned} \delta_{t}U_{i}^{n-\frac{1}{2}} =& \frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[\delta_{x}(\varphi\delta_{x} U)_{i}^{n-\frac{1}{2}}- \sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi \delta_{x} U)_{i}^{k-\frac{1}{2}} \\ &{} -a_{n-1} \delta_{x}(\varphi\delta_{x} U)_{i}^{0} \Biggr]+\frac{t_{n}^{\alpha -1}+t_{n-1}^{\alpha-1}}{2\varGamma (\alpha)}\delta_{x}( \varphi\delta_{x} U)_{i}^{0} +f_{i}^{n-\frac{1}{2}}+(R)_{i}^{n}, \end{aligned}$$

(41)

where $(R)_{i}^{n}=(R_{1})_{i}^{n-\frac{1}{2}}-(R_{2})_{i}^{n}$, $1\leq i\leq M-1$, $2\leq n\leq N$.

When $n=1$, using equality (34) at the point $(x_{i},t_{1})$ and employing the Taylor expansion, we have

$$\begin{aligned} \delta_{t} U_{i}^{\frac{1}{2}}&=\frac{\partial u}{\partial t}(x_{i},t_{1})-(R_{3})_{i} \\ &={}_{0} \mathcal{D}_{t}^{1-\alpha}\frac{\partial}{\partial x} \biggl[\varphi (x)\frac{\partial u}{\partial x} \biggr](x_{i},t_{1})+f(x_{i},t_{1})-(R_{3})_{i}, \end{aligned}$$

(42)

where

$$ (R_{3})_{i}=\tau \int_{0}^{1} \frac{\partial^{2} u}{\partial t^{2}}(x_{i},s \tau)s\,ds. $$

(43)

Using Lemma 4, we arrive at

$$\begin{aligned} \delta_{t} U_{i}^{\frac{1}{2}} =&\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)}\bigl[ \delta_{x}(\varphi\delta_{x} U)_{i}^{1}-a_{0} \delta_{x}(\varphi\delta _{x} U)_{i}^{0} \bigr]+\frac{\tau^{\alpha-1}}{\varGamma (\alpha)}\delta_{x}(\varphi\delta _{x} U)_{i}^{0} \\ &{}+f(x_{i},t_{1})+(R_{1})_{i}^{1}-(R_{3})_{i} \\ =&\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)}\bigl[\delta_{x}(\varphi\delta_{x} U)_{i}^{1}+(\alpha-1)\delta_{x}(\varphi \delta_{x} U)_{i}^{0}\bigr]+f_{i}^{1}+R_{i}, \end{aligned}$$

(44)

where

$$R_{i}=(R_{1})_{i}^{1}-(R_{3})_{i}, \quad 1\leq i\leq M-1. $$

By the previous analysis there exists a constant C, independent of h and τ, satisfying

$$\begin{aligned}& \bigl\vert R_{i}^{n}\bigr\vert \leq C\bigl( \tau^{1+\alpha}+h^{2}\bigr),\quad 1\leq i\leq M-1, 2\leq n\leq N, \end{aligned}$$

(45)

$$\begin{aligned}& \vert R_{i}\vert \leq C\bigl(\tau+h^{2}\bigr),\quad 1 \leq i\leq M-1. \end{aligned}$$

(46)

The initial and boundary conditions can be written as

$$\begin{aligned}& U_{0}^{n}=\varPhi _{1}(t_{n}),\qquad U_{M}^{n}=\varPhi _{2}(t_{n}),\quad 1\leq n \leq N, \end{aligned}$$

(47)

$$\begin{aligned}& U_{i}^{0}=\varPsi (x_{i}),\quad 0\leq i\leq M. \end{aligned}$$

(48)

Ignoring the truncation errors $R_{i}^{n}$ in (41) and $R_{i}$ in (44) and replacing the grid function $U_{i}^{n}$ with its numerical analog $u_{i}^{n}$, we arrive at the following difference scheme:

$$\begin{aligned}& \delta_{t} u_{i}^{n-\frac{1}{2}} =\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[ \delta_{x}(\varphi\delta_{x} u)_{i}^{n-\frac{1}{2}}- \sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi \delta_{x} u)_{i}^{k-\frac{1}{2}}-a_{n-1} \delta_{x}(\varphi \delta_{x} u)_{i}^{0} \Biggr] \\& \hphantom{\delta_{t} u_{i}^{n-\frac{1}{2}} ={}}{} +\frac{t_{n}^{\alpha-1}+t_{n-1}^{\alpha-1}}{2\varGamma (\alpha)} \delta _{x}(\varphi\delta_{x} u)_{i}^{0}+f_{i}^{n-\frac{1}{2}}, \quad 1\leq i\leq M-1,2\leq n\leq N, \end{aligned}$$

(49)

$$\begin{aligned}& \delta_{t} u_{i}^{\frac{1}{2}}=\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha )}\bigl[ \delta_{x}(\varphi\delta_{x} u)_{i}^{1}+( \alpha-1)\delta_{x}(\varphi\delta_{x} u)_{i}^{0} \bigr]+f_{i}^{1}, \quad 1\leq i\leq M-1, \end{aligned}$$

(50)

$$\begin{aligned}& u_{0}^{n}=\varPhi _{1}(t_{n}),\qquad u_{M}^{n}=\varPhi _{2}(t_{n}),\quad 1\leq n \leq N, \end{aligned}$$

(51)

$$\begin{aligned}& u_{i}^{0}=\varPsi (x_{i}),\quad 0\leq j\leq M. \end{aligned}$$

(52)

It is easy to see that, at each time level, the difference scheme (49)-(52) is a tridiagonal system with strictly diagonal dominant coefficient matrix, and thus the difference scheme has a unique solution, and the Thomas algorithm suits.

3 Analysis of stability and convergence of the CN-type difference scheme

3.1 Stability

Now we introduce necessary notation and lemmas, which will be used in the analysis of stability and convergence.

Define the grid function space $\mathcal{S}_{h}=\{u\mid u=(u_{0},u_{1},\ldots ,u_{M}), u_{0}=u_{M}=0\}$ on $\varOmega _{h}$. For any $v, w\in\mathcal{S}_{h}$, we define the discrete inner products and corresponding norms as follows:

$$\begin{aligned}& (v,w)_{h}=h\sum_{i=1}^{M-1}v_{i}w_{i}, \qquad \|v\|=\sqrt{(v,v)_{h}}, \\& \langle v,w\rangle=h\sum_{i=0}^{M-1} ( \delta_{x} v_{i+\frac{1}{2}} ) (\delta_{x} w_{i+\frac{1}{2}} ),\qquad \|\delta_{x} v\|=\sqrt{\langle v,v\rangle}, \\& (\delta_{x} u,\delta_{x} v)_{\varphi}=h\sum _{i=0}^{M-1}\varphi(x_{i+\frac {1}{2}}) ( \delta_{x} u_{i+\frac{1}{2}}) (\delta_{x} v_{i+\frac{1}{2}}), \qquad \| \delta_{x} u\|_{\varphi}=\sqrt{(\delta_{x} u,\delta_{x} u)_{\varphi}}, \\& \|v\|_{\infty}=\max_{0\leq i\leq M}|v_{i}|. \end{aligned}$$

Considering the smoothness of $\varphi(x)$, it is not hard to get

$$ \sqrt {c}_{1}\|\delta_{x} u\|\leq\| \delta_{x} u\|_{\varphi}\leq\sqrt {c}_{2}\| \delta_{x} u\|. $$

(53)

Lemma 5

[35]

For any grid function $u\in\mathcal{S}_{h}$,

$$\|u\|\leq\frac{L}{\sqrt{6}}\|\delta_{x} u\|. $$

We have the following properties of $a_{n}$.

Lemma 6

$$\begin{aligned}& 1=a_{0}>a_{1}>a_{2}\cdots>a_{n} \rightarrow0, \end{aligned}$$

(54)

$$\begin{aligned}& \alpha(n+1)^{\alpha-1}< a_{n}< \alpha n^{\alpha-1}, \end{aligned}$$

(55)

$$\begin{aligned}& a_{n-1}< \frac{1}{2}\bigl[\alpha n^{\alpha-1}+ \alpha(n-1)^{\alpha-1}\bigr],\quad n\geq 2, \end{aligned}$$

(56)

$$\begin{aligned}& \hat{a}_{n-1}< a_{n-1}, \qquad \hat{a}_{n-1}< a_{n-2}-a_{n-2}, \quad n\geq2, \end{aligned}$$

(57)

where $\hat{a}_{n-1}=\frac{1}{2}[\alpha n^{\alpha-1}+\alpha{(n-1)}^{\alpha-1}]-a_{n-1}$.

Proof

Noticing that $a_{n}=\alpha\int_{n}^{n+1}x^{\alpha-1}\,dx$ and $x^{\alpha -1}$ is a strictly convex and decreasing function, the first three relations hold.

From inequalities (54)-(56) we have

$$\begin{aligned} 4a_{n-1}-\bigl[\alpha n^{\alpha-1}+\alpha{(n-1)}^{\alpha-1} \bigr]&>3\alpha n^{\alpha-1}-\alpha{(n-1)}^{\alpha-1} \end{aligned}$$

(58)

$$\begin{aligned} & =\alpha n^{\alpha-1} \biggl[3- \biggl(\frac{n}{n-1} \biggr)^{1-\alpha} \biggr]>0 \end{aligned}$$

(59)

and

$$ a_{n-2}>\alpha{(n-1)}^{\alpha-1}>\frac{1}{2} \bigl[\alpha n^{\alpha-1}+\alpha {(n-1)}^{\alpha-1}\bigr], $$

(60)

so that (57) holds. □

We now give the proof of the stability of the difference scheme (49)-(52) with respect to the initial value $u_{i}^{0}$ and the inhomogeneous term f. We denote

$$f^{1}=\bigl(0,f_{1}^{1},f_{2}^{1}, \ldots,f_{M-1}^{1},0\bigr) $$

and

$$f^{n-\frac{1}{2}}=\bigl(0,f_{1}^{n-\frac{1}{2}},f_{2}^{n-\frac{1}{2}}, \ldots,f_{M-1}^{n-\frac{1}{2}},0\bigr),\quad 2\leq n\leq N. $$

Theorem 1

Let $u_{i}^{m}$, $0\leq i\leq M$, $1\leq m\leq N$, be a solution of the finite difference scheme (49)-(52) with $\varPsi _{1}=\varPsi _{2}=0$. Then we have

$$\begin{aligned} \bigl\Vert u^{m}\bigr\Vert ^{2} \leq& \bigl\Vert u^{0}\bigr\Vert ^{2} +\frac{\tau^{\alpha}}{ \varGamma (1+\alpha)} \bigl[(2-\alpha)^{2}+1\bigr]\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2} \\ &{}+\frac{L^{2}}{12c_{1}} \varGamma (1+\alpha)\tau^{2-\alpha }\cdot\bigl\Vert f^{1}\bigr\Vert ^{2} \\ &{} +\frac{L^{2}}{6c_{1}}\cdot \varGamma (\alpha)\tau\cdot T^{1-\alpha}\sum _{n=2}^{m}\bigl\Vert f^{n-\frac{1}{2}} \bigr\Vert ^{2}. \end{aligned}$$

(61)

Proof

Taking the inner product of (49) with $u^{n-\frac{1}{2}}$, we have

$$\begin{aligned} \bigl(\delta_{t} u^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr) =& \frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[ \bigl(\delta_{x} (\varphi \delta_{x} u)^{n-\frac{1}{2}}, u^{n-\frac{1}{2}} \bigr)-\sum _{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \\ &{}\cdot \bigl(\delta_{x} (\varphi\delta_{x} u)^{k-\frac{1}{2}}, u^{n-\frac{1}{2}} \bigr)+\hat{a}_{n-1} \bigl( \delta_{x} (\varphi\delta_{x} u)^{0}, u^{n-\frac {1}{2}} \bigr) \Biggr] \\ &{}+ \bigl(f^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr). \end{aligned}$$

(62)

Noticing that

$$\bigl(\delta_{t} u^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr)= \frac{1}{2\tau} \bigl(\bigl\Vert u^{n}\bigr\Vert ^{2}- \bigl\Vert u^{n-1}\bigr\Vert ^{2} \bigr) $$

and using the discrete Green formula and zero boundary conditions for every term in the right-hand side, we obtain

$$\begin{aligned} \frac{\|u^{n}\|^{2}-\|u^{n-1}\|^{2}}{2\tau} =&\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[- \bigl(\delta_{x} u^{n-\frac{1}{2}},\delta_{x} u^{n-\frac{1}{2}} \bigr)_{\varphi}+ \sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \\ &{}\cdot \bigl(\delta_{x} u^{k-\frac{1}{2}},\delta_{x} u^{n-\frac{1}{2}} \bigr)_{\varphi}-\hat{a}_{n-1} \bigl( \delta_{x} u^{0},\delta_{x} u^{n-\frac{1}{2}} \bigr)_{\varphi} \Biggr] \\ &{}+ \bigl(f^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr). \end{aligned}$$

(63)

Applying the Cauchy-Schwarz inequality, we have

$$\begin{aligned} \frac{\Vert u^{n}\Vert ^{2}-\Vert u^{n-1}\Vert ^{2}}{2\tau} \leq& \frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[-\bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2} +\frac{1}{2}\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \\ &{}\cdot\bigl(\bigl\Vert \delta_{x} u^{k-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}\bigr)+ \frac{\hat{a}_{n-1}}{2}\bigl(\bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2}\bigr) \Biggr] \\ &{}+\bigl\vert \bigl(f^{n-\frac {1}{2}},u^{n-\frac{1}{2}}\bigr)\bigr\vert . \end{aligned}$$

(64)

Letting $\frac{\tau^{r-1}}{\varGamma (1+r)}=I$, we have

$$\begin{aligned} \frac{\Vert u^{n}\Vert ^{2}-\Vert u^{n-1}\Vert ^{2}}{I\tau} \leq&-2\bigl\Vert \delta_{x} u^{n-\frac{1}{2}} \bigr\Vert _{\varphi}^{2}+(a_{0}-a_{n-1}) \bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+\frac{2}{I}| \bigl(f^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr)| \\ &{} +\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \bigl\Vert \delta_{x} u^{k-\frac {1}{2}}\bigr\Vert _{\varphi}^{2}+\hat{a}_{n-1}\bigl(\bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2}\bigr) \\ =&(\hat{a}_{n-1}-a_{n-1}-1)\bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2} \\ &{} + \hat{a}_{n-1}\bigl\Vert \delta_{x} u^{0} \bigr\Vert _{\varphi}^{2}+\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \bigl\Vert \delta_{x} u^{k-\frac{1}{2}}\bigr\Vert _{\varphi}^{2} \\ &{}+\frac{2}{I}\bigl\vert \bigl(f^{n-\frac{1}{2}},u^{n-\frac{1}{2}} \bigr)\bigr\vert . \end{aligned}$$

(65)

From (57) we know that

$$\begin{aligned} \begin{aligned} \frac{\Vert u^{n}\Vert ^{2}-\Vert u^{n-1}\Vert ^{2}}{I\tau} \leq{}&-\bigl\Vert \delta_{x} u^{n-\frac{1}{2}} \bigr\Vert _{\varphi}^{2}+(a_{n-2}-a_{n-1}) \bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2} \\ &{}+\sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \bigl\Vert \delta_{x} u^{k-\frac {1}{2}}\bigr\Vert _{\varphi}^{2}+\frac{2}{I}\bigl\vert \bigl(f^{n-\frac {1}{2}},u^{n-\frac{1}{2}}\bigr)\bigr\vert . \end{aligned} \end{aligned}$$

Summing up for $2\leq n\leq m$ and changing the summation order in the third term of the right-hand side, we get

$$\begin{aligned} \frac{\Vert u^{m}\Vert ^{2}-\Vert u^{1}\Vert ^{2}}{I\tau} \leq&-\sum_{n=2}^{m} \bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+(a_{0}-a_{m-1})\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2} \\ &{} +\sum_{k=1}^{m-1}\sum _{n=k+1}^{m}(a_{n-k-1}-a_{n-k})\bigl\Vert \delta_{x} u^{k-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \frac{2}{I}\sum_{n=2}^{m}\bigl\vert \bigl(f^{n-\frac{1}{2}},u^{n-\frac{1}{2}}\bigr)\bigr\vert \\ =&-\sum_{k=2}^{m}\bigl\Vert \delta_{x} u^{k-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+\sum_{k=1}^{m-1}(a_{0}-a_{m-k}) \bigl\Vert \delta_{x} u^{k-\frac{1}{2}}\bigr\Vert _{\varphi}^{2} \\ &{} +(a_{0}-a_{m-1})\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2}+\frac {2}{I} \sum_{n=2}^{m}\bigl|\bigl(f^{n-\frac{1}{2}}, u^{n-\frac{1}{2}}\bigr)\bigr| \\ =&\sum_{k=2}^{m-1}(-a_{m-k}) \bigl\Vert \delta_{x} u^{k-\frac {1}{2}}\bigr\Vert _{\varphi}^{2}-\bigl\Vert \delta_{x} u^{m-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+\frac{2}{I} \sum_{n=2}^{m}\bigl\vert \bigl(f^{n-\frac{1}{2}}, u^{n-\frac{1}{2}}\bigr)\bigr\vert \\ &{} +(a_{0}-a_{m-1}) \bigl(\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2}\bigr) \\ =&\sum_{k=2}^{m}(-a_{m-k}) \bigl\Vert \delta_{x} u^{k-\frac{1}{2}} \bigr\Vert _{\varphi}^{2}+(a_{0}-a_{m-1}) \bigl(\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2}\bigr) \\ &{} +\frac{2}{I}\sum_{n=2}^{m} \bigl\vert \bigl(f^{n-\frac{1}{2}}, u^{n-\frac{1}{2}}\bigr)\bigr\vert . \end{aligned}$$

(66)

Using the Cauchy inequality, (53), and Lemma 1, we have

$$ \frac{2}{I}\bigl\vert \bigl(f^{n-\frac{1}{2}}, u^{n-\frac{1}{2}}\bigr)\bigr\vert \leq\frac{L^{2}}{6c_{1}I^{2} a_{m-n}}\bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2}+a_{m-n}\bigl\Vert \delta_{x} u^{n-\frac{1}{2}}\bigr\Vert _{\varphi}^{2}. $$

(67)

Substituting (67) into (66), we have

$$ \bigl\Vert u^{m}\bigr\Vert ^{2}\leq\bigl\Vert u^{1}\bigr\Vert ^{2} +I\tau(a_{0}-a_{m-1}) \bigl(\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2} \bigr)+\sum _{n=2}^{m}\frac{\tau L^{2}}{6c_{1}I a_{m-n}}\bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2}. $$

(68)

Taking the inner product of (50) with $u^{n-\frac{1}{2}}$, we have

$$\begin{aligned} \frac{\Vert u^{1}\Vert ^{2}-\Vert u^{0}\Vert ^{2}}{2\tau} &=I \bigl[-\bigl(\delta_{x} u^{1}, \delta_{x} u^{\frac{1}{2}}\bigr)_{\varphi}+ (1-\alpha) \bigl( \delta_{x} u^{0},\delta_{x} u^{\frac{1}{2}} \bigr)_{\varphi}\bigr]+\bigl(f^{1},u^{\frac{1}{2}}\bigr) \\ &=I \bigl[-2\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ (2-\alpha) \bigl(\delta_{x} u^{0},\delta_{x} u^{\frac{1}{2}}\bigr)_{\varphi}\bigr]+\bigl(f^{1},u^{\frac{1}{2}}\bigr), \end{aligned}$$

so that

$$ \bigl\Vert u^{1}\bigr\Vert ^{2}=\bigl\Vert u^{0}\bigr\Vert ^{2}+I\tau \bigl[-4\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ 2(2-\alpha) \bigl(\delta_{x} u^{0},\delta_{x} u^{\frac{1}{2}}\bigr)_{\varphi}\bigr]+2\tau\bigl(f^{1},u^{\frac{1}{2}} \bigr). $$

(69)

Substituting (69) into (68) and using the Cauchy-Schwarz inequality again, we arrive at

$$\begin{aligned} \bigl\Vert u^{m}\bigr\Vert ^{2} \leq& \bigl\Vert u^{0}\bigr\Vert ^{2}+I\tau \bigl[-3\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ 2(2-\alpha) \bigl(\delta_{x} u^{0},\delta_{x} u^{\frac{1}{2}}\bigr)_{\varphi}\bigr] \\ &{} +I\tau a_{0}\bigl\Vert \delta_{x} u^{0} \bigr\Vert _{\varphi}^{2}+\sum_{n=2}^{m} \frac{\tau L^{2}}{6c_{1}I a_{m-n}}\bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2}+2\tau \bigl(f^{1},u^{\frac{1}{2}}\bigr) \\ \leq&\bigl\Vert u^{0}\bigr\Vert ^{2}-2I\tau\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+I\tau\bigl[ (2-\alpha)^{2}+1\bigr]\bigl\Vert \delta_{x} u^{0}\bigr\Vert _{\varphi}^{2} \\ &{} +\sum_{n=2}^{m}\frac{\tau L^{2}}{6c_{1}I a_{m-n}} \bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2}+2I\tau\bigl\Vert \delta_{x} u^{\frac{1}{2}}\bigr\Vert _{\varphi}^{2}+ \frac{L^{2}\tau }{12Ic_{1}}\bigl\Vert f^{1}\bigr\Vert ^{2}. \end{aligned}$$

(70)

Noticing that $a_{m-n}>a_{m-1}>\alpha m^{\alpha-1}>\alpha N^{\alpha -1}$, we have

$$\begin{aligned} \sum_{n=2}^{m}\frac{\tau L^{2}}{6c_{1}I a_{m-n}}\bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2} &\leq \frac{\tau L^{2}}{6c_{1}I \alpha N^{\alpha-1}}\sum _{n=2}^{m}\bigl\Vert f^{n-\frac{1}{2}} \bigr\Vert ^{2} \\ &=\frac{L^{2}}{6c_{1}}\cdot\frac{\tau^{2-\alpha} \varGamma (1+\alpha )}{\alpha N^{\alpha-1}}\sum_{n=2}^{m} \bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2} \\ &=\frac{L^{2}}{6c_{1}}\cdot \varGamma (\alpha)\tau\cdot T^{1-\alpha}\sum _{n=2}^{m}\bigl\Vert f^{n-\frac{1}{2}}\bigr\Vert ^{2}. \end{aligned}$$

(71)

Then, substituting (71) into (70), we get (61) for $2\leq m\leq N$, and (61) for $m=1$ is obvious. So the proof is completed. □

3.2 Convergence

We now consider the convergence of the difference scheme (49)-(52). Let

$$e_{i}^{n}=U_{i}^{n}-u_{i}^{n}, \quad 0\leq i\leq M, 0\leq n\leq N. $$

Subtracting (49)-(52) from (41)-(44) and (47)-(48), we get the equations for the error:

$$\begin{aligned}& \delta_{t} e_{i}^{n-\frac{1}{2}} =\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha)} \Biggl[ \delta_{x}(\varphi\delta_{x} e)_{i}^{n-\frac{1}{2}}- \sum_{k=1}^{n-1}(a_{n-k-1}-a_{n-k}) \delta_{x}(\varphi \delta_{x} e)_{i}^{k-\frac{1}{2}} \Biggr] +R_{i}^{n}, \\& \quad 1\leq i\leq M-1, 2\leq n\leq N, \end{aligned}$$

(72)

$$\begin{aligned}& \delta_{t} e_{i}^{\frac{1}{2}}=\frac{\tau^{\alpha-1}}{\varGamma (1+\alpha )} \delta_{x}(\varphi\delta_{x} e)_{i}^{1}+R_{i}, \quad 1\leq i\leq M-1, \end{aligned}$$

(73)

$$\begin{aligned}& e_{0}^{n}=0,\qquad e_{M}^{n}=0,\quad 1 \leq n\leq N, \end{aligned}$$

(74)

$$\begin{aligned}& e_{i}^{0}=0,\quad 0\leq i\leq M. \end{aligned}$$

(75)

Then from Theorem 1 we have

$$ \bigl\Vert e^{n}\bigr\Vert ^{2}\leq\frac{L^{2}}{12c_{1}} \varGamma (1+\alpha)\tau^{2-\alpha}\cdot \Vert R\Vert ^{2}+ \frac{L^{2}}{6c_{1}}\tau \varGamma (\alpha)T^{1-\alpha}\cdot\sum _{k=2}^{n}\bigl\Vert R^{k}\bigr\Vert ^{2}. $$

(76)

From (45) and (46) we have

$$\begin{aligned} \bigl\Vert e^{n}\bigr\Vert ^{2} &\leq\frac{L^{3}}{12c_{1}} \varGamma (1+\alpha)\tau^{2-\alpha}\bigl[c\bigl(\tau+h^{2}\bigr) \bigr]^{2} +\frac{L^{2}}{6c_{1}}N\tau \varGamma (\alpha)T^{1-\alpha}\bigl[c \bigl(\tau^{1+\alpha }+h^{2}\bigr)\bigr]^{2} \end{aligned}$$

(77)

$$\begin{aligned} &\leq\frac{L^{3}}{12c_{1}}\varGamma (1+\alpha) \bigl[c \bigl(\tau^{2-\frac{\alpha }{2}}+h^{2} \bigr) \bigr]^{2} +\frac{L^{2}}{6c_{1}}\varGamma (\alpha)T^{2-\alpha} \bigl[c\bigl(\tau^{1+\alpha}+h^{2}\bigr)\bigr]^{2}. \end{aligned}$$

(78)

Letting

$$ \beta=\min \biggl\{ 2-\frac{\alpha}{2},1+\alpha \biggr\} ,\qquad \hat{c}=Lc\sqrt{ \frac{\varGamma {(\alpha)}}{12c_{1}} \bigl(L\alpha+2T^{2-\alpha } \bigr)}, $$

we have the convergence in the $L_{2}$ norm.

Theorem 2

Suppose that problem (10)-(12) has a smooth solution $u(x,t)$ in the domain $[0,L]\times[0,T]$ and $u_{i}^{n}$, $0\leq i\leq M$, $1\leq n\leq N$, is a solution of the difference scheme (49)-(52). Then

$$ \max_{1\leq n\leq N} \bigl\Vert u\bigl(x_{i},t^{n} \bigr)-u_{i}^{n}\bigr\Vert \leq\hat{c} \bigl( \tau^{\beta}+h^{2}\bigr). $$

(79)

Remark

The Crank-Nicolson-type scheme involves two time levels for a Riemann-Liouville fractional subdiffusion equation with spatially variable coefficient. Therefore, we actually used recursion method to handle the analysis of stability. Then we get the convergence, and the convergence order in spatial direction is just two. It is difficult to improve the space accuracy by introducing a compact technique.

4 Numerical examples

In this section, we give two examples to testify the efficiency and convergence orders of our difference scheme.

Example 1

Consider the following problem with zero initial value:

$$\begin{aligned}& \frac{\partial u(x,t)}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl\{ \frac{\partial}{\partial x} \biggl[\bigl(x^{2}+1\bigr)\frac{\partial u}{\partial x} \biggr] \biggr\} +e^{x}(2+\alpha)t^{1+\alpha} \\& \hphantom{\frac{\partial u(x,t)}{\partial t}={}}{}-e^{x}(x+1)^{2} \cdot\frac{\varGamma (3+\alpha)}{\varGamma (2+2\alpha)}, \quad 0< x< 1, 0< t\leq1, \end{aligned}$$

(80)

$$\begin{aligned}& u(0,t)=t^{2+\alpha},\qquad u(1,t)=et^{2+\alpha},\quad 0< t \leq1, \end{aligned}$$

(81)

$$\begin{aligned}& u(x,0)=0,\quad 0\leq x\leq1. \end{aligned}$$

(82)

The exact solution is $u(x,t)=e^{x}t^{2+\alpha}$.

Let

$$\begin{aligned}& E_{L_{2}}(h,\tau)=\max_{1\leq n\leq N}\bigl\Vert u^{n}-U^{n}\bigr\Vert , \\& \operatorname{Order}(\tau)=\log_{2} \biggl(\frac{E_{L_{2}}(h,2\tau)}{E_{L_{2}}(h,\tau)} \biggr),\qquad \operatorname{Order}(h)=\log_{2} \biggl( \frac{E_{L_{2}}(2h,\tau)}{E_{L_{2}}(h,\tau)} \biggr). \end{aligned}$$

We solve problem (80)-(82) with the Crank-Nicolson-type scheme (49)-(52). Fixing the spatial step $h=1/1\text{,}000$ and taking different temporal steps, Table 1 presents the maximum $L_{2}$ norm errors and convergence orders of our schemes; fixing the temporal step $\tau =1/10\text{,}000$ and taking different spatial steps, Table 2 presents the $L_{2}$ norm errors and convergence orders in spatial direction. In both cases, we take α to be $1/3$, $1/2$, $2/3$. The results show that the Crank-Nicolson-type scheme has accuracy of order $1+\alpha$ in the temporal direction and order 2 in the spatial direction.

Table 1 The maximum $\pmb{L_{2}}$ errors and convergence orders for Example  1 where $\pmb{h=1/1\text{,}000}$

Table 2 The maximum $\pmb{L_{2}}$ errors and convergence orders for Example  1 where $\pmb{\tau=1/10\text{,}000}$

Example 2

Now we give a problem with nonzero initial value:

$$\begin{aligned}& \frac{\partial u(x,t)}{\partial t}={}_{0} \mathcal{D}_{t}^{1-\alpha} \biggl\{ \frac{\partial}{\partial x} \biggl[\bigl(x^{2}+1\bigr)\frac{\partial u}{\partial x} \biggr] \biggr\} +\cos(\pi x)\cdot(3+\alpha)t^{2+\alpha} \\& \hphantom{\frac{\partial u(x,t)}{\partial t}={}}{}+ \bigl[2\pi x \sin(\pi x)+\pi^{2} \bigl(x^{2}+1\bigr)\cos(\pi x) \bigr] \\& \hphantom{\frac{\partial u(x,t)}{\partial t}={}}{}\cdot \biggl[\frac{\varGamma (4+\alpha)}{\varGamma (3+2\alpha)}t^{2+2\alpha}+ \frac {1}{\varGamma (\alpha)}t^{\alpha-1} \biggr], \quad 0< x< 1,0< t\leq1, \end{aligned}$$

(83)

$$\begin{aligned}& u(0,t)=t^{3+\alpha}+1,\qquad u(1,t)=-t^{3+\alpha}-1,\quad 0< t \leq1, \end{aligned}$$

(84)

$$\begin{aligned}& u(x,0)=\cos(\pi x),\quad 0\leq x\leq1. \end{aligned}$$

(85)

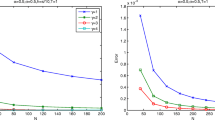
The exact solution is $u(x,t)=\cos(\pi x) (t^{3+\alpha}+1 )$. We solve problem (83)-(85) with the Crank-Nicolson-type scheme (49)-(52) and present the numerical results in Tables 3 and 4. The results show that our scheme is still efficient for nonzero initial value problems. In Figures 1 and 2, we plot surface figures of the error ($|u(x_{i},t_{n})-u_{i}^{n}|$) with different mesh sizes when $\alpha =0.1$, 0.9. These figures show that the maximum error becomes relatively smaller as the mesh size becomes smaller, which provides the validation of our results once more.

Figure 1

The error surface figures with $\pmb{h=\tau=\frac{1}{10}}$ (left) and $\pmb{h=\tau=\frac{1}{40}}$ (right) when $\pmb{\alpha=0.1}$ .

Figure 2

The error surface figures with $\pmb{h=\tau=\frac{1}{10}}$ (left) and $\pmb{h=\tau=\frac{1}{40}}$ (right) when $\pmb{\alpha=0.9}$ .

Table 3 The maximum $\pmb{L_{2}}$ errors and convergence orders for Example  2 with $\pmb{h=1/1\text{,}000}$

Table 4 The maximum $\pmb{L_{2}}$ errors and convergence orders for Example  2 with $\pmb{\tau=1/10\text{,}000}$

5 Conclusion

In this paper, we have presented a Crank-Nicolson-type difference scheme for the Riemann-Liouville fractional spatial variable coefficient subdiffusion equation. Based on the Crank-Nicolson technique and $L_{1}$ formula on the temporal direction, we proved that our difference scheme is unconditionally stable with respect to the initial value and the inhomogeneous term, and the numerical solution is convergent in the discrete $L_{2}$ norm. The convergence order is $\min \{2-\frac{\alpha}{2},1+\alpha \}$ in the temporal direction and two in the spatial direction. This scheme results in a linear system in which the coefficient matrix is a tridiagonal and strictly diagonally dominant, so it can be solved by the Thomas algorithm. Two numerical examples are given to show the efficiency of the method. It is meaningful to construct a second-order difference scheme of this type, which will be our work in the future.