1 Introduction

The compressible Euler equations are governed by

$$ \left \{ \textstyle\begin{array}{l} \rho_{t}+(\rho u)_{x} =0, \\ (\rho u)_{t}+(\rho u^{2}+p(\rho,s))_{x} =0, \\ ( \rho u^{2}/2+ \rho e)_{t}+(( \rho u^{2}/2+ \rho e +p(\rho,s))u)_{x} =0, \end{array}\displaystyle \right . $$
(1.1)

where the variables ρ, u, s, p, e denote density, velocity, specific entropy, pressure, and specific energy. Both p and e are given functions of ρ and s, satisfying the thermodynamical constraint

$$ T \, \mathrm{d} s =\mathrm{d} e + p\, \mathrm{d} \frac{1}{\rho}, $$
(1.2)

where \(T=T(\rho, s)\) is the temperature. Considerable progress has been made on the Riemann problems or other closely related problems for system (1.1) with the polytropic gas; see [1–4] and the references therein. Here, we concern ourselves with the equation of state

$$ p(\rho,s)=-A\rho^{-\alpha}, $$
(1.3)

which is called the generalized Chaplygin gas, where \(0<\alpha\le1\), \(A>0\) are constants. A substantial difference between the polytropic gas and the generalized Chaplygin gas is that the latter has a negative pressure with a positive sound speed. The generalized Chaplygin gas is used as a unified description for the recent accelerated expansion of the universe and the evolution of the perturbations of energy density. It has also emerged as a unification of dark energy and dark matter. Equation (1.3) with \(\alpha=1\) is called a Chaplygin gas, which was introduced by Chaplygin [5] and Tsien [6] as a mathematical approximation for calculating the lifting force on a wing of an airplane in aerodynamics. The reader is referred to [7–10] for more physical background on the generalized Chaplygin gas.

Recently, the (generalized) Chaplygin gas has attracted intensive attention. Brenier [11] considered the Riemann problem for the isentropic Euler equations

$$ \left \{ \textstyle\begin{array}{l} \rho_{t}+(\rho u)_{x} =0, \\ (\rho u)_{t}+(\rho u^{2}+p(\rho,s))_{x} =0, \end{array}\displaystyle \right . $$
(1.4)

with the Chaplygin gas, where the solutions with concentration were obtained when the initial data belong to a certain domain in the phase plane. Guo et al. [12] removed this constraint, and they obtained the delta shock wave solutions. Roughly speaking, the delta shock solution is a solution such that at least one of the state variables has a Dirac delta function [13]. Physically, the delta shock waves are interpreted as the process of formation of the galaxies in the universe, or the process of concentration of particles. For the theory of delta shock wave and its related topics, the reader is referred to [14] for a more detailed review. Wang [15] constructed the Riemann solutions to system (1.4) for the generalized Chaplygin gas, while the formation of a delta shock wave and vacuum state for system (1.4) as pressure vanishes was analyzed by Sheng et al. [16]. In addition, Sun [17] dealt with the Riemann problem of system (1.4) with the Coulomb-like friction term for the generalized Chaplygin gas, and the delta shock wave solutions were constructed. However, in contrast to the extensive investigations on the isentropic Euler equations (1.4) with the (generalized) Chaplygin gas, little literature contributed to the compressible Euler equations (1.1) with the (generalized) Chaplygin gas.

In [18], Kraiko studied the system (1.1) with \(p(\rho ,s)=0\), and the discontinuities which would be different from classical ones and carry mass, impulse, and energy, were introduced to construct the solution for arbitrary initial data. Since both density ρ and specific energy e involve the Dirac delta function, it is difficult to define the product of them. To avoid this difficulty, Nilsson et al. [19, 20] denoted the internal energy ρe by a new variable H and showed the processes of concentration of both mass and internal energy on the delta shock wave front. Subsequently, Cheng [21] solved the Riemann problem for (1.1) with \(p(\rho,s)=0\), where the delta shock wave with a Dirac delta function in both density and internal energy developed in the solutions. For the studies on the delta shock wave with a Dirac delta function in multiple state variables, the reader is referred to [14, 22–25]. Zhu and Sheng [26] obtained the solutions to the Riemann problem for system (1.1) with the Chaplygin gas. We notice that the delta shock wave with a Dirac delta function only in density issued in the solution. Motivated by the idea in [19, 20], in contrast to [26], we consider the compressible Euler equations of the form

$$ \left \{ \textstyle\begin{array}{l} \rho_{t}+(\rho u)_{x} =0, \\ (\rho u)_{t}+(\rho u^{2}+p(\rho,s))_{x} =0, \\ ( \rho u^{2}/2+ H)_{t}+(( \rho u^{2}/2+ H +p(\rho,s))u)_{x} =0, \end{array}\displaystyle \right . $$
(1.5)

where the state variable \(H \ge0\) is the internal energy.

We study the Riemann problem for (1.5) and (1.3) with the initial data

$$ (\rho, u, H) (0, x )= \left \{ \textstyle\begin{array}{l@{\quad}l} (\rho_{-}, u_{-}, H_{-}), & x< 0, \\ (\rho_{+}, u_{+}, H_{+}), & x> 0, \end{array}\displaystyle \right . $$
(1.6)

where \(\rho_{i} > 0\), \(u_{i}, H_{i} > 0\), \(i=-, + \), are different constants. In a recent paper, the case where \(\alpha=1\) was solved. It was found that a delta shock wave with Dirac delta function in both density and internal energy appeared in the solutions. Meanwhile, the formation mechanism of this kind of delta shock wave results from the overlapping of the linearly degenerate characteristic lines. In this article, we pay attention to the case where \(0<\alpha<1\).

In the generalized Chaplygin gas \(0<\alpha<1\), with the thermodynamical constraint (1.2), we first conduct the physically relevant region for system (1.5) and (1.3). Then, based on the projections of the classical wave curves onto the \((\rho, u)\)-plane, the Riemann problem is divided into two cases. In the case \(u_{-}-\sqrt {A}\rho_{-}^{-(1+\alpha)/2} < u_{+}+\sqrt{A}\rho_{+}^{-(1+\alpha)/2}\), by the analysis on the physically relevant region and the method of characteristic analysis, we obtain four kinds of exact solutions, which are the combination of a centered rarefaction wave, a shock wave, and a contact discontinuity. However, for the case \(u_{-}-\sqrt{A}\rho _{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho_{+}^{-(1+\alpha)/2}\), the Riemann problem cannot be solvable by a combination of these classical waves. In this case, we justify rigorously the phenomenon of the delta shock wave with a Dirac delta function in both density and internal energy. We then propose both a generalized Rankine-Hugoniot relation and an entropy condition for this type of delta shock wave. Using these relations, the delta shock wave solution is obtained in this case, in which both density and internal energy contain the Dirac delta function simultaneously. Meanwhile, the expressions for the location, speed, and weights of this type of delta shock wave are explicitly provided. Finally, we present the numerical results, performed by the Nessyahu-Tadmor scheme [27], to confirm this type of solution.

In our study, it is shown that the delta shock wave with Dirac delta function in both density and internal energy develops in the compressible Euler equations with the generalized Chaplygin gas. To the best of our knowledge, this type of delta shock wave has not been found in the previous studies on the generalized Chaplygin gas. Besides, the formation mechanism of this kind of delta shock wave in the generalized Chaplygin gas results from the overlapping of the linearly degenerate and genuinely nonlinear characteristic lines, which is substantially different from the case of the Chaplygin gas. Moreover, this type of delta shock wave has also been illustrated numerically.

This paper is organized as follows. In Section 2, we first clarify the physically relevant region for the system of generalized Chaplygin gas dynamics, then we deduce the classical wave curves. We also construct the solutions involving the classical waves. In Section 3, we analyze the phenomenon of the delta shock wave with Dirac delta function in both density and internal energy, and propose both a generalized Rankine-Hugoniot relation and an entropy condition of this type of delta shock wave. We also give the numerical results to confirm this type of delta shock wave. The conclusion is given in Section 4.

2 Solutions involving classical waves

2.1 Classical waves

We derive the physically relevant region for the system (1.5) and (1.3). One shows from (1.2) that \(T\, \mathrm{d} s =\mathrm{d} (e - \frac{A}{\alpha+1}\rho^{-(\alpha+1)}) \). Thus, there exists a function \(f(s)\) such that

$$ T=f'(s),\qquad e=\frac{A}{\alpha+1}\rho^{-(\alpha+1)}+f(s). $$

The positivity of e shows that the power function \(g(X)=\frac {A}{\alpha+1}X^{(\alpha+1)}+f(s)\), \(X \in(0, +\infty)\) takes positive values. This implies that \(f(s) \ge0\), namely, \(e-\frac{A}{\alpha +1}\rho^{-(\alpha+1)}\ge0\). Therefore, the physically relevant region is

$$ \aleph=\biggl\{ (\rho, u, H)\Big| \rho>0, H \ge\frac{A}{\alpha+1} \rho^{-\alpha }, u \in R\biggr\} . $$
(2.1)

The system (1.5) and (1.3) has three eigenvalues

$$ \lambda_{1}=u-\sqrt{A\alpha\rho^{-(\alpha+1)}}, \qquad \lambda_{2}=u, \qquad \lambda _{3}=u+\sqrt{A\alpha \rho^{-(\alpha+1)}}, $$
(2.2)

with the corresponding right eigenvectors

$$ r_{1}=\bigl(\rho,-\sqrt{A\alpha\rho^{-(\alpha+1)}},H+p \bigr)^{T},\qquad r_{2}=(0,0,1)^{T},\qquad r_{3}=\bigl(\rho,\sqrt{A\alpha\rho^{-(\alpha+1)}},H+p \bigr)^{T}, $$

satisfying \(\nabla\lambda_{1}\cdot r_{1} =\frac{\alpha-1}{2}\sqrt {A\alpha\rho^{-(\alpha+1)}}< 0\), \(\nabla\lambda_{3}\cdot r_{3} =\frac {1-\alpha}{2}\sqrt{A\alpha\rho^{-(\alpha+1)}} > 0\), \(\nabla\lambda _{2}\cdot r_{2} =0\). Hence, the first and third characteristic fields are genuinely nonlinear, while the second one is linearly degenerate.

Both (1.5) and (1.6) remain invariant under the transformation \((t,x) \to(\alpha t, \alpha x)\), \(\alpha>0\), so we need to seek a self-similar solution \((\rho, u, H)(\xi)\) (\(\xi=x/t\)). Therefore, the Riemann problem for (1.5), (1.3), and (1.6) can be reduced to the following boundary value problem at infinity:

$$ \left \{ \textstyle\begin{array}{l} -\xi\rho_{\xi}+(\rho u)_{\xi}=0, \\ -\xi(\rho u)_{\xi}+(\rho u^{2}+p)_{\xi}=0, \\ -\xi( \rho u^{2}/2 +H)_{\xi}+(( \rho u^{2}/2 +H+p)u)_{\xi}=0, \\ ( \rho, u, H)(\pm\infty)=(\rho_{\pm}, u_{\pm}, H_{\pm}). \end{array}\displaystyle \right . $$
(2.3)

For smooth solutions, we can rewrite (2.3) in the matrix form

$$ \begin{pmatrix} u-\xi& \rho& 0 \\ A\alpha\rho^{-(2+\alpha)} & (u-\xi) & 0 \\ 0 & H-A\rho^{-\alpha} & u-\xi \end{pmatrix} \begin{pmatrix} \rho \\ u \\ H \end{pmatrix} _{\xi}=0. $$
(2.4)

Thus, besides the constant solution \((\rho, u, H)= \mathrm{Const.}\), it provides either a backward centered rarefaction wave

$$ \overleftarrow{R}\mbox{:}\quad \xi=u-\sqrt{A\alpha\rho^{-(\alpha+1)}},\qquad \frac {\mathrm{d} u}{\mathrm{d} \rho}=-\sqrt{A\alpha}\rho^{-(\alpha+3)/2},\qquad \frac{\mathrm{d} H}{\mathrm{d} \rho} =(H+p)\rho^{-1}, $$
(2.5)

or a forward centered rarefaction wave

$$ \overrightarrow{R}\mbox{:}\quad \xi=u+\sqrt{A\alpha\rho^{-(\alpha+1)}},\qquad \frac {\mathrm{d} u}{\mathrm{d} \rho}=\sqrt{A\alpha}\rho^{-(\alpha+3)/2},\qquad \frac{\mathrm{d} H}{\mathrm{d} \rho} =(H+p)\rho^{-1}. $$
(2.6)

Given a left state \((\rho_{-},u_{-},H_{-})\), we integrate (2.5) and take the requirement \(\lambda_{1}(\rho_{-},u_{-}) < \lambda_{1}(\rho,u)\) to obtain the backward centered rarefaction wave curve

$$ \overleftarrow{R}(\rho_{-}, u_{-}, H_{-})\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \xi =u-\sqrt{A\alpha} \rho^{-(\alpha+1)/2}, \\ u =\frac{2\sqrt{A\alpha}}{1+\alpha}\rho^{-(\alpha+1)/2}+u_{-}- \frac{2\sqrt{A\alpha}}{1+\alpha}\rho_{-}^{-(\alpha+1)/2}, \\ H =\frac{A}{1+\alpha}\rho^{-\alpha}+\frac{\rho}{\rho_{-}}( H_{-}- \frac{A}{1+\alpha}\rho_{-}^{-\alpha}), \end{array}\displaystyle \right . \quad \rho< \rho_{-}, $$
(2.7)

which is the set of the states that can be connected to the left state \((\rho_{-},u_{-},H_{-})\) on the right by a backward centered rarefaction wave. Similarly, for a given right state \((\rho_{+},u_{+},H_{+})\), integrating (2.6) and using the requirement \(\lambda_{3}(\rho _{+},u_{+}) > \lambda_{3}(\rho,u)\), we derive the forward centered rarefaction wave curve

$$ \overrightarrow{R}(\rho_{+}, u_{+}, H_{+})\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \xi =u+\sqrt{A\alpha} \rho^{-(\alpha+1)/2}, \\ u =-\frac{2\sqrt{A\alpha}}{1+\alpha}\rho^{-(\alpha+1)/2}+u_{+}+ \frac{2\sqrt{A\alpha}}{1+\alpha}\rho_{+}^{-(\alpha+1)/2}, \\ H =\frac{A}{1+\alpha}\rho^{-\alpha}+\frac{\rho}{\rho_{+}}( H_{+}- \frac{A}{1+\alpha}\rho_{+}^{-\alpha}), \end{array}\displaystyle \right .\quad \rho< \rho_{+}, $$
(2.8)

which consists of the states that can be joined with the right state \((\rho_{+},u_{+},H_{+})\) on the left by a forward centered rarefaction wave.

For a bounded discontinuous solution with a discontinuity \(\xi=\omega\), the Rankin-Hugoniot condition for (1.5) and (1.3) is

$$ \left \{ \textstyle\begin{array}{l} -\omega[\rho]+[\rho u] =0, \\ -\omega[\rho u]+[\rho u^{2}+p] =0, \\ -\omega[ \rho u^{2}/2 +H]+[( \rho u^{2}/2 +H+p)u] =0, \end{array}\displaystyle \right . $$
(2.9)

where ω is the velocity of the discontinuity, and \([G]= G_{+}-G_{-} \), with \(G_{-}\) and \(G_{+}\) the values of the function G on the left and right-hand sides of the discontinuity, is the jump of G across the discontinuity. We obtain by calculating (2.9) either a backward shock wave

$$ \overleftarrow{S}\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \omega =u_{-}-\sqrt{\frac{\rho_{+}[p]}{\rho_{-}[\rho]}} =u_{+}-\sqrt{\frac{\rho_{-}[p]}{\rho_{+}[\rho]}}, \\ {[u]} =-\sqrt{\frac{[p]}{\rho_{+}\rho_{-}[\rho]}}[\rho], \qquad [H]=\rho ^{-1}_{-}(H_{-}+\frac{1}{2}(p_{+}+p_{-}))[\rho], \end{array}\displaystyle \right . $$
(2.10)

a contact discontinuity

$$ J\mbox{:}\quad \omega=u_{-}=u_{+}, \qquad [ \rho]=0, \qquad [u]=0,\qquad [H] \neq0, $$
(2.11)

or a forward shock wave

$$ \overrightarrow{S}\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \omega =u_{-}+\sqrt{\frac{\rho_{+}[p]}{\rho_{-}[\rho]}} =u_{+}+\sqrt{\frac{\rho_{-}[p]}{\rho_{+}[\rho]}}, \\ {[u]} =\sqrt{\frac{[p]}{\rho_{+}\rho_{-}[\rho]}}(\rho_{+}-\rho_{-}),\qquad {[H]}=\rho^{-1}_{+}(H_{+}+\frac{1}{2}(p_{+}+p_{+}))[\rho]. \end{array}\displaystyle \right . $$
(2.12)

For a given left state \((\rho_{-},u_{-},H_{-})\), by (2.10) and the entropy condition of the shock wave

$$ \lambda_{1}(\rho,u) < \omega< \lambda_{1}( \rho_{-},u_{-}),\qquad \omega< \lambda_{2}( \rho,u), $$
(2.13)

a backward shock wave curve can be expressed as

$$ \overleftarrow{S}(\rho_{-}, u_{-}, H_{-})\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \omega =u_{-}-\sqrt{\frac{\rho[p]}{\rho_{-}[\rho]}} =u-\sqrt{\frac{\rho_{-}[p]}{\rho[\rho]}}, \\ u =u_{-}-\sqrt{\frac{[p]}{\rho\rho_{-}[\rho]}}(\rho-\rho_{-}), \\ H =-\frac{1}{2}(p+p_{-})+\frac{\rho}{\rho_{-}}(H_{-}+\frac{1}{2}(p+p_{-})), \end{array}\displaystyle \right .\quad \rho>\rho_{-}, $$
(2.14)

which is the set of the states that can be connected to the left state \((\rho_{-},u_{-},H_{-})\) on the right by a backward shock wave. Using (2.11), it is easy to obtain a contact discontinuity curve

$$ J(\rho_{-}, u_{-}, H_{-})\mbox{:} \quad \omega=u=u_{-}, \qquad \rho=\rho_{-},\qquad u=u_{-},\qquad H \neq H_{-}, $$
(2.15)

which is the set of the states that can be joined with the left state \((\rho_{-},u_{-},H_{-})\) by a contact discontinuity. Besides, for a given right state \((\rho_{+},u_{+},H_{+})\), using (2.12) and the entropy condition of a shock wave,

$$ \lambda_{3}(\rho_{+},u_{+})< \omega< \lambda_{3}(\rho,u),\qquad \omega> \lambda_{2}(\rho,u), $$
(2.16)

we obtain a forward shock wave curve

$$ \overrightarrow{S}(\rho_{+}, u_{+}, H_{+})\mbox{:}\quad \left \{ \textstyle\begin{array}{l} \omega =u_{+}+\sqrt{\frac{\rho[p]}{\rho_{+}[\rho]}} =u+\sqrt{\frac{\rho_{+}[p]}{\rho[\rho]}}, \\ u =u_{+}+\sqrt{\frac{[p]}{\rho\rho_{+}[\rho]}}(\rho-\rho_{+}), \\ H =-\frac{1}{2}(p+p_{+})+\frac{\rho}{\rho_{+}}(H_{+}+\frac{1}{2}(p+p_{+})), \end{array}\displaystyle \right .\quad \rho>\rho_{+}, $$
(2.17)

which is the set of the states that can be connected to the right state \((\rho_{+},u_{+},H_{+})\) on the left by a forward shock wave.

Thus, the classical waves of system (1.5) and (1.3) contain a centered rarefaction wave, a shock wave, and a contact discontinuity.

2.2 Solutions involving the classical waves

On the physically relevant region ℵ, from the left state \(A(\rho _{-}, u_{-}, H_{-})\), we draw the curves \(\overleftarrow{R}(\rho_{-}, u_{-}, H_{-})\), \(\overleftarrow{S}(\rho_{-}, u_{-}, H_{-})\), \(\overrightarrow{R}(\rho_{-}, u_{-}, H_{-})\), and \(\overrightarrow {S}(\rho_{-}, u_{-}, H_{-})\), and from the right state \(B(\rho_{+}, u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha +1)/2}+\rho_{+}^{-(\alpha+1)/2}), H_{+})\), we draw the curves \(\overrightarrow{R}(\rho_{+}, u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha +1)/2}+\rho_{+}^{-(\alpha+1)/2}), H_{+})\), and \(\overrightarrow{S}(\rho _{+}, u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha +1)/2}), H_{+})\), where the curve \(\overrightarrow{R}(\rho_{-}, u_{-}, H_{-})\) is determined by

$$ \left \{ \textstyle\begin{array}{l} \xi =u+\sqrt{A\alpha} \rho^{-(\alpha+1)/2}, \\ u =-\frac{2\sqrt{A\alpha}}{1+\alpha}\rho^{-(\alpha+1)/2}+u_{-}+ \frac{2\sqrt{A\alpha}}{1+\alpha}\rho_{-}^{-(\alpha+1)/2}, \\ H =\frac{A}{1+\alpha}\rho^{-\alpha}+\frac{\rho}{\rho_{-}}( H_{-}- \frac{A}{1+\alpha}\rho_{-}^{-\alpha}), \end{array}\displaystyle \right .\quad \rho_{-} < \rho, $$
(2.18)

which consists of the right states that can be connected with the left state \(A(\rho_{-}, u_{-}, H_{-})\) on the right by a forward centered rarefaction wave, the curve \(\overrightarrow{S}(\rho_{-}, u_{-}, H_{-})\) is defined by

$$ \left \{ \textstyle\begin{array}{l} \omega =u_{-}+\sqrt{\frac{\rho[p]}{\rho_{-}[\rho]}} =u+\sqrt{\frac{\rho_{-}[p]}{\rho[\rho]}}, \\ u =u_{-}+\sqrt{\frac{[p]}{\rho\rho_{-}[\rho]}}(\rho-\rho_{-}), \\ H =-\frac{1}{2}(p+p_{-})+\frac{\rho}{\rho_{-}}(H_{-}+\frac {1}{2}(p+p_{-})), \end{array}\displaystyle \right .\quad \rho< \rho_{-}, $$
(2.19)

which is composed of the right states which can be joined with the left state \(A(\rho_{-}, u_{-}, H_{-})\) on the right by a forward shock wave, and the curve \(\overrightarrow{R}(\rho_{+}, u_{-}-\sqrt{A}(\rho _{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha+1)/2}), H_{+})\) is given by

$$ \left \{ \textstyle\begin{array}{l} \xi =u+\sqrt{A\alpha} \rho^{-(\alpha+1)/2}, \\ u =-\frac{2\sqrt{A\alpha}}{1 +\alpha}\rho^{-(\alpha+1)/2}+u_{-}- \sqrt {A} (\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha+1)/2}) \\ \hphantom{u ={}}{}+ \frac{2\sqrt{A\alpha}}{1+\alpha}\rho_{+}^{-(\alpha+1)/2} , \\ H =\frac{A}{1+\alpha}\rho^{-\alpha}+\frac{\rho}{\rho_{+}}( H_{+}- \frac{A}{1+\alpha}\rho_{+}^{-\alpha}), \end{array}\displaystyle \right .\quad \rho < \rho_{+}, $$
(2.20)

which consists of the states that can be connected with the right state \(B(\rho_{+}, u_{-} -\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha +1)/2}), H_{+})\) on the left by a forward centered rarefaction wave, and the curve \(\overrightarrow{S}(\rho_{+}, u_{-}-\sqrt{A}(\rho _{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha+1)/2}), H_{+})\) is expressed by

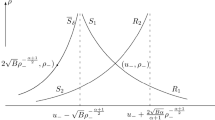
$$ \left \{ \textstyle\begin{array}{l} \omega =u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha +1)/2})+\sqrt{\frac{\rho[p]}{\rho_{+}[\rho]}} =u+\sqrt{\frac{\rho_{+}[p]}{\rho[\rho]}}, \\ u =u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha +1)/2})+\sqrt{\frac{[p]}{\rho\rho_{+}[\rho]}}(\rho-\rho_{+}), \\ H =-\frac{1}{2}(p+p_{+})+\frac{\rho}{\rho_{+}}(H_{+}+\frac {1}{2}(p+p_{+})), \end{array}\displaystyle \right .\quad \rho> \rho_{+}, $$
(2.21)

which is the set of the states that can be joined with the right state \(B(\rho_{+},u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha +1)/2}),H_{+})\) on the left by a forward shock wave. The projections of these curves onto the \((\rho, u)\)-plane are denoted by \(\overleftarrow{R}_{\rho u}(\rho_{-}, u_{-},H_{-})\), \(\overleftarrow{S}_{\rho u}(\rho_{-}, u_{-}, H_{-})\), \(\overrightarrow{R}_{\rho u}(\rho_{-}, u_{-}, H_{-})\), \(\overrightarrow{S}_{\rho u}(\rho_{-}, u_{-}, H_{-})\), \(\overrightarrow{R}_{\rho u}(\rho_{+}, u_{-}- \sqrt{A}\cdot (\rho _{-}^{-(\alpha+1)/2} +\rho_{+}^{-(\alpha+1)/2}), H_{+})\), \(\overrightarrow{S}_{\rho u}(\rho_{+}, u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha +1)/2}+\rho_{+}^{-(\alpha+1)/2}), H_{+})\), which have the straight lines \(\rho=0\), \(u=u_{-}-\sqrt{A}\rho _{-}^{-(1+\alpha)/2}\), \(u=u_{-}+\frac{2\sqrt{A\alpha}}{1+\alpha}\rho_{-}^{-(1+\alpha)/2}\), \(\rho=0\), \(\rho=0\), \(u=u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2}\) as their asymptotes. These projections divide the \((\rho, u)\)-plane into five regions, as shown in Figure 1.

Figure 1
figure 1

The projections of the curves \(\pmb{\overleftarrow{S}}\) , \(\pmb{\overleftarrow{R}}\) ,  \(\pmb{\overrightarrow{S}}\) , \(\pmb{\overrightarrow{R}}\) onto the \(\pmb{(\rho, u)}\) -plane.

Full size image

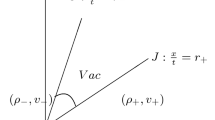
When the projection of the state \((\rho_{+}, u_{+}, H_{+})\) onto the \((\rho, u)\)-plane lies in \(I\cup \mathit{II}\cup \mathit{III} \cup \mathit{IV}\), namely, \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} < u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\), the Riemann problem can be solved in the following way. On the physically relevant region ℵ, we draw the backward wave curve \(\overleftarrow{R}(\rho_{-}, u_{-}, H_{-})\) or \(\overleftarrow{S}(\rho _{-}, u_{-}, H_{-})\), and the forward wave curve \(\overrightarrow {R}(\rho_{+}, u_{+}, H_{+})\) or \(\overrightarrow{S}(\rho_{+}, u_{+}, H_{+})\). The projections of these curves onto the \((\rho, u)\)-plane have a unique intersection point \((\rho_{\star},u_{\star})\). Then we draw the contact discontinuity curve \(J(\rho_{\star},u_{\star}, H_{-})\), which intersects the backward and forward wave curves at the unique points \((\rho_{\star_{1}},u_{\star_{1}}, H_{\star_{1}})\) and \((\rho_{\star_{2}},u_{\star_{2}}, H_{\star_{2}})\). Hence, we obtain four kinds of exact solutions, as shown in Figures 2-5. The conclusion is stated by the following theorem.

Figure 2
figure 2

The structure of solution as the projection of state ⊕ onto \(\pmb{(\rho, u)}\) -plane lies in I .

Full size image
Figure 3
figure 3

The structure of solution as the projection of state ⊕ onto \(\pmb{(\rho, u)}\) -plane lies in II .

Full size image

Theorem 1

On the physically relevant region ℵ, under the condition \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} < u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\), the Riemann problem (1.5), (1.3), and (1.6) admits four kind of exact solutions, which consist of a centered rarefaction wave, a shock wave, and a contact discontinuity besides the constant states.

3 Delta shock wave solution

3.1 Delta shock wave with Dirac delta function in both density and internal energy

We solve the Riemann problem (1.5), (1.3), and (1.6) when the projection of the state \((\rho_{+}, u_{+}, H_{+})\) onto the \((\rho, u)\)-plane lies in V, namely,

$$ u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}. $$
(3.1)

The characteristic line defined by \(x/t=\lambda_{i}\), \(i=1,2,3\) from the initial data will overlap in the domain \(\varOmega = \{(t,x)|(u_{+}+\sqrt {A\alpha}\rho_{+}^{-(1+\alpha)/2})t \le x \le(u_{-}-\sqrt{A\alpha}\rho _{-}^{-(1+\alpha)/2})t ,0\le t < +\infty\}\), as illustrated in Figure 6. Hence, the singularity will develop in Ω, while this singularity cannot be a jump with finite amplitudes.

To analyze the singularity in Ω, we first study the special case \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} = u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\). Let us consider the limit of the solution \(\rho (\xi)\), \(u(\xi)\), and \(H(\xi)\) when \(\rho_{-}\), \(u_{-}\), \(H_{-}\), \(\rho _{+}\), \(H_{+}\) are fixed, \(u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha +1)/2} +\rho_{+}^{-(\alpha+1)/2})+0\). When \(u_{+} > u_{-}-\sqrt{A}(\rho _{-}^{-(\alpha+1)/2}+\rho_{+}^{-(\alpha+1)/2})\) and the projection of the state \((\rho_{+}, u_{+}, H_{+})\) on the \((\rho, u)\)-plane lies in III, the solution is depicted in Figure 4, where

$$ \left \{ \textstyle\begin{array}{l} \rho_{\star_{1}} =\rho_{\star_{2}}=\rho_{\star},\qquad u_{\star_{1}}=u_{\star _{2}}=u_{\star}, \\ H_{\star_{1}} =\frac{1}{2}A(\rho_{-}^{-\alpha}+\rho_{\star}^{-\alpha}) +\frac{\rho_{\star}}{\rho_{-}}(H_{-}- \frac{1}{2}A(\rho_{-}^{-\alpha}+\rho_{\star}^{-\alpha})), \\ H_{\star_{2}} =\frac{1}{2}A(\rho_{+}^{-\alpha}+\rho_{\star}^{-\alpha}) +\frac{\rho_{\star}}{\rho_{+}}(H_{+}- \frac{1}{2}A(\rho_{+}^{-\alpha}+\rho_{\star}^{-\alpha})), \end{array}\displaystyle \right . $$
(3.2)

and \(u_{\star}\), \(\rho_{\star}\) are uniquely determined by

$$ \left \{ \textstyle\begin{array}{l} u_{\star}=u_{-}-\sqrt{\frac{A(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha})}{\rho_{\star}\rho_{-}(\rho_{\star}-\rho_{-})}}(\rho_{\star}-\rho_{-}),\quad \rho_{\star}>\rho_{-}, \\ u_{\star}=u_{+}+\sqrt{\frac{A(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha})}{\rho_{\star}\rho_{+}(\rho_{\star}-\rho_{+})}}(\rho_{\star}-\rho_{+}),\quad \rho_{\star}>\rho_{+}. \end{array}\displaystyle \right . $$
(3.3)

From (3.3), one shows that

$$\begin{aligned} u_{+} =&u_{-}-\sqrt{ \frac{A(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}\rho_{-}(\rho_{\star}-\rho_{-})}}(\rho_{\star}-\rho_{-}) -\sqrt{ \frac{A(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}\rho_{+}(\rho_{\star}-\rho_{+})}}(\rho_{\star}-\rho_{+}) \\ =&u_{-}-\sqrt{A}\sqrt{\bigl(\rho_{-}^{-1}- \rho_{\star}^{-1}\bigr) \bigl(\rho_{-}^{-\alpha}- \rho_{\star}^{-\alpha}\bigr)}- \sqrt{A}\sqrt{\bigl(\rho_{+}^{-1}- \rho_{\star}^{-1}\bigr) \bigl(\rho_{+}^{-\alpha}- \rho_{\star}^{-\alpha}\bigr)}. \end{aligned}$$
(3.4)

Besides, according to (2.1), one obtains that

$$ H_{-}- \frac{1}{2}A\rho_{-}^{-\alpha} >H_{-}-\frac{A}{1+\alpha}\rho_{-}^{-\alpha}\ge0,\qquad H_{+}- \frac {1}{2}A\rho_{+}^{-\alpha} >H_{+}-\frac{A}{1+\alpha}\rho_{+}^{-\alpha}\ge0. $$
(3.5)

Thus, as \(u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0\), the combination of (3.2)-(3.5) yields

$$ \left \{ \textstyle\begin{array}{l} \rho_{\star_{1}}=\rho_{\star_{2}}=\rho_{\star} \to\infty,\qquad H_{\star _{1}} \to\infty,\qquad H_{\star_{2}} \to\infty, \\ u_{\star_{1}}=u_{\star_{2}}=u_{\star} \to u_{+}+ \sqrt{A}\rho _{+}^{-(\alpha+1)/2}= u_{-}-\sqrt{A}\rho_{-}^{-(\alpha+1)/2}, \end{array}\displaystyle \right . $$
(3.6)

and then \(\overleftarrow{S}\), J and \(\overrightarrow{S}\) coincide to form a new singularity.

Figure 4
figure 4

The structure of solution as the projection of state ⊕ onto \(\pmb{(\rho, u)}\) -plane lies in III .

Full size image
Figure 5
figure 5

The structure of solution as the projection of state ⊕ onto \(\pmb{(\rho, u)}\) -plane lies in IV .

Full size image
Figure 6
figure 6

The characteristic lines when \(\pmb{u_{-}-\sqrt{A}\rho _{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho_{+}^{-(1+\alpha )/2}}\) .

Full size image

Let us calculate the total quantities of ρ, u and H between \(\overleftarrow{S}\) and \(\overrightarrow{S}\) as \(\rho_{-}\), \(u_{-}\), \(H_{-}\), \(\rho_{+}\), \(H_{+}\) are fixed, \(u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha +1)/2}+\rho_{+}^{-(\alpha+1)/2})+0\), and the projection of the state \((\rho_{+}, u_{+}, H_{+})\) on the \((\rho, u)\)-plane lies in III,

$$\begin{aligned}& \lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}\rho(\xi )\, \mathrm{d}\xi \\ & \quad =\lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}\rho_{\star }\, \mathrm{d}\xi \\ & \quad =\lim_{\rho_{\star} \to\infty}\rho_{\star} \biggl(\sqrt{A \frac{\rho _{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{+})}}+\sqrt{A\frac{\rho_{-}(\rho _{-}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{-})}} \biggr) \\ & \quad =\sqrt{A}\bigl(\rho_{-}^{(1-\alpha)/2}+\rho_{+}^{(1-\alpha)/2} \bigr) \\ & \quad \neq 0, \end{aligned}$$
(3.7)
$$\begin{aligned}& \lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}u(\xi)\, \mathrm{d}\xi \\ & \quad =\lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}u_{\star }\, \mathrm{d}\xi \\ & \quad =\lim_{\rho_{\star} \to\infty}u_{\star} \biggl(\sqrt{A \frac{\rho _{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{+})}}+\sqrt{A\frac{\rho_{-}(\rho _{-}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{-})}} \biggr) \\ & \quad =0, \end{aligned}$$
(3.8)
$$\begin{aligned}& \lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}H(\xi)\, \mathrm{d}\xi \\& \quad =\lim_{u_{+} \to u_{-}-\sqrt{A}(\rho_{-}^{-(\alpha+1)/2}+\rho _{+}^{-(\alpha+1)/2})+0} \biggl( \int_{u_{\star}-(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{-})^{-1} \rho_{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}}^{u_{\star}}H_{\star_{1}}\, \mathrm{d}\xi \\& \qquad {}+ \int_{u_{\star}}^{u_{\star}+(A\rho_{\star}^{-1}(\rho_{\star}-\rho_{+})^{-1} \rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star}^{-\alpha}))^{1/2}} H_{\star_{2}}\, \mathrm{d}\xi \biggr) \\& \quad =\lim_{\rho_{\star} \to\infty} \biggl(H_{\star_{1}}\sqrt{A \frac{\rho _{-}(\rho_{-}^{-\alpha}-\rho_{\star}^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{-})}} +H_{\star_{2}}\sqrt{A\frac{\rho_{+}(\rho_{+}^{-\alpha}-\rho_{\star }^{-\alpha})}{ \rho_{\star}(\rho_{\star}-\rho_{+})}} \biggr) \\& \quad =\sqrt{A}\biggl(\rho_{-}^{-(1+\alpha)/2}\biggl(H_{-}- \frac{A}{2}\rho_{-}^{-\alpha}\biggr) +\rho_{+}^{-(1+\alpha)/2} \biggl(H_{+}-\frac{A}{2}\rho_{+}^{-\alpha}\biggr) \biggr) \\& \quad \neq 0. \end{aligned}$$
(3.9)

Equations (3.7)-(3.9) show that \(\rho(\xi)\) and \(H(\xi)\) have the same singularity as a weighed Dirac delta function at \(\xi=u_{-}-\sqrt{A}\rho_{-}^{-(\alpha+1)/2}\), and that \(u(\xi)\) has a bounded variation. Thus, the singularity in Ω is a delta shock wave with a Dirac delta function in both ρ and H. Besides, the inequality

$$ \lambda_{1}(\rho_{+},u_{+})< \lambda_{2}(\rho_{+},u_{+})< \lambda _{3}(\rho_{+},u_{+}) < \sigma< \lambda_{1}(\rho_{-},u_{-})< \lambda_{2}( \rho_{-},u_{-})< \lambda_{3}( \rho_{-},u_{-}), $$

holds, where \(\sigma=u_{-}-\sqrt{A}\rho_{-}^{-(\alpha+1)/2}=u_{+}+\sqrt {A}\rho_{+}^{-(\alpha+1)/2}\) is the velocity of the delta shock wave. It means that none of the six characteristic lines on both sides of the delta shock wave is outgoing.

By the above analysis, for the general case \(u_{-}-\sqrt{A}\rho _{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho_{+}^{-(1+\alpha)/2}\), the delta shock wave solution which contains a Dirac delta function in both ρ and H is suggested. We first give two definitions.

Definition 1

The two-dimensional weighted delta function \(w(s)\delta_{L} \) supported on a smooth curve L parameterized as \(x=x(s)\), \(y=y(s)\) (\(c \leq s \leq d\)) is defined as

$$ \bigl\langle w(s)\delta_{L}, \phi(x,y) \bigr\rangle = \int_{c}^{d}w(s) \phi\bigl(x(s),y(s)\bigr)\, \mathrm{d}s, $$
(3.10)

for all the test functions \(\phi\in C_{0}^{\infty}(R^{ 2})\).

Definition 2

The triple distribution \((\rho, u, H)\) is a delta shock wave solution of (1.5) and (1.3) in the sense of distribution if there exist a smooth curve L and two functions \(w(t),h(t) \in C^{1}(L)\) such that ρ, u, H are of the following form:

$$ \rho=\bar{\rho}(t,x) +w(t)\delta_{L},\qquad u= \bar{u}(t,x),\qquad H = \bar {H}(t,x) +h(t)\delta_{L}, $$
(3.11)

and

$$ \left \{ \textstyle\begin{array}{l} \langle \rho, \phi_{t} \rangle + \langle \rho u, \phi_{x} \rangle =0, \\ \langle \rho u, \phi_{t} \rangle + \langle \rho u^{2}+ p, \phi_{x} \rangle =0, \\ \langle \rho u^{2}/2+H, \phi_{t} \rangle + \langle (\rho u^{2}/2+H+p)u, \phi_{x} \rangle =0, \end{array}\displaystyle \right . $$
(3.12)

for all the test functions \(\phi\in C_{0}^{\infty}( (0, +\infty) \times R)\), where \(\bar{\rho}, \bar{u}, \bar{H} \in L^{\infty}([0, +\infty) \times R; R)\), \(u|_{L}=u_{\delta}(t)\),

$$\begin{aligned}& \langle \rho, \phi \rangle = \int_{0}^{+\infty} \int_{-\infty}^{+\infty} \bar{\rho }(t,x)\phi \,\mathrm{d}x\, \mathrm{d}t +\bigl\langle w(t)\delta_{L},\phi\bigr\rangle , \\& \langle \rho u, \phi \rangle = \int_{0}^{+\infty} \int_{-\infty}^{+\infty}\bar{\rho } \bar{u}(t,x)\phi \, \mathrm{d}x\,\mathrm{d}t +\bigl\langle w(t)u_{\delta}(t) \delta_{L},\phi\bigr\rangle , \end{aligned}$$

and H has the similar integral identities as above.

With Definitions 1-2, we seek a delta shock wave solution with the discontinuity \(x=x(t)\) to (1.5) and (1.3) in the form

$$ (\rho, u, H) (t, x)= \left \{ \textstyle\begin{array}{l@{\quad}l} (\rho_{-}, u_{-}, H_{-}), & x< x(t), \\ (w(t)\delta(x-x(t)), u_{\delta}(t), h(t)\delta(x-x(t))), & x=x(t), \\ (\rho_{+}, u_{+}, H_{+}), & x > x(t), \end{array}\displaystyle \right . $$
(3.13)

where \((\rho_{i}, u_{i}, H_{i})\), \(i= -,+\) are smooth bounded solutions to (1.5) and (1.3), δ is the standard Dirac measure supported on the curve \(x(t)\), and \(w(t)\), \(h(t)\) are the weights of the delta shock wave on the state variables ρ, H. Besides, we define

$$ p=\left \{ \textstyle\begin{array}{l@{\quad}l} -A\rho_{-}^{-\alpha}, & x< x(t), \\ 0, & x=x(t), \\ -A\rho_{+}^{-\alpha}, & x>x(t). \end{array}\displaystyle \right . $$
(3.14)

Lemma 1

If the solution of the form (3.13) satisfies the following generalized Rankine-Hugoniot relation:

$$ \left \{ \textstyle\begin{array}{l} \frac{\mathrm{d}x(t)}{\mathrm{d}t} =u_{\delta}(t), \\ \frac{\mathrm{d}w(t)}{\mathrm{d}t} =u_{\delta}(t)[\rho]-[\rho u], \\ \frac{\mathrm{d}(w(t)u_{\delta}(t))}{\mathrm{d}t} =u_{\delta}(t)[\rho u]-[\rho u^{2}+p], \\ \frac{\mathrm{d}(w(t)u_{\delta}^{2}(t)/2+h(t))}{\mathrm{d}t} =u_{\delta }(t)[\rho u^{2}/2+H]-[(\rho u^{2}/2+H+p)u], \end{array}\displaystyle \right . $$
(3.15)

then it is a delta shock wave solution to (1.5) and (1.3) in the sense of distribution.

Proof

If equation (3.15) holds, then, for any test functions \(\phi\in C_{0}^{\infty}( (0, +\infty) \times R)\), by Green’s formulation and integrating by parts, we obtain

$$\begin{aligned}& \bigl\langle \rho u^{2}/2+H, \phi_{t} \bigr\rangle + \bigl\langle \bigl(\rho u^{2}/2+H+p\bigr)u, \phi_{x} \bigr\rangle \\& \quad = \int_{0}^{+\infty} \int_{-\infty}^{+\infty}\bigl(\rho u^{2}/2+H\bigr) \phi _{t}+\bigl(\bigl(\rho u^{2}/2+H+p\bigr)u\bigr) \phi_{x}\,\mathrm{d}x\,\mathrm{d}t \\& \qquad {} + \int_{0}^{+\infty}\bigl(w(t) u_{\delta}^{2}(t)/2+h(t) \bigr)\phi_{t}+\bigl(\bigl(w(t) u_{\delta}^{2}(t)/2+h(t) \bigr)u_{\delta}(t)\bigr)\phi_{x}\,\mathrm{d}t \\& \quad = \int_{0}^{+\infty} \int_{-\infty}^{x(t)}\bigl(\bigl(\rho_{-} u_{-}^{2}/2+H_{-}\bigr)\phi\bigr)_{t}+ \bigl(\bigl(\rho_{-} u_{-}^{2}/2+H_{-}+p_{-} \bigr)u_{-}\phi \bigr)_{x}\,\mathrm{d}x\,\mathrm{d}t \\& \qquad {} + \int_{0}^{+\infty} \int_{x(t)}^{+\infty}\bigl(\bigl(\rho_{+} u_{+}^{2}/2+H_{+}\bigr)\phi\bigr)_{t}+ \bigl(\bigl(\rho_{+} u_{+}^{2}/2+H_{+}+p_{+} \bigr)u_{+}\phi \bigr)_{x}\,\mathrm{d}x\,\mathrm{d}t \\& \qquad {} + \int_{0}^{+\infty}\bigl(w(t) u_{\delta}^{2}(t)/2+h(t) \bigr) \bigl(\phi_{t}+u_{\delta }(t)\phi_{x}\bigr)\, \mathrm{d}t \\& \quad = - \int_{0}^{+\infty}-\bigl(\bigl(\rho_{-} u_{-}^{2}/2+H_{-}+p_{-} \bigr)u_{-}\phi \bigr)\,\mathrm{d}t+\bigl(\bigl(\rho_{-} u_{-}^{2}/2+H_{-}\bigr)\phi\bigr)\,\mathrm{d}x \\& \qquad {} + \int_{0}^{+\infty}-\bigl(\bigl(\rho_{+} u_{+}^{2}/2+H_{+}+p_{+} \bigr)u_{+}\phi\bigr)\,\mathrm {d}t+\bigl(\bigl(\rho_{+} u_{+}^{2}/2+H_{+}\bigr)\phi\bigr)\,\mathrm{d}x \\& \qquad {} - \int_{0}^{+\infty} \phi\frac{\,\mathrm{d}(w(t) u_{\delta }^{2}(t)/2+h(t))}{\,\mathrm{d}t}\,\mathrm{d}t \\& \quad = \int_{0}^{+\infty}\phi \biggl(u_{\delta}(t)\bigl[ \rho u^{2}/2+H\bigr]-\bigl[\bigl(\rho u^{2}/2+H+p\bigr)u \bigr]-\frac{\,\mathrm{d}(w(t)u_{\delta}^{2}(t)/2+h(t))}{\,\mathrm {d}t} \biggr) \,\mathrm{d}t \\& \quad = 0, \end{aligned}$$
(3.16)

which yields the third equality of (3.12). In a similar way, one can prove the first and second equalities of (3.12). The proof is complete. □

Remark 1

The generalized Rankine-Hugoniot equation (3.15) describes the exact relationship between the limit states on two sides of a delta shock wave and the location, speed, weights, and the assignments of u on the delta shock wave.

In addition, to guarantee the uniqueness of delta shock wave solution, we propose the following entropy condition for a delta shock wave:

$$\begin{aligned} \lambda_{1}(\rho_{+},u_{+})< & \lambda_{2}(\rho_{+},u_{+})< \lambda _{3}(\rho_{+},u_{+}) \le u_{\delta}(t) \le \lambda_{1}(\rho_{-},u_{-}) \\ < &\lambda_{2}(\rho_{-},u_{-})< \lambda_{3}(\rho_{-},u_{-}), \end{aligned}$$
(3.17)

which means that all of the six characteristic lines on both sides of the delta shock wave are incoming.

Definition 3

The discontinuity satisfying (3.15) and (3.17) is called a delta shock wave, denoted by δ.

3.2 Solution involving delta shock wave

In this subsection, both the generalized Rankine-Hugoniot relation and the entropy condition for the delta shock wave will be applied to solve the Riemann problem (1.5), (1.3), and (1.6) when \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\). At this moment, this Riemann problem is reduced to the initial value problem for (3.15) and (3.17) with the initial conditions

$$ x(0)=0,\qquad u_{\delta}(0)=0,\qquad w(0)=0,\qquad h(0)=0. $$
(3.18)

From (3.15) and (3.18), it leads to

$$ \left \{ \textstyle\begin{array}{l} w(t) =x(t)[\rho]-[\rho u]t, \\ w(t)u_{\delta}(t) =x(t)[\rho u]-[\rho u^{2}+p]t, \\ w(t)u_{\delta}^{2}(t)/2+h(t) =x(t) [\rho u^{2}/2+H]-[(\rho u^{2}/2+H+p)u]t. \end{array}\displaystyle \right . $$
(3.19)

We multiply the first equation of (3.19) by \(u_{\delta}(t)\) and then subtract it from the second equation to obtain

$$ [\rho]x(t)u_{\delta}(t)-[\rho u]x(t)-[\rho u]u_{\delta}(t)t+\bigl[ \rho u^{2}+p\bigr]t=0, $$

or

$$ \frac{\mathrm{d}}{{\mathrm{d}} t} \bigl( [\rho]x^{2}(t)/2 -[\rho u]x(t)t+\bigl[\rho u^{2}+p\bigr]t^{2}/2 \bigr)=0, $$

that is,

$$ [\rho]x^{2}(t) -2[\rho u]x(t)t+\bigl[\rho u^{2}+p\bigr]t^{2}=0. $$
(3.20)

When \([\rho]=\rho_{+}-\rho_{-}=0\), we can deduce that

$$ \left \{ \textstyle\begin{array}{l} x(t) =(u_{-}+u_{+})t/2, \\ u_{\delta}(t) =(u_{-}+u_{+})/2, \\ w(t) =\rho_{-}(u_{-}-u_{+})t, \\ h(t) =-w(t)u_{\delta}^{2}(t)/2+ x(t) [\rho u^{2}/2+H]-[(\rho u^{2}/2+H+p)u]t, \end{array}\displaystyle \right . $$
(3.21)

which satisfies the entropy condition (3.17).

When \([\rho]=\rho_{+}-\rho_{-} \neq0\), noting (3.1), the discriminant of the quadratic equation (3.20) holds,

$$\begin{aligned} \varDelta &=4t^{2}\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr) \\ &=4t^{2}\bigl\{ \rho_{-}\rho_{+}[u]^{2}+A( \rho_{+}-\rho_{-}) \bigl(\rho_{+}^{-\alpha}- \rho_{-}^{-\alpha}\bigr)\bigr\} \\ &=4t^{2}\bigl\{ \rho_{+}\rho_{-} \bigl([u]^{2}-A\bigl(\rho_{-}^{-1}- \rho_{+}^{-1}\bigr) \bigl(\rho_{-}^{-\alpha}- \rho_{+}^{-\alpha}\bigr)\bigr)\bigr\} \\ &>0. \end{aligned}$$

Therefore, (3.20) admits two solutions

$$\begin{aligned}& x_{1}(t)=\frac{t}{[\rho]} \bigl([\rho u]+\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr), \end{aligned}$$
(3.22)
$$\begin{aligned}& x_{2}(t)=\frac{t}{[\rho]} \bigl([\rho u]-\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr). \end{aligned}$$
(3.23)

Let us single out an admissible solution from (3.22) and (3.23) using the entropy condition (3.17). For the solution (3.22), it shows that

$$ u_{\delta}(t)=x'_{1}(t)= \frac{1}{[\rho]} \bigl([\rho u]+\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr). $$
(3.24)

Then, by using (3.1) and noting

$$\begin{aligned}& \bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)- \bigl(\sqrt{A\alpha}\rho_{+}^{-(1+\alpha )/2}[\rho]-\rho_{-}[u] \bigr)^{2} \\& \quad = \bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr] \bigr)- \bigl(\rho_{-}\bigl(u_{-}-\bigl(u_{+}+ \sqrt {A\alpha}\rho_{+}^{-(1+\alpha)/2}\bigr)\bigr) +\sqrt{A\alpha} \rho_{+}^{(1-\alpha)/2} \bigr)^{2} \\& \quad = [\rho] \bigl(\rho_{-} \bigl(u_{+}+\sqrt{A\alpha} \rho_{+}^{-(1+\alpha)/2}-\bigl(u_{-}+ \sqrt{A} \rho_{-}^{-(1+\alpha)/2}\bigr) \bigr) \bigl(u_{+}+\sqrt{A \alpha}\rho _{+}^{-(1+\alpha)/2} \\& \qquad {} -\bigl(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} \bigr) \bigr) +A(1-\alpha)\rho_{+}^{-\alpha} \bigr), \end{aligned}$$
(3.25)
$$\begin{aligned}& \bigl(-\rho_{+}[u]-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2}[ \rho ]\bigr)^{2}-\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr) \\& \quad = \bigl(\rho_{+}\bigl(u_{-}-\sqrt{A\alpha} \rho_{-}^{-(1+\alpha)/2}-u_{+}\bigr) +\sqrt{A\alpha} \rho_{-}^{-(1+\alpha)/2} \bigr)^{2}-\bigl([\rho u]^{2}-[\rho ] \bigl[\rho u^{2}+p\bigr]\bigr) \\& \quad = [\rho] \bigl(\rho_{+} \bigl(u_{+}+\sqrt{A} \rho_{+}^{-(1+\alpha)/2}-\bigl(u_{-}- \sqrt{A\alpha} \rho_{-}^{-(1+\alpha)/2}\bigr) \bigr) \bigl(u_{+}- \sqrt{A} \rho_{+}^{-(1+\alpha)/2} \\& \qquad {}-\bigl(u_{-}-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2} \bigr) \bigr) +A(1-\alpha)\rho_{-}^{-\alpha} \bigr), \end{aligned}$$
(3.26)

we can deduce that

$$\begin{aligned}& u_{\delta}(t)-\bigl(u_{+}+\sqrt{A\alpha}\rho_{+}^{-(1+\alpha)/2} \bigr) \\& \quad = \frac{1}{[\rho]} \bigl(\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2}-\bigl(\sqrt {A\alpha} \rho_{+}^{-(1+\alpha)/2}[\rho]-\rho_{-}[u]\bigr) \bigr) \\& \quad > 0, \end{aligned}$$
(3.27)
$$\begin{aligned}& \bigl(u_{-}-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2} \bigr)-u_{\delta}(t) \\& \quad = \frac{1}{[\rho]} \bigl(\bigl(-\rho_{+}[u]-\sqrt{A\alpha} \rho_{-}^{-(1+\alpha )/2}[\rho]\bigr) -\bigl([\rho u]^{2}-[ \rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr) \\& \quad > 0, \end{aligned}$$
(3.28)

namely, \(u_{+}+\sqrt{A\alpha}\rho_{+}^{-(1+\alpha)/2} < u_{\delta}(t) < u_{-}-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2}\). However, for the solution (3.23), it is easy to see that

$$ u_{\delta}(t)= x'_{2}(t)= \frac{1}{[\rho]} \bigl([\rho u]-\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr). $$
(3.29)

As \([\rho]>0\), a combination of (3.1), (3.25), and (3.26) shows that

$$\begin{aligned}& u_{\delta}(t)-\bigl(u_{+}+\sqrt{A\alpha}\rho_{+}^{-(1+\alpha)/2} \bigr) \\& \quad = \frac{1}{[\rho]} \bigl(-\bigl([\rho u]^{2}-[\rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2}-\bigl(\sqrt {A\alpha} \rho_{+}^{-(1+\alpha)/2}[\rho]-\rho_{-}[u]\bigr) \bigr) \\& \quad < 0, \end{aligned}$$
(3.30)
$$\begin{aligned}& \bigl(u_{-}-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2} \bigr)-u_{\delta}(t) \\& \quad = \frac{1}{[\rho]} \bigl(\bigl(-\rho_{+}[u]-\sqrt{A\alpha} \rho_{-}^{-(1+\alpha )/2}[\rho]\bigr) -\bigl([\rho u]^{2}+[ \rho] \bigl[\rho u^{2}+p\bigr]\bigr)^{1/2} \bigr) \\& \quad > 0, \end{aligned}$$
(3.31)

that is, \(u_{\delta}(t) < u_{+}+\sqrt{A\alpha}\rho_{+}^{-(1+\alpha)/2} < u_{-}-\sqrt{A\alpha}\rho_{-}^{-(1+\alpha)/2}\). By the entropy condition (3.17), we choose (3.22) as an admissible solution. Thus, from (3.19), we obtain

$$ \left \{ \textstyle\begin{array}{l} x(t) =\frac{1}{[\rho]} ( [\rho u]t+w(t) ), \\ u_{\delta}(t) =\frac{1}{[\rho]} ( [\rho u]+w'(t) ), \\ w(t) = ([\rho u]^{2}-[\rho][\rho u^{2}+p])^{1/2}t, \\ h(t) =-w(t)u_{\delta}^{2}(t)/2 +x(t) [\rho u^{2}/2+H]-[(\rho u^{2}/2+H+p)u]t. \end{array}\displaystyle \right . $$
(3.32)

According to (3.21) and (3.32), with a simple calculation, we obtain the following properties of the solution to (3.15) and (3.18).

Lemma 2

On the physically relevant region ℵ, under the condition \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\), the solution to (3.15) and (3.18) has the following properties.

  1. (i)

    \(x(t)\) is a monotone function of t.

  2. (ii)

    \(u_{\delta}(t)\) is a constant value, satisfying \(u_{+}+\sqrt{A\alpha} \rho_{+}^{-(\alpha+1)/2} < u_{\delta}(t) < u_{-}-\sqrt{A\alpha} \rho_{-}^{-(\alpha+1)/2} \).

  3. (iii)

    \(w(t) \ge0\) is a monotone increasing function of t.

  4. (iv)

    \(h(t) \ge0\) is a monotone increasing function of t.

Therefore, we have the following result.

Theorem 2

On the physically relevant region ℵ, under the condition \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} \ge u_{+}+\sqrt{A}\rho _{+}^{-(1+\alpha)/2}\), the Riemann problem (1.5), (1.3) and (1.6) admits uniquely a delta shock wave solution of the form

$$ (\rho, u, H) (t, x)= \left \{ \textstyle\begin{array}{l@{\quad}l} (\rho_{-}, u_{-}, H_{-}), & x< x(t), \\ (w(t)\delta(x-x(t)), u_{\delta}(t), h(t)\delta(x-x(t))), & x=x(t), \\ (\rho_{+}, u_{+}, H_{+}), & x > x(t), \end{array}\displaystyle \right . $$
(3.33)

where \(x(t)\), \(u_{\delta}(t)\), \(w(t)\), and \(h(t)\) are shown in (3.21) for \(\rho_{-}=\rho_{+}\) or (3.32) for \(\rho_{-} \neq\rho_{+}\). See Figure  7.

Figure 7
figure 7

The structure of solution as the projection of state ⊕ onto \(\pmb{(\rho, u)}\) -plane lies in V .

Full size image

3.3 Numerical simulation to the delta shock wave solution

This subsection gives some numerical simulations for the delta shock wave solution mentioned above. In the following examples, we take \(A=3.0\), \(\alpha=0.5\), and the interval \([-2,2]\), and compute the solution using the Nessyahu-Tadmor scheme [27] with \(\mathrm{CFL}=0.475\).

Case 1. \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} = u_{+}+\sqrt {A}\rho_{+}^{-(1+\alpha)/2}\). The initial data are as follows:

$$ \begin{aligned} &\rho_{-} = 1.430, \qquad u_{-} = 2.530,\qquad H_{-} = 4.530, \\ &\rho_{+} = 3.077,\qquad u_{+} = 0.460,\qquad H_{+} = 7.560, \end{aligned} $$
(3.34)

and the numerical results are given in Figures 8-10.

Figure 8
figure 8

The density for Case 1 at \(\pmb{t=0.3}\) .

Full size image

Case 2. \(u_{-}-\sqrt{A}\rho_{-}^{-(1+\alpha)/2} > u_{+}+\sqrt {A}\rho_{+}^{-(1+\alpha)/2}\). The initial data are as follows:

$$ \begin{aligned} &\rho_{-} = 1.430,\qquad u_{-} = 2.530,\qquad H_{-} = 1.330, \\ &\rho_{+} = 7.140,\qquad u_{+} = -0.870,\qquad H_{+} = 8.160, \end{aligned} $$
(3.35)

and the numerical results are depicted in Figures 11-13.

From Figures 8 and 10 or Figures 11 and 13, it is clearly observed that both density ρ and internal energy H develop extreme concentrations, containing a Dirac delta function. Meanwhile, Figure 9 or Figure 12 indicates that the velocity u consists of two constant values separated by one discontinuity. Therefore, the above numerical results clearly confirm Theorem 2.

Figure 9
figure 9

The velocity for Case 1 at \(\pmb{t=0.3}\) .

Full size image
Figure 10
figure 10

The internal energy for Case 1 at \(\pmb{t=0.3}\) .

Full size image
Figure 11
figure 11

The density for Case 2 at \(\pmb{t=0.3}\) .

Full size image
Figure 12
figure 12

The velocity for Case 2 at \(\pmb{t=0.3}\) .

Full size image
Figure 13
figure 13

The internal energy for Case 2 at \(\pmb{t=0.3}\) .

Full size image

4 Conclusion

In this study, we completely solve the Riemann problem for the compressible Euler equations with the generalized Chaplygin gas. Its solutions exhibit five kinds of geometrical structures. It is shown that the delta shock wave with Dirac delta function in both density and internal energy develops in the solutions. To our knowledge, this type of delta shock wave has not been found in the previous investigations of the generalized Chaplygin gas. Besides, the formation mechanism of this kind of delta shock wave in the generalized Chaplygin gas results from the overlapping of the linearly degenerate and genuinely nonlinear characteristic lines, which is substantially different from the case of the Chaplygin gas.