Numerical analysis of a pseudo-compact C-N conservative scheme for the Rosenau-KdV equation coupling with the Rosenau-RLW equation

Abstract

In this paper, numerical solutions for the Rosenau-KdV equation coupling with the Rosenau-RLW equation are considered and a new C-N pseudo-compact conservative numerical scheme, which preserves the original conservative properties is designed. The proposed scheme is based on a finite difference method. The existence of the difference solutions has been shown by the Brouwer fixed point theorem. Unconditional stability, second-order convergence, and a prior error estimate of the scheme are proved by the discrete energy method. Numerical examples have been given to verify the theoretical results.

1 Introduction

The Rosenau-KdV equation coupling with the Rosenau-RLW equation (the Rosenau-KdV-RLW equation) is of the form [1]

$$ u_{t}-\gamma u_{xxt}+u_{xxxxt}+\beta u_{xxx}+u_{x}+\alpha\bigl(u^{2} \bigr)_{x}=0, $$

(1.1)

where $\alpha>0$, β, γ are real constants. A special case of its solitary wave solution is given as follows [1]:

$$\begin{aligned} u(x,t)={}&\frac{5}{456}(-25+13\sqrt{457}) \\ &{}\times\operatorname{sech}^{4} \biggl[\frac{1}{\sqrt{288}}\sqrt{-13+\sqrt{457}} \biggl(x-\frac{241+13\sqrt{457}}{266}t\biggr)\biggr]. \end{aligned}$$

(1.2)

When $\gamma=0$, system (1.1) is reduced to the Rosenau-KdV equation:

$$ u_{t}+u_{xxxxt}+\beta u_{xxx}+u_{x}+\alpha \bigl(u^{2}\bigr)_{x}=0. $$

(1.3)

On the mathematical front, Zuo obtained solitons and periodic solutions for the Rosenau-KdV equation [2]. Esfahani [3] derived the solitary wave solution for the generalized Rosenau-KdV equation. However, to the best of our knowledge, few numerical methods to the initial-boundary value problem of Rosenau-KdV equation have been studied till now [4, 5]. On the other hand, when $\beta=0$, system (1.1) is reduced to the following equation:

$$ u_{t}-\gamma u_{xxt}+u_{xxxxt}+u_{x}+ \alpha\bigl(u^{2}\bigr)_{x}=0. $$

(1.4)

This equation is usually called the Rosenau-RLW equation. The Rosenau-RLW equation (1.4) has been solved numerically by various methods. Zuo et al. [6] have proposed a nonlinear implicit conservative scheme for the general Rosenau-RLW equation. In [7, 8], Pan et al. have presented three-level linearized difference schemes for both (1.4) and the general Rosenau-RLW equation. Atouani and Omrani have developed a Galerkin finite element method for (1.4) [9]. Hu and Wang have also proposed a high-accuracy linear conservative scheme to solve (1.4) [10]. When $\gamma=\beta=0$, system (1.1) is reduced to the Rosenau equation [11]:

$$ u_{t}+u_{xxxxt}+u_{x}+\bigl(u^{2} \bigr)_{x}=0. $$

(1.5)

As is well known, the KdV equation has been developed in very wide applications and undergone research which can be used to describe wave propagation and spread interaction. In the study of the dynamics of dense discrete systems, the case of wave-wave and wave-wall interactions cannot be treated by the well-known KdV equation. In order to overcome the shortcoming of the KdV equation, Rosenau proposed the Rosenau equation (1.5) [11]. The theoretical results on existence, uniqueness, and regularity of the solution to (1.5) have been investigated by Park [12]. Many numerical schemes have been proposed for the Rosenau equation, such as the discontinuous Galerkin method [13], the $C^{1}$-conforming finite element method [14], the finite difference method [15–17], and the orthogonal cubic spline collocation method [18].

As far as computational studies are concerned, Wongsaijai and Poochinapan [1] have proposed a three-level weighted average implicit finite difference scheme to solve the Rosenau-KdV-RLW equation. However, the three-level implicit difference scheme cannot be started by itself, it is necessary to select another suitable two-level scheme to compute $u^{1}$. In their proof of Theorem 3, the authors did not consider the positive and negative of the parameter γ and so there exists the same difficulty in the following proof of their paper. Here we give a modified proof of this theorem, namely Lemma 3.1 in this article. In this paper, an attempt has been made to propose a new conservative C-N scheme for the Rosenau-KdV-RLW equation. As already pointed out by Li and Vu-Quoc [19], ‘in some areas, the ability to preserve some invariant properties of the original differential equation is a criterion to judge the success of a numerical simulation’. Fei et al. [20] also pointed out that the non-conservative difference schemes may easily show nonlinear blow-up, and the conservative difference schemes perform better than the non-conservative ones. Some conservative finite difference schemes have been proposed in the literature; numerical results of all the schemes are encouraging. In this respect, we refer the reader to [21–27], and references therein. These numerical methods may give us much help in designing a new numerical scheme for the Rosenau-KdV-RLW equation. The present scheme is two-level pseudo-compact, unconditionally stable, and of second-order accuracy, which numerically simulates the conservative laws at the same time.

The rest of the paper is as follows: In Section 2, a pseudo-compact nonlinear implicit conservative difference scheme is proposed for the Rosenau-KdV-RLW equation. The discrete conservative laws are also discussed. In Section 3, the existence of difference solutions has been shown by Brouwer fixed point theorem. The second-order convergence and stability of the scheme are proved in Section 4. In Section 5, numerical experiments are reported to verify the theoretical results.

2 A pseudo-compact C-N conservative scheme and its discrete conservative invariant

In general, the solutions of system (1.1) decay rapidly to zero for $|x|\gg0$. Therefore, numerically we can solve system (1.1) in a compact domain $\Omega=(x_{l},x_{r})$ with $-x_{l}\gg0$ and $x_{r}\gg0$. Consider the Rosenau-KdV-RLW equation

$$ u_{t}-\gamma u_{xxt}+u_{xxxxt}+\beta u_{xxx}+u_{x}+\alpha\bigl(u^{2} \bigr)_{x}=0,\quad (x,t)\in\Omega\times(0,T], $$

(2.1)

with the initial condition

$$ u(x,0)=u_{0}(x),\quad x\in[x_{l},x_{r}], $$

(2.2)

and the boundary conditions

$$ u(x_{l},t)=u(x_{r},t)=0,\qquad u_{xx}(x_{l},t)=u_{xx}(x_{r},t)=0,\quad t\in [0,T], $$

(2.3)

where $u_{0}(x)$ is a known smooth function, $\Omega=(x_{l},x_{r})$.

The IBV problems (2.1)-(2.3) are known to possess the following conservative properties [1]:

$$\begin{aligned}& Q(t)=\int_{x_{l}}^{x_{r}} u(x,t)\,\mathrm{d}x = Q(0), \end{aligned}$$

(2.4)

$$\begin{aligned}& E(t)=\|u\|^{2}_{L_{2}}+\gamma \|u_{x}\|^{2}_{L_{2}}+\|u_{xx}\|^{2}_{L_{2}}=E(0). \end{aligned}$$

(2.5)

The domain $\{(x,t)|(x,t)\in\bar{\Omega}\times[0,T]\}$ is discretized into grids described by the set ${(x_{j},t_{n})}$ of nodes, in which $x_{j}=x_{l}+jh$ ($0\le j\le J$), $t_{n}=n\tau$ ($0\le n\le N$), where $J=[\frac{x_{r}-x_{l}}{h}]$, $N=[\frac{T}{\tau}]$, h and τ are the uniform step size in the spatial and temporal direction, respectively. Denote $u^{n}_{j}\approx u(x_{j},t_{n})$. Define the discrete grid $\Omega_{h}=\{ x_{j}=x_{l}+jh| 1\le j\le J-1\}$, $\Omega_{\tau}=\{t_{n}=n\tau| 1\le n\le N-1\}$, and the extended discrete grid $\bar{\Omega}_{h}=\{x_{j}=x_{l}+jh| j=-1,0,1,\ldots,J,J+1\}$, $\bar{\Omega}_{\tau}=\{t_{n}=n\tau| 0\le n\le N\}$. Suppose $u^{n}=\{u^{n}_{j}; j=1,2,\ldots,J-1, n=1,2,\ldots,N-1\}$ is a discrete function on ${\Omega}_{h}\times{\Omega}_{\tau}$. Let $Z^{0}_{h}=\{ u^{n}=(u^{n}_{j})|u^{n}_{-1}=u^{n}_{0}=u^{n}_{J}=u^{n}_{J+1}=0, j=-1,0,1,\ldots, J,J+1\}$. For convenience, we introduce the following notations for the difference operators:

$$\begin{aligned}& \bigl(u^{n}_{j}\bigr)_{x}=\frac{u^{n}_{j+1}-u^{n}_{j}}{h},\qquad \bigl(u^{n}_{j}\bigr)_{\bar{x}}=\frac{u^{n}_{j}-u^{n}_{j-1}}{h},\\& \bigl(u^{n}_{j}\bigr)_{\hat{x}}=\frac{u^{n}_{j+1}-u^{n}_{j-1}}{2h},\qquad \bigl(u^{n}_{j}\bigr)_{t}=\frac{u^{n+1}_{j}-u^{n}_{j}}{\tau},\\& \bigl(u^{n},v^{n}\bigr)=h\sum _{j=1}^{J-1}u^{n}_{j}v^{n}_{j},\qquad \bigl\| u^{n}\bigr\| ^{2}=\bigl(u^{n},u^{n}\bigr),\qquad \bigl\| u^{n}\bigr\| _{\infty}=\max_{1\le j\le J-1}\bigl|u^{n}_{j}\bigr|. \end{aligned}$$

In the paper, C denotes a general positive constant which may have different values in different occurrences.

Based on the notations above, we propose the following pseudo-compact C-N conservative scheme for the IBV problems (2.1)-(2.3):

$$\begin{aligned}& \begin{aligned}[b] &\bigl(u^{n}_{j}\bigr)_{t}+\frac{h^{2}}{12} \bigl(u^{n}_{j}\bigr)_{x\bar{x}t} -\gamma \bigl(u^{n}_{j}\bigr)_{x\bar{x}t}+\bigl(u^{n}_{j} \bigr)_{xx\bar{x}\bar{x}t}+\frac{1}{2}\beta \bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)_{x\bar{x}\hat{x}}+\frac{1}{2}\bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)_{\hat{x}}\\ &\quad{}+\frac{1}{6}\alpha \bigl[\bigl(u^{n+1}_{j}+u^{n}_{j} \bigr) \bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)_{\hat {x}}+\bigl(\bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)^{2}\bigr)_{\hat{x}}\bigr]=0,\quad (x_{j},t_{n}) \in\Omega_{h}\times\Omega_{\tau}, \end{aligned} \end{aligned}$$

(2.6)

$$\begin{aligned}& u^{0}_{j}=u_{0}(x_{j}),\quad x_{j}\in\Omega_{h}, \end{aligned}$$

(2.7)

$$\begin{aligned}& u^{n}_{0}=u^{n}_{J}=0,\qquad \bigl(u^{n}_{0}\bigr)_{x\bar{x}}=\bigl(u^{n}_{J} \bigr)_{x\bar{x}}=0,\quad t_{n}\in\bar{\Omega}_{\tau}. \end{aligned}$$

(2.8)

For simplicity, we denote ${u}^{n+\frac{1}{2}}_{j}=\frac {u^{n+1}_{j}+u^{n}_{j}}{2}$; then the last term of (2.6) can be rewritten as follows:

$$\begin{aligned} \kappa\bigl(u^{n+1},u^{n}\bigr)=\frac{2}{3}\alpha \bigl[u^{n+\frac{1}{2}}_{j}\bigl(u^{n+\frac {1}{2}}_{j} \bigr)_{\hat{x}}+\bigl(\bigl(u^{n+\frac{1}{2}}_{j} \bigr)^{2}\bigr)_{\hat{x}}\bigr]. \end{aligned}$$

To analyze the discrete conservative laws of finite difference approximate solutions, the following lemmas should be introduced.

Lemma 2.1

[28]

For arbitrary discrete functions: $u^{n},v^{n}\in Z^{0}_{h}$, we have

$$\begin{aligned} \bigl(\bigl(u^{n}\bigr)_{x},v^{n}\bigr)=- \bigl(u^{n},\bigl(v^{n}\bigr)_{\bar{x}}\bigr),\qquad \bigl(v^{n},\bigl(u^{n}\bigr)_{x\bar{x}}\bigr)=-\bigl( \bigl(v^{n}\bigr)_{x},\bigl(u^{n} \bigr)_{x}\bigr), \end{aligned}$$

and

$$ \bigl(u^{n},\bigl(u^{n}\bigr)_{x\bar{x}}\bigr)=-\bigl( \bigl(u^{n}\bigr)_{x},\bigl(u^{n} \bigr)_{x}\bigr)=-\bigl\| u_{x}^{n}\bigr\| ^{2}. $$

Furthermore, if $(u^{n}_{0})_{x\bar{x}}=(u^{n}_{J})_{x\bar{x}}=0$, then

$$ \bigl(u^{n},\bigl(u^{n}\bigr)_{xx\bar{x}\bar{x}} \bigr)=\bigl\| u_{xx}^{n}\bigr\| ^{2}. $$

Lemma 2.2

For any two mesh functions: $u^{n},v^{n}\in Z^{0}_{h}$, we have

$$\begin{aligned} \bigl(\bigl(u^{n}\bigr)_{\hat{x}},u^{n}\bigr)=0,\qquad \bigl( \bigl(u^{n}\bigr)_{x\bar{x}\hat{x}},u^{n}\bigr)=0. \end{aligned}$$

(2.9)

Proof

For any two mesh functions: $u^{n},v^{n}\in Z^{0}_{h}$, according to the discrete boundary conditions (2.8) and the definition of $Z^{0}_{h}$, we get

$$\begin{aligned} \bigl(\bigl(u^{n}\bigr)_{\hat{x}},u^{n}\bigr)&=h\sum _{j=1}^{J-1}\bigl(u^{n}_{j} \bigr)_{\hat{x}}u^{n}_{j}=\frac {1}{2}\sum _{j=1}^{J-1}\bigl(u^{n}_{j+1}-u^{n}_{j-1} \bigr)u^{n}_{j} \\ &=\frac{1}{2}\sum_{j=1}^{J-1} \bigl(u^{n}_{j+1}u^{n}_{j}-u^{n}_{j}u^{n}_{j-1} \bigr)=0 \end{aligned}$$

(2.10)

and

$$\begin{aligned} \bigl(\bigl(u^{n}\bigr)_{x\bar{x}\hat{x}},u^{n}\bigr)&=h\sum _{j=1}^{J-1}\bigl(u^{n}_{j} \bigr)_{x\bar{x}\hat {x}}u^{n}_{j}=\frac{1}{2}\sum _{j=1}^{J-1}\bigl(\bigl(u^{n}_{j+1} \bigr)_{x\bar {x}}-\bigl(u^{n}_{j-1}\bigr)_{x\bar{x}} \bigr)u^{n}_{j} \\ &=\frac{1}{2h^{2}}\sum_{j=1}^{J-1} \bigl(u^{n}_{j+2}-2u^{n}_{j+1}+2u^{n}_{j-1}-u^{n}_{j-2} \bigr)u^{n}_{j} \\ &=\frac{1}{2h^{2}}\sum_{j=1}^{J-1} \bigl(u^{n}_{j+2}u^{n}_{j}-u^{n}_{j}u^{n}_{j-2} \bigr)-\frac {1}{h^{2}}\sum_{j=1}^{J-1} \bigl(u^{n}_{j+1}u^{n}_{j}-u^{n}_{j}u^{n}_{j-1} \bigr)=0. \end{aligned}$$

(2.11)

 □

Theorem 2.1

Suppose $u_{0}\in H^{2}_{0}[x_{l},x_{r}]$, then scheme (2.6)-(2.8) admits the following invariant:

$$\begin{aligned}& Q^{n}=h\sum_{j=1}^{J-1}u^{n}_{j}=Q^{n-1}= \cdots=Q^{0}, \end{aligned}$$

(2.12)

$$\begin{aligned}& E^{n}=\bigl\| u^{n}\bigr\| ^{2}+\biggl(\gamma- \frac{h^{2}}{12}\biggr)\bigl\| u^{n}_{x}\bigr\| ^{2} +\bigl\| u^{n}_{xx}\bigr\| ^{2}=E^{n-1}= \cdots=E^{0}. \end{aligned}$$

(2.13)

Proof

Multiplying (2.1) with h, according to the boundary conditions (2.3), then summing up for j from 1 to $J-1$, we obtain

$$\begin{aligned} h\sum_{j=1}^{J-1}\bigl(u^{n+1}_{j}-u^{n}_{j} \bigr)=0. \end{aligned}$$

(2.14)

Let

$$\begin{aligned} Q^{n}=h\sum_{j=1}^{J-1}u^{n}_{j}. \end{aligned}$$

(2.15)

Then we obtain (2.12) from (2.14).

Taking the inner product of (2.6) with $u^{n+\frac{1}{2}}$, according to boundary condition (2.8), Lemmas 2.1 and 2.2, we have

$$\begin{aligned} &\frac{1}{2\tau}\bigl(\bigl\| u^{n+1}\bigr\| ^{2}-\bigl\| u^{n}\bigr\| ^{2} \bigr)+\biggl(\gamma-\frac {h^{2}}{12}\biggr)\frac{1}{2\tau} \bigl(\bigl\| u^{n+1}_{x}\bigr\| ^{2}-\bigl\| u^{n}_{x}\bigr\| ^{2} \bigr)+\frac {1}{2\tau}\bigl(\bigl\| u^{n+1}_{xx}\bigr\| ^{2}-\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr) \\ &\quad{} +\bigl(\kappa\bigl(u^{n+1},u^{n}\bigr),u^{n+\frac{1}{2}} \bigr)=0. \end{aligned}$$

(2.16)

Note that

$$\begin{aligned} \bigl(\kappa\bigl(u^{n+1},u^{n}\bigr),u^{n+\frac{1}{2}} \bigr)={}&\frac{2}{3}\alpha h\sum_{j=1}^{J-1} \bigl\{ \bigl(u^{n+\frac{1}{2}}_{j}\bigr) \bigl(u^{n+\frac{1}{2}}_{j} \bigr)_{\hat {x}}+\bigl[\bigl(u^{n+\frac{1}{2}}_{j} \bigr)^{2}\bigr]_{\hat{x}}\bigr\} u^{n+\frac{1}{2}}_{j} \\ ={}& \frac{1}{3}\alpha\sum_{j=1}^{J-1} \bigl\{ \bigl(u^{n+\frac {1}{2}}_{j}\bigr)^{2} \bigl(u^{n+\frac{1}{2}}_{j+1}-u^{n+\frac{1}{2}}_{j-1}\bigr) + \bigl[\bigl(u^{n+\frac{1}{2}}_{j+1}\bigr)^{2}- \bigl(u^{n+\frac{1}{2}}_{j-1}\bigr)^{2}\bigr]u^{n+\frac {1}{2}}_{j} \bigr\} \\ ={}& \frac{1}{3}\alpha\sum_{j=1}^{J-1} \bigl[\bigl(u^{n+\frac{1}{2}}_{j+1}\bigr)u^{n+\frac {1}{2}}_{j}+ \bigl(u^{n+\frac{1}{2}}_{j}\bigr)^{2}\bigr]u^{n+\frac{1}{2}}_{j+1} \\ &{} -\frac{1}{3}\alpha\sum_{j=1}^{J-1} \bigl[\bigl(u^{n+\frac {1}{2}}_{j}\bigr)u^{n+\frac{1}{2}}_{j-1}+ \bigl(u^{n+\frac {1}{2}}_{j-1}\bigr)^{2}\bigr]u^{n+\frac{1}{2}}_{j} \\ ={}&0. \end{aligned}$$

(2.17)

It follows from (2.16)-(2.17) that

$$\begin{aligned} &\frac{1}{\tau}\bigl(\bigl\| u^{n+1}\bigr\| ^{2}-\bigl\| u^{n}\bigr\| ^{2} \bigr)+\biggl(\gamma-\frac{h^{2}}{12}\biggr)\frac {1}{\tau} \bigl(\bigl\| u^{n+1}_{x}\bigr\| ^{2}-\bigl\| u^{n}_{x}\bigr\| ^{2} \bigr) \\ &\quad{}+\frac{1}{\tau }\bigl(\bigl\| u^{n+1}_{xx}\bigr\| ^{2}-\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr)=0. \end{aligned}$$

(2.18)

By the definition of $E^{n}$, (2.13) holds. □

3 Estimates and existence of difference solution

Next, we analyze error estimates of solution for scheme (2.6)-(2.8).

Lemma 3.1

Suppose $u\in H^{2}_{0}[x_{l},x_{r}]$, then the estimate of the solution of the initial-boundary value problem (2.1)-(2.3) satisfies

$$\begin{aligned} \|u\|_{L_{2}}\le C, \qquad\|u\|_{L_{\infty}}\le C. \end{aligned}$$

Proof

If $\gamma> 0$, from (2.5), we have

$$ \|u\|_{L_{2}}\le C,\qquad \|u_{x}\|_{L_{2}}\le C. $$

(3.1)

By the Sobolev inequality, we obtain

$$ \|u\|_{L_{\infty}}\le C. $$

(3.2)

An application of the Hölder inequality and the Schwartz inequality yields

$$\begin{aligned} \|u_{x}\|^{2}_{L_{2}}\le\|u\|_{L_{2}} \cdot\|u_{xx}\|_{L_{2}}\le\frac {1}{2}\bigl(\|u\|^{2}_{L_{2}}+\|u_{xx}\|^{2}_{L_{2}} \bigr). \end{aligned}$$

(3.3)

If $\gamma\leq0$, it follows from (2.5) and (3.3) that

$$\begin{aligned} \biggl(1+\frac{\gamma}{2}\biggr)\|u\|_{L_{2}}+\biggl(1+ \frac{\gamma}{2}\biggr)\|u_{xx}\|_{L_{2}}\le C. \end{aligned}$$

(3.4)

We choose a suitable value of γ, such that $(1+\frac{\gamma }{2})> 0$. It follows from (3.3), (3.4), and the Sobolev inequality that

$$\begin{aligned} \|u\|_{L_{\infty}}\le C. \end{aligned}$$

(3.5)

 □

Lemma 3.2

(Discrete Sobolev inequality [29])

There exist two constants $C_{1}$ and $C_{2}$ such that

$$\begin{aligned} \bigl\| u^{n}\bigr\| _{\infty}\le C_{1}\bigl\| u^{n}\bigr\| +C_{2}\bigl\| u^{n}_{x}\bigr\| . \end{aligned}$$

Lemma 3.3

Under the conditions of Lemma 3.1, there is the estimation for the solution $u^{n}$ of scheme (2.6): $\|u^{n}\|\le C$, $\|u^{n}_{x}\|\le C$, which yields $\|u^{n}\|_{\infty}\le C$.

Proof

If $\gamma>0$, let h be small enough, such that $(\gamma-\frac{h^{2}}{12})>0$. It follows from (2.13) that

$$\begin{aligned} \bigl\| u^{n}\bigr\| \le C,\qquad \bigl\| u^{n}_{xx}\bigr\| \le C. \end{aligned}$$

(3.6)

By using Lemma 2.1 and the Schwartz inequality, we get

$$\begin{aligned} \bigl\| u^{n}_{x}\bigr\| ^{2}\le\bigl\| u^{n}\bigr\| \bigl\| u^{n}_{xx}\bigr\| \le \frac{1}{2}\bigl(\bigl\| u^{n}\bigr\| ^{2}+\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr). \end{aligned}$$

(3.7)

This together with (3.6) and Lemma 3.2 gives

$$\begin{aligned} \bigl\| u^{n}\bigr\| _{\infty}\le C. \end{aligned}$$

(3.8)

If $\gamma\leq0$, it from (2.13) and (3.7) follows that

$$\begin{aligned} \biggl[1+\frac{1}{2}\biggl(\gamma-\frac{h^{2}}{12}\biggr) \biggr]\bigl\| u^{n}\bigr\| ^{2} +\biggl[1+\frac{1}{2}\biggl( \gamma-\frac{h^{2}}{12}\biggr)\biggr]\bigl\| u^{n}_{xx}\bigr\| ^{2} \leq C. \end{aligned}$$

(3.9)

Thus, we obtain (3.8) from (3.6), (3.7), and (3.9) with $[1+\frac{1}{2}(\gamma-\frac{h^{2}}{12})]>0$. □

Remark 3.1

Lemma 3.3 implies that scheme (2.6)-(2.8) is unconditionally stable.

To prove the existence of solutions for scheme (2.6)-(2.8), the following Browder fixed point theorem should be introduced. For the proof, see [30].

Lemma 3.4

(Browder fixed point theorem)

Let H be a finite dimensional inner product space. Suppose that $g:H\to H$ is continuous and there exists an $\alpha>0$ such that $(g(x),x)>0$ for all $x\in H$ with $\|x\|=\alpha$. Then there exists $x^{*}\in H$ such that $g(x^{*})=0$ and $\|x^{*}\|\le\alpha$.

Theorem 3.1

There exists $u^{n}\in Z^{0}_{h}$ satisfying the difference scheme (2.6)-(2.8).

Proof

It follows from the original problem (2.1)-(2.3) that $u^{0}$ satisfies scheme (2.6)-(2.8). For $n\le N-1$, assume that $u^{0},u^{1},\ldots,u^{n}$ satisfy (2.6)-(2.8). Next we prove that there exists $u^{n+1}$ satisfying scheme (2.6)-(2.8).

Define an operator g on $Z^{0}_{h}$ as follows:

$$\begin{aligned} g(v)={}&2v-2u^{n}+\frac{h^{2}}{12}\bigl(2v_{x\bar{x}}-2u^{n}_{x\bar{x}} \bigr)-\gamma \bigl(2v_{x\bar{x}}-2u^{n}_{x\bar{x}} \bigr)+2v_{xx\bar{x}\bar{x}}-2u^{n}_{xx\bar {x}\bar{x}}+\tau\beta v_{x\bar{x}\hat{x}}+\tau v_{\hat{x}} \\ &{}+\frac{2}{3}\tau\alpha\bigl[vv_{\hat{x}}+\bigl((v)^{2} \bigr)_{\hat{x}}\bigr]. \end{aligned}$$

(3.10)

Doing the inner product of (3.10) with v and using (2.17), and Lemmas 2.1 and 2.2, we have

$$\begin{aligned} \bigl(g(v),v\bigr)={}& 2\|v\|^{2}-2\bigl(u^{n},v\bigr)+ \biggl(2\gamma-\frac {h^{2}}{6}\biggr)\bigl[\|v_{x}\|^{2}- \bigl(u^{n}_{x},v_{x}\bigr)\bigr]+2\|v_{xx}\|^{2}-2 \bigl(u^{n}_{xx},v_{xx}\bigr) \\ \ge{}&2\|v\|^{2}-2\bigl\| u^{n}\bigr\| \cdot\|v\|+\biggl(2\gamma- \frac{h^{2}}{6}\biggr) \bigl(\|v_{x}\|^{2}-\bigl\| u^{n}_{x}\bigr\| \cdot \|v_{x}\|\bigr) \\ &{}+2\|v_{xx}\|^{2}-2\bigl\| u^{n}_{xx}\bigr\| \cdot\|v_{xx}\| \\ \ge{}&2\|v\|^{2}-\bigl(\|u\|^{2}+\|v\|^{2}\bigr)+\biggl(\gamma-\frac {h^{2}}{12}\biggr) \bigl(\|v_{x}\|^{2}-\bigl\| u^{n}_{x}\bigr\| ^{2} \bigr) \\ &{}+2\|v_{xx}\|^{2}-\bigl(\bigl\| u^{n}_{xx}\bigr\| ^{2}+\|v_{xx}\|^{2} \bigr) \\ &\ge\|v\|^{2}+\|v_{xx}\|^{2}+\biggl(\gamma- \frac {h^{2}}{12}\biggr)\|v_{x}\|^{2}-\bigl(\bigl\| u^{n}\bigr\| ^{2}+\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr) \\ &{}-\biggl(\gamma-\frac {h^{2}}{12}\biggr)\bigl\| u^{n}_{x}\bigr\| ^{2}. \end{aligned}$$

(3.11)

If $\gamma>0$, let h be small enough, such that $(\gamma-\frac {h^{2}}{12})>0$, then for $\forall v\in Z^{0}_{h}$, we have $(g(v),v)\ge0$ with $\|v\|^{2}=\|u^{n}\|^{2}+\|u^{n}_{xx}\|^{2}+(\gamma-\frac {h^{2}}{12})\|u^{n}_{x}\|^{2}+1$.

If $\gamma\leq0$, it follows from (3.7) and (3.11) that

$$\begin{aligned} \bigl(g(v),v\bigr)\ge{}&\|v\|^{2}+\|v_{xx}\|^{2}+ \frac{1}{2}\biggl(\gamma-\frac {h^{2}}{12}\biggr) \bigl(\|v\|^{2}+\|v_{xx}\|^{2} \bigr)-\bigl(\bigl\| u^{n}\bigr\| ^{2}+\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr) \\ &{}-\biggl(\gamma -\frac{h^{2}}{12}\biggr)\bigl\| u^{n}_{x}\bigr\| ^{2} \\ &\geq\biggl[1+\frac{1}{2}\biggl(\gamma-\frac{h^{2}}{12}\biggr) \biggr]\|v\|^{2}+\biggl[1+\frac {1}{2}\biggl(\gamma- \frac {h^{2}}{12}\biggr)\biggr]\|v_{xx}\|^{2} \\ &{}- \bigl(\bigl\| u^{n}\bigr\| ^{2}+\bigl\| u^{n}_{xx}\bigr\| ^{2} \bigr). \end{aligned}$$

(3.12)

Hence, for h sufficiently small, satisfying $[1+\frac{1}{2}(\gamma -\frac{h^{2}}{12})]>0$, it is obvious that $(g(v),v)\ge0$ for $\forall v\in Z^{0}_{h}$ with $[1+\frac{1}{2}(\gamma-\frac {h^{2}}{12})]\|v\|^{2}=\|u^{n}\|^{2}+\|u^{n}_{xx}\|^{2}+1$.

To conclude, following from Lemma 3.4, there exists $v^{*}\in Z^{0}_{h}$ which satisfies $g(v^{*})=0$. Let $u^{n+1}=2v^{*}-u^{n}$, then it can be proved that $u^{n+1}$ is the solution of scheme (2.6)-(2.8). This completes the proof of Theorem 3.1. □

4 Convergence and stability of the scheme

In this section, we shall discuss the convergence and stability of scheme (2.6)-(2.8). Let $v(x,t)$ be the solution of the problem (2.1)-(2.3), $v^{n}_{j}=v(x_{j},t_{n})$, then we define the truncation error of scheme (2.6)-(2.8) as follows:

$$\begin{aligned}& \begin{aligned}[b] Er^{n}_{j}={}&\bigl(v^{n}_{j} \bigr)_{t}+\frac{h^{2}}{12}\bigl(v^{n}_{j} \bigr)_{x\bar{x}t} -\gamma\bigl(v^{n}_{j} \bigr)_{x\bar{x}t}+\bigl(v^{n}_{j}\bigr)_{xx\bar{x}\bar{x}t}+ \frac{1}{2}\beta \bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)_{x\bar{x}\hat{x}}+\frac{1}{2}\bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)_{\hat{x}}\\ &{} +\frac{1}{6}\alpha\bigl[\bigl(v^{n+1}_{j}+v^{n}_{j} \bigr) \bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)_{\hat {x}}+\bigl(\bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)^{2}\bigr)_{\hat{x}}\bigr], \quad (x_{j},t_{n}) \in\Omega_{h}\times \Omega_{\tau}, \end{aligned} \end{aligned}$$

(4.1)

$$\begin{aligned}& v^{0}_{j}=u_{0}(x_{j}),\quad (x_{j},t_{n})\in\Omega_{h}, \end{aligned}$$

(4.2)

$$\begin{aligned}& v^{n}_{0}=v^{n}_{J}=0,\qquad \bigl(v^{n}_{0}\bigr)_{x\bar{x}}=\bigl(v^{n}_{J} \bigr)_{x\bar{x}}=0,\quad (x_{j},t_{n})\in\bar{ \Omega}_{\tau}. \end{aligned}$$

(4.3)

Using a Taylor expansion, we see that $Er^{n}_{j}=O(\tau^{2}+h^{2})$ holds if $\tau,h\to0$.

Lemma 4.1

(Discrete Gronwall inequality [29])

Suppose $w(k)$, $\rho(k)$ are nonnegative mesh functions and $\rho(k)$ is nondecreasing. If $C>0$ and

$$\begin{aligned} w(k)\le\rho(k)+C\tau\sum_{l=0}^{k-1}w(l),\quad \forall k, \end{aligned}$$

then

$$\begin{aligned} w(k)\le\rho(k)e^{C\tau k}, \quad\forall k. \end{aligned}$$

Theorem 4.1

Assume that $u_{0}\in H^{2}_{0}[x_{l},x_{r}]$ and $u(x,t)\in C^{6,3}$, then the solution $u^{n}$ of the scheme (2.6)-(2.8) converges to the solution of the IBV problem (2.1)-(2.3) and the rate of convergence is $O(\tau^{2}+h^{2})$ in the $\|\cdot\|_{\infty}$ norm.

Proof

Let $e^{n}_{j}=v^{n}_{j}-u^{n}_{j}$. From (2.6)-(2.8) and (4.1)-(4.3), we obtain the following error equations:

$$\begin{aligned}& \begin{aligned}[b] Er^{n}_{j}={}&\bigl(e^{n}_{j} \bigr)_{t}+\frac{h^{2}}{12}\bigl(e^{n}_{j} \bigr)_{x\bar{x}t} -\gamma\bigl(e^{n}_{j} \bigr)_{x\bar{x}t}+\bigl(e^{n}_{j}\bigr)_{xx\bar{x}\bar{x}t}+ \frac{1}{2}\beta \bigl(e^{n+1}_{j}+e^{n}_{j} \bigr)_{x\bar{x}\hat{x}}+\frac{1}{2}\bigl(e^{n+1}_{j}+e^{n}_{j} \bigr)_{\hat {x}}\\ &{} +\frac{1}{6}\alpha\bigl[\bigl(v^{n+1}_{j}+v^{n}_{j} \bigr) \bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)_{\hat {x}}+\bigl(\bigl(v^{n+1}_{j}+v^{n}_{j} \bigr)^{2}\bigr)_{\hat{x}}\bigr]\\ &{} -\frac{1}{6}\alpha\bigl[\bigl(u^{n+1}_{j}+u^{n}_{j} \bigr) \bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)_{\hat {x}}+\bigl(\bigl(u^{n+1}_{j}+u^{n}_{j} \bigr)^{2}\bigr)_{\hat{x}}\bigr],\quad (x_{j},t_{n}) \in\Omega_{h}\times \Omega_{\tau}, \end{aligned} \end{aligned}$$

(4.4)

$$\begin{aligned}& e^{0}_{j}=0,\quad (x_{j},t_{n})\in \Omega_{h}, \end{aligned}$$

(4.5)

$$\begin{aligned}& e^{n}_{0}=e^{n}_{J}=0,\qquad \bigl(e^{n}_{0}\bigr)_{x\bar{x}}=\bigl(e^{n}_{J} \bigr)_{x\bar{x}}=0,\quad (x_{j},t_{n})\in\bar{ \Omega}_{\tau}. \end{aligned}$$

(4.6)

Taking in (4.4) the inner product with $2e^{n+\frac{1}{2}}$ (i.e. $e^{n+1}+e^{n}$), and using Lemmas 2.1 and 2.2, we obtain

$$\begin{aligned} \bigl(Er^{n},2e^{n+\frac{1}{2}}\bigr)={}&\frac{1}{\tau} \bigl(\bigl\| e^{n+1}\bigr\| ^{2}-\bigl\| e^{n}\bigr\| ^{2}\bigr)+ \frac{1}{\tau}\biggl(\gamma-\frac {h^{2}}{12}\biggr) \bigl(\bigl\| e^{n+1}_{x}\bigr\| ^{2}-\bigl\| e^{n}_{x}\bigr\| ^{2} \bigr) \\ &{}+\frac{1}{\tau }\bigl(\bigl\| e^{n+1}_{xx}\bigr\| ^{2}-\bigl\| e^{n}_{xx}\bigr\| ^{2} \bigr) +\bigl(I+II,2e^{n+\frac{1}{2}}\bigr), \end{aligned}$$

(4.7)

where

$$\begin{aligned} I=\frac{2}{3}\alpha\bigl(v^{n+\frac{1}{2}}v^{n+\frac{1}{2}}_{\hat {x}}-u^{n+\frac{1}{2}}u^{n+\frac{1}{2}}_{\hat{x}} \bigr),\qquad II=\frac{2}{3}\alpha\bigl\{ \bigl[\bigl(v^{n+\frac{1}{2}} \bigr)^{2}\bigr]_{\hat{x}}-\bigl[\bigl(u^{n+\frac {1}{2}} \bigr)^{2}\bigr]_{\hat{x}}\bigr\} . \end{aligned}$$

According to Lemmas 3.1, 3.3, and the Schwartz inequality, the fourth term of right-hand side of (4.7) is estimated as follows:

$$\begin{aligned} \bigl(I,2e^{n+\frac{1}{2}}\bigr)&=\frac{4}{3}\alpha h\sum _{j=1}^{J-1}\bigl[v^{n+\frac {1}{2}}_{j} \bigl(v^{n+\frac{1}{2}}_{j}\bigr)_{\hat{x}}-u^{n+\frac{1}{2}}_{j} \bigl(u^{n+\frac {1}{2}}_{j}\bigr)_{\hat{x}}\bigr]e_{j}^{n+\frac{1}{2}} \\ &=\frac{4}{3}\alpha h\sum_{j=1}^{J-1} \bigl[v^{n+\frac{1}{2}}_{j}\bigl(e^{n+\frac {1}{2}}_{j} \bigr)_{\hat{x}} +\bigl(v^{n+\frac{1}{2}}_{j}-u^{n+\frac{1}{2}}_{j} \bigr) \bigl(u_{j}^{n+\frac{1}{2}}\bigr)_{\hat {x}} \bigr]e_{j}^{n+\frac{1}{2}} \\ &\le Ch\sum_{j=1}^{J-1}\bigl[\bigl| \bigl(e_{j}^{n+\frac{1}{2}}\bigr)_{\hat{x}}\bigr|+\bigl|\bigl(u_{j}^{n+\frac {1}{2}} \bigr)_{\hat{x}}\bigr|\bigr]\bigl|e_{j}^{n+\frac{1}{2}}\bigr| \\ &\le C\bigl[\bigl\| e_{x}^{n+1}\bigr\| ^{2}+\bigl\| e_{x}^{n}\bigr\| ^{2} +\bigl\| e^{n+1}\bigr\| ^{2}+\bigl\| e^{n}\bigr\| ^{2} \bigr], \end{aligned}$$

(4.8)

$$\begin{aligned} \bigl(II,2e^{n+\frac{1}{2}}\bigr)&=\frac{4}{3}\alpha h\sum _{j=1}^{J-1}\bigl\{ \bigl[\bigl(v^{n+\frac{1}{2}}_{j} \bigr)^{2}\bigr]_{\hat{x}}-\bigl[\bigl(u^{n+\frac{1}{2}}_{j} \bigr)^{2}\bigr]_{\hat {x}}\bigr\} e_{j}^{n+\frac{1}{2}} \\ &=-\frac{4}{3}\alpha h\sum_{j=1}^{J-1} \bigl[\bigl(v^{n+\frac {1}{2}}_{j}\bigr)^{2}- \bigl(u^{n+\frac{1}{2}}_{j}\bigr)^{2}\bigr] \bigl(e_{j}^{n+\frac{1}{2}}\bigr)_{\hat {x}} \\ &=-\frac{4}{3}\alpha h\sum_{j=1}^{J-1}{e_{j}^{n+\frac{1}{2}} \bigl(v^{n+\frac {1}{2}}_{j}+u^{n+\frac{1}{2}}_{j}\bigr) \bigl(e_{j}^{n+\frac{1}{2}}\bigr)_{\hat{x}}} \\ &\le C\bigl[\bigl\| e_{x}^{n+1}\bigr\| ^{2}+\bigl\| e_{x}^{n}\bigr\| ^{2} +\bigl\| e^{n+1}\bigr\| ^{2}+\bigl\| e^{n}\bigr\| ^{2} \bigr]. \end{aligned}$$

(4.9)

In addition, it is obvious that

$$\begin{aligned} \bigl(Er^{n},2e^{n+\frac{1}{2}}\bigr)=\bigl(Er^{n},e^{n+1}+e^{n} \bigr)\le\bigl\| Er^{n}\bigr\| ^{2} +\frac{1}{2} \bigl(\bigl\| e^{n+1}\bigr\| ^{2}+\bigl\| e^{n}\bigr\| ^{2} \bigr). \end{aligned}$$

(4.10)

Substituting (4.9)-(4.10) into (4.7), we get

$$\begin{aligned} &\bigl\| e^{n+1}\bigr\| ^{2}-\bigl\| e^{n}\bigr\| ^{2}+\biggl( \gamma-\frac {h^{2}}{12}\biggr) \bigl(\bigl\| e^{n+1}_{x}\bigr\| ^{2}-\bigl\| e^{n}_{x}\bigr\| ^{2} \bigr)+\bigl\| e_{xx}^{n+1}\bigr\| ^{2}-\bigl\| e_{xx}^{n}\bigr\| ^{2} \\ &\quad \le C\tau \bigl(\bigl\| e^{n+1}\bigr\| ^{2} +\bigl\| e^{n}\bigr\| ^{2}+\bigl\| e_{x}^{n+1}\bigr\| ^{2}+\bigl\| e_{x}^{n}\bigr\| ^{2} \bigr)+\tau\bigl\| Er^{n}\bigr\| ^{2}. \end{aligned}$$

(4.11)

Let $B^{n}=\|e^{n}\|^{2}+(\gamma-\frac {h^{2}}{12})\|e^{n}_{x}\|^{2}+\|e_{xx}^{n}\|^{2}$. Summing up (4.11) from 0 to $n-1$ yields

$$\begin{aligned} B^{n}-B^{0}\leq C\tau\sum_{l=0}^{n-1}\bigl\| Er^{l}\bigr\| ^{2}+C \tau\sum_{l=0}^{n-1}\bigl(\bigl\| e^{l}\bigr\| ^{2}+\bigl\| e_{x}^{l}\bigr\| ^{2} \bigr). \end{aligned}$$

(4.12)

Notice that

$$ \tau\sum_{l=0}^{n-1}\bigl\| Er^{l}\bigr\| ^{2} \le n\tau\max_{0\le l\le n-1}\bigl\| Er^{l}\bigr\| ^{2}\le T\cdot \bigl[O\bigl(\tau^{2}+h^{2}\bigr)\bigr]^{2}. $$

(4.13)

From the discrete initial condition, we know that $e^{0}$ is of second-order accuracy; then

$$ B^{0}=\bigl[O\bigl(\tau^{2}+h^{2}\bigr) \bigr]^{2}. $$

(4.14)

This together with (4.13) and (4.12) gives

$$ \bigl\| e^{n}\bigr\| ^{2}+\biggl(\gamma-\frac{h^{2}}{12} \biggr)\bigl\| e^{n}_{x}\bigr\| ^{2}+\bigl\| e_{xx}^{n}\bigr\| ^{2} \leq \bigl[O\bigl(\tau^{2}+h^{2}\bigr)\bigr]^{2}+C \tau\sum_{l=0}^{n-1}\bigl(\bigl\| e^{l}\bigr\| ^{2}+\bigl\| e_{x}^{l}\bigr\| ^{2} \bigr). $$

(4.15)

If $\gamma>0$, let h be small enough, such that $(\gamma-\frac {h^{2}}{12})>0$. It follows from (4.15) and Lemma 4.1 that

$$\begin{aligned} \bigl\| e^{n}\bigr\| \le O\bigl(\tau^{2}+h^{2}\bigr),\qquad \bigl\| e_{x}^{n}\bigr\| \le O\bigl(\tau^{2}+h^{2} \bigr), \qquad\bigl\| e_{xx}^{n}\bigr\| \le O\bigl(\tau^{2}+h^{2} \bigr). \end{aligned}$$

(4.16)

According to Lemma 3.2, we obtain

$$ \bigl\| e^{n}\bigr\| _{\infty}\le O\bigl(\tau^{2}+h^{2} \bigr). $$

(4.17)

Using Lemma 2.1 and the Schwartz inequality, we have

$$ \bigl\| e_{x}^{n}\bigr\| ^{2}\le\bigl\| e^{n}\bigr\| \cdot\bigl\| e_{xx}^{n}\bigr\| \le\frac {1}{2}\bigl(\bigl\| e^{n}\bigr\| ^{2}+\bigl\| e_{xx}^{n}\bigr\| ^{2} \bigr). $$

(4.18)

If $\gamma\leq0$, it follows from (4.18) and (4.15) that

$$\begin{aligned} \biggl[1+\frac{1}{2}\biggl(\gamma-\frac {h^{2}}{12}\biggr)\biggr] \bigl(\bigl\| e^{n}\bigr\| ^{2}+\bigl\| e_{xx}^{n}\bigr\| ^{2} \bigr)\leq\bigl[O\bigl(\tau^{2}+h^{2}\bigr) \bigr]^{2}+C\tau \sum_{l=0}^{n-1} \bigl(\bigl\| e^{l}\bigr\| ^{2}+\bigl\| e_{xx}^{l}\bigr\| ^{2} \bigr). \end{aligned}$$

(4.19)

For h is sufficiently small which satisfies $[1+\frac{1}{2}(\gamma -\frac{h^{2}}{12})]>0$, according to Lemma 4.1, we get $\|e^{n}\|^{2}+\|e_{xx}^{n}\|^{2}\le[O(\tau^{2}+h^{2})]^{2}$, that is,

$$ \bigl\| e^{n}\bigr\| \le O\bigl(\tau^{2}+h^{2}\bigr),\qquad \bigl\| e_{xx}^{n}\bigr\| \le O\bigl(\tau ^{2}+h^{2} \bigr). $$

(4.20)

This together with (4.18) and Lemma 3.2 gives

$$ \bigl\| e^{n}\bigr\| _{\infty}\le O\bigl(\tau^{2}+h^{2} \bigr). $$

(4.21)

This completes the proof of Theorem 4.1. □

Similarly, the following can be proved.

Theorem 4.2

Under the conditions of Theorem 4.1, the solution of the scheme (2.6)-(2.8) is unconditionally stable in the sense of the $\|\cdot\|_{\infty}$ norm.

Theorem 4.3

Scheme (2.6)-(2.8) is uniquely solvable.

5 Numerical experiments

In this section, we will conduct some numerical experiments to verify the theoretical results obtained in the previous sections. We will measure the accuracy of the proposed scheme using the maximum norm errors defined by

$$ e^{n}_{\epsilon}=\bigl\| v^{n}-u^{n}\bigr\| _{\infty}. $$

Consider the IBV problem of the Rosenau-KdV-RLW equation (2.1)-(2.3). The exact solution of system (2.1)-(2.3) has the following form [1]:

$$ u(x,t)=\lambda\operatorname{sech}^{4}\bigl[\mu(x-ct)\bigr], $$

(5.1)

where λ, μ, and c are dependent on the following formulas:

$$ \left \{ \begin{array}{@{}l} \lambda\bigl(\alpha\lambda-840c\mu^{4} \bigr)=0,\\ \lambda\bigl(20(\beta+c\gamma)\mu^{2}+1{,}040c\mu^{4}\bigr)=0,\\ \lambda\bigl(1-c-16(\beta+c\gamma)\mu^{2}-256c\mu^{4} \bigr)=0. \end{array} \right . $$

(5.2)

In the computations, without loss of generality, we take the parameters $\beta=\gamma=1$, $\alpha=\frac{1}{2}$ [1] and $\beta=1$, $\gamma=-\frac{1}{10}$, $\alpha=\frac{1}{2}$, respectively. When we choose the parameters $\beta=\gamma=1$, $\alpha=\frac{1}{2}$, the exact solution of the problem (2.1)-(2.3) is (1.2). When we choose the parameters $\beta=1$, $\gamma=-\frac{1}{10}$, $\alpha=\frac{1}{2}$, similar to getting (1.2), we can also derive the exact solution of the problem (2.1)-(2.3), which reads

$$\begin{aligned} u(x,t) =&\frac{35}{9{,}227{,}184}(-386{,}095+5{,}915\sqrt{7{,}465}) \\ &{}\times \operatorname{sech}^{4}\biggl[\frac{1}{\sqrt{1{,}440}}\sqrt{-65+\sqrt{7{,}465}}\biggl(x- \frac{76{,}855+1{,}235\sqrt{7{,}465}}{160{,}208}t\biggr)\biggr]. \end{aligned}$$

(5.3)

It follows from (5.1) and (5.3) that the IBV problem (2.1)-(2.3) is consistent with the initial value problem (2.1)-(2.2) for $-x_{l}\gg0$, $x_{r}\gg0$. In the following numerical experiments, we always take $x_{l}=-20$, $x_{r}=40$, and $T=10$. The proposed scheme [1] is a weighted average and linearized one: when $\theta=-\frac{1}{3}$, the scheme is a non-conservative one and we denote it as Scheme I; when $\theta=\frac {1}{3}$, the scheme is a conservative one and we denote it as Scheme II. We denote the present conservative scheme (2.6) of this paper as Scheme III.

Example 1

We also choose the parameters $\beta=\gamma=1$, $\alpha =\frac{1}{2}$ [1].

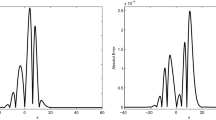
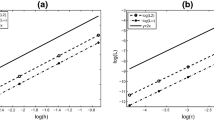
The errors in the sense of $L_{\infty}$-norm of the numerical solutions at different time t under various mesh steps $h=\tau$ are listed on Table 1. Table 1 verifies the good stability of the numerical solutions. We make a comparison between Schemes I, II, and III. The maximal errors of the numerical solutions under various mesh steps $h=\tau$ at $t=10$ are listed on Table 2. From Table 2, as to conservative schemes, it is obvious that Scheme III performs better than Scheme II in the numerical precision, but it is inferior to non-conservative Scheme I, which also shows the influence of the parameter θ on the numerical precision. In order to verify the second-order accuracy $O(\tau^{2}+h^{2})$, the convergence order figure of $\log(e^{n}_{\epsilon})\mbox{-}\log(h)$ is given in Figure 1 under various mesh steps h and τ at $t=10$. From Figure 1, it is obvious that scheme (2.6)-(2.8) is convergent in the maximum norm, and the convergence order is $O(\tau^{2}+h^{2})$. Figure 2 is presented to show the conservative laws of the discrete mass $Q^{n}$ and the discrete energy $E^{n}$ computed by scheme (2.6) when $h=\tau=0.1$. It is easy to see from Figure 2 that scheme (2.6) preserves the discrete mass and the discrete energy very well, thus it can be used for computing for a long time.

Figure 1

The convergence order for $\pmb{u^{n}}$ of Scheme III under various h and τ at $\pmb{t=10}$ when $\pmb{\beta=\gamma=1}$ , $\pmb{\alpha=\frac{1}{2}}$ .

Figure 2

Discrete conservative mass and energy computed by Scheme III with $\pmb{h=\tau=0.1}$ when $\pmb{\beta=\gamma=1}$ and $\pmb{\alpha=\frac{1}{2}}$ .

Table 1 Maximal errors of numerical solutions at different time t with various $\pmb{h=\tau}$ for Scheme III when $\pmb{\beta=\gamma=1}$ , $\pmb{\alpha=\frac{1}{2}}$

Table 2 The comparison of maximal errors of numerical solutions at $\pmb{t=10}$ with various $\pmb{h=\tau}$ for Scheme I, II, and III when $\pmb{\beta =\gamma=1}$ , $\pmb{\alpha=\frac{1}{2}}$

The curves of the solitary waves with time computed by Scheme III of this paper with $h=\tau=0.1$ are given in Figure 3, the waves at $t=5, 10$ agree with the ones at $t=0$ quite well, which also demonstrates the accuracy of the scheme.

Figure 3

Exact solutions of $\pmb{u(x,t)}$ at $\pmb{t=0}$ and numerical solutions computed by Scheme III with $\pmb{h=\tau=0.1}$ at $\pmb{t=5}$ and 10.

Example 2

We take the parameters $\beta=1$, $\gamma=-\frac {1}{10}$, $\alpha=\frac{1}{2}$.

In Example 2, the maximal errors of the numerical solutions at different time t for Scheme III are listed on Table 3. We also give numerical results for Schemes I and II when parameters $\beta=1$, $\gamma =-\frac{1}{10}$, and $\alpha=\frac{1}{2}$: the errors $e^{n}_{\epsilon}$ of the numerical solutions with various $h=\tau$ at $t=10$ are listed on Table 4. Tables 3 and 4 show the good stability of the numerical solutions. The convergence order figure of $\log(e^{n}_{\epsilon})\mbox{-}\log (h)$ is given in Figure 4 under various mesh steps h and τ at $t=10$. Figure 4 shows that scheme (2.6)-(2.8) is convergent in the maximum norm and the convergence order is $O(\tau ^{2}+h^{2})$. Figure 5 is given to verify the conservative laws of the discrete mass $Q^{n}$ and the discrete energy $E^{n}$ computed by Scheme III of the present paper when $h=\tau=0.1$. The discrete mass $Q^{n}$ and the discrete energy $E^{n}$ computed by the conservative Scheme II are shown in Figure 6 when $h=\tau=0.1$. It is easy to see from Figures 5 and 6 that Schemes II and III both preserve conservative invariant very well.

Figure 4

The convergence order for $\pmb{u^{n}}$ of Scheme III under various h and τ at $\pmb{t=10}$ when $\pmb{\beta=1}$ , $\pmb{\gamma=-\frac{1}{10}}$ , $\pmb{\alpha=\frac{1}{2}}$ .

Figure 5

Discrete conservative mass and energy computed by Scheme III with $\pmb{h=\tau=0.1}$ when $\pmb{\beta=1}$ , $\pmb{\gamma=-\frac{1}{10}}$ , $\pmb{\alpha=\frac{1}{2}}$ .

Figure 6

Discrete conservative mass and energy computed by Scheme II with $\pmb{h=\tau=0.1}$ when $\pmb{\beta=1}$ , $\pmb{\gamma=-\frac{1}{10}}$ , $\pmb{\alpha=\frac{1}{2}}$ .

Table 3 Maximal errors of numerical solutions at different time t with various $\pmb{h=\tau}$ for Scheme III when $\pmb{\beta=1}$ , $\pmb{\gamma=-\frac{1}{10}}$ , $\pmb{\alpha=\frac{1}{2}}$

Table 4 Maximal errors of numerical solutions at $\pmb{t=10}$ with various $\pmb{h=\tau}$ for Scheme I, II when $\pmb{\beta=1}$ , $\pmb{\gamma=-\frac{1}{10}}$ , $\pmb{\alpha=\frac{1}{2}}$

The curves of the solitary waves with time computed by Schemes II and III of this paper with $h=\tau=0.2$, $h=\tau=0.1$ are given in Figures 7 and 8, respectively, the waves at $t=5, 10$ agree with the ones at $t=0$ quite well, which also demonstrates the accuracy of both schemes. From the numerical results, the present conservative scheme of this paper is efficient and accurate, which also demonstrates that a further discussion of the positive and negative of the parameter γ is necessary.

Figure 7

Exact solutions of $\pmb{u(x,t)}$ at $\pmb{t=0}$ and numerical solutions computed by Scheme III with $\pmb{h=\tau=0.1}$ at $\pmb{t=5}$ and 10.

Figure 8

Exact solutions of $\pmb{u(x,t)}$ at $\pmb{t=0}$ and numerical solutions computed by Scheme II with $\pmb{h=\tau=0.2}$ at $\pmb{t=5}$ and 10.