A new conservative nonlinear high-order compact finite difference scheme for the general Rosenau-RLW equation

Abstract

In this paper, a new conservative high-order compact finite difference scheme is studied for the initial-boundary value problem of the generalized Rosenau-regularized long wave equation. We design new conservative nonlinear fourth-order compact finite difference schemes. It is proved by the discrete energy method that the compact scheme is uniquely solvable; we have the energy conservation and the mass conservation for this approach in discrete Sobolev spaces. The convergence and stability of the difference schemes are obtained, and its numerical convergence order is $O(\tau^{2}+h^{4})$ in the $L^{\infty}$-norm. Furthermore, numerical results are given to support the theoretical analysis. Numerical experiment results show that the theory is accurate and the method is efficient and reliable.

1 Introduction

In this paper, we consider the following initial-boundary value problem of the Generalized Rosenau-RLW Regularized Long Wave (RLW) equation (GRRLW):

$$\begin{aligned}& u_{t}+u_{xxxxt}-u_{xxt}+u_{x}+ \bigl(u^{p}\bigr)_{x}=0,\quad (x,t)\in \Omega\times(0,T], \end{aligned}$$

(1.1)

$$\begin{aligned}& u(x_{l},t)=u(x_{r},t)=0,\qquad u_{xx}(x_{l}, t)=u_{xx}(x_{r},t)=0,\quad t\in (0,T], \end{aligned}$$

(1.2)

$$\begin{aligned}& u(x,0)=u_{0}(x),\quad x\in\Omega, \end{aligned}$$

(1.3)

where $p\geq2$ is a positive integer, $\Omega=(x_{l}, x_{r})$ and $u_{0}(x)$ are known smooth functions. Let $H_{0}^{2}(\Omega)=\{v(x)\in H^{2}(\Omega)\mid v(x_{l},t)=v(x_{r},t)=0, v_{xx}(x_{l}, t)=v_{xx}(x_{r},t)=0\}$. The initial-boundary value problem (1.1)-(1.3) possesses the following conservative quantities:

$$\begin{aligned}& E(t)=\|u\|^{2}_{L^{2}}+\|u_{x}\|^{2}_{L^{2}}+ \|u_{xx}\| ^{2}_{L^{2}}=E(0), \end{aligned}$$

(1.4)

$$\begin{aligned}& Q(t)=\int_{x_{l}}^{x_{r}}u(x,t)\,dx=\int _{x_{l}}^{x_{r}}u(x,0)\,dx=Q(0). \end{aligned}$$

(1.5)

For the Schrödinger equation, the Cahn-Hilliard equation, and the Klein-Gordon equation, the existence and uniqueness of numerical solutions were discussed in [1–5], respectively. The convergence and stability of the finite difference schemes were proved in the theory, and their numerical convergence orders are $O(\tau^{2}+h^{2})$. In [6–12], some new finite difference schemes for the initial-boundary value problem of the RLW equation were considered. Two types of conservative finite difference schemes were proposed in [13], which depended on the choice of a parameter. On the basis of the prior estimates as regards the norms, the convergence of the difference solution was proved with order $O(\tau^{2}+h^{2})$ in the energy norm in [14, 15]. For the Cahn-Hilliard equation, a three-level linearized high-order compact difference scheme was derived. The unique solvability and unconditional convergence of the difference solution were proved. The convergence order is $O(\tau^{2}+h^{4})$ in the maximum norm in [16]. In [17], a new conservative difference scheme for the general Rosenau-RLW equation was proposed. In [18], Pan and Zhang proposed a conservative linearized difference scheme for the general Rosenau-RLW equation which was unconditionally stable and second-order convergent and simulates conservative laws at the same time. In [19], the initial-boundary value problem for the Rosenau-RLW equation was studied. One proposed a three-level linear finite difference scheme, which has the theoretical accuracy of $O(\tau^{2}+h^{4})$.

This paper is organized as follows. In Section 2, a nonlinear and conservative difference scheme for the GRRLW equation is constructed, and the discrete conservative laws of the difference scheme are discussed. The unique solvability of the numerical solutions is also given. In Section 3, the prior error estimates for a fourth-order finite difference approximation of the GRRLW equation are obtained, and the convergence and stability of the difference scheme are proved. Numerical experiments are reported in Section 4.

2 Finite difference scheme and conservation law

Let $h=(x_{r}-x_{l})/J$ be the uniform step size in the spatial direction for positive integer J. Let τ denote the uniform step size in the temporal direction. Denote $x_{j}=x_{l}+jh$ ($0\leq j\leq J$), $t^{n}=n\tau$ ($0\leq n\leq N$). Let $U^{n}_{j}$ denote the approximation of $u(x_{j}, t_{n})$, and let

$$ \mathbf{R}^{J}_{0}= \bigl\{ V_{j}=(V_{j})_{j \in\mathbb{Z}} \mid V_{0}=V_{J}=0 \bigr\} . $$

As usual, the following notations will be used:

$$\begin{aligned}& \delta_{x}V^{n}_{i}=\frac{V^{n}_{i+1}-V^{n}_{i}}{h},\qquad \delta_{\hat{x}}V^{n}_{i}=\frac{V^{n}_{i+1}-V^{n}_{i-1}}{2h},\qquad \delta_{\bar{x}}V^{n}_{i}=\frac{V^{n}_{i+2}-V^{n}_{i-2}}{4h}, \\ & \delta^{2}_{x}V_{i}^{n}= \frac{V_{i+1}^{n}-2V^{n}_{i}+V_{i-1}^{n}}{h^{2}}, \qquad\delta^{4}_{x}V_{i}^{n}= \delta^{2}_{x}\bigl( \delta ^{2}_{x}V_{i}^{n} \bigr), \qquad\partial_{t}V^{n}_{i}=\frac {V_{i}^{n+1}-V^{n}_{i}}{\tau}, \\ & V^{n+\frac{1}{2}}_{i}=\frac{V^{n+1}_{i}+V^{n}_{i}}{2},\qquad \mathcal{A}_{1}V_{i}= \biggl(1+\frac{h^{2}}{12}\delta^{2}_{x} \biggr)V_{i}, \qquad\mathcal{A}_{2}V_{i}= \biggl(1+ \frac{h^{2}}{6}\delta ^{2}_{x} \biggr)V_{i}. \end{aligned}$$

We now introduce the discrete $L^{2}$-inner product and the associated norm

$$(U, V)_{h}=h\sum_{i=1}^{J-1}U_{i}V_{i},\quad U, V\in \mathbf{R}_{0}^{J}, \qquad \|V\|_{h}=(V,V)_{h}^{\frac{1}{2}}. $$

The discrete $H^{m}$-seminorm $|\cdot|_{m,h}$, the $H^{m}$-norm $\|\cdot\|_{m,h}$ and the $L^{\infty}$-norm $\|\cdot\|_{\infty,h}$ are defined, respectively, as

$$\begin{aligned}& |V|_{m,h}= \Biggl(h\sum_{i=0}^{J-m}\bigl| \hat{\delta }^{m}_{x}V_{i}\bigr|^{2} \Biggr)^{\frac{1}{2}},\qquad \|V\|_{m,h} = \Biggl(\sum _{s=0}^{m}|V|^{2}_{s,h} \Biggr)^{\frac {1}{2}},\qquad \|V\|_{\infty,h}=\max _{0\leq i\leq J}|V_{i}|, \end{aligned}$$

where the $\hat{\delta}_{x}^{m}$ ($m\geq1$) denote the mth-order forward difference quotient operators in the x direction. It is convenient to let $L^{2}_{h}(\Omega_{h})$ and $H^{m}_{h}(\Omega_{h})$ ($m\geq1$) denote the normed vector space, respectively, as

$$\begin{aligned}& L^{2}_{h}(\Omega_{h}):=\bigl\{ \mathbf{R}^{J}_{0},\|\cdot\|_{h}\bigr\} , \qquad H^{m}_{h}(\Omega_{h}):=\bigl\{ \mathbf{R}^{J}_{0},\|\cdot\|_{m,h}\bigr\} , \end{aligned}$$

where $\Omega_{h}=\{x_{j}=x_{l }+jh\mid 0< j<J\}$.

For the discretization of the first-order derivatives $u_{x}$, the second-order derivatives $u_{xx}$ and the fourth-order derivatives $u_{xxxx}$ of the function $u(x)$, we have the following formulas:

$$\begin{aligned}& \mathcal{A}_{1}u_{xx}(x_{i})= \delta^{2}_{x}u(x_{i})+O\bigl(h^{4} \bigr) \quad\Rightarrow\quad u_{xx}(x_{i})= \mathcal{A}_{1}^{-1}\delta^{2}_{x}u(x_{i})+O \bigl(h^{4}\bigr), \\& \mathcal{A}_{2}u_{x}(x_{i})= \delta_{\hat{x}}u(x_{i})+O\bigl(h^{4}\bigr) \quad \Rightarrow\quad u_{x}(x_{i})=\mathcal{A}_{2}^{-1} \delta_{\hat{x}}u(x_{i})+O\bigl(h^{4}\bigr), \\& \mathcal{A}_{2}u_{xxxx}(x_{i})= \delta^{4}_{x}u(x_{i})+O\bigl(h^{4} \bigr) \quad\Rightarrow\quad u_{xxxx}(x_{i})= \mathcal{A}_{2}^{-1}\delta^{4}_{x}u(x_{i})+O \bigl(h^{4}\bigr), \end{aligned}$$

omitting the small terms $O(h^{4})$, we obtain the approximation of $u_{xx}$, $u_{x}$, and $u_{xxxx}$ as

$$\begin{aligned}& \mathcal{A}_{1}u_{xx}(x_{i})\approx \delta^{2}_{x}U_{i} \ \quad\Rightarrow\quad u_{xx}(x_{i})\approx \mathcal{A}_{1}^{-1} \delta^{2}_{x}U_{i}, \\& \mathcal{A}_{2}u_{x}(x_{i})\approx \delta_{\hat{x}}U_{i} \ \quad\Rightarrow\quad u_{x}(x_{i}) \approx \mathcal{A}_{2}^{-1}\delta_{\hat{x}}U_{i}, \\& \mathcal{A}_{2}u_{xxxx}(x_{i})\approx \delta^{4}_{x}U_{i} \ \quad\Rightarrow \quad u_{xxxx}(x_{i})\approx \mathcal{A}_{2}^{-1} \delta^{4}_{x}U_{i}, \end{aligned}$$

where $U_{i}$ is the approximation of $u(x_{i})$. The corresponding matrix form is

$$\begin{aligned}& M_{1}(\Pi_{h}u_{xx})\approx\delta^{2}_{x}U \quad\Rightarrow \quad \Pi_{h}u_{xx}\approx M_{1}^{-1}\delta^{2}_{x}U, \\& M_{2}(\Pi_{h}u_{x})\approx\delta_{\hat{x}}U \quad\Rightarrow\quad \Pi_{h}u_{x}\approx M_{2}^{-1}\delta_{\hat{x}}U, \\& M_{2}(\Pi_{h}u_{xxxx})\approx\delta^{4}_{x}U \quad\Rightarrow\quad \Pi_{h}u_{xxxx}\approx M_{2}^{-1}\delta^{4}_{x}U, \end{aligned}$$

where

$$\begin{aligned}& U=(U_{1}, U_{2}, \ldots, U_{J-1}), \\& \Pi_{h}u_{x}=\bigl(u_{x}(x_{1}),u_{x}(x_{2}), \ldots,u_{x}(x_{J-1})\bigr), \\& \Pi_{h}u_{xx}=\bigl(u_{xx}(x_{1}),u_{xx}(x_{2}), \ldots,u_{xx}(x_{J-1})\bigr), \\& \Pi_{h}u_{xxxx}=\bigl(u_{xxxx}(x_{1}),u_{xxxx}(x_{2}), \ldots,u_{xxxx}(x_{J-1})\bigr), \end{aligned}$$

and

$$\begin{aligned}& M_{1}=\frac{1}{12} \left .\begin{pmatrix} 10&1&0&\ldots&0&0\\ 1&10&1&\ldots&0&0\\ \vdots&\vdots&\vdots&\ldots&\vdots&\vdots\\ 0&0&0&\ldots&1&10 \end{pmatrix} \right ._{(J-1)\times(J-1)}, \\& M_{2}=\frac{1}{6} \left .\begin{pmatrix} 4&1&0&\ldots&0&0\\ 1&4&1&\ldots&0&0\\ \vdots&\vdots&\vdots&\ldots&\vdots&\vdots\\ 0&0&0&\ldots&1&4 \end{pmatrix} \right ._{(J-1)\times(J-1)}. \end{aligned}$$

Imposing the compact difference scheme of the GRRLW equations (1.1)-(1.3) gives

$$\begin{aligned}& \begin{aligned}[b] &\partial_{t}U^{n}_{i}+ \mathcal{A}_{2}^{-1}\delta_{x}^{4} \partial _{t}U^{n}_{i}+\mathcal{A}_{2}^{-1} \delta_{\hat{x}}U^{n+\frac {1}{2}}_{i}-\mathcal{A}_{1}^{-1} \delta_{x}^{2}\partial _{t}U^{n}_{i} \\ &\quad{}+\frac{4p}{3(p+1)}\bigl[\bigl(U_{i}^{n+\frac{1}{2}} \bigr)^{p-1}\delta_{\hat {x}}U_{i}^{n+\frac{1}{2}}+ \delta_{\hat{x}}\bigl(U_{i}^{n+\frac {1}{2}}\bigr)^{p} \bigr] \\ &\quad{}-\frac{p}{3(p+1)}\bigl[\bigl(U_{i}^{n+\frac{1}{2}} \bigr)^{p-1}\delta_{\bar {x}}U_{i}^{n+\frac{1}{2}}+ \delta_{\bar{x}}\bigl(U_{i}^{n+\frac{1}{2}}\bigr)^{p} \bigr] =0, \\ &\quad{} 1\leq i\leq J-1, 0\leq n\leq N-1, \end{aligned} \end{aligned}$$

(2.1)

$$\begin{aligned}& U^{n}_{0}=U^{n}_{J}=0, \qquad \delta^{2}_{x}U^{n}_{0}= \delta^{2}_{x}U^{n}_{J}=0, \quad 0\leq n \leq N, \end{aligned}$$

(2.2)

$$\begin{aligned}& U_{i}^{0}=u_{0}(x_{i}),\quad 0\leq i \leq J. \end{aligned}$$

(2.3)

Lemma 2.1

[20]

The eigenvalues of the matrices $M_{1}$, $M_{2}$ are, respectively, in the following forms:

$$\begin{aligned}& \lambda_{M_{1},k}=\frac{1}{6} \biggl(5+\cos\frac{k\pi}{J} \biggr),\qquad \lambda_{M_{2},k}=\frac{1}{3} \biggl(2+\cos \frac{k\pi}{J} \biggr),\quad k=1,2,\ldots, J-1. \end{aligned}$$

For the real symmetric positive definite matrices $M_{1}$, $M_{2}$, we let $H_{1}=M_{1}^{-1}$ and $H_{2}=M_{2}^{-1}$. Then $H_{1}$, $H_{2}$ are also real symmetric positive definite matrices. Now, we introduce the following discrete norm:

$$\begin{aligned} \bigl\| |V|\bigr\| _{1,h}=\bigl[(H_{1} \delta_{x}V,\delta_{x}V)\bigr]^{\frac{1}{2}},\qquad \bigl\| |V| \bigr\| _{2,h}=\bigl[\bigl(H_{2}\delta^{2}_{x}V, \delta^{2}_{x}V\bigr)\bigr]^{\frac{1}{2}},\quad V\in \mathbf{R}^{J}_{0}. \end{aligned}$$

(2.4)

Lemma 2.2

The discrete norms $\||\cdot|\|_{l,h}$ and $|\cdot|_{l,h}$ ($l=1,2$) are equivalent. In fact, for any grid function $V\in \mathbf{R}^{J}_{0}$, we have

$$\begin{aligned} c_{1}|V|_{1,h}\leq\bigl\| |V|\bigr\| _{1,h}\leq c_{2}|V|_{1,h},\qquad c_{1}|V|_{2,h}\leq \bigl\| |V|\bigr\| _{2,h}\leq c_{3}|V|_{2,h}, \end{aligned}$$

(2.5)

where $c_{1}=1$, $c_{2}=\sqrt{\frac{3}{2}}$, $c_{3}=\sqrt{3}$.

Proof

It follows from Lemma 2.1 that the eigenvalues of $H_{1}$ and $H_{2}$ satisfy

$$\begin{aligned} 1\leq\lambda_{H_{1},k}\leq\frac{3}{2},\qquad 1\leq \lambda_{H_{2},k}\leq3, \quad k=1,2,\ldots,J-1. \end{aligned}$$

these give the spectral radius $\rho(H_{1})\leq\frac{3}{2}$, $\rho(H_{2})\leq3$, and consequently

$$\begin{aligned}& 1\leq\|H_{1}\|=\bigl\| \rho(H_{1})\bigr\| \leq \frac{3}{2}, \qquad 1\leq\|H_{2}\|=\bigl\| \rho(H_{2}) \bigr\| \leq3. \end{aligned}$$

(2.6)

Thus we have

$$ \begin{aligned} &|V|_{1,h}^{2} \leq(H_{1}\delta_{x}V,\delta_{x}V)_{h} \leq\|H_{1}\| (\delta_{x}V,\delta_{x}V)_{h} \leq\frac{3}{2}|V|_{1,h}^{2}, \\ &|V|_{2,h}^{2}\leq\bigl(H_{2}\delta^{2}_{x}V, \delta^{2}_{x}V\bigr)_{h}\leq\| H_{2}\| \bigl(\delta^{2}_{x}V,\delta^{2}_{x}V \bigr)_{h}\leq3|V|_{2,h}^{2}. \end{aligned} $$

(2.7)

 □

Lemma 2.3

[17]

For $U,V\in\mathbf{R}_{0}^{J}$, we have

$$\begin{aligned}& (\delta_{\hat{x}} U,V)_{h}=-( U,\delta_{\hat{x}}V)_{h}, \qquad (\delta_{\bar{x}} U,V)_{h}=-( U,\delta_{\bar{x}} V)_{h}. \end{aligned}$$

Lemma 2.4

[21]

For any discrete function $V\in\mathbf{R}_{0}^{J}$, we have interpolation formulas as follows:

$$ \|V\|_{k,h}\leq K_{0}\|V\|_{n,h}^{\frac{k}{n}} \|V\|_{h}^{1-\frac{k}{n}}, $$

(2.8)

for $0\leq k\leq n$, and

$$ \|V\|_{\infty,h}\leq K\|V\|_{n,h}^{\frac{1}{n}}\|V \|_{h}^{1-\frac{1}{n}}, $$

(2.9)

for $n\geq1$, where $K_{0}$ and K are constants independent of h and V.

Lemma 2.5

[21]

For $V\in H^{1}_{h}(\Omega_{h})$, we have

$$\|V\|_{h}^{2}\leq K_{1}|V|_{1,h}^{2}, $$

where $K_{1}$ is a constant independent of h and V.

Lemma 2.6

[22]

For $V\in H^{2}_{h}(\Omega_{h})$, we have

$$\begin{aligned} |V|_{1,h}^{2}\leq K_{2}|V|_{2,h}^{2}, \end{aligned}$$

where $K_{2}$ is a constant independent of h and V.

Lemma 2.7

[23]

Let $(H,(\cdot,\cdot)_{h})$ be a finite-dimensional inner product space, $\|\cdot\|_{h}$ be the associated norm, and $g:H\longrightarrow H$ be continuous. Assume, moreover, that $\exists\alpha>0$, $\forall z\in H$, $\|z\|_{h}=\alpha$, $(g(z),z)\geq0$. Then there exists a $z^{*}\in H$ such that $g(z^{*})=0$ and $\|z^{*}\|_{h}\leq\alpha$.

Lemma 2.8

[19]

Suppose that the discrete function $\{\omega^{n}\mid n=0,1,2,\ldots,N; N\tau=T\}$ satisfies the inequality

$$\begin{aligned} \omega^{n}-\omega^{n-1}\leq A\tau\omega^{n}+B\tau \omega^{n-1}+C_{n}\tau, \end{aligned}$$

where A, B, and $C_{n}$ are nonnegative constants. Then

$$\begin{aligned} \max_{1\leq n\leq N}\bigl|\omega^{n}\bigr|\leq \Biggl( \omega^{0}+\tau\sum^{N}_{l=1}C_{l} \Biggr)e^{2(A+B)T}, \end{aligned}$$

where τ is sufficiently small, such that $(A+B)\tau\leq\frac{N-1}{2N}$ ($N>1$).

The matrix form of the difference scheme (2.1)-(2.3) can be written as

$$\begin{aligned}& \begin{aligned}[b] &\partial_{t}U^{n}+H_{2} \delta_{x}^{4}\partial_{t}U^{n}+H_{2} \delta _{\hat{x}}U^{n+\frac{1}{2}}-H_{1}\delta_{x}^{2} \partial _{t}U^{n} \\ &\quad{}+\frac{4p}{3(p+1)}\bigl[\bigl(U^{n+\frac{1}{2}}\bigr)^{p} \delta_{\hat {x}}U^{n+\frac{1}{2}}+\delta_{\hat{x}} \bigl(U_{i}^{n+\frac {1}{2}} \bigr)^{p}\bigr] \\ &\quad{}-\frac{p}{3(p+1)}\bigl[\bigl(U^{n+\frac{1}{2}}\bigr)^{p-1} \delta_{\bar {x}}U^{n+\frac{1}{2}}+\delta_{\bar{x}} \bigl(U^{n+\frac{1}{2}} \bigr)^{p}\bigr]=0, \quad 0\leq n\leq N-1, \end{aligned} \end{aligned}$$

(2.10)

$$\begin{aligned}& U^{n}|_{\partial\Omega_{h}}=0, \qquad \delta^{2}_{x}U^{n}|_{\partial\Omega_{h}}=0, \quad 0\leq n\leq N, \end{aligned}$$

(2.11)

$$\begin{aligned}& U^{0}_{i}=u_{0}(x_{i}), \quad 0\leq i\leq J. \end{aligned}$$

(2.12)

Let $\mathbf{Z}_{h}^{0}=\{V_{j}=(V_{j})_{j \in\mathbb{Z}}\mid V_{0}=V_{J}=0, \delta_{x}^{2}V_{0}=\delta_{x}^{2}V_{J}=0\}$, obviously, the solution $U^{n}\in\mathbf{Z}_{h}^{0}$ of the difference scheme (2.1)-(2.3), then there are the following lemmas:

Theorem 2.9

Assume $u_{0}\in H_{0}^{2}(\Omega)$, then the finite difference scheme (2.1)-(2.3) is conservative for the discrete energy and the discrete mass, i.e.

$$\begin{aligned} E^{n}=\bigl\| U^{n}\bigr\| ^{2}_{h}+ \bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{1,h}+\bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{2,h}=\cdots =E^{0} \end{aligned}$$

(2.13)

and

$$Q^{n}=h\sum_{j=1}^{J-1}U_{j}^{n}=Q^{n-1}= \cdots=Q^{0}. $$

Proof

Taking the inner product of (2.10) with $2U^{n+\frac{1}{2}}$, we obtain

$$\begin{aligned} &\bigl(\partial_{t}U^{n},2U^{n+\frac{1}{2}} \bigr)_{h}+\bigl(H_{2}\delta _{x}^{4} \partial_{t}U^{n},2U^{n+\frac{1}{2}}\bigr)_{h} + \bigl(H_{2}\delta_{\hat{x}}U^{n+\frac{1}{2}},2U^{n+\frac {1}{2}} \bigr)_{h} \\ &\quad{}-\bigl(H_{1}\delta_{x}^{2} \partial_{t}U^{n},2U^{n+\frac{1}{2}}\bigr)_{h} + \frac{4p}{3(p+1)}\bigl(\bigl(\bigl(U^{n+\frac{1}{2}}\bigr)^{p-1} \delta_{\hat {x}}U^{n+\frac{1}{2}}+\delta_{\hat{x}} \bigl(U^{n+\frac {1}{2}} \bigr)^{p}\bigr),2U^{n+\frac{1}{2}}\bigr)_{h} \\ &\quad{}-\frac{p}{3(p+1)}\bigl(\bigl(\bigl(U^{n+\frac{1}{2}} \bigr)^{p-1}\delta_{\bar{x}} U^{n+\frac{1}{2}}+\delta_{\bar{x}} \bigl(U^{n+\frac{1}{2}}\bigr)^{p}\bigr),2U^{n+\frac{1}{2}} \bigr)_{h}=0, \end{aligned}$$

(2.14)

letting

$$\begin{aligned}& \phi(U,U)=\frac{4p}{3(p+1)}\bigl(U^{p-1}\delta_{\hat{x}} U+ \delta_{\hat{x}}\bigl(U^{p}\bigr)\bigr), \\& \psi(U,U)=\frac{p}{3(p+1)}\bigl(U^{p-1}\delta_{\bar{x}}U+ \delta_{\bar {x}}\bigl(U^{p}\bigr)\bigr), \end{aligned}$$

from Lemma 2.3, we have

$$\begin{aligned} \bigl(\phi(U,U),U\bigr)_{h} =&\frac{4p}{3(p+1)} \bigl(U^{p-1}\delta_{\hat{x}} U+\delta_{\hat{x}} \bigl(U^{p}\bigr),U\bigr)_{h} \\ =&\frac{4p}{3(p+1)}\bigl[\bigl(U^{p-1}\delta_{\hat{x}} U,U \bigr)_{h}+\bigl(\delta _{\hat{x}}\bigl(U^{p}\bigr),U \bigr)_{h}\bigr] \\ =&\frac{4p}{3(p+1)}\bigl[\bigl(\delta_{\hat{x}}U,U^{p} \bigr)_{h}-\bigl(\delta_{\hat{x}} U,U^{p} \bigr)_{h}\bigr]=0 \end{aligned}$$

(2.15)

and

$$\begin{aligned} \bigl(\psi(U,U),U\bigr)_{h} =&\frac{p}{3(p+1)} \bigl(U^{p-1}\delta_{\bar{x}} U+\delta_{\bar{x}} \bigl(U^{p}\bigr),U\bigr)_{h} \\ =&\frac{p}{3(p+1)}\bigl[\bigl(U^{p-1}\delta_{\bar{x}} U,U \bigr)_{h}+\bigl(\delta_{\bar {x}}\bigl(U^{p}\bigr),U \bigr)_{h}\bigr] \\ =&\frac{p}{3(p+1)}\bigl[\bigl(\delta_{\bar{x}} U,U^{p} \bigr)_{h}-\bigl(\delta_{\bar{x}} U,U^{p} \bigr)_{h}\bigr]=0. \end{aligned}$$

(2.16)

Thus from (2.14)-(2.16), we can obtain

$$ \bigl(\bigl\| U^{n+1}\bigr\| ^{2}_{h}- \bigl\| U^{n}\bigr\| ^{2}_{h}\bigr)+\bigl(\bigl\| \bigl|U^{n+1}\bigr| \bigr\| ^{2}_{1,h}-\bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{1,h} \bigr)+\bigl(\bigl\| \bigl|U^{n+1}\bigr|\bigr\| ^{2}_{2,h}- \bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{2,h}\bigr)=0. $$

(2.17)

Let $E^{n}$ denote the following discrete energy:

$$\begin{aligned} E^{n}=\bigl\| U^{n}\bigr\| ^{2}_{h}+ \bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{1,h}+\bigl\| \bigl|U^{n}\bigr| \bigr\| ^{2}_{2,h}, \end{aligned}$$

(2.18)

then from (2.17), we get

$$\begin{aligned} E^{n}=E^{n-1}=\cdots=E^{0}. \end{aligned}$$

Multiplying (2.1) with h, according to the boundary condition (2.2), summing for j from 1 to $J-1$, we obtain

$$ h\sum_{j=1}^{J-1}\bigl(U_{j}^{n+1}-U_{j}^{n} \bigr)=0, $$

letting

$$Q^{n}=h\sum_{j=1}^{J-1}U_{j}^{n}, $$

then we have

$$Q^{n}=Q^{n-1}=\cdots=Q^{0}. $$

This completes the proof. □

Lemma 2.10

Assume $u_{0}\in H_{0}^{2}(\Omega)$, then there is the estimation for the solution of the difference scheme (2.1)-(2.3)

$$\begin{aligned} \bigl\| U^{n}\bigr\| _{1,h}\leq\sqrt{\frac{(2K_{2}+1)E^{0}}{K_{2}+1}},\qquad \bigl\| U^{n}\bigr\| _{\infty,h}\leq K\sqrt{\frac{(2K_{2}+1)E^{0}}{K_{2}+1}}. \end{aligned}$$

Proof

From Lemma 2.2, Lemma 2.6, and Theorem 2.9, we have

$$\begin{aligned} \biggl(\frac{K_{2}+1}{K_{2}} \biggr)\bigl|U^{n}\bigr|^{2}_{1,h}+ \bigl\| U^{n}\bigr\| ^{2}_{h}\leq\bigl\| U^{n} \bigr\| ^{2}_{h}+\bigl|U^{n}\bigr|^{2}_{1,h}+\bigl|U^{n}\bigr|^{2}_{2,h} \leq E^{0}, \quad n\geq0. \end{aligned}$$

Hence, we can get

$$\bigl\| U^{n}\bigr\| _{1,h}=\sqrt{ \bigl\| U^{n}\bigr\| ^{2}_{h}+\bigl|U^{n}\bigr|^{2}_{1,h}} \leq\sqrt {E^{0}+\frac{K_{2}E^{0}}{K_{2}+1}} =\sqrt{\frac{(2K_{2}+1)E^{0}}{K_{2}+1}}. $$

It follows from Lemma 2.4 that

$$\begin{aligned} \bigl\| U^{n}\bigr\| _{\infty,h}\leq K\bigl\| U^{n}\bigr\| _{1,h}\leq K \sqrt{\frac{(2K_{2}+1)E^{0}}{K_{2}+1}}. \end{aligned}$$

This completes the proof. □

Lemma 2.11

For $V \in\mathbf{Z}_{h}^{0}$, we have

$$ \|\delta_{\bar{x}}V\|_{h}^{2} \leq\| \delta_{\hat{x}}V\|_{h}^{2} \leq\|\delta_{x}V \|_{h}^{2}. $$

Proof

From the definition of $\|\cdot\|_{h}$, we have

$$\begin{aligned} \|\delta_{\bar{x}}V\|_{h}^{2} =&h\sum ^{J-2}_{j=2}(\delta_{\bar{x}}V_{j})^{2} =\frac{h}{4}\sum^{J-2}_{j=2}( \delta_{\hat{x}}V_{j+1}+\delta_{\hat {x}}V_{j-1})^{2} \\ =&\frac{h}{4}\sum^{J-2}_{j=2}\bigl(( \delta_{\hat {x}}V_{j+1})^{2}+(\delta_{\hat{x}}V_{j-1})^{2}+2( \delta_{\hat {x}}V_{j+1}) (\delta_{\hat{x}}V_{j-1}) \bigr) \leq\|\delta_{\hat{x}}V\|_{h}^{2} \end{aligned}$$

and

$$\begin{aligned} \|\delta_{\hat{x}}V\|_{h}^{2} =&h\sum ^{J-1}_{j=1}(\delta_{\hat{x}}V_{j})^{2} =\frac{h}{4}\sum^{J-1}_{j=1}( \delta_{x}V_{j}+\delta_{x}V_{j-1})^{2} \\ =&\frac{h}{4}\sum^{J-1}_{j=1}\bigl(( \delta_{x}V_{j})^{2}+(\delta _{x}V_{j-1})^{2}+2( \delta_{x}V_{j}) (\delta_{x}V_{j-1}) \bigr) \leq\|\delta_{x}V\|_{h}^{2}. \end{aligned}$$

The proof is completed. □

Theorem 2.12

The difference scheme (2.1)-(2.3) is uniquely solvable.

Proof

For a fixed n, (2.10) can be written as

$$\begin{aligned} &U^{n+\frac{1}{2}}-U^{n}+H_{2} \delta_{x}^{4}\bigl(U^{n+\frac {1}{2}}-U^{n}\bigr)+ \frac{\tau}{2}H_{2}\delta_{\hat{x}}U^{n+\frac{1}{2}} -H_{1}\delta_{x}^{2}\bigl(U^{n+\frac{1}{2}}-U^{n} \bigr) \\ &\quad{}+\frac{\tau}{2}\phi\bigl(U^{n+\frac{1}{2}},U^{n+\frac{1}{2}}\bigr)- \frac {\tau}{2}\psi\bigl(U^{n+\frac{1}{2}},U^{n+\frac{1}{2}}\bigr)=0, \end{aligned}$$

(2.19)

we define F on $\mathbf{Z}_{h}^{0}$ as follows:

$$\begin{aligned} F(\xi) =&\xi-U^{n}+H_{2}\delta_{x}^{4} \xi-H_{2}\delta _{x}^{4}U^{n}+ \frac{\tau}{2}H_{2}\delta_{\hat{x}} \xi \\ &{}-H_{1}\delta_{x}^{2}\xi+H_{1} \delta_{x}^{2}U^{n}+\frac{\tau }{2}\phi(\xi, \xi)-\frac{\tau}{2}\psi(\xi,\xi), \end{aligned}$$

(2.20)

obviously, F is continuous. Computing the inner product of (2.20) with ξ and considering $(\phi(\xi,\xi),\xi)_{h}=0$, $(\psi(\xi,\xi),\xi)_{h}=0$ and $(H_{2}\delta_{\hat{x}}\xi, \xi)_{h}=0$, we obtain

$$\begin{aligned} \bigl(F(\xi),\xi\bigr)_{h} =&\|\xi\|_{h}^{2}- \bigl(U^{n},\xi\bigr)_{h}+\bigl\| |\xi|\bigr\| _{2,h}^{2}- \bigl(H_{2}\delta _{x}^{2}U^{n}, \delta_{x}^{2}\xi\bigr)_{h}+\bigl\| |\xi|\bigr\| ^{2}_{1,h}+\bigl(H_{1}\delta_{x}^{2}U^{n}, \xi\bigr)_{h} \\ \geq&\|\xi\|_{h}^{2}-\frac{1}{2}\bigl(\|\xi \|_{h}^{2}+\bigl\| U^{n}\bigr\| _{h}^{2} \bigr)+\bigl\| |\xi|\bigr\| _{2,h}^{2}+\bigl\| |\xi|\bigr\| _{1,h}^{2} \\ &{}-\bigl(H_{2}\delta_{x}^{2}U^{n}, \delta_{x}^{2}\xi\bigr)_{h}+\bigl(H_{1} \delta _{x}^{2}U^{n},\xi\bigr)_{h} \\ \geq&\frac{1}{2}\bigl(\|\xi\|_{h}^{2}- \bigl\| U^{n}\bigr\| _{h}^{2}\bigr)+\bigl\| |\xi|\bigr\| _{1,h}^{2}+\bigl\| |\xi|\bigr\| _{2,h}^{2}- \frac{1}{2}\bigl(\bigl\| |\xi|\bigr\| _{2,h}^{2}+\bigl\| \bigl|U^{n}\bigr|\bigr\| _{2,h}^{2}\bigr) \\ &{}-\frac{1}{2}\bigl(\bigl\| |\xi|\bigr\| _{1,h}^{2}+ \bigl\| \bigl|U^{n}\bigr|\bigr\| _{1,h}^{2}\bigr) \\ =&\frac{1}{2}\bigl(\|\xi\|^{2}_{h}- \bigl\| U^{n}\bigr\| ^{2}_{h}\bigr)+\frac{1}{2}\bigl\| |\xi | \bigr\| ^{2}_{2,h}+\frac{1}{2}\bigl\| |\xi|\bigr\| ^{2}_{1,h}- \frac{1}{2}\bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{2,h}- \frac{1}{2}\bigl\| \bigl|U^{n}\bigr|\bigr\| ^{2}_{1,h} \\ \geq&\frac{1}{2}\|\xi\|_{h}^{2}-\frac{1}{2} \bigl(\bigl\| U^{n}\bigr\| _{h}^{2}+\bigl\| \bigl|U^{n}\bigr| \bigr\| _{1,h}^{2}+\bigl\| \bigl|U^{n}\bigr|\bigr\| _{2,h}^{2} \bigr). \end{aligned}$$

Hence, for all $\xi\in\mathbf{Z}_{h}^{0}$, let $\|\xi\|_{h}^{2}=\|U^{n}\|^{2}_{h}+\||U^{n}|\|_{1,h}^{2}+\||U^{n}|\| _{2,h}^{2}+1$, then there exists $(F(\xi),\xi)_{h}>0$. It follows from Lemma 2.7 that there exists a $\xi^{*}\in\mathbf{Z}_{h}^{0}$ which satisfies $F(\xi^{*})=0$. Let $U^{n+1}=2\xi^{*}-U^{n}$, then it can be proved that $U^{n+1}\in\mathbf{Z}_{h}^{0}$ is the solution of scheme (2.1)-(2.3).

Next, we will give the uniqueness of the difference solution. Assume that $U^{n}$ and $V^{n}$ satisfy scheme (2.1)-(2.3), letting $w^{n}=V^{n}-U^{n}$, we have

$$\begin{aligned} &\partial_{t}w^{n}+H_{2} \delta_{x}^{4}\delta_{t}w^{n}+H_{2} \delta _{\hat{x} }w^{n+\frac{1}{2}}-H_{1}\delta_{x}^{2} \partial_{t}w^{n} \\ &\qquad{}+\bigl[\phi\bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\phi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr)\bigr] -\bigl[\psi \bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\psi\bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}} \bigr)\bigr] \\ &\quad=0. \end{aligned}$$

(2.21)

Computing the inner product of (2.21) with $2w^{n+\frac{1}{2}}$, we have

$$\begin{aligned} 0 =&\bigl(\bigl\| w^{n+1}\bigr\| _{h}^{2}- \bigl\| w^{n}\bigr\| _{h}^{2}\bigr)+\bigl(\bigl\| \bigl|w^{n+1}\bigr| \bigr\| _{2,h}^{2}-\bigl\| \bigl|w^{n}\bigr|\bigr\| _{2,h}^{2} \bigr)+\bigl(\bigl\| \bigl|w^{n+1}\bigr|\bigr\| _{1,h}^{2}- \bigl\| \bigl|w^{n}\bigr|\bigr\| _{1,h}^{2}\bigr) \\ &{}+2\tau\bigl(\phi\bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\phi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr),w^{n+\frac{1}{2}}\bigr)_{h} \\ &{}-2\tau\bigl(\psi\bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\psi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr),w^{n+\frac{1}{2}}\bigr)_{h}, \end{aligned}$$

(2.22)

by Lemma 2.10, we can estimate (2.22) as follows:

$$\begin{aligned} &\bigl(\phi\bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\phi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr), w^{n+\frac{1}{2}}\bigr)_{h} \\ &\quad=\frac{4ph}{3(p+1)}\sum_{i=1}^{J-1} \bigl[\bigl(V_{i}^{n+\frac {1}{2}}\bigr)^{p-1} \delta_{\hat{x}} V^{n+\frac{1}{2}}_{i}-\bigl(U_{i}^{n+\frac {1}{2}} \bigr)^{p-1}\delta_{\hat{x}} U^{n+\frac{1}{2}}_{i} \bigr]w^{n+\frac {1}{2}}_{i} \\ &\qquad{}+\frac{4ph}{3(p+1)}\sum_{i=1}^{J-1} \bigl[\delta_{\hat{x}}\bigl(V^{n+\frac {1}{2}}_{i} \bigr)^{p}-\delta_{\hat{x}}\bigl(U^{n+\frac {1}{2}}_{i} \bigr)^{p}\bigr]w^{n+\frac{1}{2}}_{i} \\ & \quad\leq \frac{2p}{3(p+1)}\max\bigl\{ K_{3}^{p-1},(p-1)K_{3}^{p-1} \bigr\} \bigl(\bigl\| w^{n+1}\bigr\| _{1,h}^{2}+\bigl\| w^{n} \bigr\| _{1,h}^{2}\bigr), \end{aligned}$$

(2.23)

$$\begin{aligned} &\bigl(\psi\bigl(V^{n+\frac{1}{2}},V^{n+\frac{1}{2}}\bigr)-\psi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr),w^{n+\frac{1}{2}}\bigr)_{h} \\ &\quad=\frac{ph}{3(p+1)}\sum_{i=2}^{J-2} \bigl[\bigl(V_{i}^{n+\frac {1}{2}}\bigr)^{p-1} \delta_{\bar{x}} V^{n+\frac{1}{2}}_{i}-\bigl(U_{i}^{n+\frac {1}{2}} \bigr)^{p-1}\delta_{\bar{x}} U^{n+\frac{1}{2}}_{i} \bigr]w^{n+\frac {1}{2}}_{i} \\ &\qquad{}+\frac{ph}{3(p+1)}\sum_{i=2}^{J-2} \bigl[\delta_{\bar{x}}\bigl( V^{n+\frac {1}{2}}_{i} \bigr)^{p}-\delta_{\bar{x}}\bigl( U^{n+\frac {1}{2}}_{i} \bigr)^{p}\bigr]w^{n+\frac{1}{2}}_{i} \\ & \quad\leq\frac{p}{6(p+1)}\max\bigl\{ K_{3}^{p-1},(p-1)K_{3}^{p-1} \bigr\} \bigl(\bigl\| w^{n+1}\bigr\| _{1,h}^{2}+\bigl\| w^{n} \bigr\| _{1,h}^{2}\bigr), \end{aligned}$$

(2.24)

where $K_{3}=K\sqrt{\frac{(2K_{2}+1)E^{0}}{K_{2}+1}}$. Substituting (2.23) and (2.24) into (2.22), from Lemma 2.2, we obtain

$$\begin{aligned} &\bigl(\bigl\| w^{n+1}\bigr\| _{h}^{2}+ \bigl\| \bigl|w^{n+1}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|w^{n+1}\bigr|\bigr\| _{2,h}^{2}\bigr)-\bigl(\bigl\| w^{n}\bigr\| _{h}^{2}+ \bigl\| \bigl|w^{n}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|w^{n}\bigr|\bigr\| _{2,h}^{2}\bigr) \\ &\quad\leq\frac{5p\tau}{3(p+1)}\max\bigl\{ K_{3}^{p-1},(p-1)K_{3}^{p-1} \bigr\} \bigl(\bigl\| w^{n+1}\bigr\| _{1,h}^{2}+\bigl\| w^{n} \bigr\| _{1,h}^{2}\bigr) \\ &\quad\leq K_{4}\tau\bigl(\bigl\| \bigl|w^{n+1}\bigr|\bigr\| _{1,h}^{2}+ \bigl\| \bigl|w^{n}\bigr|\bigr\| _{1,h}^{2}\bigr) \\ &\quad\leq K_{4}\tau\bigl(\bigl\| w^{n+1}\bigr\| _{h}^{2}+ \bigl\| \bigl|w^{n+1}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|w^{n+1}\bigr| \bigr\| _{2,h}^{2}\bigr) \\ &\qquad{}+K_{4}\tau\bigl(\bigl\| w^{n}\bigr\| _{h}^{2}+ \bigl\| \bigl|w^{n}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|w^{n}\bigr| \bigr\| _{2,h}^{2}\bigr), \end{aligned}$$

(2.25)

where $K_{4}=\frac{5p}{3(p+1)}\max\{K_{3}^{p-1},(p-1)K_{3}^{p-1}\}$.

Choosing small enough τ, we obtain by Lemma 2.8

$$ \bigl\| w^{n}\bigr\| _{h}^{2}+ \bigl\| \bigl|w^{n}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|w^{n}\bigr| \bigr\| _{2,h}^{2}=0. $$

(2.26)

This completes the proof. □

3 Convergence and stability of the difference solution

In this section, we will consider the convergence and stability of the finite difference scheme (2.1)-(2.3). Assume that the solution $u(x,t)$ of (1.1)-(1.3) is sufficiently smooth. We define the net function $u_{i}^{n}=u(x_{i},t_{n})$ and the truncation errors as follows:

$$\begin{aligned}& \begin{aligned}[b] &\partial_{t}u^{n}_{i}+ \mathcal{A}_{2}^{-1}\delta_{x}^{4} \partial _{t}u^{n}_{i}+\mathcal{A}_{2}^{-1} \delta_{\hat{x}}u^{n+\frac {1}{2}}_{i}-\mathcal{A}_{1}^{-1} \delta_{x}^{2}\partial _{t}u^{n}_{i} \\ &\quad{}+\frac{4p}{3(p+1)}\bigl[\bigl(u_{i}^{n+\frac{1}{2}} \bigr)^{p-1}\delta_{\hat {x}}u_{i}^{n+\frac{1}{2}}+ \delta_{\hat{x}}\bigl(u_{i}^{n+\frac{1}{2}}\bigr)^{p} \bigr] \\ &\quad{}-\frac{p}{3(p+1)}\bigl[\bigl(u_{i}^{n+\frac{1}{2}} \bigr)^{p-1}\delta_{\bar {x}}u_{i}^{n+\frac{1}{2}}+ \delta_{\bar{x}}\bigl(u_{i}^{n+\frac {1}{2}}\bigr)^{p} \bigr] =r_{i}^{n}, \\ &\quad{} 1\leq i\leq J-1, 0\leq n\leq N-1, \end{aligned} \end{aligned}$$

(3.1)

$$\begin{aligned}& u^{n}_{0}=u^{n}_{J}=0, \qquad \delta^{2}_{x}u^{n}_{0}= \delta^{2}_{x}u^{n}_{J}=0, \quad 0\leq n \leq N, \end{aligned}$$

(3.2)

$$\begin{aligned}& u_{i}^{0}=u_{0}(x_{i}), 0\leq i\leq J. \end{aligned}$$

(3.3)

Suppose that $u_{0} \in H_{0}^{2}(\Omega)$ and $u(x, t)\in C^{6,4}$, then from Taylor’s expansion, the truncation errors of scheme (3.1) satisfy

$$\begin{aligned} \bigl|r_{i}^{n}\bigr|=O\bigl(\tau^{2}+h^{4} \bigr), \quad \mbox{as } \tau\rightarrow0, h\rightarrow0. \end{aligned}$$

(3.4)

Theorem 3.1

Suppose that $u_{0} \in H_{0}^{2}(\Omega)$ and $u(x, t)\in C^{6,4}$, then the solution of the difference scheme (2.1)-(2.3) converges to the solution of the problem (1.1)-(1.3) with order $O(\tau^{2}+h^{4})$ by the $L^{\infty}$ norm.

Proof

Subtracting (2.1)-(2.3) from (3.1)-(3.3) letting $e_{i}^{n}=u^{n}_{i}-U^{n}_{i}$, we obtain

$$\begin{aligned}& \begin{aligned}[b] &\partial_{t}e^{n}+H_{2} \delta_{x}^{4}\delta_{t}e^{n}+H_{2} \delta _{\hat{x}}e^{n+\frac{1}{2}}-H_{1}\delta_{x}^{2} \partial_{t}e^{n} +\bigl[\phi\bigl(u^{n+\frac{1}{2}},u^{n+\frac{1}{2}} \bigr)-\phi\bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr)\bigr] \\ &\qquad{}-\bigl[\psi\bigl(u^{n+\frac{1}{2}},u^{n+\frac{1}{2}}\bigr)-\psi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr)\bigr]=r^{n},\quad 0\leq n \leq N-1, \end{aligned} \end{aligned}$$

(3.5)

$$\begin{aligned}& e^{n}|_{\partial\Omega_{h}}=0, \qquad \delta^{2}_{x}e^{n}|_{\partial\Omega_{h}}=0, \quad 0\leq n\leq N, \end{aligned}$$

(3.6)

$$\begin{aligned}& e_{i}^{0}=0,\quad 0\leq i\leq J. \end{aligned}$$

(3.7)

Computing the inner product of (3.5) with $2e^{n+\frac{1}{2}}$, we have

$$\begin{aligned} &2\tau\bigl(r^{n},e^{n+\frac{1}{2}}\bigr)_{h} \\ &\quad=\bigl(\bigl\| e^{n+1}\bigr\| _{h}^{2}-\bigl\| e^{n} \bigr\| _{h}^{2}\bigr) +\bigl(\bigl\| \bigl|e^{n+1}\bigr| \bigr\| _{1,h}^{2}-\bigl\| \bigl|e^{n}\bigr|\bigr\| _{1,h}^{2} \bigr)+\bigl(\bigl\| \bigl|e^{n+1}\bigr|\bigr\| _{2,h}^{2}- \bigl\| \bigl|e^{n}\bigr|\bigr\| _{2,h}^{2}\bigr) \\ &\qquad{}+2\tau\bigl(\phi\bigl(u^{n+\frac{1}{2}},u^{n+\frac{1}{2}}\bigr)-\phi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr),e^{n+\frac{1}{2}}\bigr)_{h} \\ &\qquad{}-2\tau\bigl(\psi\bigl(u^{n+\frac{1}{2}},u^{n+\frac{1}{2}}\bigr)-\psi \bigl(U^{n+\frac {1}{2}},U^{n+\frac{1}{2}}\bigr),e^{n+\frac{1}{2}}\bigr)_{h}. \end{aligned}$$

(3.8)

Similarly to the proof of Theorem 2.12, we have

$$\begin{aligned} &\bigl(\bigl\| e^{n+1}\bigr\| _{h}^{2}+ \bigl\| \bigl|e^{n+1}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|e^{n+1}\bigr| \bigr\| _{2,h}^{2}\bigr)- \bigl(\bigl\| e^{n} \bigr\| _{h}^{2}+\bigl\| \bigl|e^{n}\bigr|\bigr\| _{1,h}^{2}+ \bigl\| \bigl|e^{n}\bigr|\bigr\| _{2,h}^{2}\bigr) \\ &\quad\leq\tau\bigl\| r^{n}\bigr\| ^{2}_{h}+K_{5} \tau\bigl(\bigl\| e^{n+1}\bigr\| _{h}^{2}+\bigl\| \bigl|e^{n+1}\bigr| \bigr\| _{1,h}^{2}+\bigl\| \bigl|e^{n+1}\bigr|\bigr\| _{2,h}^{2} \bigr) \\ &\qquad{}+K_{5}\tau\bigl(\bigl\| e^{n}\bigr\| _{h}^{2}+ \bigl\| \bigl|e^{n}\bigr|\bigr\| _{1,h}^{2}+\bigl\| \bigl|e^{n}\bigr| \bigr\| _{2,h}^{2}\bigr), \end{aligned}$$

(3.9)

where $K_{5}=K_{4}+\frac{1}{2}$. Let $B^{n}=\|e^{n}\|_{h}^{2}+\||e^{n}|\|_{1,h}^{2}+\||e^{n}|\|_{2,h}^{2}$, then (3.9) can be rewritten as

$$\begin{aligned} B^{n+1}-B^{n}\leq\tau\bigl\| r^{n} \bigr\| _{h}^{2}+\tau K_{5}\bigl(B^{n+1}+B^{n} \bigr). \end{aligned}$$

(3.10)

Choosing small enough τ, from Lemma 2.8, we obtain

$$ B^{n}\leq C\bigl(B^{0}+\bigl( \tau^{2}+h^{4}\bigr)^{2}\bigr). $$

(3.11)

From the discrete initial conditions, we know that

$$\begin{aligned} B^{0}\leq O\bigl(\tau^{2}+h^{4} \bigr)^{2}. \end{aligned}$$

(3.12)

Then we have

$$ \bigl\| e^{n}\bigr\| _{h}\leq O\bigl( \tau^{2}+h^{4}\bigr), \qquad \bigl\| \bigl|e^{n}\bigr| \bigr\| _{1,h}\leq O\bigl(\tau^{2}+h^{4}\bigr), \qquad \bigl\| \bigl|e^{n}\bigr|\bigr\| _{2,h}\leq O\bigl(\tau^{2}+h^{4} \bigr). $$

(3.13)

By Lemma 2.2, we obtain

$$ \bigl|e^{n}\bigr|_{1,h}\leq O\bigl(\tau^{2}+h^{4} \bigr), \qquad \bigl|e^{n}\bigr|_{2,h}\leq O\bigl(\tau^{2}+h^{4} \bigr). $$

(3.14)

It follows from Lemma 2.4 that

$$ \bigl\| e^{n}\bigr\| _{\infty,h}\leq O\bigl( \tau^{2}+h^{4}\bigr). $$

(3.15)

This completes the proof. □

We can similarly prove the stability of the difference solution.

Theorem 3.2

Under the conditions of Theorem  3.1, the solution of conservative finite difference scheme (2.1)-(2.3) is stable by the $L^{\infty}$ norm.

4 Numerical experiments

In this section, numerical results are provided to demonstrate the accuracy and efficiency of the compact scheme (2.1)-(2.3). The exact solution of the system (1.1)-(1.3) is

$$\begin{aligned} u(x,t)=\exp \biggl(\frac{\ln\frac {(p+1)(3p+1)(p+3)}{2(p^{2}+3)(p^{2}+4p+7)}}{p-1} \biggr) \operatorname {sech}^{\frac{4}{p-1}} \biggl( \biggl(\frac{p-1}{\sqrt {4p^{2}+8p+20}} \biggr) (x-ct) \biggr), \end{aligned}$$

(4.1)

where $c=\frac{p^{4}+4p^{3}+14p^{2}+20p+25}{p^{4}+4p^{3}+10p^{2}+12p+21}$ is the wave velocity. In order to compare with the literature [17], we choose $x_{l}=-30$, $x_{r}=120$, and consider three cases: $p=2$, $p=3$ and $p=6$ in Tables 1, 2, and 3, respectively. Tables 1, 2, and 3 give the errors in the sense of the $L^{\infty}$-norm of the numerical solutions under various steps of $\tau=h=0.4, 0.2, 0.1, 0.05$ at $t=60$ for $p=2, 3 \mbox{ and }6$.

Table 1 The errors of numerical solutions at $\pmb{t=60}$ with $\pmb{\tau=h}$ for $\pmb{p=2}$

Table 2 The errors of numerical solutions at $\pmb{t=60}$ with $\pmb{\tau=h}$ for $\pmb{p=3}$

Table 3 The errors of numerical solutions at $\pmb{t=60}$ with $\pmb{\tau=h}$ for $\pmb{p=6}$

Denote

$$\mbox{order}1=\log_{2}^{\frac{E(\tau, 2h)}{E(\tau, h)}},\qquad \mbox{order}2= \log_{2}^{\frac{E(2\tau, h)}{E(\tau, h)}}, $$

where $E(\tau, h)=\|u^{n}-U^{n}\|_{\infty, h}$. First, we test the spatial errors and convergence orders by letting h vary and fixing the time step size τ sufficiently small to avoid contamination of the temporal. Table 4 shows the numerical results when $\tau= \frac{1}{1{,}000}$, $h = \frac{150}{125}$, $h = \frac{150}{250}$, $h=\frac{150}{500}$, and $h = \frac{150}{1{,}000}$. It can be seen from Table 4 that the convergence order of the compact difference scheme (2.1)-(2.3) is about 4 with respect to the spatial step size.

Table 4 The maximum norm errors and spatial convergence order with fixed time step $\pmb{\tau=\frac{1}{1{,}000}}$

We further test the temporal errors and convergence orders. Fix $h =0.1$, a value small enough so that the spatial error is negligible as compared with the temporal error. Take $\tau= \frac{1}{10}, \frac{1}{20}, \frac{1}{40}, \frac{1}{80}$, respectively. Table 5 shows that the convergence order of the compact difference scheme (2.1)-(2.3) with respect to the temporal variable is about 2.

Table 5 The maximum norm errors and temporal convergence order with the fixed space step $\pmb{h=0.1}$

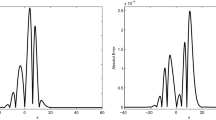
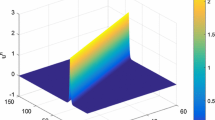
Figures 1, 2, and 3 plot the conservative law of discrete energy $E^{n}$, computed by scheme (2.1)-(2.3) with $\tau=0.5$, $h=0.2$ for $p=2, 3 \mbox{ and }6$. Figures 4, 5, and 6 plot the exact solutions at $t=0$ and the numerical solutions computed by scheme (2.1)-(2.3) with $\tau=0.1$, $h=0.2$ at $t=30, 60$, which also show the accuracy of scheme (2.1)-(2.3).

Figure 1

Discrete energy $\pmb{E^{n}}$ with $\pmb{\tau=0.5}$ , $\pmb{h=0.2}$ at various t for $\pmb{p=2}$ .

Figure 2

Discrete energy $\pmb{E^{n}}$ with $\pmb{\tau=0.5}$ , $\pmb{h=0.2}$ at various t for $\pmb{p=3}$ .

Figure 3

Discrete energy $\pmb{E^{n}}$ with $\pmb{\tau=0.5}$ , $\pmb{h=0.2}$ at various t for $\pmb{p=6}$ .

Figure 4

Numerical solution $\pmb{U^{n}}$ with $\pmb{p=2}$ and $\pmb{\tau=0.1}$ , $\pmb{h=0.2}$ .

Figure 5

Numerical solution $\pmb{U^{n}}$ with $\pmb{p=3}$ and $\pmb{\tau=0.1}$ , $\pmb{h=0.2}$ .

Figure 6

Numerical solution $\pmb{U^{n}}$ with $\pmb{p=6}$ and $\pmb{\tau=0.1}$ , $\pmb{h=0.2}$ .