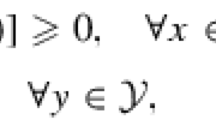An inexact generalized PRSM with LQP regularization for structured variational inequalities and its applications to traffic equilibrium problems

Abstract

As one of the operator splitting methods, the Peaceman-Rachford splitting method (PRSM) has attracted considerable attention recently. This paper proposes a generalized PRSM for structured variational inequalities with positive orthants. In fact, we apply the well-developed LQP regularization to regularize the subproblems of the recently proposed strictly contractive PRSM, thus the resulting subproblems reduce to two nonlinear equation systems, which are much easier to solve than the subproblems of PRSM. Furthermore, these two nonlinear equations are allowed to be solved inexactly. For the new method, we prove its global convergence and establish its worst-case convergence rate in the ergodic sense. Numerical experiments show that the proposed method is quite efficient for the traffic equilibrium problems with link capacity bound.

1 Introduction

In this paper, we focus on the variational inequalities with separable structures and positive orthants. That is, find $u^{*}\in\Omega$ such that

$$ \bigl(u-u^{*}\bigr)^{\top}T\bigl(u^{*}\bigr)\geq0,\quad u\in \Omega, $$

(1)

with

$$u=\left ( \textstyle\begin{array}{@{}c@{}} x\\ y \end{array}\displaystyle \right ),\qquad T(u)=\left ( \textstyle\begin{array}{@{}c@{}} f(x)\\ g(y) \end{array}\displaystyle \right ),\qquad \Omega=\bigl\{ (x,y)|Ax+By=b, x \in\mathcal{R}^{m}_{+}, y\in\mathcal{R}^{n}_{+}\bigr\} , $$

where $f:\mathcal{X}\rightarrow\mathcal{R}^{m}$ and $g:\mathcal {Y}\rightarrow\mathcal{R}^{n}$ are continuous and monotone operators; $A\in\mathcal{R}^{l\times m}$ and $B\in\mathcal {R}^{l\times n}$ are given matrices; $b\in\mathcal{R}^{l}$ is a given vector. Problem (1) is a standard mathematical model arising from several scientific fields and admits a large number of applications in network economics, traffic assignment, game theoretic problems, etc.; see [1–3] and the references therein. Throughout, we assume that the solution of Problem (1) (denoted by $\Omega^{*}$) is nonempty.

By attaching a Lagrange multiplier vector $\lambda\in\mathcal{R}^{l}$ to the linear constraints $Ax+By=b$, Problem (1) can be equivalently transformed into the following compact form, denoted by $\operatorname{VI}(\mathcal{W},Q)$: Find $w^{*}\in \mathcal{W}$, such that

$$ \bigl(w-w^{*}\bigr)^{\top}Q\bigl(w^{*}\bigr)\geq0,\quad \forall w\in \mathcal{W}, $$

(2)

where

$$w=\left ( \textstyle\begin{array}{@{}c@{}} x\\ y\\ \lambda \end{array}\displaystyle \right ),\qquad Q(w)=\left ( \textstyle\begin{array}{@{}c@{}}f(x)-A^{\top}\lambda\\ g(y)-B^{\top}\lambda\\ Ax+By-b \end{array}\displaystyle \right ),\qquad \mathcal{W}= \mathcal{R}^{m}_{+}\times\mathcal{R}^{n}_{+}\times \mathcal{R}^{l}. $$

We denote by $\mathcal{W}^{*}$ the solution of $\operatorname{VI}(\mathcal{W},Q)$. Obviously, $\mathcal{W}^{*}$ is nonempty under the assumption that $\Omega ^{*}$ is nonempty. In addition, due to the monotonicity of $f(\cdot)$ and $g(\cdot)$, the mapping $Q(\cdot)$ of $\operatorname{VI}(\mathcal{W},Q)$ is also monotone.

A simple but powerful operator splitting algorithm in the literature is the alternating direction method of multipliers (ADMM) proposed in [4–6]. For the developments of ADMM on structured variational inequalities (2), we refer to [7–9]. Similar to ADMM, the Peaceman-Rachford splitting method (PRSM) is also a simple algorithm for Problem (2); see [10–12]. For solving (2), the iterative scheme of PRSM is

$$ \left \{ \textstyle\begin{array}{l} 0\leq x^{k+1}\perp \{f(x^{k+1})-A^{\top}[\lambda^{k}-\beta (Ax^{k+1}+By^{k}-b)]\}\geq0, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-\beta(Ax^{k+1}+By^{k}-b), \\ 0\leq y^{k+1}\perp \{g(y^{k+1})-B^{\top}[\lambda^{k+\frac{1}{2}}-\beta (Ax^{k+1}+By^{k+1}-b)]\}\geq0, \\ \lambda^{k+1}=\lambda^{k+\frac {1}{2}}-\beta(Ax^{k+1}+By^{k+1}-b), \end{array}\displaystyle \right . $$

(3)

where $\beta>0$ is a penalty parameter. Different from the ADMM, the PRSM updates the Lagrange multiplier twice at each iteration. However, the global convergence of PRSM cannot be guaranteed without any further assumptions on the model (2). To solve this issue, He et al. [13] developed the following strictly contractive PRSM (SC-PRSM):

$$ \left \{ \textstyle\begin{array}{l} 0\leq x^{k+1}\perp \{f(x^{k+1})-A^{\top}[\lambda^{k}-\beta (Ax^{k+1}+By^{k}-b)]\}\geq0, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-r\beta(Ax^{k+1}+By^{k}-b), \\ 0\leq y^{k+1}\perp \{g(y^{k+1})-B^{\top}[\lambda^{k+\frac{1}{2}}-\beta (Ax^{k+1}+By^{k+1}-b)]\}\geq0, \\ \lambda^{k+1}=\lambda^{k+\frac {1}{2}}-r\beta(Ax^{k+1}+By^{k+1}-b), \end{array}\displaystyle \right . $$

(4)

where $r\in(0,1)$ is an underdetermined relaxation factor. The global convergence of SC-PRSM is proved via the analytic framework of contractive type methods in [13].

Note that the computational load of SC-PRSM (4) relies on the resulting two complementarity problems, which are computationally expensive, especially for large-scale problems. Therefore, how to alleviate the difficulty of these subproblems deserves intensive research. In this paper, motivated by well-developed logarithmic-quadratic proximal (LQP) regularization proposed in [14], we regularize the two complementarity problems in (4) by LQP, which forces the solutions of the two complementarity problems to be interior points of $\mathcal{R}^{m}_{+}$ and $\mathcal{R}^{n}_{+}$, respectively, thus the two complementarity problems reduce to two easier nonlinear equation systems. On the other hand, it is well known that the generalized ADMM [15, 16] includes the classical ADMM as a special case, and it can numerically accelerate the original ADMM with some values of the relaxation factor. Therefore, inspired by the above analysis, we get the following iterative scheme:

$$ \left \{ \textstyle\begin{array}{l} 0\leq x^{k+1}\perp \{f(x^{k+1})-A^{\top}[\lambda^{k}-\beta (Ax^{k+1}+By^{k}-b)] \\ \hphantom{0\leq{}}{}+R[(x^{k+1}-x^{k})+\mu(x^{k}-P_{k}^{2}(x^{k+1})^{-1})]\}\geq 0, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-r\beta(Ax^{k+1}+By^{k}-b), \\ 0\leq y^{k+1}\perp \{g(y^{k+1})-B^{\top}[\lambda^{k+\frac{1}{2}}-\beta (\alpha Ax^{k+1}-(1-\alpha)(By^{k+1}-b)+By^{k+1}-b)] \\ \hphantom{0\leq {}}{}+S[(y^{k+1}-y^{k})+\mu(y^{k}-Q_{k}^{2}(y^{k+1})^{-1})]\}\geq0, \\ \lambda^{k+1}=\lambda^{k+\frac{1}{2}}-\beta[\alpha Ax^{k+1}-(1-\alpha )(By^{k+1}-b)+By^{k+1}-b], \end{array}\displaystyle \right . $$

(5)

where $\alpha\in(0,2)$, $r\in(0,2-\alpha)$, and $\mu\in(0,1)$ are three constants, and $R=\operatorname{diag}(r_{1},r_{2},\ldots, r_{m})\in\mathcal {R}^{m\times m}$ and $S=\operatorname{diag}(s_{1},s_{2},\ldots,s_{n})\in\mathcal {R}^{n\times n}$ are symmetric positive definite matrices, $P_{k}=\operatorname {diag}(1/x^{k}_{1},1/x^{k}_{2},\ldots,1/x^{k}_{m})$, $Q_{k}=\operatorname{diag}(1/y^{k}_{1},1/y^{k}_{2},\ldots,1/y^{k}_{n})$, and $(x^{k+1})^{-1}$ (or $(y^{k+1})^{-1}$) is a vector whose jth element is $1/x^{k+1}_{j}$ (or $1/y^{k+1}_{j}$). By Lemma 2.2 (see Section 2), the new iterate $(x^{k+1}, y^{k+1})$ generated by (5) lies in the interior of $\mathcal{R}^{m+n}$, provided that the previous iterate $(x^{k}, y^{k})$ does. Therefore, the two complementarity problems in (5) can reduce to the nonlinear equation systems, and we get the following iterative scheme:

$$ \left \{ \textstyle\begin{array}{l} f(x^{k+1})-A^{\top}[\lambda^{k}-\beta (Ax^{k+1}+By^{k}-b)]+R[(x^{k+1}-x^{k})+\mu(x^{k}-P_{k}^{2}(x^{k+1})^{-1})]=0, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-r\beta(Ax^{k+1}+By^{k}-b), \\ g(y^{k+1})-B^{\top}[\lambda^{k+\frac{1}{2}}-\beta(\alpha Ax^{k+1}-(1-\alpha)(By^{k+1}-b)+By^{k+1}-b)] \\ \quad {}+S[(y^{k+1}-y^{k})+\mu(y^{k}-Q_{k}^{2}(y^{k+1})^{-1})]=0, \\ \lambda^{k+1}=\lambda^{k+\frac{1}{2}}-\beta[\alpha Ax^{k+1}-(1-\alpha )(By^{k+1}-b)+By^{k+1}-b]. \end{array}\displaystyle \right . $$

Obviously, the above iterative scheme includes two nonlinear equations, which are not easy to solve exactly in many applications. This motivates us to propose the following inexact version:

$$ \left \{ \textstyle\begin{array}{l} \mbox{Find } x^{k+1}\in R^{m}_{++}, \mbox{such that } \|x^{k+1}-x_{*}^{k+1}\|\leq v_{k}, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-r\beta(Ax^{k+1}+By^{k}-b), \\ \mbox{Find } y^{k+1}\in R^{n}_{++}, \mbox{such that } \| y^{k+1}-y_{*}^{k+1}\|\leq v_{k}, \\ \lambda^{k+1}=\lambda^{k+\frac{1}{2}}-\beta[\alpha Ax^{k+1}-(1-\alpha )(By^{k+1}-b)+By^{k+1}-b], \end{array}\displaystyle \right . $$

(6)

where $\{v_{k}\}$ is a nonnegative sequence satisfying $\sum_{k=0}^{\infty}v_{k}<+\infty$, and $x_{*}^{k+1}$, $y_{*}^{k+1}$ satisfy

$$\begin{aligned}& f\bigl(x_{*}^{k+1}\bigr)-A^{\top}\bigl[\lambda^{k}- \beta \bigl(Ax_{*}^{k+1}+By^{k}-b\bigr)\bigr]+R\bigl[ \bigl(x_{*}^{k+1}-x^{k}\bigr)+\mu\bigl(x^{k}-P_{k}^{2} \bigl(x_{*}^{k+1}\bigr)^{-1}\bigr)\bigr]=0 , \\& g\bigl(y_{*}^{k+1}\bigr)-B^{\top}\bigl[\lambda_{*}^{k+\frac{1}{2}}- \beta \bigl(\alpha Ax_{*}^{k+1}-(1-\alpha) \bigl(By_{*}^{k+1}-b \bigr)+By_{*}^{k+1}-b\bigr)\bigr] \\& \quad {}+S\bigl[\bigl(y_{*}^{k+1}-y^{k} \bigr) +\mu\bigl(y^{k}-Q_{k}^{2} \bigl(y_{*}^{k+1}\bigr)^{-1}\bigr)\bigr]=0 . \end{aligned}$$

Here $\lambda_{*}^{k+\frac{1}{2}}=\lambda^{k}-r\beta(Ax_{*}^{k+1}+By^{k}-b)$.

The rest of this paper is organized as follows. In Section 2, we summarize preliminaries which are useful for further discussion, and we present the new method. In Section 3, the global convergence and the worst-case convergence rate in the ergodic sense of the new method are proved. In Section 4, we apply the proposed method to solve the traffic equilibrium problems with link capacity bound. Finally, some concluding remarks are made in Section 5.

2 Preliminaries

In this section, we first of all summarize some notations and lemmas which are used frequently in the sequent analysis, and then present our proposed method in detail.

First, we define four matrices as follows:

$$ \begin{aligned} &M=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} I_{m}&0&0\\ 0&I_{n}&0\\ 0&-\beta B&(r+\alpha) I_{l} \end{array}\displaystyle \right ), \\ &P= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} (1+\mu)R&0&0\\ 0&(1+\mu)S+\beta B^{\top}B&(1-r-\alpha)B^{\top}\\ 0&-B&\frac{1}{\beta}I_{l} \end{array}\displaystyle \right ), \end{aligned} $$

(7)

and

$$ \begin{aligned} &N=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}}\mu R&0&0\\ 0&\mu S&0\\ 0&0&0 \end{array}\displaystyle \right ), \\ &H= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} (1+\mu)R&0&0\\ 0&(1+\mu)S+\frac{\beta}{r+\alpha} B^{\top}B&\frac{1-r-\alpha}{r+\alpha }B^{\top}\\ 0&\frac{1-r-\alpha}{r+\alpha}B&\frac{1}{\beta(r+\alpha)}I_{l} \end{array}\displaystyle \right ). \end{aligned} $$

(8)

The four matrices M, P, N, H just defined satisfy the following assertions.

Lemma 2.1

If $\mu\in(0,1)$, $\alpha\in(0,2)$, $r\in(0,2-\alpha)$, and R, S are symmetric positive definite, then we have:

• (1) The matrices M, P, H defined, respectively, in (7), (8) have the following relationship:

  $$ HM=P. $$

  (9)

• (2) The two matrices H and $\tilde{H}:=P^{\top}+P-M^{\top}HM-2N$ are symmetric positive definite.

Proof

Item (1) holds evidently. As for item (2), it is obvious that H and H̃ are symmetric. Now, we prove that they are positive definite. Note that $\mu\in(0,1)$, $\alpha\in(0,2)$, and $r\in(0,2-\alpha)$. Then for any $w=(x,y,\lambda)\neq0$, we get

$$\begin{aligned} w^{\top}Hw =& (1+\mu)\Vert x\Vert _{R}^{2}+(1+\mu)\Vert y\Vert _{S}^{2}+ \frac{1}{r+\alpha} \biggl(\beta \Vert By\Vert ^{2}+2(1-r-\alpha) \lambda^{\top}By+\frac{1}{\beta} \Vert \lambda \Vert ^{2} \biggr) \\ \geq& (1+\mu)\Vert x\Vert _{R}^{2}+(1+\mu)\Vert y \Vert _{S}^{2}+\frac{2}{r+\alpha} \min\{2-r-\alpha,r+\alpha \}\Vert By\Vert \cdot \Vert \lambda \Vert \\ \geq& (1+\mu)\Vert x\Vert _{R}^{2}+(1+\mu)\Vert y \Vert _{S}^{2}, \end{aligned}$$

(10)

where the inequality follows from the Cauchy-Schwartz inequality. If $x\neq0$ or $y=0$, then from (10), we have $w^{\top}Hw>0$. Otherwise $x=0$, $y=0$, and $\lambda\neq0$, then we have $w^{\top}Hw=\frac {\|\lambda\|^{2}}{\beta(r+\alpha)}>0$. Thus, H is positive definite. As for H̃, using (9), we have

$$\begin{aligned} \tilde{H} =&P^{\top}+P-M^{\top}HM-2N \\ =&P^{\top}+P-M^{\top}P-2N \\ =&\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}}(1-\mu)R& 0& 0 \\ 0& (1-\mu)S& 0 \\ 0& 0 &\frac{2-(r+\alpha )}{\beta}I_{l} \end{array}\displaystyle \right ). \end{aligned}$$

Therefore H̃ is positive definite. The proof is complete. □

The following lemma lists a fundamental assertion with respect to the LQP regularization, which was proved in [17].

Lemma 2.2

Let $\bar{P}=\operatorname{diag}(p_{1},p_{2},\ldots,p_{t})\in \mathcal{R}^{t\times t}$ be a positive definite diagonal matrix, $q(u)\in\mathcal{R}^{t}$ be a monotone mapping of u with respect to $\mathcal{R}^{t}_{++}$, and $\mu\in(0,1)$. For a given $\bar{u}\in\mathcal{R}^{t}_{++}$, we define $\bar{U}:=\operatorname {diag}(\bar{u}_{1},\bar{u}_{2},\ldots,\bar{u}_{t})$. Then the equation

$$ q(u)+\bar{P}\bigl[(u-\bar{u})+\mu\bigl(\bar{u}-\bar{U}u^{-1}\bigr) \bigr]=0 $$

has the unique positive solution u. In addition, for this positive solution $u\in\mathcal{R}^{t}_{++}$ and any $v\in\mathcal{R}^{t}_{+}$, we have

$$ (v-u)^{\top}q(u)\geq\frac{1+\mu}{2}\bigl(\|u-v \|^{2}_{\bar {P}}-\|\bar{u}-v\|^{2}_{\bar{P}}\bigr)+ \frac{1-\mu}{2}\|\bar{u}-u\|^{2}_{\bar{P}}. $$

(11)

Now we present the generalized PRSM with LQP regularization for solving the Problem (2).

Remark 2.1

Note that Algorithm 1 includes many LQP-type methods as special cases, such as:

• If $r=0$ and $v_{k}=0$ (∀k), we obtain the generalized alternating direction method with LQP regularization proposed in [18].

• If $\alpha=1$, we obtain a method similar to the method proposed in [19], and their difference only lies in the latter is designed for the separable convex programming.

Algorithm 1

A generalized PRSM with LQP regularization for $\operatorname{VI}(\mathcal{W},Q)$

Remark 2.2

Obviously, by the relationship of the PRSM and the generalized ADMM presented in [20], the iterative scheme (6) is equivalent to

$$ \left \{ \textstyle\begin{array}{l} \mbox{Find } x^{k+1}\in R^{m}_{++}, \mbox{such that } \|x^{k+1}-x_{*}^{k+1}\|\leq v_{k}, \\ \tilde{\lambda}^{k+\frac{1}{2}}=\lambda^{k}-\mu\beta(Ax^{k+1}+By^{k}-b), \\ \mbox{Find } y^{k+1}\in R^{n}_{++}, \mbox{such that } \| y^{k+1}-y_{**}^{k+1}\|\leq v_{k}, \\ \lambda^{k+1}=\tilde{\lambda}^{k+\frac{1}{2}}-\beta(Ax^{k+1}+By^{k+1}-b), \end{array}\displaystyle \right . $$

where $\mu=\alpha-1+r$ and $y_{**}^{k+1}$ satisfy

$$\begin{aligned}& g\bigl(y_{**}^{k+1}\bigr)-B^{\top}\bigl[ \lambda_{*}^{k+\frac{1}{2}}-\beta \bigl(Ax_{*}^{k+1}+By_{**}^{k+1}-b \bigr)\bigr] \\& \quad {}+S\bigl[\bigl(y_{**}^{k+1}-y^{k}\bigr) + \mu\bigl(y^{k}-Q_{k}^{2}\bigl(y_{**}^{k+1} \bigr)^{-1}\bigr)\bigr]=0 . \end{aligned}$$

Obviously, when $\alpha=1$, $r=0$, that is, $\tilde{\lambda}^{k+\frac {1}{2}}={\lambda}_{*}^{k+\frac{1}{2}}=\lambda^{k}$, the above iterative scheme reduces to the first inexact ADMM with LQP in [21].

3 Global convergence and convergence rate

In this section, we aim to prove the global convergence of Algorithm 1, and establish its worst-case convergence rate in a nonergodic sense.

To prove the global convergence, we need to define some auxiliary sequences as follows:

$$ \lambda_{*}^{k+1}=\lambda_{*}^{k+\frac{1}{2}}-\beta \bigl(Ax_{*}^{k+1}+By_{*}^{k+1}-b \bigr) , $$

and

$$ {w}_{*}^{k+1}=\left ( \textstyle\begin{array}{@{}c@{}} {x}_{*}^{k+1}\\ {y}_{*}^{k+1}\\ {\lambda}_{*}^{k+1} \end{array}\displaystyle \right ) \quad \mbox{and}\quad \hat{w}^{k}=\left ( \textstyle\begin{array}{@{}c@{}}\hat{x}^{k}\\ \hat{y}^{k}\\ \hat{\lambda}^{k} \end{array}\displaystyle \right )=\left ( \textstyle\begin{array}{@{}c@{}}{x}_{*}^{k+1}\\ {y}_{*}^{k+1}\\ \lambda^{k}-\beta(A{x}_{*}^{k+1}+By^{k}-b) \end{array}\displaystyle \right ). $$

(12)

Thus, based on (6) and (12), we immediately have

$$\begin{aligned}& {x}_{*}^{k+1}=\hat{x}^{k}, \qquad {y}_{*}^{k+1}= \hat{y}^{k},\qquad \lambda _{*}^{k+\frac{1}{2}}=\lambda^{k}-r\bigl( \lambda^{k}-\hat{\lambda}^{k}\bigr) , \\& \lambda_{*}^{k+1}=\lambda^{k}-\bigl[(r+\alpha) \bigl( \lambda^{k}-\hat {\lambda}^{k}\bigr)-\beta B \bigl(y^{k}-\hat{y}^{k}\bigr)\bigr] . \end{aligned}$$

This and (7), (11) show that

$$ w_{*}^{k+1}=w^{k}-M\bigl(w^{k}- \hat{w}^{k}\bigr). $$

(13)

Lemma 3.1

The sequence $\{w_{*}^{k}\}$ defined by (12) and the sequence $\{w^{k}\}$ generated by Algorithm 1 satisfy the following inequality:

$$ \bigl\Vert w_{*}^{k+1}-w^{k+1}\bigr\Vert _{H}\leq\rho v_{k}, \quad \forall k\geq0, $$

(14)

where $\rho>0$ and H is defined by (8).

Proof

By the definitions of $\lambda^{k+1}$ and $\lambda _{*}^{k+1}$, we have

$$ \lambda_{*}^{k+1}-\lambda^{k+1}=(1+r)\beta A \bigl(x^{k+1}-x_{*}^{k+1}\bigr)+\beta B\bigl(y^{k+1}-y_{*}^{k+1} \bigr) . $$

This and (6), (12) imply (14) immediately. The lemma is proved. □

Lemma 3.2

If $w^{k}=w^{k+1}$, then $w^{k+1}=(x^{k+1},y^{k+1},\lambda^{k+1})$ produced by Algorithm 1 is a solution of $\operatorname{VI}(\mathcal{W},Q)$.

Proof

For any $x\in\mathcal{R}^{m}_{+}$, applying Lemma 2.2 to the x-subproblem of (6) by setting $\bar{u}=x^{k}$, $u=\hat{x}^{k}$, $v=x$, and

$$ q(u)=f\bigl(\hat{x}^{k}\bigr)-A^{\top}\bigl[ \lambda^{k}-\beta\bigl(A\hat{x}^{k}+By^{k}-b\bigr) \bigr] $$

in (11), we have

$$\begin{aligned}& \bigl(x-\hat{x}^{k}\bigr)^{\top}\bigl\{ f\bigl( \hat{x}^{k}\bigr)-A^{\top}\bigl[\lambda^{k}-\beta \bigl(A\hat {x}^{k}+By^{k}-b\bigr)\bigr]\bigr\} \\& \quad \geq \frac{1+\mu}{2}\bigl(\bigl\Vert \hat{x}^{k}-x\bigr\Vert ^{2}_{R}-\bigl\Vert x^{k}-x\bigr\Vert ^{2}_{R}\bigr)+\frac{1-\mu }{2}\bigl\Vert x^{k}-\hat{x}^{k}\bigr\Vert ^{2}_{R} \\& \quad = \frac{1+\mu}{2}\bigl(\bigl\Vert \hat{x}^{k}-x\bigr\Vert ^{2}_{R}-\bigl\Vert x^{k}-\hat{x}^{k}+ \hat{x}^{k}-x\bigr\Vert ^{2}_{R}\bigr)+ \frac{1-\mu}{2}\bigl\Vert x^{k}-\hat{x}^{k}\bigr\Vert ^{2}_{R} \\& \quad = (1+\mu)\biggl[\bigl(\hat{x}^{k}-x\bigr)^{\top}R\bigl( \hat{x}^{k}-x^{k}\bigr)-\frac{1}{2}\bigl\Vert x^{k}-\hat {x}^{k}\bigr\Vert ^{2}_{R} \biggr]+\frac{1-\mu}{2}\bigl\Vert x^{k}-\hat{x}^{k}\bigr\Vert ^{2}_{R} \\& \quad = (1+\mu) \bigl(\hat{x}^{k}-x\bigr)^{\top}R\bigl( \hat{x}^{k}-x^{k}\bigr)-\mu\bigl\Vert x^{k}- \hat{x}^{k}\bigr\Vert ^{2}_{R}, \end{aligned}$$

from which we get

$$ \bigl(x-\hat{x}^{k}\bigr)^{\top}\bigl[(1+\mu)R \bigl(x^{k}-\hat{x}^{k}\bigr)-f\bigl(\hat {x}^{k} \bigr)+A^{\top}\hat{\lambda}^{k}\bigr]\leq\mu\bigl\Vert x^{k}-\hat{x}^{k}\bigr\Vert ^{2}_{R}. $$

(15)

For any $y\in\mathcal{R}^{n}_{+}$, applying Lemma 2.2 to the y-subproblem of (6) by setting $\bar{u}=y^{k}$, $u=\hat{y}^{k}$, $v=y$, and

$$ q(u)=g\bigl(\hat{y}^{k}\bigr)-B^{\top}\bigl[ \lambda_{*}^{k+\frac{1}{2}}-\beta \bigl(\alpha A\hat{x}^{k}-(1-\alpha) \bigl(B\hat{y}^{k}-b\bigr)+B\hat{y}^{k}-b\bigr)\bigr] $$

in (11), we have

$$\begin{aligned}& \bigl(y-\hat{y}^{k}\bigr)^{\top}\bigl\{ g\bigl( \hat{y}^{k}\bigr)-B^{\top}\bigl[\lambda_{*}^{k+\frac {1}{2}}-\beta \bigl(\alpha A\hat{x}^{k}-(1-\alpha) \bigl(B\hat{y}^{k}-b \bigr)+B\hat {y}^{k}-b\bigr)\bigr]\bigr\} \\& \quad \geq \frac{1+\mu}{2}\bigl(\bigl\Vert \hat{y}^{k}-y\bigr\Vert ^{2}_{S}-\bigl\Vert y^{k}-y\bigr\Vert ^{2}_{S}\bigr)+\frac{1-\mu }{2}\bigl\Vert y^{k}-\hat{y}^{k}\bigr\Vert ^{2}_{S} \\& \quad = (1+\mu) \bigl(\hat{y}^{k}-y\bigr)^{\top}S\bigl( \hat{y}^{k}-y^{k}\bigr)-\mu\bigl\Vert y^{k}- \hat{y}^{k}\bigr\Vert ^{2}_{S}, \end{aligned}$$

from the above inequality and $\lambda_{*}^{k+\frac{1}{2}}-\beta(\alpha A\hat{x}^{k}-(1-\alpha)(B\hat{y}^{k}-b)+B\hat{y}^{k}-b)=\hat{\lambda }^{k}+(1-r-\alpha)(\lambda^{k}-\hat{\lambda}^{k})-\beta B(\hat{y}^{k}-y^{k})$, we get

$$\begin{aligned} \begin{aligned}[b] &\bigl(y-\hat{y}^{k}\bigr)^{\top}\bigl\{ \bigl[(1+ \mu)S+\beta B^{\top}B\bigr]\bigl(y^{k}-\hat {y}^{k} \bigr)-g\bigl(\hat{y}^{k}\bigr)+B^{\top}\hat{ \lambda}^{k}-(1-r-\alpha)B^{\top}\bigl(\hat { \lambda}^{k}-\lambda^{k}\bigr)\bigr\} \\ &\quad \leq\mu\bigl\Vert y^{k}-\hat{y}^{k}\bigr\Vert ^{2}_{S}. \end{aligned} \end{aligned}$$

(16)

In addition, from (12) again, we have

$$ \bigl(A\hat{x}^{k}+B\hat{y}^{k}-b\bigr)-B \bigl(\hat{y}^{k}-y^{k}\bigr)+\frac {1}{\beta}\bigl(\hat{ \lambda}^{k}-\lambda^{k}\bigr)=0. $$

(17)

Then, combining (15), (16), (17), for any $w=(x,y,\lambda)\in\mathcal {W}$, we have

$$\begin{aligned}& \bigl(\hat{w}^{k}-w\bigr)^{\top} \left \{ \left ( \textstyle\begin{array}{@{}c@{}}f(\hat{x}^{k})-A^{\top}\hat{\lambda}^{k} \\ g(\hat{y}^{k})-B^{\top}\hat{\lambda}^{k} \\ A_{1}\hat{x}_{1}^{k}+A_{2}\hat{x}_{2}^{k}-b \end{array}\displaystyle \right )\right. \\& \qquad {}+\left. \left ( \textstyle\begin{array}{@{}c@{}}(1+\mu)R(\hat{x}_{1}^{k}-x_{1}^{k}) \\ (1-r-\alpha)B^{\top}(\hat{\lambda}^{k}-\lambda^{k})+[(1+\mu)S+\beta B^{\top}B](\hat{y}^{k}-y^{k}) \\ -B(\hat{y}^{k}-y^{k})+(\hat{\lambda}^{k}-\lambda^{k})/\beta \end{array}\displaystyle \right ) \right \} \\& \quad \leq \mu\bigl\Vert x^{k}-\hat{x}^{k}\bigr\Vert ^{2}_{R}+\mu\bigl\Vert y^{k}- \hat{y}^{k}\bigr\Vert ^{2}_{S}. \end{aligned}$$

Then, recalling the definitions of P in (7) and N in (8), the above inequality can be written as

$$ \bigl(\hat{w}^{k}-w\bigr)^{\top}Q\bigl( \hat{w}^{k}\bigr)\leq\bigl\Vert w^{k}-\hat{w}^{k} \bigr\Vert ^{2}_{N}-\bigl(w-\hat{w}^{k} \bigr)^{\top}P\bigl(w^{k}-\hat{w}^{k}\bigr), \quad \forall w\in\mathcal{W}. $$

(18)

In addition, if $w^{k}=w^{k+1}$, then we have $w^{k}=\hat{w}^{k}$, which together with (18) indicates that

$$\bigl(w-\hat{w}^{k}\bigr)^{\top}Q\bigl(\hat{w}^{k} \bigr)\geq0, \quad \forall w\in\mathcal{W}. $$

This implies that $\hat{w}^{k}=(\hat{x}_{1}^{k},\hat{x}_{2}^{k},\hat{\lambda}^{k})$ is a solution of $\operatorname{VI}(\mathcal{W},Q)$. Since $\hat{w}^{k}=w^{k+1}$, therefore $w^{k+1}$ is also a solution of $\operatorname{VI}(\mathcal{W},Q)$. This completes the proof. □

The next lemma further refines the right term of (17) and express it in terms of some quadratic terms, and its proof is motivated by Lemma 3.3 in [13].

Lemma 3.3

Let the sequence $\{w^{k}\}$ be generated by Algorithm 1. Then, for any $w\in\mathcal{W}$, we have

$$\begin{aligned}& \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{N}-\bigl(w-\hat{w}^{k}\bigr)^{\top}P\bigl(w^{k}-\hat {w}^{k}\bigr) \\& \quad =\frac{1}{2}\bigl(\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2}-\bigl\Vert w-w_{*}^{k+1}\bigr\Vert ^{2}_{H}\bigr)- \frac{1}{2}\bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{\tilde{H}}. \end{aligned}$$

(19)

Proof

Taking $a=w$, $b=\hat{w}^{k}$, $c=w^{k}$, $d=w_{*}^{k+1}$ in the identity

$$(a-b)^{\top}H(c-d)=\frac{1}{2}\bigl(\Vert a-d\Vert _{H}^{2}-\Vert a-c\Vert _{H}^{2} \bigr)+\frac{1}{2}\bigl(\Vert c-b\Vert _{H}^{2}- \Vert d-b\Vert _{H}^{2}\bigr), $$

we get

$$\begin{aligned}& \bigl(w-\hat{w}^{k}\bigr)^{\top}H\bigl(w^{k}-w_{*}^{k+1} \bigr) \\& \quad =\frac{1}{2}\bigl(\bigl\Vert w-w_{*}^{k+1}\bigr\Vert _{H}^{2}-\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2}\bigr)+\frac{1}{2}\bigl(\bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert _{H}^{2}- \bigl\Vert w_{*}^{k+1}-\hat{w}^{k}\bigr\Vert _{H}^{2}\bigr), \end{aligned}$$

which combined with (9) and (13) yields

$$\begin{aligned}& \bigl(w-\hat{w}^{k}\bigr)^{\top}P \bigl(w^{k}-\hat{w}^{k}\bigr) \\& \quad =\frac{1}{2}\bigl(\bigl\Vert w-w_{*}^{k+1}\bigr\Vert _{H}^{2}-\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2}\bigr)+ \frac{1}{2}\bigl(\bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert _{H}^{2}-\bigl\Vert w_{*}^{k+1}- \hat{w}^{k}\bigr\Vert _{H}^{2}\bigr). \end{aligned}$$

(20)

For the last term of (20), we have

$$\begin{aligned}& \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert _{H}^{2}-\bigl\Vert w_{*}^{k+1}- \hat{w}^{k}\bigr\Vert _{H}^{2} \\& \quad = \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert _{H}^{2}-\bigl\Vert \bigl(w^{k}- \hat{w}^{k}\bigr)-\bigl(w^{k}-w_{*}^{k+1}\bigr)\bigr\Vert _{H}^{2} \\& \quad = \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert _{H}^{2}-\bigl\Vert \bigl(w^{k}- \hat{w}^{k}\bigr)-M\bigl(w^{k}-\hat{w}^{k}\bigr) \bigr\Vert _{H}^{2} \\& \quad = 2\bigl(w^{k}-\hat{w}^{k}\bigr)^{\top}HM \bigl(w^{k}-\hat{w}^{k}\bigr)-\bigl(w^{k}- \hat{w}^{k}\bigr)^{\top}M^{\top}HM \bigl(w^{k}-\hat{w}^{k}\bigr) \\& \quad = \bigl(w^{k}-\hat{w}^{k}\bigr) \bigl(P^{\top}+P-M^{\top}HM\bigr) \bigl(w^{k}-\hat{w}^{k}\bigr). \end{aligned}$$

Substituting it in (20), we obtain (19). The proof is complete. □

The following theorem indicates the sequence generated by Algorithm 1 is Fejèr monotone with respect to $\mathcal{W}^{*}$.

Theorem 3.1

Let $\{w^{k}\}$ be the sequence generated by Algorithm 1. Then, for any $w^{*}\in\mathcal{W}^{*}$, we have

$$ \bigl\Vert w_{*}^{k+1}-w^{*}\bigr\Vert _{H}^{2}\leq\bigl\Vert w^{k}-w^{*}\bigr\Vert _{H}^{2}-\bigl\Vert w^{k}-\hat {w}^{k} \bigr\Vert ^{2}_{\tilde{H}}. $$

(21)

Proof

From (18), (19), and the monotonicity of Q, we obtain

$$\begin{aligned}& \bigl(\hat{w}^{k}-w\bigr)^{\top}Q(w) \\& \quad \leq \bigl(\hat{w}^{k}-w\bigr)^{\top}Q\bigl( \hat{w}^{k}\bigr) \\& \quad \leq \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{N}-\bigl(w-\hat{w}^{k}\bigr)^{\top}P\bigl(w^{k}-\hat{w}^{k}\bigr) \\& \quad = \frac{1}{2}\bigl(\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2}-\bigl\Vert w-w_{*}^{k+1}\bigr\Vert ^{2}_{H}\bigr)-\frac{1}{2}\bigl\Vert w^{k}-\hat {w}^{k}\bigr\Vert ^{2}_{\tilde{H}}. \end{aligned}$$

(22)

The assertion (21) follows immediately by setting $w=w^{*}\in\mathcal {W}^{*}$ in (22). The theorem is proved. □

Now, we are ready to prove the global convergence of Algorithm 1.

Theorem 3.2

The sequence $\{w^{k}\}$ generated by Algorithm 1 converges to some $w^{\infty}$, which belongs to $\mathcal{W}^{*}$.

Proof

First, by (21), for any given $w^{*}\in\mathcal{W}^{*}$, we have

$$ \bigl\Vert w_{*}^{k+1}-w^{*}\bigr\Vert _{H}\leq\bigl\Vert w^{k}-w^{*}\bigr\Vert _{H} , $$

which together with (14) implies that

$$ \bigl\Vert w^{k+1}-w^{*}\bigr\Vert _{H}\leq\bigl\Vert w^{k+1}-w_{*}^{k+1}\bigr\Vert _{H}+\bigl\Vert w_{*}^{k+1}-w^{*}\bigr\Vert _{H}\leq\rho v_{k}+\bigl\Vert w^{k}-w^{*}\bigr\Vert _{H} . $$

Therefore, for any $l\leq k$, we have

$$\bigl\Vert w^{k+1}-w^{*}\bigr\Vert _{H}\leq\bigl\Vert w^{l}-w^{*}\bigr\Vert _{H}+\rho\sum _{i=l}^{k}v_{i}. $$

Since $\sum_{k=0}^{\infty}v_{k}<+\infty$, there is a constant $C_{w^{*}}>0$, such that

$$ \bigl\Vert w^{k+1}-w^{*}\bigr\Vert _{H}\leq C_{w^{*}}< +\infty,\quad \forall k\geq0. $$

(23)

Therefore the sequence $\{w^{k}\}$ generated by Algorithm 1 is bounded. Furthermore, it follows from (14), (21), (23) that

$$\begin{aligned}& \bigl\Vert w^{k+1}-w^{*}\bigr\Vert _{H}^{2} \\& \quad = \bigl\Vert \bigl(w^{k+1}-w_{*}^{k+1}\bigr)+ \bigl(w_{*}^{k+1}-w^{*}\bigr)\bigr\Vert _{H}^{2} \\& \quad \leq \bigl\Vert w^{k+1}-w_{*}^{k+1}\bigr\Vert _{H}^{2}+2\bigl\Vert w^{k+1}-w_{*}^{k+1} \bigr\Vert _{H}\times\bigl\Vert w_{*}^{k+1}-w^{*}\bigr\Vert _{H}+\bigl\Vert w_{*}^{k+1}-w^{*}\bigr\Vert _{H}^{2} \\& \quad \leq \bigl\Vert w^{k}-w^{*}\bigr\Vert _{H}^{2}- \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{\tilde{H}}+2\rho v_{k}\bigl\Vert w^{k}-w^{*}\bigr\Vert _{H}+\rho^{2}v_{k}^{2} \\& \quad \leq \bigl\Vert w^{k}-w^{*}\bigr\Vert _{H}^{2}- \bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{\tilde{H}}+2\rho v_{k}C_{w^{*}}+ \rho^{2}v_{k}^{2}. \end{aligned}$$

(24)

Then, summing the inequality (24) over $k=0,1,\ldots$ and by $\sum_{k=0}^{\infty}v_{k}<+\infty$, we have

$$\sum_{k=0}^{\infty}\bigl\Vert w^{k}-\hat{w}^{k}\bigr\Vert ^{2}_{\tilde{H}} \leq\bigl\Vert w^{0}-w^{*}\bigr\Vert _{H}^{2}+ \sum_{k=0}^{\infty}\bigl(2\rho v_{k}C_{w^{*}}+\rho^{2}v_{k}^{2} \bigr)< +\infty, $$

which implies that

$$ \lim_{k\rightarrow\infty}\bigl\Vert w^{k}- \hat{w}^{k}\bigr\Vert ^{2}_{\tilde{H}}=0. $$

(25)

Thus the sequence $\{\hat{w}^{k}\}$ is also bounded, and thus it has at least one cluster point. Let $w^{\infty}$ be a cluster point of $\{\hat {w}^{k}\}$ and let the subsequence $\{\hat{w}^{k_{j}}\}$ converge to $w^{\infty}$. Then, by (18) and (25), we can get

$$ \lim_{k\rightarrow\infty}\bigl(w-\hat{w}^{k} \bigr)^{\top}Q\bigl(\hat {w}^{k}\bigr)\geq0,\quad \forall w\in \mathcal{W}. $$

(26)

That is,

$$\bigl(w-w^{\infty}\bigr)^{\top}Q\bigl(w^{\infty}\bigr) \geq0, \quad \forall w\in\mathcal{W}, $$

which implies that $w^{\infty}\in\mathcal{W}^{*}$. By (24), we have

$$ \bigl\Vert w^{k+1}-w^{\infty}\bigr\Vert _{H}^{2}\leq\bigl\Vert w^{l}-w^{\infty}\bigr\Vert _{H}^{2}+\sum_{i=l}^{\infty}\bigl(2\rho v_{i}C_{w^{*}}+\rho^{2}v_{i}^{2} \bigr), \quad \forall k\geq0, \forall l\leq k. $$

(27)

From $\lim_{k\rightarrow\infty}\|w^{k}-\hat{w}^{k}\|_{\tilde{H}}=0$ and $\{\hat{w}^{k_{j}}\}\rightarrow w^{\infty}$, for any given $\epsilon>0$, there exists an integer $j_{0}$, such that

$$\bigl\Vert w^{k_{j_{0}}}-w^{\infty}\bigr\Vert _{\tilde{H}}< \frac{\epsilon}{\sqrt{2}}\quad \mbox{and}\quad \sum_{i=k_{j_{0}}}^{\infty}\bigl(2\rho v_{i}C_{w^{*}}+\rho^{2}v_{i}^{2} \bigr)< \frac {\epsilon^{2}}{2}. $$

Therefore, for any $k\geq k_{j_{0}}$, it follows from the above two equalities and (27) that

$$\bigl\Vert w^{k+1}-w^{\infty}\bigr\Vert _{\tilde{H}}\leq \sqrt{\bigl\Vert w^{k_{j_{0}}}-w^{\infty}\bigr\Vert _{\tilde{H}}^{2}+\sum_{i=k_{j_{0}}}^{\infty}\bigl(2\rho v_{i}C_{w^{*}}+\rho ^{2}v_{i}^{2} \bigr)}< \epsilon, $$

which combining with the positive definite of H̃ indicates that the sequence $\{w^{k}\}$ converges to $w^{\infty}\in\mathcal{W}^{*}$. This completes the proof. □

Now, we are going to establish the convergence rate of Algorithm 1 in a nonergodic sense.

Theorem 3.3

Let $\{w^{k}\}$ be the sequence generated by Algorithm 1. Then, for any $w\in\mathcal{W}$, we have

$$ (\tilde{w}_{t}-w)^{\top}Q(w)\leq \frac{1}{t+1} \Biggl( \frac{1}{2}\bigl\Vert w^{0}-w\bigr\Vert ^{2}_{H}+\rho\sum_{k=0}^{t}v_{k} \bigl\Vert w-w^{k+1}\bigr\Vert _{H} \Biggr), $$

(28)

where $\tilde{w}_{t}=(\sum_{k=0}^{t}\hat{w}^{k})/(t+1)$.

Proof

From (22), we have

$$\bigl(w-\hat{w}^{k}\bigr)^{\top}Q(w)+\frac{1}{2}\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2}\geq \frac{1}{2}\bigl\Vert w-w_{*}^{k+1}\bigr\Vert ^{2}_{H}, \quad \forall w\in\mathcal{W}. $$

It follows from (14) that

$$\begin{aligned}& \bigl\Vert w-w_{*}^{k+1}\bigr\Vert ^{2}_{H} \\& \quad \geq \bigl(\bigl\Vert w-w^{k+1}\bigr\Vert _{H}- \bigl\Vert w^{k+1}_{*}-w^{k+1}\bigr\Vert _{H} \bigr)^{2} \\& \quad = \bigl\Vert w-w^{k+1}\bigr\Vert _{H}^{2}-2 \bigl\Vert w-w^{k+1}\bigr\Vert _{H}\times\bigl\Vert w^{k+1}_{*}-w^{k+1}\bigr\Vert _{H}+\bigl\Vert w^{k+1}_{*}-w^{k+1}\bigr\Vert _{H}^{2} \\& \quad \geq \bigl\Vert w-w^{k+1}\bigr\Vert _{H}^{2}-2 \rho v_{k}\bigl\Vert w-w^{k+1}\bigr\Vert _{H}, \quad \forall w\in\mathcal{W}. \end{aligned}$$

From the above two inequalities, we get

$$\begin{aligned}& \bigl(w-\hat{w}^{k}\bigr)^{\top}Q(w)+\frac{1}{2}\bigl\Vert w-w^{k}\bigr\Vert _{H}^{2} \\& \quad \geq \frac{1}{2}\bigl\Vert w-w^{k+1}\bigr\Vert _{H}^{2}-\rho v_{k}\bigl\Vert w-w^{k+1} \bigr\Vert _{H},\quad \forall w\in\mathcal{W}. \end{aligned}$$

Summing the above inequality over $k=0,1,\ldots,t$, we obtain

$$\begin{aligned} \begin{aligned} &\Biggl[ (t+1)w- \Biggl( \sum_{k=0}^{t} \hat{w}^{k} \Biggr) \Biggr]^{\top}Q(w)+\frac{1}{2}\bigl\Vert w^{0}-w\bigr\Vert ^{2}_{H} \\ &\quad \geq \frac{1}{2}\bigl\Vert w-w^{t+1}\bigr\Vert _{H}^{2}-\rho\sum_{k=0}^{t}v_{k} \bigl\Vert w-w^{k+1}\bigr\Vert _{H} \\ &\quad \geq -\rho\sum_{k=0}^{t}v_{k} \bigl\Vert w-w^{k+1}\bigr\Vert _{H},\quad \forall w\in \mathcal{W}. \end{aligned} \end{aligned}$$

Using the notation of $\tilde{w}_{t}$, we have

$$(w-\tilde{w}_{t})^{\top}Q(w)+\frac{1}{2(t+1)}\bigl\Vert w^{0}-w\bigr\Vert ^{2}_{H}\geq- \frac{\rho }{t+1} \sum_{k=0}^{t}v_{k} \bigl\Vert w-w^{k+1}\bigr\Vert _{H},\quad \forall w\in \mathcal{W}. $$

The assertion (28) follows from the above inequality immediately. The proof is completed. □

Remark 3.1

From the proof of Theorem 3.2, there is a constant $D>0$, such that

$$\bigl\Vert w^{k}\bigr\Vert _{H}\leq D \quad \mbox{and} \quad \bigl\Vert \hat{w}^{k}\bigr\Vert _{H}\leq D, \quad \forall k\geq0. $$

Since $\tilde{w}_{t}=(\sum_{k=0}^{t}\hat{w}^{k})/(t+1)$, thus, we also have $\|\tilde{w}_{t}\|\leq D$. Denote $E_{1}=\sum_{k=0}^{\infty}v_{k}<+\infty$. For any $w\in\mathcal{B}_{\mathcal{W}}(\tilde{w}_{t})=\{w\in\mathcal{W}|\| w-\tilde{w}_{t}\|_{H}\leq1\}$, by (28), we get

$$\begin{aligned}& (\tilde{w}_{t}-w)^{\top}Q(w) \\& \quad \leq \frac{1}{t+1} \Biggl(\frac{1}{2}\bigl(\bigl\Vert w^{0}-\tilde{w}_{t}\bigr\Vert _{H}+\Vert \tilde{w}_{t}-w\Vert _{H}\bigr)^{2}+\rho\sum _{k=0}^{t}v_{k}\bigl(\bigl\Vert \tilde{w}_{t}-w^{k+1}\bigr\Vert _{H}+\Vert \tilde{w}_{t}-w\Vert _{H}\bigr) \Biggr) \\& \quad \leq \frac{1}{t+1} \biggl( \frac{1}{2}(2D+1)^{2}+\rho E_{1}(2D+1) \biggr). \end{aligned}$$

Then, for any given $\epsilon>0$, the above inequality shows that after at most $\lceil(2D+1)(2D+1+2\rho E_{1})/(2\epsilon)-1\rceil$ iterations, we can get

$$(\tilde{w}_{t}-w)^{\top}Q(w)\leq\epsilon,\quad \forall w\in \mathcal {B}_{\mathcal{W}}(\tilde{w}_{t}). $$

This indicates that $\tilde{w}_{t}$ is an approximate solution of $\operatorname{VI}(\mathcal{W}, Q)$ with an accuracy of $\mathcal{O}(1/t)$. Thus a worst-case $\mathcal{O}(1/t)$ convergence rate of Algorithm 1 in the ergodic sense is established.

4 Numerical experiments

In this section, we apply Algorithm 1 to the traffic equilibrium problem with link capacity bound [22], which has been well studied in the literature of transportation. All codes were written by Matlab R2010a and conducted on a ThinkPad notebook with a Pentium (R) Dual-Core CPU T4400@2.2 GHz, 2GB of memory.

Consider a network $[\mathcal{N},\mathcal{L}]$ of nodes $\mathcal{N}$ and directed links $\mathcal{L}$, which is depicted in Figure 1, and consists of 20 nodes, 28 links and 8 O/D pairs.

Figure 1

A directed network with 20 nodes and 28 links.

We use the following symbols. a: a link; p: a path; ω: an origin/destination (O/D) pair of nodes; $\mathcal{P}_{\omega}$: the set of all paths connecting the O/D pair ω; Â: the path-arc incidence matrix; E: the path-O/D pair incident matrix; $x_{p}$: the traffic flow on the path p; $\hat{f}_{a}$: the link load on the link a; $d_{\omega}$: the traffic amount between the O/D pair ω. Thus, the link-flow vector f̂ is given by

$$\hat{f}=\hat{A}^{\top}x $$

and the O/D pair-traffic amount vector d is given by

$$d=E^{\top}x. $$

Let $t(\hat{f})=\{t_{a},a\in\mathcal{L}\}$ be the vector of link travel costs, which is given in Table 1. For a given link travel cost vector t, the path travel cost vector θ is given by

$$\theta=\bar{A}t(\hat{f})\quad \mbox{and}\quad \theta(x)=\hat{A}t\bigl(\hat {A}^{\top}x\bigr). $$

Associated with every O/D pair ω, there is a travel disutility $\eta_{\omega}(d)$, which is defined by

$$ \eta_{\omega}(d)=-m_{\omega}d_{\omega}+q_{\omega}, \quad \forall \omega, $$

(29)

and the parameters $m_{\omega}$, $q_{\omega}$ are given in Table 2. Now, the traffic network equilibrium problem is to seek the path-flow pattern $x^{*}$ [22]:

$$x^{*}\geq0, \quad \bigl(x-x^{*}\bigr)^{\top}\hat{F}\bigl(x^{*}\bigr)\geq0, \quad \forall x\in\mathcal{S}:=\bigl\{ x\in\mathcal{R}^{n}| \hat{A}^{\top}x\leq b, x\geq0\bigr\} , $$

where

$$\hat{F}_{p}(x)=\theta_{p}(x)-\eta_{\omega}\bigl(d(x) \bigr),\quad \forall\omega,p\in\mathcal {P}_{\omega}, $$

and b is the given link capacity vector. Using matrices  and E, a compact form of mapping is $\hat {F}(x)=\hat{A}t(\hat{A}^{\top}x)-E\eta(E^{\top}x)$. Introducing a slack variable $y\geq0$ and setting $g(y)=0$, $B=I$, the above problem can be converted into Problem (1). That is,

$$ \bigl(u-u^{*}\bigr)^{\top}T\bigl(u^{*}\bigr)\geq0, \quad u\in \Omega, $$

(30)

with

$$u=\left ( \textstyle\begin{array}{@{}c@{}}x\\ y \end{array}\displaystyle \right ),\qquad T(u)=\left ( \textstyle\begin{array}{@{}c@{}}\hat{F}(x)\\ 0 \end{array}\displaystyle \right ),\qquad \Omega=\bigl\{ (x,y)| \hat{A}^{\top}x+y=b, x\geq0, y\geq0\bigr\} . $$

When $v_{k}=0$ ($\forall k\geq0$), the implementation details of the two nonlinear equations of Algorithm 1 at each iteration are

$$\left \{ \textstyle\begin{array}{l} -[\lambda^{k}-\beta(y^{k+1}+\hat{A}^{\top}x^{k}-b)]+S[(y^{k+1}-y^{k}) +\mu(y^{k}-Q_{k}^{2}(y^{k+1})^{-1})]=0, \\ \lambda^{k+\frac{1}{2}}=\lambda^{k}-r\beta(y^{k+1}+\hat{A}^{\top}x^{k}-b), \\ \hat{F}(x^{k+1})-\hat{A}[\lambda^{k+\frac{1}{2}}-\beta[\alpha y^{k+1}-(1-\alpha)(\hat{A}^{\top}x^{k+1}-b)+\hat{A}^{\top}x^{k+1}-b] \\ \quad {}+R[(x^{k+1}-x^{k})+\mu(x^{k}-P_{k}^{2}(x^{k+1})^{-1})]]=0, \\ \lambda^{k+1}=\lambda^{k+\frac{1}{2}}-\beta[\alpha y^{k+1}-(1-\alpha )(\hat{A}^{\top}x^{k+1}-b)+\hat{A}^{\top}x^{k+1}-b]. \end{array}\displaystyle \right . $$

For the y-subproblem, it is easy to get its solution explicitly [23]:

$$y^{k+1}_{j}=\frac{-ss_{j}^{k}+\sqrt{(ss_{j}^{k})^{2}+4\mu s_{j}(\beta +s_{j})(y_{j}^{k})^{2}}}{2(\beta+s_{j})}, $$

where

$$ss^{k}=-\lambda^{k}+\beta\bigl(\hat{A}^{\top}x^{k}-b\bigr)-(1-\mu)Sy^{k}. $$

For the x-subproblem, we use the LQP-type method developed in [24] to solve it. In the test, we take $x^{0}=(1,1,\ldots,1)^{\top}$, $y^{0}=(1,1,\ldots,1)^{\top}$, and $\lambda^{0}=(0,0,\ldots,0)^{\top}$ as the starting point. For the test problem, the stopping criterion is

$$\max \biggl\{ \frac{\Vert e_{x}(w^{k})\Vert _{\infty}}{ \Vert e_{x}(w^{0})\Vert _{\infty}},\bigl\Vert e_{y} \bigl(w^{k}\bigr)\bigr\Vert _{\infty},\bigl\Vert e_{\lambda}\bigl(w^{k}\bigr)\bigr\Vert _{\infty}\biggr\} \leq\epsilon, $$

where

$$e\bigl(w^{k}\bigr):=\left ( \textstyle\begin{array}{@{}c@{}}e_{x}(w^{k})\\ e_{y}(w^{k})\\ e_{\lambda}(w^{k}) \end{array}\displaystyle \right )=\left ( \textstyle\begin{array}{@{}c@{}}x^{k}-P_{\mathcal{R}^{n}_{+}}\{x^{k}-[\hat{F}(x^{k})-\hat {A}\lambda^{k}]\}\\ y^{k}-P_{\mathcal{R}^{n}_{+}}[y^{k}+\lambda^{k}]\\ \hat{A}^{\top}x^{k}+y^{k}-b \end{array}\displaystyle \right ). $$

In the test, we take $\mu=0.01$, $\beta=0.8$, $r=0.8$, $R=100I$, $S=0.9I$. To illustrate the superiority of Algorithm 1, we also implement the inexact ADMM (denoted by IADMM) presented in [25] to solve this example under the same computational environment. The numerical results for different capacities ($b=30$ and $b=40$) and different ϵ and α are listed in Table 1, where the numbers in the tuplet ‘$\cdot/\cdot$’ represents, respectively, the numbers of iterations (Iter.) and the CPU time in seconds. Numerical results in Table 3 indicate that Algorithm 1 is an efficient method for the traffic equilibrium problem with link capacity bound, and it is superior to the IADMM in terms of number of iteration and CPU time. Furthermore, the two criteria of Algorithm 1 decrease with respect to α, as one has pointed in [26].

Table 1 The link traversing cost functions $\pmb{t_{a}(\hat{f})}$

Table 2 The O/D pairs and the parameters in ( 25 )

Table 3 Numerical results for different ϵ , α , and link capacity b

In addition, for the test problem with $b=40$, the optimal link-flow (Flow) vector $\hat{A}x^{*}$ and the toll charge (Charge) on the congested link $-\lambda^{*}$ are listed in Table 4.

Table 4 The optimal link flow and the toll charge on the link with $\pmb{b=40}$

5 Conclusions

In this paper, we have proposed an inexact generalized PRSM with LQP regularization for the structured variational inequalities, for which one only needs to solve two nonlinear equations approximately at each iteration. Under mild conditions, we have proved the global convergence of the new method and establish its convergence rate. Numerical results about the traffic equilibrium problem with link capacity bound indicate that the new method is quite efficient.