Dynamic interference for uplink SCMA in large-scale wireless networks without coordination

Abstract

Fast varying active transmitter sets are a key feature of wireless communication networks with very short length transmissions arising in communications for the Internet of Things. As a consequence, the interference is dynamic, leading to non-Gaussian statistics. At the same time, the very high density of devices is motivating non-orthogonal multiple access (NOMA) techniques, such as sparse code multiple access (SCMA). In this paper, we study the statistics of the dynamic interference from devices using SCMA. In particular, we show that the interference is α-stable with non-trivial dependence structure for large-scale networks modeled via Poisson point processes. Moreover, the interference on each frequency band is shown to be sub-Gaussian α-stable in the special case of disjoint SCMA codebooks. We investigate the impact of the α-stable interference on achievable rates and on the optimal density of devices. Our analysis suggests that ultra dense networks are desirable even with α-stable interference.

1 Introduction

Mordern wireless communication networks are increasingly heterogeneous. This heterogeneity stems from non-uniform placement of access points and variations in transmit power constraints and a characteristic of network employing small cells and ad hoc networks. Another form of heterogeneity is due to differences in the services that networks provide. For instance, there are key differences in quantity and type of data, as well as transmission protocols between networks supporting standard cellular or WLAN communication and machine-to-machine (M2M) communications, which are increasingly ubiquitous with the rapid development of the Internet of Things (IoT) [1].

In standard cellular services, data transmissions typically vary between 1 KB and 2 MB per transmission for text and image transfers and up to 3 GB for video transmission [2]. On the other hand, in M2M communications, data transmission is of the order of 1 MB per month [3]. Transmissions in M2M are therefore very short in time. As a consequence, the active set of transmitting devices at each time can change rapidly. A natural question is how devices should operate in this setting. In particular, what are the statistical properties of the resulting interference (is it even Gaussian?), and what interference mitigation strategies are appropriate?

In the uplink—where a large number of devices connect to one or more access points—one interference mitigation strategy is to ensure that device transmissions are nearly orthogonal. That is, transmisssions overlap on different frequencies, different times, different spatial dimensions, or different power levels. This approach falls under the class of non-orthogonal multiple access (NOMA) transmission strategies [4].

One promising NOMA strategy is sparse code multiple access (SCMA) for OFDM systems [5]. In this strategy, users can transmit on a sparse subset of all frequency bands, analogous to CDMA where in contrast, the coding is performed over time slots. We remark that SCMA falls in the class of code-based NOMA as opposed to the pure power NOMA strategy, which exploits differences in received power levels to discriminate between users via successive interference cancellation [6].

In this paper, we assess the impact of rapidly changing active transmitter sets—or dynamic interference—in large-scale wireless networks with SCMA, such as in M2M. We consider a worst-case scenario where the network is interference-limited, uncoordinated, and the locations of interferers are governed by a homogeneous Poisson point process. This setup is relevant for networks supporting the Internet of Things and in large-scale sensor networks, where transmitting devices are very simple and have limited ability to coordinate. In particular, limited coordination arises in the grant free scenarios recently considered in the context of NOMA [6], where devices randomly access time-frequency resources. In many cases, such random access is necessary due to the use of low-power, low-cost devices. A coordinated channel has high power usage due to the need for control signals. This is not realistic with ultra-low power devices.

The study of interference in wireless networks has a long history. An early significant contribution was due to Middleton [7, 8] where it was established that the electromagnetic interference probability density function is represented via an infinite series, leading to the Middleton class A and class B models. Reduced to two terms to simplify derivations, the resulting distribution is called the Bernoulli-Gaussian model [9, 10]. Around the year 2000, work on Ultra Wide Band (UWB) communications also gave rise to many empirical modeling approaches. These works are relevant because the topologies are similar and impulsive radio transmissions gave rise to dynamic interference. The empirical models are often based on pragmatic choices, which provide a good fit with simulated data and analytical solutions for the maximum likelihood detector [11–13].

Dynamic interference in wireless networks without SCMA was introduced in [14, 15] by considering fast-varying (symbol-by-symbol) active transmitter sets, with locations governed by a homogeneous Poisson point process. In particular, it was shown that the interfering signal power in each time-slot follows the α-stable law, which is widely used to model impulsive noise signals [16]. Further analysis of these models via stochastic geometry [17, 18] has established that the α-stable interference model is a good approximation of the true interference distribution when the radius of the network is large and there are no guard zones [19–21].

The class of α-stable random variables are well-known to model impulsive signals; however, unlike Gaussian models, α-stable models are challenging to study due to the absence of a closed-form probability density function [22]. Although an expression without a closed-form for the error probability in the presence of α-stable interference was derived in [14], little is known about achievable rates and the optimal density of devices in this scenario and in particular for networks using SCMA.

1.1 Methods and overview of contributions

In this paper, we study the statistics of dynamic interference in large-scale networks exploiting SCMA. Unlike existing work on SCMA, we consider the presence of dynamic interference. Accounting for the impact of dynamic interference is critical as the resulting high amplitude interference is known to have an important impact on key network performance indicators (e.g., bit error rate and capacity [23]). As Gaussian interference models underestimate the probability of such high amplitude interference, the resulting design can be highly suboptimal.

A key focus, unlike existing work on dynamic interference, is not only on the statistics of interference but also on the dependence between the signals on different bands. Our main result is to establish that when devices randomly and independently select frequency bands to transmit on—i.e., the non-zero elements of the SCMA codebook—the resulting interference is an α-stable random vector. However, the interference on each band is not in general independent. To study this dependence structure, we focus on a particular class of SCMA codebooks where devices transmit on a restricted set of bands. For this class of SCMA codebooks detailed in the sequel, we show that the resulting dynamic interference has sub-Gaussian α-stable dependence structure.

We then study achievable rates in the presence of isotropic α-stable noise, which is a special case of sub-Gaussian α-stable noise for which rate bounds are not currently known. Based on the achievable rate, we study consequences for network design and in particular the impact of device density on the area spectral efficiency. This provides new insights into the design of networks in the presence of dynamic interference by characterizing the optimal device density. Moreover, the characterization of the achievable rate provides a basis for network optimization, e.g., power control. Finally, we discuss the general problem of characterizing the dependence structure induced by general SCMA codebooks. In particular, we propose an approach based on copulas and investigate consequences for signal detection.

The paper is organized as follows. In Section 2, the setup is formalized for large-scale SCMA-based wireless networks with dynamic interference. In Section 3, the statistics of the dynamic interference are characterized and shown to follow the law of an α-stable random vector. In Section 4, we study achievable rates in α-stable noise and the impact on device density. In Section 5, we discuss our results and in Section 8, we conclude.

2 Problem formalization

Consider an uplink single-cell network in which the simultaneous transmissions from a large number of devices are received by a single access point at the origin. The device transmissions are over a subset of orthogonal bands $\mathcal {B} = \{1,2,\ldots,K\}$.

At each time slot t, each device independently transmits with probability p≪1. The subset of transmitting devices is governed by a Poisson point process Φ_t with intensity λ. Since p≪1, the distance from devices in Φ_t, denoted by r_j, and devices in $\Phi _{t^{\prime }}$ corresponding to another time t≠t^′, denoted by $r_{j^{\prime }}$, to the access point are modeled as independent random variables. That is, for a device j in Φ_t and a device j^′ in $\Phi _{t^{\prime }}$ we have $\text {Pr}\left (r_{j} \leq R|r_{j^{\prime }}\right) = \text {Pr}(r_{j} \leq R)$.

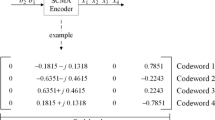
In a given time slot, each device j seeks to transmit a message W_j uniformly drawn from the set $\mathcal {W}_{j} = \{1,2,\ldots,M\}$ over n channel uses. M is the number of different messages that the device can transmit. We denote by m the number of bands that each device can use to transmit their data. Each device is also equipped with an encoder $\mathcal {E}_{j}: \mathcal {W}_{j} \rightarrow \mathbb {C}^{K\times n}$, which maps each message to n SCMA codewords in $\mathbb {C}^{K}$, allowing for vector codewords¹. One SCMA codeword is composed of m non-zero elements selected from the set of all subsets $\mathcal {B}_{m}$, which consists of all subsets of {1,2,…,K} with size m.

We are interested in two classes of SCMA codebooks. In the first class, any set in $\mathcal {B}_{m}$ can be selected by a device, where the non-zero elements of each codeword are assumed to be independently chosen for each device. This first case is referred to as the general random SCMA codebook.

In the second class of SCMA codebooks, only disjoint elements of $\mathcal {B}_{m}$ can be selected. In this case, there are $\left \lfloor \frac {K}{m} \right \rfloor$ codewords. If two devices choose different codebooks (i.e., different elements of $\mathcal {B}_{m}$), then there is no interference. On the other hand, if two devices choose the same element of $\mathcal {B}_{m}$, then they will interfere on all bands with a non-zero signal. This second case is referred to as the disjoint random SCMA codebook. These codebooks are detailed further in Section 3.

Accounting for the contributions of all transmitting devices at time t, the received signal at the access point on band k in the interference limited regime is given by:

$$\begin{array}{*{20}l} y_{k}(t) &= \sum\limits_{j \in \Phi_{t}} h_{j,k}(t)r_{j}(t)^{-\eta/2}x_{j,k}(t), \\ t &= 1,2,\ldots,n \end{array} $$

(1)

where $h_{j,k} \sim \mathcal {CN}(0,1)$ is the Rayleigh fading coefficient of the j-th device on band k, r_j(t) is the distance from the device j to the access point, and η>2 is the path-loss exponent. We remark that Rayleigh fading models are appropriate for IoT applications indoor or in dense environments such as those that arise in city centers [24]. Although we do not treat other fading models further in this paper, we remark that if the input signal x_j,k(t) is isotropic and has finite power, then our results also apply to Rician or Nakagami fading.

We can now formalize the key question that we address in the remainder of this paper:

• What are the statistics of the interference in SCMA networks with fast-varying active transmitter sets? In particular, what is the distribution of theK-dimensional random vector Z(t), t=1,2,…with elements

  $$\begin{array}{*{20}l} Z_{k}(t) = \sum\limits_{j \in \Phi_{t}} h_{j,k}(t)r_{j}(t)^{-\eta/2}x_{j,k}(t) \end{array} $$

  (2)

  corresponding to the interference from the devices on band k at time t?

3 Interference characterization

In this section, we investigate the effect of rapidly changing active transmitter sets on the interference statistics, that is, we characterize the distribution of dynamic interference. A key feature of dynamic interference is its impulsive nature, which we formally establish by showing that the interference on each band follows the α-stable distribution under the assumptions in Section 2. We also study the dependence structure of the random vector arising from the interference on each band.

3.1 Preliminaries

Before characterizing the interference statistics, we review definitions and important properties of α-stable random variables and vectors. The α-stable random variables are a key class of random variables with heavy-tailed probability density functions, which have been widely used to model impulsive signals [16, 22]. The probability density function of an α-stable random variable is parameterized by four parameters: the exponent 0≤α≤2; the scale parameter $\gamma \in \mathbb {R}_{+}$; the skew parameter β∈[−1,1]; and the shift parameter $\delta \in \mathbb {R}$. As such, a common notation for an α-stable random variable X is X∼S_α(γ,β,δ). In the case β=δ=0, X is said to be a symmetric α-stable random variable.

In general, α-stable random variables do not have closed-form probability density functions. Instead, they are usually represented by their characteristic function, given by ([22], Eq. 1.1.6)

$$ \begin{aligned} &\mathbb{E}\left[e^{i\theta X}\right]\\ &= \left\{\begin{array}{c} \exp\left\{-\gamma^{\alpha}|\theta|^{\alpha}\left(1 - i\beta(\text{sign}\theta)\tan \frac{\pi\alpha}{2}\right) + i\delta\theta\right\},\\ \alpha \neq 1 \\ \exp\left\{-\gamma|\theta|\left(1 + i\beta\frac{2}{\pi}(\text{sign} \theta)\log|\theta|\right) + i\delta\theta\right\}, \\ \alpha = 1 \end{array}\right. \end{aligned} $$

(3)

In addition to the characteristic function, symmetric α-stable random variables admit a series representation. This is known as the LePage series and is detailed in the following theorem (a proof is available in ([22], Theorem 1.4.2), which will play a key role in our analysis of dynamic interference.

Theorem 1

Let 0<α<2, (Γ_i, i=1,2,…) be a Poisson process of rate 1 and W₁,W₂,… be a sequence of independent and identically distributed symmetric² random variables. Then, the sum ${\sum \nolimits }_{i=1}^{\infty } \Gamma _{i}^{-1/\alpha }W_{i}$ converges almost surely to a random variable X whose distribution is $S_{\alpha }\left (\left (C_{\alpha }^{-1}\mathbb {E}\left [\left (|W_{1}|^{\alpha }\right)^{1/\alpha }\right ]\right),0,0\right)$, where

$$\begin{array}{*{20}l} C_{\alpha} = \left\{ \begin{array}{ll} \frac{1 - \alpha}{\Gamma(2-\alpha)\cos(\pi\alpha/2)},&\text{if}~\alpha \neq 1\\ 2/\pi,&\text{if}~\alpha = 1. \end{array} \right. \end{array} $$

(4)

It is possible to extend the notion of an α-stable random variable to the multivariate setting. A sufficient condition for a random vector X to be a symmetric α-stable random vector is that the marginal distributions of the elements of X are symmetric α-stable³. In general, d-dimensional symmetric α-stable random vectors are represented via their characteristic function, given by [22]

$$\begin{array}{*{20}l} \mathbb{E}\left[e^{i\boldsymbol{\theta}\cdot \mathbf{X}}\right] = \exp\left(-{\int\nolimits}_{\mathbb{S}^{d-1}} \left|\sum\limits_{k=1}^{d} \theta_{k} s_{k}\right|^{\alpha}\Gamma(d\mathbf{s})\right), \end{array} $$

(5)

where Γ is the unique symmetric measure on the d-dimensional unit sphere $\mathbb {S}^{d-1}$. A particular class of α-stable random vectors are an instance of the sub-Gaussian α-stable random vectors⁴, defined as follows.

Definition 1

Any vector X distributed as X=(A^1/2G₁,…,A^1/2G_d), where

$$\begin{array}{*{20}l} A \sim S_{\alpha/2}\left(\left(\cos \pi\alpha/4\right)^{2/\alpha},1,0\right), \end{array} $$

(6)

and $\mathbf {G} = \left [G_{1},\ldots,G_{d}\right ]^{T} \sim \mathcal {N}\left (\mathbf {0},\sigma ^{2}\mathbf {I}\right)$ is called a sub-Gaussian α-stable random vector in $\mathbb {R}^{d}$ with underlying Gaussian vector G.

Sub-Gaussian random vectors are typically characterized by either the scale-mixture representation in Definition 1 or via their characteristic function ([22], Proposition 2.5.5) as detailed in the following proposition.

Proposition 1

Let X be a symmetric α-stable random vector in $\mathbb {R}^{d}$. Then, the following statements are equivalent:

• 1. X is sub-Gaussian α-stable with an underlying Gaussian vector having i.i.d. $\mathcal {N}\left (0,\sigma ^{2}\right)$ components.

• 2. The characteristic function of X is of the form

  $$\begin{array}{*{20}l} \mathbb{E}\left[e^{i\boldsymbol{\theta} \cdot \mathbf{X}}\right] = \exp\left(-2^{-\alpha/2}\sigma^{\alpha}\|\boldsymbol{\theta}\|^{\alpha}\right). \end{array} $$

  (7)

Sub-Gaussian α-stable random vectors are preserved under orthogonal transformations. The following proposition provides further characterizations of sub-Gaussian α-stable random vectors via their relationship to orthogonal transformations⁵.

Proposition 2

Let $\mathcal {O}(d)$ be the set of real orthogonal matrices and $\mathbf {U} \in \mathcal {O}(d)$. Then, $\mathbf {Z} \overset {d}{=} \mathbf {U}\mathbf {Z}$ holds for all $\mathbf {U} \in \mathcal {O}(d)$ if and only if Z is a sub-Gaussian α-stable random vector with an underlying Gaussian vector having i.i.d. $\mathcal {N}\left (0,\sigma ^{2}\right)$ components.

Proof

See Section 6. □

Sub-Gaussian α-stable random vectors also play an important role in studying complex α-stable random variables, that is, a random variable with α-stable distributed real and imaginary components. In particular, the generalization of sub-Gaussian α-stable random variables to the complex case is known as the class of isotropic α-stable random variables, defined as follows.

Definition 2

Let Z₁,Z₂ be two symmetric α-stable random variables. The complex α-stable random variable Z=Z₁+iZ₂ is isotropic if it satisfies the condition:

• $\mathbf {C1:} e^{i\phi }Z \overset {(d)}{=} Z$ for any ϕ∈ [ 0,2π).

The random vector Z is said to be induced by the isotropic α-stable random variable Z. Due to the fact that baseband signals are typically complex, isotropic α-stable random variables will play an important role in the interference characterization.

The following proposition ([22], Corollary 2.6.4) highlights the link between isotropic α-stable random variables and sub-Gaussian α-stable random vectors.

Proposition 3

Let 0<α<2. A complex α-stable random variable Z=Z₁+iZ₂ is isotropic if and only if there are two independent and identically distributed zero-mean Gaussian random variables G₁,G₂ with variance σ² and a random variable A∼S_α/2((cos(πα/4))^2/α,1,0) independent of (G₁,G₂)^T such that (Z₁,Z₂)^T=A^1/2(G₁,G₂)^T. That is, (Z₁,Z₂)^T is a sub-Gaussian α-stable random vector.

We remark that isotropic complex α-stable random variables are closely related to sub-Gaussian random vectors as can be observed from a comparison with Definition 1. Moreover, unlike the isotropic (or circularly symmetric) Gaussian case (α=2), isotropic α-stable random variables with α<2 do not have independent real and imaginary components. This dependence arises from the characterization in Proposition 3 through the dependence of the α-stable random variable A in both the real and imaginary components.

3.2 Interference for general random SCMA codebooks

We now study the statistics of the interference from devices under the general SCMA codebook setup detailed in Section 2. We first consider the distribution of the interference on each band. In particular, we characterize the distribution of:

$$\begin{array}{*{20}l} Z_{k}(t) = \sum\limits_{j \in \Phi_{t}} h_{j,k}(t)r_{j}(t)^{-\eta/2}x_{j,k}(t),~k = 1,\ldots,K. \end{array} $$

(8)

Consider the scenario of a general SCMA codebook, where each device selects the m bands that it transmits on from a distribution P_m on $\mathcal {B}_{m}$, independently of the other devices. For example, suppose that device j selects bands uniformly from $\mathcal {B}_{m}$ then the probability that it transmits on band k at time t is $q = \frac {\stackrel {K -1}{m-1}}{\stackrel {K}{m}}$. As such, the devices that transmit on band k also form a homogeneous Poisson point process with rate λq. In this case, the following theorem holds.

Theorem 2

Suppose that

$$\begin{array}{*{20}l} \mathbb{E}\left[\left(\text{Re}\left(h_{j,k}(t)r_{j}(t)^{-\eta/2}x_{j,k}(t)\right)\right)^{\eta/4}\right] < \infty. \end{array} $$

(9)

Further, suppose that each device selects m bands from a given distribution P_m on $\mathcal {B}_{m}$, independently of the other devices. Then, Z_k(t)converges almost surely to an isotropic $\frac {4}{\eta }$-stable random variable.

Proof

Using the mapping theorem for PPPs [25], it follows that $\{r_{l}^{2}\}_{l}$ is a one-dimensional Poisson point process with intensity λπ ([21], Theorem 1). Since the codebooks for each device are independent, the hypothesis of the theorem implies that the LePage representation in Theorem 1 holds. It then follows that the interference has real and imaginary parts that are almost surely symmetric $\frac {4}{\eta }$-stable random variables. Since we consider Rayleigh fading, h_l,nx_l,n is isotropic and condition C1 for isotropic α-stable random variables is also satisfied, as required. □

A consequence of Theorem 2 is that the interference random vector Z(t) is an α-stable random vector when devices use general SCMA codebooks. This is in sharp contrast to standard models for non-dynamic interference, which are typically Gaussian.

Although Z(t) is an α-stable random vector, the dependence structure remains unspecified. We note that unlike Gaussian interference models, the dependence structure is not characterized through the covariance matrix. In fact, the covariance of α-stable random variables is either infinite or undefined, depending on the value of 0<α<2. Next, we study the dependence structure for the special case of disjoint random SCMA codebooks, where each device transmits on one of a family of disjoint sets consisting of m bands.

3.3 Interference for disjoint random SCMA codebooks

We now consider the case where devices transmit using disjoint random SCMA codebooks. Given K bands it is possible to obtain ⌊K/m⌋ disjoint subsets. Devices are said to use disjoint random SCMA codebooks if they are restricted to transmitting on one of these ⌊K/m⌋ disjoint subsets of $\mathcal {B}$, and the set of m bands is selected uniformly. In this section, we characterize the statistics of the interference vector arising from the use of disjoint random SCMA codebooks.

To begin, consider the case where devices use SCMA codewords that have non-zero values on disjoint sets of bands. By the independent thinning theorem for Poisson point processes [25], the interference on bands in different disjoint subsets in $\mathcal {B}_{m}$ are independent. Therefore, the key challenge is to establish the dependence of interference on bands within the same disjoint subset in $\mathcal {B}_{m}$.

Consider a given disjoint subset in $\mathcal {B}_{m}$ and denote the interference on these m bands as Z_m(t). In this case, the received signal vector at the access point on the m bands under consideration can then be written as:

$$\begin{array}{*{20}l} \mathbf{y}_{m}(t) = r_{1}^{-\eta/2}\mathbf{h}_{1,m} \circ \mathbf{x}_{1,m}(t) + \mathbf{Z}_{m}(t), \end{array} $$

(10)

where ∘ is the Hadamard element-wise product and

$$\begin{array}{*{20}l} \mathbf{Z}_{m}(t) = \sum\limits_{j \in \Phi_{t}} r_{j}(t)^{-\eta/2}\mathbf{h}_{j,m}(t) \circ \mathbf{x}_{j,m}(t) \end{array} $$

(11)

The statistics of the interference random vector Z_m are given in the following theorem. The proof is provided in Section 3.5.

Theorem 3

The interference Z_m induced by disjoint random SCMA codebooks follows the sub-Gaussian α-stable distribution with an underlying Gaussian vector having i.i.d. $\mathcal {N}\left (0,\sigma _{\mathbf {Z}}^{2}\right)$ components, α=4/η and parameter

$$\begin{array}{*{20}l} \sigma_{\mathbf{Z}} = \left(\pi \lambda q_{D} C^{-1}_{\frac{4}{\eta}} \mathbb{E}\left[\left|\text{Re}(h_{1,1}x_{1,1})\right|^{\frac{4}{\eta}}\right]\right)^{\eta/4}, \end{array} $$

(12)

where $q_{D} = \frac {1}{\lfloor K/m \rfloor }$ and $C_{\frac {4}{\eta }}$ as defined in Theorem 1.

3.4 Numerical results

To illustrate the dependence structure resulting from sub-Gaussian α-stable interference. Interference samples are generated from a network of devices distributed uniformly on a disc of radius R=500 m and number of access points drawn from a Poisson distribution with parameter πR²λ with λ=0.1. These samples approximate a realization of a Poisson point process with rate λ [25].

Figure 1 plots samples obtained from the real and imaginary parts of interference on a single band. Observe that the samples are distributed isotropically as expected from Theorem 2. Figure 2 plots the real parts of interference samples from two bands b₁,b₂ in a disjoint SCMA codebook with b₁,b₂ in the same disjoint subset. Observe that the samples exhibit the same dependence structure as in Fig. 1, which is consistent with Theorem 3.

Fig. 1

Scatter plot of samples from the real and imaginary parts of interference on a single band. Samples generated from a network of devices distributed uniformly on a disc of radius R=500 m and number of access points drawn from a Poisson distribution with parameter πR²λ with λ=0.1

Fig. 2

Scatter plot of samples from the real parts of interference drawn from two distinct bands, b₁,b₂. Samples generated from a network of devices using a disjoint SCMA codebook. Bands b₁,b₂ lie in the same disjoint subset. The distribution of devices is the same as Fig. 1

Figure 3 plots the real parts of interference samples from two bands b₁,b₂ in a general SCMA codebook with b₁ selected with probability 1/2 and b₂ selected with probability 1/3 if b₁ is selected and probability 2/3 if b₁ is not selected. This scenario can occur in codebooks constructed to reduce decoding complexity. Observe that the dependence structure differs from Fig. 2, which demonstrates that SCMA codebooks can have dependence structures that do not arise from sub-Gaussian random α-stable random vectors. In Section 5, we discuss methods to model this dependence in a tractable manner.

Fig. 3

Scatter plot of samples from the real parts of interference drawn from two distinct bands, b₁,b₂. Samples generated from a network of devices using a codebook with b₁ selected with probability 1/2 and b₂ selected with probability 1/3 if b₁ is selected and 2/3 if b₁ is not selected. The distribution of devices is the same as Fig. 1

3.5 Proof of Theorem 3

We first establish that the elements of Z_m are complex α-stable random variables. Without loss of generality, consider the first element of Z_m, denoted by Z₁, given by:

$$\begin{array}{*{20}l} Z_{1} = \sum\limits_{j \in \Phi_{t}} r_{j}^{-\eta/2}h_{j,1}x_{j,1}. \end{array} $$

(13)

Giving each element of Φ an index in $\mathbb {N}$, we write

$$\begin{array}{*{20}l} Z_{1} = \sum\limits_{j=1}^{\infty} r_{j}^{-\eta/2}h_{j,1}x_{j,1}. \end{array} $$

(14)

Let z_j=h_j,1x_j,1 and denote the real an imaginary parts as z_j,r and z_j,i, respectively. We then have

$$\begin{array}{*{20}l} Z_{1} = \sum\limits_{j=1}^{\infty} r_{j}^{-\eta/2}(z_{j,r} + {iz}_{j,i}). \end{array} $$

(15)

Now, recall that the distances $\{r_{j}\}_{j=1}^{\infty }$ are from points in a homogeneous PPP to the origin. Using the mapping theorem, it follows that $\left \{r_{j}^{2}\right \}_{j=1}^{\infty }$ with intensity q_Dλπ. It then follows from the LePage series representation in Theorem 1 that Z₁ converges almost surely to Z_r+iZ_i, where Z_r and Z_i are symmetric 4/η-stable random variables. Morever, $e^{i\theta }Z_{1} \overset {d}{=} Z_{1}$ since for each j, $e^{i\theta }h_{j,1}x_{j,1} \overset {d}{=} h_{j,1}x_{j,1}$ by the fact that the Rayleigh fading coefficient is isotropic. Therefore, by Proposition 3, it follows that an equivalent representation of Z₁ is a two-dimensional real sub-Gaussian α-stable random vector.

By applying the same argument to each element of Z_m, it follows that it is a complex 4/η-stable random vector. We now need to show that stacking the real valued representation of each element of Z_m yields a sub-Gaussian α-stable random vector. Let Z^′ be the vector obtained by stacking the real and imaginary parts of Z_m.

To proceed, we will apply Proposition 2. In particular, let $\mathbf {U} \in \mathcal {O}(2m)$ (recall that $\mathcal {O}(2m)$ is the set of real orthogonal matrices of dimensions 2m×2m). Further, let $Z^{\prime }_{j,l}$ represent the real or imaginary part of the interference on a band k due to device j, which is given by

$$\begin{array}{*{20}l} Z^{\prime}_{j,l} = r_{j}^{-\eta/2}\left(\text{Re}(h_{j,k})\text{Re}(x_{j,k}) - \text{Im}(h_{j,k})\text{Im}(x_{j,k})\right) \end{array} $$

(16)

in the case that $Z^{\prime }_{j,l}$ corresponds to a real part. A similar expression can be also obtained for the case of an imaginary part. For both cases, $Z^{\prime }_{j,l} = r_{j}^{-\eta /2}\left (f_{j,k}\text {Re}\left (x_{j,k}\right) + g_{j,k}\text {Im}\left (x_{j,k}\right)\right)$, where f_j,k and g_j,k are Gaussian with variance 1/2 due to the fact that h_j,k is a Rayleigh fading coefficient. As such, the vector of interference from device j can be written as $\mathbf {Z}^{\prime }_{j} = r_{j}^{-\eta /2}(\mathbf {f} \cdot \text {Re}(\mathbf {x}_{j}) + \mathbf {g} \cdot \text {Im}(\mathbf {x}_{j}))$. Since U is orthogonal it then follows that $\mathbf {U}\mathbf {f} \overset {d}{=} \mathbf {f}$ and $\mathbf {U}\mathbf {g} \overset {d}{=} \mathbf {g}$, which implies that $\mathbf {UZ^{\prime }} \overset {d}{=} \mathbf {Z}^{\prime }$. Since the choice of $\mathbf {U} \in \mathcal {O}(2m)$ is arbitrary, the result then follows by applying Proposition 2.

4 Achievable rates with dynamic interference

At present, the capacity of dynamic interference channels has not been established even for single frequency systems. To this end, in this section, we study achievable rates for dynamic interference channels. Although our focus is on single frequency systems, it is also applicable to SCMA-based systems when each band is treated separately.

As shown in Theorem 2, the interference on each band is isotropic α-stable distributed. To study achievable rates in this interference, we introduce the additive isotropic α-stable noise (AIαSN) channel. In particular, the output of the AIαSN channel is given by

$$\begin{array}{*{20}l} y = r_{d}^{-\eta/2}h_{d}X_{d} + Z. \end{array} $$

(17)

where r_d is the distance from a device to its serving access point located at the origin, $h_{d} \sim \mathcal {CN}(0,1)$ is the Rayleigh fading coefficient and X_d is the baseband emission for the device under consideration, and Z is the isotropic α-stable distributed interference. Unlike the capacity of the power constrained Gaussian noise channel, tractable expressions are not known for the power constrained AIαSN channel. For this reason, it is desirable to consider alternative constraints.

One choice of constraints is the combination of amplitude and fractional moment constraints. In particular, the input signal X_d in (17) is required to satisfy

$$\begin{array}{*{20}l} \mathbb{E}\left[\left|\text{Re}(X_{d})\right|^{\zeta}\right] &\leq c\\ \mathbb{E}\left[\left|\text{Im}(X_{d})\right|^{\zeta}\right] &\leq c \\ \left|\text{Re}(X_{d})\right| &\leq A\\ \left|\text{Im}(X_{d})\right| &\leq A, \end{array} $$

(18)

where 0<ζ<α. Note that the presence of the amplitude constraint ensures that the input has finite moments, including power.

To characterize the capacity of the AIαSN channel in (17) subject to the constraints in (18), we proceed in two steps. First, we relax the amplitude constraints and consider the optimization problem given by

$$ \begin{aligned} & \underset{\mu \in \mathcal{P}}{\text{maximize}} & I(X_{d};y)\\ & \text{subject to} & \mathbb{E}\left[\left|\text{Re}(X_{d})\right|^{\zeta}\right] \leq c,\\ & & \mathbb{E}\left[\left|\text{Im}(X_{d})\right|^{\zeta}\right] \leq c,\\ \end{aligned} $$

(19)

where $\mathcal {P}$ is the set of probability measures on $\mathbb {C}$ and 0<ζ<α. The unique (see [26]) solution to (19) is lower bounded in the following theorem.

Theorem 4

For fixed r_d and h_d, the capacity of the additive isotropic $\frac {4}{\eta }$-stable noise channel in (17) subject to the fractional moment constraints in (19) is lower bounded by:

$$\begin{array}{*{20}l} C_{L} = \frac{\eta}{4}\log\left(1 + \frac{\left(\sqrt{2|r_{d}^{-\frac{\eta}{2}}h_{d}|^{2}}\left(\frac{c}{C(\zeta, \frac{4}{\eta})}\right)^{\frac{1}{\zeta}}\right)^{\frac{4}{\eta}}}{\sigma_{\mathbf{N}}^{\frac{4}{\eta}}}\right), \end{array} $$

(20)

where Γ(·) is the Gamma function and

$$\begin{array}{*{20}l} C\left(\zeta,\frac{4}{\eta}\right) = \frac{2^{\zeta+1}\Gamma\left(\frac{\zeta + 1}{2}\right)\Gamma(-\eta \zeta/4)}{\frac{4}{\eta}\sqrt{\pi}\Gamma(-\zeta/2)}. \end{array} $$

(21)

Proof

We consider the case that X_d is an isotropic α-stable random variable satisfying the constraints in (19). By Theorem 5 in [26], the mutual information of the channel Y=X_d+Z is derived using the stability property; i.e., Y is an isotropic α-stable random variable since X_d and Z are. The mutual information is then given by

$$\begin{array}{*{20}l} I(X_{d};Y) = \frac{\eta}{4}\log\left(1 + \frac{\left(\sqrt{2}\left(\frac{c}{C\left(\zeta,\frac{4}{\eta}\right)}\right)^{1/\zeta}\right)^{\frac{4}{\eta}}}{\sigma_{\mathbf{N}}^{\frac{4}{\eta}}}\right) \end{array} $$

(22)

The result then follows by observing that $r_{d}^{-\frac {\eta }{2}}h_{d}X_{d}$ is also an isotropic $\frac {4}{\eta }$-stable random variable with parameter $|r_{d}^{-\frac {\eta }{2}}h_{d}|\sigma _{\mathbf {N}}$ using the fact that X_d is isotropic and ([22], Property 1.2.3). □

Remark 1

Note that the achievable rate derived in Theorem 4 bears similarities to the capacity of additive white Gaussian noise channels, but is not the same. A key difference is the absence of the noise variance, which is in fact infinite for α-stable noise models. Instead, the parameter σ_N characterizes the statistics of the noise.

The achievable rates from Theorem 4 are obtained by using input signals that are isotropic α-stable random variables, which do not satisfy the amplitude constraints in (18). The second step in characterizing the capacity of the AIαSN channel subject to (18) is therefore to consider a truncated isotropic α-stable input. This guarantees the amplitude constraints are satisfied and, as we will show, yields a mutual information in the AIαSN channel that is well approximated by Theorem 4 for a sufficiently large truncation level T.

The truncated isotropic α-stable random variables are defined as follows. Let X be an isotropic α-stable random variable, with real part X_r and imaginary part X_i. The truncation of X, denoted by X_T, is given by

$$\begin{array}{*{20}l} X_{T} = \left\{ \begin{array}{ll} X,\\ \qquad\qquad\,\text{if}~|X_{r}| \leq T,~|X_{i}| \leq T \\ \text{sign}(X_{r})T + {iX}_{i},\\ \qquad\qquad\,\text{if}~|X_{r}| > T,~|X_{i}| \leq T \\ X_{r} + i\text{sign}(X_{i}) T,\\ \qquad\qquad\,\text{if}~|X_{r}| \leq T,~|X_{i}| > T \\ \text{sign}(X_{r}) T + i\text{sign}(X_{i}) T,\\ \qquad\qquad\,\text{if}~|X_{r}| > T,~|X_{i}| > T. \end{array}\right. \end{array} $$

(23)

Using the truncated isotropic α-stable input, an achievable rate of the amplitude and fractional moment constrained AIαSN channel is obtained by evaluating the mutual information I(y;X_T), where y is the output of the channel in (17). In fact, using a similar argument to that for the power constrained Gaussian noise channel [27], it is straightforward to show that all rates R<I(y;X_T) are achievable by using a codebook consisting of 2^nR codewords Wⁿ(1),…,Wⁿ(2^nR) with W_i(w), i=1,2,…,n, w=1,2,…,2^nR independent truncated isotropic α-stable random variables.

Unfortunately, truncated isotropic α-stable inputs do not lead to a closed-form mutual information for the channel in (17). In fact, only scaling laws for the capacity have been recently derived for real-valued inputs [28, 29]. In order to characterize the achievable rates in the presence of dynamic interference, we therefore approximate I(X_T;y) by the lower bound in Theorem 4.

To verify that this approximation is indeed accurate, we numerically compute the mutual information I(X_T;y) and compare it with the result in Theorem 4 in Figs. 4 and 5 for α=1.7 and α=1.3, respectively. Observe that for a sufficiently large truncation level, the approximation based on Theorem 4 is in good agreement with I(X_T;y). Moreover, the achievable rate is significantly larger than the case of a Gaussian input. This suggests that Gaussian signaling is not necessarily desirable in the presence of dynamic interference with the constraints in (18).

Fig. 4

Achievable rates for an AIαSN channel with α=1.7, σ_N=0.1 and a constraint $\mathbb {E}[|X|] \leq 1$. The curves correspond to a Gaussian input, an isotropic α-stable input and a truncated isotropic α-stable input (defined in (23))

Fig. 5

Achievable rates for an AIαSN channel with α=1.3, σ_N=0.5 and a constraint $\mathbb {E}[|X|] \leq 1$. The curves correspond to a Gaussian input, an isotropic α-stable input and a truncated isotropic α-stable input (defined in (23))

In light of the validity of the achievable rate approximation based on Theorem 4, we now turn to characterizing the effect of device density in large-scale networks with dynamic interference.

4.1 Area spectral efficiency analysis

In this section, we investigate the effect of device density λ on network performance. In particular, we study the area spectral efficiency, which is defined as the expected total rate per square meter. We focus on the setting where each device is associated to its own access point and the other devices introduce interference.

The area spectral efficiency captures the tradeoff between the distance between each device and its base station as well as the increasing interference as the device density increases. Formally, let A₁⊂A₂⊂⋯ be a sequence of discs such that Area(A_n)→∞ as n→∞. The area spectral efficiency is then given by

$$\begin{array}{*{20}l} \zeta = {\lim}_{n\rightarrow \infty} \frac{1}{\text{Area}(A_{n})} \mathbb{E}\left[\sum\limits_{i \in \Phi(A_{n})} R_{i}(A_{n})\right], \end{array} $$

(24)

where Φ(A_n) is the PPP Φ restricted to the disc A_n and R_i(A_n) corresponds to the achievable rate with a truncated isotropic α-stable input and devices in Φ(A_n).

The area spectral efficiency for this model is given in the following theorem.

Theorem 5

The area spectral efficiency with device locations governed by a homogeneous PPP Φ with rate λ and truncated isotropic α-stable inputs is given by

$$\begin{array}{*{20}l} \zeta = \lambda \mathbb{E}_{r_{d},h_{d}}[R_{i}], \end{array} $$

(25)

where R_i is the achievable rate of the AIαSN channel with a truncated isotropic α-stable input and devices in Φ.

Proof

See Section 7. □

As observed in Section 4, R_i=I(y_i;X_T) does not have a closed-form expression which makes characterizing the area spectral efficiency ζ challenging. To proceed, we exploit the approximation of I(y_i;X_T) based on Theorem 4. In particular, we obtain the following approximation for the area spectral efficiency:

$$\begin{array}{*{20}l} \zeta &\approx \frac{\lambda\eta}{4}\\ &\quad \times \mathbb{E}_{r_{d},h_{d}}\left[\log\left(1 + \frac{\left(\sqrt{2|r_{d}h_{d}|^{2}}\left(\frac{c}{C(r,\frac{4}{\eta})}\right)^{\frac{1}{r}}\right)^{\frac{4}{\eta}}}{\pi\lambda C_{\frac{\eta}{4}}^{-1}\mathbb{E}\left[\left|\text{Re}(h_{k}x_{k})\right|^{\frac{4}{\eta}}\right]}\right)\right] \end{array} $$

(26)

which is tight when the truncation level for the input T is sufficiently large. Further insight into the approximation error can be obtained numerically, such as in Figs. 4 and 5.

The expression in (26) provides insight into the effect of the device density λ. In particular, consider a function of the form

$$\begin{array}{*{20}l} f(\lambda) = \lambda \log\left(1 + \frac{1}{\lambda}\right), \end{array} $$

(27)

which captures the dependence of the spatial rate density approximation in (26) on the device density λ. Since we are interested in studying the impact of device density, to apply Leibniz’s rule in (26). it is sufficient to consider (27). Evaluating the derivative yields $f^{\prime }(\lambda) = \log \left (1 + \frac {1}{\lambda }\right) - \frac {1}{1 + \lambda }$.

Since $\log x > 1 - \frac {1}{x}$ for x>1, it follows that $\log \left (1 + \frac {1}{\lambda }\right) > \frac {1}{1 + \lambda }$ and hence for λ>0, f^′(λ)>0. This implies that the area spectral efficiency ζ is an increasing function of the density λ (illustrated in Fig. 6). We therefore conclude that dense networks maximize the area spectral efficiency. We remark that dense networks are also desirable for slowly varying active interferer sets [30]. This implies that although the optimal signaling strategy for each link is no longer Gaussian, the basic network structure is the same both for dynamic interference and interference arising from a slowly varying active interferer set.

Fig. 6

Plot of f(λ) in (27)

5 Discussion

In Section 3, we established that the interference is α-stable in networks with SCMA and fast-varying active transmitter sets. Moreover, in the special case of disjoint random SCMA codebooks, the interference vector on bands within a disjoint set is sub-Gaussian α-stable while bands in different disjoint sets are independent. A natural question is therefore how the dependence structure for general SCMA codebooks can be characterized. One approach to resolving this problem is to exploit a copula representation of the dependence structure, which has been proposed in [31].

In particular, let $\phantom {\dot {i}\!}F_{\mathbf {Z}_{2K}}$ be the joint distribution of the real interference random vector Z_2K obtained by stacking real and imaginary parts as detailed in Section 3. We seek a simple and general characterization of the joint distribution. To this end, let C_Z be a copula, which is a function [0,1]^2K→[0,1]. Since the elements of Z_2k are α-stable random variables, it follows that the cumulative distribution function (CDF) of each element is continuous, denoted by F. As a consequence, there exists a unique copula C_Z such that the joint distribution of Z_2k can be written as

$$\begin{array}{*{20}l} &F_{\mathbf{Z}_{2K}}(z_{1,r},z_{1,i},\ldots,z_{K,r},z_{K,i}) \\ &= C_{Z}(F(z_{1,r}),F(z_{1,i})\ldots,F(z_{K,r}),F(z_{K,i})) \end{array} $$

(28)

by Sklar’s theorem [32].

Note that the copula provides a representation of the dependence structure, independent of the marginal distributions. That is, random vectors can be characterized in terms of the marginal distributions and the copula. In particular, the joint distribution of Z_2K can be characterized by the univariate α-stable distributions of each z_k,r and z_k,i and the copula C_Z. In this case, the probability distribution density is given by:

$$\begin{array}{*{20}l} &f_{\mathbf{Z}_{2K}}(z_{1,r},z_{1,i},\ldots,z_{K,r},z_{K,i}) \\ &= c_{Z}\left(F_{1,r}(z_{1,r}),F_{1,i}(z_{1,i})\ldots,F_{K,r}(z_{K,r}),F_{K,i}(z_{K,i})\right)\\ &~\prod\limits^{K}_{k=1}f_{k,r}(z_{k,r})f_{k,i}(z_{k,i}) \end{array} $$

(29)

where c_Z is the density function of the copula C_Z and has such a form that $c_{Z}(u_{1},\ldots,u_{n})=\frac {{\partial }^{n} C_{Z}(u_{1},\ldots,u_{n})}{\partial u_{1},\ldots,\partial u_{n}}$

This divides the density into two components, the copula component and the independent component consisting of the marginal distributions, which provides a basis for optimizing receiver structures and other system components. In particular, we desire a tractable copula C for which detection rules can be derived.

As an example, consider the standard Archimedean copula

$$\begin{array}{*{20}l} C_{Z}(u_{1},\ldots,u_{n}) = \phi^{-1}\left(\sum\limits_{i=1}^{n} \phi(u_{i})\right) \end{array} $$

(30)

where the generator ϕ:[0,1]→[0,∞] is a continuous and completely monotonic function such that ϕ(1)=0. In this case, the density function is given by:

$$\begin{array}{*{20}l} c_{Z}(u_{1},\ldots,u_{n}) = \psi^{(n)}\left(\sum\limits_{i=1}^{n} \phi(u_{i})\right)\prod\limits^{n}_{i=1}\phi^{\prime}(u_{i}). \end{array} $$

(31)

where ψ=ϕ⁻¹ is the inverse generator.

This representation of the dependence structure for the interference forms a basis for maximum likelihood decoding schemes at the receiver, which are otherwise intractable. Indeed, the log-likelihood ratio (LLR) Λ(Z_2K) for BPSK transmissions and additive vector symmetric α-stable noise can be written as [33, 34]:

$$\begin{array}{*{20}l} &\Lambda(\mathbf{Z}_{2K})\\ &= \log \frac{f_{\mathbf{Z}_{2K}}\left(z_{1,r}-1,z_{1,i}-1,\ldots,z_{K,r}-1,z_{K,i}- 1\right)}{f_{\mathbf{Z}_{2K}}\left(z_{1,r}+1,z_{1,i}+1,\ldots,z_{K,r}+1,z_{K,i}+1\right)} \\ &= \sum_{k=1}^{K} \log \frac{f(z_{k,r}-1)f(z_{k,i}-1)}{f(z_{k,r}+1)f(z_{k,i}+1)}\\ &\quad+ \log \frac{c_{Z}\left(F(z_{1,r}-1),\ldots,F(z_{K,i}- 1)\right)}{c_{Z}\left(F(z_{1,r}+1),\ldots,F(z_{K,i}+1)\right)}\\ &= \Lambda_{\bot}(\mathbf{Z}_{2K}) +\Lambda_{c}(\mathbf{Z}_{2K}) \end{array} $$

(32)

where Λ_⊥(Z_2K) is the independent component of the LLR arising from the marginal distributions and Λ_c(I_2K) is the component of the LLR depending on the copula and represents the dependence structure. This representation provides a clear separation between the independent and the dependent components, which may be useful in the design of efficient receivers.

However, there are still some challenging issues. As shown in (30), Archimedean copulæ assume the same dependence structure of each pair (u_k,u_j). On the other hand, the dependence of the pair (F(z_k,r),F(z_k,i)) arises from the sub-Gaussian α-stable distribution by Theorem 2 and in general will be different from the distribution of the pairs (F(z_k,r),F(z_j,r)),k≠j or (F(z_k,r),F(z_j,i)),k≠j. Hence, even if it allows for more tractable expressions [33, 34], the Archimedean family may not be an appropriate choice. It remains an open question to select useful general copula representations for dynamic interence with dynamic interference and SCMA codebooks.

6 Proof of Proposition 2

The proof follows a similar argument as for isotropic complex α-stable random variables ([22], Theorem 2.6.3). We first show that if Z is a d-dimensional sub-Gaussian α-stable random vector, then UZ is also sub-Gaussian α-stable. Since Z is sub-Gaussian α-stable, then it admits a scale mixture representation A^1/2G, where $\mathbf {G} \sim \mathcal {N}\left (0,\sigma ^{2} \mathbf {I}\right)$. Therefore, we can write UZ=A^1/2UG, which implies that UZ is sub-Gaussian α-stable if $\mathbf {U}\mathbf {G} \sim \mathcal {N}\left (0,\sigma _{U}^{2}\mathbf {I}\right)$ for some σ_U>0. This holds since the covariance matrix of UG is given by $\Sigma _{\mathbf {U}} = \mathbb {E}\left [\mathbf {U}\mathbf {G}\mathbf {G}^{T}\mathbf {U}^{T}\right ] = \sigma ^{2}\mathbf {I}$ by the orthogonality of U.

We now show that $\mathbf {Z} \overset {d}{=} \mathbf {U}\mathbf {Z}$ for all $\mathbf {U} \in \mathcal {O}(d)$ implies that Z is sub-Gaussian α-stable. The characteristic function of Z is given by:

$$\begin{array}{*{20}l} \mathbb{E}\left[e^{i\boldsymbol{\theta}\cdot \mathbf{Z}}\right] &= \exp\left(-{\int\nolimits}_{\mathbb{S}^{d-1}} |\boldsymbol{\theta} \cdot \mathbf{s}|^{\alpha}\Gamma(\mathrm{d}\mathbf{s})\right)\\ &\overset{(a)}{=} \exp\left(-{\int\nolimits}_{\mathbb{S}^{d-1}} |\mathbf{U}\boldsymbol{\theta}\cdot \mathbf{s}|^{\alpha}\Gamma(\mathrm{d}\mathbf{s})\right)\\ &= \exp\left(-{\int\nolimits}_{\mathbb{S}^{d-1}} |\boldsymbol{\theta} \cdot \mathbf{t}|^{\alpha} \Gamma_{\mathbf{U}}(\mathrm{d}\mathbf{t})\right), \end{array} $$

(33)

where (a) holds since orthogonal transformations preserve the magnitude of the inner product in $\mathbb {R}^{d}$. It then follows that for any Borel set $B \subset \mathbb {R}^{d}$, we have Γ_U(B)=Γ(UB) by the uniqueness of the spectral measure. Since $\mathbf {U} \in \mathcal {O}(d)$ is arbitrary, it follows that Γ_U=Γ for all $\mathbf {U} \in \mathcal {O}(d)$. As such, Γ is uniform on $\mathbb {S}^{d-1}$, which by ([22], Theorem 2.5.5) implies that Z is sub-Gaussian α-stable.

7 Proof of Theorem 5

In order to compute the area spectral efficiency ζ, observe that for a given A_n, the random variables R_i(A_n) are identically distributed (but not independent) since the distances r_d are independent and identically distributed, and the locations of the devices are independently and uniformly distributed in A_n conditioned on the number of devices N(A_n) in A_n [25]. By the strong law of large numbers for PPPs [35], $\frac {N(A_{n})}{\text {Area}(A_{n})} \cong \lambda ~\mathrm {a.s.}$ as n→∞. Let ε>0, it then follows that

$$\begin{array}{*{20}l} \zeta &= {\lim}_{n \rightarrow \infty} \frac{1}{\text{Area}(A_{n})} \mathbb{E}\left[\sum\limits_{i=1}^{\text{Area}(A_{n}) \frac{N(A_{n})}{\text{Area}(A_{n})}} R_{i}(A_{n})\right]\\ &= {\lim}_{n \rightarrow \infty} \frac{1}{\text{Area}(A_{n})}\\ &\quad \times\left(\mathbb{E}\left[\sum\limits_{i=1}^{\lfloor \text{Area}(A_{n}) \lambda_{1} \rfloor} R_{i}(A_{n})|\lambda_{1} \in [\lambda - \epsilon, \lambda + \epsilon]\right]\right.\\ &\quad \left. \times \text{Pr}(\lambda_{1} \in [\lambda - \epsilon,\lambda + \epsilon])\right.\\ &\quad \left. + \mathbb{E}\left[\sum\limits_{i=1}^{\lfloor \text{Area}(A_{n}) \lambda_{1} \rfloor} R_{i}(A_{n})|\lambda_{1} \not\in [\lambda - \epsilon, \lambda + \epsilon]\right]\right.\\ &\quad \left. \times \text{Pr}(\lambda_{1} \not\in [\lambda - \epsilon,\lambda + \epsilon])\right) \end{array} $$

(34)

A direct consequence of the strong law of large numbers of PPPs is that as n→∞, Pr(λ₁∈[λ−ε,λ+ε])→1.

Next, for sufficiently large n select A_n such that λArea(A_n) is an integer and ε>0 sufficiently small such that λArea(A_n) is the only integer in [λ−ε,λ+ε]. It then follows that

$$\begin{array}{*{20}l} \zeta &= {\lim}_{n \rightarrow \infty} \frac{1}{\text{Area}(A_{n})} \text{Area}(A_{n}) \lambda \mathbb{E}[R_{i}(A_{n})]\\ &= \lambda {\lim}_{n \rightarrow \infty} \mathbb{E}[R_{i}(A_{n})]. \end{array} $$

(35)

To evaluate ${\lim }_{n \rightarrow \infty } \mathbb {E}[R_{i}(A_{n})]$, let $y_{i,A_{n}}$ be the received signal at the access point served by the i-th device in Φ(A_n). For fixed r_d,h_d, $\phantom {\dot {i}\!}R_{i}(A_{n}) = I(y_{i,A_{n}};X_{T})$. From the LePage series representation of the interference in Theorem 1, it follows that the signal received by the access point served by the i-th device in Φ satisfies $y_{i} \overset {(d)}{=} r_{d}^{-\frac {\eta }{2}}h_{d}X_{T} + I,~\mathrm {a.s.}$ as n→∞.

Since the conditions in ([36], Theorem 1) hold, it follows that for fixed r_d,h_d we have $I(y_{i,A_{n}};X_{T}) \rightarrow I(y_{i};X_{T})$ as n→∞. As R_i(A_n) is positive and R_i(A_n)→R_i as n→∞, we then obtain the desired result.

8 Conclusions

An important feature of wireless communication networks supporting the IoT is that devices can transmit very small amounts of data leading to dynamic interference. In this paper, we have studied the problem of dynamic interference when devices exploit the NOMA strategy SCMA. In particular, we established that the interference is characterized by a multivariate α-stable distribution. This work also considered the impact of α-stable interference on network design. We have derived achievable rates for a class of NOMA networks and shown that the area spectral efficiency increases with the density of devices.

An avenue of future research is the study of dynamic interference in networks using SCMA codebooks that have reduced decoding complexity. The design of such codebooks motivates the study of a general class of vector additive α-stable noise channels for which fundamental limits on data rates are not known.