1 Introduction

With the deployment of massive antennas and the utilization of higher-frequency spectrum like millimeter wave, the next-generation wireless networks are envisioned to provide higher service quality for communications as well as sensing functionality to support many emerging applications like smart manufacturing, environment monitoring and intelligent transportation, etc. [1]. To achieve this target, the integrated sensing and communication (ISAC) technique has been recognized as a key enabler and gained paramount interest from both academia and industry [1, 2].

Contrary to the traditional systems where the communication and radar sensing are usually designed independently and deployed separately, ISAC aims to realize the dual functionality in a unified system by the sharing of frequency, hardware and the joint signal processing design [3,4,5,6]. In ISAC, the implementation of digital processing technology on the radar sensing and communication facilitates the sharing of hardware components, making it possible to build a unified and simple structure with reduced device size and energy consumption. Moreover, by co-designing the waveform, the dual functionality can be operated simultaneously and achieve a higher spectral and time efficiency. The paper [7] considers the employment of the ISAC technique for assisting orthogonal time frequency space (OTFS) transmission in both uplink and downlink vehicular communication systems. Authors in [8] propose to jointly design the dual-functional transmit signals occupying several subcarriers to realize multi-user OFDM communications and detect one moving target in the presence of clutters. Beyond the sharing of time-spectral resources, the interplay between communication information and sensing information in ISAC will be beneficial to both functionalities [9]. For example, the information distributed on a communication network can be used in radar sensing applications to increase detection probability and estimation precision, while the radar sensing can assist the proactive resource management in wireless communications.

In this work, we consider the multi-input multi-output (MIMO) ISAC waveform design in wireless multi-user (MU) networks and investigate the joint information and sensing beamforming optimization problem to ensure high-quality dual functionalities in both communication and sensing. The beamforming designs for mitigating the interference between a communication system and a coexisting radar system have been widely studied [10,11,12,13,14,15,16]. While these designs are effective to control the interference, the beamforming designs are separate in two systems and they often need extra centralized entities to exchange knowledge such as the interference channel information and radar waveform parameters between the two systems, causing high system complexity and increased energy consumption [17]. ISAC, which brings the radar and communication systems together, can avoid this issue and enable the dual functions by proper time frequency resource allocation [6, 18,19,20]. For instance, the work [18] studied a time-division-based ISAC system to implement a spectrum-sharing dual-function signaling. While the probing capabilities of orthogonal frequency division multiplexing (OFDM) waveforms were studied in [3, 6, 19, 20], though the hardware is shared, the integration between sensing and communication in most of these works [18, 19] is still weak as the dual functionalities operate in different time slots or frequency bands. Besides, some of these existing schemes [6, 20] are based on a single directional antenna and thereby suffer from a notable degradation in signal-to-noise-ratio (SNR) when the communication receivers are not physically located within the radar lobe. As a result, they are not able to illuminate multiple targets and communicate with multiple users simultaneously.

While the aforementioned works did not fully integrate the sensing and communication, the recent works [3, 17, 21,22,23,24,25] stepped further into a stronger integration via considering the unified waveform design in the context of MU-MIMO. In paper [22], the authors introduced an approach to dual-function radar communications using waveform diversity in tandem with sidelobe control by designing two transmit beamforming weight vectors. The paper [26] proposed a quadrature amplitude modulation (QAM)-based dual-function radar communications (DFRC) strategy which exploits sidelobe control and waveform diversity to transmit communication information. However, both of these two papers only considered limited desired direction set. It will limit the performance of sensing when the targets located out of the direction set. The paper [23] proposed an antenna-selection-based signaling strategy for DFRC systems to embed communication symbols into transmit array configurations. But the usage of transmit antennas for the dual function individually prevents the system from making use of the whole antennas, limiting both the performance of sensing and communication. Authors in [27] tackled the joint design of the DFRC transmitter and of the radar, and user receivers and formulate a general resource allocation problem. But both radar-centric and communication-centric designs cannot achieve scalable trade-off between the two functions. In [25], a joint sensing and communication model is considered and the modulation symbol is precoded by the communication beamforming vector and the sensing beamforming vector to sense the target while serving the communication user. In [17], the authors designed the array probing signal to match the desired radar transmit beampattern and minimize the interference power at communication receivers. In the work [21], a transmit beamforming design was proposed wherein the communication waveform was also utilized as a radar sensing waveform. In these works, the communication waveform is also used for target sensing, and thus, the available degrees of freedom (DoF) for sensing is equal to the number of communication users [3]. When the number of users is small, it incurs a loss of DoF of sensing and may lead to distortion of radar beampattern. To address this issue, the authors of [3] employed an additional sensing waveform and proposed to jointly optimize both communication and sensing waveforms, which not only greatly improves the design flexibility but also makes fully use of the DoF of antenna arrays. Instead of minimizing the mismatch between a desired sensing waveform, the work [24] introduced the Cramer–Rao bound (CRB) as the measure of sensing performance and used it in the ISAC joint waveform design. A CRB-minimization problem was formulated under per-user SINR constraints, and the authors demonstrated that the proposed beamforming design could achieve a better sensing performance than its counterparts based on the beampattern matching [3].

In this paper, we propose a framework for ISAC beamforming in a multi-user and multi-target multi-input multi-output (MUMT-MIMO) network, with a specific emphasis on optimization of the target estimation performance measured by the CRB for unbiased estimators, subject to the communication sum-rate constraint as well as the transmit power budget limit. Specifically, in the MUMT-MIMO network, we consider two connected base stations (BSs) collaborating in a bi-static sensing mode for the target sensing. At the same time, the transmit BS also sends information data streams to communication users. Compared with the mono-static sensing mode in [3, 24, 28] that requires full-duplexing and suffers from self-interference, the bi-static sensing avoids this problem as the transmission of sensing signals and the reception of reflected signals are separate at different BSs. In our formulated beamforming design problem, the CRB of target parameters is minimized to improve the sensing performance. Different from the work [24] that considers minimizing the CRB of one subset of parameters (angles or reflection coefficients) of a single target only and [29, 30] that emphasize the localization accuracy by CRB of locations of the targets, we consider multiple targets and minimize the CRB of all the parameters including angle of arrival (AoA), angle of departure (AoD) and reflection coefficient simultaneously in the formulation. By doing that, the designed beamforming can achieve a better sensing performance [31]. In addition, unlike the individual SINR constraint for each user equipment (UE) in [3], the sum-rate constraint is considered in our design to guarantee the network throughput performance.

While the resultant joint information and sensing beamforming problem is highly non-convex and challenging to solve, we first devise an effective algorithm by the weighted mean square error minimization (WMMSE) [32] and semidefinite relaxation (SDR) techniques. Although the WMMSE–SDR method can converge properly and one can show that the SDR is tight without performance loss, its computational complexity can be high when the numbers of targets and transmit antennas are large. To alleviate the computational burden of the WMMSE–SDR algorithm, we further develop a low-complexity algorithm for the joint beamforming design by leveraging fractional programming (FP) [33] and first-order algorithms for min–max problems (e.g., the smoothed gradient descent–ascent (SGDA) [34]). For example, in paper [35, 36], the authors make use of the fractional programming transformation to transform the non-convex sum-rate objective function into a convex form with introduce auxiliary variables and both of them specialize in single-ratio problems. We are the first to apply the quadratic transform for FP to solve the CRB-minimization problem. The main contributions of our work are summarized as follows.

  • We formulate a new joint ISAC beamforming design problem in a multi-user and multi-target MIMO network for simultaneous target sensing and communications. The formulated problem considers the comprehensive optimization of the CRB of all the parameters of multiple targets while guaranteeing the network throughput (sum rate) for communication users.

  • We devise an effective WMMSE–SDR algorithm for handling the joint beamforming design problem and show that SDR is in fact tight and incurs no performance loss.

  • By leveraging the tightness of SDR and the FP techniques, we further show that the joint beamforming problem can be equivalently reformulated as a min–max–min problem with simple constraints. This allows us to combine the block coordinate descent (BCD) method and the SGDA algorithm to devise a low-complexity FP-SGDA algorithm. It is shown that the FP-SGDA algorithm can achieve almost the same performance as the WMMSE–SDR algorithm but has a significantly reduced complexity.

  • We evaluate the proposed algorithms by extensive simulations. The numerical results reveal that the minimization of CRB of all parameters achieves a better sensing performance than that of partial parameters only. In addition, it demonstrates that our proposed FP-SGDA algorithm solves the beamforming problem efficiently with greatly reduced computation time.

The remainder of this paper is organized as follows. In Sect. 2, we introduce the system model and formulate the beamforming design problem by deriving the CRB for radar sensing and sum rate for communication. Sections 3 and 4 elaborate on the design of WMMSE–SDR and FP-SGDA to solve the formulated problem. Simulation results are presented in Sect. 5. Finally, Sect. 6 provides concluding remarks.

Notations Column vectors and matrices are, respectively, written in boldfaced lowercase and uppercase letters, e.g., \({\textbf{a}}\) and \({\textbf{A}}\). The superscripts \((\cdot )^{\mathrm{T}}\), \(\bar{(\cdot )}\) and \((\cdot )^{\mathrm{H}}\) represent the transpose, conjugate and Hermitian transpose, respectively. \({\textbf{I}}_{K}\) is the \(K \times K\) identity matrix; \(\Vert {\textbf{a}}\Vert\) denotes the Euclidean norm of vector \({\textbf{a}}\), and \(||\cdot ||_{F}\) denotes the Frobenius norm. \(\odot\) denotes the Hadamard (element-wise) matrix product. \(\Im (\cdot )\) and \(\Re (\cdot )\) represent the imaginary and real part of a complex value, respectively. \(\{a_{i}\}\) denotes the set of all \(a_{i}\) with subscripts i covering all the admissible integers.

2 Dual-functional system model and problem formulation

In this section, we build the signal and channel model for the MIMO communication and sensing systems followed by formulating the joint information and sensing signal beamforming design problem.

2.1 Signal model

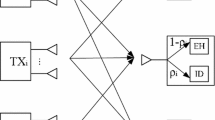
We consider a dual-functional MUMT-MIMO ISAC system in Fig. 1a.Footnote 1 The transmit BS, which is equipped with \(N_{t}\) transmit antennas, sends communication signals to \(N_{u}\) single-antenna UEs, while transmits the probing signals to the L targets. At the same time, the sensing BS with \(N_{s}\) receiving antennas receives the signals reflected by these targets and performs sensing operation collaboratively with the transmit BS in a bi-static mode. Without loss of generality, we assume \(N_{u} < N_{s} \le N_{t}\). For both transmit BS and sensing BS, we assume a uniform linear array (ULA) with half-wavelength separation, i.e., \(d=\lambda /2\) with \(\lambda = c/f_{\mathrm{c}}\), c the speed of light, and \(f_{\mathrm{c}}\) the carrier frequency.

Fig. 1
figure 1

Illustration of the system and transmitter model

Full size image

As shown in Fig. 1b, at the transmit BS, both the communication and sensing functionalities operate simultaneously by joint beamforming; each data symbol \(s_{i} \in {\mathbb{C}}\) for the i-th communication UE and the sensing signal \({\textbf{s}}_{s} \in {\mathbb{C}}^{N_{t} \times 1}\) are first precoded by a digital precoding vector \({\textbf{w}}_{i} \in {\mathbb{C}}^{N_{t}}\) and a digital precoding matrix \({\textbf{W}}_{s} \in {\mathbb{C}}^{N_{t}\times N_{t}}\), respectively. The corresponding transmitted baseband signal \({\textbf{x}}\in {\mathbb{C}}^{N_{t}}\) integrated by \(s_{i}\) and \({\textbf{s}}_{s}\) is a weighted sum of communication symbols and radar waveforms given by

$${\textbf{x}}_{t} = \sum _{i = 1}^{ N_{u}}{\textbf{w}}_{i}s_{i} + {\textbf{W}}_{s}{\textbf{s}}_{s}.$$
(1)

Without loss of generality, the transmit signals satisfy the following assumptions:

  1. 1.

    Both the signals \(s_{i}\) for communication and \({\textbf{s}}_{s}\) for sensing are zero-mean and wide-sense stationary stochastic process;

  2. 2.

    The communication signals intended to different users are uncorrelated, namely \({\mathbb{E}}\{s_{i}s_{j}\} = 0\) for \(i\ne j\), and \({\mathbb{E}}\{|s_{i}|^{2}\} = 1\);

  3. 3.

    The sensing signals sent from different antennas are uncorrelated with each other, i.e., \({\mathbb{E}}\{{\textbf{s}}_{s}{\textbf{s}}_{s}^{\mathrm{H}}\} = {\textbf{I}}_{N_{t}}\). In practice, the corresponding waveform can be generated by pseudorandom coding [37,38,39,40,41].

  4. 4.

    Both \(s_{i}\) and \({\textbf{s}}_{s}\) are known at the transmit BS and the sensing BS. For example, the information can be exchanged among BSs via an fiber-optic backhaul.

2.2 Sensing channel model

As shown in Fig. 1a, since the transmit BS and sensing BS work in a bi-static mode of passive sensing, it means that the transmitter and receiver are located in different places. Therefore, the AoD and AoA are different. Denote \(\theta _{\ell }, \phi _{\ell }\) as the AoD and AoA of the \(\ell\)-th target to the transmit BS and the sensing BS, respectively, \(\ell = 1, \dots , L\). Then, the transmit array response vector and the receive array response vector can be expressed as

$$\begin{aligned} {\textbf{v}}(\theta _{\ell })&= [1, e^{j\pi \sin (\theta _{\ell })},\ldots ,e^{j\pi (N_{t}-1)\sin (\theta _{\ell })}]^{\mathrm{T}},\\ {\textbf{a}}(\phi _{\ell })&= [1, e^{j\pi \sin (\phi _{\ell })},\ldots ,e^{j\pi (N_{t}-1)\sin (\phi _{\ell })}]^{\mathrm{T}}, \end{aligned}$$
(2)

respectively. Correspondingly, the channel response matrix from the transmit BS to the sensing BS \({\textbf{G}}\in {\mathbb{C}}^{N_{s}\times N_{t}}\) can be modeled as

$$\begin{aligned} {\textbf{G}}= \sum _{\ell =1}^{L}b_{\ell }{\textbf{a}}(\phi _{\ell }){\textbf{v}}(\theta _{\ell })^{{\mathrm{T}}}, \end{aligned}$$
(3)

where \(b_{\ell }\in {\mathbb{C}}\) is the reflection coefficient accounting for the path loss, including the distance information and the radar cross section (RCS) of the \(\ell\)-th target. Since the sensing task is typically accomplished within a few milliseconds [42], the sensing channel (3) is assumed to be quasi-static, and the parameters \(\{\phi _{\ell }, \theta _{\ell }, b_{\ell }\}_{\ell =1}^{L}\) maintain unchanged during the sensing period. Meanwhile, it is assumed that the channel state information (CSI) of the downlink (DL) communication channel from transmit BS to UE i \({\textbf{h}}_{i} \in {\mathbb{C}}^{N_{t}}, i = 1, \ldots , N_{u}\) is available to the transmit BS.

2.3 Problem formulation

To facilitate the dual functionalities of the DL communication and the target sensing, the beamformer \(\{{\textbf{w}}_{i}\}\) and \({\textbf{W}}_{s}\) are jointly designed in the ISAC system. In this subsection, the performance metrics for the communication as well as the target sensing are described firstly, based on which the joint beamforming optimization problem is formulated.

2.3.1 Information throughput

With the transmitted signal \({\textbf{x}}_{t} \in {\mathbb{C}}^{N_{t}}\) in (1), the received signal \(y_{i}\in {\mathbb{C}}\) at UE i can be written as

$$\begin{aligned} y_{i}&={\textbf{h}}_{i}^{\mathrm{H}}{\textbf{x}}_{t} + n_{i},\\&= {\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}s_{i} + \sum _{j\ne i}^{N_{u}}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{j}s_{j} + {\textbf{h}}_{i}^{\mathrm{H}} {\textbf{W}}_{s}{\textbf{s}}_{s} + n_{i},\end{aligned}$$
(4)

in which \(n_{i} \sim {\mathcal{C}}{\mathcal{N}}(0, \sigma ^{2}_{i})\) is the additive white Gaussian noise (AWGN) at UE i. In (4), the first term is the desired signal for the i-th communication UE, while the second term and the third term are the interference caused by the signals to the other UEs and the sensing signals, respectively. To this end, the signal-to-interference plus noise ratio (SINR) at the i-th communication UE can be expressed as

$$\begin{aligned} {\textsf{SINR}}_{i} = \frac{|{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}|^{2}}{\sum _{j\ne i}^{N_{u}}|{\textbf{h}}^{\mathrm{H}}_{i}{\textbf{w}}_{j}|^{2} + |{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{R}}_{s}{\textbf{h}}_{i}| + \sigma _{i}^{2}}, \end{aligned}$$
(5)

where \({\textbf{R}}_{s} = {\textbf{W}}_{s}{\textbf{W}}_{s}^{\mathrm{H}}\) denotes the sensing covariance matrix. The overall throughput (sum rate) of the DL communication in the network is

$$\sum _{i=1}^{N_{u}}r_{i} =\sum _{i=1}^{N_{u}}\log \left( 1 + {\textsf{SINR}}_{i}\right) .$$
(6)

2.3.2 Sensing CRB

Similar to (4), the reflected signal received at the sensing BS is

$${\textbf{y}}_{s} ={\textbf{G}}\left( {\textbf{W}}_{s}{\textbf{s}}_{s}+ \sum _{i=1}^{N_{u}}{\textbf{w}}_{i}s_{i}\right) + {\textbf{n}}_{s},$$
(7)

with \({\textbf{n}}_{s} \sim {\mathcal{C}}{\mathcal{N}}({\textbf{0}}, \sigma ^{2}_{s} {\textbf{I}}_{N_{s}})\) being the AWGN. Note here both the sensing signal \({\textbf{s}}_{s}\) and the communication signal \({\textbf{s}}_{i}\) can be used for sensing since they are known by the sensing BS.

Combining (3) and (7), the received signal \({\textbf{y}}_{s}\) can be written as

$$\begin{aligned} {\textbf{y}}_{s} = {\textbf{A}}{\textbf{B}}{\textbf{V}}^{\mathrm{T}} \left( {\textbf{W}}_{s}{\textbf{s}}_{s}+ \sum _{i=1}^{N_{u}}{\textbf{w}}_{i}s_{i}\right) + {\textbf{n}}_{s} \end{aligned}$$
(8)

where

$$\begin{aligned} {\textbf{A}}&= {\textbf{A}}({\varvec{\phi }}) = [{\textbf{a}}(\phi _{1}),\ldots ,{\textbf{a}}(\phi _{L})],\\ {\textbf{V}}&= {\textbf{V}}({\varvec{\theta }}) = [{\textbf{v}}(\theta _{1}),\ldots ,{\textbf{v}}(\theta _{L})],\\ {\varvec{\phi }}&= [\phi _{1},\ldots ,\phi _{L}],\\ {\varvec{\theta }}&= [\theta _{1},\ldots ,\theta _{L}],\\ {\textbf{b}}&= [b_{1},\ldots ,b_{L}]^{\mathrm{T}},\\ {\textbf{B}}&= {\text{diag}}({\textbf{b}}), \end{aligned}$$
(9)

and \({{\text{diag}}}({\textbf{b}})\) represents a diagonal matrix with \(b_{\ell }\) being its diagonal entries.

From the perspective of target sensing, the parameter estimation accuracy is of the main interest in the work, where we adopt the CRB to evaluate the performance of the target sensing for the beamforming design. The CRB represents the best performance of any unbiased estimators [43] and is widely applied to assess the sensing performance. As shown in [24], the CRB-minimization beamformers outperform other methods based on beampattern matching for target sensing. Denote the parameters of the targets as \({\varvec{\phi }}, {\varvec{\theta }}, {\textbf{b}}_{R}, {\textbf{b}}_{i}\), where \({\textbf{b}}_{R} = \Re ({\textbf{b}})\) and \({\textbf{b}}_{i} = \Im ({\textbf{b}})\). Given the received signal \({\varvec{y}}\) in (8), the Fisher information matrix (FIM) w.r.t. \({\varvec{\phi }}, {\varvec{\theta }}, {\textbf{b}}_{R}, {\textbf{b}}_{i}\) can be derived as

$$\begin{aligned}{\textbf{M}}= \frac{2}{\sigma ^{2}_{s}} \begin{bmatrix} \Re ({\textbf{M}}_{{\varvec{\phi }}{\varvec{\phi }}}) &{}\quad \Re ({\textbf{M}}_{{\varvec{\phi }}{\varvec{\theta }}}) &{}\quad \Re ({\textbf{M}}_{{\varvec{\phi }}{\textbf{b}}}) &{}\quad -\Im ({\textbf{M}}_{{\varvec{\phi }}{\textbf{b}}}) \\ \Re ^{\mathrm{T}}({\textbf{M}}_{{\varvec{\phi }}{\varvec{\theta }}}) &{}\quad \Re ({\textbf{M}}_{{\varvec{\theta }}{\varvec{\theta }}}) &{}\quad \Re ({\textbf{M}}_{{\varvec{\theta }}{\textbf{b}}}) &{}\quad -\Im ({\textbf{M}}_{{\varvec{\theta }}{\textbf{b}}}) \\ \Re ^{\mathrm{T}}({\textbf{M}}_{{\varvec{\phi }}{\textbf{b}}}) &{}\quad \Re ^{\mathrm{T}}({\textbf{M}}_{\theta {\textbf{b}}}) &{}\quad \Re ({\textbf{M}}_{{\textbf{b}}{\textbf{b}}}) &{}\quad -\Im ({\textbf{M}}_{{\textbf{b}}{\textbf{b}}})\\ -\Im ^{\mathrm{T}}({\textbf{M}}_{{\varvec{\phi }}{\textbf{b}}}) &{}\quad -\Im ^{\mathrm{T}}({\textbf{M}}_{{\varvec{\theta }}{\textbf{b}}}) &{}\quad -\Im ^{\mathrm{T}}({\textbf{M}}_{{\textbf{b}}{\textbf{b}}}) &{}\quad \Re ({\textbf{M}}_{{\textbf{b}}{\textbf{b}}}) \end{bmatrix}, \end{aligned}$$
(10)

where

$$\begin{aligned} {\textbf{M}}_{{\varvec{\phi }}{\varvec{\phi }}}&= ({\dot{{\textbf{A}}}}^{\mathrm{H}}{\dot{{\textbf{A}}}})\odot ({\bar{{\textbf{B}}}}{\textbf{V}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{V}}{\textbf{B}}), \end{aligned}$$
(11a)
$$\begin{aligned} {\textbf{M}}_{{\varvec{\phi }}{\varvec{\theta }}}&=({\dot{{\textbf{A}}}}^{\mathrm{H}}{\textbf{A}})\odot , ({\bar{{\textbf{B}}}}{\dot{{\textbf{V}}}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{V}}{\textbf{B}}), \end{aligned}$$
(11b)
$$\begin{aligned} {\textbf{M}}_{{\varvec{\phi }}{\textbf{b}}}&=({\dot{{\textbf{A}}}}^{\mathrm{H}}{\textbf{A}})\odot ({\textbf{V}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{V}}{\textbf{B}}), \end{aligned}$$
(11c)
$$\begin{aligned} {\textbf{M}}_{{\varvec{\theta }}{\varvec{\theta }}}&= ({\textbf{A}}^{\mathrm{H}}{\textbf{A}})\odot ({\bar{{\textbf{B}}}}{\dot{{\textbf{V}}}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\dot{{\textbf{V}}}}{\textbf{B}}), \end{aligned}$$
(11d)
$$\begin{aligned} {\textbf{M}}_{{\varvec{\theta }}{\textbf{b}}}&= ({\textbf{A}}^{\mathrm{H}}{\textbf{A}})\odot ({\textbf{V}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\dot{{\textbf{V}}}}{\textbf{B}}), \end{aligned}$$
(11e)
$$\begin{aligned} {\textbf{M}}_{{\textbf{b}}{\textbf{b}}}&=({\textbf{A}}^{\mathrm{H}}{\textbf{A}})\odot ({\textbf{V}}^{\mathrm{H}}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{V}}), \end{aligned}$$
(11f)
$$\begin{aligned} {\dot{{\textbf{A}}}}({\varvec{\phi }})&= \left[ \frac{\partial {\textbf{a}}(\phi _{1})}{\partial \phi _{1}},\ldots , \frac{\partial {\textbf{a}}(\phi _{L})}{\partial \phi _{L}}\right] , \end{aligned}$$
(11g)
$$\begin{aligned} {\dot{{\textbf{V}}}}({\varvec{\theta }})&= \left[ \frac{\partial {\textbf{v}}(\theta _{1})}{\partial \theta _{1}},\ldots , \frac{\partial {\textbf{v}}(\theta _{L})}{\partial \theta _{L}}\right] , \end{aligned}$$
(11h)

and

$$\begin{aligned} {\textbf{R}}_{{\textbf{x}}_{t}} = \sum _{i = 1}^{N_{u}}{\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}} + {\textbf{R}}_{s}. \end{aligned}$$
(12)

The details of the derivation of (10), (11), (12) are given in “Appendix 1.” Notice that \({\textbf{M}}\in {\mathbb{C}}^{4L \times 4L}\). Given \({\textbf{M}}\), the CRB matrix for the target sensing is given by \({\textbf{C}}= {\textbf{M}}^{-1}\).

Based on the sum-rate expression in (6) and the CRB matrix \({\textbf{C}}\) derived before, the joint information and sensing beamforming design problem to achieve the dual functionalities in the ISAC system can be formulated as

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s}\succeq 0 \end{array}}\, &{\text{Tr}}(\Lambda _{{\varvec{\alpha }}} {{\textbf{M}}^{-1}}) \end{aligned}$$
(13a)
$$\begin{aligned}{\text{s.t.}}\, &\sum _{i=1}^{N_{u}}r_{i} \ge r_{m}, \end{aligned}$$
(13b)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}\Vert {\textbf{w}}_{i}\Vert ^{2} + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{aligned}$$
(13c)

where \(\Lambda _{{\varvec{\alpha }}} = {\text{diag}}\{\alpha _{1},\ldots ,\alpha _{4L}\}\) is a diagonal matrix with \(\alpha _{\ell} , \ell =1,\ldots ,4L\), being the weights for different target parameters, and P is the maximum transmission power of the transmit BS. With defined weights \(\alpha _{\ell }, \ell = 1,\ldots ,4L\), sum rate \(r_{m}\) and the power P, problem (13) aims to improve the sensing performance via minimizing the trace of the weighted CRB matrix in (13a) while guaranteeing the DL communication performance of the network by imposing the sum-rate constraint in (13b). The constraint (13c) is to ensure the system to meet the total transmit power limit. It is necessary to point out that, compared with existing works [24, 31], our formulation in (13a) incorporates the CRB of all the sensing parameters instead of only parts of them. As demonstrated in [31], the minimization of CRB of more parameters could achieve a better accuracy for the parameter estimation, which will also be verified in Sect. 5.

While CRB is a function of \({\varvec{\phi }}, {\varvec{\theta }}, {\textbf{b}}_{R}, {\textbf{b}}_{i}\) as can be seen in (10), problem (13) can be interpreted as optimizing the beamformers \(\{{\textbf{w}}_{i}\}, {\textbf{W}}_{s}\) with respect to targets of interest with the potential values of \(\{b_{\ell }, \theta _{\ell }, \phi _{\ell }\}\). This is quite typical in the target tracking scenario where we wish to beamform toward an estimated/predicted direction to track the movement of the target [24, 31]. Thus, these parameters are assumed to be known and incorporated into the optimization.

Problem (13) is very challenging to solve because of the non-convexity of (13b) and \({\textbf{M}}^{-1}\) in (13a). What’s more, the high dimension of \({\textbf{M}}\) makes it unrealistic to give explicit expression of \({\textbf{M}}^{-1}\). In what follows, we address these challenges to solve problem (13) and develop two computationally efficient beamforming algorithms.

3 Proposed WMMSE–SDR algorithm

In this section, we tackle the intricate joint beamforming problem (13). The ingredients are to leverage the seminal WMMSE algorithm [32] to deal with the sum-rate constraint while using the SDR to overcome the non-convexity in the CRB function.

To elaborate this, firstly, note that by the epigraph form, we can write the objective of (13) as \(\sum _{\ell =1}^{4L} \alpha _{\ell} t_{\ell}\) and have additional constraints \({\textbf{e}}_{\ell} ^{\mathrm{T}} {\textbf{M}}^{-1} {\textbf{e}}_{\ell} \le t_{\ell} , \ell =1,\ldots ,4L,\) where \({\textbf{e}}_{\ell} \in {\mathbb{R}}^{4L}\) is the \(\ell\)-th column of the identity matrix \({\textbf{I}}_{4L}\), and \(\{t_{\ell} \}\) is introduced slack variables. Then, by applying the Schur complement [44], we can reformulate (13) into the following problem

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}\succeq 0 \end{array}, \{t_{\ell }\}}\, &\sum _{\ell =1}^{4L}\alpha _{\ell }t_{\ell } \end{aligned}$$
(14a)
$$\begin{aligned} \mathrm{s.t.}\, &\left[ \begin{array}{ll} {\textbf{M}}&{}\quad {\textbf{e}}_{\ell }\\ {\textbf{e}}_{\ell }^{\mathrm{T}} &{}\quad t_{\ell } \end{array}\right] \succeq 0,\quad \ell =1,\ldots ,4L, \end{aligned}$$
(14b)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}r_{i} \ge r_{m}, \end{aligned}$$
(14c)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}\Vert {\textbf{w}}_{i}\Vert ^{2} + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{aligned}$$
(14d)

As seen, we no longer deal with \({\textbf{M}}^{-1}\) in (14).

As mentioned before, another challenge for solving problem (14) is the non-convex sum-rate constraint (14c). Note that, unlike the SINR constraints considered in [24], directly application of SDR to constraint (14c) does not yield a tractable form. Instead, we exploit the relation between the rate expression and mean square error (MSE), following the WMMSE method [32]. The WMMSE algorithm addresses weighted sum-rate maximization by solving a problem equivalent to it, i.e., with the same optimal solution, and amenable for block coordinate descent [45]. With the assumption provided in Sect. 2.1, the equivalent problem is given by a weighted sum mean square error minimization problem (15) as illustrated in Theorem 1 [32].

$$\begin{aligned} \max \sum _{i=1}^{N_{u}}r_{i} = N_{t} - \min _{\begin{array}{c} \{v_{i}\}, \{u_{i}\},\\ \{{\textbf{w}}_{i}\}, {\textbf{W}}_{s} \end{array}} \sum _{i=1}^{N_{u}}, (v_{i}e_{i}-\log (v_{i})), \end{aligned}$$
(15)

in which \(e_{i}\) is the MSE of the estimated data symbol and transmitted data symbol given by

$$\begin{aligned} e_{i}&= {\mathbb{E}}{|\hat{s_{i}} -s_{i}|^{2}}\\&= |(u_{i}y_{i}-s_{i})|^{2}\\&=\left| \left( 1-u_{i}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}\right) \right| ^{2} + |u_{i}|^{2}\left( \sum _{j\ne i}|{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{j}|^{2}+ {\textbf{h}}_{i}^{\mathrm{H}}{\textbf{R}}_{s}{\textbf{h}}_{i}\right) + \sigma _{i}^{2}\left| u_{i}\right| ^{2}, \end{aligned}$$
(16)

and \(v_{i}\) is the user weight, \(u_{i}\) is the receiver gain, and both of them are the introduced auxiliary variables need to be optimized. Problem (15) is convex in in each individual \(\{v_{i}\}\) and \(\{u_{i}\}\) with fixed \(\{{\textbf{w}}_{i}\}\) and \({\textbf{W}}_{s}\), and hence, the partial optimization problem can be easily solved and a local optimum can be obtained by iteratively minimizing the cost function with respect to one variable while keeping the others fixed.

Based on (15), problem (14) is updated to

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}, \{t_{\ell }\} \end{array}}\, &\sum _{\ell =1}^{4L}\alpha _{\ell }t_{\ell } \end{aligned}$$
(17a)
$$\begin{aligned} \mathrm{s.t.}\, &\left[ \begin{array}{ll} {\textbf{M}}&{}\quad {\textbf{e}}_{\ell }\\ {\textbf{e}}_{\ell }^{\mathrm{T}} &{}\quad t_{\ell } \end{array}\right] \succeq 0, \quad \ell =1,\ldots ,4L, \end{aligned}$$
(17b)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}\Vert {\textbf{w}}_{i}\Vert ^{2} + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{aligned}$$
(17c)
$$\sum _{i=1}^{N_{u}} (v_{i}e_{i}-\log (v_{i})) \le N_{t} - r_{m},$$
(17d)
$$\begin{aligned}&{\textbf{R}}_{s}\succeq 0. \end{aligned}$$
(17e)

Until now, the constraint (17d) is convex and the MSE \(e_{i}\) in (16) is also convex w.r.t. each variable.Footnote 2 However, problem (17) is still hard to solve due to the intricate non-convex mapping from \(\{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}\) to \({\textbf{M}}\) in (10) and (11). To handle it, we adopt the popular semidefinite relaxation (SDR) technique [31]. By defining \({\textbf{R}}_{i} = {\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}\), \({\textbf{R}}_{{\textbf{x}}_{t}}\) in (12) can be written as

$$\begin{aligned} {\textbf{R}}_{{\textbf{x}}_{t}} = \sum _{i = 1}^{N_{u}}{\textbf{R}}_{i} +{\textbf{R}}_{s}. \end{aligned}$$
(18)

Therefore, by SDR, \({\textbf{M}}\) becomes a linear function of \({\textbf{R}}_{i}\) and \({\textbf{R}}_{s}\). On the other hand, the MSE \(e_{i}\) in (17d) can be expressed by \({\textbf{R}}_{{\textbf{x}}_{t}}\) as follows

$$\begin{aligned} e_{i} = 1-2\Re \big (u_{i}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}\big ) + |u_{i}|^{2}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{R}}_{{\textbf{x}}_{t}}{\textbf{h}}_{i} + \sigma _{i}^{2}|u_{i}|^{2}.\end{aligned}$$
(19)

Therefore, problem (17) is updated to (20) as follows

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\}, \{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}, \{t_{\ell }\} \end{array}}\, &\sum _{\ell =1}^{4L}\alpha _{\ell }t_{\ell } \end{aligned}$$
(20a)
$$\begin{aligned} \mathrm{s.t.}\, &{\textbf{R}}_{s}\succeq 0, \end{aligned}$$
(20b)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}{\mathrm{Tr}}({\textbf{R}}_{i}) + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{aligned}$$
(20c)
$$\sum _{i=1}^{N_{u}} (v_{i}e_{i}-\log (v_{i})) \le N_{t} - r_{m}.$$
(20d)
$$\left[ \begin{array}{ll} {\textbf{M}}&{}\quad {\textbf{e}}_{\ell }\\ {\textbf{e}}_{\ell }^{\mathrm{T}} &{} \quad t_{\ell } \end{array}\right] \succeq 0, \quad \ell =1,\ldots ,4L,$$
(20e)
$$\begin{aligned}&{\textbf{R}}_{i} = {\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}. \end{aligned}$$
(20f)

In problem (20), the only non-convex constraint is (20f). By SDR, we relax the constraint to \({\textbf{R}}_{i} \succeq {\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}\) which, by the Schur complement, is equivalent to the following linear matrix inequality (LMI)

$$\begin{aligned} \left[ \begin{array}{ll} {\textbf{R}}_{i} &{}\quad {\textbf{w}}_{i}\\ {\textbf{w}}_{i}^{\mathrm{H}} &{}\quad 1 \end{array}\right] \succeq 0,\quad i = 1,\ldots ,N_{u}. \end{aligned}$$
(21)

Based on the above derivations, problem (17) can be updated to

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\}, \{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}, \{t_{\ell }\} \end{array}}\, &\sum _{l=1}^{4L}\alpha _{\ell }t_{\ell } \end{aligned}$$
(22a)
$$\begin{aligned} \mathrm{s.t.}\, &{\textbf{R}}_{s}\succeq 0, \end{aligned}$$
(22b)
$$\begin{aligned}&\sum _{i=1}^{N_{u}}{\mathrm{Tr}}({\textbf{R}}_{i}) + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{aligned}$$
(22c)
$$\sum _{i=1}^{N_{u}} (v_{i}e_{i}-\log (v_{i})) \le N_{t} - r_{m},$$
(22d)
$$\begin{aligned}&\left[ \begin{array}{ll} {\textbf{M}}&{}\quad {\textbf{e}}_{\ell }\\ {\textbf{e}}_{\ell }^{\mathrm{T}} &{}\quad t_{\ell } \end{array}\right] \succeq 0,\quad \ell =1,\ldots ,4L, \end{aligned}$$
(22e)
$$\left[ \begin{array}{ll} {\textbf{R}}_{i} &{}\quad {\textbf{w}}_{i}\\ {\textbf{w}}_{i}^{\mathrm{H}} &{}\quad 1 \end{array}\right] \succeq 0,\quad i=1,\ldots ,N_{u}.$$
(22f)

As seen, given \(\{v_{i}\}, \{u_{i}\}\), the remaining part of problem (22) is an SDP that can be efficiently solved with off-the-shelf solvers, such as \({\textsf{CVX}}\) [46]. Once the SDP is solved, \(\{v_{i}\}, \{u_{i}\}\) can be updated at each r-th iteration with the following closed-form expressions

$$\begin{aligned} u_{i}^{r+1}&\leftarrow \left[ {\textbf{h}}_{i}^{\mathrm{H}}\left( \sum _{j=1}^{N_{u}}{\textbf{R}}_{j}^{r+1}+{\textbf{R}}_{s}^{r+1}\right) {\textbf{h}}_{i}+\sigma _{i}^{2}\right] ^{-1}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}^{r+1}, \forall i, \end{aligned}$$
(23a)
$$\begin{aligned} v_{i}^{r+1}&\leftarrow \left( 1-\bar{u}_{i}^{r+1}{\textbf{h}}_{i}^{\mathrm{H}}{\textbf{w}}_{i}^{r+1}\right) ^{-1}, \forall i. \end{aligned}$$
(23b)

The alternating updates proceed iteratively until convergence. The details of the proposed WMMSE–SDR algorithm for problem (22) are given in Algorithm 1.

figure a

It is necessary to point out that the equality in (21) may not be satisfied by the solution of a general SDP problem (22) after SDR. In that case, \({\textbf{R}}_{i}\) is not rank-1 and only an approximate solution \({\textbf{w}}_{i}\) can be attained, which could bring performance loss. However, it is interesting to find in the work that a rank-1 solution of problem (22) is always achievable from the points obtained by Algorithm 1. In particular, Theorem 1 holds for problem (22).

Theorem 1

  1. (1)

    Algorithm 1 converges, and any limit point is a KKT solution of (22).

  2. (2)

    For any feasible solution \(\{\{{\hat{t}}_{\ell }\},\{{\hat{{\textbf{R}}}}_{i}\}, {\hat{{\textbf{R}}}}_{s}\}\) of problem (22), one can construct

    $$\begin{aligned} \tilde{t}_{\ell }&= {\hat{t}}_{\ell }, \ell = 1, \ldots , 4L, \end{aligned}$$
    (24a)
    $$\begin{aligned} {\tilde{{\textbf{w}}}}_{i}&= \frac{{\hat{{\textbf{R}}}}_{i}{\textbf{h}}_{i}}{\sqrt{{\textbf{h}}_{i}^{\mathrm{H}}{\hat{{\textbf{R}}}}_{i}{\textbf{h}}_{i}}}, i=1, \ldots , N_{u}, \end{aligned}$$
    (24b)
    $$\begin{aligned} {\tilde{{\textbf{R}}}}_{i}&= {\tilde{{\textbf{w}}}}_{i}{\tilde{{\textbf{w}}}}_{i}^{\mathrm{H}}, i=1, \ldots , N_{u}, \end{aligned}$$
    (24c)
    $$\begin{aligned} {\tilde{{\textbf{R}}}}_{s}&= \sum _{i = 1}^{N_{u}}{\hat{{\textbf{R}}}}_{i} +{\hat{{\textbf{R}}}}_{s} - \sum _{i=1}^{N_{u}}{\tilde{{\textbf{R}}}}_{i}, \end{aligned}$$
    (24d)

    which is also a feasible solution of (22).

Proof

See “Appendix 2.” \(\square\)

Theorem 1 implies that SDR is in fact tight to problem (22), since by (24b) and (24d) one can always construct a rank-one feasible solution \({\tilde{{\textbf{R}}}}_{i}\) together with \({\tilde{{\textbf{R}}}}_{s}\) for (22). Thus, \({\tilde{{\textbf{w}}}}_{i}\) and \({\tilde{{\textbf{R}}}}_{s}\) is a feasible solution to problem (17). Then, the sensing beamforming \({\tilde{{\textbf{W}}}}_{s}\) can be extracted from \({\tilde{{\textbf{R}}}}_{s}\) by Cholesky decomposition or eigenvalue decomposition. Lastly, the tightness of SDR implies that with fixed \(\{u_{i}, v_{i}\}\) problem (17) has the strong duality.

Corollary 1

With fixed \(\{u_{i},v_{i}\}\), problem (17) has a zero duality gap with its Lagrange dual.

Proof

With \(\{u_{i}\}\) and \(\{v_{i}\}\) fixed, problem (22) is convex w.r.t. \(\{\{{\textbf{w}}_{i}\}, \{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}\}\}\), so it has no duality gap with its dual problem, which is given by

$$\begin{aligned} \max _{\begin{array}{c} \lambda \ge 0, \mu \ge 0, \Gamma _{i}\succeq 0, \Xi _{s}\succeq 0, \{\xi _{\ell }\ge 0\} \end{array}}\, \left\{ \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\},{\textbf{R}}_{s} \end{array}} {\mathcal{L}}(\Omega _{1})\right\} , \end{aligned}$$
(25)

where the Lagrangian function is

$$\begin{aligned} {\mathcal{L}}(\Omega _{1})&=\sum _{\ell =1}^{4L}\alpha _{\ell }t_{\ell } - {\mathrm{Tr}}(\Xi _{s}{\textbf{R}}_{s}) \\&\quad + \mu \left[ \left( \sum _{i=1}^{N_{u}}{\mathrm{Tr}}({\textbf{R}}_{i}) + {\mathrm{Tr}}({\textbf{R}}_{s}) \right) - P_{T}\right] \\&\quad +\lambda \left[ \sum _{i=1}^{N_{u}}\ (v_{i}e_{i}-\log (v_{i})) - N_{t} + r_{m}\right] \\&\quad - \sum _{\ell = 1}^{4L}\xi _{\ell }\left( {\textbf{e}}_{\ell }^{\mathrm{T}}{\textbf{M}}^{-1}{\textbf{e}}_{\ell }-t_{\ell }\right) + \sum _{i = 1}^{N_{u}}{\mathrm{Tr}}\left[ \Gamma _{i}\left( {\textbf{R}}_{i}-{\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}\right) \right] , \end{aligned}$$
(26)

and \(\Omega _{1} \triangleq \{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\},\{{\textbf{R}}_{s}\}, \lambda , \mu , \{\Gamma _{i}\}, \Xi _{s}, \{\xi _{\ell }\}\}\).

Because of the tightness of SDR \({\textbf{R}}_{i} = {\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}\), the last term of (26) will be zero, making (25) the same as the dual problem of (17), which is given by

$$\begin{aligned} \max _{\begin{array}{c} \lambda \ge 0, \mu \ge 0, \Xi _{s}\succeq 0, \{\xi _{\ell }\ge 0\} \end{array}}\, \left\{ \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} {\mathcal{L}}(\Omega _{2})\right\} , \end{aligned}$$
(27)

where the Lagrangian function is

$$\begin{aligned} {\mathcal{L}}(\Omega _{2})&=\sum _{\ell =1}^{4L}\alpha _{\ell }t_{\ell }- {\mathrm{Tr}}(\Xi _{s}{\textbf{R}}_{s}) \\&\quad + \mu \left[ \left( \sum _{i=1}^{N_{u}}{\mathrm{Tr}}({\textbf{w}}_{i}{\textbf{w}}_{i}^{\mathrm{H}}) + {\mathrm{Tr}}({\textbf{R}}_{s}) \right) - P_{T}\right] \\&\quad +\lambda \left[ \sum _{i=1}^{N_{u}}\ \left( v_{i}e_{i}-\log (v_{i})\right) - N_{t} + r_{m}\right] + \sum _{\ell = 1}^{4L}\xi _{\ell }\left( {\textbf{e}}_{\ell }^{\mathrm{T}}{\textbf{M}}^{-1}{\textbf{e}}_{\ell }-t_{\ell }\right) , \end{aligned}$$
(28)

and \(\Omega _{2} \triangleq \{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{s}\}, \lambda , \mu , \Xi _{s}, \{\xi _{\ell }\}\}\).

Thus, under the equivalence between (17) and (22) built in Theorem 1, there is zero gap between problem (17) and its dual problem. That completes the proof. \(\square\)

4 Proposed FP-SGDA algorithm

While the proposed WMMSE–SDR algorithm can achieve a KKT point, it needs to solve an SDP in Step 3, which is usually of high computational complexity with \(O(L^3 + L^{2}N_{t}^{2}+L^{2}N_{s}^{2} + LN_{t}^{2} + N_{u}N_{t}^{2})\). Therefore, it necessitates to tailor a computation-efficient algorithm. To accomplish the task, we resort to the FP techniques and the primal-dual relation to transform the original problem (13) to a min–max problem with simple constraints, which then can be efficiently handled by low-complexity algorithms base on the tightness of SDR proved by Theorem 1 and the zero duality in Corollary 1 for the subproblem.

Firstly, problem (17) can be equivalently written as

$$\begin{aligned} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\} \end{array}}\, &\sum _{\ell =1}^{4L}\alpha _{\ell }{\textbf{e}}_{\ell }^{\mathrm{T}}{\textbf{M}}^{-1}{\textbf{e}}_{\ell } \\ \mathrm{s.t.}\, &\{\{{\textbf{w}}_{i}\},{\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}\}\in {\mathcal{C}}_{1}, \end{aligned}$$
(29)

in which \({\mathcal{C}}_{1}\) is defined as the variable set of (29) given by,

$${\mathcal{C}}_{1}\triangleq \left\{ \{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}\left| \begin{array}{l}{\textbf{R}}_{s} \succeq 0,\\\sum _{i=1}^{N_{u}} (v_{i}e_{i}-\log (v_{i})) \le N_{t} - r_{m}, \\ \sum _{i=1}^{N_{u}}\Vert {\textbf{w}}_{i}\Vert ^{2} + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \end{array}\right. \right\} .$$

For such a problem, the FP is introduced to avoid dealing with \({\textbf{M}}^{-1}\) directly.

FP refers to a family of optimization problems that involve ratio term(s). Compared with the literature of FP that specialize in single-ratio problems [47, 48], the quadratic transform proposed by [33] can recast the original problem to a form amenable to iterative optimization with decoupled numerator and denominator of each ratio term by introducing some suitable auxiliary variables. This decoupling feature of the proposed quadratic transform can convert the original non-convex problem into a sequence of convex problems, making it particularly suited for the coordinated resource optimization problem across multiple cells in a wireless cellular network. To deal with the FP problem (29) which in a multidimensional complex case where the numerators are vectors and the denominators are matrices, the following lemma is given.

Lemma 1

[33] Consider the following sum of fractional terms

$$\sum _{m=1}^{M}{\varvec{a}}_{m}^{\mathrm{H}}{\textbf{B}}_{m}^{-1}{\varvec{a}}_{m},$$
(30)

where each \({\varvec{a}}_{m} \in {\mathbb{C}}^d\), and \({\textbf{B}}_{m} \in {\mathbb{C}}^{d\times d}\) is Hermitian, for \(m=1,\dots ,M\). Then, the above term is equal to

$$\begin{aligned} \max _{\{{\textbf{y}}_{m} \in {\mathbb{C}}^{d}\}_{m=1}^M}\, \sum _{m=1}^{M}\left( 2\Re \left\{ {\textbf{y}}_{m}^{\mathrm{H}}{\varvec{a}}_{m}\right\} -{\textbf{y}}_{m}^{\mathrm{H}}{\textbf{B}}_{m}{\textbf{y}}_{m}\right) . \end{aligned}$$
(31)

Regard \({\textbf{M}}\) and \({\textbf{e}}_{\ell }\) as \({\textbf{B}}\) and \({\textbf{a}}_{m}\) in Lemma 1, respectively, and introducing auxiliary variables \(\{{\textbf{y}}_{\ell }\in {\mathbb{C}}^{4L}\}_{\ell =1}^{4L}\), problem (29) can be transformed to

$$\begin{aligned} \min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}, \{v_{i}\}, \{u_{i}\}\}\in {\mathcal{C}}_{1} \end{array}} \left\{ \max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \sum _{\ell =1}^{4L}\left( 2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} -{\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right) \right\} . \end{aligned}$$
(32)

Notice that problem (32) successfully circumvents dealing with the intricate \({\textbf{M}}^{-1}\) in problem (29) directly. Let us rewrite problem (32) by separating \(\{\{u_{i}\}, \{v_{i}\}\}\) and \(\{\{{\textbf{w}}_{i}\}, {\textbf{R}}_{i}\}\) as

$$\begin{aligned} \min _{\begin{array}{c} \{\{v_{i}\}, \{u_{i}\}\}\in {\mathcal{C}}_{1} \end{array}} \left\{ \min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\}, {\textbf{R}}_{s}\}\in {\mathcal{C}}_{1} \end{array}} \left\{ \max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \sum _{\ell =1}^{4L}\left( 2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} -{\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right) \right\} \right\} , \end{aligned}$$
(33)

and consider the inner min–max problem when \(\{\{u_{i}\}, \{v_{i}\}\}\) is fixed. After SDR by (18) and (21), the inner min–max problem is

$$\begin{aligned} \min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}\}\in {\mathcal{C}}_{2} \end{array}} \left\{ \max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \sum _{\ell =1}^{4L}\left( 2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} -{\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right) \right\} , \end{aligned}$$
(34)

in which \({\mathcal{C}}_{2}\) is defined by

$${\mathcal{C}}_{2}\triangleq \left\{ \{{\textbf{w}}_{i}\}, {\textbf{R}}_{s} \left| \begin{array}{l}{\textbf{R}}_{s} \succeq 0,\\ \sum _{i=1}^{N_{u}} (v_{i}e_{i}-\log (v_{i})) \le N_{t} - r_{m}, \\ \sum _{i=1}^{N_{u}}{\mathrm{Tr}}({\textbf{R}}_{i}) + {\mathrm{Tr}}({\textbf{R}}_{s}) \le P, \\ \left[ \begin{array}{ll} {\textbf{R}}_{i} &{} {\textbf{w}}_{i}\\ {\textbf{w}}_{i}^{\mathrm{H}} &{} 1 \end{array}\right] \succeq 0,\; i=1,\ldots ,N_{u} \end{array}\right. \right\} .$$

Because problem (34) is concave in \(\{{\textbf{y}}_{\ell }\}\) and convex in \(\{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}\}\), the order of min–max in (34) can be changed to max–min as

$$\begin{aligned}&\max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \left\{ \min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}\}\in {\mathcal{C}}_{2} \end{array}} \sum _{\ell =1}^{4L}\left( 2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} -{\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right) \right\} \end{aligned}$$
(35a)
$$\begin{aligned} =&\max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \left\{ \sum _{\ell =1}^{4L}2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} + \min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\},\{{\textbf{R}}_{i}\}, {\textbf{R}}_{s}\}\in {\mathcal{C}}_{2} \end{array}} \sum _{\ell =1}^{4L} -{\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right\} . \end{aligned}$$
(35b)

Since the SDR is tight according to Theorem 1, the inner SDR minimization problem in (35b) is equivalent to

$$\min _{\begin{array}{c} \{\{{\textbf{w}}_{i}\},{\textbf{R}}_{s}\}\in {\mathcal{C}}_{1} \end{array}}-\sum _{\ell =1}^{4L} {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell } .$$
(36)

According to Corollary 1, problem (36) has no duality gap, and thus can be solved by considering its Lagrangian dual

$$\begin{aligned} \max _{\begin{array}{c} \lambda \ge 0, \mu \ge 0 \end{array}} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} {\mathcal{L}}(\Omega ), \end{aligned}$$
(37)

where \(\lambda ,\mu\) are the dual variables, \(\Omega = \{\{{\textbf{w}}_{i}\},{\textbf{R}}_{s}, \lambda , \mu \}\) are the variable set, and

$$\begin{aligned} {\mathcal{L}}(\Omega )=&-\sum _{\ell =1}^{4L}\left( {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{M}}{\textbf{y}}_{\ell }\right) + \lambda \left[ \sum _{i=1}^{N_{u}}\ (v_{i}e_{i}-\log (v_{i})) - N_{t}+r_{m}\right] \\&+ \mu \left[ \left( \sum _{i=1}^{N_{u}}\Vert {\textbf{w}}_{i}\Vert ^{2} + {\mathrm{Tr}}({\textbf{R}}_{s}) \right) - P\right] . \end{aligned}$$
(38)

Therefore, problem (35b) is further equivalent to

$$\begin{aligned}&\max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\} \end{array}}\, \left\{ \sum _{\ell =1}^{4L}2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} + \max _{\begin{array}{c} \lambda \ge 0, \mu \ge 0 \end{array}} \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} {\mathcal{L}}(\Omega ) \right\} \end{aligned}$$
(39a)
$$\begin{aligned} =&\max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\},\lambda \ge 0, \mu \ge 0 \end{array}}\, \left\{ \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} \sum _{\ell =1}^{4L}2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} + {\mathcal{L}}(\Omega ) \right\} . \end{aligned}$$
(39b)

Incorporating the minimization over \(\{u_{i},v_{i}\}\), problem (32) is equivalent to

$$\begin{aligned} \min _{\begin{array}{c} \{u_{i},v_{i}\} \end{array}}\left\{ \max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\},\lambda \ge 0, \mu \ge 0 \end{array}}\, \left\{ \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} \sum _{\ell =1}^{4L}2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} + {\mathcal{L}}(\Omega ) \right\} \right\} . \end{aligned}$$
(40)

It is not difficult to check that the objective function in (40) is convex in each variable of \(\{v_{i}\}\) and \(\{u_{i}\}\), concave w.r.t \(\{{\textbf{y}}_{\ell }\}, \lambda , \mu\), but non-convex in \(\{\{{\textbf{w}}_{i}\},{\textbf{R}}_{s}\}\). In the work, we adopt BCD algorithm to update \(\{v_{i}\}, \{u_{i}\}\) and the inner max–min problem alternatively. With \(\{v_{i}\}, \{u_{i}\}\) fixed, the inner max–min problem can be solved by the SGDA algorithm [34] that is designed for non-convex–concave problems. The SGDA is very computationally efficient since it takes only a single-loop update in each iteration. Specifically, by introducing auxiliary sequences \(\{{\hat{{\textbf{w}}}}_{i}\}\) and \({\hat{{\textbf{R}}}}_{s}\), the following problem can be built from the inner max–min problem in (40)

$$\begin{aligned} \max _{\begin{array}{c} \{{\textbf{y}}_{\ell }\}, \lambda \ge 0, \mu \ge 0 \end{array}}\Bigg \{ \min _{\begin{array}{c} \{{\textbf{w}}_{i}\},{\textbf{R}}_{s} \end{array}} \, \Bigg \{&\sum _{\ell =1}^{4L}2\sqrt{\alpha _{\ell }}\Re \left\{ {\textbf{y}}_{\ell }^{\mathrm{H}}{\textbf{e}}_{\ell }\right\} + {\mathcal{L}}(\Omega )\\&+ \frac{p}{2}\sum _{i = 1}^{N_{u}}||{\textbf{w}}_{i}-{\hat{{\textbf{w}}}}_{i}||^{2} + \frac{q}{2}||{\textbf{R}}_{s}-{\hat{{\textbf{R}}}}_{s}||_{F}\Bigg \}\Bigg \}, \end{aligned}$$
(41)

where p and q are constants. When SGDA is applied to (40), gradient ascent and gradient descent are conducted alternatingly over the objective function of problem (41), while the auxiliary sequences are updated through a averaging step. That gives the FP-SGDA algorithm for the joint beamforming optimization problem (13). The details of the proposed FP-SGDA algorithm are summarized in Algorithm 2.

figure b

In Algorithm 2, \(\gamma , \beta\) and c are step sizes and the expressions of \(\nabla _{{\textbf{w}}_{i}} {\mathcal{L}}(\Omega )\) and \(\nabla _{{\textbf{R}}_{s} } {\mathcal{L}}(\Omega )\) are

$$\begin{aligned} \nabla _{{\textbf{w}}_{i}}{\mathcal{L}}(\Omega ) =\, &-\sum _{\ell =1}^{4L}\left( \sum _{jk}^{4}{\textbf{M}}^{{\textbf{C}}}_{jk}{\bar{{\textbf{D}}}}_{{\textbf{y}}_{\ell ,i}}{\textbf{M}}^{{\textbf{A}}}_{jk}{\textbf{D}}_{{\textbf{y}}_{\ell ,k}}{\textbf{M}}^{{\textbf{B}}}_{jk}{\textbf{w}}_{i}\right. \\ {}&\left. +\left( {\textbf{M}}^{{\textbf{C}}}_{jk}{\textbf{D}}^{\mathrm{H}}_{{\textbf{y}}_{\ell ,j}}{\textbf{M}}^{{\textbf{A}}}_{jk}{\textbf{D}}_{{\textbf{y}}_{\ell ,k}}{\textbf{M}}^{{\textbf{B}}}_{jk}\right) ^{\mathrm{T}}{\bar{{\textbf{w}}}}_{i}\right) \\&+ \lambda \left( \sum _{j=1}^{N_{u}}v_{j}|u_{j}|^{2}{\textbf{h}}_{j}{\textbf{h}}_{j}^{\mathrm{H}}\right) {\textbf{w}}_{i}-2\lambda v_{i}u_{i}{\textbf{h}}_{i} + 2\delta {\textbf{w}}_{i},\\ \nabla _{{\textbf{R}}_{s}}{\mathcal{L}}(\Omega ) =&-\sum _{\ell =1}^{4L}\left( \sum _{jk}^{4}{\textbf{M}}^{{\textbf{C}}}_{jk}{\bar{{\textbf{D}}}}_{{\textbf{y}}_{\ell ,j}}{\textbf{M}}^{{\textbf{A}}}_{jk}{\textbf{D}}_{{\textbf{y}}_{\ell ,k}}{\textbf{M}}^{{\textbf{B}}}_{jk}\right) \\&+ \lambda \left( \sum _{j=1}^{N_{u}}v_{j}|u_{j}|^{2}{\textbf{h}}_{j}{\textbf{h}}_{j}^{\mathrm{H}}\right) + \mu {\textbf{I}}_{N_{t}}, \end{aligned}$$
(42)

where \({\textbf{y}}_{\ell }=[{\textbf{y}}_{\ell ,1}^{\mathrm{T}},\ldots ,{\textbf{y}}_{\ell ,4}^{\mathrm{T}}]^{\mathrm{T}}\) and \({\textbf{D}}_{{\textbf{y}}_{\ell ,k}} = {\text{diag}}({\textbf{y}}_{\ell ,k})\). As expressed in (10), \({\textbf{M}}\) is a \(4L\times 4L\) block matrix, where each sub-block expressed in (11) can be written in the following unified form

$$\begin{aligned} {\textbf{M}}_{jk} = {\textbf{M}}^{{\textbf{A}}}_{jk} \odot {\textbf{M}}^{{\textbf{B}}}_{jk}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{M}}^{{\textbf{C}}}_{jk},\quad j = 1,\ldots ,4,k = 1,\ldots ,4. \end{aligned}$$
(43)

For example, \({\textbf{M}}_{11}\triangleq {\textbf{M}}_{{\varvec{\phi }}{\varvec{\phi }}} = {\textbf{M}}^{{\textbf{A}}}_{11} \odot {\textbf{M}}^{{\textbf{B}}}_{11}{\bar{{\textbf{R}}}}_{{\textbf{x}}_{t}}{\textbf{M}}^{{\textbf{C}}}_{11}\), where \({\textbf{M}}^{{\textbf{A}}}_{11} = {\dot{{\textbf{A}}}}^{\mathrm{H}}{\dot{{\textbf{A}}}}, {\textbf{M}}^{{\textbf{B}}}_{11} = {\bar{{\textbf{B}}}}{\textbf{V}}^{\mathrm{H}}\) and \({\textbf{M}}^{{\textbf{C}}}_{11} = {\textbf{V}}{\textbf{B}}\).

In FP-SGDA algorithm, it has the computational complexity with \(O(LN_{t}^{2} + L^{2}N_{s}^{2} + LN_{t} + N_{u}N_{t})\), which is much smaller than that in WMMSE–SDR algorithm. It is also verified by the simulation results.

5 Simulation results and discussion

In this section, the performance of our proposed ISAC beamforming algorithms is evaluated extensively through simulation. The network consists of \(N_{u} = 5\) UEs and \(L = 5\) targets. The number of antennas equipped at both BSs is \(N_{s} = N_{t} = 20\). The carrier frequency is 2.35 GHz and the signal bandwidth is 100 MHz. The path loss between the UE and the transmit BS is set as \(128.1 + 37.6\log _{10}({\text{d}})\) (dB), in which d is the distance between BS and UE [49]. The power spectral density of is − 174 dBm/Hz . The transmit BS is located at \((x,y) =(0, 0)\) m, and the sensing BS is at (0, 500) m. As shown in Fig. 2, the targets and UEs are randomly located in a rectangular area enclosed by the magenta dotted line and that by the dotted line, respectively. Two scenarios with different distributions of UE’s location are considered. In scenario 1, UEs are located near the targets to sense and the directions of them to the BSs are close. In scenario 2, UEs are located far away from the targets and they have different directions to the BSs. Totally 500 Monte Carlo realizations of typologies are conducted and the performance is averaged over them. Unless specified otherwise, the weights of CRB for all parameters are set as \(\alpha _{\ell } = 1\). The maximum transmit power is \(P = 30\) (dBm), and the sum-rate threshold is \(r_{m} = 20\) (bits/s/Hz). The initial values of \(\{{\varvec{w}}_{i}^0\}\) are set via the zero-forcing beamforming for both WMMSE–SDR and FP-SGDA. The step sizes in FP-SGDA are set as \(\gamma = 0.01\) and \(\beta = c = 0.02\). In our experiments, the MATLAB is operated on the platform with CPU of i7-9800X and GPU of RTX-3080Ti.

Fig. 2
figure 2

Two scenarios of different network typologies

Full size image

5.1 Comparison between WMMSE–SDR and FP-SGDA beamforming

In this subsection, the performance of the proposed WMMSE–SDR and FP-SGDA beamforming schemes is compared in terms of the convergence behavior and the computational time.

5.1.1 Convergence behavior

Figure 3 presents the convergence behaviors of the proposed algorithms. One can observe that the objective value \({\mathrm{Tr}}({\textbf{M}}^{-1})\) obtained by WMMSE–SDR and that by FP-SGDA decrease quickly. While both algorithms converge to almost the same objective value within a few iterations, it shows that WMMSE–SDR takes fewer iterations to converge. An interesting phenomenon in Fig. 3 is that both the two algorithms will converge a little faster with a larger transmit power budget P.

Fig. 3
figure 3

Comparison of convergence of WMMSE–SDR and FP-SGDA

Full size image

Compared with scenario 1, the ISAC system in scenario 2 achieves a lower objective value during the iteration, corresponding to a better sensing performance. This is because that the communication signals received at UEs are more easily to be interfered by the sensing signals when the targets and UEs are located close to each other. As a consequence, more power will be allocated to communication to meet the throughput requirement in scenario 1, and the corresponding sensing performance is degraded.

5.1.2 Impact of power and sum-rate constraint

Figure 4 demonstrates the achieved value of the trace of CRB matrix versus the sum-rate threshold \(r_{m}\) under different transmit power limits. In both scenarios, the achieved value of the trace increases with a higher threshold of sum rate. This is reasonable as more power will be used for communication to satisfy a more stringent throughput requirement. Moreover, with more transmit power budget, the attained CRB values will go down and the sensing performance is improved.

Fig. 4
figure 4

Comparison of Tr(CRB) of WMMSE–SDR and FP-SGDA algorithms

Full size image

In both scenarios, the trend of curves of WMMSE–SDR and that of FP-SGDA are similar. FP-SGDA obtains almost the same values as WMMSE–SDR. In addition, under the same power and sum-rate constraint settings, the obtained CRB in scenario 2 is smaller than that of scenario 1, which is in accordance with our expectation.

5.1.3 Computational time

As analyzed in Sect. 4, one big advantage of the proposed FP-SGDA is its lower computational complexity to WMMSE–SDR. To demonstrate that, the computational time (in seconds) of the two proposed algorithms versus the number of targets with different number of transmit antennas is listed in Table 1.

Table 1 Comparison of computational time (s) of WMMSE–SDR and FP-SGDA algorithms
Full size table

As shown in Table 1, the computational time of WMMSE–SDR and that of FP-SGDA increase with more targets to be sensed and more antennas equipped at BSs, because the increase of number of targets L and the number of antennas \(N_{t}\) will lead to a problem of a larger dimension and increased complexity.

More importantly, Table 1 shows that FP-SGDA reduce the computational time significantly. In fact, the averaged computational time of FP-SGDA is only 3–4% of that of WMMSE–SDR, under the same setting of L and \(N_{t}\). It verifies the effectiveness of our designs to reduce the computational complexity in the proposed FP-SGDA. And its computational advantage seems more significant with a larger number of targets and transmit antennas. In addition, it showcases that the computational time of FP-SGDA is less sensitive to the increase of \(N_{t}\), making it more appealing to the massive MIMO scenarios.

As the two proposed algorithms attain almost the same objective values, while FP-SGDA admits much better computational efficiency, it is compared with other benchmark schemes in the next subsection.

5.2 Comparison of improvement for parameter estimation

In this subsection, the achieved performance of our considered joint beamforming formulation is compared with other benchmark schemes. Specifically, the following schemes are evaluated for comparison.

  • Com.: Problem (13) is solved with the sum-rate threshold set as the objective value of the classical sum-rate maximization problem obtained by the WMMSE algorithm [32]. In this scheme, the network throughput is more emphasized.

  • AOD (\({\textbf{M}}_{11}\)): Problem (13) is solved with the objective function changed to \({\mathrm{Tr}}({\textbf{M}}_{11}^{-1})\). In this scheme, the channel parameters AOA and reflection coefficient \(\{{\varvec{\theta }}, {\varvec{v}}\}\) are assumed to be known, and only the minimization of the CRB of AOD \({\varvec{\phi }}\) is considered.

  • AOD (\(\alpha _{\ell }\)): Problem (13) is solved with the weights in the objective function set to \(\alpha _{\ell } = 1, \ell =1,\ldots ,L\) and \(\alpha _{\ell } = 0, \ell =L+1,\ldots ,4L\). Note that, different from that in AOD (\({\textbf{M}}_{11}\)), this scheme treats the other parameters including AoA and reflection coefficient unknown here.

  • All para: Problem (13) is solved with \(\alpha _{\ell } = 1, \ell =1,\ldots ,4L\) in the objective function with \({\mathrm{Tr}}(\Lambda _{{\varvec{\alpha }}}{\textbf{M}}^{-1})\). In this scheme, the minimization of the CRB of all parameters \(\{{\varvec{\phi }}, {\varvec{\theta }}, {\textbf{b}}_{R}, {\textbf{b}}_{i}\}\) is considered in the optimization.

  • Sen.: Problem (13) is solved by setting the sum-rate constraint as \(r_{m} = 0\). The target sensing is more emphasized in this scheme.

Figure 5 presents the values of MSE and Tr(CRB) obtained by the beamforming optimized from all the aforementioned schemes above with FP-SGDA. MUSIC algorithm is applied to acquire the AoD estimation. \({\text{MSE}}(\cdot )\) is calculated by the summation of the mean square errors of the estimated and true AoDs. \({\mathrm{Tr}}({\text{CRB}})(\cdot )\) corresponds to the achieved summation of the CRB of AoD \({\varvec{\phi }}\). The values of \({\text{MSE}}(\cdot )\) are depicted by points, while values of \({\mathrm{Tr}}({\text{CRB}})(\cdot )\) are illustrated by dotted lines.

Fig. 5
figure 5

Comparison of MSE and Tr(CRB) for parameter estimation

Full size image

One can see from Fig. 5 that all the schemes can provide higher estimation accuracy when the transmit power is increased. Among all the schemes, the sensing performance of Com. is the worst as it emphasizes the most on communication and nearly all the power is allocated to the data transmission. In contrast, Sen. gets the best estimation accuracy, because it considers the optimization of sensing performance only. Besides, All para attains the better performance than AOD (\(\alpha _{\ell }\)). The reason is that the sensing of different parameters for each target indeed impacts each other. As illustrated in [31], the optimization of CRB of AoD solely could deteriorate the estimation of the reflection coefficient, since the obtained beampattern has a notch at the direction to the target when the minimization of the CRB of reflection coefficients is ignored. The phenomenon here is consistent with what demonstrated in [31]. Comparing AOD (\({\textbf{M}}_{11}\)) with AOD (\(\alpha _{\ell }\)), one can observe that the performance of the two schemes is very near, while the latter one achieve slightly better performance. This is in accordance with our expectation since AOD (\({\textbf{M}}_{11}\)) ignores the uncertainty of the other unknown parameters in the optimization.

5.3 Discussion

We conduct extensive simulations to evaluate our proposed WMMSE–SDR and FP-SGDA in various scenarios under different power and sum-rate constraints. The numerical results show that our proposed algorithms can improve the sensing performance effectively and converge within only a few iterations. It also showcases that the sensing performance that is evaluated by the achieved trace of the weighted CRB of parameters will be improved with an increased transmit power and degraded with a more stringent sum-rate threshold. The phenomenon reveals the trade-off between sensing and information transmission under limited power. In addition, the comparison of the computational time demonstrates that FP-SGDA does not only achieve almost the same sensing performance as WMMSE–SGDA, but also significantly reduces the computational time. It verifies the efficacy of our proposed low-complexity designs. Moreover, the proposed MUMT-ISAC framework is also compared with other benchmark schemes, including one scheme considering the minimization of CRB of partial parameters only, one treating partial parameters as deterministic, one focused more on sensing and another one emphasizing sensing. The comparison presents that our proposed framework achieves the best balance between sensing and information transmission. In a nutshell, the simulation verifies the effectiveness of our proposed MUMT-ISAC framework. It shows our proposed joint beamforming algorithms can effectively improve the estimation accuracy and ensure a high communication throughput with highly reduced computational complexity.

6 Conclusion

In this paper, we have investigated the joint information and sensing beamforming design problem in MUMT-MIMO ISAC systems. We have proposed a new MUMT-MIMO ISAC framework where two BSs collaborate to sense targets in a bi-static mode, while the transmit BS sends information streams to communication users simultaneously. To improve the sensing performance and ensure a high communication throughput, we have formulated a beamforming problem to minimize the trace of the weighted CRB of target parameters subject to the sum-rate constraint. To solve the intricate non-convex problem, we have proposed a WMMSE–SDR algorithm, which can achieve a KKT point of the problem. In addition, we have proved the tightness of SDR and developed a low-complexity FP-SGDA algorithm. Through extensive simulation, we found that our proposed algorithms can achieve a promising sensing and communication performance, and the FP-SGDA algorithm can significantly reduce the computational time. Besides the parameters considered in this paper, range and Doppler are also the directions for future research.