Background

Genomic prediction of genetic merit, using SNP markers, is now routinely used in animal and plant breeding to identify superior breeding individuals and so accelerate genetic gain [1–3]. Genomic prediction methodology is also increasingly used in human disease studies for the inference of genetic architecture, the identification of causal mutations (QTL mapping), and prediction of disease risk [4–8].

Genomic predictions are often implemented using linear prediction models, especially best linear unbiased prediction (BLUP) or Genomic BLUP (GBLUP), which assume that all the SNPs contribute small effects to the trait and these effects are derived from a normal distribution [1, 4, 9]. While BLUP based genomic predictions have certainly been successful in increasing genetic gain in livestock and crops [10, 11], this approach does have some limitations. One limitation is that the prediction accuracy does not persist well across multiple generations, because the severe shrinkage in these models results in the effect of causative mutation being “smeared” across many markers encompassing long chromosome segments – in other words a linear combination of effects of a large number of markers is used to capture the effect of a QTL. After several generations, the association between markers and QTL might be broken down by recombination, thereby reducing prediction accuracy. The smearing of effect of causative mutations across many SNP also results in imprecise QTL mapping with BLUP methods.

To address these problems, Bayesian mixture models (nonlinear prediction e.g. Bayes A, B, C, and R) [1, 6, 12–15] assume non-normal prior distributions of SNP effects. One example of a flexible approach, BayesR [14] defines a mixture model with SNP effects following a mixture of four normal distributions with zero, very small, small and moderate variances. In practice, the prediction accuracy of Bayesian mixture models (including BayesR) has been shown to be equal or superior to that of GBLUP for both human diseases and dairy cattle milk production traits [15–25].

In addition to the prediction of breeding values and future phenotypes using genotype data, Bayesian models (such as BayesR) can be used to map the causal polymorphisms (quantitative trait loci or QTL). For this purpose they have some advantages over traditional single SNP regression, which is commonly used to analyse genome wide association studies (GWAS) [16–24]. Single SNP regression fits one SNP at a time as a fixed effect and tests the significance of the association between the SNP and the trait, while ignoring all other SNPs. To protect against performing multiple tests, stringent P-values (P < 5*10−8) are used. This method of analysis has three limitations:1) The effect of those SNPs declared significant is usually over-estimated; 2) multiple SNPs in linkage disequilibrium with the same QTL may show an association with the trait leading to imprecision in mapping the QTL; 3) many QTL are not detected at all because no SNP reaches the stringent P-value for association with the trait. By comparison, Bayesian mixture models fit all SNPs simultaneously by treating the SNP effects as random effects drawn from a prior distribution. For example, the BayesR model has been implemented for QTL detection in the dairy cattle genome and for human disease traits [15]. The results show that BayesR can increase the power of identifying the known genes in contrast with GBLUP and GWAS.

Even though nonlinear models are attractive, one limitation is that nonlinear models typically require long computational times. Due to the hierarchical estimation of posterior distributions of SNP effects and their variances, nonlinear models have usually been implemented with Markov Chain Monte Carlo (MCMC). This requires a large number of iterations with time per iteration scaled linearly with the number of markers (m) and the number of individuals (n). Genomic data sets are now often very large and are rapidly becoming larger. For human, 300,000 to 9 million SNPs arrays genotyped on up to 253 K individuals [26, 27] are available for association studies and disease/fitness prediction. In dairy cattle, whole genome sequence data including 39 million variants has been published by the 1000 bull genomes project [28]. When confronted with such huge genomic data, Bayesian methods can be so computationally expensive that it is not possible to use them.

Two approaches have been used to develop more computationally efficient algorithms for implementing Bayesian mixture models. One is to modify MCMC with speed-up schemes. For example, Moser et al. [8] introduced a “500SNPs” scheme to pick 500 SNPs with non-zero effects to be updated instead of all the SNPs. Such modification schemes could reduce the running time by 3 ~ 6 fold. Calus et al. [29] proposed a right-hand-side updating algorithm to cluster multiple SNPs (similar to a haplotype) to be updated as one during MCMC iterations. The results on 50 K SNP panels demonstrated up to 90 % reduction in computational time without reducing prediction accuracy. The other approach is to introduce heuristic methods (e.g. iterated conditional expectation, ICE; expectation maximisation, EM) as an alternative to MCMC. There are a wide range of fast versions of Bayesian approaches to genomic prediction using these methods (including fastBayesB, emBayesB, emBayesR) [30–35], which are several orders faster than MCMC implementations. However, none of these algorithms gives consistently as high prediction accuracy as their MCMC counterparts. The EM method of Wang et al. [30], emBayesR, gave higher accuracy than ICE based methods but still had a reduction in accuracy of 5 % ~ 7 % for traits with mutations of moderate to large effect. In other words, the heuristic approximations works best when there are no mutations of moderate to large effect, otherwise accuracy can be compromised. This is undesirable, especially when the largest advantage of the non-linear Bayesian methods over BLUP is observed when there are mutations of moderate to large effect (where moderate effect can mean a QTL explaining 1 % of the variance if the data set is large)!

Motivated by the deficiency of both MCMC (long computing terms) and fast versions of nonlinear models (lower prediction accuracy with some genetic architectures), we hypothesise that a hybrid scheme, beginning with EM iterations and finishing with MCMC sampling iterations, would give similar prediction accuracy to a full MCMC implementation, while having a significant speed advantage. Here we propose a hybrid algorithm (termed HyB_BR) of Expectation-Maximisation (EM) (emBayesR) and MCMC under the BayesR model. The algorithm also incorporates a speed-up scheme where only a proportion of SNP continue to be sampled in MCMC iterations. In comparison with emBayesR [30], the main improvement is that HyB_BR introduces a limited number of MCMC iterations after EM to improve the solutions from emBayesR.

To evaluate the predictive ability and computational efficiency of HyB_BR, prediction accuracy was compared with BayesR and GBLUP in two data sets. The first data set was 800 K SNP genotypes in 16,214 Holstein and Jersey bulls and cows. The prediction accuracy within these breeds and in a third breed (Aussie Red) was evaluated. The results showed that HyB_BR achieved very similar prediction accuracy to BayesR, while reducing the running time by up to 17 fold, and overcoming the limitations of slightly reduced accuracy of emBayesR. As a result of running the algorithm, the posterior probability of each SNP being in the model was derived, and this was used for QTL mapping. The resulting QTL regions were compared between the approaches and with previous literature reports. The results demonstrated that HyB_BR has enough power to detect the major known genes affecting milk production traits in dairy cattle as well as some novel regions. HyB_BR was also evaluated in a second data set - the Welcome Trust Case Control Consortium (WTCCC) human disease data set [27]. The results demonstrated that HyB_BR is a promising method for risk prediction and genetic architecture inference for human disease traits as well.

Methods

The mixture data model

The overall model at the level of the data for HyB_BR (independent of MCMC and EM implementation) including all the relevant parameters and priors is described first. The model assumes that y, the phenotypic records of n individuals, is a linear model of fixed effects (β), SNP effect (g), random polygenic effects (v) and environmental errors (e):

$$ \mathbf{y}=\mathbf{X}\boldsymbol{\upbeta } +\mathbf{Zg}+\mathbf{W}\mathbf{v}+\mathbf{e}, $$
(1)

where,

β = vector of p fixed effects, following uninformative priors.

g = vector of m SNP effects. For each SNP, \( {g}_i\sim b\left(i,1\right)\times N\left(0,0*{\sigma}_g^2\right)+b\left(i,2\right)\times N\left(0,0.0001*{\sigma}_g^2\right)+b\left(i,3\right)\times N\left(0,0.001*{\sigma}_g^2\right)+b\left(i,4\right)\times N\left(0,0.01*{\sigma}_g^2\right), \)in which σ 2 g is the genetic variance of the trait and b(i, k) is a scalar with two possible values {0, 1}, determining whether or not the effect of the i th SNP is derived from the k th distribution.

Pr = vector of probabilities where Pr k  = scalar with the value range between 0 and 1. The parameter Pr defines the proportion of all the SNPs following each of four normal distributions k. Pr k is assumed to follow a Dirichlet distribution with the parameter α = (1, 1, 1, 1)T.

v = vector of q polygenic effects (breeding values, for the proportion of variance not explained by the SNP), with v ~ N(0, A σ 2 a ), A is the q × q pedigree-based relationship matrix, σ 2 a is the polygenic variance, q is the number of individuals in the pedigree.

e = vector of n residual errors. For cattle data, e ~ N(0, Eσ 2 e ), where E is a n × n diagonal matrix so that the error variance associated with different records can vary. For example, for bulls, the phenotype would be daughter yield deviations, which would have a lower error variance than the trait deviations (TD) of cows [36]. For human data where all phenotypes have the same magnitude of error, E matrix can be replaced by the identity matrix I.

X = n × p design matrix, allocating phenotypes y to fixed effects β.

Z = a n × m genotype matrix with elements \( {\mathbf{z}}_{\mathrm{ij}}=\left({\mathbf{s}}_{\mathrm{ij}}-2{p}_i\right)/\sqrt[2]{2{p}_i\left(1-{p}_i\right)} \), in which s ij is the genotypes of the j th individual for the i th SNP (0, 1 or 2 copies of the second allele), and p i is the allele frequency of each SNP i.

W = n × q design matrix, aims at allocating the q × 1 vector of polygenic effects to y.

Note that model (1) extends the model used by Wang et al. [30] to include fixed effects, polygenic effects and weights.

The prior distribution of each SNP effect g i conditional on b(i, k) is

$$ \mathrm{p}\left({g}_i\Big|b\left(i,k\right)\right)=\left\{\begin{array}{c}\hfill \delta \left({g}_i\right),\ b\left(i,1\right)=1\ \hfill \\ {}\hfill \frac{1}{\sqrt{2\pi {\upsigma}_{\mathrm{i}}^2\left[k\right]}} \exp \left(-\frac{g_i^2}{2{\upsigma}_{\mathrm{i}}^2\left[k\right]}\right),\ b\left(i,k\right)=1\left(k=2,3,4\right)\hfill \end{array}\right.\ . $$

Where, δ(gi) denotes the Dirac delta function with all probability mass at gi = 0.

The joint distribution p(g i , b(i, k)|Pr k ) (i.e. conditional on Pr k ) can be written as:

$$ \begin{array}{l}p\left({g}_i,b\left(i,k\right)\Big|P{r}_k\right)={\displaystyle {\prod}_{k=1}^4p}\left({g}_i\Big|b\left(i,k\right)\right)\times p\left(b\left(i,k\right)\Big|P{r}_k\right)\\ {}\kern3.5em ={\left(\updelta \left({g}_i\right)P{r}_1\right)}^{b\left(i,1\right)}{{\displaystyle {\prod}_{k=2}^4\left(\frac{1}{\sqrt{2{\uppi \upsigma}_{\mathrm{i}}^2\left[k\right]}} \exp \left(-\frac{g_i^2}{2{\upsigma}_{\mathrm{i}}^2\left[k\right]}\right)P{r}_k\right)}}^{b\left(i,k\right)}\end{array} $$
(2)

The implementation of HyB_BR with the mixture model defined above consists of two components: 1) The Expectation-Maximization module. HyB_BR first implements the EM iterations under the mixture Gaussian model (Eq. 2) to give approximations for the parameter set including SNP effects g, proportion of SNP in each distribution Pr, error variance σ 2 e , and polygenic variance σ 2 a . For the estimation of each SNP effect, the PEV (predicted error variance) correction is introduced to account for the errors which are generated from the estimations of all other SNP effects (detailed in Additional file 1). 2) MCMC module. Once the EM steps are converged, the output values of the parameters are used in the modified MCMC iterations as the start values. For the final step, a MCMC scheme is implemented with a limited number of iterations.

EM module

In the following EM modules, the parameter set θ = {g, Pr, β, v, σ 2 e } will be estimated by their maximum a posteriori (MAP) value. Similar to emBayesR [30], all the parameters θ were estimated according to the expectation-maximisation process with steps:

  1. i)

    Define the log likelihood f(y|θ) of the data under the data model (1).

  2. ii)

    Derive the log posterior function of the parameters using Bayes’ theorem. Following Bayes’ theorem, the log posterior distribution of the parameter sets θ is based on the rule logp(θ|y) ∝ logf(y|θ) + logp(θ), with p(θ) the prior for the parameter.

  3. iii)

    Take the expectation on the posterior function over the missing data.

  4. iv)

    Differentiate the expected posterior function and solve for this equal to zero to obtain MAP (Maximum A Posterior) of the parameter set θ.

In the Expectation-maximization implementation, the posterior distributions for each parameter p(θ|y) are obtained while “integrating out” the other parameters. For example, for the estimation of each SNP effect g i (SNP i in the vector g), we maximize the posterior distribution of each SNP effect p(g i |y, b(i, k), Prk, β, v, σ 2 e ) by integrating out the other SNP effects g j ≠ i , the parameters b(i, k), β, v, but we fix the proportion parameter Prk and the error variance σ 2 e at their maximum posterior estimates. In the following, we will detail the inference process for several key parameters including SNP effects (g), the mixing parameters (Pr k ), fixed effects (β), polygenic effects (v) and the error variance (σ 2 e ) separately:

  1. 1)

    Estimation of SNP effects g

As in our EM version of BayesR [30], in HyB_BR we will update the estimated effect of SNPs one at a time. Therefore, we rewrite Zg in Eq. (1) as the sum of the effect of the current SNP Z i g i and the combined effect of all other SNP effects u i (u i  = ∑ j ≠ i Z j g j ). We rewrite the model (1) as:

$$ \mathbf{y}=\mathbf{X}\boldsymbol{\upbeta } +{\mathbf{Z}}_{\mathbf{i}}{g}_i+{\mathbf{u}}_{\boldsymbol{i}}+\mathbf{W}\mathbf{v}+\mathbf{e} $$
(3)

where, g i (the effect of SNP i) is the i th element of the vector g, and u i  = ∑ j ≠ i Z j g j .

We estimate of ĝ i by the value of g i that maximises the posterior probability \( \mathrm{P}\left({g}_i\Big|\mathbf{y},\widehat{\mathbf{P}}\mathbf{r},\widehat{\upsigma_e^2}\right) \) where \( \widehat{\mathbf{P}}\mathbf{r} \) and \( \widehat{\upsigma_e^2} \) are the MAP estimates of Pr and σ 2 e conditional on y.

To perform this, we first introduce “missing data” (b(i, k), β, v, u i ), and then “integrate them out” via the Expectation-Maximisation steps. In detail, the marginal posterior distribution of each SNP effect g i can be written as:

\( p\left({g}_i,b\left(i,k\right)\Big|\mathbf{y},\boldsymbol{\upbeta}, \mathbf{v},{\mathbf{u}}_{\boldsymbol{i}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)\propto p\left(\mathbf{y}\Big|{g}_i,b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},{\mathbf{u}}_{\boldsymbol{i}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)p\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right). \)

Under the model (3), the first term \( p\left(\mathbf{y}\Big|{g}_i,b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},{\mathbf{u}}_{\boldsymbol{i}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right) \) is obtained according to the following normal distribution:

y − Xβ − Z i g i  − Wv − u i  ~ N(0, Eσ 2e ),

which can be transformed as:

$$ {\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathbf{i}}{g}_i\sim N\left(0,\ \mathbf{E}{\upsigma}_{\mathrm{e}}^2\right), $$

Where, e* = y − Xβ − Wv − u i .

Therefore, the term \( p\left(\mathbf{y}\Big|{g}_i,b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},{\mathbf{u}}_{\boldsymbol{i}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right) \) can be written as: \( p\left(\mathbf{y}\Big|{g}_i,{\mathbf{u}}_{\boldsymbol{i}},b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)=\frac{1}{{\left(2\pi \widehat{\sigma_e^2}\right)}^{\frac{n}{2}}}\frac{1}{\left|\mathbf{E}\right|} exp\left[-\frac{1}{2\widehat{\sigma_e^2}}\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{g}_i\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{g}_i\right)\right] \)

Then the log likelihood function is:

$$ logp\left(\mathbf{y}\Big|{g}_i,{\mathbf{u}}_{\boldsymbol{i}},b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)=-\frac{\mathrm{n}}{2} \log \widehat{\upsigma_{\mathrm{e}}^2}- \log \left|\mathbf{E}\right|-\frac{1}{2\widehat{\upsigma_{\mathrm{e}}^2}}\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{g}_i\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{g}_i\right) $$
(4)

Ignoring an additive constant, the second term \( p\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right) \) is defined in the Eq. (2). Then the log of \( p\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right) \) is:

$$ \begin{array}{l} logp\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right)=b\left(i,1\right) \log \left(\delta \left({g}_i\right){\widehat{Pr}}_1\right)\\ {}\kern15em +{\displaystyle {\sum}_{\mathrm{k}=2}^4b}\left(i,k\right)\left(-\frac{1}{2}{ \log \upsigma}_i^2\left[k\right]-\frac{g_i^2}{2{\upsigma}_i^2\left[k\right]}+ \log {\widehat{Pr}}_{\mathrm{k}}\right)\end{array} $$
(5)

Treating (e*, b(i, k)) as missing data and omitting the terms without g i , the expectation of the log marginal posterior of each SNP effect is:

$$ \begin{array}{l}{E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left({g}_i,b\left(i,k\right)\Big|\mathbf{y},\boldsymbol{\upbeta}, \mathbf{v},{\mathbf{u}}_{\boldsymbol{i}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)\\ {}={E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left(\mathbf{y}\Big|{g}_i,{\mathbf{u}}_{\boldsymbol{i}},b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)+{E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right)\end{array} $$

According to Eq (4), the expectation of the first term is:

$$ \begin{array}{l}{E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left(\mathbf{y}\Big|{g}_i,{\mathbf{u}}_{\boldsymbol{i}},b\left(i,k\right),\boldsymbol{\upbeta}, \mathbf{v},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)\kern0.5em \\ {}\kern3em \propto -\frac{1}{2\widehat{\upsigma_{\mathrm{e}}^2}}\left\{\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{\mathrm{g}}_{\mathrm{i}}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left({\mathbf{e}}^{*}-{\mathbf{Z}}_{\mathrm{i}}{\mathrm{g}}_{\mathrm{i}}\right)+tr\left({\mathbf{E}}^{-1}\mathrm{P}\mathrm{E}\mathrm{V}\left({\mathbf{e}}^{*}\right)\right)\right\}\end{array} $$
(6)

According to the Eq. (5), the expectation of the second term is:

$$ \begin{array}{l}{E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left({g}_i,b\left(i,k\right)\Big|{\widehat{Pr}}_k\right)\\ {}\propto P\left(i,1\right) \log \left(\delta \left({g}_i\right){\widehat{Pr}}_1\right)+{\displaystyle {\sum}_{\mathrm{k}=2}^4P}\left(i,k\right)\left(-\frac{1}{2}{ \log \upsigma}_i^2\left[k\right]-\frac{g_i^2}{2{\upsigma}_i^2\left[k\right]}+ \log {\widehat{Pr}}_{\mathrm{k}}\right)\end{array} $$
(7)

Where, \( P\left(i,k\right)=E\left(b\left(i,k\right)\Big|\mathbf{y},\ {\widehat{Pr}}_k\right) \). The term P(i, k) can be derived as in the Additional file 2.

Hence, in the Maximisation steps of EM, we differentiate Eqs. (6) and (7) with respect to ĝ i , and then obtain an estimate for the SNP effect as:

$$ \begin{array}{l}\frac{\partial {E}_{{\mathbf{e}}^{*},b\left(i,k\right)} logp\left({g}_i,{\mathbf{u}}_{\boldsymbol{i}},b\left(i,k\right)\Big|\mathbf{y},\widehat{\boldsymbol{\upbeta}},\widehat{\mathbf{v}},\widehat{\upsigma_{\mathrm{e}}^2},\ {\widehat{Pr}}_k\right)}{\partial {\mathrm{g}}_i}=\left[-{\displaystyle \sum_{\mathrm{k}=2}^4\frac{P\left(i,k\right)}{\upsigma_i^2\left[k\right]}}-\frac{{\mathbf{Z}}_{\mathrm{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathbf{i}}}{\widehat{\upsigma_{\mathrm{e}}^2}}\right]{g}_i+\frac{{\mathbf{Z}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{e}}^{*}}{\widehat{\upsigma_{\mathrm{e}}^2}}=0\\ {}{\widehat{g}}_i={\left[{\mathbf{Z}}_{\mathrm{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathrm{i}}+{\displaystyle {\sum}_{k=1}^4\left(P\left(i,k\right)\widehat{\upsigma_{\mathrm{e}}^2}{\upsigma}_i^2\left[k\right]\right)}\right]}^{-1}\left[{\mathbf{Z}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{e}}^{*}\right]\end{array} $$
(8)
  1. 2)

    Estimation of parameter Pr

This follows a common method for an EM algorithm to analyse a mixture of distributions. We introduce the ‘missing data’ b(i, k) which is the indicator variable that indicates which of the k = 4 distributions SNP effect i is drawn from. The posterior distribution of proportion parameter Pr is:

$$ p\left(\mathbf{Pr},\mathbf{b}\Big|\mathbf{y}\right)\propto p\left(\mathbf{y}\Big|\mathbf{b}\right)p\left(\mathbf{b}\Big|\mathbf{Pr}\right)p\left(\mathbf{Pr}\right) $$

Where,

The term p(y|b) does not involve Pr. So when we differentiate with respect to Pr, this term will drop out and therefore can be ignored.

$$ \begin{array}{l}p\left(\mathbf{b}\Big|\mathbf{Pr}\right)={\displaystyle {\prod}_{i=1}^n{\displaystyle {\prod}_{k=1}^4{\left(P{r}_k\right)}^{b\left(i,k\right)}}}\\ {}p\left(\mathbf{Pr}\right)=\kern0.5em {\displaystyle {\prod}_{k=1}^4P{r}_k}\kern1em \end{array} $$

Therefore, the log posterior expression of Pr can be written as:

$$ \begin{array}{l} logp\left(\mathbf{Pr},\mathbf{b}\Big|\mathbf{y}\right)\propto logp\left(\mathbf{b}\Big|\mathbf{Pr}\right)+ logp\left(\mathbf{Pr}\right)\\ {}\kern11em ={\displaystyle {\sum}_{i=1}^n{\displaystyle {\sum}_{k=1}^4b}}\left(i,k\right) logP{r}_k+{\displaystyle {\sum}_{k=1}^4 logP{r}_k.}\end{array} $$

Treating b as the missing data and defining P(i, k) = E(b(i, k)|y, Pr k ), the expectation of the posterior can be written as:

$$ {E}_{\mathbf{b}\Big|\mathbf{y}} logp\left(\mathbf{Pr},\mathbf{b}\Big|\mathbf{y}\right)={\displaystyle {\sum}_{i=1}^n{\displaystyle {\sum}_{k=1}^4P}}\left(i,k\right) logP{r}_k+{\displaystyle {\sum}_{k=1}^4 logP{r}_k.} $$
(9)

Introducing Lagrange multiplier λ to account for the constraint that ∑ 4 k = 1 Pr k  = 1 and differentiate with respect to Pr k , the parameter Pr can be estimated by:

$$ \begin{array}{l}\frac{\partial {\mathrm{E}}_{\mathbf{b}\Big|\mathbf{y}}\left[ logp\left(\mathbf{Pr},\mathbf{b}\Big|\mathbf{y}\right)+\uplambda \left({\displaystyle {\sum}_{\mathrm{k}=1}^4}P{r}_k-1\right)\right]}{\partial P{r}_k}=\frac{{\displaystyle {\sum}_{i=1}^m}P\left(i,k\right)}{P{r}_k}+\frac{1}{P{r}_k}+\lambda =0\\ {}\kern8.5em P{r}_k=\frac{{\displaystyle {\sum}_{\mathrm{i}=1}^m}P\left(i,k\right)+1}{{\displaystyle {\sum}_{k=1}^4}\left({\displaystyle {\sum}_{i=1}^m}\kern0.5em P\left(i,k\right)+1\right)}\end{array} $$
(10)

The computation of P(i, k) is given in the Additional file 2.

  1. 3)

    Estimation of fixed effects (β) and the error variance (σ 2 e )

Since fixed effects (β) and the error variance has uninformative priors, their posterior distribution is:

$$ p\left({\sigma}_e^2,\boldsymbol{\upbeta}, \widehat{\mathbf{g}}\Big|\mathbf{y}\right)=\frac{1}{{\left(2\pi {\sigma}_e^2\right)}^{\frac{n}{2}}}\frac{1}{\left|\mathbf{E}\right|} exp\left[-\frac{1}{2{\sigma}_e^2}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}\right)\right] $$

As \( \mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}=\mathbf{e} \), the full log likelihood based on this model is:

$$ logp\left({\sigma}_e^2,\boldsymbol{\upbeta}, \widehat{\mathbf{g}}\Big|\mathbf{y}\right)=-\frac{\mathrm{n}}{2}{ \log \upsigma}_{\mathrm{e}}^2+\frac{1}{2{\upsigma}_{\mathrm{e}}^2}\mathbf{e}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{e} $$
(11)

Treating e as the missing data, the expectation of the Eq. (11) can be expressed as

$$ \begin{array}{l}{\mathrm{E}}_{\mathbf{e}\Big|\mathbf{y}} logp\left({\sigma}_e^2,\boldsymbol{\upbeta}, \widehat{\mathbf{g}}\Big|\mathbf{y}\right)\\ {}={\mathrm{E}}_{\mathbf{e}\Big|\mathbf{y}}\left[-\frac{\mathrm{n}}{2}{ \log \upsigma}_{\mathrm{e}}^2+\frac{1}{2{\upsigma}_{\mathrm{e}}^2}\mathbf{e}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{e}\right]\\ {}=-\frac{\mathrm{n}}{2}{ \log \upsigma}_{\mathrm{e}}^2+\frac{1}{2{\upsigma}_{\mathrm{e}}^2}\left[\mathbf{e}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{e}+tr\left({\mathbf{E}}^{-1}\mathrm{P}\mathrm{E}\mathrm{V}\left(\mathbf{e}\right)\right)\right]\end{array} $$

In theory, PEV(e) ≠ PEV(e*) due to e = e* + Z i g i . However, since each SNP effect is shrunk severely towards zero by GBLUP [4], we approximate PEV(e) ≅ PEV(e*). The calculation of the term PEV(e*) is detailed in the Additional file 1.

Therefore, differentiating the equation E e|y logp(σ 2 e , β, ĝ|y) with regard to σ 2e and b, we achieve:

$$ \widehat{\upsigma_{\mathrm{e}}^2}=\frac{1}{\mathrm{n}}\left[\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}\right)+tr\left({\mathbf{E}}^{-1}\mathrm{P}\mathrm{E}\mathrm{V}\left({\mathbf{e}}^{*}\right)\right)\right] $$
(12)
$$ \widehat{\boldsymbol{\upbeta}}={\left(\mathbf{X}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{X}\right)}^{-1}\mathbf{X}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{W}\widehat{\mathbf{v}}\right) $$
(13)
  1. 4)

    Estimation of polygenic effects (v)

Under the model (1), the conditional posterior density function of polygenic effects v is:

$$ p\left(\mathbf{v}\Big|\mathbf{y}\right)=p\left(\mathbf{y}\Big|\mathbf{v},\widehat{\mathbf{g}},\widehat{\boldsymbol{\upbeta}},\widehat{\sigma_e^2}\right)p\left(\mathbf{v}\right) $$

Where,

$$ p\left(\mathbf{y}\Big|\mathbf{v},\widehat{\mathbf{g}},\widehat{\boldsymbol{\upbeta}},\widehat{\sigma_e^2}\right)=\frac{1}{{\left(2\pi {\sigma}_e^2\right)}^{\frac{n}{2}}}\frac{1}{\left|\mathbf{E}\right|} exp\left[-\frac{1}{2{\sigma}_e^2}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\widehat{\mathbf{g}}-\mathbf{W}\mathbf{v}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\widehat{\boldsymbol{\upbeta}}-\mathbf{W}\mathbf{v}\right)\right] $$
(14)
$$ p\left(\mathbf{v}\right)=\frac{1}{{\left(2\pi {\upsigma}_{\mathrm{a}}^2\right)}^{\frac{q}{2}}}\frac{1}{\left|\mathbf{A}\right|} exp\left[-\frac{1}{2{\sigma}_a^2}\mathbf{v}\mathit{\hbox{'}}\;{\mathbf{A}}^{-1}\mathbf{v}\right] $$
(15)

Therefore, the log posterior based on Eqs. (14) and (15) is:

$$ \begin{array}{l} logp\left(\mathbf{v}\Big|\mathbf{y}\right)= logf\left(\mathbf{y}\Big|\mathbf{v},\widehat{\mathbf{g}},\widehat{\boldsymbol{\upbeta}},\widehat{\sigma_e^2}\right)+ logp\left(\mathbf{v}\right)\\ {}=\left[-\frac{\mathrm{n}}{2} \log \widehat{\upsigma_{\mathrm{e}}^2}- \log \left|\mathbf{E}\right|+\frac{1}{2\widehat{\upsigma_{\mathrm{e}}^2}}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\widehat{\boldsymbol{\upbeta}}-\mathbf{W}\mathbf{v}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\widehat{\boldsymbol{\upbeta}}-\mathbf{W}\mathbf{v}\right)\right]\\ {}+\left[-\frac{\mathrm{q}}{2}{ \log \upsigma}_{\mathrm{a}}^2- \log \left|\mathbf{A}\right|+\frac{1}{2{\upsigma}_{\mathrm{a}}^2}\mathbf{v}\mathit{\hbox{'}}\;{\mathbf{A}}^{-1}\mathbf{v}\right]\end{array} $$
(16)

According to the equation \( \mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\boldsymbol{\upbeta } -\mathbf{W}\widehat{\mathbf{v}}=\mathbf{e} \), the Eq. (16) can be written as:

$$ \begin{array}{l} logp\left(\mathbf{v}\Big|\mathbf{y}\right)= logf\left(\mathbf{y}\Big|\mathbf{v},\widehat{\mathbf{g}},\widehat{\boldsymbol{\upbeta}},\widehat{\sigma_e^2}\right)+ logp\left(\mathbf{v}\right)\\ {}=\left[-\frac{\mathrm{n}}{2} \log \widehat{\upsigma_{\mathrm{e}}^2}- \log \left|\mathbf{E}\right|+\frac{1}{2\widehat{\upsigma_{\mathrm{e}}^2}}\mathbf{e}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{e}\right]\\ {}+\left[-\frac{\mathrm{q}}{2}{ \log \upsigma}_{\mathrm{a}}^2- \log \left|\mathbf{A}\right|+\frac{1}{2{\upsigma}_{\mathrm{a}}^2}\mathbf{v}\mathit{\hbox{'}}\;{\mathbf{A}}^{-1}\mathbf{v}\right]\end{array} $$
(17)

Taking expectation over the missing data e, we get:

$$ \begin{array}{l}{\mathrm{E}}_{\mathbf{e}\Big|\mathbf{y}} logp\left(\mathbf{v}\Big|\mathbf{y}\right)=\left[-\frac{\mathrm{n}}{2} \log \widehat{\upsigma_{\mathrm{e}}^2}- \log \left|\mathbf{E}\right|+\frac{1}{2\widehat{\upsigma_{\mathrm{e}}^2}}\mathbf{e}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{e}+tr\left({\mathbf{E}}^{-1}\mathrm{P}\mathrm{E}\mathrm{V}\left(\mathbf{e}\right)\right)\right]\\ {}\kern9.5em +\left[-\frac{\mathrm{q}}{2}{ \log \upsigma}_{\mathrm{a}}^2- \log \left|\mathbf{A}\right|+\frac{1}{2{\upsigma}_{\mathrm{a}}^2}\mathbf{v}\mathit{\hbox{'}}\;{\mathbf{A}}^{-1}\mathbf{v}\right]\end{array} $$
(18)

Differentiating the Eq. (18) with regards to v, we get:

$$ \widehat{\mathbf{v}}={\left(\mathbf{W}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{W}{\upsigma}_{\mathrm{a}}^2+{\upsigma}_{\mathrm{e}}^2{\mathbf{A}}^{-1}\right)}^{-1}{\upsigma}_{\mathrm{a}}^2\mathbf{W}\hbox{'}{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{X}\widehat{\boldsymbol{\upbeta}}\right) $$
(19)

Where, for simplicity, the variance σ 2a . will be fixed as the specified value from GBLUP estimation.

Table 1 lists all the parameters and their equation derived from EM steps.

Table 1 The list of all the estimated parameters including the possibility for each SNP (P(i, k)), the proportion parameter (Pr), each SNP effect (g i ), error variance (σ 2 e ), fixed effect (β), and polygenic effects v and the according equation derived from EM steps
Full size table

Steps for EM module

The overall procedure of EM is described by means of the pseudo code, steps ①~⑦. Here we will detail these steps according to their sequence appearing in the pseudocode descriptions:

  • Step EM_①: Initialise the parameters g, Pr, σ 2 i and Construct X, A, G, E, W matrices. Similar to emBayesR [30], the starting values of g and Pr were set as g = 0.01 and Pr = {0.5, 0.487, 0.01, 0.003}, while σ 2 i  = {0, 0.0001 * σ 2g , 0.001 * σ 2g , 0.01 * σ 2g }. The genetic variance σ 2g and polygenic variance σ 2a are obtained from GBLUP. Both variances won’t be updated during EM iterations.

    The n × 3 matrix X is a design matrix, allocating the phenotypes to fixed effects. In our case, the matrix X is set up with the first column being the mean, the second and third columns defining the breeds (Holstein or Jersey) and sex (bulls or cows) of the cattle. For example, if the i th animal is a Holstein bull, then x i,2 = 1 with x i,3 = 0.

    The Pedigree relationship matrix A is built using Henderson’s rules [37]; while the genomic relationship matrix G is constructed using the equation G = ZZ ' /n. Diagonal error matrix E is calculated following Garrick et al. [36], and the index matrix W maps individuals in the pedigree to the phenotypes if they have ones.

  • Step EM_②: Calculate the PEV matrix under model 1 (Additional file 1). Then using PEV matrix, calculate \( tr\left({\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathbf{i}}{\mathbf{Z}}_{\mathbf{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}\mathbf{P}\mathbf{E}{\mathbf{V}}_{{\mathbf{u}}_1}\left(\mathbf{e}\right)\right) \) which is used in the equation for \( {E}_{e^{*}} logP\left(i,k\right) \) (Additional file 2). In theory, the calculation of this term should be updated each EM iteration, which is time consuming. To avoid huge computational burden, the PEV matrix is treated as constant value for the term \( tr\left({\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathbf{i}}{\mathbf{Z}}_{\mathbf{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}\mathbf{P}\mathbf{E}{\mathbf{V}}_{{\mathbf{u}}_1}\left(\mathbf{e}\right)\right) \) in front of EM loop.

    Then for each SNP i (i in 1 to m)

  • Step EM_③: Correct y for the effects of all other SNPs except current SNP i with equation \( {\mathbf{y}}^{\dagger }=\mathbf{y}-{\displaystyle {\sum}_{\mathrm{j}\ne \mathrm{i}}\kern0.5em {\mathbf{Z}}_{\mathbf{j}}}\kern0.5em {\widehat{\mathrm{g}}}_{\mathrm{j}}-\mathbf{X}\widehat{\mathbf{b}}-\mathbf{W}\widehat{\mathbf{v}}. \)

  • Step EM_④: Estimate the probability that the effect of SNP i is from one of four normal distributions \( {E}_{e^{*}} logP\left(i,k\right) \) with the equation (S3). After this, P(i, k) is calculated with the equation \( exp\left({E}_{e^{*}} log{P}_{ik}/{\displaystyle {\sum}_{k=1}^4 exp\kern0.5em }\left({E}_{e^{*}} log{P}_{ik}\right)\right) \) (S4).

  • Step EM_⑤: the SNP effect ĝ i is updated via Eq. (8).

    After effects have been estimated for all SNP,

  • Step EM_⑥: Estimate σ 2 e with Eq. (12), fixed effects β with Eq. (13), update Pr k with Eq. (10), and update polygenic effects v with the Eq. (19).

  • Step EM_⑦: Assess convergence criterion (ĝ l − ĝ l − 1) ' (ĝ l − ĝ q − 1)/((ĝ l' ĝ l) ≤ 10− 10 with l being the EM iterations number. If not converged, then return to Step ③ for the next EM iteration; otherwise, exit the EM iterations and return the estimates of parameters from the final iterations.

Modified MCMC module with speed-up scheme

The outputs of the EM including SNP solutions, polygenic effects, error variance and genetic variance are used as starting values of parameters for the MCMC module, which allows MCMC to begin with no burn in.

The MCMC module of HyB_BR implements the same Gibbs sampling processes as BayesR [15] but modified with one speed-up scheme as follows. Over the first 500 iterations, the average probability that the SNP effect is zero (p(i, 1)) is calculated. If p(i, 1) ≥ a, then the SNP effect is set to zero and is not updated in future iterations.

The test for selecting a reasonable value of the parameter a was conducted as follows. The impact of value of a from 0.85 to 0.95 on prediction accuracy was investigated for the milk production traits and fertility, Fig. 1. The results show that criterion p(i, 1)≥, 1, is the lowest threshold which gives an accuracy very close to the maximum. The criterion means SNP i has more than 90 % probability of having no effect.

Fig. 1
figure 1

The trend of prediction accuracy according to a range of values of the threshold parameter a

Full size image

The modified MCMC steps can then be described as follows:

  • Step MCMC_①: sampling the error variance \( {\widehat{\upsigma}}_{\mathrm{e}}^2 \) according to the distribution \( {\widehat{\upsigma}}_{\mathrm{e}}^2\sim Inv-{\upchi}^2\left(n-2,\frac{{{\mathbf{y}}^{*}}^{\hbox{'}}{\mathbf{E}}^{-1}{\mathbf{y}}^{*}}{n-2}\right) \), with \( {\mathbf{y}}^{*}=\left(\mathbf{y}-\mathbf{Zg}-\mathbf{X}\widehat{\boldsymbol{\upbeta}}-\mathbf{W}\widehat{\mathbf{v}}\right). \)

  • Step MCMC_②: sampling the fixed effects β from the distribution \( N\Big(\ {\boldsymbol{\upbeta}}_{\mu },{\left(\mathbf{X}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{X}\right)}^{-1}{\widehat{\upsigma}}_{\mathrm{e}}^2 \)), with \( {\boldsymbol{\upbeta}}_{\mu }={\left(\mathbf{X}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{X}\right)}^{-1}\mathbf{X}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\left(\mathbf{y}-\mathbf{Z}\widehat{\mathbf{g}}-\mathbf{W}\widehat{\mathbf{v}}\right) \).

  • Step MCMC_③: Polygenic variance is sampled \( {\widehat{\upsigma}}_{\mathrm{a}}^2\sim Inv-{\upchi}^2\left(n-2,\frac{\widehat{\mathbf{v}}\mathit{\hbox{'}}\;{\mathbf{A}}^{-1}\widehat{\mathbf{v}}}{n-2}\right) \).

  • Step MCMC_④: The polygenic effects are sampled from normal distribution N(μ, s), with the mean \( \mu =\widehat{\mathbf{v}} \) from Eq. (19) and the variance\( s={\left(\mathbf{W}\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}\mathbf{W}+{\mathbf{A}}^{-1}{\upsigma}_{\mathrm{e}}^2/{\upsigma}_{\mathrm{a}}^2\right)}^{-1}. \)

    Then for each SNP i (i in 1 to m),

  • Step MCMC_⑤: Implement the speed-up scheme : if (iterations > 500) and (P(i, 1) > 0.9), then stop updating this SNP i.

    Else,

  • Step MCMC_⑥: Estimate the log likelihood that the effect of SNP i is from one of four normal distributions L(g i |σ 2 i [k]). Following the derivation steps of Kemper et al. [15], the optimised equation of the log likelihood function is

    \( \begin{array}{c}L\left({g}_i\Big|{\upsigma}_i^2\left[k\right]\right)=-\frac{1}{2}\left\{ \log \left({\upsigma}_i^2\left[k\right]{\mathbf{Z}}_{\mathbf{i}}^{\boldsymbol{\hbox{'}}}{\mathbf{Z}}_{\mathbf{i}}+{\upsigma}_{\mathrm{e}}^2\right)+{\left(\left({e}^{*}\right)\mathit{\hbox{'}}\;{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathbf{i}}\right)}^2{\upsigma}_i^2\left[k\right]{\upsigma}_{\mathrm{e}}^{-2}/\left({\upsigma}_i^2\left[k\right]{\mathbf{Z}}_{\mathbf{i}}^{\boldsymbol{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathbf{i}}+{\upsigma}_{\mathrm{e}}^2\right)\right\}\\ {}+ log{ \Pr}_{\mathrm{k}},\end{array} \)

    with e* = y − Xβ − u − Wv.

    After this, P(i, k) is calculated with the equation:\( exp\Big(L\left({g}_i\Big|{\upsigma}_i^2\left[k\right]\right)/{\displaystyle {\sum}_{k=1}^4 exp\kern0.5em }\left(L\left({g}_i\Big|{\upsigma}_i^2\left[k\right]\right)\right) \)

  • Step MCMC_⑦: Sample ĝ i with N(μ, s), \( \mu ={\left[{\mathbf{Z}}_{\mathrm{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathrm{i}}+\frac{\widehat{\upsigma_{\mathrm{e}}^2}}{\upsigma_i^2\left[k\right]}\right]}^{-1}\left[{\mathbf{Z}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}\ {e}^{*}\right] \), and \( s={\left[{\mathbf{Z}}_{\mathrm{i}}^{\mathit{\hbox{'}}}{\mathbf{E}}^{-1}{\mathbf{Z}}_{\mathrm{i}}+\frac{\widehat{\upsigma_{\mathrm{e}}^2}}{\upsigma_i^2\left[k\right]}\right]}^{-1} \).

  • Step MCMC_⑧: Update Pr ~ Dirichlet(β1 + 1, β2 + 1, β3 + 1, β4 + 1),where β1, β2, …, β4 are the number of SNPs in one of four normal distributions.

    Return to MCMC step 1.

    HyB_BR was written in the C++ programming language.

Data

Cattle

One thousand seven hundred forty-five Holstein and Jersey cattle and 114 Australian Red bulls were genotyped with the 777 K Illumina HD bovine SNP chip. 15,049 Holstein and Jersey bulls and cows, 249 Australian red bulls and cows were genotyped with the 54 K Illumina Bovine SNP array. After stringent quality control and SNP filtering described in [14], there were 632,003 SNPs remaining for animals genotyped with the 777 K SNP panel, and 43,425 SNPs remaining for animals genotyped with the 54 K SNP array. Animals genotyped with the 43,425 SNPs, were imputed to 632,003 SNP genotypes using Beagle 3.0 [38]. Therefore, the total data set was 17,157 cattle of three breeds with real or imputed genotypes for 632,003 SNP.

The phenotypes include milk yield, protein yield, fat percent(fat%), and cow fertility. The heritability of these traits varies from 0.33 (for milk yield, protein yield and fat%), to 0.03 (for cow fertility). The fertility (reproductive performance of dairy cows) is usually measured according to calving interval (CI, the number of days between successive calvings), days from calving to first service (CFS), pregnancy diagnosis, lactation length (LL), and survival to second lactation on Australian Holstein and Jersey cows [39, 40]. Here, the fertility phenotype was calving interval (CI). Here, the fertility phenotype is mainly derived from CI. The phenotypes for all the traits were daughter trait deviations (DTD) for bulls (the average of their daughters phenotypes, corrected for fixed effects), and trait deviations (TD) for cows (as described by Kemper et al. [15]). For genomic prediction, the data was separated into a reference set, where SNP effects were estimated, and validation sets, where the prediction accuracy was assessed, and the division of animals into reference and validation sets was by year of birth (youngest animals in validation set). The reference data includes bulls and cows from two breeds (Holstein and Jersey), and the predictions were evaluated in the other animals of the same breeds or in a breed (Aussie red) not included in the reference set. The exact number of individuals in these data sets for each trait is given in Table 2.

Table 2 The number of individuals in the reference sets and validations sets related to three traits including Milk yield (MilkY), Protein yield (ProtY), Fat Percent (Fat%) and Fertility
Full size table

To compare the computational time required by the different genomic prediction methods, we also used three reference sets with increasing different numbers of animals; Ref 1_ CATTLE had 3049 Holstein bulls; Ref 2_CATTLE had 11,527 Holstein bulls and cows, while Ref 3_CATTLE was the complete reference data set with 16,214 animals.

For the EM module, estimates of three variance components (σ 2 e , σ 2 v , σ 2 g ) were required as the input. We ran Asreml4.0 [41] (which is implemented with GBLUP methods) on these data sets to estimate these variance parameters and the results are listed in Table 3.

Table 3 Three input variance parameters related to the reference data sets
Full size table

The correlation between GEBV and DTD in the validation sets was used as a proxy for prediction accuracy. The regression of DTD on GEBV in the validation sets was used to investigate if any of the methods resulted in biased predictions.

Case/Control human disease trait data

For predicting human disease risk, seven disease traits of the Welcome Trust Case Control Consortium (WTCCC) genomic data [27] including bipolar disorder (BD), coronary artery disease (CAD), Crohn’s disease (CD), Hypertension (HT), rheumatoid arthritis (RA), type 1 diabetes (T1D), and type 2 diabetes (T2D) were used. Following the steps of strict QC on SNP data [7, 8, 42] with Plink [43], we had seven combined case/control data sets (one for each trait) with different number of markers and records listed in Table 4. The input parameters of seven datasets for HyB_BR including error variance and genetic variance were calculated by GCTA [44], given in Table 4. To assess prediction accuracy, for each disease, we randomly generated 20 splits of the data with 80 % of individuals for the reference set and 20 % for the validation set. To assess the prediction ability, the area under the ROC curve (AUC) [45] was calculated.

Table 4 The size and genetic architecture of seven combined control/case data sets
Full size table

Results

Compute time comparison of HyB_BR and BayesR

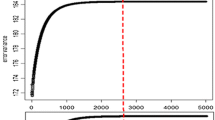
To compare computational efficiency, HyB_BR without the speed-up scheme (labelled as Hyb_BR_Orig), HyB_BR with the speed-up scheme and pure MCMC BayesR were implemented on three data sets with 632,003 markers but different numbers of records, varying from 3049 in Ref 1_CATTLE, 11,527 in Ref 2_CATTLE, to 16,214 in Ref 3_CATTLE. As used by Kemper et al. [15], pure MCMC BayesR required 40,000 iterations of complexity O(mn) with parameters estimated from samples from the posterior distributions (m is the number of markers and n is the number of individuals). The first 20,000 iterations were removed as burn in. The MCMC module of HyB_BR used only 4000 iterations and burn-in was replaced by the EM (400 iterations to convergence). 4000 cycles for the MCMC module were used after comparing results with increasing number of iterations. The results showed that 4000 were necessary to achieve maximum prediction accuracy (Fig. 2).

Fig. 2
figure 2

Prediction accuracy with an increasing number of MCMC iterations for BayesR

Full size image

The prediction accuracy was evaluated for milk yield with a reference set containing the Holstein and Jersey bulls&cows data.

With the smallest data set (Ref 1_CATTLE), 5 h compute time was required for HyB_BR compared with 96 h for BayesR MCMC (Fig. 3); 35 h required by HyB_BR instead of 410 h of BayesR for Ref 2_CATTLE; And in Ref 3_CATTLE, 42 h for HyB_BR_sp but 720 h for BayesR. These results suggest HyB_BR is at least 10 times faster than BayesR MCMC, with the speed advantage increasing as data sets became larger (17 times faster with the largest data set). The HyB_BR speed up scheme reduced compute time by approximately 50 %, compared to HyB_BR_Orig without the speed up scheme (Fig. 3), with no reduction in the prediction accuracy (Tables 5, 6 and 7).

Fig. 3
figure 3

Computational time in hours required for BayesR, HyB_BR_Orig, and HyB_BR_sp on three reference sets (Ref 1_CATTLE, Ref 2_CATTLE, Ref 3_CATTLE)

Full size image
Table 5 The accuracy and bias of with-breed prediction of GBLUP, BayesR(BR), emBayesR (EM), and HyB_BR (HB)
Full size table
Table 6 The accuracy and bias of multi-breeds prediction of GBLUP, BayesR(BR), emBayesR (EM), and HyB_BR (HB)
Full size table
Table 7 The accuracy and bias of across-breeds prediction of BayesR, GBLUP, and HyB_BR
Full size table

These timings were recorded on a server with Intel E5-2680 2.7GHz processors and 384GB of 1333 MHz RAM.

The accuracy and bias of within-breeds, multi-breeds and across-breeds prediction for four complex dairy traits

Genomic prediction with a single breed reference

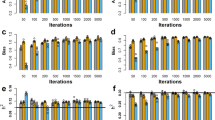
For the within-breed prediction (that is, when a Holstein reference was used to estimate SNP effects used for calculating GEBV in a Holstein validation set, and likewise for Jersey) in Table 5, HyB_BR performed as well as BayesR for all traits, including fat%. Both BayesR and HyB_BR had a 1 % ~ 6 % superiority of accuracy over GBLUP for Milk yield, Protein yield and Fat%, but had no advantage for fertility. Similarly, for the prediction of Jersey validation with Jersey reference, BayesR and HyB_BR had a consistent advantage over GBLUP for milk production traits, but not for fertility. Especially, for the trait Fat%, BayesR and HyB_BR gave very similar results, with a 17 % increase in accuracy (0.79 vs 0.73 in Holstein and 0.71 vs 0.54 in Jersey) of genomic prediction over GBLUP, as well as a 5 % increase in accuracy over emBayesR. HyB_BR and BayesR also gave regression coefficients closer to one than GBLUP for most traits.

Genomic prediction with a multi-breed reference

When predicting the Holstein or Jersey validation with the combined Holstein and Jersey reference, HyB_BR had the same accuracy as BayesR, Table 5. Compared with GBLUP, BayesR and HyB_BR gave consistently higher accuracy increase for the milk production traits, though this was not observed for fertility. And for the prediction of Jersey validation set, BayesR and HyB_BR improved accuracy for the milk production traits by 11 % compared with GBLUP. The results show that there are small but consistent accuracy improvements as a result of using the multi-breed reference (compare Tables 5 and 6), consistent with the results of Kemper et al. [15] and Hoze et al. [46].

Also, including polygenic effects (estimated using the pedigree) in the model can improve the prediction accuracy by 1 ~ 2 %, at least for milk production traits, Tables 5 and 6. However, for fertility the introduction of polygenic effects for all the prediction methods did not impact the accuracy at all.

Compared with GBLUP and emBayesR, BayesR and HyB_BR gave less biased predictions for milk production traits. However for fertility the regression values far from one indicate bias, from all methods – the low accuracy of fertility phenotypes, including in the validation set, likely contributes to this.

Genomic prediction across breeds

For predicting Australian Red validation bulls (an additional breed to those in the reference set), BayesR and HyB_BR gave higher accuracy than GBLUP for all traits (Table 7).

Across all the prediction results shown in Tables 5, 6 and 7, emBayesR had a 2 % ~ 5 % reduction in accuracy compared with BayesR and HyB_BR for fat%, while BayesR and HyB_BR gave almost identical accuracies in all cases.

Inferred genetic architecture and QTL mapping for dairy production and fertility traits

Bayes R described the genetic architecture of a trait by the posterior proportion of SNPs in each of the four different distributions. Table 8 reported the estimated proportion in each of four distributions from BayesR, emBayesR, and HyB_BR. The number of SNPs falling into the distribution with the largest variance was similar for all three methods. Compared with BayesR, HyB_BR tended to estimate more SNPs (up to 5 %) in the distribution with variance 0.001 * σ 2 g , and 0.0001 * σ 2 g . In contrast to HyB_BR, emBayesR tended to estimate that a higher proportion of SNPs have no effect than does BayesR. This may explain the lower accuracy it achieves.

Table 8 The number of SNPs in each of four distributions
Full size table

QTL mapping for dairy production and fertility traits

Both BayesR and HyB_BR estimate the posterior probability that every SNP has a non-zero effect on the trait. This is useful for QTL mapping – SNP with very high posterior probabilities of having a non-zero effect should be strongly associated with causal mutations (e.g. Moser et al. [8], Kemper et al. [15]). Then, QTL mapping from BayesR and HyB_BR can be conducted by plotting the posterior probability of each SNPs having a non-zero effect on the trait by genome position, and then comparing the genome location of the effects with a high posterior probability of being in the largest distribution for each method.

The estimated posterior possibilities of all the SNPs (y axis) related to four different traits were plotted according to the positions (base pairs) of SNPs on the whole genome (x axis) in Figs. 4, 5, 6 and 7. The top SNPs with high posterior possibilities were picked up according to the number of SNPs in the variance 0.01 * σ 2 g (the total number of markers * Pr [4]). Table 9 listed all the top SNPs in the variance related to the previously reported genes with a effect on milk production including CSF2RB [47], GC [48], GHR/CCL28 [18], PAEP [17], MGST1 [49], and DGAT1 [16]. Both BayesR and HyB_BR identified all of these regions, which demonstrated that HyB_BR can perform QTL mapping with similar precision to BayesR. For example, HyB_BR could detect the DGAT1 as well as BayesR shown in Fig. 6 (Fat%).

Fig. 4
figure 4

Mapping all the SNPs’ posterior possibilities estimated from BayesR and HyB_BR across the whole chromosome related to milk yield. The posterior possibility is calculated based on the sum of the posterior possibilities P(i, k) of each SNP with non-zero variances written as ∑ 4 k = 2 P(i, k). The blue circle is the SNPs (picked up based on the high posterior possibility following in the distribution with largest variances) with location information mapped to known genes

Full size image
Fig. 5
figure 5

Mapping all the SNPs’ posterior possibilities estimated from BayesR and HyB_BR across the whole chromosome related to protein yield. The posterior possibility is calculated based on the sum of the posterior possibilities P(i, k) of each SNP with non-zero variances written as ∑ 4 k = 2 P(i, k). The blue circle is the SNPs (picked up based on the high posterior possibility following in the distribution with largest variances) with location information mapped to known genes

Full size image
Fig. 6
figure 6

Mapping all the SNPs’ posterior possibilities estimated from BayesR and HyB_BR across the whole chromosome related to Fat percent (Fat%). The posterior possibility is calculated based on the sum of the posterior possibilities P(i, k) of each SNP with non-zero variances written as ∑ 4 k = 2 P(i, k). The blue circle is the SNPs (picked up based on the high posterior possibility following in the distribution with largest variances) with location information mapped to known genes

Full size image
Fig. 7
figure 7

Mapping all the SNPs’ posterior possibilities estimated from BayesR and HyB_BR across the whole chromosome related to fertility. The posterior possibility is calculated based on the sum of the posterior possibilities P(i, k) of each SNP with non-zero variances written as ∑ 4 k = 2 P(i, k). The blue circle is the SNPs (picked up based on the high posterior possibility following in the distribution with largest variances) with location information mapped to known genes

Full size image
Table 9 The list of identified causal mutations by both BayesR and HyB_BR
Full size table

The application of HyB_BR to predict the risk of Human disease traits and infer genetic architecture for these traits

In the human data, cross validation was used to estimate the accuracy of HyB_BR. As there were 20 replicates of 20/80 split (validation/reference), we evaluated the mean of the AUC for each disease shown in Table 10. Analysis methods compared were GBLUP implemented in GCTA [44], BayesR from Moser et al. [8], and HyB_BR. The standard deviations of the accuracy (across the 20 replicates) were also listed in the parenthesis of Table 10. HyB_BR and BayesR performed equally well across all seven traits, with the same prediction accuracy for each trait. For the diseases of CD, RA, and T1D, BayesR and HyB_BR had significantly higher accuracy than GBLUP. Especially for T1D, BayesR and HyB_BR could have up to 12 % accuracy increase compared with GBLUP. However, for other traits including BD, CAD, HT, and T2D, BayesR and HyB_BR did not show any superiority over GBLUP. The underlying architecture of these traits might explained this, as suggested by Moser et al. [8]. In detail, for CD, RA and T1D, there are known mutations of moderate to large effect, and the mixture assumptions of BayesR and HyB_BR can take advantage of this. However, for four other diseases including BD, CAD, HT, and T2D, there are no known mutations of moderate to large effect, and this is reflected in the genetic architecture for these diseases inferred by HyB_BR.

Table 10 The prediction performance evaluated by the Area under curve (AUC) of GBLUP, BayesR and HyB_BR on seven diseases
Full size table

The genetic architecture of human disease traits

The inferred genetic architecture was different for each of the seven diseases (Table 11). For example, the genetic architecture of BD is controlled by many SNPs (9077 for HyB_BR; 9611 for BayesR) with small effects (the variance 0.0001σ 2 g ), but just 3 SNPs with large effects (the variance 0.01σ 2 g ). These numbers demonstrated the polygenic architecture of BD. On the contrary, for T1D, there was relatively smaller number of SNPs (3544 for HyB_BR; 2750 for BayesR) with small effects but many more SNPs (almost 200) with large effects. The proportion numbers from Fig. 8 also demonstrated this (in accordance with the results from Moser et al. [8]). Large proportion of SNPs with small effects (the variance 0.0001σ 2 g ) controlled the polygenic architecture of the diseases BD (98.76 % for HyB_BR; 99.55 % for BayesR), CAD (97.31 % for HyB_BR; 96.8 % for BayesR), HT (96.96 % for HyB_BR; 98.09 % for BayesR), and T2D (95.14 % for HyB_BR; 97.79 % for BayesR). For these diseases, the mixture model of BayesR and HyB_BR did not have much advantage. However, relatively larger proportions of SNPs with moderate effects (the variance 0.001σ 2 g ) existed for the traits RA (0.77 % for HyB_BR; 0.93 % for BayesR) and T1D(5.02 % for HyB_BR; 5.54 % for BayesR). For these two traits controlled by major genes, BayesR and HyB_BR gave substantially greater accuracy than GBLUP, which explained the results for prediction accuracy (Table 10).

Table 11 The number of SNPs in each proportion of four distributions estimated by BayesR, and HyB_BR on seven human diseases
Full size table
Fig. 8
figure 8

The inferred genetic architecture of seven human diseases from BayesR and HyB_BR. The blue bar is the proportion of SNPs in Pr [2] (with the variance 0.0001 * σ 2 g ), which is estimated by the number of SNP in Pr [2] divided by the total number of SNPs with nonzero variance. The red bar is the proportion of SNPs with the variance 0.001 * σ 2 g , estimated by the number of SNP in Pr [3] divided by the total number of SNPs with nonzero variance. The green bar is the proportion of SNPs with the variances 0.01 * σ 2 g , estimated by the number of SNPs in Pr [2] divided by the total number of SNPs with nonzero variance

Full size image

Compared with BayesR, HyB_BR detected the same number of SNPs with moderate variance (the variance 0.01 * σ 2 g ) but appeared to systematically detect more SNPs in the proportion of small variance (the variance 0.0001 * σ 2 g ), similar to the results observed for the comparison of BayesR and HyB_BR in in dairy cattle data (Table 8).

Discussion

We have presented a novel and computationally efficient algorithm termed HyB_BR for simultaneous genomic prediction and QTL mapping. A pure EM algorithm was less accurate for some traits, while pure MCMC requires very long computation times. Therefore, HyB_BR implements the EM algorithm followed by a limited number of MCMC iterations. In this way, the algorithm takes advantage of the features of an EM algorithm (rapid convergence) and the higher accuracy from MCMC implementations in a hybrid scheme. Our accuracies of genomic prediction for complex traits in human and cattle from HyB_BR are almost identical to those from the full MCMC implementation of the Bayesian mixture model, with a 10 fold or greater reduction in computing time required.

For the pure MCMC algorithm, the burn-in stage can account for up to 50 % of the total running time. One of the key advantages of HyB_BR is that the EM module effectively replaces the burn-in cycles that are usually required for MCMC. Based on the starting point from EM (with very limited number of iterations; less than 500 iterations), the running time of HyB_BR can be much reduced.

The pure EM algorithm, EmBayesR [30] has been demonstrated to be much faster than BayesR, but had lower accuracy for some traits, particularly those with mutations of moderate to large effect. For example, when implemented on the trait fat% in dairy cattle, emBayesR had a decreased accuracy of 5 % ~ 7 % compared to BayesR. One possible explanation is that emBayesR shrinks SNP effects too much (shown in Table 8). This could be because the PEV that is used to account for the error of the effects of all the other SNPs while estimating the effect of the current SNP is only an approximation. The introduction of PEV correction is based on one observation: previous fast algorithm studies (especially Iterative conditional expectation algorithms) assumed the effects of the other SNPs were estimated perfectly while estimating the effect of the current SNP, leading to poor performance [30]. Therefore, EmBayesR and the EM part of HyB_BR allow for the errors in the effect of other SNPs and other location parameters by using the PEV. The calculation of the PEV from GBLUP is carried out before the iterations to estimate the effects of each SNP. And since the normal priors from GBLUP model do not allow for SNPs of moderate to large effects, such PEV calculation is an approximation and this may be one reason for loss of accuracy in the EM. To deal with this, HyB_BR further implements a small number of MCMC iterations to improve the outcome of pure EM steps.

HyB_BR has three advantages. First, as the size of genomic data increases, the computational efficiency of HyB_BR without burn-in stage (a small number of O(mn) iterations), is greater than BayesR by full MCMC. And when implemented with the speed-up scheme described in the methods, computational time can be reduced even further, by sampling a reduced set of SNPs in the MCMC module, apparently with no loss of accuracy (but critically the information from the SNPs that are not sampled remains in the posterior proportions of SNPs in each distribution). Second, the prediction accuracy of HyB_BR is comparable to BayesR in all cases including dairy cattle and human disease prediction shown in Tables 5, 6 and 7, and Table 10. Third, HyB_BR, like BayesR, is flexible with respect to the genetic architecture of complex traits. As shown in Tables 5, 6 and 7, HyB_BR performs well on four different complex traits, with architecture ranging from highly polygenic architecture to genetic architecture controlled by major genes. In addition to the prediction on the continuous quantitative traits of dairy cattle, the investigation on the risk prediction of seven case/control human diseases with binary 0/1 phenotypes shows HyB_BR and BayesR perform on this type of data, Table 10. Finally, the posterior probabilities of SNP having a nonzero effect from HyB_BR can be used for QTL mapping, Fig. 6.

Implementing genomic prediction methods with whole genome sequence data may improve the prediction accuracy and accelerate the discovery of causal variants. However, for this to occur, more computationally efficient genomic prediction algorithms are required. Compared with BayesR, the predicted time of HyB_BR on different number of markers with the same reference phenotypesis listed in Table 12. The time is estimated linearly on the number of markers and individuals. When the number of markers reaches 30 million (the number of variants discovered in the 1000 bull genomes project, Daetwyler et al. [28]), the running time of BayesR is around 34,170 h, which is impractical. On the contrary, on the same data with 30 million of variants, HyB_BR is predicted to require 2010 h. It may be possible to reduce this further by optimising the code even more. Therefore, as the size of genomic data increases, HyB_BR will remain feasible well beyond the point where the use of BayesR is impractical.

Table 12 The predicted computational time (in hours) of HyB_BR and BayesR on high density data with different number of variants and the same number of individuals (16,214)
Full size table

While HyB_BR performs well with computational efficiency and robust prediction accuracy, there are at least still two strategies that could be used to further improve efficiency. There is one key part of EM module that consumes running time and memory: the calculation of tr(E − 1 Z i Z ' i E − 1 PEV) for each SNP in front of EM iterations. In detail, the calculation of tr(E − 1 Z i Z ' i E − 1 PEV) requires the time complexity of \( O\left(\frac{1}{2}m{n}^2\right) \), which accounts for almost 2/3 of the computational time required for the EM module even though the calculation is made in front of the EM iterations. Therefore, a future task is to implement a multi-threaded version to improve speed. The threshold of limiting the number of SNPs to be updated requires further study. Currently we define the threshold as T: if(P(i, 1) > 0.9), which is applicable for the current data. However, it’s uncertain whether or not such a threshold is suitable for other types of data.

HyB_BR has some features in common with other mixture methods such as BSLMM [6], and BOLT-LMM [25]. All of these methods declared the merit of computational efficiency with time complexity O(mn) but under different mixture models. In detail, BSLMM assumed a large proportion of SNPs with small effects (under BLUP models), while others had large effects (under Bayesian sparse regression models; the mixture of two normal priors). Due to limited number of SNPs implemented for MCMC sampling (large proportion of SNPs are under GBLUP models), BSLMM could be computationally efficient. However, compared with the mixture of four normal distributions by BayesR which provided great flexibility with respect genetic architecture, the flexibility of BSLMM with respect to different genetic architectures required further investigation. Another algorithm is BOLT-LMM, which has been developed mainly for the association studies. BOLT-LMM incorporated Bayesian mixture models to improve the power of GWAS with appealing outcomes. Instead of MCMC sampling, BOLT-LMM implemented iterative conditional expectation (ICE) algorithm on a mixture of two normal distributions to improve the computational speed with the approximated computational complexity O(mn). There could be three limitations with this method: 1) ICE algorithms did not account for the PEVs from all other SNP effects during the estimation of current SNP effect. On practical data sets, ICE could lead to the loss of prediction accuracy. BOLT-LMM introduced LD score regression technique to calibrate the prediction errors. However, since the calibrating factor was constant across all the SNPs (the prediction error variance regarding each SNP differs according to our equation (E − 1 Z i Z ' i E − 1 PEV)), such calibration scheme seem not to be effective to solve the problem. 2) The leave-one-chromosome-out scheme implemented in BOLT-LMM might perform well for GWAS but not be suitable for simultaneous genomic prediction. 3) BOLT-LMM treated each SNP effect as a fixed effect for the association statistics. This combined with the stringent significance threshold for multiple testing, leaded to the over-estimation for SNP effects. Another efficient method for genomic prediction termed MultiBLUP [7] introduced SNPs clusters into BLUP models according to its adaptive algorithm. For each SNP class, the linear combination models (using genomic relationship matrix) similar to GBLUP were implemented. MultiBLUP has been demonstrated to be computationally efficient with robust prediction accuracy in the human data sets. However, when moved to dairy cattle genomic data sets, there is long Linkage disequilibrium (LD) between markers, which might be easily broken up by multiBLUP models.

Conclusions

In summary, HyB_BR is a computationally efficient method for simultaneous genomic prediction, QTL mapping and inference of genetic architecture. The hybrid scheme of MCMC and EM decreases computational time by a factor of at least 10 fold with no reduction in prediction accuracy. The HyB_BR algorithm makes simultaneous genomic prediction, QTL mapping and inference of genetic architecture feasible in extremely large genomic data sets including whole genome sequence data.