1 Introduction

Safety is the most important property of a passenger railway vehicle. The fatigue strength of a vehicle loading structure has a substantial impact on its safety, and thus must be comprehensively assured. A series of fatigue strength analysis methods for welded railway vehicle structures have been introduced to date [1], including fatigue assessment for constant amplitude loading by the endurance limit, evaluation of fatigue test programs by cumulative damage, and evaluation of simulated multiple body systems by cumulative damage. These methods are commonly applied in the railway industry [2,3,4,5,6].

Han et al. [7] introduced a static load test method and evaluated experimentally the static strength for the bogie frame of an urban maglev train. Linhart et al. [8] carried out high-cycle fatigue tests with an evaluation of fatigue limit on large model components of bars with press fitted hubs made of three railway axle steels. Wu et al. [9] proposed a new crack closure based fatigue crack growth rate model in terms of low cycle fatigue behavior and improved threshold stress intensity factor range at different loading ratios. The predicted results were in good agreement with the experimental data of the railway axle used steels. Bertini et al. [10] investigated the fatigue resistance of a typical welded joint employed in railway bogie manufacturing. Zhou et al. [11] carried out stress tests of high-speed train axles along the rebuilt railway line and Jingjin intercity railway line. The S-N curve parameters with different notches and the corresponding fatigue limits were calculated. Milovanović et al. [12] studied a methodology used to identify causes of cracking nearby the welded joint on the underframe of wagon type Sgmns for the transportation of containers and swap bodies. As part of the Euraxles project, a series of full-scale axles fatigue tests were carried out [13]. The fatigue limits and the stress concentration factors were verified. However, most published research are not determined based on actual, on-track test programs of the structure in question.

The speed and efficiency of train travel has been continually modernized over recent decades, so the real load situation of vehicles may differ substantially from the standard. Furthermore, the vehicle structures may crack unexpectedly during the service period [14]. The load situation of railway vehicles have been researched recently. By use of a reliable test technology, Ren et al. [15] tested the axle spring forces of the high speed EMU on the Beijing-Tianjin railway line. Zhu et al. [16] carried out theoretical research and experimental validation to investigate load spectra of high-speed trains bogie frames. Wu et al. [17] investigated the post-derailment dynamic behavior of the half car and verified the proposed post-derailment dynamic model.

The bogie frame is one of the most important parts of the railway vehicle [18,19,20,21,22]. It plays a significant role in controlling wheel sets on the railway, and it carries the brakes, motors, gear boxes, and suspensions while sustaining the static weight of the car body. To this effect, the load conditions of the bogie frame are highly complex and accurately assessing its fatigue strength is very challenging. Numerous welded structures of railway vehicles are safety critical [23, 24]. The dynamic stress on-track test, one of the most feasible and effective approaches to obtaining fatigue stress cycles [25], was utilized in this study on a long-term China high-speed train program to explore the dynamic stress response of the bogie frame. The results were used to build a new method for evaluating the on-track fatigue damage of the bogie frame.

2 Dynamic Stress Test Program

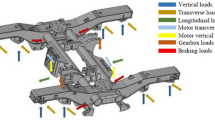
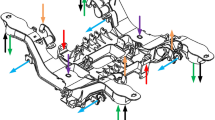
Figure 1 shows the dynamic stress test point distribution of the China high-speed train bogie frame. The strain gauge is disposed at the junction of the weld metal and the base metal, as shown in Figure 2. The tested vehicle was still in service on several railway lines including Beijing West-Guangzhou South, Beijing West-Taiyuan-Guangzhou South, and others throughout the duration of the dynamic stress test program.

Figure 1
figure 1

Dynamic stress test point distribution on the high-speed train bogie frame

Full size image
Figure 2
figure 2

Strain gauge paste mode of the testing points

Full size image

The bogie frame was subjected to a combined, multi-level stress during train operation. To facilitate follow-up analysis, the multi-level stress was transformed into equivalent constant amplitude stress based on the fatigue damage consistency law. In other words, equivalent stress is the most important parameter for fatigue.

According to the rules of the rain flow count method, the stress spectrum must first be obtained from the test data before calculating the fatigue damage under Miner damage accumulation theory based on the stress spectrum. The tested fatigue damage D1, according to the tested miles L1 (km), is:

$$D_{1} = \sum\limits_{i = 1}^{a} {\frac{{n_{i} }}{{N_{i} }}} + \sum\limits_{j = 1}^{b} {\frac{{n_{j} }}{{N_{j} }}} = \sum\limits_{i = 1}^{a} {\frac{{n_{i} \sigma_{i}^{{m_{1} }} }}{{C_{1} }}} + \sum\limits_{j = 1}^{b} {\frac{{n_{j} \sigma_{j}^{{m_{2} }} }}{{C_{2} }}} ,$$
(1)

S-N curve parameters can be determined based on Ref. [26].

The fatigue damage of equivalent stress σe after 2 × 106 cycles is denoted as D. The following equation makes D equal to the total fatigue damage of the train according to the whole service life miles L (km):

$$D = \frac{{N\sigma_{e}^{{m_{1} }} }}{{C_{1} }}.$$
(2)

On the basis of the fatigue damage consistency law, tested damage D1 should be equal to the entire damage D per kilometer:

$$\frac{D}{L} = \frac{{D_{1} }}{{L_{1} }}.$$
(3)

Eq. (3) can be written as a stress-type equation:

$$\frac{{N\sigma_{e}^{{m_{1} }} }}{{C_{1} L}} = \sum\limits_{i = 1}^{a} {\frac{{n_{i} \sigma_{i}^{{m_{1} }} }}{{C_{1} L_{1} }}} + \sum\limits_{j = 1}^{b} {\frac{{n_{j} \sigma_{j}^{{m_{2} }} }}{{C_{2} L_{1} }}} ,$$
(4)

where

$$\sigma_{e} = \left( {\frac{L}{{L_{1} N}}\sum\limits_{i = 1}^{a} {n_{i} \sigma_{i}^{{m_{1} }} } + \frac{{LC_{1} }}{{L_{1} C_{2} N}}\sum\limits_{j = 1}^{b} {n_{j} \sigma_{j}^{{m_{2} }} } } \right)^{1/ {m_1}} .$$
(5)

Engineers often utilize the linear S-N curve to ensure structural safety [27]. Let C2 = C1, m2 = m1 so that Eq. (5) becomes:

$$\sigma_{e} = \left( {\frac{L}{{L_{1} N}}\sum\limits_{k = 1}^{a + b} {n_{k} \sigma_{k}^{{m_{1} }} } } \right)^{1/ {m_1}} .$$
(6)

Eq. (6) is the equivalent stress amplitude calculation formula based on the measured data. L equals 12 million km, according to the known high-speed train service life.

The dynamic stress responses of the bogie frame were obtained by the test program as the train ran on the Taiyuan-Guangzhou South line. The equivalent stress amplitudes according to Eq. (6) of each tested stress point are shown in Table 1.

Table 1 Equivalent stress values of the frame under uniform operation (MPa)
Full size table

A long-term tracking dynamic stress test was conducted on a passenger-carrying operation train with regular maintenance on common tracks, which represent the normal level. The equivalent stress amplitudes of D10 and D11 along with the operating mileage from 18.5 × 104 km to 95.7 × 104 km are shown in Figures 3 and 4.

Figure 3
figure 3

Equivalent stress amplitudes of D10 along with operating mileage

Full size image
Figure 4
figure 4

Equivalent stress amplitudes of D11 along with operating mileage

Full size image

3 Methodology

If the whole service miles of bogie frame is cut into x pieces, the fatigue damage of each piece can be calculated as follows:

$$D_{i = 1,2 \ldots x} = \frac{{\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} N}}{{C_{1} }}\frac{{L_{i} }}{L}.$$
(7)

The whole fatigue damage of the bogie frame in total service miles is:

$$D = \sum\limits_{i = 1}^{x} {D_{i} } = \sum\limits_{i = 1}^{x} {\left[ {\frac{{\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} N}}{{C_{1} }}\frac{{L_{i} }}{L}} \right]} .$$
(8)

Because the ratio between test miles L1 and whole service miles L is the probability of each equivalent stress amplitude tested, Eq. (8) can be rewritten as follows:

$$\begin{aligned} D & = \sum\limits_{i = 1}^{x} {\left[ {\frac{{\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} N}}{{C_{1} }} \cdot p\left( {\sigma_{e} } \right)_{i} } \right]} \hfill \\ & = \frac{N}{{C_{1} }}\sum\limits_{i = 1}^{x} {\left[ {\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} p\left( {\sigma_{e} } \right)_{i} } \right]} . \hfill \\ \end{aligned}$$
(9)

As the piece number x increases towards infinity, Eq. (9) can be rewritten in integral form:

$$\begin{aligned} D & = \mathop {\lim }\limits_{x \to \infty } \frac{N}{{C_{1} }}\sum\limits_{i = 1}^{x} {\left[ {\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} p\left( {\sigma_{e} } \right)_{i} } \right]} \hfill \\ & = \frac{N}{{C_{1} }}\int {\left[ {\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} p\left( {\sigma_{e} } \right)_{i} } \right]{\text{d}}\left( {\sigma_{e} } \right)_{i} .} \hfill \\ \end{aligned}$$
(10)

The following equation makes [σe] equal to the damage consistency equivalent stress amplitude according to the entire service mileage of the bogie frame:

$$\left( {\left[ {\sigma_{e} } \right]} \right)^{{m_{1} }} = \int_{{}}^{{}} {\left[ {\left( {\sigma_{e} } \right)_{i}^{{m_{1} }} p\left( {\sigma_{e} } \right)_{i} } \right]{\text{d}}\left( {\sigma_{e} } \right)_{i} } ,$$
(11)

where the key to acquiring the damage consistency equivalent stress amplitude is in determining the probability distribution of tested equivalent stress amplitude.

4 Application and Discussion

By comparison between Figures 3 and 4, the equivalent stress amplitudes of D11 were selected to determine the probability distribution of tested equivalent stress amplitude on account of their randomness. Table 2 shows the tested equivalent stress amplitude values of D11 in different operation routes according to the information shown in Figure 4.

Table 2 Tested equivalent stress values of D11 in different railway tracks (MPa)
Full size table

Due to the regular maintenance of railway lines and rail vehicles, the running performance of rail vehicles is relatively stable. It is reasonable to suppose that deviations among the tested equivalent stress amplitudes are caused by stochastic factors when running conditions are constant. The tested equivalent stress amplitudes can be written in the following form according to the error analysis theory:

$$\sigma_{e} = \sigma + \varepsilon (0,s^{2} ).$$
(12)

Predictably, the equivalent stress amplitude is in normal distribution N(σ, s2), so the whole service life fatigue damage of the bogie frame can be calculated as following formula under the “3σ Principle”:

$$D = \frac{N}{{C_{1} }}\int\limits_{\sigma - 3s}^{\sigma + 3s} {(\sigma_{e} )^{{m_{1} }} } \cdot \frac{1}{{\sqrt {2\uppi} s}}e^{{ - \frac{{(\sigma_{e} - \sigma )^{2} }}{{2s^{2} }}}} {\text{d}}(\sigma_{e} ).$$
(13)

Because the tested equivalent stress amplitude belongs to a small sample size, the Anderson–Darling test method was used to test whether the equivalent stress amplitude followed a normal distribution. The test statistic AD value can be determined as follows:

$$A^{2} = - n - \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {2i - 1} \right)\left( {\ln F\left( {X_{i} } \right) + \ln \left( {1 - F\left( {X_{n + 1 - i} } \right)} \right)} \right)} .$$
(14)

Small A value indicates that the tested equivalent stress amplitude obeys normal distribution. Normal distribution test conclusions are reflected by P-values, which can be acquired as follows:

$$A^{{{\prime }2}} = A^{2} \times \left( {1 + \frac{0.75}{n} + \frac{2.25}{{n^{2} }}} \right).$$
(15)

When \(13 > A^{{{\prime }2}} > 0.600\),

$$P = \exp \left( {0.9177 - 4.279 \times A^{{{\prime }2}} - 1.38 \times \left( {A^{{{\prime }2}} } \right)^{2} } \right).$$
(16)

When \(0.600 > A^{{{\prime }2}} > 0.340\),

$$P = \exp \left( {0.9177 - 4.279 \times A^{{{\prime }2}} - 1.38 \times \left( {A'^{2} } \right)^{2} } \right).$$
(17)

When \(0.340 > A^{{{\prime }2}} > 0.200\),

$$P = \exp \left( { - 8.318 + 42.796 \times A^{{{\prime }2}} - 59.938 \times \left( {A^{{{\prime }2}} } \right)^{2} } \right).$$
(18)

When \(A^{{{\prime }2}} < 0.200,\)

$$P = \exp \left( { - 13.436 + 101.14 \times A^{{{\prime }2}} - 223.73 \times \left( {A^{{{\prime }2}} } \right)^{2} } \right).$$
(19)

When the confidence coefficient is 95%, the assumption that tested equivalent stress amplitude closely obeys a normal distribution should be rejected if P < 0.05. The data shown in Table 2 was tested by Anderson–Darling test method to obtain the results shown in Table 3; said data does indeed follow normal distribution.

Table 3 Normal test result of D11 testing point by Anderson–Darling test method
Full size table

Table 4 shows the damage consistency equivalent stress amplitude of each railway line, which corresponds to fatigue damage, calculated by the method introduced in Section 3. Different railway lines exhibited different fatigue damage values, even on twin lines (e.g., Beijing West-Guangzhou South versus Guangzhou South-Beijing West). To compute the fatigue damage of the bogie frame as accurately as possible over the entire service life, both the damage consistency equivalent stress amplitude of each railway line train running and the operation schedule of the train are needed. These values allow the whole service life fatigue damage of the bogie frame to be calculated as follows:

Table 4 Damage consistency equivalent stress amplitude of each railway line (MPa)
Full size table
$$D = \frac{N}{{C_{1} }}\sum\limits_{i = 1}^{a} {\left[ {\sigma_{e} } \right]_{i}^{{m_{1} }} p_{i} } .$$
(20)

The complex load conditions of the bogie frame create different stress responses across different locations on the frame, so the mean value are also disparate. The difference between the standard deviations merit further research. The data in Table 1 was transformed into a new sample group to analyze the distributed standard deviation parameters as follows:

$$\left( {\sigma_{e}^{{\prime }} } \right)_{ij} = \left( {\sigma_{e} } \right)_{ij} - \frac{1}{j}\sum\limits_{j = 1}^{n} {\left( {\sigma_{e} } \right)_{ij} } .$$
(21)

The standard deviation parameters of the testing points are relatively uniform if the new sample group can be represented by a normal distribution. The Anderson–Darling normality test results are shown in Table 5, where the new sample can be considered to have a significant normal distribution. The estimated distribution parameters of each bogie frame testing point are shown in Table 6, where no standard deviations exceed 3 except the D24 testing point, which is slightly greater than 3; point D24 is located in the connection region of the frame and power device gear-box.

Table 5 Normal test result of new sample group by Anderson–Darling method
Full size table
Table 6 Estimated distribution parameters of each bogie frame testing point
Full size table

Based on the above analysis, the equivalent stress amplitude of the frame can be represented by a normal distribution within 12 million km and the standard deviation is generally 3 or less. To make the integral part of Eq. (13) equal G, G is expressed as follows:

$$G = \int\limits_{\sigma - 3s}^{\sigma + 3s} {(\sigma_{e} )^{{m_{1} }} } \cdot \frac{1}{{\sqrt {2\pi } s}}e^{{ - \frac{{(\sigma_{e} - \sigma )^{2} }}{{2s^{2} }}}} {\text{d}}(\sigma_{e} ).$$
(22)

G value reflects the fatigue damage of the bogie frame. Its value was consistently calculated to be under the mean value 10–90 MPa, with standard deviation of 0.5–3 (Figure 5). Its projection along standard deviation direction is shown in Figure 6, where the width of the data line represents the impact of standard deviation to the G value.

Figure 5
figure 5

G values under the mean value 10‒90 MPa, standard deviation 0.5–3

Full size image
Figure 6
figure 6

G value projection along standard deviation direction

Full size image

The small range of the standard deviation indicates that fatigue damage is mainly affected by the mean value. Therefore, an accurate mean value estimate of equivalent stress amplitude distribution is an essential component of the on-track dynamic stress fatigue test program.

5 Conclusions

Studies have shown that high-speed train bogie frame fatigue damage contains randomness though in the same operation route. The evaluation method proposed in this paper can be adapted to accurately assess the fatigue damage of the bogie frame. Several characteristics of the fatigue damage to the bogie frame were identified here by analyzing actual dynamic stress testing data.

  1. (1)

    The equivalent stress amplitude on behalf of the bogie frame fatigue damage can be obtained by integral based on normal distribution and 3σ Principle, especially when conditions are constant. The mean value of distribution parameters is dependent on the specific location of the test point; the standard deviation maximum value is about 3. Standard deviation does not significantly affect fatigue damage, but mean value has a great effect on it, so the mean value evaluation accuracy should be the primary focus in establishing the test program.

  2. (2)

    Bogie frame fatigue damage differs when the train runs on different operation routes, even across twin lines. When the damage consistency equivalent stress amplitude of each running railway line and the operation schedule of the train are known a priori, the whole service life fatigue damage of the bogie frame can be calculated precisely. Fatigue damage varies across specific locations on the frame, but the dynamic stress responses of the region connected to the power system are generally more random than the responses in other regions.