1 Introduction

With the rapid development of urban areas, there is an urgent need for efficient and convenient transportation systems. Metro systems have appeared and been developed as the focal point of urban railway construction [1]. The development of urban rail transit is of great significance for solving urban traffic problems. However, with the increasing passenger capacity of metro vehicles and the gradual deterioration of operating conditions, the reliability requirements of vehicle components could be much stricter. As one of the core components of a vehicle bogie, the frame not only plays the role of bridge to transmit the vibration between vehicle body and wheelsets, but also takes various loads during the operation [2]. Therefore, studies on the fatigue strength and reliability of bogie frames are also developing. Since the late twentieth century, a large number of structural strength tests have been carried out on bogie frames, and relevant standards have been established, including the UIC 615-4 standard [3] and EN 13749 standard [4]. However, the actual situation shows that, compared with the standards, the signals collected during the line tracking test will be more helpful for studying the dynamic response characteristics of bogie frames in real operating conditions.

Dynamic stress is a key index which reflects the fatigue characteristics of the bogie frame. The values of dynamic stress at any part of the frame can be obtained through measurements in a line tracking test, which comprehensively represent the effects of various excitations during vehicle operation. In the early stage, the Qingdao Sifang Vehicle Research Institute conducted studies on the dynamic stress of a railway vehicle, where data for fatigue analysis were obtained regarding multiple routes. Yaohui [5] established a dynamic model of the vehicle considering the effect of bogie frame modalities, and used the finite element method to calculate the dynamic stress spectrum. Longxiu and Shouguang [6] conducted systematic research on how to test the stress spectrum of the welded bogie structure of a high-speed passenger vehicle and how to determine the critical fatigue locations. Daoyun [7] introduced kernel density estimation to overcome the limitations of parameter methods in estimating the distribution of a dynamic stress spectrum. It proved that this method has certain errors and is slightly conservative in fitting and estimating the dynamic stress spectrum, but it is very useful for ensuring structural safety during operation. Qiang [8] established the stress–time history based on measurements of line tracking tests and analyzed the dynamic stress characteristics using rainflow counting. Fan [9] studied the influence of speed level, curve radius, and switch conditions on dynamic stress by establishing a dynamic model and changing the line conditions. Qiushi [10] obtained the probability distribution characteristics of the load and extrapolated the dynamic stress test data from small to large samples using the multi-sample kernel density extrapolation method. He proposed a quantitative evaluation method using a matrix gray correlation analysis to evaluate the closeness correlation and similarity correlation of the rainflow matrix before and after extrapolation. Stichel [11] established a multi-rigid body dynamic model of the bogie frame and conducted fatigue analysis based on the dynamic stress data of the key control positions during actual operation. Zehsaz [12] analyzed the effect of vehicle speed on the stress distribution at different parts of the vehicle structure. He established a two-axle bogie model using the finite element analysis method and obtained the static and dynamic loads under different conditions. Equivalent stress was used in the strength calculation, and the results showed that there was always a maximum stress in the bogie frame, and the increase of bogie rotation speed significantly affected the stress increment of the bogie frame.

In the study of the fatigue strength and fatigue life of the bogie frame, Chinese scholars have focused on obtaining data through line tracking tests and analyzing the fatigue life of key structures from the perspectives of time and frequency domains after data processing. Li [13] focused on the Beijing Metro Line 2 and evaluated the fatigue strength of the bogie frame by combining line tracking measurements and finite element modeling. Xihong [14] transformed the asymmetric cyclic stress spectrum measured on the line into a symmetric cyclic stress spectrum based on the average stress sensitivity coefficient, and proposed a fatigue life prediction method for welded structures based on the principles of fatigue strength evaluation and linear fatigue cumulative damage criteria. Pengpeng [15] compiled a stress spectrum for fatigue reliability analysis based on line tracking measured data, constructed a one-dimensional Brownian motion equation for equivalent stress and fatigue strength, and proposed an equivalent time-varying dynamic stress–strength interference model for the bogie frame to analyze the relationship between fatigue life and its reliability. Hua [16] established an optimization function based on the principle of damage consistency and used the load–stress transfer coefficient matrix in the optimization function to derive an experimental load spectrum suitable for deriving experimental data from large-scale measured dynamic stress data.

It can be seen that related studies are based on data collected from actual line tests, indicating that if the tracking test time is too short, there may be significant errors between the statistical stress spectrum obtained based on small sample sizes and the actual stress spectrum. Generally speaking, the longer the tracking test time selected, the more the established stress spectrum is in line with the actual fatigue condition of the vehicle. However, there are also problems such as long test time, high test cost, and high difficulty. On the whole, a longer line test is not necessarily better. Currently, there is limited research on the shortest tracking period required to cover the actual operational damage, and it is necessary to infer the minimum testing period for stress based on the distribution characteristics of the spectrum in order to reduce testing costs. Therefore, this paper first conducts actual line dynamic strength tracking tests on the bogie frame. The statistical dynamic stress spectrum of the typical fatigue control positions of the frame is obtained through rainflow counting, and Weibull distribution fitting is performed to obtain the scale and shape parameter samples at different fatigue control points. Then, sampling, variance homogeneity testing, and t-tests are performed to study the optimization of the line tracking test period.

2 The Pre-processing of Stress

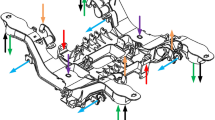
The bogie frame carries and transmits various loads when operating in lines, and these main loads on the bogie frame are shown in Fig. 1. Under the action of loads, the stress of each part on the frame also changes with time, which can be referred to as stress–time history. In engineering practice, the indirect method is generally used for safe and reliable stress measurement. Its principle is that loads can cause small strain on the surface of a metal structure. Therefore, by measuring the values of the strain \(\epsilon\) at the selected position, Hooke’s law can be used to obtain the stress \(\sigma\), as shown in Eq. (1):

$$\begin{aligned} \sigma =E\epsilon \end{aligned}$$
(1)

The measurement is mainly achieved through the 1/4 strain measurement group bridge method. A strain resistance is arranged at the fatigue control position of the frame, and three temperature compensation plates are attached beside it to form the Wheatstone bridge so that the influence of temperature on signals can be reduced [17]. According to the relevant standards and practical experience with loading tests of bogie frames, we consider proportional stress, where we maintain the hypothesis that the principal stress directions and ratios remain constant throughout the loading history. The generated signals are collected by the SoMat eDAQ platform. Then, NCODE professional software is used to process the measured data, including balance adjustment, zero bleaching, filtering, removing abnormal burrs, and other processing steps, and finally, the stress–time history can be used to compile the stress spectrum.

Fig. 1
figure 1

The loads on the bogie frame

Full size image

3 Compilation and Distribution Fitting of the Stress Spectrum

3.1 Compilation of the Stress Spectrum

The strain data obtained by data collection equipment is irregular and constantly changing with time, so it is difficult to directly carry out fatigue assessment using time domain signals. The interaction between amplitude and frequency is the primary reason for structure failure. Therefore, the rainflow counting method is used to process time domain signals into a series of amplitudes and frequencies, which is widely used in the research of fatigue damage and life prediction. A study by Zhao et al. [18] gave application examples of compression, extrapolation, superposition, and time domain reconstruction of a load spectrum based on the rainflow counting method. A study by Men et al. [19] obtained a load distribution matrix using the rainflow counting method based on the test data of typical pavement and reinforced road. Therefore, the time domain signal is processed by the rainflow counting method to obtain multiple stress cycles, and then the wave center method can be used to compile the stress spectrum.

The compilation method is as follows:

  1. (1)

    Obtain the maximum and minimum values of amplitude, and then determine the class interval according to the level of spectrum as shown in Eq. (2):

    $$D = (F_{{{\text{max}}}} - F_{{{\text{min}}}} /N){\text{ }}$$
    (2)

    where D is the spectrum interval, \(F_{{{\text{max}}}}\) is the maximum value of amplitude, \(F_{{{\text{min}}}}\) is the minimum value of amplitude, and N is the spectrum level, generally with 8, 16, 32, and 64.

  2. (2)

    After the group interval is obtained, the up and down limit values of the stress responding to each level can be calculated through Eq. (3) as follows:

    $$\begin{gathered} F_{{i_{{{\text{up}}}} }} = F_{{{\text{min}}}} + D \times i \hfill \\ F_{{i_{{{\text{down}}}} }} = F_{{{\text{min}}}} + D \times (i - 1) \hfill \\ \end{gathered}$$
    (3)

    where \(i=1,2,...,N\).

  3. (3)

    After determining the amplitude of each level of the spectrum, the cycle of the rainflow series is graded, the cumulative frequency of each level is obtained, and finally the stress spectrum is obtained.

3.2 The Distribution Fitting of the Stress Spectrum

The relation between stress amplitude and frequency is studied using mathematical statistics. The amplitude of the spectrum is regarded as a random variable, and the frequency is regarded as the frequency distribution to obtain the stress distribution. Studies have shown that structural stress amplitudes generally follow Weibull distribution [20]. Xiangpo [21] et al. concluded through research and analysis that, compared with normal distribution, log-normal distribution, exponential distribution, and other common distributions, three-parameter Weibull distribution has strong adaptability to a variety of data forms. This distribution fitting method demonstrates robustness in handling variations in data distribution and non-normality, common challenges in fatigue testing where samples often exhibit nonuniformity. The amplitude and probability density of randomly selected measurement points on a certain day are shown in Fig. 2. It can be preliminarily believed that the stress amplitude and probability density can be fitted by three-parameter Weibull distribution. The probability density function of Weibull distribution is shown as Eq. (4):

$$\begin{aligned} f(x)=\frac{\beta }{\alpha }\left[ \frac{x-\mu }{\alpha }\right] ^{\beta -1} \exp \left\{ -\left( \frac{x-\mu }{\alpha } \right) ^\beta \right\} , (x\ge \mu ) \end{aligned}$$
(4)

where \(\alpha\), \(\beta\), and \(\mu\) are the scale parameter, shape parameter, and position parameter describing the Weibull distribution, respectively. \(\alpha\) reflects the dispersion of data, and \(\beta\) reflects the shape of the function curve. The reliability function is shown as Eq. (5):

$$\begin{aligned} P(x)=1- \exp \left\{ -\left( \frac{x-\mu }{\alpha } \right) ^\beta \right\} , (x\ge \mu ) \end{aligned}$$
(5)

The logarithm of the reliability function is taken twice to obtain the linear regression in Eq. (6):

$$\begin{aligned} Y=A+BX \end{aligned}$$
(6)

where \(Y=\ln \ln \frac{1}{p}\), \(X=\ln (x-\mu )\), \(B=\beta\), and \(A=-\beta \ln (\alpha )\).

Fig. 2
figure 2

The probability density curve of the stress amplitude of a random measurement point

Full size image

It is preliminarily assumed that the amplitude and probability density of the stress spectrum conform to the Weibull distribution. \((x_i,p_i)\) is obtained by processing the measured data of the line, where \(x_i\) is the amplitude, and \(p_i\) is the reliability. Combining with the equation obtained after the logarithm of the Weibull distribution reliability function twice, a new data sample \((X_i,Y_i)\) can be obtained. The measured stress spectrum of a certain day is selected for distribution fitting to obtain the linear regression equation of eight stress measurement points and corresponding three parameter values of their Weibull distribution, and then the significance test is carried out with the F-test method. The null hypothesis is that \(H_0: B=0\), and the alternative hypothesis is that \(H_1: B\ne 0\). If \(H_0\) is rejected, it is considered that there is a linear relationship between the data, and the linear regression effect is significant. If \(H_0\) is accepted, it is considered that there is no linear relationship between the data, and the effect of linear regression is not significant.

The fitting parameters and significance test results of eight stress measurement points are listed in Table 1. The F-values of the F-test statistics are all greater than the critical value when the significance level is 0.5, indicating that the hypothesis of a significant linear relationship between variables X and Y is accepted with 95% confidence. The test shows that the linear relationship of the regression equation is significant, and the stress spectrums of all eight measurement points satisfy the three-parameter Weibull distribution. By putting the fitting parameter results into the probability density expression of Weibull distribution, the specific probability density function satisfied by the stress of each measurement point can be obtained, and the function curve can be drawn. Comparing the function curve with the actual probability results in Fig. 3, it can be seen that the three-parameter Weibull distribution can effectively reflect the stress spectrum distribution of the measurement points in different fatigue control areas of the frame.

Fig. 3
figure 3

Probability density distribution and fitting Weibull distribution of stress amplitude of different measurement points

Full size image
Table 1 Stress spectrum distribution fitting parameters of measurement points and significance test results
Full size table

4 Statistical Inference of Weibull Distribution Parameters

4.1 Normality Test of Weibull Distribution Parameters

The three parameters of Weibull distribution are obtained by fitting the measurement data of the whole test period. If we take these fitting parameters as random variables and the distribution and find the distribution characteristics of fitting parameters, then certain statistics can be used to replace the corresponding fitting parameter variable, and the overall distribution of the stress spectrum can be obtained under a 95% confidence level. In this paper, a single-sample Kolmogorov–Smirnov (K-S) method is used to test the normality of the distribution form of the fitting parameter population. The significance level \(\alpha\) is set as 0.05. The null hypothesis is that the parameter variables follow normal distribution, and the alternative hypothesis is that the parameter variables do not follow normal distribution. If the P-value is not greater than the significance level \(\alpha\), the population distribution of the samples is significantly different from the normal distribution. If the P-value is greater than the significance level, the null hypothesis is accepted, and there is no significant difference between the population distribution of the samples and the normal distribution. The results of K-S test on fitting parameter of Weibull distribution are listed in Table 2.

Table 2 The K-S test results of Weibull distribution of different measurement points
Full size table

According to the above K-S test results, the P-values of the normality test of the three fitting parameters from stress measurement points 2D6, 2D9, 4HZ1, and 2HC2 are all higher than the significance level of 0.05, indicating that the hypothesis that fitting parameters meet the normal distribution cannot be rejected under 95% confidence level. Therefore, all the variables of three parameters from above measurement points meet the normal distribution. The mean value and standard deviation can be calculated from the normal distribution. The mean values are taken to represent the corresponding fitting parameters, and then the overall distribution of stress spectrum can be obtained under a 95% confidence level. According to the compiling of the stress spectrum, a one-dimensional spectrum is only associated with the amplitude of stress. Therefore, the stress spectrum at high confidence level can be inferred by figuring out the Weibull distribution function of amplitude. These statistical methods contribute to ensuring that the extracted parameters represent the overall distribution, enhancing the methodology’s adaptability to data variability.

4.2 The Compilation of the Statistical Stress Spectrum

  1. (1)

    The characteristics of the stress spectrum: Taking measurement point 2D6 as an example, the three parameter values from Weibull distribution of the stress spectrum can be obtained as follows: scale parameter \(\alpha =1.1845\), shape parameter \(\beta =0.6375\), and location parameter \(\mu =0.9387\). Then the probability density function of the three-parameter Weibull distribution can be obtained as follows:

    $$\begin{aligned} f(x)= & {} \frac{0.6375}{1.1845}\left[ \frac{x-0.9387}{1.1845}\right] ^{0.6375-1}\nonumber \\{} & {} \exp \left\{ -\left( \frac{x-0.9387}{1.1845} \right) ^{0.6375} \right\} , (x\ge 0.9387) \end{aligned}$$
    (7)

    The reliability function of three-parameter Weibull distribution is:

    $$\begin{aligned} P(x)=1- \exp \left\{ -\left( \frac{x-0.9387}{1.1845} \right) ^{0.6375} \right\} , (x\ge 0.9387) \end{aligned}$$
    (8)

    The probability density function of the stress spectrum under a 95% confidence level is compared with the probability density function inferred from the data for a certain day, and the comparison results are shown in Fig. 4. It can be seen that the two curves are basically coincident, which means that the probability density function under a 95% confidence level is equivalent to the probability density function result inferred from every independent day within the study range.

  2. (2)

    Statistical inference of stress maximum: Conver [22] proposed that cycles of \(10^6\) times could cover all the loads with low occurrence probability and severe conditions. However, according to the spectrum compiled from the line testing data, the number of cycles has not reached \(10^6\) times, which cannot be directly applied to the fatigue test. At the same time, it is uncertain whether the stress maximum values on the operating line are included in the actual test stress spectrum. Thus, taking the occurrence of stress maximum in cycle of \(10^6\) times as the basis for inference, the total cumulative frequency of the stress is extended to \(10^6\) times. Then, the probability of occurrence of the maximum value is set as \(10^6\) and then substituted into the transcendental probability function shown in Eq. (9) so the stress maximum can be calculated as the following equation:

    $$\begin{aligned} P(x)=1-\int _{-\infty }^{x}f(x)dx=10^{-6} \end{aligned}$$
    (9)

    Taking measurement point 2D6 as an example, the fitting parameters \(\alpha\), \(\beta\), and \(\mu\) of the Weibull distribution are known. When the level of stress spectrum is selected as 64, the upper limit of stress amplitude corresponding to level 64 can be calculated through Eq. (9), where the probability of occurrence of stress amplitude maximum is \(P(X)=10^{-6}\), and the stress amplitude maximum is then obtained as \(X_{max}=73.8\) MPa. Similarly, the stress amplitude maximum values of measurement points 2D9, 4HZ1, and 2HC2 can be inferred. The stress amplitude maximum values from the stress spectrum of a certain day are randomly selected and compared with the inferred stress amplitude maximum values, which are listed in Table 3. It can be seen that the stress amplitude maximum values inferred from Weibull distribution are all larger than those of the measured data spectrum. Since the number of cycles in a single day test is less than \(10^6\), it can be considered that the stress amplitude maximum values predicted by Weibull distribution meet the requirements of covering the whole life cycle of vehicle operation, which is in line with the actual situation.

  3. (3)

    Comparison of statistical stress spectrum and measured stress spectrum

Fig. 4
figure 4

The probability density function of 95% confidence and one-way inference

Full size image
Table 3 The statistical inference of stress amplitude maximum
Full size table

According to the results obtained above, all stress amplitude values corresponding to 64 levels of each measurement point are obtained first, and the group interval of the stress amplitude is close to the group interval of the measured stress spectrum. The frequency corresponding to each level of amplitude is solved through the probability density function, and then the statistical stress spectrum with a 95% confidence level could be compiled. Taking measurement point 2D6 as an example, the amplitude and frequency of the inferred statistical stress spectrum with a 95% confidence level and the measured single-day stress spectrum are compared, which can be seen in Fig. 5. The comparative analysis reveals that stress amplitudes at all levels within the statistical stress spectrum consistently surpass those observed in the measured stress spectrum. Moreover, the frequency of stress amplitudes at each level is also notably higher. This observation signifies that the damage induced at each level by the statistical spectrum encompasses and surpasses the damage incurred by the measured spectrum. In essence, the statistical stress spectrum, by consistently exhibiting larger stress amplitudes and frequencies across all levels, is positioned to cover and encapsulate the fatigue-related damage observed in the measured spectrum. The consistent trend of larger stress amplitudes and frequencies across various measurement points, besides 2D6, further solidifies the robustness and generalizability of this conclusion.

Fig. 5
figure 5

Comparison of amplitude and frequency between the statistical spectrum and measured spectrum of measurement point 2D6

Full size image

4.3 Linear Damage Accumulation and Failure Criteria

After the compilation of the statistical stress spectrum, it can also be used to calculate the damage for different measurement points. The Miner damage theory is widely used in engineering practice for cumulative damage calculation [23]. The damage of all stress levels is calculated separately; these damages can be superimposed linearly. After the statistical inference of a statistical spectrum from a measured spectrum, the stress level series \(S_1\),\(S_2\),...,\(S_k\) can be obtained, and its corresponding frequency is \(n_1\),\(n_2\),...,\(n_k\). Then, according to the S-N curve of the relevant materials, the fatigue life can be also obtained as \(N_1\),\(N_2\),...,\(N_k\). Therefore, Miner’s theory can be expressed as Eq. (10):

$$\begin{aligned} D_s=\sum _{i=1}^{k}\frac{n_i}{N_i}=\sum _{i=1}^{k}\frac{n_i S_i^m}{C} \end{aligned}$$
(10)

where \(D_s\) is the damage calculated from the statistical spectrum, k is the spectrum level, and C and m are the S-N curve parameters. By using Eq. (10) to calculate the damage for selected measurement points according to the statistical stress spectrum, the results show that the damage is relatively larger than the value calculated from the measured spectrum. This again shows that the statistical stress spectrum, exhibiting larger stress amplitudes and frequencies across all levels, is positioned to cover and encapsulate the fatigue-related damage observed in the measured spectrum.

The fracture is considered to happen when damage \(D_c\) finally accumulates to 1, which can be used as the fatigue evaluation criteria. If the calculated damage is larger than \(D_c\), it can be assumed that failure would occur.

5 Optimization of Tracking Test Period on Bogie Operation

In practice, enough samples are often obtained through a tracking test for the compilation of a stress spectrum, and then the statistical spectrum is inferred and analyzed through the population distribution function. In order to ensure the accuracy and reliability of the analysis results, it is necessary to track the number of test samples in sufficient quantity. However, there is no in-depth study on the requirement of the number of samples. The tracking test in this paper lasted for 16 months, and the effective data collected was as long as 6 months, and the collection of corresponding samples cost a lot of resources. In order to improve efficiency, it is necessary to determine the minimum number of samples reflecting the characteristics of the population distribution, that is, how long the tracking test period needs to be investigated.

5.1 Normality Test of Grouping Parameters

According to the above statistical inference of Weibull distribution parameters, eight stress measurement points are selected as the study objects. The collected samples data are divided evenly into three groups on average according to the number of samples, and K-S tests are carried out on fitting parameters (like scale parameter \(\alpha\) and shape parameter \(\beta\)) of different measurement points in each interval, which can be used to determine whether each parameter of the measurement points meets the normal distribution. Taking stress measurement point 2D6 as an example, the K-S test results are listed in Table 4.

Table 4 K-S test results of distribution parameters of measurement point 2D6 in different groups
Full size table

The obtained results indicate that the P-values from all conducted tests surpass the predetermined significance level of 0.05. This observation leads to the conclusion that under a 95% confidence level, the assumption that each fitting parameter of the measurement point adheres to a normal distribution cannot be rejected. This statistical inference holds true for each fitting parameter within the studied measurement points. Similar results are consistently observed across various measurement points within each group. Therefore, it can be deduced that the fitting parameters of different measurement points within each group also conform to a normal distribution

5.2 Determination of Minimum Sample Size

Based on the above data grouping, under a 95% confidence level, the K-S test is carried out for the fitting parameters of each group so as to test whether the parameters of each group meet the normal distribution. The sample size of parameters meeting the normal distribution is denoted as Q. Under the condition of following normal distribution, the random sampling is realized by programming, and the sample size obtained by sampling is denoted as q (q = 2, 3, 4, 5...). The t-test is carried out for the samples extracted from any group and its corresponding total sample, and the significance test level is set as 0.05. If the mean and variance of population distributions obtained from the two samples are the same, it is considered that the sample size q can be used to replace the group of population samples. The data collected at stress measurement point 2D6 in the first group are taken as an example to discuss its scale parameter variables . Its sample size Q is 60. Random sampling is carried out for the population samples within the group. In order to ensure the sample size obtained by sampling is more reliable, 50 groups are selected, and the sample size obtained by each group is q (q = 2, 3, 4, 5, 6...). When the number of groups that do not meet the t-test within 50 groups is no more than 2, then it can be concluded that the sample size of the current grouping can replace the total sample number under a 95% confidence level.

Taking the first group of sampled data as an example, the Levene test of homogeneity of variance and t-test of the sample and the population are conducted, and the results are listed in Table 5.

Table 5 Results for Levene test of homogeneity of variance and t-test for independent sample
Full size table

It can be seen from Table 5 that the F-statistic is 0.008 and the P-value is 0.927, which is larger than the significance test level of 0.05, so the hypothesis of no significant difference in variance is accepted. Table 8 also shows that the t-statistic value is 0.297 and the P-value is 0.768, which is also larger than the significance test level of 0.05. Therefore, the null hypothesis of the t-test is accepted. Under the significance test level of 0.05, it is determined that there is no significant difference between the mean values of the samples and the population.

The Levene test of homogeneity of variance and t-test are carried out for 50 groups of samples and the population successively, so as to ensure that the sample size obtained from sampling is more reliable. The initial value of sample size q is set as 2, and the t-test is conducted for each group of samples and the population samples. When q is given any value and the number of groups that do not meet the t-test is larger than 2, then q is increased by 1, and 50 groups are selected again to repeat the test steps. The test can be stopped only when the number of groups that do not meet the t-test within 50 groups is no more than 2. Finally, in the first group, the minimum number of samples of stress measurement point 2D6 is 3. The same method is used to obtain the minimum number of samples of other measurement points in different groups. The minimum number of samples of all measurement points in each group are shown in Table 6.

Table 6 The minimum number of samples in different groups of measurement points
Full size table

Comparing the minimum number of parameter samples of different measurement points under the same group, the highest value is taken as the minimum number of samples under the same group. From the comparison in Table 6, it can been seen that for stress measurement points, the minimum number of samples for the first group is 15, the minimum number of samples for the second group is 6 and the minimum number of samples for the third group is 8. Therefore, for the whole test period, when under a 95% confidence level, at least 29 single-day data samples need to be collected to reflect the overall distribution.

Therefore, the testing time required for collected data is reduced, making the measurement process more flexible, and testers can reasonably arrange time, improving efficiency. The determination of the minimum sample size representing the overall distribution optimizes tracking test periods. This ensures that the shortest tracking test period adequately reflects the overall stress distribution of typical fatigue control parts, allowing for efficient testing planning and execution.

6 Conclusions

Due to concerns related to testing cost and operational safety, tracking the entire service period of a metro vehicle becomes impractical. Hence, there arises an imperative to investigate the minimum tracking period necessary for a high-reliability life evaluation. Our methodology recognizes the impracticality of recording all dynamic stress data throughout the entire service period. By strategically utilizing limited dynamic stress data samples, we achieve a cost-effective approach, optimizing resource utilization while still providing valuable insights into the fatigue characteristics of the metro bogie frame.

The analysis explores stress in eight key fatigue control points during different operating periods. Utilizing the rainflow counting method, the stress spectrum measurements are compiled, and the fitting and testing of a three-parameter Weibull distribution are conducted, confirming the suitability of these measurement points for the distribution under a 95% confidence condition. Obtaining scale parameter and shape parameter samples for different fatigue control parts provides a robust statistical foundation.

Additionally, the mean value is used to replace each parameter variable to achieve the three-parameter Weibull distribution function of the population. Therefore, the maximum values of measurement points are calculated, and the statistical spectrum is also compiled, facilitating the statistical inference of the shortest tracking test period capable of representing the overall data distribution. The inclusion of variance homogeneity testing and t-tests further underscores the method’s statistical rigor.

Results indicate that under the 95% confidence level, the study determines the minimum sample size required to represent the distribution characteristics of the sample population. Specifically, at least 29 single-day test samples are necessary to effectively represent the sample distribution for all stress measurement points throughout the entire test cycle.

This paper is based on a long-term tracking experiment on a specific type of bogie, and the obtained dataset is extensive, providing significant advantages in the inference of the stress spectrum. There are also limitations and prospects of the proposed method: the collected data are representative but may not be universally applicable. In order to enhance the widespread applicability of the data, it is advisable to conduct additional tests on different lines and various types of bogie structures. Likewise, in the study of the minimum sample size for data, due to the wide range of collected data, the division is based solely on averaging according to the number of samples. In order to make the research conclusions more universally applicable, a more in-depth investigation into interval division should be conducted.