Numerical solution of nonlinear Hammerstein integral equations via Sinc collocation method based on double exponential transformation

Abstract

In this paper, numerical solution of nonlinear Hammerstein integral equations via collocation method based on double exponential transformation is considered. Some remarks with respect to the computational cost and stability and implementation are discussed. Examples are presented to illustrate effectiveness of method.

Introduction

In this paper, we consider the nonlinear Hammerstein integral equations of this form:

$$u\left(x\right)=g\left(x\right)+\lambda {\int }_{\Gamma }K(x,t)F(t,u(t\left)\right)\mathit{\text{dt}},x,t\in \Gamma =[a,b],$$

(1)

where a,b, and λ are real constants; g(x),K(x,t), and F(t,u(t)) are given functions; and u(x) is to be determined. Equation 1 is applied in various areas of electromagnetic, fluid dynamics, reformulation of two-point boundary value problems [1]. Many different methods are usually used to solve Equation 1 such as the polynomial approximation [2], radial basis function [3], Adomian decomposition method [4], Chebyshev and Taylor collocation [5], and wavelets [6].

The Sinc method is a powerful numerical tool for finding fast and accurate solutions in various areas of problems. In [7, 8], a full overview of the Sinc function and appropriate conditions and theorems have been discussed. In [9], the Sinc collocation method for numerical solutions of Hammerstein integral equations was used. Double exponential transformation, abbreviated as DE was first proposed by Takahasi and Mori [10] in 1974 for one-dimensional numerical integration, and it has come to be widely used in applications. It is known that the double exponential transformation gives an optimal result for the numerical evaluation of definite integrals of an analytic function [11–13]. Indeed it has been demonstrated that the use of the Sinc method in cooperation with the DE transformation gives highly efficient numerical methods for approximation of function, indefinite numerical integration, and solution of differential equations [14]. However, Sugihara [15–17] has recently found that the errors in the Sinc numerical methods are O(exp(−c N/l o g N)) with some c>0, which is also practically meaningful.

The main purpose of the present research is to consider the numerical solution of Hammerstein integral equations based on double exponential transformation and investigate computational cost and stability and implementation of the algorithm. Also, some remarkable properties of this method are explained.

The layout of the paper is as follows: in the “Methods” section, we give basic definitions, assumptions and preliminaries of the Sinc approximations and main idea of the work. In the “Results and discussion” section, the proposed algorithm is applied to solve some nonlinear Hammerstien integral equations and the details of the numerical implementation and some experimental results are mentioned; finally, the “Conclusion” section, contains the conclusion remarks.

Algorithm 1

Methods

Basic definitions and preliminaries

Let f be a function defined on $ℝ$, h>0 as the step size, and then the Whittaker cardinal defined by the series

$$C(f,h)\left(x\right)=\sum _{j=-\infty }^{\infty }f\left(\mathit{\text{jh}}\right)S(j,h)\left(x\right),$$

(2)

whenever this series is convergent, and

$$S(j,h)\left(x\right)=\frac{sin\left[\pi \right(x-\mathit{\text{jh}})/h]}{\pi (x-\mathit{\text{jh}})/h},j=0,\pm 1,\pm 2,\mathrm{...},$$

(3)

where S(j,h)(x) is known as j−t h Sinc function evaluated at x. Throughout this paper, let d>0 and D _d denote the region {z=x+i y |y|<d} in the complex plan $\mathcal{C}$ and ϕ the conformal map of a simply connected domain D in the complex domain onto D _d , such that ϕ(a)=−∞,ϕ(b)=∞, where a,b are boundary points of D with a,b∈∂ D. Let ψ denote the inverse map of ϕ, and let the arc Γ, with end points a,b (a,b∈Γ), given by Γ=ψ(−∞,∞). For h>0, let the points x _k on Γ given by x _k =ψ(k h), k∈Z.

Moreover, let us consider H¹(D _d ) be the family of all functions g analytic in D _d , such that

$$\begin{array}{c}{N}_1(g,D_d)=\underset{є\to 0}{lim}{\int }_{\partial D_{d\left(є\right)}}\left|g\right(t\left)\right|\left|\mathit{\text{dt}}\right|<\infty ,\\ D_{d\left(є\right)}=\{t\in C,|\mathit{\text{Ret}}|<\frac{1}{є},|\mathit{\text{Imt}}|<d(1-є\left)\right\}.\end{array}$$

We recall the following definition from [10, 16], which will become instrumental in establishing our useful formulas:

Definition 1

A function g is said to decay double exponentially if there exist constants α and C, such that

$$\left|g\right(t\left)\right|\le Cexp(-\alpha exp|t\left|\right),t\in (-\infty ,\infty ).$$

Equivalently, a function g is said to decay double exponentially with respect to conformal map ϕ if there exist positive constants α and C such that

$$\left|g\right(\varphi \left(t\right)\left){\varphi }^{\prime }\right(t\left)\right|\le Cexp(-\alpha exp|t\left|\right),t\in (-\infty ,\infty ).$$

Here, we suppose that $K_{\varphi }^{\alpha }\left(D_d\right)$ denote the family of functions g, where g(ϕ(t))ϕ^′(t) belongs to H¹(D _d ) and decays double exponentially with respect to ϕ. If f belongs to $K_{\varphi }^{\alpha }\left(D_d\right)$ with respect to ϕ, then we have the following formulas for definite and indefinite integrals based on DE transformation which is given and fully discussed in [18]:

$$\begin{array}{c}{\int }_a^{b}f\left(x\right)\mathit{\text{dx}}=h\sum _{j=-N}^{j=N}f\left(\varphi \right(\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ +O(exp(\frac{-2\mathrm{\pi dN}}{\text{log}(2\mathrm{\pi dN}/\alpha )}\left)\right)\end{array}$$

(4)

and

$$\begin{array}{c}{\int }_a^{s}f\left(x\right)\mathit{\text{dx}}=h\sum _{j=-N}^{j=N}f\left(\varphi \right(\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ \times (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\frac{\pi {\varphi }^{-1}\left(s\right)}{h}-\mathrm{j\pi }\left)\right)\\ +O(\frac{\text{log}N}{N}exp(-\frac{\mathrm{\pi dN}}{\text{log}(\mathrm{\pi dN}/\alpha )}\left)\right),\end{array}$$

where

$$\varphi \left(t\right)=\frac{b-a}{2}\text{tan}h\left(\frac{\pi }{2}\text{sin}\mathit{\text{ht}}\right)+\frac{a+b}{2},$$

(5)

$${\varphi }^{\prime }\left(t\right)=\frac{b-a}{2}\frac{\pi /2\text{cos}h\left(t\right)}{\text{cos}{h}^2(\pi /2\text{sin}h(t\left)\right).}$$

(6)

Also, S i(t) is the Sine integral defined by:

$$\mathit{\text{Si}}\left(t\right)={\int }_0^t\frac{\text{sin}w}{w}\mathit{\text{dw}},$$

and the mesh size h satisfies $h=\frac{1}{N}log(\mathrm{\pi dN}/\alpha )$.

Main idea

To apply DE transformation for approximation of Equation 1, first, we use indefinite integration for the second term of its right-hand side:

$$\begin{array}{c}{\int }_a^{x}K(x,t)F(t,u(t\left)\right)\mathit{\text{dt}}\simeq h\sum _{j=-N}^{N}K(x,\varphi (\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\frac{\pi {\varphi }^{-1}\left(x\right)}{h}-\mathrm{j\pi }\left)\right)F_j.\end{array}$$

(7)

Similarly, for definite integral we have:

$${\int }_a^{b}K(x,t)F(t,u(t\left)\right)\mathit{\text{dt}}\simeq h\sum _{j=-N}^{N}K(x,\varphi (\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right))F_j,$$

where F _j =F(t _j ,u(t _j )),j=−N...N. If we substitute Equation 7 in right-hand side of Equation 1,

$$\begin{array}{c}u\left(x\right)-h\sum _{j=-N}^{N}K(x,\varphi (\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ \times (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\frac{\pi {\varphi }^{-1}\left(x\right)}{h}-\mathrm{j\pi }\left)\right)F_j\simeq g\left(x\right).\end{array}$$

(8)

To find unknown F _j =F(t _j ,u(t _j ),j=−N...N, we can apply the Sinc collocation points x _k as x _k =ϕ(k h),k=−N...N, so we have the following nonlinear system of (2N+1)(2N+1) unknown F _j :

$$\begin{array}{c}u\left(x_k\right)-h\sum _{j=-N}^{N}K(x_k,\varphi (\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ \times (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\pi (k-j)\left)\right)F_j=g\left(x_k\right).k,j=-\mathrm{N..N.}\end{array}$$

(9)

By solving a system of nonlinear equations, we obtain approximate solution u _j which corresponds to the exact solution u(x _j ) at the Sinc points x _k =ϕ(k h). To obtain an approximation in arbitrary x, we use a method similar to the Nyström method [19] for the Volterra integro differential equation:

$$\begin{array}{c}{u}_N\left(x\right)=g\left(x\right)+\mathrm{\lambda h}\sum _{j=-N}^{N}K(x,\varphi (\mathit{\text{jh}}\left)\right){\varphi }^{\prime }\left(\mathit{\text{jh}}\right)\\ \times (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\frac{\pi {\varphi }^{-1}\left(x\right)}{h}-\mathrm{j\pi }\left)\right))F_j.\end{array}$$

(10)

By using the notations

$$\begin{array}{l}\mathbf{A}=\left(a_{\mathit{\text{kj}}}\right),a_{\mathit{\text{kj}}}=\left[K\right(x_k,\varphi \left(\mathit{\text{jh}}\right)\left){\varphi }^{\prime }\right(\mathit{\text{jh}})\\ \times (\frac{1}{2}+\frac{1}{\pi }\mathit{\text{Si}}(\pi (k-j)\left)\right)],k,j=-\mathrm{N..N}\\ \mathbf{U}={(u_{-N},\dots ,u_N)}^t,\mathbf{g}={\left(g\right(x_{-N}),\dots ,g(x_N\left)\right)}^t,\\ \mathbf{F}={(F_{-N},\dots ,F_N)}^t,\end{array}$$

the system in Equation 9 can be shown in matrix form:

$$\mathbf{U}-\mathbf{A}\mathbf{F}=\mathbf{g}.$$

(11)

Finally, we give Algorithm 1 to compute numerical solution of Equation 1.

Results and discussion

Numerical experiments

In this section, three examples are presented based on Algorithm 1 to illustrate the effectiveness and importance of proposed method. All programs have been provided by Maple 13. Also, in order to show the error and the accuracy of approximation, we apply the following criteria: 1) Absolute error between the exact and approximate solution (L _∞ error norm) is defined for M=2N+1 by

$$\parallel .{\parallel }_{\infty }=\mathit{\text{Ma}}{x}_{i=-\mathrm{N..N}}\left|u\right(x_i)-u_M(x_i\left)\right|.$$

(12)

• 2) The L ₂ error norm is defined by

  $$\parallel .{\parallel }_2=\sqrt{\sum _{i=-N}^N{\left[u\right(x_i)-u_M(x_i\left)\right]}^2}.$$

  (13)

• 3) The root mean square (RMS) is defined by

  $$\mathit{\text{RMS}}=\sqrt{\frac{1}{M}\sum _{-N\le i\le N}{\left[u\right(x_i)-u_M(x_i\left)\right]}^2,}$$

  (14)

where M=2N+1 is the number of test points (Sinc points). 4) Run time of program which is showed by T(s), (s means second).

Example 1

Consider the integral equation [3]:

$$\begin{array}{c}u\left(x\right)=1+\stackrel{2}{sin}\left(x\right)+{\int }_0^x-3sin(x-t)u^2\left(t\right)\mathit{\text{dt}},0\le x\le 1\end{array}$$

(15)

with the exact solution: u(x)= cos(x). To obtain results, we take three sample numbers of basic functions, such as N=5,8,11. Also, in order to have better results, we concentrate on the mentioned criteria as runtime (column T(s) in Table 1), infinity norm (column ∥.∥ _∞ ), L₂ error norm (column ∥.∥₂), RMS error (column RMS), condition number (column Cond based on infinity norm). The results in Sinc collocation method are shown in Table 1.

Table 1 Results of Example 1 by Sinc collocation method

As observed in Table 1, numerical results show simplicity and very good accuracy of the method. By decreasing the number of basic functions, the errors have been decreased. Also, in comparison with the results of [3], which used MQ Radial Basis function, condition number in each row is very small, which is a good factor in the Sinc method. For example, in the Sinc method for N=10, we have a 21×21 system of nonlinear equations, with condition number 7.19E+000, but in [3], condition number is 2.45E+013, which is very noticeable. Also, we must notice the size of system which in this case is 10×10. Run time of program in comparison with the size of nonlinear system in the Sinc method is remarkable. Figure 1 shows the exact and the approximate solution of this example.

Figure 1

The exact u(x) and the approximate u _N (x) solution of Example 1 for N=5 .

Example 2

Consider the following integral equation [9]:

$$u\left(x\right)=exp(x+1)-{\int }_0^{1}exp(x-2t)u^3\left(t\right)\mathit{\text{dt}},0\le x\le 1$$

(16)

with the exact solution: u(x)= exp(x).

In this example, results show good approximation based on the Sinc collocation method. Clearly, these remarkable factors are mostly due to structure of coefficient matrix which is very important. Also, in [9], Sinc collocation with single transformation $\varphi \left(x\right)=ln\left(\frac{x}{1-x}\right)$ was applied and for N=35 maximum error. ∥.∥ _∞ =9.37E−10 was obtained which in comparison with double exponential transformation is very remarkable since in this manner, the size of nonlinear system is 71×71. Figure 2 shows convergence behavior of the Sinc collocation method in terms of infinity norm versus reciprocal of number of collocation points N. Similar to column ∥.∥ _∞ in Table 2, Figure 2 shows that infinity norm decreases by increasing the number of collocation points. Figure 3 shows the exact and approximate solution of this example.

Figure 2

The plot of error (with infinity norm) versus N in Example 2.

Table 2 Results of Example 2 by Sinc collocation method

Figure 3

u(x) the exact and u _N (x) the approximate solution of Example 2 with N=3 .

Example 3

Consider the following nonlinear Hammerstein integral equation [9]:

$$u\left(x\right)={\int }_0^1\mathit{\text{xt}}{u}^2\left(t\right)\mathit{\text{dt}}-\frac{5}{12}x+1,0\le x\le 1$$

(17)

with the exact solution: $u\left(x\right)=1+\frac{1}{3}x$

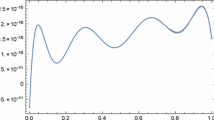
The results in Table 3, show the efficiency and rate of convergence of the method. By decreasing the number of basic functions, the errors have been decreased. Condition number in each row is small, that is a good factor in Sinc method. This property is caused by special structure of coefficient Matrix. In comparison with [9] by single exponential transformation and maximum error ∥.∥ _∞ =5.88E−9 with N=45, results in Table 3 are very considerable. Figure 4 shows convergence behavior of Sinc collocation method. Also, Figure 5 shows the exact and the approximate solution of this example.

Figure 4

The plot of error (with infinity norm) versus N in Example 3.

Table 3 Results of Example 3 by Sinc collocation method

Figure 5

The exact u(x) and the approximate u _N (x) solution of Example 3 with N=3 .

However, the results show that the proposed method is practically reliable. Also, Sinc collocation method gives better accuracy in very small run time with low computational cost. Based on results and other works [20, 21], the Sinc collocation method gives better accuracy at the computational cost; also, the implementing and coding are very easy.

Conclusion

We applied the Sinc collocation method based on double exponential transformation to nonlinear Hammerstein integral equations. The Sinc collocation method in run time and condition number have good reliability and efficiency. Also, we can improve the accuracy of the solution by selecting the appropriate shape parameters and selecting the large values of N. Results show the high accuracy of method by taking this view that storing in time and memory is another useful property in the Sinc method. In addition, this method is portable to other areas of problems and is easy to program.