Numerical solutions of nonlinear Fisher's reaction–diffusion equation with modified cubic B-spline collocation method

Abstract

In this paper, a numerical method is proposed to approximate the numeric solutions of nonlinear Fisher's reaction–diffusion equation with modified cubic B-spline collocation method. The method is based on collocation of modified cubic B-splines over finite elements, so we have continuity of the dependent variable and its first two derivatives throughout the solution range. We apply modified cubic B-splines for spatial variable and derivatives, which produce a system of first-order ordinary differential equations. We solve this system by using SSP-RK54 scheme. The proposed method needs less storage space that causes less accumulation of numerical errors. The numerical approximate solution to the nonlinear Fisher's reaction–diffusion equation has been computed without using any transformation and linearization process. Illustrative three test examples are included to establish the effectiveness and pertinence of the technique. Easy and economical implementation is the strength of this method.

Introduction

We consider the nonlinear Fisher's reaction–diffusion equation

$$\frac{\partial u}{\partial t}=\alpha \frac{{\partial }^{2}u}{\partial x^2}+\beta u\left(1-u\right),a\le x\le b,t>0,$$

(1.1)

with the initial and boundary conditions

$$u\left(x,0\right)=u_0\left(x\right),a\le x\le b$$

(1.2)

$$u\left(a,t\right)=g_0\left(t\right),u\left(b,t\right)=g_1\left(t\right),t\in \left[0,t\right].$$

(1.3)

The properties of Fisher's equation have been contrived theoretically by many authors. The analysis of travelling wave solution of Fisher's equation has been studied by many computational approaches. Travelling wave fronts have important applications in various fields of science and engineering, for example, chemistry, biology, and medicine [1]. One of the first numerical solutions was described by Gazdag and Canosa [2] with a pseudo-spectral approach. Ablowitz and Zepetella [3] have established an explicit solution of Fisher's equation for a special wave speed. Twizell et al. [4] and Parekh and Puri [5] have demonstrated implicit and explicit finite-differences algorithms to discuss the numerical study of Fisher's equation. Tang and Weber [6] have proposed a Galerkin finite element method for solving Fisher's equation. Mickens [7] has introduced a best finite-difference scheme for Fisher's equation. Mavoungou and Cherruault [8] have depicted a numerical study of Fisher's equation by Adomian's method. Qiu and Sloan [9] have used a moving mesh method for numerical solution of Fisher's equation. Al-Khaled [10] has proposed the sinc collocation method for Fisher's equation. Zhao and Wei [11] have presented a comparison of the discrete singular convolution and three other numerical schemes for solving Fisher's equation. Wazwaz and Gorguis [12] have given the exact solutions to Fisher's equation and to a nonlinear diffusion equation of the Fisher type by employing the Adomian decomposition method. Olmos and Shizgal [13] have constructed the numerical solutions to Fisher's equation using a pseudo-spectral approach. Mittal and Kumar [14] and El-Azab [15] have contrived Fisher's equation by applying the wavelet Galerkin method. Recently, Sahin et al. [16] have applied the B-spline Galerkin approach to find numerical solution of Fisher's equation. Cattani and Kudreyko [17] have developed multiscale analysis of the Fisher equation. Mittal and Jiwari [18] have developed a numerical study of Fisher's equation by using differential quadrature method. Mittal and Arora [19] have presented efficient numerical solution of Fisher's equation by using B-spline collocation method.

In this paper, we have presented a simple numerical method that uses modified cubic B-spline for the spatial derivatives which produce a system of first-order ordinary differential equations. We solve this system by using SSP-RK54 scheme. This method needs less storage space that causes less accumulation of numerical errors. The approximate numerical solution to the nonlinear Fisher's reaction–diffusion equation has been computed without using any transformation and linearization process.

This paper is organized as follows: In the ‘Description of the methods’ section, description of cubic B-spline collocation method is explained. In the ‘Modified cubic B-spline collocation method’ section, procedure for implementation of present method is described for Equations 1.1 to 1.3. In the ‘The initial vector α⁰’ section, procedure to obtain an initial vector which is required to start our method is explained. We have discussed three test examples to authenticate the adaptability and accuracy of the presented method in the ‘Numerical experiments and discussion’ section, followed by the ‘Conclusions’ section that briefly summarizes the numeric approximate outcomes.

Description of the methods

In the cubic B-spline collocation method, the approximate solution can be written as a linear combination of cubic B-spline basis functions for the approximation space under consideration.

We consider a mesh a = x₀ < x₁, …, x_N − 1 < x _N  = b as a uniform partition of the solution domain a ≤ x ≤ b by the knots xj with $h=x_j-x_{j-1}=\frac{b-a}{N},j=1,\dots ,N$.

Our numerical treatment for solving Equation 1.1 using the collocation method with cubic B-splines is to find an approximate solution U^N(x,t) to the exact solution u(x,t) in the form

$$U^N\left(x,t\right)={\displaystyle \sum }_{j=-1}^{N+1}{\alpha }_j\left(t\right)B_j\left(x\right),$$

(2.1)

where α _j (t) are unknown time-dependent quantities to be determined from the boundary conditions and collocation from the differential equation.

The cubic B-spline B _j (x) at the knots is given by

$$B_j\left(x\right)=\frac{1}{h^3}\left\{\begin{array}{cc}\hfill {\left(x-x_{j-2}\right)}^3\hfill & \hfill \mathit{x\epsilon }\left[x_{j-2},x_{j-1}\right)\hfill \\ \hfill {\left(x-x_{j-2}\right)}^3-4{\left(x-x_{j-1}\right)}^3\hfill & \hfill \mathit{x\epsilon }\left[x_{j-1},x_j\right)\hfill \\ \hfill \begin{array}{c}\hfill {\left(x_{j+2}-x\right)}^3-4{\left(x_{j+1}-x\right)}^3\hfill \\ \hfill \begin{array}{c}\hfill {\left(x_{j+2}-x\right)}^3\hfill \\ \hfill 0\hfill \end{array}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \mathit{x\epsilon }\left[x_j,x_{j+1}\right)\hfill \\ \hfill \begin{array}{c}\hfill \mathit{x\epsilon }\left[x_{j+1},x_{j+2}\right)\hfill \\ \hfill \mathit{otherwise}\hfill \end{array}\hfill \end{array}\hfill \end{array}\right\}$$

(2.2)

where B₁,B₀,B₁,…, B_{N − 1}B _N ,B_{N + 1} forms a basis over the region a ≤ x ≤ b.

Each cubic B-spline covers four elements, so each element is covered by four cubic B-splines. The values of B _j (x) and its derivative may be tabulated as in Table 1.

Table 1 Coefficient of cubic B-splines and its derivatives at knots x _j

Using approximate function (2.1) and cubic B-spline function (2.2), the approximate values of UN(x) and its two derivatives at the knots/nodes are determined in terms of the time parameters αj as follows:

$$\begin{array}{l}{U}_j={\alpha }_{j-1}+4{\alpha }_j+{\alpha }_{j+1}\\ h{U}_j\prime =3\left({\alpha }_{j+1}-{\alpha }_{j-1}\right)\\ h^2{U}_j\prime \prime =6\left({\alpha }_{j-1}-2{\alpha }_j+{\alpha }_{j+1}\right)\end{array}$$

(2.3)

Modified cubic B-spline collocation method

In this paper, we have used the following modification in cubic B-spline basis functions to solve Fisher's equation. In the proposed method, there is a necessity to modify the cubic B-spline basis functions into a new set of basis functions in such manner, so we obtained a diagonally dominant system of differential equations for handling with Dirichlet boundary conditions. The procedure for modifying the basis functions is given as follows:

$${\tilde{B}}_0\left(x\right)=B_0\left(x\right)+2B_{-1}\left(x\right)$$

$${\tilde{B}}_1\left(x\right)=B_1\left(x\right)-B_{-1}\left(x\right)$$

$${\tilde{B}}_j\left(x\right)=B_j\left(x\right),j=2,\dots ,N-2$$

(3.1)

$${\tilde{B}}_{N-1}\left(x\right)=B_{N-1}\left(x\right)-B_{N+1}\left(x\right)$$

$${\tilde{B}}_N\left(x\right)=B_N\left(x\right)+2B_{N+1}\left(x\right)$$

Now, we consider the approximate solution using the modified cubic B-spline basis functions in the form

$$\begin{array}{l}{U}^N\left(x_0,t\right)=g_0\left(t\right),\mathrm{for}j=0\\ U^N\left(x_j,t\right)={\displaystyle \sum }_{j=0}^N{\alpha }_j{\tilde{B}}_j\left(x\right),\mathrm{for}j=1,\dots ,N-1\\ U^N\left(x_N,t\right)=g_1\left(t\right),\mathrm{for}j=N\end{array}$$

(3.2)

To apply the proposed method with the modified set of cubic B-spline basis functions ${\tilde{B}}_j\left(x\right),j=0,\dots ,N$ to Equations 1.1 to 1.3, we proceed as follows:

Our numerical treatment for solving Equation 1.1 using the collocation method with modified cubic B-splines is to find an approximate solution U^N(x,t) to the exact solution u(x,t) which is given in (3.2), where α _j (t) are time-dependent quantities to be determined from the boundary conditions and collocation from the differential equation.

Using approximate solution (3.2) and modified cubic B-spline function (3.1), the approximate values of U _t ^N(x) at the knots/nodes are determined in terms of the time parameters α _j as follows:

$$\begin{array}{l}{\left(U_t\right)}_0={\dot{g}}_0\left(t\right),\mathrm{for}j=0\\ {\left(U_t\right)}_j={\displaystyle \sum }_{j=0}^N{\dot{\alpha }}_j{\tilde{B}}_j\left(x\right),\mathrm{for}j=1,\dots ,N-1\\ {\left(U_t\right)}_N={\dot{g}}_1\left(t\right),\mathrm{for}j=N\end{array}$$

(3.3)

Using (3.1) and Table 1 in (3.3), we obtained

$$\begin{array}{l}{\left(U_t\right)}_0=6{\dot{\alpha }}_0,\mathrm{for}j=0\\ {\left(U_t\right)}_j={\dot{\alpha }}_{j-1}+4{\dot{\alpha }}_j+{\dot{\alpha }}_{j+1},\mathrm{for}j=1,\dots ,N-1\\ {\left(U_t\right)}_N=6{\dot{\alpha }}_N,\mathrm{for}j=N\end{array}$$

(3.4)

Using (3.1) to (3.4) in (1.1) to (1.3), we have

$$6{\dot{\alpha }}_0={\dot{g}}_0\left(t\right),\mathrm{for}j=0$$

$$\begin{array}{ll}{\displaystyle \sum }_0^{N+1}{\dot{\alpha }}_j{\tilde{B}}_j\left(x\right)=& \alpha \left\{{\displaystyle \sum }_0^{N+1}{\alpha }_j{\tilde{B}}_j\text{'}\text{'}\left(x\right)\right\}\\ +\beta \left\{{\displaystyle \sum }_0^{N+1}{\alpha }_j{\tilde{B}}_j\left(x\right)\right\}\left\{1-{\displaystyle \sum }_0^{N+1}{\alpha }_j{\tilde{B}}_j\left(x\right)\right\},\end{array}$$

$$\mathrm{for}j=1,\dots ,N-1$$

$$6{\dot{\alpha }}_N={\dot{g}}_1\left(t\right),\mathrm{for}j=N$$

(3.5)

Using (3.2) to (3.4) in (3.5), we get a system of ordinary differential equations of the form

$$A\dot{\alpha }=\phi$$

(3.6)

$$\begin{array}{ll}\mathrm{\text{where}}& A=\left[\begin{array}{cc}\hfill 6\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 4\hfill & \hfill 1\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill 1\hfill & \hfill 4\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 6\hfill \end{array}\right],\\ \dot{\alpha }=\left[\begin{array}{c}\hfill {\dot{\alpha }}_0\hfill \\ \hfill {\dot{\alpha }}_1\hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill {\dot{\alpha }}_{N-1}\hfill \\ \hfill {\dot{\alpha }}_N\hfill \end{array}\right],\mathrm{\phi \phi }=\left[\begin{array}{c}\hfill {\mathrm{\phi \phi }}_0\hfill \\ \hfill {\mathrm{\phi \phi }}_1\hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill {\mathrm{\phi \phi }}_{N-1}\hfill \\ \hfill {\mathrm{\phi \phi }}_N\hfill \end{array}\right]\end{array}$$

$${\mathrm{\phi \phi }}_0={\dot{g}}_0\left(t\right),\mathrm{for}j=0$$

$${\mathrm{\phi \phi }}_j=\alpha \left({\alpha }_{j-1}-2{\alpha }_j+{\alpha }_{j+1}\right)+\beta \left({\alpha }_{j-1}+4{\alpha }_j+{\alpha }_{j+1}\right)\left\{1-\left({\alpha }_{j-1}+4{\alpha }_j+{\alpha }_{j+1}\right)\right\}$$

$$\mathrm{for}j=1,\dots ,N-1$$

$${\mathrm{\phi \phi }}_N={\dot{g}}_1\left(t\right),\mathrm{for}j=N$$

Here A is the (N + 1) × (N + 1) tridiagonal matrix and φφ is the (N + 1)-order vector which depends on the boundary conditions.

Now, we solve the first-order ordinary differential equation system (3.6) by using SSP-RK54 scheme [20]. Once the parameter α⁰ has been determined at a specified time level, we can compute the solution at the required knots. In (3.6), first we solve this system for vector $\dot{\alpha }$ by using a variant of the Thomas algorithm only once at each time level t > 0, then we get a first-order system of ordinary differential equations which can be solved for vector α by using SSP-RK54 scheme, and consequently, the solution U^N(x,t) is completely known.

The initial vector α⁰

The initial vector α⁰ can be obtained from the initial condition and boundary values of the derivatives of the initial condition as the following expressions:

$$U\left(x_j,0\right)=g_0\left(0\right),j=0,$$

$$U\left(x_j,0\right)=\mathrm{\phi \phi }\left(x_j\right),j=1,\dots ,N-1$$

$$U\left(x_j,0\right)=g_1\left(0\right),j=N.$$

This yields a (N + 1) × (N + 1) system of equations of the form

Aα⁰ = b, (4.1)

where

$$\begin{array}{l}A=\left[\begin{array}{cc}\hfill 6\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 4\hfill & \hfill 1\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill 1\hfill & \hfill 4\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 6\hfill \end{array}\right],{\alpha }^0=\left[\begin{array}{c}\hfill {\alpha }_0^0\hfill \\ \hfill {\alpha }_1^0\hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill {\alpha }_{N-1}^0\hfill \\ \hfill {\alpha }_N^0\hfill \end{array}\right],\mathrm{and}\\ b=\left[\begin{array}{c}\hfill g_0\left(0\right)\hfill \\ \hfill \mathrm{\phi \phi }\left(x_1\right)\hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill \mathrm{\phi \phi }\left(x_{N-1}\right)\hfill \\ \hfill g_1\left(0\right)\hfill \end{array}\right]\end{array}$$

The solution of (4.1) can be found using the Thomas algorithm.

Numerical experiments and discussion

In order to show the utility and adaptability of the method, it is tested on the following three test examples.

Example 1. We consider Equation 1.1 as given in [6] with initial condition

$$u_0\left(x\right)={\mathrm{sech}}^2\left(10x\right),$$

(5.1)

and boundary conditions are

$${lim}_{x\to -\infty }u\left(x,t\right)=0\mathrm{and}{lim}_{x\to \infty }u\left(x,t\right)=0.$$

(5.2)

For all cases, we set α = 0.1, β = 1.0, h = 0.05, and ∆t = 0.005.

The space scale L is adjusted to ensure that there is sufficient space for waves to propagate.

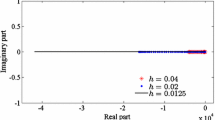
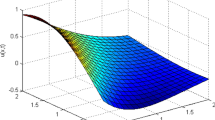
The contour plots of u at different t are shown in Figures 1, 2, 3, and 4.

Figure 1

Approximate solutions at t = 0 to 0.2 with step size h = 0. 05.

Figure 2

Approximate solutions at t = 0 to 5 with step size h = 0.5.

Figure 3

Approximate solutions at t = 0 to 40 with step size h = 2.

Figure 4

Approximate solutions at t = 0 to 40 with step size h = 2.

Figure 1 is for a short period of time, showing the results or t = 0 to 0.2 with step size h = 0.05. At the very beginning, near x = 0, u _xx < 0 with a large absolute value, but the reaction term u(1 − u) is quite small, that is, the effect of diffusion dominates over the effect of reaction, so the peak goes down rapidly and gets flatter.

Figure 2 is for the period of time for t = 0 to 5 with step size h = 0.5. It shows that after the peak of the contour arrives at the lowest level, the reaction term dominates the diffusion (gradually), so it begins to go up and flatten itself until at the top u = 1.

Figure 3 is for the period of time t = 0 to 40 with step size h = 2. It shows that after the peak has returned to its original position, the contour on the top becomes flatter and flatter. So, after a long time, the contour looks like a bell with a flat top and very steep lateral sides, which propagate to the left and right symmetrically. The wave fronts (i.e., the lateral sides) approach a fixed shape, and their propagating speed approaches a constant value c.

Finally, in Figure 4, we show the results for the initial condition

$$u_0\left(x\right)=0.1{\mathrm{sech}}^2\left(10x\right)$$

Example 2. We consider Equation 1.1 as given in [19] with α = 1 as

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+\beta u\left(1-u\right),$$

(5.3)

and boundary conditions are

$$\underset{x\to -\infty }{\lim }u\left(x,t\right)=1.0\mathrm{and}\underset{x\to \infty }{\lim }u\left(x,t\right)=0.$$

(5.4)

The exact solution of Equation 5.3 is taken as

$$u\left(x,t\right)=\frac{1}{{\left[1+\exp \left(\left(\sqrt{\frac{\beta }{6}}\right)x-\left(\frac{5\beta }{6}\right)t\right)\right]}^2}$$

(5.5)

The numerical solution of Equation 5.3 with given boundary conditions by taking [a, b] = [−0.2, 0.8] has been computed at β = 2,000, 5,000, and 10,000 with ∆t = 0.0001. The number of partitions is taken 40 for β = 2,000, 5,000, and 120 for β = 10,000.

The computed results are presented graphically to compare results with other researchers. Results obtained are found in good agreement with the results obtained by Olmos and Shizgal [13] and Mittal and Arora [19].

Figures 5, 6, and 7 have depicted the exact and numerical solutions at different times.

Figure 5

Time-dependent profiles versus x for ρ = 2, 000 and N = 200 at t = 0. 002, 0.003, 0.004, 0.005, 0.006, 0.007.

Figure 6

Time-dependent profiles versus x for ρ = 5, 000 and N = 200 at t = 0. 001, 0.002, 0.003, 0.004, 0.005.

Figure 7

Time-dependent profiles versus x for ρ = 10,000 and N = 200 at t = 0.001, 0.0015, 0.002, 0.0025, 0.003,0.0035.

For β = 10,000, results are also presented in a tabular form in Tables 2 and 3 to compare with the exact solutions.

Table 2 Comparison of numerical and exact solutions

Table 3 Comparison of numerical and exact solutions

Example 3. We consider Fisher's equation as given in [19]

$$\frac{\partial u}{\partial t}=\alpha \frac{{\partial }^{2}u}{\partial x^2}-b{u}^2+\mathit{au},$$

(5.6)

where t ∈ [0,t], 0 < t < ∞, −∞ < x < ∞ with initial condition

$$u\left(x,0\right)=-\frac{1}{4}\frac{a}{b}\left[{\mathrm{sech}}^2\left(-\sqrt{\frac{a}{24c}}x\right)-2\tanh \left(-\sqrt{\frac{a}{24c}}x\right)-2\right]$$

(5.7)

and boundary conditions are

$$\underset{x\to -\infty }{\lim }u\left(x,t\right)=0.5\mathrm{and}\underset{x\to \infty }{\lim }u\left(x,t\right)=0.$$

(5.8)

The exact solution of the problem is given as

$$\begin{array}{ll}u\left(x,t\right)& =-\frac{1}{4}\frac{a}{b}[{\mathrm{sech}}^2\left(\pm \sqrt{\frac{a}{24c}}x+\frac{5a}{12}t\right)\\ -2\tanh \left(\pm \sqrt{\frac{a}{24c}}x+\frac{5a}{12}t\right)-2].\end{array}$$

(5.9)

The solution of the equation predicts a wave front of increasing allele frequency that propagates through the population. Only original alleles are present in front of the wave, and behind the wave is an area taken by over the mutant allele. In short, this equation states that the change of the density of labeled particles at a given time depends on the infection rate −bu² + au and the diffusion in the neighboring area.

The term au measures the infection rate, which is proportional to the product of the density of the infected and uninfected particles. The term −bu² shows how fast the infected particles are diffusing. Some authors have already found an analytical solution [12, 17] of Equation 5.6 for the initial condition (5.7). This solution presents a shock-like travelling wave. The amplitude of the wave is proportional to $\frac{a}{b}$. It means that the amplitude increases as the coefficient a increases, but decreases as b increases. The support of the wave is defined by $\sqrt{\frac{24c}{a}}$. The rate of the wave propagation is $\frac{\left(\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$\sqrt{6}$}\right.\right)}{\sqrt{\mathit{ac}}}$

The solution of Equation 5.6 is found out by using the B-spline collocation method for a = 0.5, b = c = 1.0.

The results obtained are shown in Tables 4 and 5 and compared with the solutions obtained in [17] and [19] with the exact solution. Figure 8 shows the time-dependent profile versus x with h = 0.25 and ∆t = 0.01, where [x _L , x _R ] = [−30, 30], at t = 1, 2, 3, 4, 5.

Table 4 Comparison of numerical and exact solutions at t = 2

Table 5 Comparisons of numerical and exact solutions at t = 4

Figure 8

Approximate solutions at t = 1 to 5 with step 1.

Conclusions

In this paper, we have developed a collocation method for solving nonlinear Fisher's reaction–diffusion equation with Dirichlet's boundary conditions using modified cubic B-spline basis functions. In the present method, we apply modified cubic B-splines for spatial variable and derivatives, which produce a system of first-order ordinary differential equations. The resulting systems of ordinary differential equations are solved by using SSP-RK54 scheme. The numerical approximate solutions to nonlinear Fisher's reaction–diffusion equation have been computed without using any transformation and linearization process. This method is tested on three test examples, and the approximate numerical outcomes obtained are comparable with existing solutions found in the literature. Easy and economical implementation is the strength of this method. The computed results justify the advantage of this method.