Abstract
This paper investigates security-oriented beamforming designs in a relay network composed of a source-destination pair, multiple relays, and a passive eavesdropper. Unlike most of the earlier works, we assume that only statistical information of the relay-eavesdropper channels is known to the relays. We propose beamforming solutions for amplify-and-forward (AF) and decode-and-forward (DF) relay networks to improve secrecy capacity. In an AF network, the beamforming design is obtained by approximating a product of two correlated Rayleigh quotients to a single Rayleigh quotient using the Taylor series expansion. Our study reveals that in an AF network, the secrecy capacity does not always grow as the eavesdropper moves away from the relays or as total relay transmit power increases. Moreover, if the destination is nearer to the relays than the eavesdropper is, a suboptimal power is derived in closed form through monotonicity analysis of secrecy capacity. While in a DF network, secrecy capacity is a single Rayleigh quotient problem which can be easily solved. We also found that if the relay-eavesdropper distances are about the same, it is unnecessary to consider the eavesdropper in a DF network. Numerical results show that for either AF or DF relaying protocol, the proposed beamforming scheme provides higher secrecy capacity than traditional approaches.
Similar content being viewed by others
1. Introduction
Cooperative communications, in which multiple nodes help each other transmit messages, has been widely acknowledged as an effective way to improve system performance [1–3]. However, due to the broadcast property of radio transmission, wireless communication is vulnerable to eavesdropping which consequently makes security schemes of great importance as a promising approach to communicate confidential messages.
The traditional secure communication schemes rely on encryption techniques where secret keys are used. However, as the high-layer secure protocols have attracted growing attacks in recent years, the implementation of security schemes at physical layer becomes a hotspot. It was first proved by Wyner that it is possible to communicate perfectly at a non-zero rate without a secret key if the eavesdropper has a worse channel than the destination [4]. This work was extended to Gaussian channels in [5] and to fading channels in [6]. Recently, there has been considerable work on secure communication in wireless relay networks (WRNs) [7–15]. A widely acknowledged measurement of system security in WRNs is the maximal rate of secret information exchange between source and destination which is defined as secrecy capacity. A decode-and-forward (DF)-based cooperative beamforming scheme which completely nulls out source signal at eavesdropper(s) was proposed in [7], and this work was extended to the amplify-and-forward (AF) protocol and cooperative jamming in [8]. Hybrid beamforming and jamming was investigated in [9] where one relay was selected to cooperate and the other to make intentional interference in a DF network. Combined relay selection and cooperative beamforming schemes for DF networks were proposed in [10] where two best relays were selected to cooperate. The authors of [11, 12] considered the scenario where the relay(s) could not be trusted in cooperative MIMO networks. Additionally, a new metric of system security is brought up in [13] as intercept probability and optimal relay selection schemes for AF and DF protocols based on the minimization of intercept probability were proposed.
In earlier works, it is widely assumed that the relays have access to instantaneous channel state information (CSI) of relay-eavesdropper (RE) channels [7, 8, 13–15]. This assumption is ideal but unpractical in a real-life wiretap attack since the malicious eavesdropper would not be willing to share its instantaneous CSI. Thus, security schemes using instantaneous CSI of the eavesdropper cannot be adopted anymore. However, the instantaneous CSI of relay-destination (RD) channels is available since the destination is positive. The statistical information of the RE channels is also available through long-term supervision of the eavesdropper's transmission [9]. It is worth mentioning that even if the relays do not have access to the perfect CSI of RD channels, they can still estimate these channels by training sequences and perform beamforming based on the estimated CSI [16].
Our focus is on secrecy capacity, and we are interested in maximizing it with appropriate weight designs of relays. The remainder of this paper is organized as follows. Section 2 introduces system model under AF and DF protocols using relay beamforming. The optimization problem in an AF network is addressed and solved in Section 3 along with some analyses of secrecy capacity. Section 4 provides the optimal beamforming design for a DF network along with a surprising finding that considering the eavesdropper sometimes may not be necessary. Numerical results are given in Section 5 to compare the performances of different designs, and Section 6 provides some concluding remarks.
2. System model
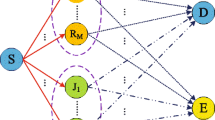
Consider a cooperative wireless network consisting of a source node S, a legitimate destination D, an eavesdropper E, and M relays R i , i = 1,…, M as shown in Figure 1. Each node is equipped with single antenna working in half-duplex mode. Assume that there is no direct link between the source and the destination/eavesdropper, i.e., neither the destination nor the eavesdropper is in the coverage area of the source. For notational convenience, we denote the source-relay (SR) channels as f i , the RD channels as g i , and the RE channels as h i . All the channels are modeled as independent and identically distributed (i.i.d.) Rayleigh fading channels, i.e., , , and . Considering the path loss effect and setting the path loss exponent to 4 (for an urban environment), we have , , and , where dAB is the distance between nodes A and B. We assume the relays to know instantaneous CSI of SR channels and RD channels, but only statistical information of RE channels. Without loss of generality, we also assume the additive noises to be i.i.d. and follow a distribution.
2.1 Amplify-and-forward
In an AF protocol, the source broadcasts in the first hop where the information symbol s is selected from a codebook and is normalized as E|s|2 = 1, and Ps is the transmit power. The received signal at R i is
where v i is the additive noise at R i .
In the second hop, each relay forwards a weighted version of the noisy signal it just received. More specifically, R i normalizes r i with a scaling factor and then transmits a weighted signal t i = w i ρ i r i . The transmit power of R i is P i = |w i |2. The received signal at the destination is
where w = (w1, …, w M )T, ρ fg = (ρ1f1g1, …, ρ M f M g M )T, ρ g = (ρ1g1, …, ρ M g M )T, v = (v1, …, v M )T, and vD represents additive white Gaussian noise (AWGN) at the destination. The total relay transmit power is wHw = P.
Meanwhile, the eavesdropper also gets a copy of s:
where ρ fh = (ρ1f1h1, …, ρ M f M h M )T, ρ h = (ρ1h1, …, ρ M h M )T, and vE represents AWGN at the eavesdropper.
2.2 Decode-and-forward
In a DF protocol, the first hop is the same as in an AF protocol. While in the second hop, instead of simply amplifying the received signal, R i decodes the message s and multiplies it with a weighted factor w i to generate the transmit signal t i = w i s. The transmit power of R i is still P i = |w i |2. The received signals at the destination and the eavesdropper can be expressed, respectively, as
and
where g = (g1, …, g M )T and h = (h1, …, h M )T.
3. Distributed beamforming design for AF
In the following sections, we consider the security issue of the above relay network. The metric of interest is secrecy capacity which is defined as
where , , and γD and γE are received signal-to-noise ratios (SNRs) at the destination and the eavesdropper, respectively. We aim to improve CS by exploiting appropriate beamforming designs. The following subsection describes the proposed beamforming design for an AF network.
3.1 Proposed design for AF (P-AF)
In distributed beamforming schemes, the relays compute the received SNRs at the destination and the eavesdropper from Equations 2 and 3, respectively, as
and
where Γ g = diag(ρ12|g1|2, …, ρ M 2|g M |2), , and Now we discuss how to design w to maximize CS, and the proposed solution is denoted by . It is obvious that maximizing CS is equivalent to maximizing . Hence, in what follows, the objective function will be .
Substituting Equations 7 and 8 into , we have
where . This is a product of two correlated Rayleigh quotients [17] which is generally difficult to maximize. However, it would be much easier to get a suboptimal solution if we approximate the objective function to a single Rayleigh quotient.
Rewrite the optimization problem as
Denote the matrices D h + P- 1I, Γ g + P- 1I, and Γ h + P- 1I as A, B, and C, respectively. For simplicity, we also let a i , b i , and c i represent the i th diagonal entry of A, B, and C, respectively, and define p = (P1, …, P M )T.
Since P i = |w i |2, the denominator can be rewritten as . According to the Taylor series expansion ,
if we expand f(p) at . Since
where and , we have . Substituting this partial derivative into (11), we further have where . It can be proved that K is negligible either with small P or large P if we make a commonly used assumption that the SR distances are about the same (see Appendix for details). Thus, we omit this part and rewrite f(p) approximately as
So the optimization problem in (9) can be approximated to
This is a single Rayleigh quotient problem. It has been reported in [17] that if U is Hermitian and V is positive definite Hermitian, for any non-zero column vector x, we have where λmax(V-1U) is the largest eigenvalue of V-1U. The equality holds if x = c umax(V-1U) where c can be any non-zero constant and umax(V-1U) is the unit-norm eigenvector of V-1U corresponding to λmax(V-1U). As a result, the optimal solution to (14) is
where Φ = A- 1B- 1C(Psρ fg ρ fg H + Γ g + P- 1I).
To show the agreement of the approximated denominator and the exact denominator, we calculated them numerically, and the results are shown in Figure 2. The channel information we used are listed in Table 1 where f = (f1, …, f M )T, g = (g1, …, g M )T, and . f and g are generated randomly.
For comparison purpose, we present two other beamforming designs. First, for the optimization of a product of two correlated Rayleigh quotient problems, a method was proposed recently in [8] to maximize the upper and lower bounds. Note that where and . is bounded as
As a result, the bounds maximization design for AF (B-AF) should be
We also address the traditional design for AF (T-AF) where the eavesdropper is ignored and the goal is to maximize CD. It can be easily proved that the optimal solution is where cAF is a constant chosen to satisfy .
3.2 Discussion about secrecy capacity in AF networks
It is natural to conjecture that secrecy capacity would grow as the eavesdropper moved away or as the total relay transmit power increased. However, we find that this conjecture is not always right.
For simplicity, we assume the distances between relays are much smaller than those between the relays and the source, so the path losses of the SR channels are almost the same. The same assumption is also made to the destination/eavesdropper. Denote the SR, RD, and RE distances as dSR, dRD, and dRE, respectively, and the corresponding channel variances as , , and , respectively.
Proposition 1. If the destination is much nearer to the relays than the eavesdropper is in an AF network, C S does not always grow as the total relay transmit power increases, and a suboptimal value of the total relay transmit power is found as
Proof. Recall that . No matter how we design the beamforming vector w, is bounded as
Due to the difficulty of calculating the eigenvalues of Φ, we replace the non-diagonal elements in Φ with their mean value 0 and the i th diagonal element with where . Thus, Φ becomes λ(P)I after replacement.
Define . Now we investigate the monotonicity of CS(P). The first-order derivatives of CS(P) and λ(P) can be computed, respectively, as
and
By setting , we obtain the positive stationary point of CS(P) as described in (18).
If dRE > dRD (), ∀P∈(0, Psubopt), we have ; ∀P∈(Psubopt, + ∞), we have . Hence, if the destination is much nearer than the eavesdropper is, CS(P) is an increasing function over (0, Psubopt) and a decreasing function over (Psubopt, + ∞), which means that CS(Psubopt) is the maximum of CS(P).
This monotonicity of CS and the accuracy of Psubopt under the case of dRE > dRD will be verified in the next section. It needs to be pointed out that the above analysis is not for any certain design, so the optimal value of P for a certain design would be different from but around Psubopt. It also needs to be pointed out that the replacement of the channel coefficients in Φ with their mean values may result in the loss of the security benefit that is supposed to be achieved by exploiting the perfect CSI of SR and RD channels. This loss does not affect the monotonicity of CS greatly under the case of dRE > dRD because the destination is much nearer and therefore much more advantageous in communication than the eavesdropper is. However, when dRE < dRD (or dRE = dRD), such replacement becomes inappropriate, since the instantaneous CSI of f i and g i improves the system security significantly.
We can further compute the second-order derivatives of CS(P) and λ(P), respectively, as
and
It can be observed from (22) that the positivity of depends on the value of P. Thus, CS(P) is neither convex nor concave.
Remark 1. In an AF network, if the total relay transmit power is large, the AWGNs in the second hop are negligible compared to the forwarded versions of the AWGNs in the first hop. Thus, can be approximately written as
This equation does not involve , which implies CS is a constant in this case wherever the eavesdropper is.
4. Distributed beamforming design for DF
This section focuses on the security-oriented beamforming design for DF protocol. Similar to the design for AF protocol, the mission is to find the optimal design under a total relay transmit power constraint to maximize secrecy capacity.
4.1 Proposed design for DF (P-DF)
From Equations 4 and 5, the received SNRs at the destination and the eavesdropper are obtained, respectively, as follows:
Let be the optimal solution of the proposed design, then
For comparison purpose, we also address the traditional design for DF (T-DF) and denote the solution by . The optimization problem is formulated as , and the optimal solution is obviously where cDF is a constant chosen to satisfy the power constraint .
4.2 Discussion about secrecy capacity in DF networks
It is a natural thought that no matter under what channel assumption, secrecy capacity achieved by security-oriented designs would be higher than that achieved by traditional designs. However, the fact is that these designs may have the same performance which means that sometimes we can just ignore the eavesdropper.
Remark 2. In a DF network, if the RE distances are about the same (which is widely assumed), it is unnecessary to consider the eavesdropper as the security-oriented design and the traditional design are indeed the same.
Noticing that in this scenario, we can write D h as . Thus, one can rewrite (27) as . Since
we have umax(I + P ggH) = umax(P ggH). Thus, which is the same as .
5. Numerical results
In this section, we investigate the performance of the above beamforming designs numerically. The simulation environment follows the model of Section 2. We perform Monte Carlo experiments consisting of 10,000 independent trials to obtain the average results.
Assume the number of relays is M = 6, and the source transmit power is Ps = 10 dB. In order to show the influence of the RE distance in AF protocol, we fix the source at (0,0), the destination at (2,0), and the relays at (1,0) and move the eavesdropper from (1.25,0) to (5,0). We assume that the distances between relays are much smaller than SR/RD/RE distances. Therefore, the SR channels and RD channels follow a distribution, and the RE distance dRE varies from 0.25 to 4.
Figure 3 shows the relationship between average secrecy capacity and total relay transmit power with the eavesdropper in different locations using P-AF design. We can see that if the eavesdropper is nearer to the relays than the destination is, the relays should use the maximal power to transmit. However, if the destination is much nearer, there is an optimal value of total relay transmit power which is about 12 dB under the case of dRE = 2, while the theoretical value in (18) is which is not very accurate but close. The reason is that Psubopt satisfies while the optimal power for P-AF design should satisfy . However, it is difficult to express λmax(Φ) in terms of the total relay transmit power and the channel coefficients, not to mention to solve the latter equation analytically. It can also be seen that as the total relay transmit power increases, the secrecy capacity tends to keep constant no matter where the eavesdropper is.
Figure 4 compares different AF beamforming designs. It can be seen that the B-AF design shows a slight advantage over the T-AF design only when the total relay transmit power is small in the dRE = 1/2 case, while our proposed design always performs the best.
The relationship between average secrecy capacity and total relay transmit power with the eavesdropper in different locations using P-DF design is demonstrated in Figure 5. We still assume the RE distances to be the same. Results show that the secrecy capacity of a DF network grows as the total relay transmit power increases or as the eavesdropper moves away.
To verify Remark 2, we now examine the P-DF design and T-DF design under different variance assumptions of the RE channels.
Case 1:
Case 2:
Case 3:
The average secrecy capacities of P-DF and T-DF designs under different RE channel assumptions are demonstrated in Figure 6. Our design outperforms the traditional design in case 1 and case 2. While in case 3, the two designs have the same performance. This indicates that the greater the RE channels differ from each other, the more superior the P-DF design is. If the RE distances are almost the same, the eavesdropper can be ignored.
6. Conclusions
In this paper, we focused on security-oriented distributed beamforming designs for relay networks in the presence of a passive eavesdropper. We provided two beamforming designs under a total relay transmit power constraint, one of which is for AF and the other is for DF. Each design is to maximize secrecy capacity by exploiting information of SR, RD, and RE channels. To derive the beamforming solution for AF requires approximating the optimization objective by using the Taylor series expansion, while the solution for DF is obtained much more easily. We also found that secrecy capacity does not always grow if the relays use more power to transmit or if the eavesdropper gets farther from the relays, and that taking the eavesdropper into consideration is not always necessary. Moreover, for AF, we derived a suboptimal value of the total relay transmit power if the destination is nearer than the eavesdropper is. Numerical results showed the efficiency of the proposed designs.
Appendix
Noticing that
we have with small P, and
with large P. If we make the assumption that the SR distances are all about the same, i.e., the 's are about the same (which is also assumed in [8]), and replace |f i |2 in the expression of with its mean value , we have
Thus, K ≈ 0 with large P.
References
Sendonaris A, Erkip E, Aazhang B: User cooperative diversity-part I: system description. IEEE Trans. Commun. 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperative diversity-part II: implementation aspects and performance analysis. IEEE Trans. Commun. 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC: Cooperative diversity in wireless networks: efficient protocols and outage behaviour. IEEE Trans. Inf. Theory 2004, 51(12):3062-3080.
Wyner AD: The wire-tap channel. Bell Syst. Tech. J. 1975, 54(8):1355-1387. 10.1002/j.1538-7305.1975.tb02040.x
Leung-Yan-Cheong SK, Hellman ME: The Gaussian wiretap channels. IEEE Trans. Inf. Theory 1978, 24(4):451-456. 10.1109/TIT.1978.1055917
Gopala PK, Lai L, Gamal HE: On the secrecy capacity of fading channels. IEEE Trans. Inf. Theory 2008, 54(10):4687-4698.
Dong L, Zhu H, Petropulu AP, Poor HV: Secure wireless communication via cooperation. In The 46-th Annual Allerton Conference on Communication, Control and Computing. Urbana-Champaign, IL, USA; 23–26 September 2008:1132-1138.
Dong L, Han Z, Petropulu AP, Poor HV: Improving wireless physical layer security via cooperating relays. IEEE Trans. Signal Process. 2010, 58(3):1875-1888.
Krikidis I, Thompson S, McLaughlin S: Relay selection for secure cooperative networks with jamming. IEEE Trans. Wirel. Commun. 2009, 8(10):5003-5011.
Kim J, Ikhlef A, Schober R: Combined relay selection and cooperative beamforming for physical layer Security. IEEE J. Commun. Netw. 2012, 14(4):364-373.
Jeong C, Kim I-M, Kim DI: Joint secure beamforming design at the source and the relay for an amplify-and-forward MIMO untrusted relay system. IEEE Trans. Signal Process. 2012, 60(1):310-325.
He X, Yener A: End-to-end secure multi-hop communication with untrusted relays. IEEE Trans. Wirel. Commun. 2013, 12(1):1-11.
Zou Y, Wang X, Shen W: Optimal relay selection for physical-layer security in cooperative wireless networks. IEEE J. Select. Areas Commun. 2013, 31(10):2099-2111.
Yang Y, Li Q, Ge J, Ching PC: Cooperative secure beamforming for AF relay networks with multiple eavesdroppers. IEEE Signal Process. Lett. 2013, 20(1):35-38.
Wang H-M, Luo M, Yin Q, Xia X-G: Hybrid cooperative beamforming and jamming for physical-layer security of two-way relay networks. IEEE Trans. Inf. Forensics Secur. 2013, 8(12):2007-2020.
Chen Z, Li H, Cui G, Rangaswamy M: Adaptive transmit and receive beamforming for interference mitigation. IEEE Signal Process. Lett. 2014, 21(2):235-239.
Zhang X: Matrix Analysis and Applications. Tsinghua University Press, Beijing; 2004:528-541.
Acknowledgements
This work is supported by the Natural Science Foundation of China under Grants 61372126 and 61302101, and the open research fund of National Mobile Communications Research Laboratory in Southeast University under Grant 2012D11.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
An erratum to this article can be found online at 10.1186/1687-6180-2014-129.
An erratum to this article is available at http://dx.doi.org/10.1186/1687-6180-2014-129.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qian, M., Liu, C. & Fu, Y. Distributed beamforming designs to improve physical layer security in wireless relay networks. EURASIP J. Adv. Signal Process. 2014, 56 (2014). https://doi.org/10.1186/1687-6180-2014-56
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2014-56