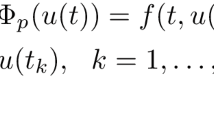Abstract
The authors consider the following impulsive differential equations involving the one-dimensional singular p-Laplacian: , , , , , , , , , where and are two parameters. Several new and more general existence and multiplicity results are derived in terms of different values of and . In this case, our results cover equations without impulsive effects and are compared with some recent results.
Similar content being viewed by others
1 Introduction
The theory and applications of the fourth-order ordinary differential equation are emerging as an important area of investigation; it is often referred to as the beam equation. In [1], Sun and Wang pointed out that it is necessary and important to consider various fourth-order boundary value problems (BVPs for short) according to different forms of supporting. Owing to its importance in engineering, physics, and material mechanics, fourth-order BVPs have attracted much attention from many authors; see, for example [2–29] and the references therein.
Very recently, Zhang and Liu [30] studied the following fourth-order four-point boundary value problem without impulsive effect:
where , . By using the upper and lower solution method, fixed point theorems, and the properties of the Green’s function and , the authors give sufficient conditions for the existence of one positive solution.
In this paper, we investigate the existence of positive solutions of fourth-order impulsive differential equations with two parameters
where and are two parameters, , , is a p-Laplace operator, i.e., , , , , ω is a nonnegative measurable function on , on any open subinterval in which may be singular at and/or , () (where m is fixed positive integer) are fixed points with , , where and represent the right-hand limit and left-hand limit of at , respectively. In addition, ω, f, , g, and h satisfy
(H1) ;
(H2) with for all t and ;
(H3) with () for all t and ;
(H4) are nonnegative and , , where
Some special cases of (1.1) have been investigated. For example, Bai and Wang [14] studied the existence of multiple solutions of problem (1.1) with , , and for . By using a fixed point theorem and degree theory, the authors proved the existence of one or two positive solutions of problem (1.1).
Feng [31] considered problem (1.1) with , , for and . By using a suitably constructed cone and fixed point theory for cones, the author proved the existence results of multiple positive solutions of problem (1.1).
Motivated by the papers mentioned above, we will extend the results of [14, 30, 31] to problem (1.1). We remark that on impulsive differential equations with a parameter only a few results have been obtained, not to mention impulsive differential equations with two parameters; see, for instance, [32–34]. However, these results only dealt with the case that and .
The rest of the paper is organized as follows: in Section 2, we state the main results of problem (1.1). In Section 3, we provide some preliminary results, and the proofs of the main results together with several technical lemmas are given in Section 4.
2 Main results
In this section, we state the main results, including existence and multiplicity of positive solutions for problem (1.1).
We begin by introducing the notation
We also choose four numbers r, , , and R satisfying
where δ is defined in (3.20).
Theorem 2.1 Assume that (H1)-(H4) hold.
-
(i)
If and , then there exist and such that, for any and , problem (1.1) has a positive solution , with
(2.2) -
(ii)
If and , then there exist and such that, for any and , problem (1.1) has a positive solution with
(2.3) -
(iii)
If , then there exist and such that, for any and , problem (1.1) has at least two positive solutions and with
(2.4)
Theorem 2.2 Assume that (H1)-(H4) hold.
-
(i)
If and , then there exist and such that, for any and , problem (1.1) has a positive solution , with property (2.2).
-
(ii)
If and , then there exist and such that, for any and , problem (1.1) has a positive solution , with property (2.3).
-
(iii)
If , then there exist and such that, for any and , problem (1.1) has at least two positive solutions and with
(2.5)
3 Preliminaries
Let , and
Then is a real Banach space with norm
where , .
A function with is called a solution of problem (1.1) if it satisfies (1.1).
We shall reduce problem (1.1) to an integral equation. To this goal, firstly by means of the transformation
we convert problem (1.1) into
and
Lemma 3.1 If (H1), (H2), and (H4) hold, then problem (3.3) has a unique solution x given by
where
Proof The proof of Lemma 3.1 is similar to that of Lemma 2.1 in [31]. □
Write . Then from (3.6) and (3.7), we can prove that and have the following properties.
Proposition 3.1 If (H4) holds, then we have
where
Remark 3.1 From (3.6) and (3.11), we obtain
Lemma 3.2 If (H1), (H3), and (H4) hold, then problem (3.4) has a unique solution y and y can be expressed in the form
where
Proof The proof of Lemma 3.2 is similar to that of Lemma 2.2 in [31]. □
From (3.14) and (3.15), we can prove that and have the following properties.
Proposition 3.2 If (H4) holds, then we have
where
Suppose that y is a solution of problem (1.1). Then from Lemma 3.1 and Lemma 3.2, we have
Define a cone in by
where
It is easy to see K is a closed convex cone of .
Define an operator by
From (3.21), we know that is a solution of problem (1.1) if and only if y is a fixed point of operator .
Lemma 3.3 Suppose that (H1)-(H4) hold. Then and is completely continuous.
Proof The proof of Lemma 3.3 is similar to that of Lemma 2.4 in [31]. □
To obtain positive solutions of problem (1.1), the following fixed point theorem in cones is fundamental, which can be found in [[35], p.94].
Lemma 3.4 Let P be a cone in a real Banach space E. Assume , are bounded open sets in E with , . If
is completely continuous such that either
-
(a)
, and , , or
-
(b)
, and , ,
then A has at least one fixed point in .
Remark 3.2 To make the reader clear what , , , and mean, we give typical examples of and , e.g.,
with , where .
4 Proofs of the main results
For convenience we introduce the following notation:
and
where is a constant.
Proof of Theorem 2.1 Part (i). Noticing that , () for all t and , we can define
where , and
Let
Then, for and , , we have
which implies that
If , , then there exist , , and such that
where satisfies
satisfies
Let . Thus, when we have
and then we get
where
and
It follows from (4.4) and (4.5) that
Applying (b) of Lemma 3.4 to (4.1) and (4.6) shows that has a fixed point with . Hence, since for we have , , it follows that (2.2) holds. This gives the proof of part (i).
Part (ii). Noticing that , () for all t and , we can define
where , and
Let
Then, for and , , we have
which implies that
If , , then there exist , , and such that
where and satisfy (4.2) and (4.3), respectively.
Similar to the proof of (4.6), we can prove that
Applying (a) of Lemma 3.4 to (4.7) and (4.8) shows that has a fixed point with . Hence, since for we have for , it follows that (2.3) holds. This gives the proof of part (ii).
Consider part (iii). Choose two numbers and satisfying (2.1). By part (i) and part (ii), there exist and such that
Since , from the proof of part (i) and part (ii), it follows that
and
Applying Lemma 3.4 to (4.9)-(4.11) shows that has two fixed points and such that and . These are the desired distinct positive solutions of problem (1.1) for and satisfying (2.4). Then the result of part (iii) follows. □
Proof of Theorem 2.2 Part (i). Noticing that , () for all t and , we can define
where , and
Let
Then, for and , , we have
Similar to the proof of (4.5), we can prove
It follows from (4.12) and (4.13) that
If , , then there exist , , and such that
where satisfies
satisfies
Let . Thus, when we have
and then we get
This yields
Applying (b) of Lemma 3.4 to (4.14) and (4.17) shows that has a fixed point with . Hence, since for we have , , it follows that (2.2) holds. This gives the proof of part (i).
Part (ii). Noticing that , () for all t and , we can define
where , and
Let
Then, for and , , we have
Similar to the proof of (4.5), we can prove
It follows from (4.18) and (4.19) that
If , , then there exist , , and such that
where and satisfy (4.15) and (4.16), respectively.
Therefore, for , we obtain
This yields
Applying (a) of Lemma 3.4 to (4.20) and (4.21) shows that has a fixed point with . Hence, since for we have , , it follows that (2.3) holds. This gives the proof of part (ii).
Consider part (iii). Choose two numbers and satisfying (2.1). By part (i) and part (ii), there exist and such that
Since , from the proof of part (i) and part (ii), it follows that
and
Applying Lemma 3.4 to (4.22)-(4.24) shows that has two fixed points and such that and . These are the desired distinct positive solutions of problem (1.1) for and satisfying (2.5). Then the proof of part (iii) is complete. □
Remark 4.1 Comparing with Feng [31], the main features of this paper are as follows.
-
(i)
Two parameters and are considered.
-
(ii)
, not only for .
-
(iii)
It follows from the proof of Theorem 2.1 that the conditions of Corollary 3.2 in [31] are not the optimal conditions, which guarantee the existence of at least one positive solution for problem (1.1). In fact, if , or , , we can prove that problem (1.1) has at least one positive solution, respectively.
References
Sun J, Wang X: Monotone positive solutions for an elastic beam equation with nonlinear boundary conditions. Math. Probl. Eng. 2011. 10.1155/2011/609189
Yao Q: Positive solutions of nonlinear beam equations with time and space singularities. J. Math. Anal. Appl. 2011, 374: 681-692. 10.1016/j.jmaa.2010.08.056
Yao Q: Local existence of multiple positive solutions to a singular cantilever beam equation. J. Math. Anal. Appl. 2010, 363: 138-154. 10.1016/j.jmaa.2009.07.043
O’Regan D: Solvability of some fourth (and higher) order singular boundary value problems. J. Math. Anal. Appl. 1991, 161: 78-116. 10.1016/0022-247X(91)90363-5
Wei Z: A class of fourth order singular boundary value problems. Appl. Math. Comput. 2004, 153: 865-884. 10.1016/S0096-3003(03)00683-0
Yang B: Positive solutions for the beam equation under certain boundary conditions. Electron. J. Differ. Equ. 2005., 2005: Article ID 78
Zhang X: Existence and iteration of monotone positive solutions for an elastic beam equation with a corner. Nonlinear Anal., Real World Appl. 2009, 10: 2097-2103. 10.1016/j.nonrwa.2008.03.017
Gupta GP: Existence and uniqueness theorems for the bending of an elastic beam equation. Appl. Anal. 1988, 26: 289-304. 10.1080/00036818808839715
Gupta GP: A nonlinear boundary value problem associated with the static equilibrium of an elastic beam supported by sliding clamps. Int. J. Math. Math. Sci. 1989, 12: 697-711. 10.1155/S0161171289000864
Graef JR, Yang B: On a nonlinear boundary value problem for fourth order equations. Appl. Anal. 1999, 72: 439-448. 10.1080/00036819908840751
Agarwal RP: On fourth-order boundary value problems arising in beam analysis. Differ. Integral Equ. 1989, 2: 91-110.
Davis J, Henderson J: Uniqueness implies existence for fourth-order Lidstone boundary value problems. Panam. Math. J. 1998, 8: 23-35.
Kosmatov N: Countably many solutions of a fourth order boundary value problem. Electron. J. Qual. Theory Differ. Equ. 2004., 2004: Article ID 12
Bai Z, Wang H: On the positive solutions of some nonlinear fourth-order beam equations. J. Math. Anal. Appl. 2002, 270: 357-368. 10.1016/S0022-247X(02)00071-9
Bai Z, Huang B, Ge W: The iterative solutions for some fourth-order p -Laplace equation boundary value problems. Appl. Math. Lett. 2006, 19: 8-14. 10.1016/j.aml.2004.10.010
Liu X-L, Li W-T: Existence and multiplicity of solutions for fourth-order boundary values problems with parameters. J. Math. Anal. Appl. 2007, 327: 362-375. 10.1016/j.jmaa.2006.04.021
Bonanno G, Bella B: A boundary value problem for fourth-order elastic beam equations. J. Math. Anal. Appl. 2008, 343: 1166-1176. 10.1016/j.jmaa.2008.01.049
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Appl. Anal. 1995, 59: 225-231. 10.1080/00036819508840401
Han G, Xu Z: Multiple solutions of some nonlinear fourth-order beam equations. Nonlinear Anal. 2008, 68: 3646-3656. 10.1016/j.na.2007.04.007
Zhang X, Ge W: Symmetric positive solutions of boundary value problems with integral boundary conditions. Appl. Math. Comput. 2012, 219: 3553-3564. 10.1016/j.amc.2012.09.037
Zhai C, Song R, Han Q: The existence and the uniqueness of symmetric positive solutions for a fourth-order boundary value problem. Comput. Math. Appl. 2011, 62: 2639-2647. 10.1016/j.camwa.2011.08.003
Zhang X, Feng M, Ge W: Symmetric positive solutions for p -Laplacian fourth order differential equation with integral boundary conditions. J. Comput. Appl. Math. 2008, 222: 561-573. 10.1016/j.cam.2007.12.002
Zhang X, Feng M, Ge W: Existence results for nonlinear boundary-value problems with integral boundary conditions in Banach spaces. Nonlinear Anal. 2008, 69: 3310-3321. 10.1016/j.na.2007.09.020
Zhang X, Liu L: A necessary and sufficient condition of positive solutions for fourth order multi-point boundary value problem with p -Laplacian. Nonlinear Anal. 2008, 68: 3127-3137. 10.1016/j.na.2007.03.006
Aftabizadeh AR: Existence and uniqueness theorems for fourth-order boundary value problems. J. Math. Anal. Appl. 1986, 116: 415-426. 10.1016/S0022-247X(86)80006-3
Kang P, Wei Z, Xu J: Positive solutions to fourth-order singular boundary value problems with integral boundary conditions in abstract spaces. Appl. Math. Comput. 2008, 206: 245-256. 10.1016/j.amc.2008.09.010
Xu J, Yang Z: Positive solutions for a fourth order p -Laplacian boundary value problem. Nonlinear Anal. 2011, 74: 2612-2623. 10.1016/j.na.2010.12.016
Webb JRL, Infante G, Franco D: Positive solutions of nonlinear fourth-order boundary value problems with local and non-local boundary conditions. Proc. R. Soc. Edinb. 2008, 138: 427-446.
Ma H: Symmetric positive solutions for nonlocal boundary value problems of fourth order. Nonlinear Anal. 2008, 68: 645-651. 10.1016/j.na.2006.11.026
Zhang X, Liu L: Positive solutions of fourth-order four-point boundary value problems with p -Laplacian operator. J. Math. Anal. Appl. 2007, 336: 1414-1423. 10.1016/j.jmaa.2007.03.015
Feng M: Multiple positive solutions of four-order impulsive differential equations with integral boundary conditions and one-dimensional p -Laplacian. Bound. Value Probl. 2011. 10.1155/2011/654871
Hao X, Liu L, Wu Y: Positive solutions for second order impulsive differential equations with integral boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2011, 16: 101-111. 10.1016/j.cnsns.2010.04.007
Sun J, Chen H, Yang L: The existence and multiplicity of solutions for an impulsive differential equation with two parameters via a variational method. Nonlinear Anal. TMA 2010, 73: 440-449. 10.1016/j.na.2010.03.035
Ning P, Huan Q, Ding W: Existence result for impulsive differential equations with integral boundary conditions. Abstr. Appl. Anal. 2013. 10.1155/2013/134691
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones. Academic Press, New York; 1988.
Acknowledgements
This work is sponsored by the project NSFC (11301178, 11171032) and the Fundamental Research Funds for the Central Universities (2014MS58). The authors are grateful to anonymous referees for their constructive comments and suggestions, which has greatly improved this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
XZ completed the main study and carried out the results of this article. MF checked the proofs and verified the calculation. All the authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, X., Feng, M. Positive solutions for classes of multi-parameter fourth-order impulsive differential equations with one-dimensional singular p-Laplacian. Bound Value Probl 2014, 112 (2014). https://doi.org/10.1186/1687-2770-2014-112
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2014-112